Both the mechanical and hydraulic properties of soil are crucial for the geotechnical design in practical engineering. It is noted that the hydraulic properties of soil are mainly governed by the pore size distribution which can be expressed by using a mathematical equation called the pore size distribution function (PSDF). Tuli et al.[1] indicated that both water and air flow in soil are governed by the geometrical pore space in soil. Much research[210] indicated that both the air and water coefficient of permeability for a saturated/unsaturated soil can be estimated from the PSDF. Vanapalli et al.[1113] indicated that the shear strength of the unsaturated soil can also be estimated from the PSDF. Zhai et al.[14] also proposed a method to estimate the tensile strength of the unsaturated sandy soils from the PSDF. Therefore, the concept of PSDF is crucial for engineers to understand the mechanical and hydraulic properties of the soil.
The soil-water characteristic curve (SWCC) is commonly considered to be analogous to the PSDF[2,7,9,15]. It is noted that the PSDF can behave with one peak point (normally named as the unimodal shape of SWCC) or two peak points (normally named as the bimodal shape of SWCC). The measured SWCC in the gravimetric water content, w-SWCC, for a deformable soil can be in a bimodal shape but the converted SWCC in the degree of saturation, S-SWCC, for the same soil can be in a unimodal shape. The discrepancy in the shapes of w-SWCC and S-SWCC has rarely been discussed.
In this paper, the framework from Zhai et al.[16] was used for the simulation of the variation of the PSDF when the soil undergoes a de-saturation process. It shows that the soil has an initial bimodal shape PSDF and gradually changes into a unimodal shape PSDF with the increase in the soil suction during the de-saturation process. The experimental data from the published literature shows good agreements with the simulated results from the method proposed in this study.
1 Pore Size Distribution Function
Childs et al.[1718] proposed the concept of the PSDF and the PSDF was firstly used by Childs and Collis-George[2] for the calculation of the water flow in soil. Diamond[19] introduced two methodologies for the determination of the PSDF. One is the mercury intrusion porosimetry method which is commonly named as the MIP test and the other is the capillary condensation method which is commonly named as the SWCC test. Recently, Spaans et al.[2023] showed that the PSDF can also be determined indirectly using the soil freezing characteristic curve (SFCC). However, the SFCC is out the scope of this paper and not discussed.
In the SWCC measurements, the experimental data is collected as the discrete points and these data points are finally represented by a continuous mathematical equation. This continuous mathematical equation is commonly named as the SWCC equation, which is widely used by engineers to estimate the degree of saturations corresponding to different soil suctions. Many researchers proposed different forms of SWCC equations[15,2426]. Based on Refs.[79], the S-SWCC can be considered as the integration of the PSDF. As a result, the SWCC equation can also be used to represent the PSDF. In this study, Fredlund and Xing’s equation[15], which is one of the most popular SWCC equations, is adopted.
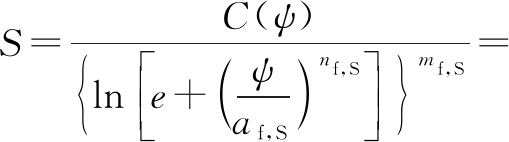

(1)
where af,S, nf,S, mf,S are the fitting parameters for the S-SWCC equation; Cr is an input value for a rough estimation of the residual suction; S is the degree of saturation; and ψ is the soil suction. Fredlund and Xing[15] illustrated that Eq.(1) was the integration of the PSDF. As a result, the PSDF can be obtained by differentiating Eq.(1). In addition, due to a wide range of suction or pores size, both the SWCC and PSDF are commonly plotted in a semi-log scale (i.e., suction or pore size are in log scale). As a result, the mathematical equation for the representation of the PSDF can be obtained as follows:
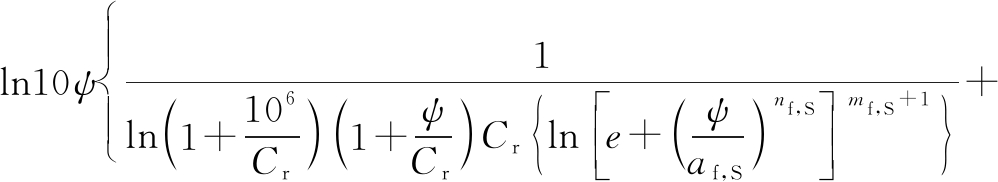
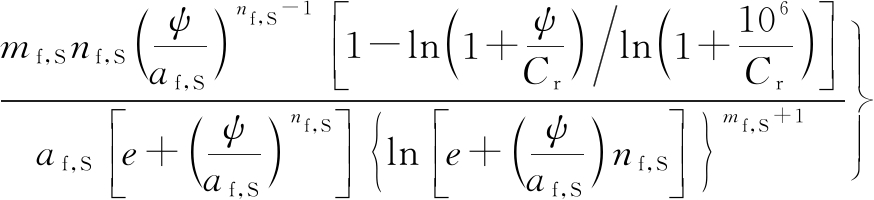
(2)
where psd(ψ) is the pore size density. As illustrated in Eq.(2), the PSDF can be represented by fitting parameters af,S, nf,S, mf,S in Fredlund and Xing’s equation[15]. The values of these fitting parameters are crucial for the shapes of the PSDF.
2 Framework for the Simulation of PSDF
It is noted that the soil with an initial loose condition can be compressed during the de-saturation process. The soil volume change during the de-saturation process can be described by the shrinkage curve (SC) and Fredlund et al.[27] proposed a mathematical equation for the representation of the SC.
(3)
where ash is the minimum void ratio; bsh is the slope of the line of tangency; and csh is the curvature of the shrinkage curve.
In this paper, Fredlund et al.’s equation[27] was used to calculate the void ratios of soil corresponding to different water contents. On the other hand, Zhai et al.[16] proposed a framework for the estimation of w-SWCCs of soil with different densities. Both the measured data of w-SWCC for the soil under a loose condition and the shrinkage curve are used as the input parameters for the development of the framework. The proposed framework of PSDFs is developed by the steps as follows:
1) Use Fredlund and Xing’s equation[15] to fit with the measured w-SWCC data and the obtained SWCC is called SWCC0, which represents the PSDF of soil under an initial loose condition.
2) Use Fredlund et al.’s equation[27] to fit with measured shrinkage curve and determine the fitting parameters in Fredlund et al.’s equation[27].
3) Divide SWCC0 into certain segments by points 1 to N, as illustrated in Fig.1, and calculate the void ratios of each point, using Fredlund et al.’s equation[27], as illustrated in Fig.2.
4) Develop the framework of S-SWCCs, as shown in Fig.3, considering different void ratios as illustrated in Tab.1. As shown in Tab.1, Gs is the specific gravity of soil, which is a constant, and Gsw/e defines the degree of saturation S.
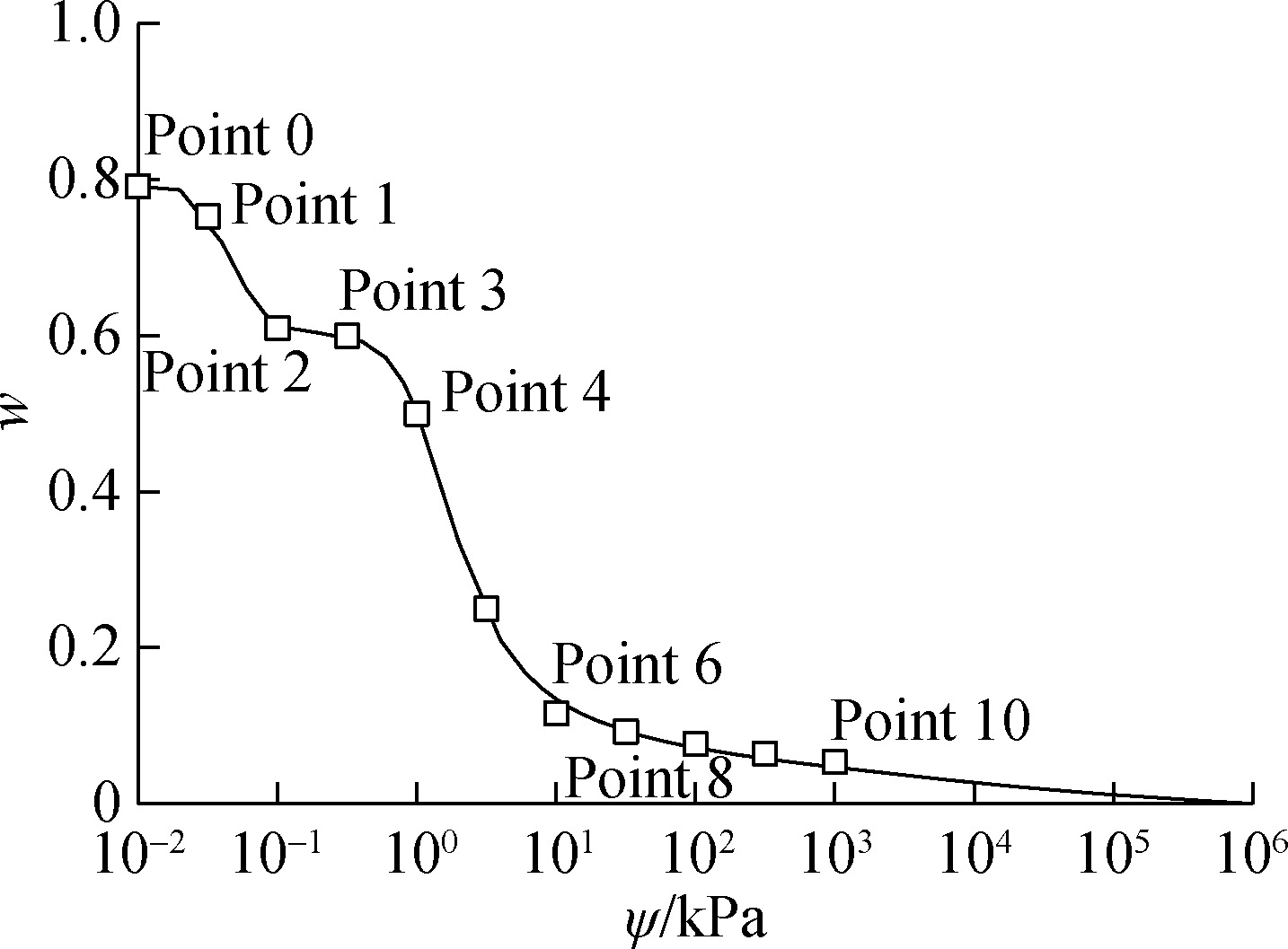
Fig.1 A typical bimodal shape w-SWCC
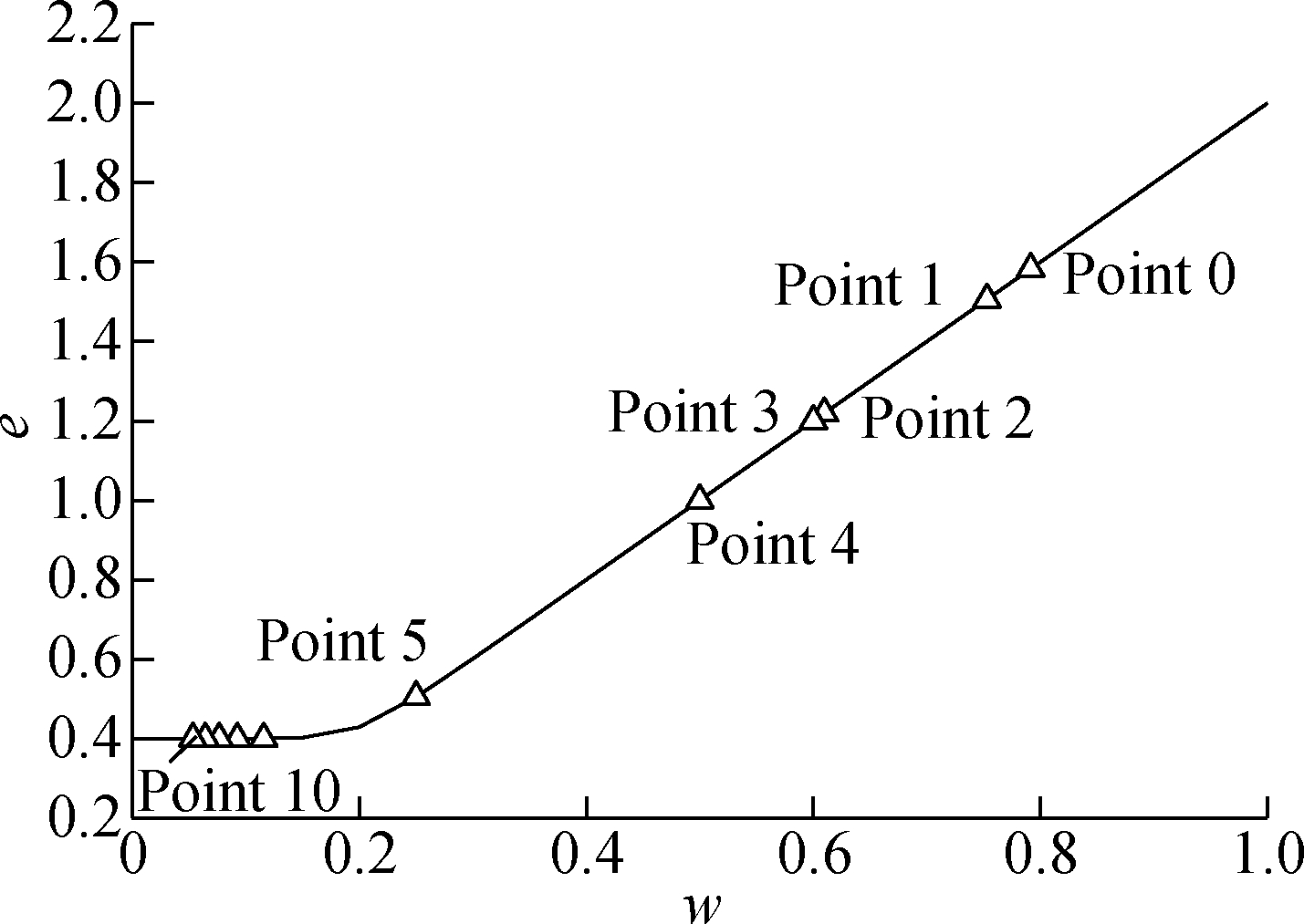
Fig.2 A typical shrinkage curve
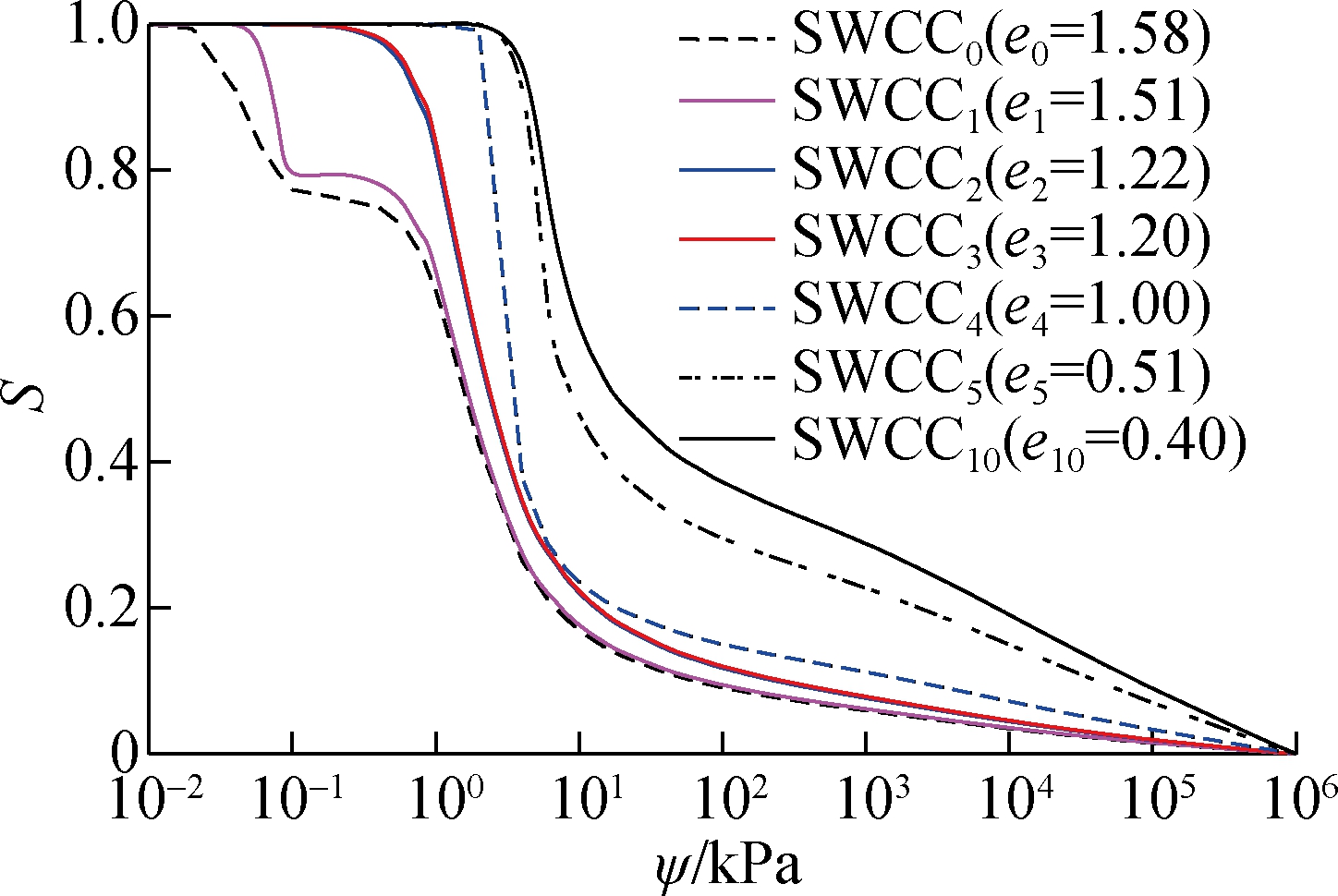
Fig.3 Family of the converted S-SWCCs
5) Convert the S-SWCCs in the framework into PSDFs, as illustrated in Fig.4, using Kelvin’s capillary law.
As shown in Fig.2, the void ratios from Point 6 to Point 10 are constant, which indicates that there is no more volume change after Point 5. As a result, the final point (Point 10) is adopted to calculate the S-SWCC for the soil under the densest condition. The calculated degrees of saturation considering different void ratios are illustrated in Tab.1.
Tab.1 Converted degrees of saturation for the development of the proposed framework
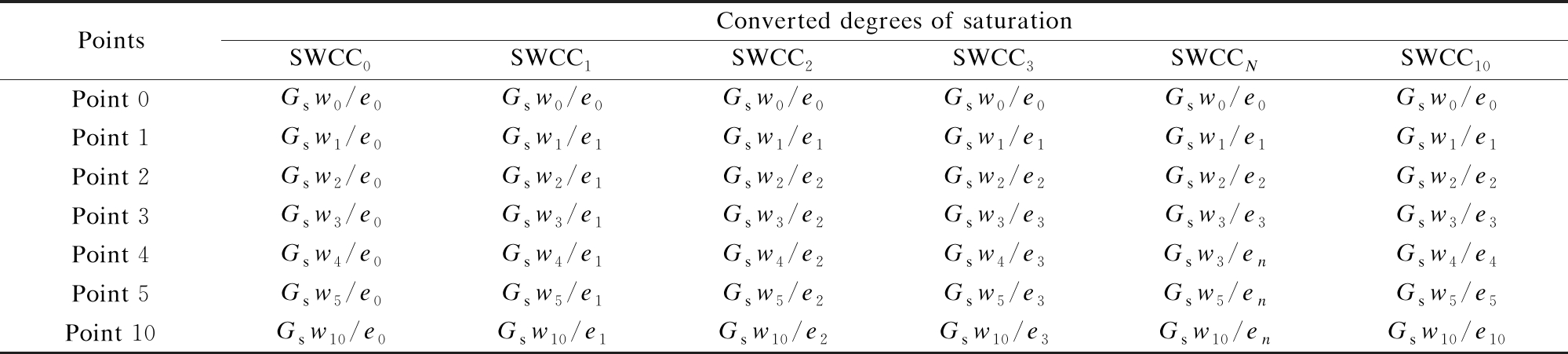
PointsConverted degrees of saturationSWCC0SWCC1SWCC2SWCC3SWCCNSWCC10Point 0Gsw0/e0Gsw0/e0Gsw0/e0Gsw0/e0Gsw0/e0Gsw0/e0Point 1Gsw1/e0Gsw1/e1Gsw1/e1Gsw1/e1Gsw1/e1Gsw1/e1Point 2Gsw2/e0Gsw2/e1Gsw2/e2Gsw2/e2Gsw2/e2Gsw2/e2Point 3Gsw3/e0Gsw3/e1Gsw3/e2Gsw3/e3Gsw3/e3Gsw3/e3Point 4Gsw4/e0Gsw4/e1Gsw4/e2Gsw4/e3Gsw3/enGsw4/e4Point 5Gsw5/e0Gsw5/e1Gsw5/e2Gsw5/e3Gsw5/enGsw5/e5Point 10Gsw10/e0Gsw10/e1Gsw10/e2Gsw10/e3Gsw10/enGsw10/e10

Fig.4 Changes in PSDF due to shrinkage of soil during the w-SWCC measurement
Fredlund and Xing’s equation[15] was adopted to fit with the calculated degree of saturations, as shown in Tab.1, and obtain SWCC0 to SWCCN. The experimental data shows bimodal shapes, and the methodology suggested by Zhai et al.[28]was used in the fitting procedure. Consequently, the fitted curves from SWCC0 to SWCC10 are obtained and illustrated in Fig.3. Subsequently, the best fitted SWCCs in Fig.3 are differentiated to obtain psd(ψ), as shown in Fig.4.
As the characteristics of pore-size distribution of soil can be clearly explored by the MIP test, the MIP test results from the published literature are adopted for the verification of the proposed model. Most of the results from the MIP test are presented as the accumulated volume (or segments of volume) with respect to the diameter of pores. Therefore,to be consistent with the MIP testing results, Fig.4 is further converted by using Kelvin’s capillary law and illustrated in Fig.5. During the conversion, a constant angle α is assumed to be zero and the segments of volume with respect to different radii of the pores are obtained by multiplying the pore-size density by the porosity.
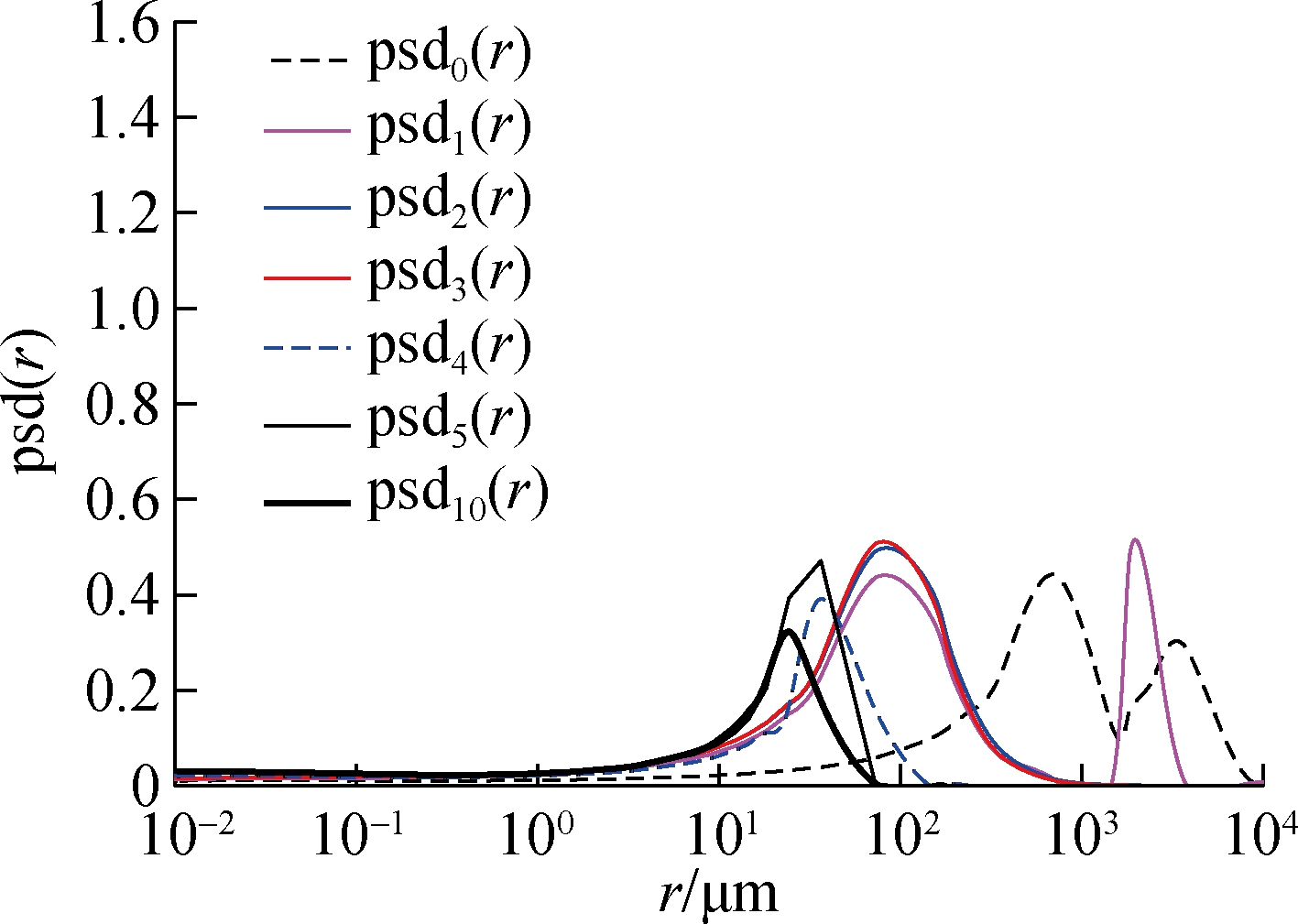
Fig.5 Illustration of the converted pore size density
As illustrated in Fig.5, the pore size density changes from psd0(r) to psd10(r) with the decrease in the void ratio. Both psd0(r) and psd1(r) exhibit the bimodal shapes while the other psd(r) shows the unimodal shapes. In other words, the PSDF of soil can be changed from a bimodal shape to a unimodal shape with the decrease in the void ratios. In addition, it seems that the pores with radii less than 10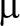 m are not compressed any more with the decrease in the void ratios and the pore radius corresponding to the maximum density (or peak point) decreases with the decrease in void ratios. As a result, Fig.5 indicates that the pores in the soil are compressed gradually from large pores to small pores during the de-saturation process and there is a certain range of small pores that cannot be compressed with the increase in soil suction.
m are not compressed any more with the decrease in the void ratios and the pore radius corresponding to the maximum density (or peak point) decreases with the decrease in void ratios. As a result, Fig.5 indicates that the pores in the soil are compressed gradually from large pores to small pores during the de-saturation process and there is a certain range of small pores that cannot be compressed with the increase in soil suction.
3 Comparison between Estimated PSDF from the Framework and Measured Data from MIP test
To verify the conclusions from the proposed framework (see Fig.5), both the experimental data of SWCC measurement and the SC are required as the input parameters. Meanwhile, the MIP testing results are also required for the verification of the estimated PSDF. In this case, the experimental data for the Chataignier clay from Li et al.[29] were selected and adopted in this paper. Both the measured SWCC and the shrinkage curve for the Chataignier clay are shown in Fig.6 and Fig,7, respectively. The MIP testing results for the Chataignier clay with different void ratios are illustrated in Fig.8. As the measured SWCC exhibits a bimodal shape, the procedure recommended by Zhai et al.[28] was used to fit Fredlund and Xing’s equation[15] with the experimental data. The fitting parameters for the bimodal SWCC are illustrated in Fig.6.
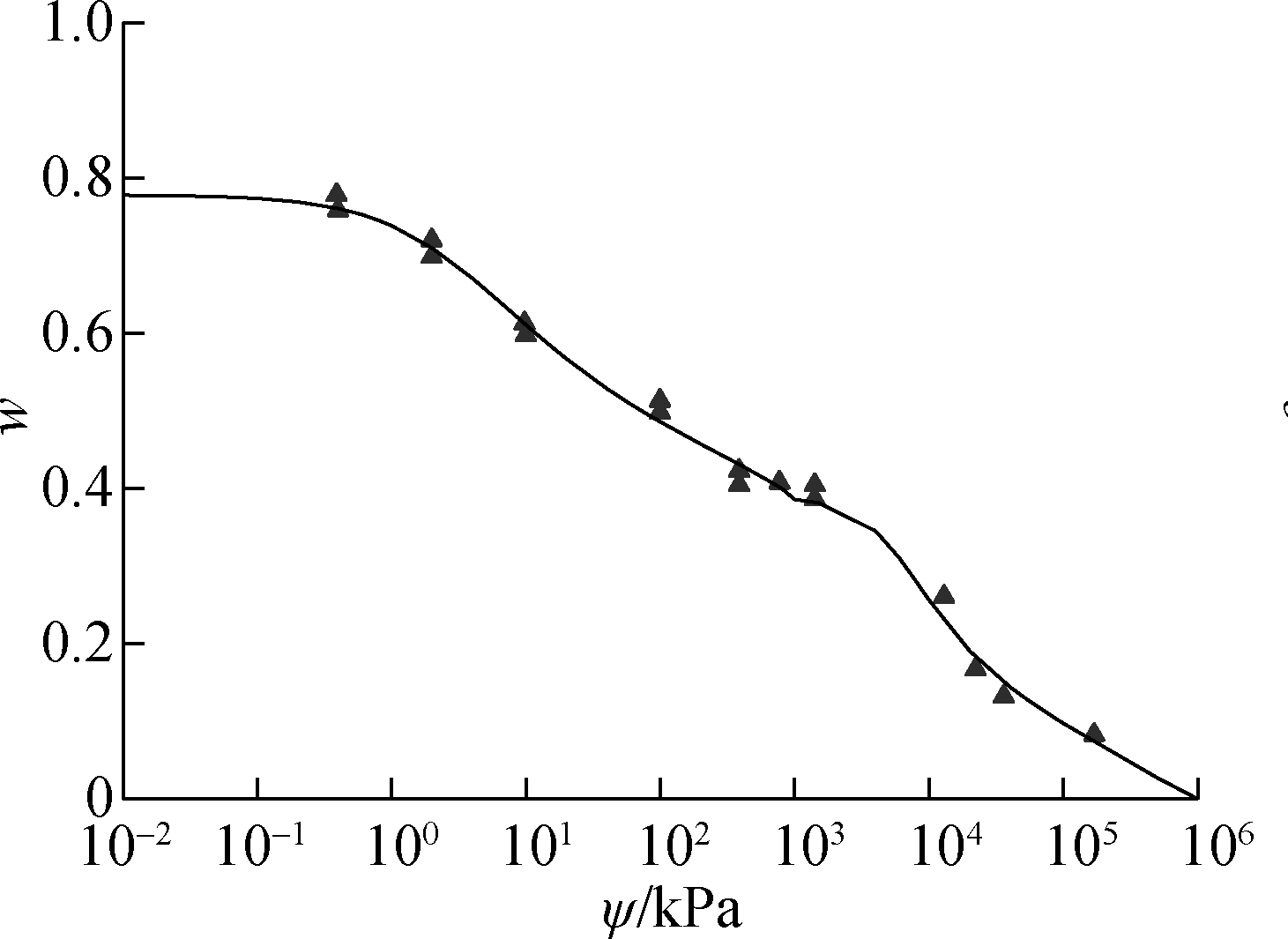
Fig.6 The measured w-SWCC for the Chataignier clay from Li et al.[30]
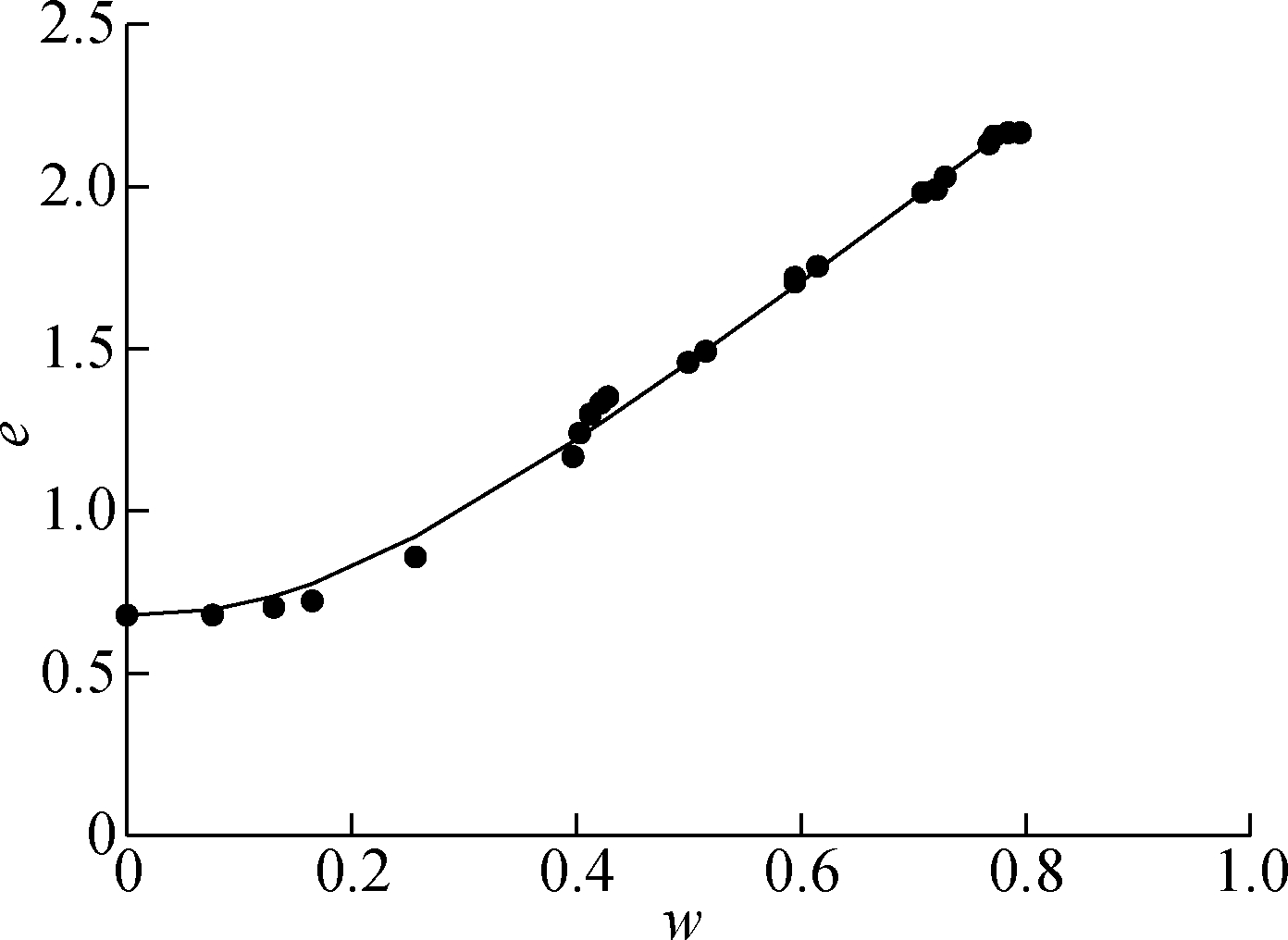
Fig.7 The measured shrinkage curve for the Chataignier clay from Li et al.[29]
Fig.8 The MIP testing results for the Chataignier clay with different soil suctions
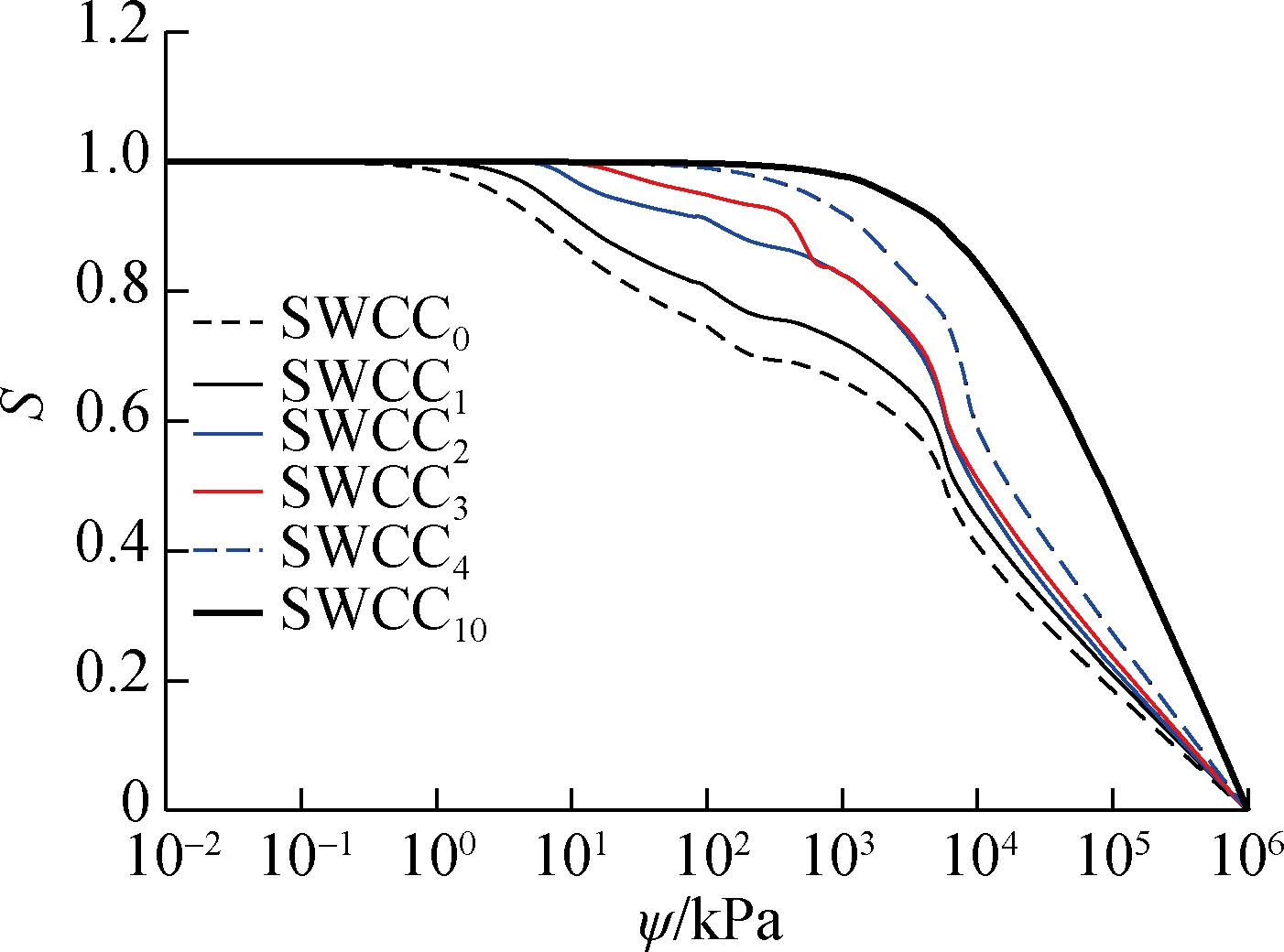
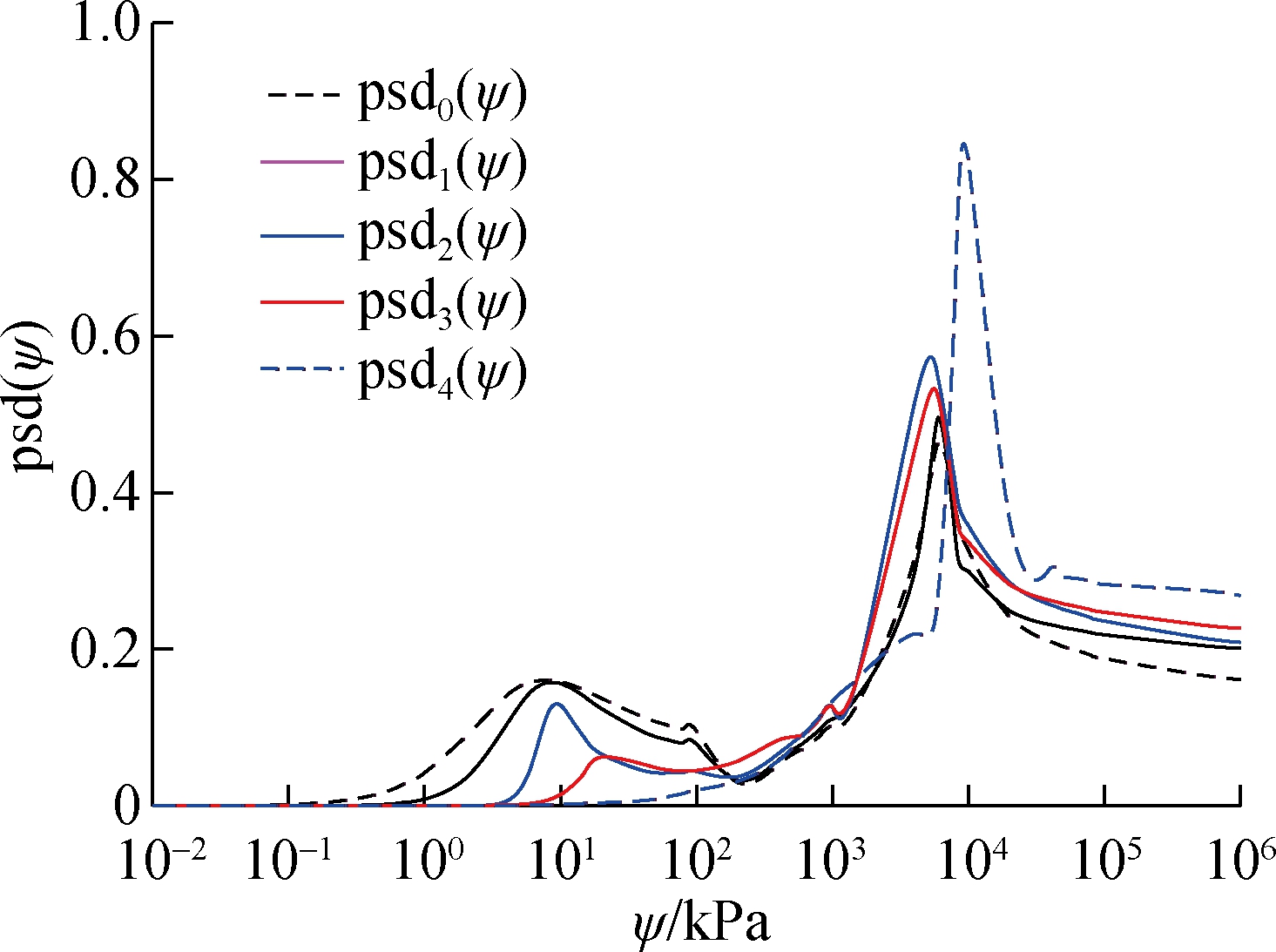
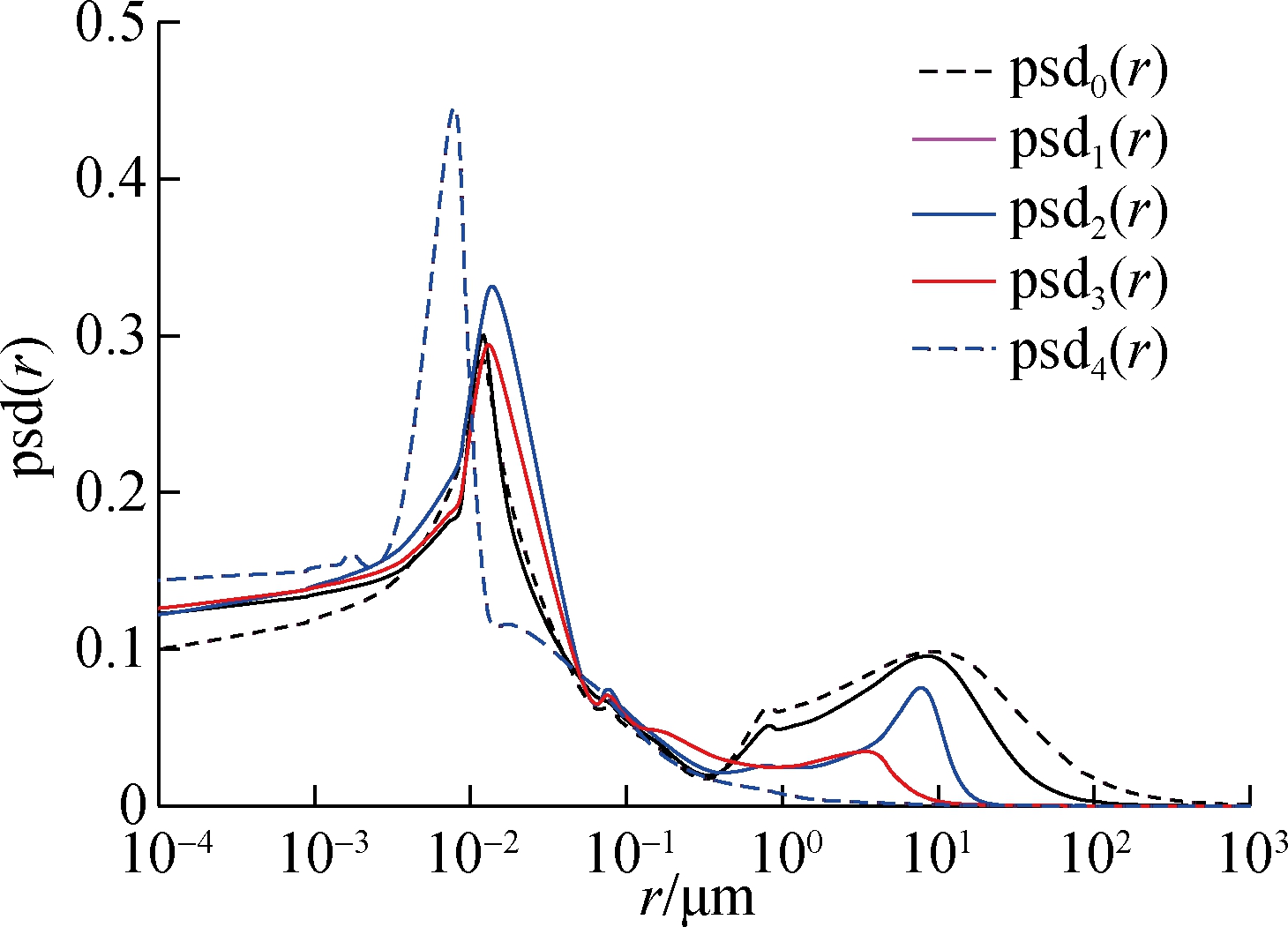
Fredlund et al.’s equations[27]are used to fit with the experimental data as shown in Fig.7. The methodology from Zhai et al.[16] was used to develop the framework of PSDFs following the steps illustrated in Section 2. The estimated S-SWCCs, psd(ψ) and psd(r) are illustrated in Fig.9.
(a)
(b)
(c)
Fig.9 The estimated SWCCs, psd(ψ) and psd(r) for the Chataignier clay. (a) S-SWCCs from measured w-SWCC and the SC; (b) psd(ψ) from the framework; (c) psd(r) from the framework
The trends of the estimated psd(r) as shown in Fig.9(c)are consistent with the MIP testing results as shown Fig.8. It should be noted that psd(r) illustrated in Fig.9(c) was estimated from the measured w-SWCC which collects limited data points within the entire suction range. In other words, the spans between the SWCC data are much wider than those between the MIP testing data. As a result, the estimated psd(r) is less accurate than that obtained from the MIP tests. However, the results in Fig.8 and Fig.9(c) indicate that the trends of psd(r) from both methods are matched well with each other. It is also observed that there is a slight discrepancy between the pore radii corresponding to the peak point from the estimated framework and MIP test due to the constant contact angle adopted in the analyses. Based on Kelvin’s capillary law, the correlation between suction and pore radius is affected by the contact angle. Recently, many reports [3034]indicated that the contact angle of soil may not necessarily have to be zero. Therefore, the discrepancy can be minimized by adopting a contact angle greater than zero.
From Fig.8 and Fig.9(c), it is also observed that the initial loose soil has a bimodal shape PSDF and the shape can be gradually changed to a unimodal shape. Therefore, it is more accurate to indicate the void ratio (or stress level) of soil before describing the shape of the SWCC (or PSDF) for the soil since it can exhibit a bimodal shape under a loose condition while exhibiting a unimodal under a dense condition.The conclusion agrees with the observations from Dieudonné et al[3536].
4 Conclusion
A simulation method of the PSDF for the deformable soil was proposed. The simulated results illustrating the variation of the PSDF were compared with the experimental results by using the MIP tests. In the low suction range, which is corresponding to a high void ratio, the experimental results from MIP tests show that PSDF for the Chataignier clay behaves in a bimodal shape. With the increase in the suction levels, the PSDFs gradually change from a bimodal shape into a unimodal shape. The simulated results from the proposed method indicate that a bimodal PSDF for a soil under a loose condition, corresponding to a high void ratio, can be gradually changed into a unimodal PSDF with the decrease in the void ratio. As a result, the simulated results agree well with the experimental data from the MIP test. The proposed method provides an alternative method for the estimation of the variation of PSDF for a deformable soil.
[1] Tuli A, Hopmans J W, Rolston D E, et al. Comparison of air and water permeability between disturbed and undisturbed soils[J].Soil Science Society of America Journal, 2005, 69(5): 13611371. DOI:10.2136/sssaj2004.0332.
[2] Childs E C, Collis-George N. The permeability of porousmaterials[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1950, 201(1066): 392405.DOI:10.1098/rspa.1950.0068.
[3] Marshall T J. A relation between permeability and sizedistribution of pores[J].Journal of Soil Science, 1958, 9(1):18.DOI:10.1111/j.1365-2389.1958.tb01892.x.
[4] Kunze R J, Uehara G, Graham K. Factors important in the calculation of hydraulic conductivity[J].Soil Science Society of America Journal, 1968, 32(6): 760765. DOI:10.2136/sssaj1968.03615995003200060020x.
[5] Mualem Y. A new model for predicting the hydraulic conductivity of unsaturated porous media[J]. Water Resources Research, 1976, 12(3): 513522.DOI:10.1029/WR012i003p00513.
[6] Fredlund D G, Xing A Q, Huang S Y. Predicting the permeability function for unsaturated soils using the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 533546. DOI:10.1139/t94-062.
[7] Zhai Q, Rahardjo H. Estimation of permeability functionfrom the soil-water characteristic curve[J].EngineeringGeology, 2015, 199: 148156. DOI:10.1016/j.enggeo.2015.11.001.
[8] Zhai Q, Rahardjo H, Satyanaga A. A pore-size distribution function based method for estimation of hydraulic properties of sandy soils[J]. Engineering Geology, 2018, 246: 288292.DOI:10.1016/j.enggeo.2018.09.031.
[9] Zhai Q, Rahardjo H, Satyanaga A, et al. Role of the pore-size distribution function on water flow in unsaturated soil[J]. Journal of Zhejiang University-SCIENCE A, 2019, 20(1): 1020. DOI:10.1631/jzus.A1800347.
[10] Zhai Q, Rahardjo H, Satyanaga A. Estimation of air permeability function from soil-water characteristic curve[J]. Canadian Geotechnical Journal, 2019, 56(4): 505513. DOI:10.1139/cgj-2017-0579.
[11] Vanapalli S K, Fredlund D G, Pufahl D,et al. Model for the prediction of shear strength with respect to soil suction[J]. Canadian Geotechnical Journal, 1996, 33(3): 379392. DOI:10.1139/t96-060.
[12] Zhai Q, Rahardjo H, Satyanaga A,et al. Estimation of unsaturated shear strength from soil-water characteristic curve[J]. Acta Geotechnica, 2019, 14(6): 19771990. DOI:10.1007/s11440-019-00785-y.
[13] Zhai Q, Rahardjo H, Satyanaga A, et al. Effect of the uncertainty in soil-water characteristic curve on the estimated shear strength of unsaturated soil[J]. Journal of Zhejiang University-SCIENCE A, 2020, 21(4): 317330. DOI:10.1631/jzus.a1900589.
[14] Zhai Q, Rahardjo H, Satyanaga A,et al. Estimation of tensile strength of sandy soil from soil-water characteristic curve[J]. Acta Geotechnica, 2020: 111. DOI:10.1007/s11440-020-01013-8.
[15] Fredlund D G, Xing A Q. Equations for the soil-water characteristic curve[J]. Canadian Geotechnical Journal, 1994, 31(4): 521532. DOI:10.1139/t94-061.
[16] Zhai Q, Rahardjo H, Satyanaga A,et al. Framework to estimate the soil-water characteristic curve for soils with different void ratios[J]. Bulletin of Engineering Geology and the Environment[J/OL] (2020-05-08) [2020-08-20].https://link.springer.com/content/pdf/10.1007/s10064-020-01825-8.pdf.
[17] Childs E C. The use of soil moisture characteristics in soil studies[J]. Soil Science, 1940, 50(4): 239252. DOI:10.1097/00010694-194010000-00001.
[18] Childs E C. Stability of clay soils[J]. Soil Science, 1942, 53(2): 7992. DOI:10.1097/00010694-194202000-00001.
[19] Diamond S. Pore size distributions in clays[J]. Clays and Clay Minerals, 1970, 18(1): 723. DOI:10.1346/ccmn.1970.0180103.
[20] Spaans E J A, Baker J M. The soil freezing characteristic: Its measurement and similarity to the soil moisture characteristic[J]. Soil Science Society of America Journal, 1996, 60(1): 1319. DOI:10.2136/sssaj1996.03615995006000010005x.
[21] Koopmans R W R, Miller R D. Soil freezing and soil water characteristic curves[J]. Soil Science Society of America Journal, 1966, 30(6): 680685. DOI:10.2136/sssaj1966.03615995003000060011x.
[22] Azmatch T F, Sego D C, Arenson L U, et al. Using soil freezing characteristic curve to estimate the hydraulic conductivity function of partially frozen soils[J]. Cold Regions Science and Technology, 2012, 83/3: 103109. DOI:10.1016/j.coldregions.2012.07.002.
[23] Ren J P, Vanapalli S K. Comparison of soil-freezing and soil-water characteristic curves of two Canadian soils[J]. Vadose Zone Journal, 2019, 18(1): 114. DOI:10.2136/vzj2018.10.0185.
[24] Brooks R H, Corey A T. Hydraulic properties of porous media[J]. American Society of Agricultural Engineers,1964, 7: 2628. DOI:10.1016/j.trc.2012.10.009.
[25] van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892898. DOI:10.2136/sssaj1980.03615995004400050002x.
[26] Satyanaga A, Rahardjo H, Leong E C, et al. Water characteristic curve of soil with bimodal grain-size distribution[J]. Computers and Geotechnics, 2013, 48: 5161. DOI:10.1016/j.compgeo.2012.09.008.
[27] Fredlund M D, Wilson G W, Fredlund D G. Representation and estimation of the shrinkage curve[C]//Proceedings of the 3rd Internationl Conference on Unsaturated Soils. Recife, Brazil, 2002: 145149.
[28] Zhai Q, Rahardjo H, Satyanaga A. Effect of bimodal soil-water characteristic curve on the estimation of permeability function[J]. Engineering Geology, 2017, 230: 142151. DOI:10.1016/j.enggeo.2017.09.025.
[29] Li Z S, Benchouk A, Derfouf F E M, et al. Global representation of the drying-wetting curves of four engineering soils: Experiments and correlations[J]. Acta Geotechnica, 2018, 13(1): 5171. DOI:10.1007/s11440-017-0527-3.
[30] Goebel M, Bachmann J, Woche S K, et al. Water potential and aggregate size effects on contact angle and surface energy[J]. Soil Science Society of America Journal, 2004, 68(2): 383393. DOI:10.2136/sssaj2004.3830.
[31] Woche S K, Goebel M O, Kirkham M B, et al. Contact angle of soils as affected by depth, texture, and land management[J]. European Journal of Soil Science, 2005, 56(2): 239251. DOI:10.1111/j.1365-2389.2004.00664.x.
[32] Ramírez-Flores J C, Woche S K, Bachmann J, et al. Comparing capillary rise contact angles of soil aggregates and homogenized soil[J]. Geoderma, 2008, 146(1/2): 336343. DOI:10.1016/j.geoderma.2008.05.032.
[33] Ganz C, Bachmann J, Lamparter A, et al. Specific processes during in situ infiltration into a sandy soil with low-level water repellency[J]. Journal of Hydrology, 2013, 484: 4554. DOI:10.1016/j.jhydrol.2013.01.009.
[34] Cai G Q, Zhou A N, Sheng D C. Permeability function for unsaturated soils with different initial densities[J]. Canadian Geotechnical Journal, 2014, 51(12): 14561467. DOI:10.1139/cgj-2013-0410.
[35] Dieudonné A, Della Vecchia G, Charlier R, et al. Influence of microfabric evolution on the retention behaviour of compacted clayey soils[M]//Unsaturated Soils: Research & Applications. CRC Press, 2014: 679684. DOI:10.1201/b17034-95.
[36] Gao Y, Sun D A. Soil-water retention behavior of compacted soil with different densities over a wide suction range and its prediction[J]. Computers and Geotechnics, 2017, 91: 1726. DOI:10.1016/j.compgeo.2017.06.016.