With the significant growth of various wireless applications, spectrum resources are becoming more scarce. Cognitive radio(CR)is proposed as a promising technology to improve the utilization of the radio frequency spectrum^[1]. Opportunistic spectrum access is an important access means for CR, in which the secondary users(SUs)can opportunistically utilize the unused frequency bands that belong to the primary users(PUs). Therefore, spectrum sensing plays a crucial role in opportunistic spectrum access without causing detrimental interference with the PUs^[2]. Recently, various spectrum sensing methods have been developed to conduct spectrum detection, such as coherent detection, feature detection and energy detection. In this paper, we focus on energy detection since it is simple and able to detect the primary signal without any prior information. However, due to the noise uncertainty, multipath fading or hidden terminal problem, these sensing methods inevitably suffer from unreliable sensing results. To improve the sensing reliability and accuracy, cooperative spectrum sensing(CSS)has attracted extensive attention and applications for CR^[3-4].

CSS is an effective technique for mitigating the detrimental impacts of channel fading in CR^[5-14]. In CSS, multiple SUs individually report their local sensing results to the FC, which makes a global decision to determine whether a PU is present in the authorized band. In Ref.[5], a sensing-throughput tradeoff problem for the CSS scenario was formulated to find the optimal sensing time and the fusion threshold k that maximize the throughput of the SUs, but it did not consider the reporting channel errors between the SUs and the FC. The optimal N-out-of-K rule over imperfect reporting channels were derived by Banavathu et al.^[6] for heterogeneous CRNs.However, they did not consider the protection constraint for the PU. The throughput of CRNs with CSS using the m-out-of-K rule was maximized by optimizing the m value and the K value while guaranteeing sufficient protection for the PU^[7], but they did not optimize the spectrum sensing parameters. A fusion rule based on dynamic grouping was proposed for the distributed CSS in heterogeneous CRNs, where the SUs in different groups were assigned different weights to achieve information fusion^[8], whereas the authors assumed that no burst errors were present in the reporting channels.

The above works^[5-8] are mainly concerned with the user cooperation in a single-channel scenario, whereas practical CR usually has multiple PU channels that can be utilized by SUs. Therefore, joint sensing of multiple channels is necessary in CRNs as it can provide more transmission opportunities for SUs and thus improve the system throughput. Considering the variety of sensing performances and channel utilizations for a multi-channel scenario,Huang et al.^[9] studied the optimization of the cognitive terminal assignment strategy in the coordinated spectrum sensing but without optimizing the sensing time and detection threshold. Yu et al.^[10] maximized the average throughput of multi-channel CR under the constraints of detection probability for each channel by jointly optimizing the sensing time, SU assignment and energy detection threshold. Azarfar et al.^[11] investigated the problem of joint transmission and CSS strategy optimization for a multi-user multi-channel dynamic spectrum access networks. However, Refs.[9-11] assumed that the reporting channels between the cognitive users and the fusion center(FC)are error-free, which is not realistic in practical CR systems since the reporting channels also suffer multi-path fading or interferences^[12-14]. Both the sensing parameters and the reporting channel errors have an important influence on the performance of CSS, and the PUs have the priority over SUs in using the licensed spectrum. Therefore, in this paper, we take all of these factors into account and investigate the throughput maximization problem for multichannel CSS with reporting channel errors under hard decision fusion rules.

First, the global detection and false-alarm probabilities in terms of reporting channel errors at the FC are derived. Then, the throughput maximization problem for multi-channel CSS is formulated while giving all the PUs effective protection by jointly optimizing the sensing time, detection threshold and SU assignment. To tackle the non-convex optimization problem, the optimal energy detector threshold at each channel is derived first. Then, a sub-optimal greedy algorithm is proposed to obtain the optimal SU assignment and the optimal sensing time to maximize the spectrum access opportunities. The numerical results are presented to compare the performance between the proposed algorithm and the exhaustive search algorithm under perfect and imperfect reporting channels. The impacts of reporting error probability and channel utilization on the throughput are also analyzed.

In this paper, a CRN with a FC,N primary channels, and M SUs is investigated. We consider the case where the SUs outnumber the channels, i.e., M>N. Hence, a couple of SUs can cooperate to sense the same channel. Each channel is licensed to one PU, and at a particular period of time, the channel may be inactive and is available for the SUs to transmit data. However, before utilizing the spectrum, the SUs have to sense the channel state(i.e., inactive ‘0'and active ‘1')by energy detection and only access the inactive channel. We assume that at least one SU is assigned to sense one PU channel and one SU is only allowed to sense one PU channel. The cooperation among M SUs is controlled by the FC.

Each frame for channel i includes sensing slot τ_s, reporting slot τ_r and transmission slot Tⁱ_d. The PU is supposed to be either absent or present during the entire frame period T. We assume that the FC assigns m_i SUs to sense the i-th channel. During the sensing slot, m_i SUs individually perform spectrum sensing to detect the channel state that the FC assigns, and then send their sensing results to the FC in the reporting slot. Finally, the FC makes a global decision regarding the status of each channel.

The reliability of local spectrum sensing is usually evaluated by two performance metrics, namely, false-alarm probability and detection probability. The former represents the probability that the SU falsely identifies the free channel as being busy while the latter denotes the probability that the SU correctly identifies the busy channel as being busy. The probabilities of false alarm and detection over channel i can be given as^[10]

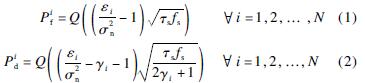
where Q(x)=1/((2π)^1/2)∫^∞_xexp(-(t²)/2)dt; σ²_n is the noise variance; ε_i is the energy detector threshold of the i-th channel; f_s is the sampling frequency; γ_i is the received signal-to-noise ratio(SNR)of primary signal at the SUs on channel i. To facilitate the analysis, the received SNRs at the SUs for the same primary channel are assumed to be the same. With a given target 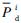value, Pⁱ_f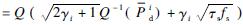, where Q^-1(x)is the inverse function of Q(x), and for a given pair of 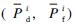, P^-i_f), the required sensing time to achieve these targets on channel i can be given as τⁱ_s=(Q^-1()-

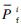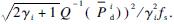
CSS is applied to improve the sensing performance by combining the sensing decisions from different spatially located SUs. Basically, CSS is performed in two successive phases: sensing and reporting. Several SUs independently sense the channel in the sensing phase and then forward their local decisions to the FC in the reporting phase. Finally, by fusing all local decisions, the FC makes a global decision on the existence of the PU.

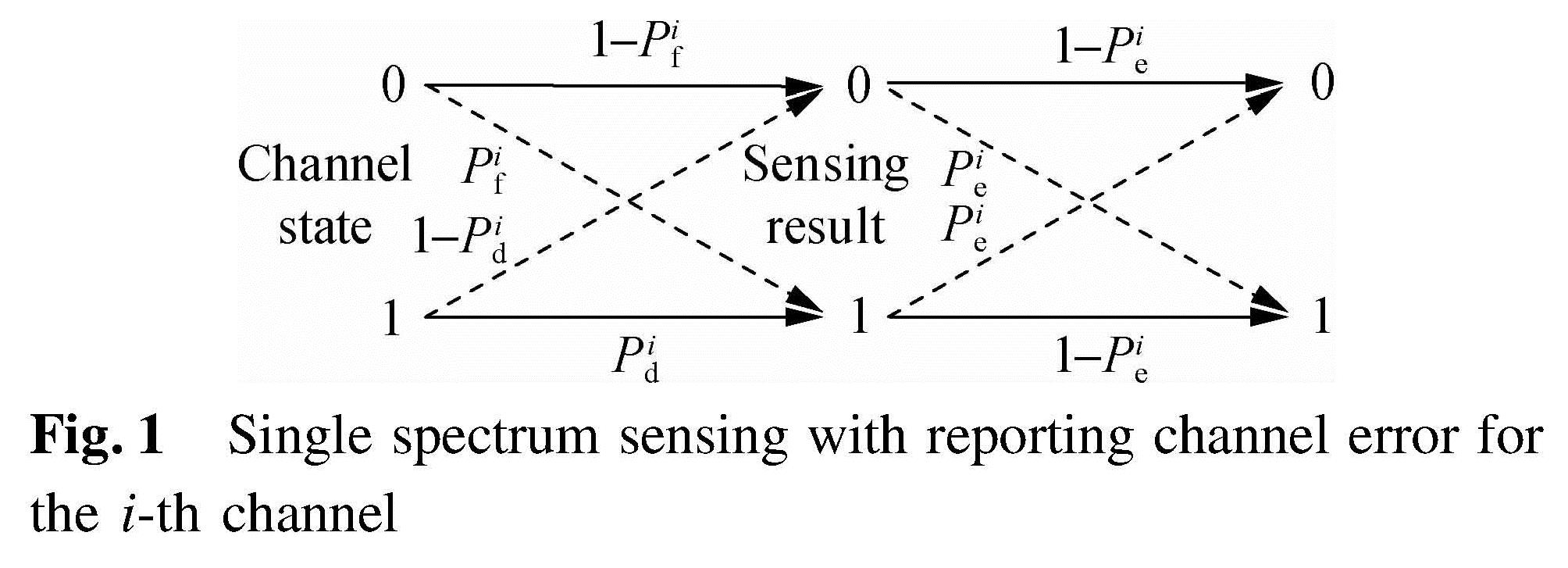
In reality, the reporting channels in CSS are imperfect since they will suffer multi-path fading and shadowing, which will inevitably deteriorate the cooperation detection performance.As shown in Fig. 1, if a SU senses that the i-th channel is inactive and reports its sensing result to the FC through a fading channel, the FC will likely receive an error result that channel i is active(which is marked in bold). In this paper, we assume that the SUs which sense the same channel have identical local sensing performance and experience the same but independent reporting channel fading. Denote Pⁱ_e as the reporting channel error probability between the SUs and FC over the i-th channel. Then, the effective false alarm probability and detection probability at the FC for the i-th channel are^[6-7]

Pⁱ_fe=Pⁱ_f(1-Pⁱ_e)+(1-Pⁱ_f)Pⁱ_e=f(Pⁱ_f)(3)

Pⁱ_de=Pⁱ_d(1-Pⁱ_e)+(1-Pⁱ_d)Pⁱ_e=f(Pⁱ_d)(4)

where f is a function which is defined as f(x)=(1-2x)Pⁱ_e+x.

Fig.1 Single spectrum sensing with reporting channel error for the i-th channel

In this paper, we consider two hard decision fusion rules: “OR” rule and “AND” rule, which pertain to the extreme cases of the voting rule and have been widely used.

1)“OR” rule. In this rule, the FC announces that the i-th channel is active when at least one of the local decisions says that the PU is active on channel i. Considering the impacts of imperfect reporting channels, the global false probability Qⁱ_fe and detection probability Qⁱ_de for channel i can be given as ^[13]

Qⁱ_fe=1-[1-f(Pⁱ_f)]^m_i(5)

Qⁱ_de=1-[1-f(Pⁱ_d)]^m_i(6)

2)“AND” rule.In this rule, the FC announces that the i-th channel is active when all the local decisions say that the PU is active on channel i. Again, under the same conditions, the global false probability Qⁱ_fe and detection probability Qⁱ_de for channel i can be expressed as

Qⁱ_fe=[f(Pⁱ_f)]^m_i(7)

Qⁱ_de=[f(Pⁱ_d)]^m_i(8)

The usage of each channel is modeled as an alternative renewal process with active and inactive states. The durations of the active and inactive states on channel i are assumed to be exponentially distributed with mean values of αⁱ₁ and αⁱ₀, respectively^[9]. Thus, the probability density functions of active and inactive periods on channel i can be, respectively, given as

pⁱ₁(t)=1/(αⁱ₁)exp(-(t)/(αⁱ₁))(9)

pⁱ₀(t)=1/(αⁱ₀)exp(-(t)/(αⁱ₀))(10)

Accordingly, let μ_i denote the utilization of channel i, i.e., the active state probability of PUs on channel i. It can be computed as

μ_i=(αⁱ₁)/(αⁱ₀+αⁱ₁)i=1,2,…,N(11)

Considering the effects of false alarm and missed detection,there are two cases that the SUs can operate on channel i: 1)When the channel is inactive, and the FC correctly determines it with probability(1-μ_i)(1-Qⁱ_fe); 2)When the channel is active, while the FC falsely determines it as inactive with probability μ_i(1-Qⁱ_de). Let Cⁱ₀ and Cⁱ₁ denote the achievable transmission rate of SUs if they are allowed to operate on the i-th channel in the absence and the presence of the PU, respectively, and define γⁱ₀ and γⁱ₁ as the corresponding SNR of the secondary transmission link on the i-th channel when the PU is absent and present.Then, we have Cⁱ₀=log₂(1+γⁱ₀), Cⁱ₁=log₂(1+γⁱ₁). Thus, for channel i, the average throughput of the SUs under these two cases can be given as

Rⁱ₀(τ_s,ε_i,m_i)=(Tⁱ_dCⁱ₀)/T(1-μ_i)(1-Qⁱ_fe(τ_s,ε_i,m_i))(12)

Rⁱ₁(τ_s,ε_i,m_i)=(Tⁱ_dCⁱ₁)/(T)μ_i(1-Qⁱ_de(τ_s,ε_i,m_i))(13)

where Tⁱ_d=T-τ_s-m_iτ_r. Therefore, the average throughput of the SUs on the i-th channel is given as

R_i(τ_s,ε_i,m_i)=Rⁱ₀(τ_s,ε_i,m_i)+Rⁱ₁(τ_s,ε_i,m_i)

In this paper, our aim is to maximize the average throughput of SUs while protecting all the PUs from harmful interference by jointly optimizing the sensing duration, energy detection threshold and SU assignment. Therefore, the optimization problem for multi-channel CSS with reporting channel errors can be formulated as

P1: 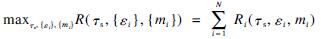(14)

s.t.

Qⁱ_de≥φ_i(14a)

Qⁱ_fe≤φ_i(14b)

0≤τ_s≤T-m_iτ_r(14c)

1≤m_i≤M(14d)

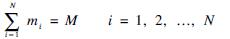(14e)

where φ_i is the minimum target detection probability on channel i which protects the PU; φ_i is the maximum false alarm probability on channel i to ensure the opportunistic spectrum access of SUs.

The operation of the SUs in case 2)experiences interference from the PU.Therefore, we have Cⁱ₀>Cⁱ₁. Generally,Qⁱ_fe<Qⁱ_de. Moreover, in CRNs, we care more about the channels that are not fully utilized, such as the channels with μ_i≤0.5. Based on these considerations, we conclude that Rⁱ₁(τ_s,ε_i,m_i)Rⁱ₀(τ_s,ε_i,m_i). Hence, for convenience, the following formula will be used as the objective function rather than(14).

(15)

In Problem P1, we can find that both Qⁱ_de and Qⁱ_fe are determined by the sensing time τ_s, the energy detector threshold ε_i, the number of cooperative SUs m_i and the reporting channel error probability Pⁱ_e. Due to the complicated coupling among the optimization variables, Problem P1 is non-convex.In this section, to make the problem tractable, the optimal energy detector threshold on channel i is derived first. Then, a sub-optimal greedy algorithm is developed to obtain the optimal SU assignment and the optimal sensing time.

Problem P1 achieves the optimal solution when the constraint(14a)is equal.The proof is similar to Ref.[10].Here, we only explain it briefly. To maximize the achievable average throughput of SUs, according to Eq.(15), the global false alarm probability Qⁱ_fe(τ_s,ε_i,m_i)needs to be minimized, that is, the sensing threshold ε_i needs to be maximized as the value of Qⁱ_fe(τ_s,ε_i,m_i)is inversely proportional to ε_i. When ε_i is maximized, Qⁱ_de(τ_s,ε_i,m_i)is minimized. Namely, Qⁱ_de=φ_i. Therefore, for any given pair of τ_s and m_i, according to Eq.(2), the sensing threshold ε_i which satisfies(14a)can be derived as

ε_i=σ²_n[((2γ_i+1)/(τ_sf_s))^1/2Q^-1(β_i)+γ_i+1](16)

We assume that the target detection probabilities on all channels are equal. Generally, φ_i is chosen to be close to but less than 1, especially in the low SNR regime.For channel i, with Qⁱ_de=φ_i,Qⁱ_fe≤φ_i, we have τ_s≥τ_i, where τ_i=((Q^-1(δ_i)-(2γ_i+1)^1/2Q^-1(β_i))/(γ_i(f_s)^1/2))². For the “AND” rule, δ_i=((φⁱ)^m_i-Pⁱ_e)/(1-2Pⁱ_e), β_i=((φ_i)^m_i-Pⁱ_e)/(1-2Pⁱ_e). For the “OR” rule, δ_i=((1-φⁱ)^m_i+Pⁱ_e-1)/(2Pⁱ_e-1), β_i=((1-φⁱ)^m_i+Pⁱ_e-1)/(2Pⁱ_e-1).

Based on the above discussions, Problem P1 can be simplified to Problem P2 as

P2: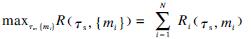(17)

s.t.

0≤τ_s≤T-m_iτ_r(17a)

1≤m_i≤M(17b)

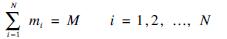(17c)

To solve problem P2, we transform problem P2 to P3.

P3:max_{mi}R({m_i})=R^*₂({m_i})(18)

s.t.

1≤m_i≤M(18a)

(18b)

where R^*₂({m_i})is the optimal objective value of Problem P4 with a given {m_i} value.

P4: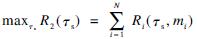(19)

s.t.

0≤τ_s≤T-m_iτ_r(19a)

Following a similar process as adopted in Ref.[5], we can also prove that R₂(τ_s)of Problem P4 is a unimodal function. Hence, the optimal sensing time in problem P4 can be obtained by efficient search algorithms such as the binary searching method. Algorithm 1 presents the proposed greedy algorithm to achieve the optimal sensing time and the optimal SU assignment.

Algorithm 1 Greedy algorithm

Input: T, f_s, τ_r, M, N, φ_i.

Output:The optimal SUs assignment {m_i}.

Initialization: Pⁱ_e, μ_i, γ_i, γⁱ₀,m^j={m_i}^j={1,1,…,1}, j←0.

while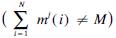

for all i=1 to N do

Let m^j+1←m^j.

Let m^j+1(i)←m^j(i)+1.

For the given m^j+1, find the maximum average throughput 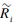by solving P4.

endfor

Find i^* that maximize the then let m^j+1←m^j,m^j+1(i^*)←m^j(i^*)+1.

j←j+1.

end while

The optimal SUs assignment {m_i} is obtained, and the corresponding optimal sensing time can be obtained by solving P4.

The computational times of solving Problem P4 by the proposed greedy algorithm are compared with the exhaustive algorithm as shown in Tab.1 with N=5 given^[10]. We can see that when M>N, the proposed greedy algorithm only requires(M-N)N optimization operations. Given N, the complexity of the greedy algorithm only linearly increases with the increase in the number of SUs, while as M-N increases, the complexity of the exhaustive search algorithm rapidly increases. Thus, the proposed algorithm is much easier and faster than the exhaustive algorithm, especially when M and N are large.

Tab.1 Comparison of the complexity

In this section, simulation results are presented to verify the effectiveness of the proposed algorithm. For comparison, we also provide the exhaustive algorithm^[10], in which all the possible combinations of {m_i} are searched. Unless otherwise specified, the number of channels N=5, the frame time slot T=100 ms, the sampling frequency f_s=6 MHz, and the reporting time of each SU τ_r=10 μs. Moreover, the target detection probabilities φⁱ on all channels are set to be 0.9, the channel utilizations μ_i on all channels vary from 0.2 to 0.5 randomly, and the received SNRs γ_i on all channels are randomly generated in the range of -20 to -15 dB.The reporting error probability Pⁱ_e on each channel ranges from 0.003 to 0.008 randomly. The channels are assumed to be block faded and the SNRs γⁱ₀ of the secondary transmission links are ergodic, stationary and exponentially distributed with the mean 20 dB. In this paper, the numerical results are obtained by averaging over 1 000 independent simulation runs.

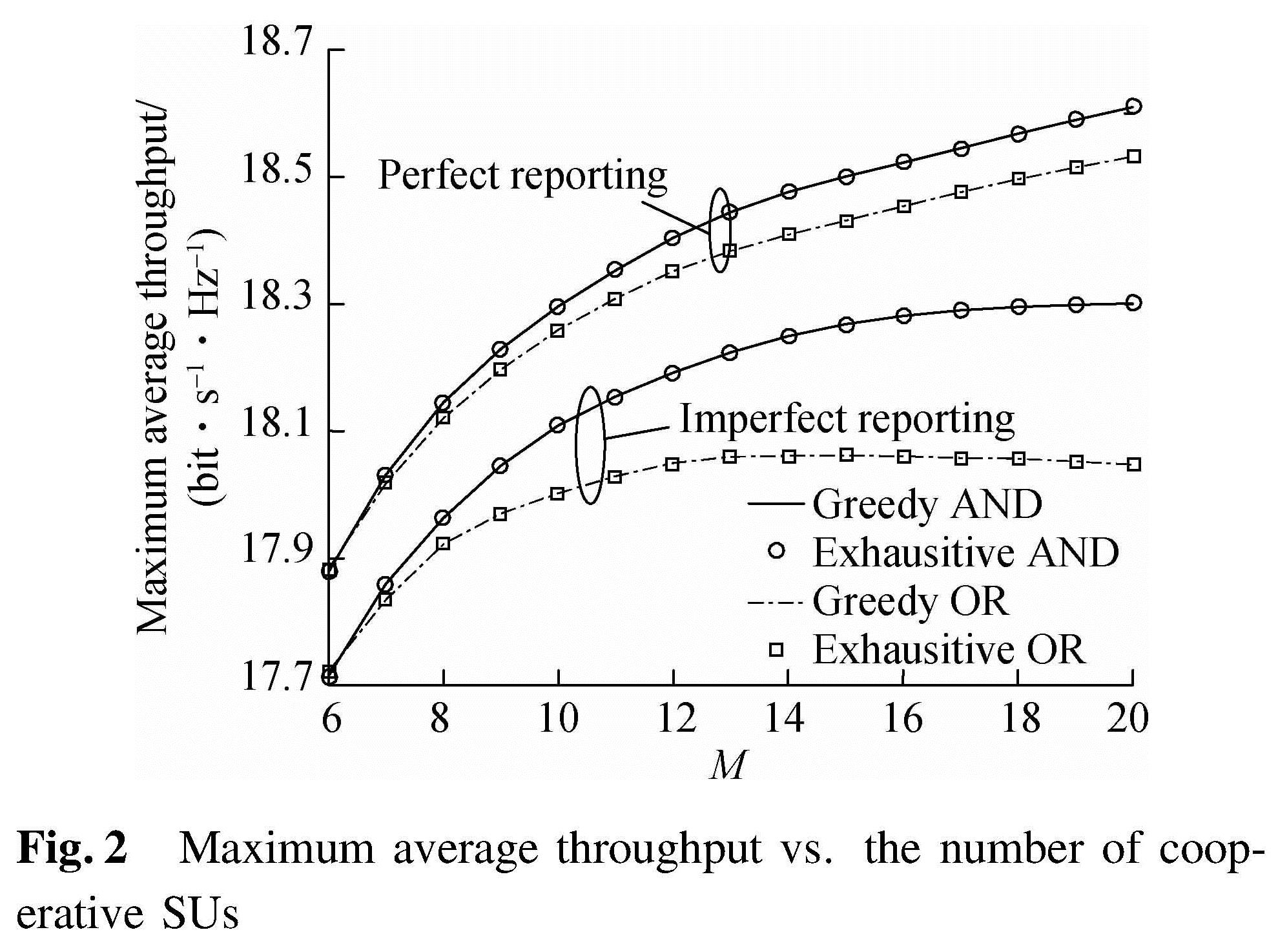
In Fig.2, the maximum average throughput versus the number of cooperative SUs under perfect and imperfect reporting channels are plotted for the proposed greedy algorithm and the existing exhaustive algorithm. It is evident that the maximum average throughputs of these two algorithms match well with each other. We can see that the average throughput of the “AND” rule is superior to that of the “OR” rule. This is because the global false-alarm probability of the “AND” rule is lower compared with “OR” rule, and therefore, more transmission opportunities can be offered to SUs to transmit data, thus improving the average throughput of the system.It is also observed that the imperfect reporting channels indeed worsen the global detection performance and cause the throughput to decrease.

Fig.2 Maximum average throughput vs. the number of cooperative SUs

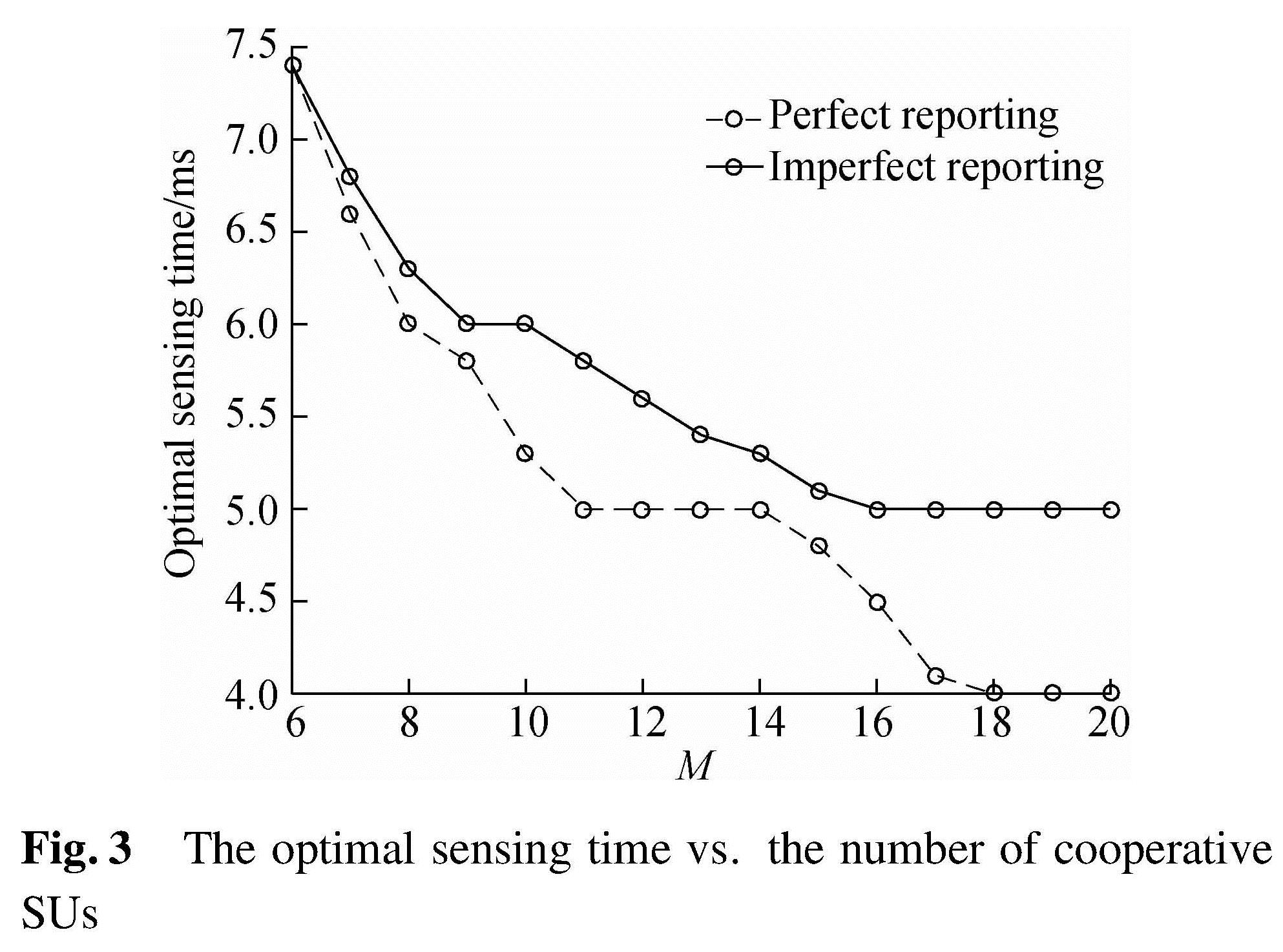
Fig.3 illustrates the optimal sensing time versus the number of cooperative SUs under perfect and imperfect reporting channels for the “AND” rule. It is observed that as the number of cooperative SUs increases, the optimal sensing time decreases. Besides, with a given number of SUs, the optimal sensing time is longer under imperfect reporting.Hence, less time will be left for data transmission, resulting in the throughput degradation of the system.

Fig.3 The optimal sensing time vs. the number of cooperative SUs

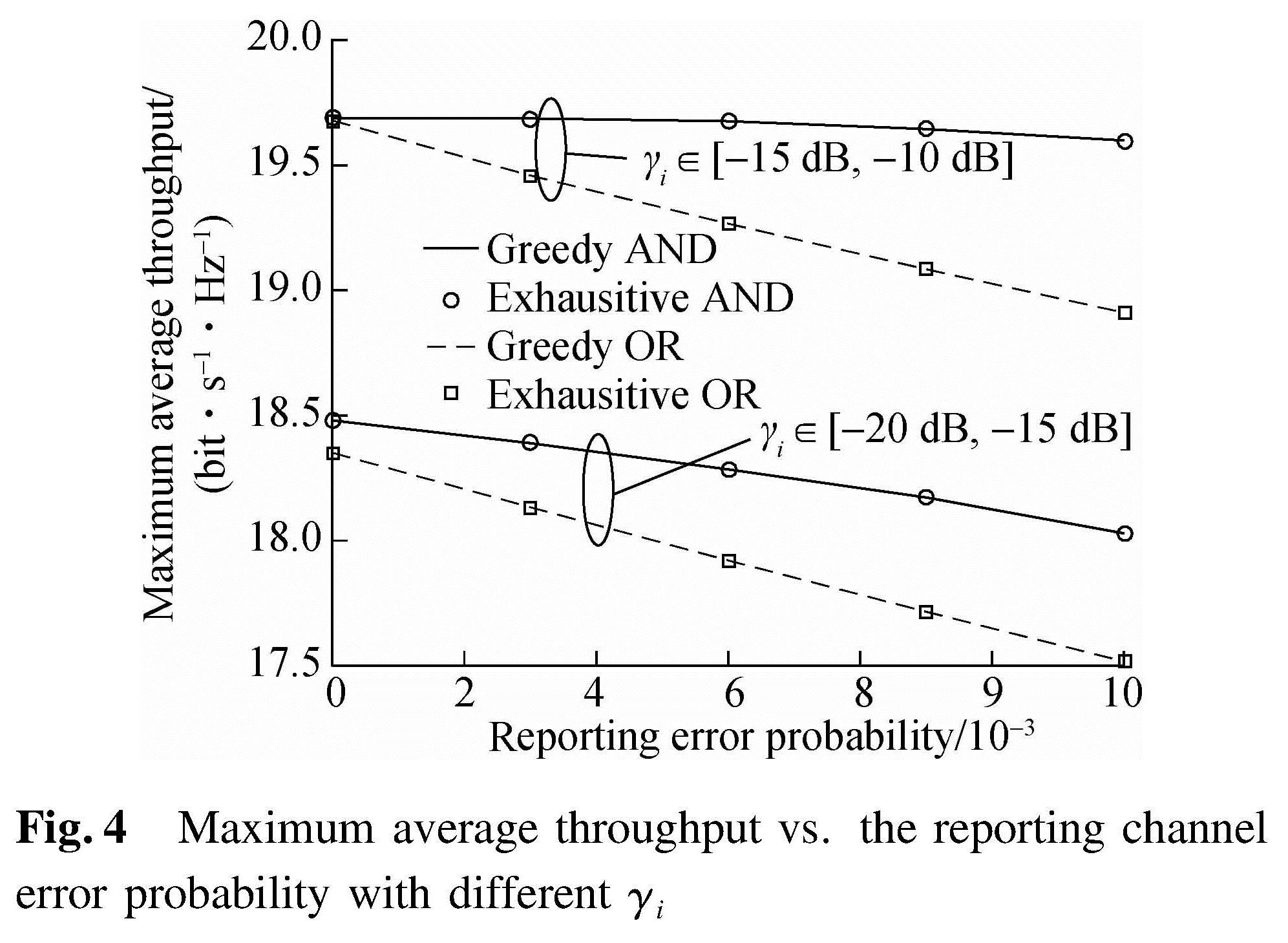
Fig.4 shows the maximum average throughput versus the reporting channel error probability with different γ_i for the proposed greedy algorithm and the exhaustive algorithm. In this figure, the reporting error probabilities on different channels are assumed to be the same. Similar to Fig.2, the proposed greedy algorithm coincides with the exhaustive solution. It can be seen that the throughput displays a more obvious decreasing trend with lower SNR. Hence, the reporting channel errors should not be ignored especially when the SNR environment is poor. Besides, compared to the “OR” rule, the throughput of the “AND” rule decreases slightly and is affected little by the reporting errors under higher SNR. This is because in the “AND” rule, the FC declares that a channel is active when all the local decisions say that it is active, and thus the robustness against reporting channel errors can be improved.

Fig.4 Maximum average throughput vs. the reporting channel error probability with different γi

Fig.5 shows the maximum average throughput versus sensing time with different channel utilizations μ_i. It is seen that the larger the channel utilization, the lower the maximum average throughput. This is because larger channel utilization implies that the channel is busy most of the time and the SUs will have little chance to access the channel, and thus the throughput declines. Moreover, we can discover that at first, the “OR” rule has a greater throughput than the “AND” rule. However, when the sensing time further increases, the throughput of the “AND” rule is larger instead. The reason is that when the sensing time is short, the “OR” rule has a lower global false alarm probability; when the sensing time is long enough, the “AND” rule has a lower false alarm probability instead, which indicates that more unused spectrum can be exploited by the SUs, thus improving their average throughput.

Fig.5 Maximum average throughput vs. sensing time with different μi

1)In this paper, we investigated the throughput maximization problem for multiple channel CSS over imperfect reporting channels. Considering the impact of reporting channel errors, the effective false alarm probability and detection probability at the FC are derived.

2)The detection threshold, sensing duration and SUs assignment are jointly optimized to maximize the average throughput of SUs while maintaining the quality of service of all PU channels.A sub-optimal greedy algorithm is developed to obtain the optimal sensing time and the SUs assignment.

3)Numerical results show that the proposed greedy algorithm achieves the same performance as that of the exhaustive search algorithm but with a much lower complexity, and the average throughput under the imperfect reporting channels is always lower than that under the perfect case.