In recent years, wireless sensor networks (WSNs) have been applied in forest monitoring, target tracking, disaster relief, etc. Data collection is one of the most important operations in WSNs. With the development of unmanned aerial vehicles (UAVs), using UAVs in data collection of WSNs has become a hot topic. However, how to efficiently collect data by optimizing the trajectory of UAVs in WSNs is still an open problem which needs further study.
Many approaches have been proposed for data collection in UAV-aided WSNs. These approaches can be classified into two categories. In the first category, Ebrahimi et al.[1-2] proposed the compressive data gathering (CDG) algorithm to compress the data uploaded by the sensor nodes (SNs) to the UAV. A data collection framework was designed to improve data collection efficiency in Refs.[3-4]. In Ref.[5], the balanced network communication protocol (BNCP) was proposed to improve the transmission efficiency during data collection. Zhan et al.[6] jointly optimized the UAV trajectory and node wake-up scheduling to minimize the mission completion time among all UAVs. Zeng et al.[7] jointly optimized the UAV trajectory and the total mission completion time, as well as communication time allocation among SNs to minimize the total UAV energy consumption. Cheng et al.[8] used the traveling salesman problem (TSP) algorithm to plan a traveling path for mobile sinks to reduce the delay time of data gathering. From the perspective of data compression, collection framework, routing protocols, and path planning, these studies enable the UAV to minimize the energy consumption of the UAV or SNs when collecting data. However, the timeliness of the collected data is rarely considered. SNs continuously generate sensing data and the size of the node buffer is limited. If time-sensitive data is not collected in time, it will overflow the buffer and lose its value. In addition, in scenarios such as target tracking, disaster monitoring, and emergency rescues, if the abnormal data can be quickly collected, some actions can be taken to avoid greater losses. Therefore, timely collection of time-sensitive data becomes crucial.
In the second category, some approaches are proposed to collect time-sensitive data. Kaul et al.[9] proposed a metric of age of information (AoI) to measure how new the information is. AoI is defined as the time that has passed since the latest information was generated. Two different AoI indices, namely maximum AoI and average AoI, were proposed in Ref.[10], and dynamic programming (DP) and the genetic algorithm (GA) were used to optimize these two indices. Abd-Elmagid et al.[11-12] studied the long-term weighted sum-AoI minimization problem. In Ref.[13], authors specifically defined the AoI as the time which has elapsed from the moment that the node generates the data packet to the time that the UAV collects the data packet. The outdated packets are minimized in the system through reinforcement learning (RL). As for the time constrained IoT devices, Samir et al.[14] proposed a UAV trajectory planning scheme to maximize the number of served IoT devices. Hu et al.[15] jointly optimized the UAV’s trajectory, the time required for energy harvesting and data collection to minimize the average AoI of the collected data. Li et al.[16] proposed a UAV-aided data collection scheme to minimize the total mission time for emergency applications. Liu et al.[17] proposed a trajectory planning policy to maximize information currency which is measured by the AoI of each sensor node. Similar to the concept of AoI, Turgut et al.[18] put forward a model of the value of information (VoI) and proposed an intruder tracking scheme taking into account the VoI. Bidoki et al.[19] further described the value of information (VoI) which decays with time and proposed a sleep scheduling scheme to maximize the VoI and minimize energy cost. Khan et al.[20] used the metric of VoI in underwater wireless sensor networks and proposed a greedy path planning (GPP) strategy to collect data. In addition, the metric of VoI is also applied to cloud computing resource planning[21] and endangered species monitoring[22].
These VoI related approaches did not consider the time limit of the UAV flight. In this paper, we aim to maximize the VoI of the collected data in a given period for UAV-aided WSNs. The main contributions of this paper are summarized as follows. First, a UAV-aided WSNs model is proposed for data collection under a more practical Rician channel. Based on the model, the data collection problem is formulated as a mixed integer non-linear program (MINLP). Secondly, the formulated problem is divided into two sub-problems according to the node type, and the maximum VoI first and successive convex approximation (MVF-SCA) algorithm for UAV trajectory planning is proposed to maximize the VoI of the collected data within flight time. Finally, a series of simulations are performed and simulation results show that the VoI collected by the proposed algorithm is higher than that of the classic TSP algorithm and the GPP algorithm.
1 System Model
1.1 Network model
In this paper, WSNs are considered for deployment in forest areas for routine data collection and timely warning of unusual events such as fires or illegal biological invasions. The network model is shown in Fig.1, which consists of a series of sensor nodes and a UAV.M sensor nodes are randomly distributed in the target area, which is represented by the set S={1,2,…,M}. i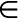 S is used as the index of the node. SNs record the surrounding temperature, humidity and pictures within a collection period. It is assumed that SNs can be divided into two categories according to the collected information. One is the common nodes (CNs), represented by set Sc. The data collected by CNs is routine data within the preset normal range with a low degree of emergency. The other is the key nodes (KNs), represented by set Sk. The data sensed by KNs is abnormal data, which is not within the preset normal range and has a high degree of emergency, S=Sc∪Sk.
S is used as the index of the node. SNs record the surrounding temperature, humidity and pictures within a collection period. It is assumed that SNs can be divided into two categories according to the collected information. One is the common nodes (CNs), represented by set Sc. The data collected by CNs is routine data within the preset normal range with a low degree of emergency. The other is the key nodes (KNs), represented by set Sk. The data sensed by KNs is abnormal data, which is not within the preset normal range and has a high degree of emergency, S=Sc∪Sk.
Fig.1 Data collection model in UAV-aided WSNs
The UAV flies above the target monitoring area and collects the data from the SNs. Due to physical limitations, the endurance of the UAV is limited, and the battery needs to be replaced or charged in time when it is low. So, we suppose that the flight time of a collection is T. Assuming that the UAV flies at a fixed altitude of H meters above the ground during the collection period T, the flight trajectory projected by the UAV on the ground can be represented as q(t), 0≤t≤T. Divide T into N equal time slots with n = 1,2,…,N as the index, and the length of each slot is denoted as δt. When δt is small enough, the position change of the UAV in δt is negligible compared with the distance from the node to the UAV. Since T is divided into N time slots, the trajectory q(t) can be discretized into a sequence {q[n], 1≤n≤N}, and q[n]  R2×1 represents the horizontal coordinate of the UAV in time slot n. The initial position and end position of the UAV are denoted by q0 and qF
R2×1 represents the horizontal coordinate of the UAV in time slot n. The initial position and end position of the UAV are denoted by q0 and qF R2×1, respectively, which can be determined by specific application scenarios.
R2×1, respectively, which can be determined by specific application scenarios.
The goal of this system is to optimize the trajectory and radio resource allocation of the UAV to maximize the VoI collected within flight time T. Therefore, the rest of this section introduces the channel model between the UAV and the nodes, the data transmission model and the value of the information model.
1.2 Channel model
In most literature, in order to facilitate optimization, the channel between the UAV and nodes is modeled as a deterministic LoS channel and follows the free space path loss model. However, this simplified model is actually inaccurate in urban and suburban areas, because it ignores random shadowing and small-scale fading. Therefore, our system adopts a more practical Rician channel to model the transmission channel between the UAV and nodes. The channel coefficient between node i and the UAV in time slot n can be expressed as
(1)
where βi[n] is a large-scale average channel power gain that takes into account signal attenuation, including path loss and shadowing; ![]()
The communication between the UAV and node is shown in Fig.2. Assume that the distance between the UAV and node i at time slot n is represented by di[n], and di[n] is calculated as
(2)
where H is the height of the UAV; q[n] denotes the projection coordination of the UAV’s position on the ground; wi is the coordinate of the node.
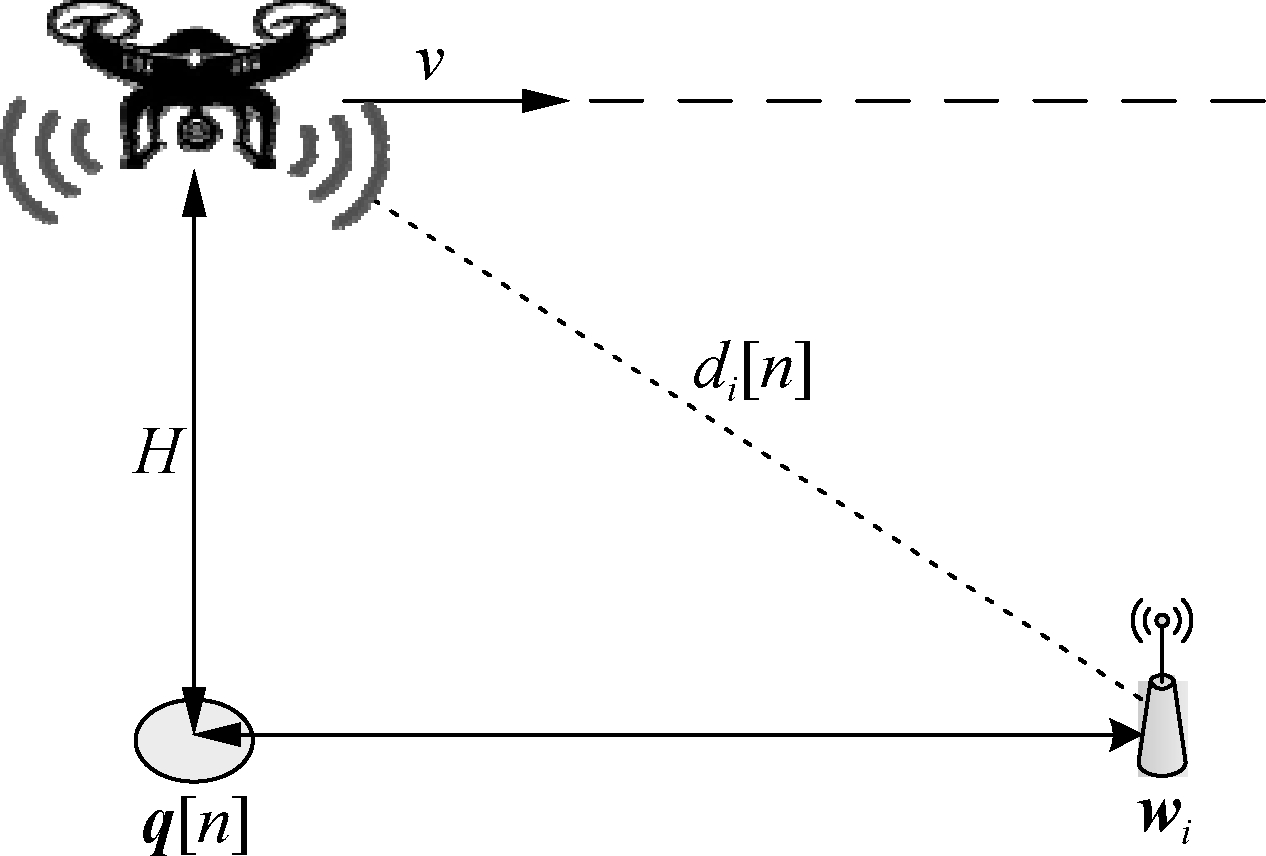
Fig.2 Communication between the UAV and node
Then, the average channel power gain βi[n] is modeled as
βi[n]=β0di[n]-α
(3)
where β0 is the average channel power gain when the reference distance d0=1 m, and α represents the path loss exponent, which is generally greater than or equal to 2 for the Rician fading channel.
The small scale fading ![]() can be written as
can be written as
(4)
where K>0 is the Rician factor used to specify the power ratio between the LoS and Rayleigh fading components. ![]()
1.3 Data transmission model
Assuming that node i uploads data to the UAV with constant power P, the received power of the UAV in time slot n is expressed as
Pi[n]=P|hi[n]|2
(5)
Then, the signal-to-noise ratio (SNR) γi[n] of node i in time slot n is calculated as
(6)
where σ2 is the noise power. The instantaneous achievable rate ((bit·s-1)/Hz) of node i in time slot n can be expressed as
(7)
where ![]() ∀n, i
∀n, i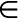 S, and the allocation of radio resources should meet the following requirements:
S, and the allocation of radio resources should meet the following requirements:
(8)
1.4 Value of information model
The VoI is a metric originally proposed in game theory which represents the price that the best player is willing to pay for a piece of information. This metric is used in WSN’s latest research and it is a way to assign higher values to recently detected data. The VoI of the sensing data is the highest at the moment of the event, and then decreases with time. Different attenuation models can be used to design VoI functions to meet the requirements of different application scenarios, such as the ramp function, stair function, and exponential function. Ideally, these functions should be constructed based on actual statistical data. In order to maintain generality, this paper uses a decaying exponential function to simulate the VoI function Vi(t).
Vi(t)=Ae-B(t-τ0)
(9)
where A>0 represents the initial VoI of the node; B is the decay speed of VoI; τ0 is the time of occurrence of abnormal events. The higher the value of A, the higher the initial VoI of the node, while the greater the value of B, the faster the attenuation of VoI.
Fig.3 shows the VoI function curves with different A and B, which can be viewed as three different data emergency levels in WSNs. It can be seen from Fig.3 that events with higher A and B values (A2=10, B2=0.3) are more urgent and will expire in about 15 min, while events with lower A and B values (A1=5, B1=0.1) will expire in about 30 min. The data collected by CNs is routine data within the preset normal range with a low degree of emergency, while the data collected by KNs is abnormal data with a high degree of emergency. Therefore, the VoI of KNs can be represented by the VoI attenuation curve, while the VoI unattenuation curve (A3=1, B3=0) can be used to represent the VoI of CNs.
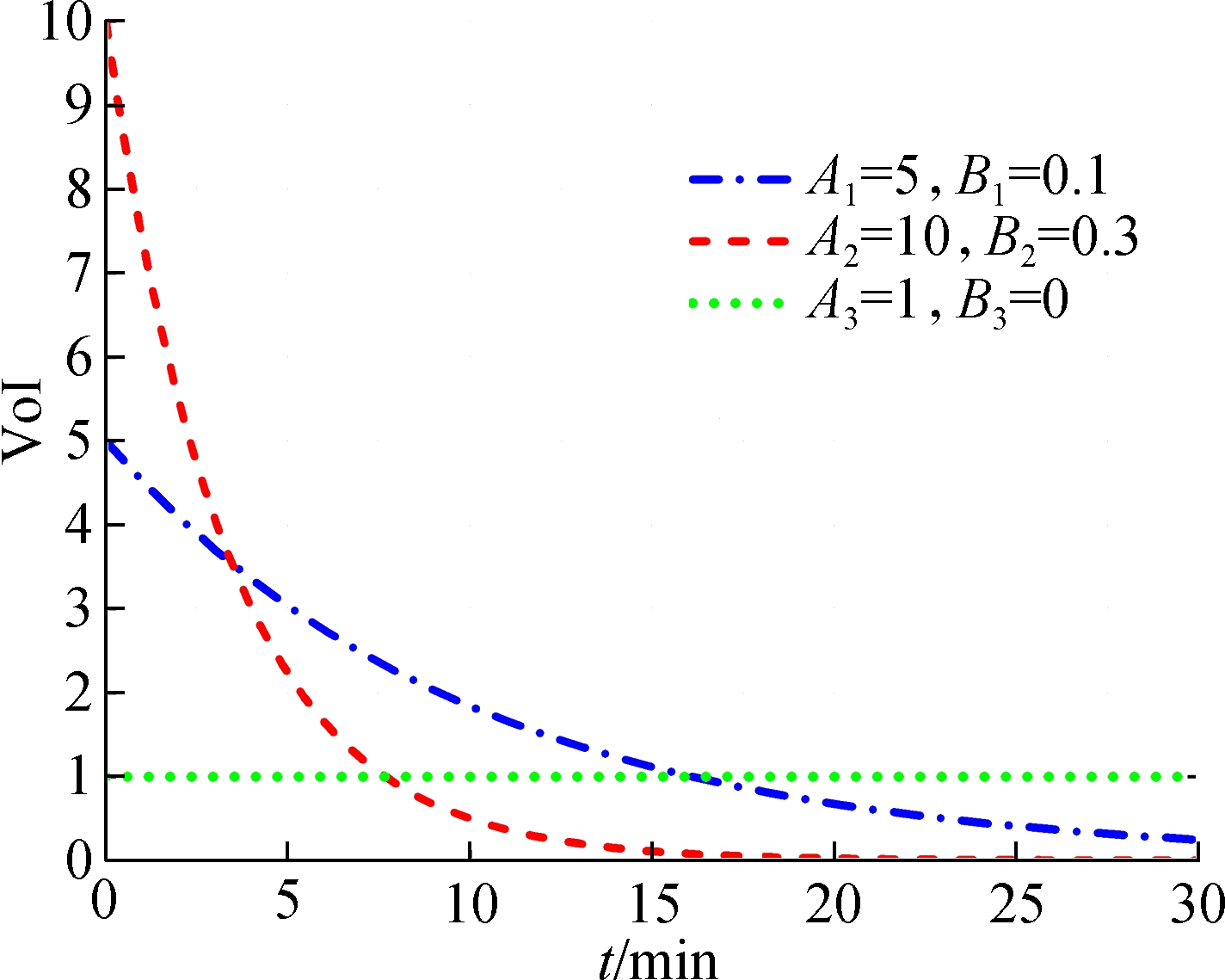
Fig.3 VoI functions with different parameters
2 Problem Formulation
In order to express the optimization problem with a mathematical formula, we define sets, parameters and variables for formulating our problem.S={1,2,…,M} is the collection of SNs, where M is the number of total SNs. Q={q[n]} is the trajectory sequence of the UAV, where q[n] is the UAV’s location at time slot n, 1≤n≤N. ![]() is the set of radio resource proportions allocated to nodes. Smin is the minimum amount of data collected by the node. Vi means that if node i uploads at least Smin data before the data deadline, and the UAV can obtain the corresponding VoI of Vi. xi is a binary variable taking the value 1 if the UAV can successfully collect the minimum amount of data Smin from node i; 0 otherwise. X={xi,∀i} is the set of the node collection strategy. rmin is the frequency band utilization required to transmit the minimum data amount Smin, where rmin=Smin/(Bδt) in (bit·s-1)/Hz; B represents the channel bandwidth in Hz; and δt is the length of the time slot. Dmax is the distance a UAV flies at maximum speed vmax in a time slot δt, where Dmax=vmaxδt in meter.
is the set of radio resource proportions allocated to nodes. Smin is the minimum amount of data collected by the node. Vi means that if node i uploads at least Smin data before the data deadline, and the UAV can obtain the corresponding VoI of Vi. xi is a binary variable taking the value 1 if the UAV can successfully collect the minimum amount of data Smin from node i; 0 otherwise. X={xi,∀i} is the set of the node collection strategy. rmin is the frequency band utilization required to transmit the minimum data amount Smin, where rmin=Smin/(Bδt) in (bit·s-1)/Hz; B represents the channel bandwidth in Hz; and δt is the length of the time slot. Dmax is the distance a UAV flies at maximum speed vmax in a time slot δt, where Dmax=vmaxδt in meter.
The objective of this paper is to jointly optimize the UAV’s trajectory and radio resource allocation so as to maximize the VoI collected by the UAV within flight time T. Then, the proposed optimization problem P1 is formulated as
(10)
(10a)
xi∈{0,1} i∈S
(10b)
(10c)
q[n+1]-q[n]≤Dmax ∀n≤N-1
(10d)
q[1]=q0, q[N]=qF
(10e)
Constraint (10a) ensures that the UAV collects the data of node i within T at least Smin. Constraint (10b) specifies the value range of the binary variable xi. Constraint (10c) prevents the UAV from wasting resources on SNs that cannot upload data within the deadline. If the node is not selected to upload data (xi=0), then ![]() and the UAV does not allocate the spectrum to node i. The flight distance constraint of the UAV in a time slot δt is expressed by constraint (10d). Constraint (10e) specifies that the initial and final flight positions of the UAV are at q0 and qF, respectively. In practical applications, data collectors can determine the starting and ending position of the UAV based on many factors, such as the location of its management property, regulations or charging stations.
and the UAV does not allocate the spectrum to node i. The flight distance constraint of the UAV in a time slot δt is expressed by constraint (10d). Constraint (10e) specifies that the initial and final flight positions of the UAV are at q0 and qF, respectively. In practical applications, data collectors can determine the starting and ending position of the UAV based on many factors, such as the location of its management property, regulations or charging stations.
According to the observation, problem P1 is a mixed integer non-linear program (MINLP), which is NP-hard due to the existence of the binary variable xi and the non-convex constraint (10a). In the next section, the MVF-SCA algorithm is proposed to obtain a sub-optimal solution of problem P1, which is a position sequence that guides the UAV to maximize the collected VoI in the flight period.
3 MVF-SCA Algorithm
As problem P1 proposed in Section 2 is a mixed integer non-convex problem, it is generally difficult to obtain the optimal solution. Therefore, in this paper, our goal is to obtain an efficient sub-optimal solution of P1. First, according to the different node types, problem P1 is divided into two sub-problems. Then, the MVF-SCA algorithm will be proposed to plan the trajectory of the UAV.
The flow chart of the MVF-SCA trajectory planning algorithm is shown in Fig.4. If there is time-sensitive abnormal data in the monitoring area, namely KNs, then the UAV uses the MVF algorithm to fly to the KNs as a priority to collect node data. Otherwise, the UAV uses efficient SCA algorithms for routine data collection. If an area of the UAV is abnormal in the routine data collection process, the node sends a data collection request to the UAV, and the UAV responds to the request, changes the flight path and uses the MVF algorithm to collect abnormal data.
The MVF-SCA algorithm is not only suitable for time-insensitive daily data collection, but also can timely collect time-sensitive abnormal data in the region. Next, the MVF algorithm for collecting the KNs and the SCA algorithm for collecting CNs are described.
Fig.4 The flow chart of the MVF-SCA algorithm
3.1 MVF algorithm
The data stored in KNs is an abnormal value that exceeds the preset value range. Due to the limited cache area of the node, if the abnormal data is not uploaded to the UAV in time before the cache area overflows, there may be a problem of data loss or being overwritten by other data. Therefore, it needs to be collected in time. Due to the timeliness of KNs, in order to maximize the VoI collected from KNs, the UAV should fly to the location of KNs at the maximum speed and collect data from the KNs first. In addition, in order to speed up the collection rate, KNs should occupy the entire spectrum when uploading data, that is, ![]() ∀i
∀i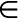 Sk. Therefore, the sub-problem P2 can be specifically expressed as
Sk. Therefore, the sub-problem P2 can be specifically expressed as
(11)
(11a)
xi∈{0,1} i∈Sk
(11b)
q[n+1]-q[n]≤Dmax ∀n≤N-1
(11c)
q[1]=q0, q[N]=qF
(11d)
For the trajectory planning of the UAV collecting KNs, we propose the MVF algorithm, which allows the UAV to plan the trajectory according to the VoI of KNs, giving priority to the node with the largest VoI. Among all the KNs that need to be collected, the UAV will first collect the node with the largest VoI in the uncollected node. If the UAV can arrive at the node and collect enough data in the rest time slot, then the UAV will fly to the node to collect data; otherwise, the UAV will select another node from the unmarked nodes and carry out a similar process. The pseudo-code of the MVF algorithm is shown as follows.
Algorithm 1 The MVF algorithm for collecting data of KNs
Input: q0, vmax, Smin, T, δt; the location of all KNs; the initial VoI of all KNs.
Sort all KNs based on their initial VoI.
Calculate the distance from the KN to the current location of the UAV dU2N
Set the number of time slots N←T/δt
Set the updated time N′←N
for i Sk do
Sk do
Select the node with the highest VoI among unmarked nodes
Find the minimum time to collect the KN and update the flying time N′
Update the location of the UAV
else
Mark the KN and update the flying time N′
end if
end for
Output: The trajectory for the UAV collecting the data of KNs.
3.2 SCA algorithm
Next, the collection of CNs will be considered. Since the VoI of CNs is a constant, maximizing the VoI of CNs is to maximize the number of collections of CNs within T. Therefore, the sub-problem P3 can be specifically expressed as
(12)
(12a)
xi∈{0,1} i∈Sc
(12b)
(12c)
q[n+1]-q[n]≤Dmax n≤N-1 (12d)
q[1]=q0, q[N]=qF
(12e)
The sub-problem P3 is still an integer non-convex problem, which is difficult to solve. First, we relax the binary variable xi to let it to be continuous from 0 to 1, but the relaxed version of P3 is still non-convex. Secondly, we introduce the slack variable B= ![]()
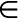 Sc} and
Sc} and ![]()
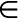 Sc}. Let Qr={qr[n],∀n} represent the given trajectory in the r-th iteration. Then, similar to Ref.[23], log2(1+γi[n]) can be expanded by the first-order Taylor. By using the convex approximation of q[n]-wi2 to approximate the function log2(1+γi[n]), the following inequality can be obtained in the r-th iteration.
Sc}. Let Qr={qr[n],∀n} represent the given trajectory in the r-th iteration. Then, similar to Ref.[23], log2(1+γi[n]) can be expanded by the first-order Taylor. By using the convex approximation of q[n]-wi2 to approximate the function log2(1+γi[n]), the following inequality can be obtained in the r-th iteration.
![]() ·
·
(q[n]-wi2-qr[n]-wi2)
(13)
where
(14)
(15)
(16)
Then, problem P3 can be rephrased as problem P4 as follows:
(17)
(17a)
(17b)
(17c)
0≤xi≤1 i∈Sc
(17d)
(17e)
(17f)
q[n+1]-q[n]≤Dmax ∀n≤N-1
(17g)
q[1]=q0, q[N]=qF
(17h)
Consider constraint (17b), the non-convexity factor 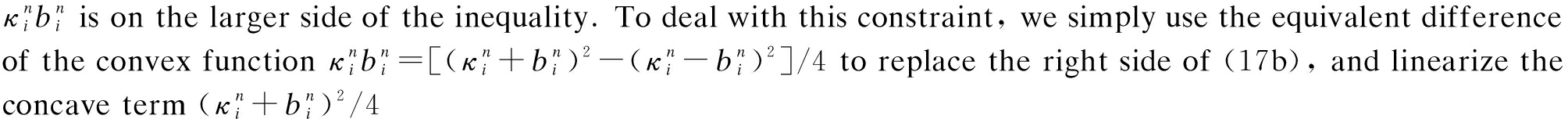 of the constraint at the r-th iteration. Therefore, constraint (17b) is approximate as
of the constraint at the r-th iteration. Therefore, constraint (17b) is approximate as
![]()
![]()
(18)
Using the above approximation, problem P3 can be converted into a convex problem. We optimize the problem by iteratively updating parameters ![]() Algorithm 2 summarizes the SCA algorithm.
Algorithm 2 summarizes the SCA algorithm.
Algorithm 2 SCA algorithm for collecting data of CNs
Input: Smin ; the error tolerance ε.
Set initial trajectory Qr={qr[n],∀n}, the resource allocation ![]() ∀n,i,r=1
∀n,i,r=1
While (Obj(r -1)-Obj(r))>ε do
Solve the convex problem P4 by interior-point solvers to obtain the trajectory qr+1[n], ∀n,
![]()
 Sc
Sc
Update the trajectory of the UAV
Update the resource allocation
r←r+1
End while
Output: The trajectory for the UAV collecting the data of CNs.
4 Performance Evaluation
4.1 Simulation environment
We assume that SNs are randomly distributed in the target region and the scale of the target region is 500 m×500 m. The CVX toolbox and the numerical convex solver SDPT3 are used to solve our optimization problem. We set the initial and final positions of the UAV to the center of the target area ([250, 250]). The algorithm is run in Windows 10 with a CPU i7-6700. Details of the parameters in the simulation are listed in Tab.1.
Tab.1 Parameters for simulations

ParameterValueNetwork size/(m×m)500×500Node transmission power P/W0.2UAV altitude H/m50Channel power gain β0/dB-60Noise power σ2/dBm-110Maximum UAV speed vmax/(m·s-1)30Error tolerance ε10-3Slot length δt/s0.01Path loss exponent α2.5
4.2 Performance evaluation
4.2.1 Complexity analysis
In this part, the complexity of the proposed MVF-SCA algorithm will be evaluated. In order to collect KNs data faster, we use the MVF algorithm. The next node to be collected by the UAV preferentially selects the node with the largest VoI, and allocates all radio resources to this node when collecting. This is essentially a greedy algorithm with a time complexity of O(n). In order to collect more CNs data in the remaining flight time after collecting KNs, we use the SCA algorithm. For the SCA algorithm, the overall complexity of problem P4 depends on the solver used to solve P4. In particular, problem P4 is a convex problem, so several interior-point solvers can be used to solve it. Therefore, we use the number of Newton steps expressed in Cs as an indicator of its complexity. In practice, the Newton step depends on the size of the problem and the number of recursive iterations before converging from a given initial point. Based on Ref.[24], the worst case Cs that reached the local solution in problem P4 can be expressed as follows: Cs is proportional to the square root of the problem size, where the problem size is the total number of variables for the optimization problem. Solving problem P4 requires constantly iterating and updating variables. In the worst case, all SNs are CNs, M is the number of CNs and N is the number of time slots, then there are 3MN+2N+M variables in problem P4. Therefore, in each iteration, the complexity of solving problem P4 is approximately ![]() where R is a finite number of iterations, depending on the value of the tolerance ε.
where R is a finite number of iterations, depending on the value of the tolerance ε.
4.2.2 Trajectory planning
The trajectory of the UAV planned by the MVF-SCA algorithm is shown in Fig.5. There are 4 KNs and 16 CNs in the network. The UAV starts from the central point of the monitoring area [250,250] and returns after a collection period T. In order to maximize the total VoI collected, the UAV first collects the KNs represented by the red asterisk mark. The UAV adjusts the trajectory to collect the most urgent KNs. When collecting CNs represented by the green dots marks, the UAV can allocate radio resources to collect multiple nodes in the same time slot. The black cross mark represents the node that has not been collected by the UAV or that has not uploaded the minimum amount of data in the collection period T.
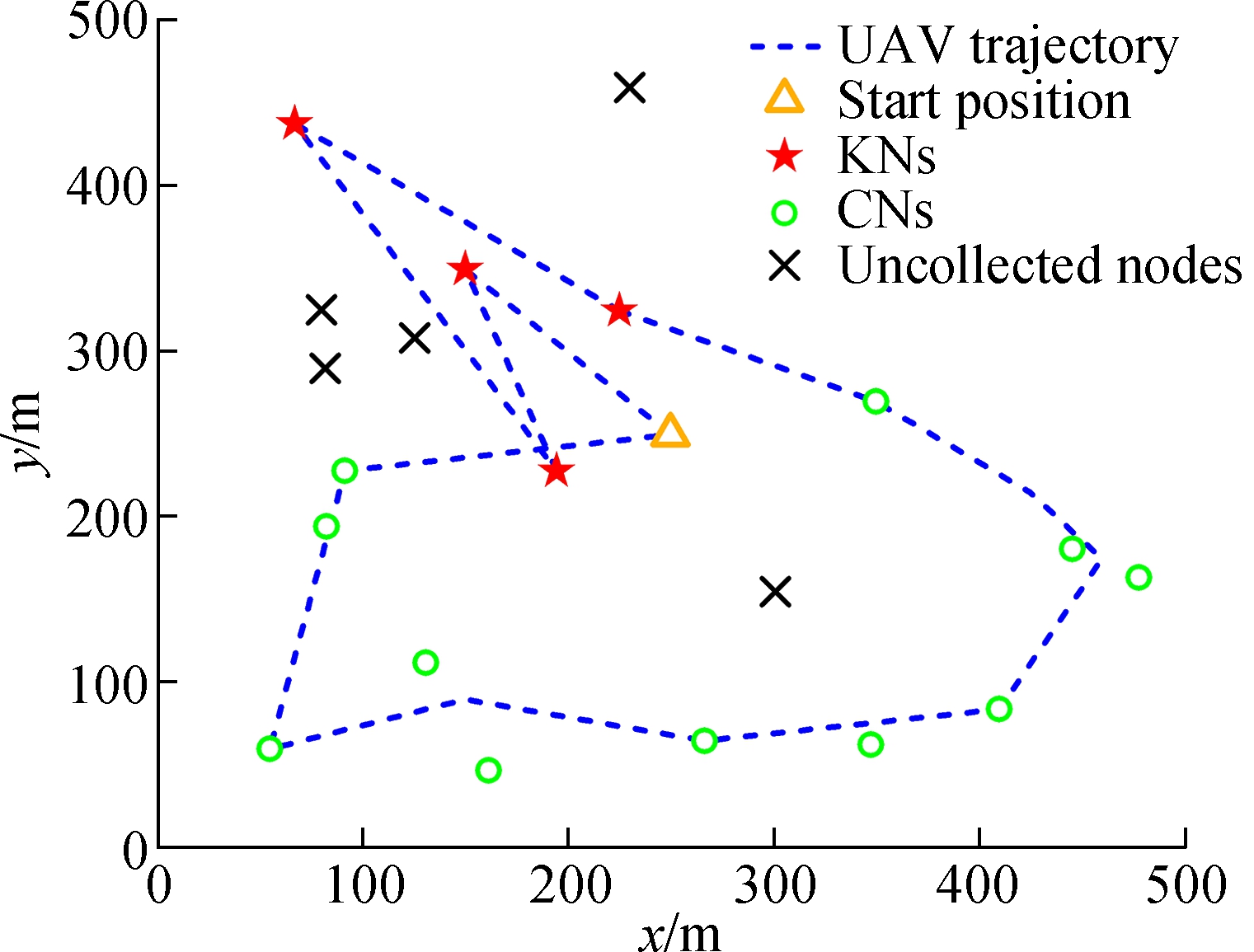
Fig.5 UAV trajectory planning by the MVF-SCA algorithm
4.2.3 Data collection
The performance of the proposed MVF-SCA algorithm is compared with that of the classical TSP algorithm[8] and the GPP algorithm[20]. Fig.6 shows the change of VoI collected by the UAV in collection period T as the number of network nodes increases. In the simulation, we maintained that KNs accounted for 20% of the total SNs. The increase in the number of nodes leads to the increase in the density of network nodes, which will help the UAV to collect more nodes in T and obtain a greater VoI. The MVF-SCA algorithm proposed has an improvement of about 15% compared with the TSP algorithm, and an improvement of about 30% compared with the GPP algorithm.

Fig.6 The comparison of collected VoI by different algorithms
Finally, the effect of the minimum data amount Smin on the performance of different algorithms is studied. As shown in Fig.7, when Smin=0 Mbit, there is no requirement for the amount of data uploaded by the node. As long as the UAV collects data greater than 0 bit at the node to obtain the VoI of the node, the VoI collected by the UAV is the largest. As Smin increases, the total VoI collected during the flight time T of the proposed MVF-SCA algorithm, GPP algorithm and TSP algorithm has decreased by varying degrees. As Smin becomes larger, the time for the UAV to collect a node becomes longer, so that the number of nodes collected within the limited flight time T decreases, and the VoI of the collected data decreases accordingly. The proposed MVF-SCA algorithm is always better than the GPP algorithm and TSP algorithm for the same Smin collection performance, because the MVF-SCA algorithm jointly optimizes the UAV trajectory and radio resource allocation for different attributes of the nodes.

Fig.7 The collected VoI vs. the minimum data amount Smin
5 Conclusions
1) The data collection problem in UAV-aided WSNs is investigated in this paper. The Rician model and the concept of VoI are considered.
2) The problem is formulated as a mixed integer non-linear program problem which is non-convex. The problem is then transferred to two sub-problems according to the node type. A UAV trajectory planning algorithm is proposed to solve the two problems.
3) Simulation results show that the VoI collected by the proposed algorithm can improve by 15% to 30% compared with the classical TSP algorithm and the GPP algorithm.
[1]Ebrahimi D, Sharafeddine S, Ho P H, et al. Data collection in wireless sensor networks using UAV and compressive data gathering[C]//2018 IEEE Global Communications Conference (GLOBECOM). Abu Dhabi, UAE, 2018: 1-7. DOI:10.1109/glocom.2018.8647924.
[2]Ebrahimi D, Sharafeddine S, Ho P H, et al. UAV-aided projection-based compressive data gathering in wireless sensor networks[J]. IEEE Internet of Things Journal, 2019, 6(2): 1893-1905. DOI:10.1109/jiot.2018.2878834.
[3]Ghorbel M B, Rodriguez-Duarte D, Ghazzai H, et al. Joint position and travel path optimization for energy efficient wireless data gathering using unmanned aerial vehicles[J]. IEEE Transactions on Vehicular Technology, 2019, 68(3): 2165-2175. DOI:10.1109/tvt.2019.2893374.
[4]Cao H R, Liu Y X, Yue X J, et al. Cloud-assisted UAV data collection for multiple emerging events in distributed WSNs[J]. Sensors, 2017, 17(8): 1818. DOI:10.3390/s17081818.
[5]Qin Y, Boyle D, Yeatman E. A novel protocol for data links between wireless sensors and UAV based sink nodes[C]//2018 IEEE 4th World Forum on Internet of Things (WF-IoT). Singapore, 2018: 371-376. DOI:10.1109/wf-iot.2018.8355154.
[6]Zhan C, Zeng Y. Completion time minimization for multi-UAV-enabled data collection[J]. IEEE Transactions on Wireless Communications, 2019, 18(10): 4859-4872. DOI:10.1109/twc.2019.2930190.
[7]Zeng Y, Xu J, Zhang R. Energy minimization for wireless communication with rotary-wing UAV[J].IEEE Transactions on Wireless Communications, 2019, 18(4): 2329-2345. DOI:10.1109/twc.2019.2902559.
[8]Cheng C F, Yu C F. Datagathering in wireless sensor networks: A combine-TSP-reduce approach[J]. IEEE Transactions on Vehicular Technology, 2016, 65(4): 2309-2324. DOI:10.1109/tvt.2015.2502625.
[9]Kaul S, Yates R, Gruteser M. Real-time status: How often should one update?[C]//2012 Proceedings—IEEE INFOCOM. Orlando, FL, USA, 2012: 2731-2735. DOI:10.1109/infcom.2012.6195689.
[10]Liu J, Wang X J, Bai B, et al. Age-optimal trajectory planning for UAV-assisted data collection[C]//2018 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS). Honolulu, HI, USA, 2018: 553-558. DOI:10.1109/infcomw.2018.8406973.
[11]Abd-Elmagid M A, Ferdowsi A, Dhillon H S, et al. Deep reinforcement learning for minimizing age-of-information in UAV-assisted networks[C]//2019 IEEE Global Communications Conference (GLOBECOM). Waikoloa, HI, USA, 2019: 1-6. DOI:10.1109/globecom38437.2019.9013924.
[12]Abd-Elmagid M A, Pappas N, Dhillon H S. On the role of age of information in the Internet of Things[J]. IEEE Communications Magazine, 2019, 57(12): 72-77. DOI:10.1109/mcom.001.1900041.
[13]Li W Y, Wang L, Fei A G. Minimizing packet expiration loss with path planning in UAV-assisted data sensing[J]. IEEE Wireless Communications Letters, 2019, 8(6): 1520-1523. DOI:10.1109/lwc.2019.2925796.
[14]Samir M, Sharafeddine S, Assi C M, et al. UAV trajectory planning for data collection from time-constrained IoT devices[J]. IEEE Transactions on Wireless Communications, 2020, 19(1): 34-46. DOI:10.1109/twc.2019.2940447.
[15]Hu H M, Xiong K, Qu G, et al. AoI-minimal trajectory planning and data collection in UAV-assisted wireless powered IoT networks[J]. IEEE Internet of Things Journal, 2020. DOI:10.1109/jiot.2020.3012835.
[16]Li J X, Zhao H T, Wang H J, et al. Joint optimization on trajectory, altitude, velocity, and link scheduling for minimum mission time in UAV-aided data collection[J]. IEEE Internet of Things Journal, 2020, 7(2): 1464-1475. DOI:10.1109/jiot.2019.2955732.
[17]Liu J, Tong P, Wang X J, et al. UAV-aided data collection for information freshness in wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2020. DOI:10.1109/twc.2020.3041750.
[18]Turgut D, Boloni L. A pragmatic value-of-information approach for intruder tracking sensor networks[C]//2012 IEEE International Conference on Communications (ICC). Ottawa, ON, Canada, 2012: 4931-4936. DOI:10.1109/icc.2012.6364380.
[19]Bidoki N H, Baghdadabad M B, Sukthankar G, et al. Joint value of information and energy aware sleep scheduling in wireless sensor networks: a linear programming approach[C]//2018 IEEE International Conference on Communications (ICC). Kansas City, MO,USA, 2018: 1-6. DOI:10.1109/icc.2018.8422392.
[20]Khan F, Butt S, Khan S, et al. Value ofinformation based data retrieval in UWSNs[J]. Sensors, 2018, 18(10): 3414-3441. DOI:10.3390/s18103414.
[21]Bölöni L, Turgut D. Value of information based scheduling of cloud computing resources[J]. Future Generation Computer Systems, 2017, 71: 212-220. DOI:10.1016/j.future.2016.10.024.
[22]Xu J, Solmaz G, Rahmatizadeh R, et al. Providing distribution estimation for animal tracking with unmanned aerial vehicles[C]//2018 IEEE Global Communications Conference (GLOBECOM). Abu Dhabi, UAE, 2018: 1-6. DOI:10.1109/glocom.2018.8647784.
[23]Zhan C, Zeng Y, Zhang R. Energy-efficient data collection in UAV enabled wireless sensor network[J]. IEEE Wireless Communications Letters, 2018, 7(3): 328-331. DOI:10.1109/lwc.2017.2776922.
[24]Arfaoui M A, Ghrayeb A, Assi C M. Secrecy performance of multi-user MISO VLC broadcast channels with confidential messages[J]. IEEE Transactions on Wireless Communications, 2018, 17(11): 7789-7800. DOI:10.1109/twc.2018.2871055.