With the rapid development of the IoTs, energy harvesting has been regarded as a favorable supplement to drive the numerous sensors in the emerging IoT [1]. Due to several key advantages such as being pollution free, having a long lifetime, and energy self-sustainability, the energy harvesting systems (EHSs) are competitive in a wide spectrum of applications[2].
The EHS generally consists of an antenna either separating or shared with data communications, an energy harvesting device (EHD) converting the RF signal from energy sources (ESs) to power, and a battery that stores the harvested energy[3]. According to different ESs, the RF-based energy harvesting system can be classified into two categories: EHS with ambient ESs and EHS with a dedicated ES[3].
Recent research of the EHS mainly focuses on how to effectively utilize energy from ambient or dedicated ESs[4-6]. In Ref.[4], an energy neutrality theorem for EHN was proposed and it was proved that perpetual operation can be achieved by maintaining the energy neutrality of EHN. Then, an adaptive duty cycle (ADC) control method was further proposed in order to assign the duty cycle online to achieve the perpetual operation of EHN. In Ref.[5], a reinforcement learning-based energy management scheme was proposed to achieve the sustainable operation of EHN. In Ref.[6], a fuzzy Q-leaning-based power management scheme was proposed for EHN under energy neutrality criteria. To achieve the sustainable operation of EHN, the duty cycle is decided from the fuzzy inference system for the EHN. In fact, all the research managed to adjust power in the EHS with ambient ESs to maximize the utilization of the harvested energy. However, due to the lack of the contact between the ESs and EHDs, the energy transmission period in the EHS with ambient ESs are more uncontrollable and unstable. However, in the EHS with a dedicated ES, the progress of energy transmission can be scheduled effectively due to the dedicated ES which is installed to power the EHDs. Hence, some research began to focus on the EHS with a dedicated ES. In Ref.[3], a two-step dual tunnel energy requesting (DTER) strategy was proposed to minimize the energy consumption at both the EHD and the ES on timely data transmission. However, these existing strategies did not consider the exhaustion or overflow of the battery’s energy during the transmission. Hence, this paper will concentrate on the online energy management strategies to improve system stability in terms of the battery’s deficit charges and overcharges.
In this paper, a Q-learning-based energy transmission scheduling algorithm is proposed to improve the EHS with a dedicated ES. Based on the basic theories of the Q-learning algorithm[7], an energy transmission scheduling algorithm is used to decrease energy consumption through adjusting transmitted energy. By using the energy scheduling scheme in this paper, the EHS can adjust the transmitted energy of ES timely and effectively to change the energy consumption. First, the system model of the EHS is presented in detail. Then, a multi-objective optimization problem is formulated to improve system performance in terms of the battery’s deficit charges and overcharges. Next, a Q-learning-based scheduling algorithm is proposed for the optimization problem. Finally, the simulation results and conclusions are presented, respectively.
1 System Model
Consider an RF-based EHS, where the EHD requests and harvests energy from the ES, as shown in Fig.1. The harvested energy stored in the EHD’s battery is consumed to send out data. Moreover, the system time is assumed to be equally divided into N time slots and Tn(1≤n≤N), the duration of time slot n is constant and selected to be less than the channel coherence time. Therefore, the channel states remain invariant over each time slot but vary across successive time slots. Assume that the fading of the wireless channel follows a correlated Rayleigh fading channel model[8]. Using the ellipsoidal approximation, the CSI can be deterministically modeled as[9]
gn=hn10-vn/10
(1)
where vn is the uncertain parameter and θ denotes the uncertainty bound which is a non-negative constant; gn and hn denote the actual and estimated channel gains at time slot n, respectively.
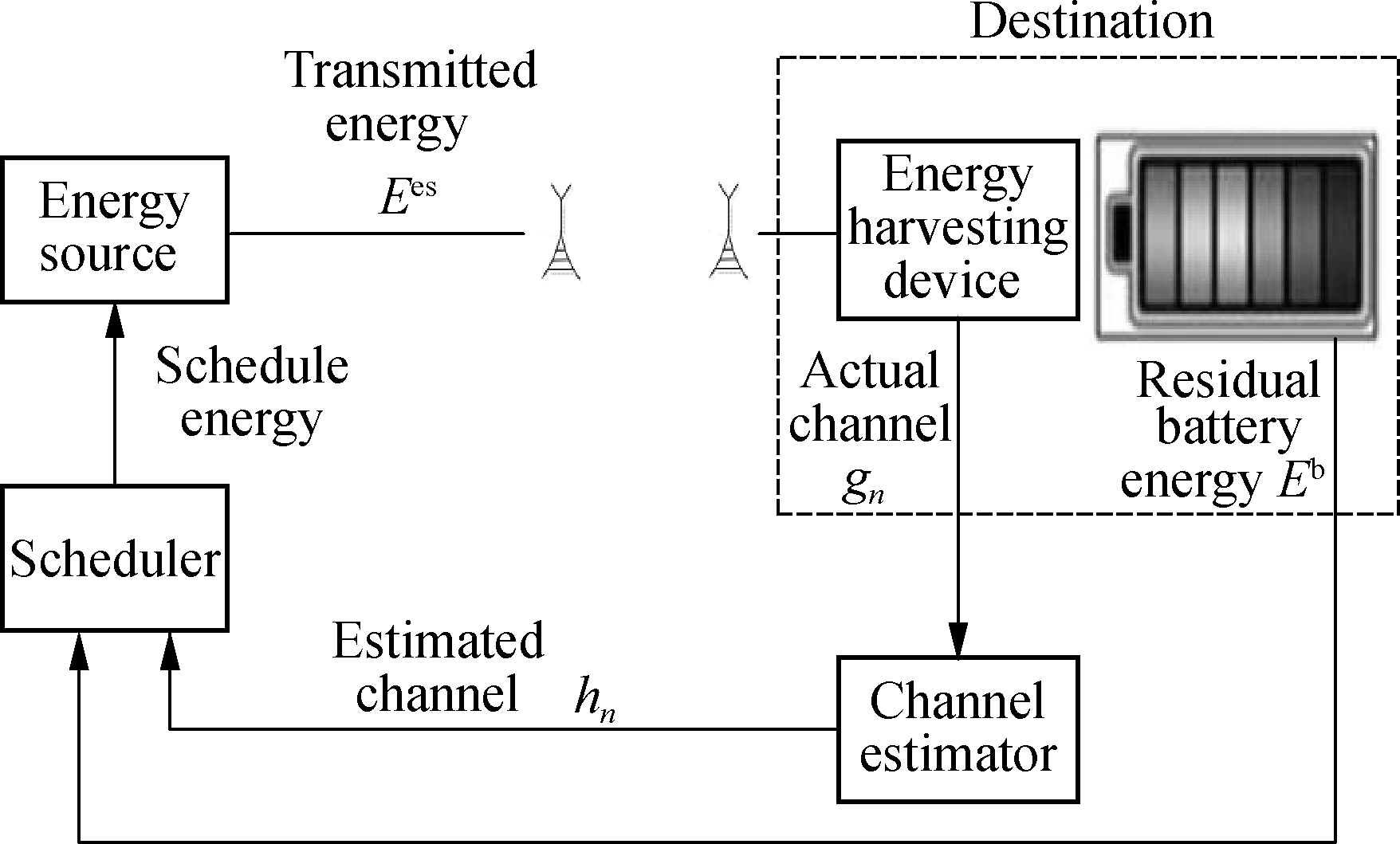
Fig.1 The energy-harvesting system
To charge the EHD, we assume that the ES transmits energy at a constant power pes. First, before the EHD receives energy at time slot n, the voltage and energy stored in the battery are denoted as vn and 
Then, after energy harvesting, the voltage of the battery will increase by ΔVn. Mathematically, the charging function can be deduced as[10]
Vn=Vm(1-e-t′/(RC))
(2)
(3)
(4)
(5)
where t′ is the time consumed during charging the voltage of the battery from 0 to Vn with Vm volts of voltage; Vm is the maximum voltage that the battery can approach. R and C are the resistance and capacitance of the charging circuit in EHD, respectively. Eq.(2) represents that the battery needs to spend time t′ on voltage changing from 0 to Vn and Eq.(3) represents that the voltage changes from Vn to Vn+ΔVn after energy harvest at time slot n. Eq.(4) and Eq.(5) reflect the relationship between the battery’s voltage and stored energy. Using Eq.(2) to Eq.(5), the charge duration can be derived as
(6)
where 
Considering that the bad channel states can significantly reduce the efficiency of the battery charge, it is assumed that if the channel state at time slot n is bad, the ES will not send energy to the destination node. Hence, Eq.(6) can be further improved as
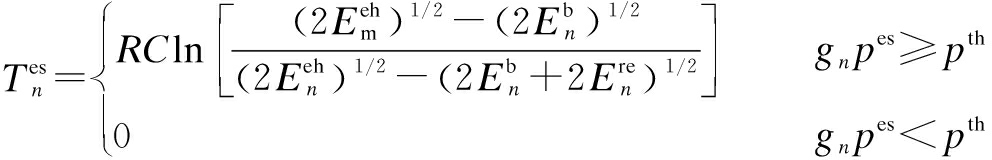
(7)
where pth denotes the charge power of a battery.
At time slot n, it is assumed that the EHD sends data at transmitted power 
Then, the residual energy at time slot n+1 can be determined as
(8)
where T is the value of the working period of EHD Tn; 
is the real received energy of the battery, and its relationship with energy transmitted by ES is
(9)
where η represents the conversion efficiency of a battery.
2 Problem Formulation
To efficiently make use of scarce transmission resources, multiple objectives should be considered simultaneously. The primary objective is to save energy consumption. In a practical system, most of the energy is consumed for wireless transmission. Therefore, the primary objective becomes how to save transmission energy. According to Eq.(6), the consumed energy is mainly affected by 
Hence, adjusting it properly can significantly reduce the consumed energy. Obviously, the primary objective can be described mathematically by minimizing Eq.(7). After each charge, the EHD can stop working due to the low residual energy of the battery. To prevent this situation, the residual energy of the battery at each time slot should be no less than the minimum energy that ensures normal working. Therefore, the condition of the battery’s energy exhaustion at time slot n can be described as
(10)
where υ represents the minimum capacity percentage of the battery that can keep EHD normally. Meanwhile, due to the limitation of the storage size, the overflow of the battery’s energy will occur when the received energy is too large. Therefore, how to avoid overcharges of the battery should be taken into account as well. The condition of the battery’s overcharge at time slot n can be described as
(11)
In most cases, it is unlikely that the three objectives can simultaneously be optimized by the same solution. Therefore, some tradeoff between the above three objectives is needed to ensure satisfactory system performance. The most well-known tradeoff method is the weighted sum method[11]. Accordingly, the multi-objective optimization problem can be converted into the following minimization problem,
(12)
where E(·) is the expectation operator; I(·) is an indicator function and is used to show the occurrence of overcharges or deficit charges; τ and μ are two small positive constants, which are used to adjust the weight of deficit charges and overcharges of the battery during the optimization.
3 Online Scheduling Algorithm
In this section, optimization problem Eq.(12) is transformed into a reinforcement learning problem. The Q-learning algorithm first creates a Q-table which records the Q-value of all the combinations of states and actions. Then, through training, the Q-value converges and the EHS can choose the best 
at every state according to the maximum or minimum value in the Q-table. The elements in Eq.(12) can be mapped into Q-learning elements as follows.
3.1 State
Channel state and residual battery energy are continuous variables, which should be converted into discrete and finite. Therefore, we divided the ranges of the continuous variable into several intervals. If different variables are located in the same interval, they are regarded the same. To distinguish these intervals, we use continuous natural numbers to label them and these numbers can be regarded as different states.
In the proposed scheduling scheme, the channel states are assumed to be discrete and finite.Without loss of generality, the range of the estimated channel gain can be divided into D states. The states can be defined as
(13)
where 0<ω1<ω2<…<ωD-1. Therefore, at time slot n, the channel state can be determined as
(14)
Similarly, the residual battery energy, which is also assumed to be discrete and finite, can be divided into E states as follows:
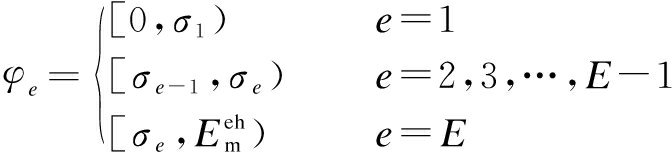
(15)
where 
At time slot n, the residual energy state can be determined as
(16)
Using the residual energy and channel states, the current composite state of the system is defined in a vector as
Sn={Hn,En}
{1,2,3,…,D}×{1,2,3,…，E}
(17)
Eq.(17) represents that every state can be mapped into the only combination of Hn and En.
3.2 Action
Obviously, the charging duration can be viewed as an action. Assume that the actions are discrete and divided into N levels. Therefore, the set of available actions can be given as
(18)
3.3 Cost
In the optimization problem Eq.(12), the objective is to save energy consumption, avoid overflow of a battery’s energy and prevent a battery from draining. Therefore, the total cost is determined as
(19)
As different circumstances have different QoS requirements, by adjusting μ and τ, the reward function is generic enough to satisfy different requirements in real systems.
3.4 Action selection
Using the states, actions and cost functions defined above, the received energy at time slot n can be selected by
(20)
where 
In matrix Q, the value of an arbitrary element is equal to the summation of its cost and the minimum discounted value of Q over all possible actions in the next state.
After selecting the proper action, the next state of battery energy En+1 can be determined by Eq.(8) and Eq.(16). Also, the next channel state Hn+1 can be obtained by Eq.(14). Hence, combined with the information of En+1 and Hn+1, the next state Sn+1 is determined as well. Accordingly, matrix Q will be updated as
(21)
where α is the time-varying learning rate parameter; γ is the discount factor. The detailed procedures of the algorithm are shown in Algorithm 1.
Algorithm 1 The Q-learning-based scheduling algorithm
Step 1 Initialization.
Step 2 If rand()<ε, randomly select an action from An. Else, select an action using Eq.(19).
Step 3 Calculate the cost using Eq.(18) and then determine next state Sn+1.
Step 4 Update Q by Eq.(20).
Step 5 n=n+1 , then go to step 2.
4 Simulation and Results
Under the same simulation environments, the proposed algorithm is compared with the constant strategy algorithm and the on-demand dynamic strategy algorithm[3] in terms of the battery’s deficit charges, the battery’s overcharges and the total consumed energy. The proposed algorithm and the reference algorithms are, respectively, deployed at most 100 times in one trial, and the trial is repeated 1 000 times. In other words, the ES transmits energy to EHD in each trial, which will not stop unless the battery’s energy is exhausted or transmission is carried out more than 100 times. After trials are completed, the data from simulations will be collected to analyze the performance of the algorithms.
4.1 Simulation settings
The constant energy transmitting power of energy source node pes=10 W. The capacitance C and resistance R of EHD are 1 kΩ and 2 nF, respectively. The maximum capacity of the battery in energy harvesting device 
is 2 nJ. To maintain the normal function of EHD, the minimum capacity percentage of a battery υ is 5%. The constant parameters in Eq.(12) are 0.4 and 0.2. Considering that at every time slot, the ES cannot obtain information about energy consumption during the EHD’s data transmission, the power used in sending the data by an energy harvesting device can be assumed to obey a uniform distribution, and the maximum power is set to be 
mW. Then, the proposed algorithm and the reference algorithms can be simulated to compare their performance.
4.2 Performance comparison
For comparison purpose, the reference algorithms are described as follows.
1) The constant strategy algorithm. In this strategy, the EHD transmits constant energy. When the residual energy of a battery is not greater than half of 
the EHD will request a replenishment and charge the battery to 95% of the maximum capacity according to Eq.(7) and Eq.(9).
2) The on-demand dynamic strategy algorithm. To avoid the overflow of arriving energy when the residual energy of a battery is too high, the ES adjusts its transmission energy adaptively based on the status of battery storage. The higher the occupancy of the storage, the greater the applied transmission energy. The occupancies of battery storage and the corresponding transmission energy are 
With this strategy, the EHD is scheduled to request adequate energy for the next data transmission.
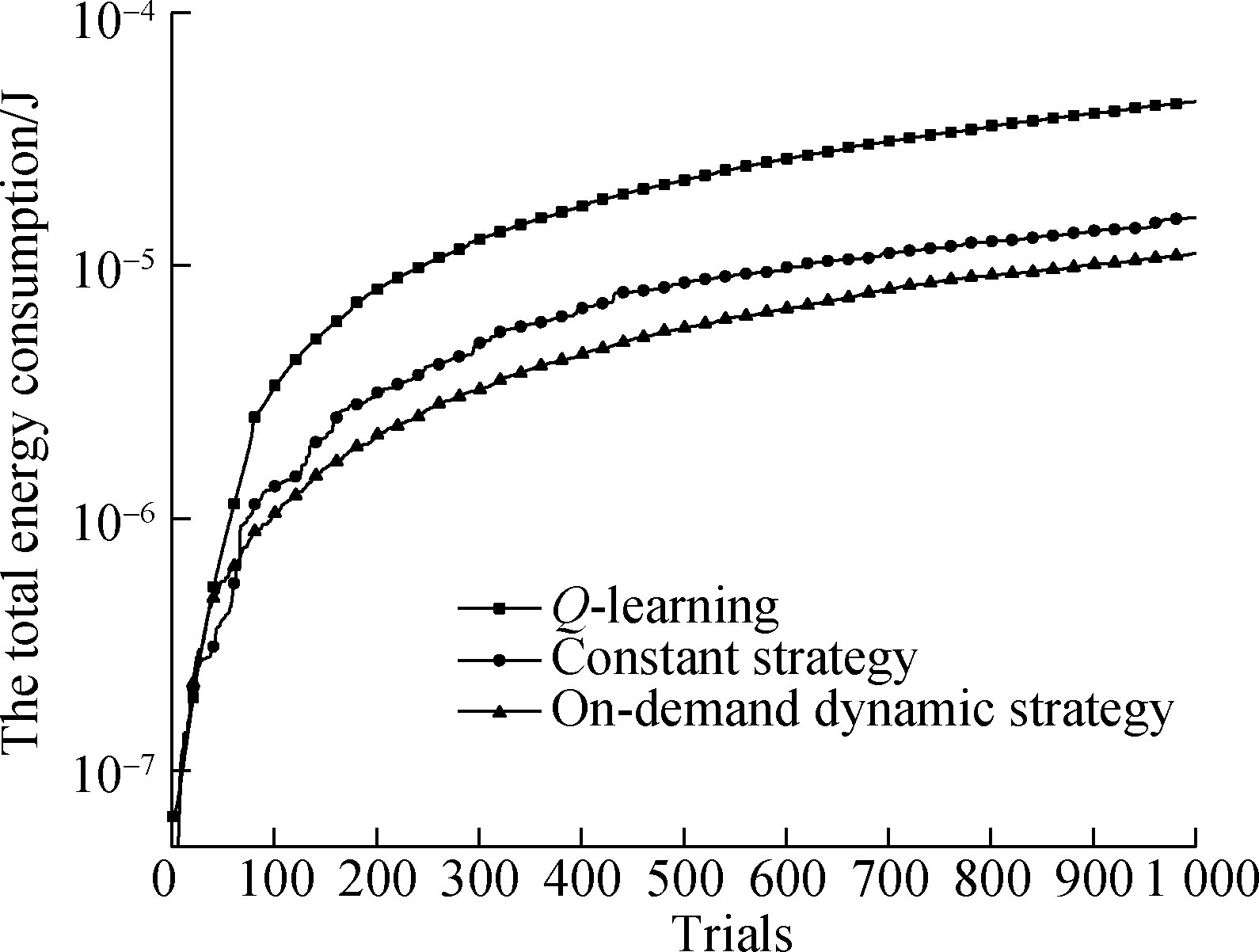
Fig.2 shows the performance comparison between the proposed Q-learning algorithm and reference algorithms. In Fig.2(a), it is noted that the Q-learning algorithm achieves an excellent performance in terms of the battery’s deficit charges. As the reference algorithms do not consider the effect of the battery’s deficit charges, the battery’s energy cannot be prevented from becoming exhausted during trials and the occurrence of the battery’s deficit charges increases with the trials’ continuation. In Fig.2(b), the preference algorithms outperform the Q-learning algorithm slightly in the overcharges. The reason is that both the constant strategy and on-demand strategy algorithms have considered the restriction of overcharges so that the overflow of the battery’s energy never occurs during trials. In Fig.2(c), both the reference algorithms consume less energy than the Q-learning algorithm, but this consequence is based on the degradation in its performance of the battery’s deficit charges. To sum up, although the Q-learning algorithm seems to consume more energy than the reference algorithms, it actually provides better system stability during the energy transmission period.
For the Q-learning algorithm, the size of action space can be an important factor that influences algorithm performance. To verify how action space size affects algorithm performance, the simulations of the Q-learning algorithm with different action space sizes are executed under the same simulation environment. The results are shown in Fig.3.
(a)
(b)
(c)
Fig.2 The performance comparison between the proposed Q-learning algorithms and the reference algorithms. (a) The battery’s deficit charges; (b) The battery’s overcharges; (c) The total consumed energy
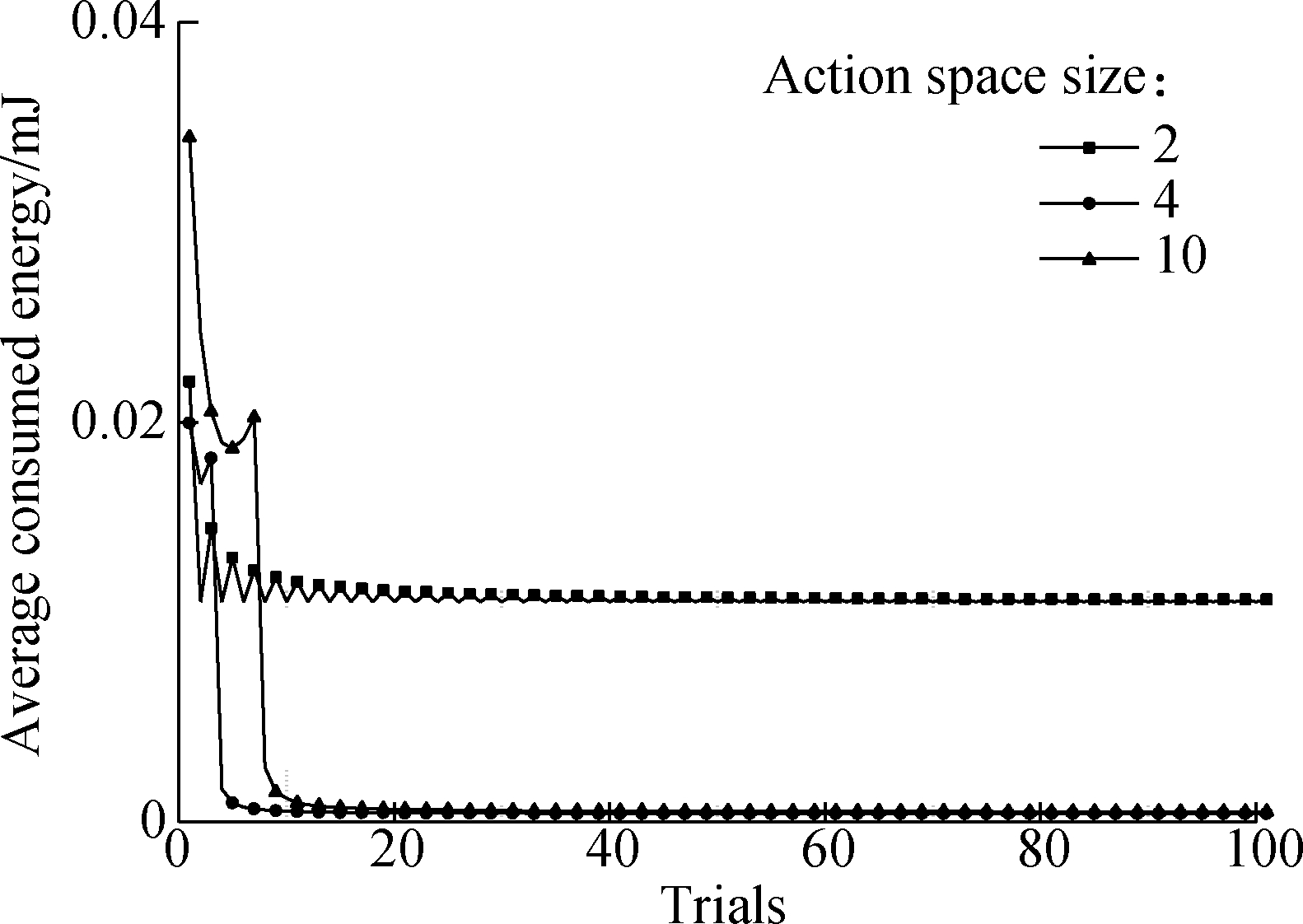
Fig.3 The averaged energy consumption of the Q-learning algorithms with different sizes of action space
Assume that the size of state space is kept at 10 during simulations. It can be seen that a large action space will result in longer convergence time[12], which is also demonstrated in Fig.3. Through the accumulated information of multiple iterations, the information of CSI will be obtained. In other words, the Q-learning algorithm spends time in learning before the first 20 trials. In the practical, for the first 20 trials, the system is in the progress of learning, and thus the derived results are not optimal. After the first 20 trials of learning, the system can grasp the best strategy of all the states and the averaged energy consumption of the ES converges to a constant value. In addition, the action space never becomes as large as possible. If the action space is large enough to obtain the optimal averaged energy consumption, a larger action space will only extend the convergence time without reducing energy consumption.
5 Conclusions
1) The proposed Q-learning algorithm can solve the proposed issue and achieves acceptable system performance over different Rayleigh fading channels in terms of energy consumption, a battery’s deficit charges and overcharges.
2) Compared with the two reference algorithms, the Q-learning algorithm shows a significant advantage in avoiding a battery’s energy from becoming exhausted. From the practical view, it is worthwhile to sacrifice performance in energy consumption in exchange for better system stability.
3) The size of action space can affect the Q-learning algorithm’s performance. A small action space causes a shorter convergence time, but cannot converge to the optimal solution. In fact, the Q-learning algorithm with a larger action space can effectively reduce energy consumption during a long time energy transmission.
[1]Adila A S, Husam A, Husi G. Towards the self-powered internet of things (IoT) by energy harvesting: Trends and technologies for green IoT[C]// 2018 2nd International Symposium on Small-scale Intelligent Manufacturing Systems (SIMS). Cavan, Ireland, 2018: 1-5.
[2]Kamalinejad P, Mahapatra C, Sheng Z, et al. Wireless energy harvesting for the internet of things[J]. IEEE Communications Magazine, 2015,53(6): 102-108. DOI: 10.1109/MCOM.2015.7120024.
[3]Luo Y, Pu L N, Zhao Y X, et al. DTER: Optimal two-step dual tunnel energy requesting for RF-based energy harvesting system[J].IEEE Internet of Things Journal, 2018, 5(4): 2768-2780. DOI:10.1109/jiot.2018.2813429.
[4]Kansal A, Hsu J, Zahedi S, et al. Power management in energy harvesting sensor networks[J]. ACM Transactions on Embedded Computing Systems, 2007,6(4): 32. DOI：10.1145/1274858.1274870.
[5]Hsu R C, Liu C T, Wang H L. A reinforcement learning-based ToD provisioning dynamic power management for sustainable operation of energy harvesting wireless sensor node[J].IEEE Transactions on Emerging Topics in Computing, 2014, 2(2): 181-191. DOI:10.1109/tetc.2014.2316518.
[6]Hsu R C, Lin T. A fuzzy Q-learning based power management for energy harvest wireless sensor node[C]// 2018 Int Conf HPCS. Orléans, France, 2018: 957-961.
[7]Mastronarde N, van der Schaar M. Joint physical-layer and system-level power management for delay-sensitive wireless communications[J].IEEE Transactions on Mobile Computing, 2013, 12(4): 694-709. DOI:10.1109/tmc.2012.36.
[8]Ertel R B, Reed J H. Generation of two equal power correlated Rayleigh fading envelopes[J].IEEE Communications Letters, 1998, 2(10): 276-278. DOI:10.1109/4234.725222.
[9]Wang J B, Feng M, Song X Y, et al. Imperfect CSI based joint bit loading and power allocation for deadline constrained transmission[J].IEEE Communications Letters, 2013, 17(5): 826-829. DOI:10.1109/lcomm.2013.031313.122583.
[10]Luo Y, Pu L, Zhao Y, et al. Optimal energy requesting strategy for rf-based energy harvesting wireless communications[C]// IEEE Conf Comput Commun. Atlanta, GA, USA, 2017: 1-9.
[11]Liu G P, Whidborne J F, Yang J B, et al. Multiobjective optimisation and control[J]. Wetlands Ecology & Management, 2003, 17(2):157-164. DOI:10.1007/s11273-008-9090-x.
[12]Mitchell T M, Carbonell J G, Michalski R S. Machine learning[M]. Boston, MA, USA: Springer, 1986:39-42.