The explosive growth of data poses a huge challenge in terms of the efficiency and difficulty of data processing[1]. As the increasing data volumes are being accumulated, a powerful computation capability is required to extract information. Previously, homogeneous computing that improved the performance of computational components was no longer sufficient to meet the performance requirements of large-scale scientific and engineering computing[2]. The heterogeneous distributed computing system, as a new carrier of computing mode, is a computing platform that interconnects a series of computing resources with different performances through networks[3], which can provide significant computing power. Grid computing[4], cloud computing[5], edge computing[6] and mobile cloud computing[7] have been developed as typical heterogeneous distributed computing systems in recent years.
Workflow is an application process that can be fully automated. It is commonly used to describe scientific computational problems with large structures and complex logical processes, and has important practical implications[8]. It is widely used in geophysics, astronomy, bioinformatics and other fields[9]. At the same time, it has a natural close coupling with heterogeneous distributed systems due to the characteristics of workflow. In addition, research on the combination of them is ongoing. Task scheduling is the main object of the workflow research, and its essence is to solve the mapping between precedence constrained tasks and computing resources to achieve optimization goals, such as shortening workflow execution time, reducing execution costs, lowering energy consumption, or improving system reliability[10-16]. As a common quality of service (QoS) element, time has always been an important goal of research due to its significance[17-20].
The problem of minimizing the execution time of workflows in low complexity situations has been studied extensively, but many algorithms only focus on different performance and communication overheads of the processor to formulate scheduling strategies. However, few have incorporated the structure of the workflow, such as the depth and out-degree of task, into the strategy. The out-degree, as an important factor controlling workflow formation, should be taken into account in this problem. Many researchers have also experimentally adjusted the magnitude of the out-degree to control the number of parallel tasks at the same level. Moreover, since the quality of the solution is very sensitive to the priority assignment of tasks, the out-degree facilitates the obtaining of more accurate task priorities. Moreover, the levelization strategy can place tasks with identical depth at the same level and select the task with the highest out-degree among them for priority scheduling, which can effectively reduce the workflow scheduling completion time by eliminating scheduling blocking while maximizing the parallelism of currently ready tasks.
On the basis of the preceding thoughts, this paper presents the following algorithms: level and out-degree earliest-finish-time (LOEFT), level heterogeneous selection value (LHSV), and heterogeneous priority earliest-finish-time (HPEFT). These algorithms are divided into three stages, namely, task levelization, task prioritization, and processor allocation. In the task levelization and task prioritization stages, a more precise task queue, which largely determines the completion time of the workflow, is obtained. In the processor allocation phase, the task queue is acquired to achieve the precise positioning of the processor to minimize the completion time of the workflow. Heterogeneous selection value (HSV) and earliest-finish-time (EFT) are two indicators used as the bases for different algorithms to allocate processors. Simulation experiments demonstrate that the LOEFT, LHSV, and HPEFT algorithms can simply and efficiently achieve the workflow of the makepan minimization, and the LOEFT algorithm has the most optimal scheduling results.
1 Related Works
Among the workflow scheduling time optimization algorithms, list heuristics has attracted widespread attention due to its efficiency and practicality[21]. The classical heterogeneous earliest-finish-time (HEFT), which was proposed by Topcuoglu et al.[17], achieved high performance in terms of robustness and schedule length. However, in more complex cases, the HEFT algorithm often fails to achieve desired scheduling results. On the basis of the HEFT algorithm, Bittencourt et al. [18] proposed the Lookahead algorithm, which sets up a prediction mechanism to schedule the current task to the processor that minimizes the EFT of all subsequent tasks; unfortunately, its complexity is high. The improved heterogeneous earliest time (IHEFT) algorithm proposed by Wang et al. [19] considers the minimum value of the upward weight on different resources as the ranking criterion. However, this approach cannot achieve good scheduling results in large-scale workflows. The HSV algorithm proposed by Xie et al. [20] can effectively reduce scheduling imprecision caused by differences in computing resources. Nevertheless, in some types of applications, the HSV algorithm will break the precedence constraint between tasks, posing a serious threat to system security while prolonging the makespan. Sih et al.[22] proposed a non-preemptive DAG workflow dynamic-level-scheduling (DLS) algorithm for DAG workflows, which not only takes into account the communication overhead between processing units, but also integrates the processing unit interconnection topology information and supplements it with time (communication overhead) and space (processing unit load) scheduling to eliminate resource competition. It also constantly adjusts the task priority to fit the compute nodes. The authors start from the homogeneous computing system and gradually extend to the heterogeneous computing system. Daoud et al. [23] invented the longest-dynamic-critical-path (LDCP) algorithm for task scheduling in processor-limited heterogeneous computing environments. The LDCP algorithm is a static list heuristic scheduling algorithm, and as such, it can be divided into three phases. The first stage is the task sorting stage, where at each step of the algorithm, the maximum value of the sum of task execution time and communication time on the path from the entry task to the exit task is the author’s LDCP, and the tasks are sorted according to it. The second stage is the processor selection stage. Based on the insertion scheduling strategy[24], the task is assigned to the processor that will allow it to obtain the minimum completion time. The third stage is the state update stage. Once the running processor of the task has been assigned, the system must update the state information in time to reflect this scheduling. The experimental results show that LDCP is superior to the HEFT and DLS algorithms in reducing the workflow completion time, but it has a higher time complexity than the HEFT algorithm.
Apart from list scheduling algorithms, other types of algorithms can be classified into clustering and task duplication heuristic algorithms[17]. Huang et al. [25] proposed three new task clustering approaches, critical path clustering heuristic (CPCH), larger edge first heuristic (LEFH), and critical child first heuristic (CCFH), attempting to minimize the communication cost over the execution path to obtain better workflow scheduling performance. The proposed scheme is evaluated through a series of simulation experiments and compared with other cluster-based task graph scheduling methods. The experimental results show that the proposed CPCH, LEFH, and CCFH significantly outperform the typical schemes, with an average makepan performance improvement of up to 21% for workflows with a large communication computation ratio (CCR). Similar to clustering heuristics, which aim to eliminate inter-processor communication overhead, duplication-based algorithms are proposed to replicate their forerunners using idle slots in processors. In Ref. [26], a workflow scheduling algorithm for heterogeneous cloud environments based on task duplication is presented. The algorithm is divided into two stages. The first stage computes the priority of all tasks and the second stage schedules task replication by computing the data arrival time from one task to another task. The proposed algorithm aims at minimizing the workflow execution time and maximizing the resource utilization. Simulation experiments verify the advantages of the proposed algorithm in terms of makespan and average cloud utilization.
2 System Models
The scheduling system model comprises of a target computing environment and an application model. The target computing environment is assumed to be set P, which is comprised of different p independent types of processors that are fully connected. In addition, all inter-processor communications are assumed to perform without contention in a fully connected topology.
Workflow can usually be represented by a directed acyclic graph (DAG), whose model is G=(T, E, W, C). Among them, T represents the set of all nodes, T={t1, t2, t3,…, tn}. Each node represents a task ti in the application; E represents a set of directed edges that are constrained between tasks, that is, ei,j ∈E indicates that task tj can be started after the execution of ti. ti is a predecessor task, and tj is a successor task. Nodes without predecessor tasks are entry tasks and are marked as tentry. Nodes without successor tasks are exit tasks and are marked as texit. Fig.1 is a schematic of Montage workflow DAG applied to astronomical observation.
W is expressed as a computation cost matrix of size |P|×|T|, where |P| represents the number of processors, |T| represents the number of tasks to be executed, and wi,k represents the execution time of task ti on processor pk. C is represented as the communication cost matrix of size |T|×|T|, and ci,j represents the communication overhead on edge ei,j. Tab.1 shows an example of the computation cost matrix of the Montage workflow in Fig.1.

Fig.1 Montage workflow DAG graph
Tab.1 Sample computation costs

Processort1t2t3t4t5t6t7t8t9t10t11t12t13t14t15t16t17t18t19t20p114131113121372116212314206182617151711p21619138131615191861657912149112415p3918191710912237161211161320181413127
In accordance with the task depth value, the workflow is divided into several independent task sets from top to bottom to maximize the parallelism of tasks at the same level. In G=(T, E, W, C), if the level of the predecessor task ti is expressed as level (ti), then the level of its direct successor task is expressed as level(ti)+1, and the specific definition is
(1)
where pred (ti) is the set of immediate predecessors of task ti.
Similar to Ref.[20], the heterogeneity of the computing node is considered in the model, and the execution time of each task on different processors is calculated to improve accuracy. The specific calculation process is
(2)
where succ (ti) is the set of immediate successors of task ti.
Based on the previous equation, the heterogeneous upward rank value is defined as
(3)
The out-degree of a task (outd(ti)) is also a factor that affects the priority of the task. If the task with a larger outd(ti) is not scheduled first, then all subsequent tasks will not be ready, thereby prolonging the makespan of the workflow. Similar to Ref.[20], the product of the average upward ranking value and the out-degree is used as the ranking criterion for task priority. This value is called the heterogeneous priority rank value (HPRV). The calculation formula is
HPRV(ti)=outd(ti)×hranku(ti)
(4)
EST(t,p) represents the earliest execution time available for task t on processor p. Correspondingly, the earliest execution completion time of task t on processor p is called the earliest finish time and is expressed as EFT(t,p). The specific definitions are shown as
EST(ti,pk)=
(5)
EFT(ti,pk)=EST(ti,pk)+wi,k
(6)
where avail[pk] is the EST when processor pk is ready for execution; AFT(tj) is the actual execution finish time of task tj. The maximum value of the start time of the predecessor task of tj triggering ti is selected in each calculation to ensure that all data needed by task ti has arrived at processor pk.
HSV combines the principles of “looking up” and “looking down” to consider the EFT and the longest distance exit time (LDET) to achieve processor allocation. The specific definition is
HSV(ti,pk)=EFT(ti,pk)×LDET(ti,pk)
(7)
where LDET(ti, pk) represents the longest time that ti takes from processor pk to exit task texit. The calculation formula is
LDET(ti,pk)=ranku(ti,pk)-wi,k
(8)
3 Algorithms
The LOEFT, LHSV, and HPEFT algorithms belong to the list scheduling algorithm. The basic idea is to construct an ordered task queue by assigning priorities to each task in the task graph. Assigning each task in the task queue, in turn, can complete the workflow. The processor minimizes time until all nodes in the task list have been scheduled. The specific process and pseudo code are as follows.
3.1 LOEFT algorithm
The LOEFT algorithm can be divided into three stages:task levelization, task prioritization, and processor allocation. In the first stage, the workflow is divided into a hierarchical set taskGroups composed of several groupk in accordance with the depth value k. In the second stage, the HPRV corresponding to task t in each groupk is calculated in turn, and the non-increasing order is placed in groupk on the basis of the HPRV. In the third stage, the processor with the minimum EFT is assigned to the current task. The specific steps are shown in Algorithm 1.
Algorithm 1 LOEFT algorithm
Input: DAG workflow G=(T, E, W, C), processors set P;
Output: task scheduling sequence SL.
taskGroups=∅;
calculate the depth value k of each task t according to Eq.(1);
calculate the HPRV of each task t according to Eq.(4);
group t with the same depth value k into groupk, and all groupk form taskGroups;
sort groupk in taskGroups in ascending order according to the value of k;
sort tasks in groupk in non-increasing order according to the HPRV;
for all groupk∈taskGroups do
for all t∈groupk do
calculate the EFT(t,p) of t on each processor p according to Eq. (6);
assign t onto the processor p with the smallest EFT(t,p);
save t-p pairs into the scheduling sequence SL;
end for
end for
return SL;
3.2 LHSV algorithm
The LHSV algorithm is also divided into three stages: task levelization, task prioritization, and processor allocation. Among them, the former two phases are the same as the LOEFT algorithm, and the processor allocation phase assigns the processor with the smallest HSV value to the current task. The specific steps are shown in Algorithm 2.
Algorithm 2 LHSV algorithm
Input: DAG workflow G=(T, E, W, C), processors set P;
Output: task scheduling sequence SL.
taskGroups = ∅;
calculate the depth valuek of each task t according to Eq.(1);
calculate the HPRV of each task t according to Eq.(4);
groupt with the same depth value k into groupk, and all groupk form taskGroups;
sort groupk in taskGroups in ascending order according to the value of k;
sort tasks in groupk in non-increasing order according to the HPRV;
for all groupk∈ taskGroups do
for all t ∈ groupk do
calculate the HSV (t,p) of t on each processor p according to Eq.(7);
assign t onto processor p with the smallest HSV (t,p);
save t-p pairs into the scheduling sequence SL;
end for
end for
return SL;
3.3 HPEFT algorithm
The HPEFT algorithm is divided into two stages, namely, task prioritization and processor allocation. The stages are the same as the latter two stages of the LOEFT algorithm, respectively. The specific steps are shown in Algorithm 3.
Algorithm 3 HPEFT Algorithm
Input: DAG Workflow G = (T, E, W, C), processors set P;
Output: task scheduling sequence SL.
calculate the HPRV of each task t in G according to Eq.(4);
sort tasks in G in non-increasing order according to the HPRV;
for all t ∈ G do
calculate the EFT(t,p) of t on each processor p according to Eq.(6);
assign t onto the processor p with the smallest EFT(t,p);
save t-p pairs into the scheduling sequence SL;
end for
return SL;
In the task levelization phase, all tasks are classified into different groups according to their own depth, and thus the time complexity is O(t2); in the task prioritization and processor allocation phase, all tasks and processors need to be traversed, which can be done in O(p×t2). Therefore, the time complexity of the LOEFT, LHSV and HPEFT algorithms are all O(p×t2), which is identical to that of the algorithm HEFT.
4 Experiments and Results
The HEFT algorithm was selected for comparison with LOEFT, LHSV, and HPEFT, and all algorithms were written in Java in a MacPro Workstation with Intel Xeon Quad-Core@2.80 GHz, 4 Cores, and 16 GB DDR3 RAM as the hardware configuration.Fast Fourier transform (FFT), Gaussian elimination (GE), Laplace, and random DAG instances generated by the Task Graph Generator (TGG)[27] are analyzed. TGG is a handy, easy to use tool specially designed to be used to develop task graphs that are needed for research works in the areas of task scheduling. Meanwhile, some parameters for generating task graphs, which are also consistently used in Refs. [17, 28-29], are given in Tab.2.
Tab.2 The important parameter settings of task graph generator
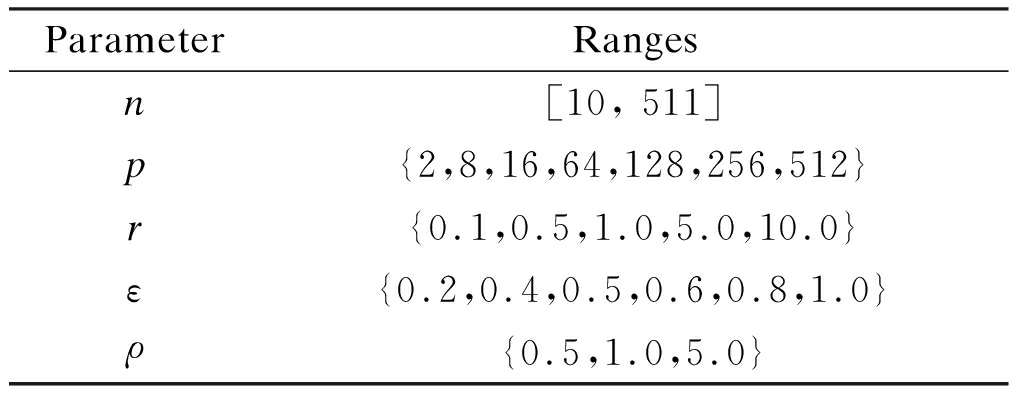
ParameterRangesn[10, 511]p{2,8,16,64,128,256,512}r{0.1,0.5,1.0,5.0,10.0}ε{0.2,0.4,0.5,0.6,0.8,1.0}ρ{0.5,1.0,5.0}
In particular, n denotes the number of DAG nodes; p denotes the number of processors. r means the communication-to-computation ratio; the smaller the ratio, the higher the communication cost, and vice versa. ε is the heterogeneous factor; the smaller the factor, the higher the homogeneity. ρ is the parallelism factor; the larger the factor, the higher the parallelism of application. Then, TGG takes these parameters as input and outputs some text files, which stores task-to-processor mappings, computation cost values, communication cost values, etc. Based on these output files, we further extract the values, construct the topology, and then import them into the algorithm to observe the resulting output. In each round of simulation, we try to diversify the combination of parameters as much as possible in order to simulate reality.
The two metrics, R and S, are presented to measure the performance of the algorithm. R is the normalization of the scheduling length, that is
(9)
where the denomination is the summation of the minimum computation cost of the critical path execution time, and the molecule m is the actual execution time. The lowest R indicates the best algorithm with respect to performance.
S denotes the speedup, which is computed by dividing the minimum sequential execution time by the actual execution time m of the algorithm, which can be expressed as
(10)
where the sequential execution time is computed by assigning all tasks to a single processor that minimizes the cumulative computation costs. Contrary to R, the highest S indicates the best algorithm with respect to performance.
The R and S values change with time. Smaller R value and larger S value indicate a greater efficiency of the algorithm.
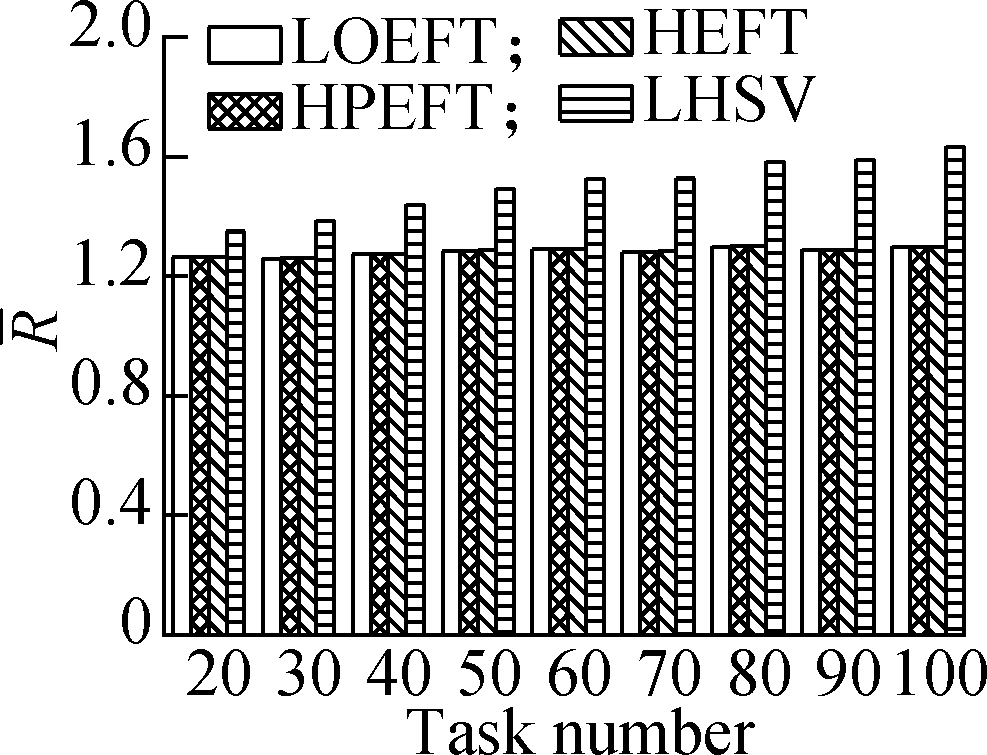
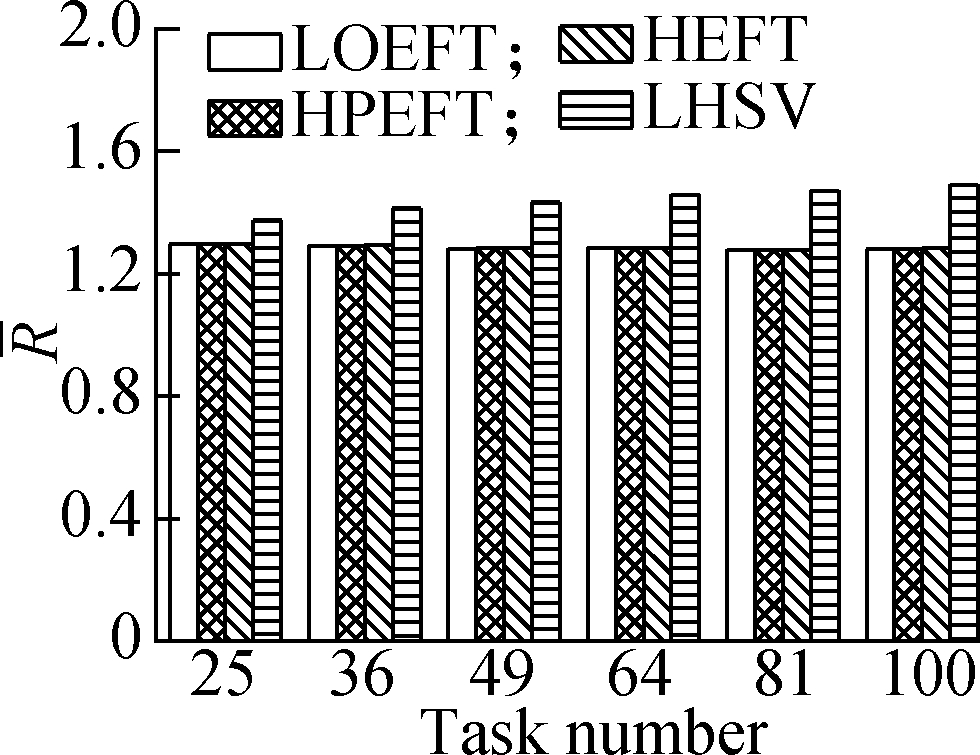
Experiment 1 This compares the change trend of the R value of each algorithm under the four different DAG workflows when the number of tasks changes. The specific steps are as follows: fixing other parameters (p, r, ε, and ρ) and changing the number of tasks. The results are shown in Fig.2. The experimental analysis shows that the LOEFT algorithm performs best with the increase in the number of tasks. Its average R value is 4.5% lower than that of the HEFT algorithm. In addition, the R value of the HPEFT algorithm is 0.3% higher than that of the HEFT algorithm. The LHSV algorithm is 8.9% higher than the HEFT algorithm. Moreover, the HPEFT algorithm is almost similar to the HEFT algorithm given that they share a similar philosophy when dealing with task scheduling. Meanwhile, the LOEFT and LHSV algorithms use task-level strategies to increase the number of concurrent tasks at the same level. However, the HSV value, which is adopted by the LHSV algorithm during the processor allocation phase, is equal to 0 when the iterating task is an exit task due to LDET(texit) = 0, that leads to a random choice of the processors to texit, thereby potentially extending the workflow completion time.
(a)

(b)
(c)
(d)
Fig.2 Average R under different task numbers. (a) Random DAG; (b) GE; (c) FFT; (d) Laplace
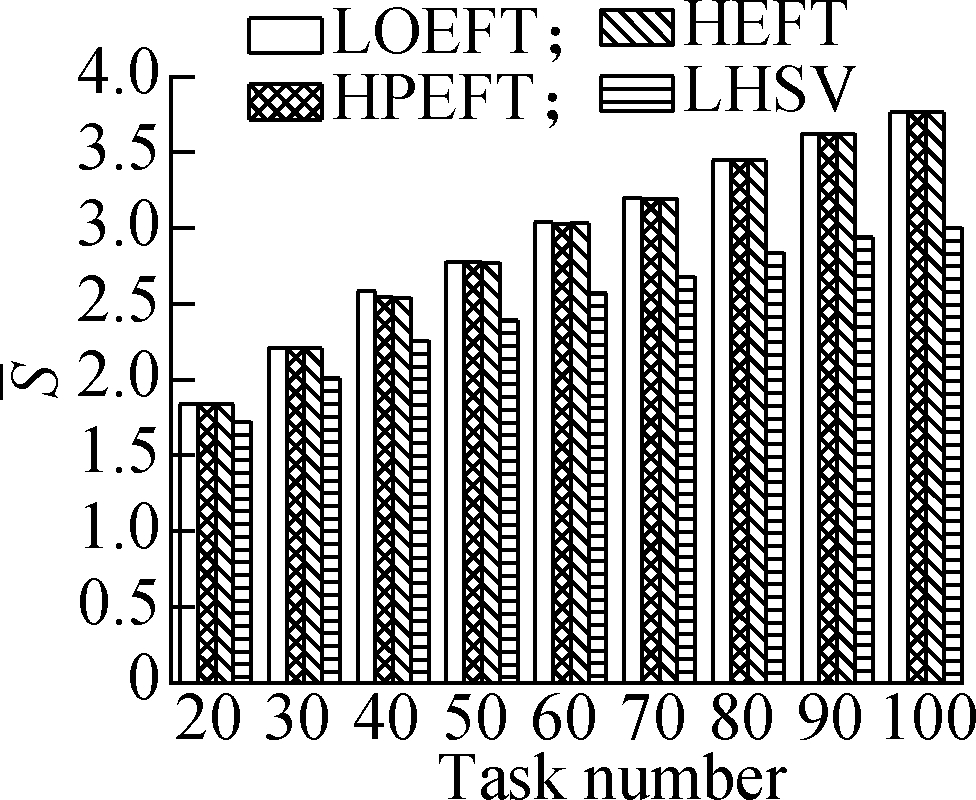
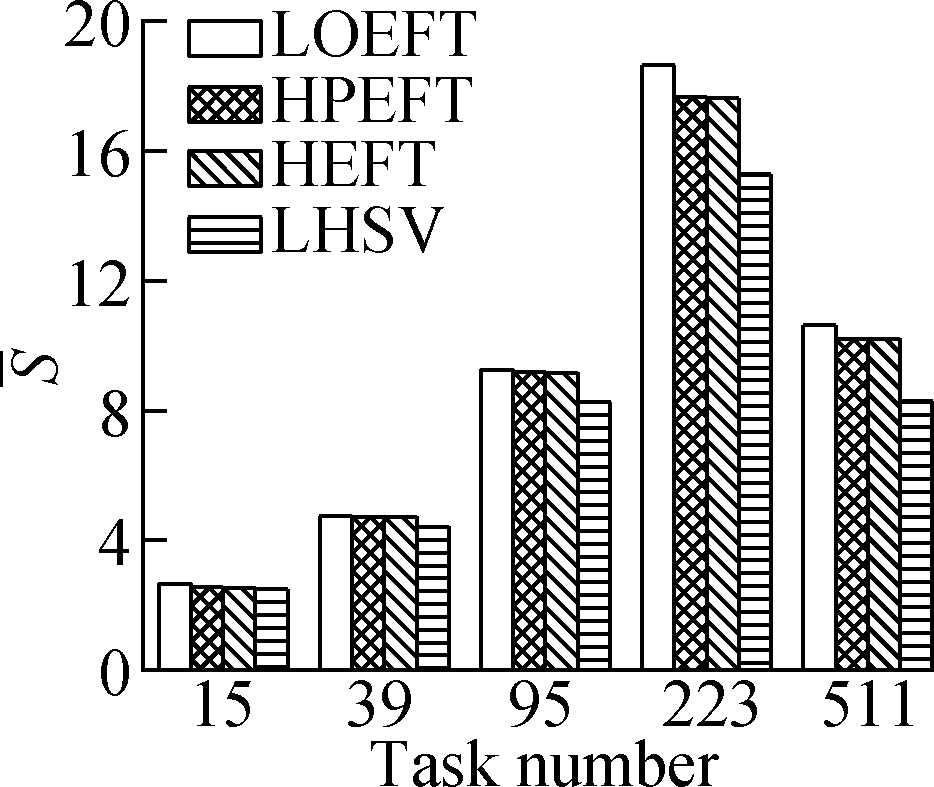
Experiment 2 This compares the trend of the S value of each algorithm under the four different DAG workflows when the number of tasks changes. The specific steps are the same as experiment 1. The results are shown in Fig.3. Through the experimental analysis, it is proved that with the increase in the number of tasks, the LOEFT algorithm shows the best performance among four approaches, with the S value being 3.1% higher than the HEFT algorithm. The HPEFT algorithm has the closest trend to the HEFT algorithm, and its S value is reduced by 0.2%. The LHSV algorithm has the worst performance, and its S value is reduced by 7.8%. The task priority phase of the LOEFT and the HPEFT algorithms is the same as their processor allocation phase. The LOEFT algorithm’s task-depth based levelization strategy increases the number of concurrent releases between tasks, and the LOEFT algorithm can obtain more accurate task prioritization, which reduces the difference caused by the processor performance difference.
(a)

(b)
(c)

(d)
Fig.3 Average S under different task numbers. (a) Random DAG; (b) GE; (c) FFT; (d) Laplace
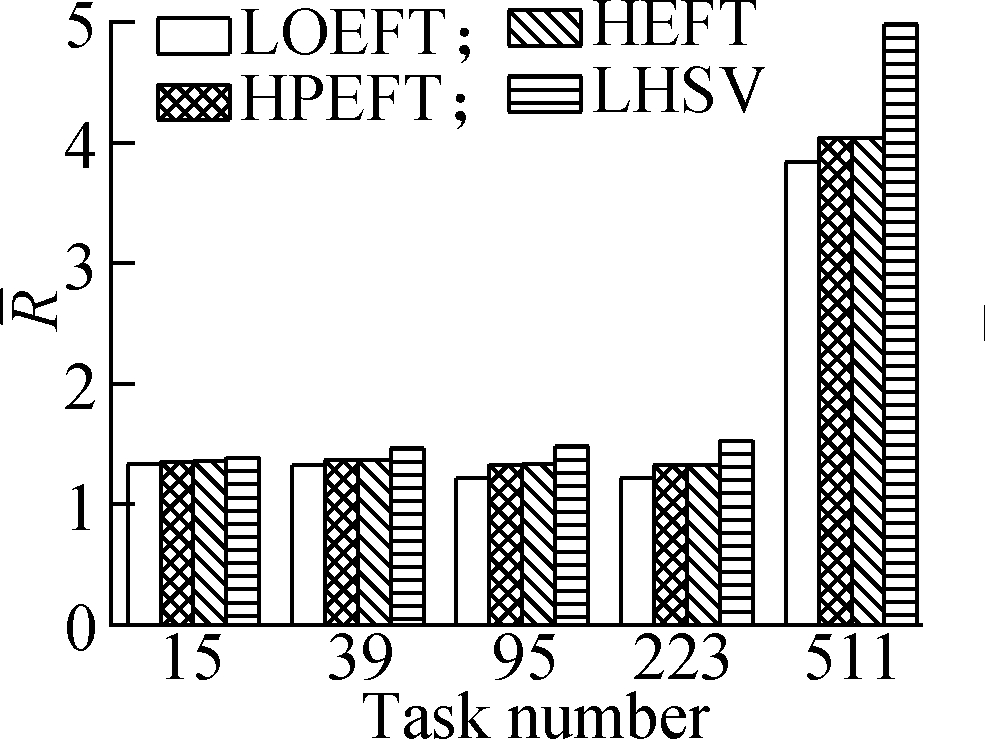
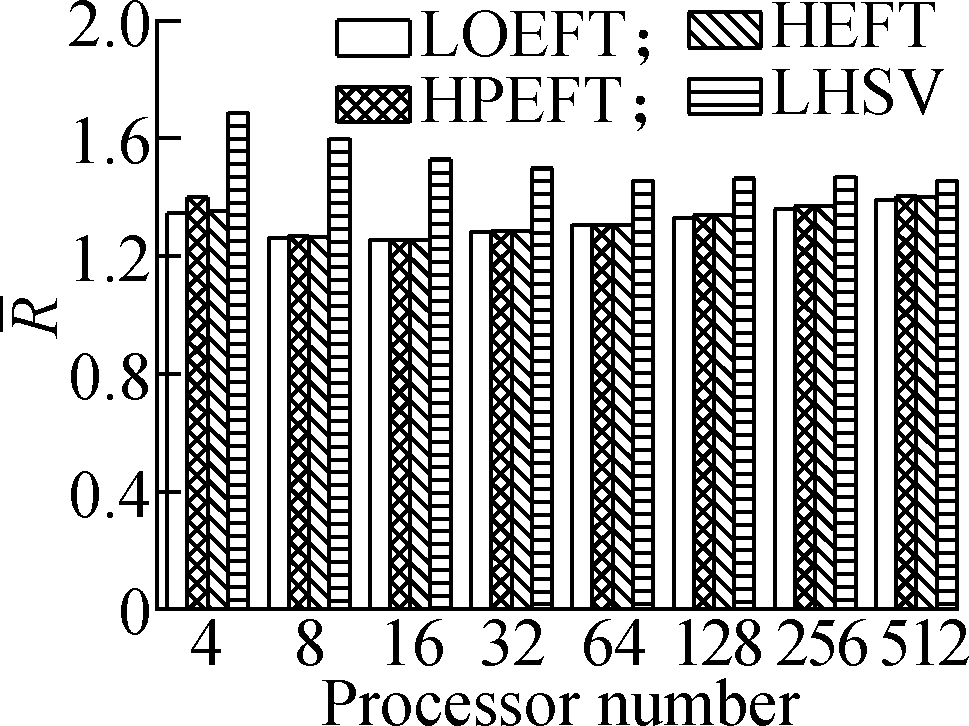
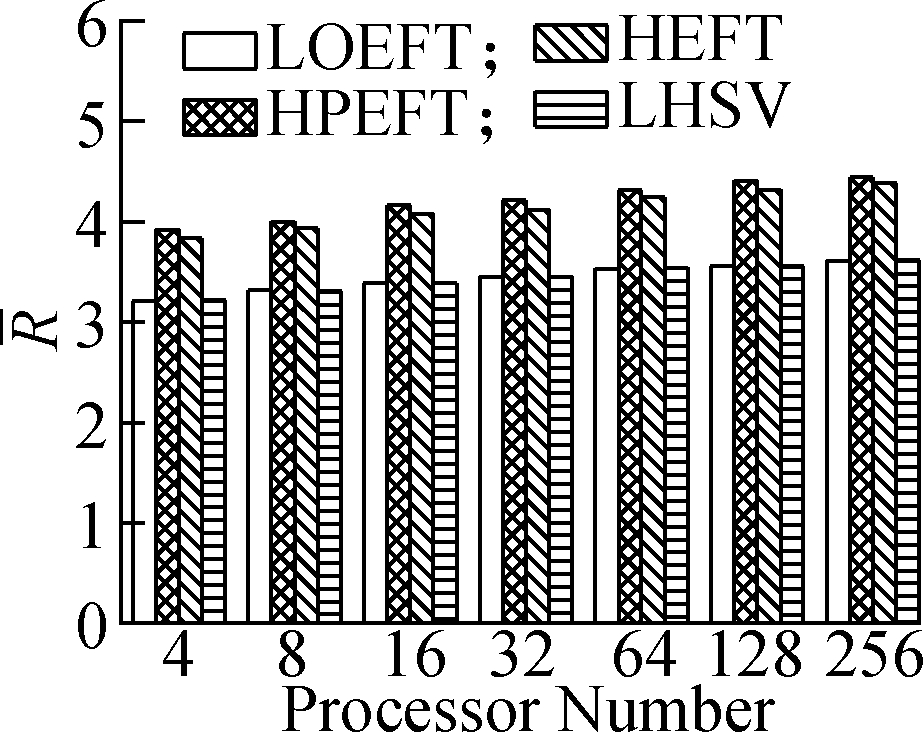
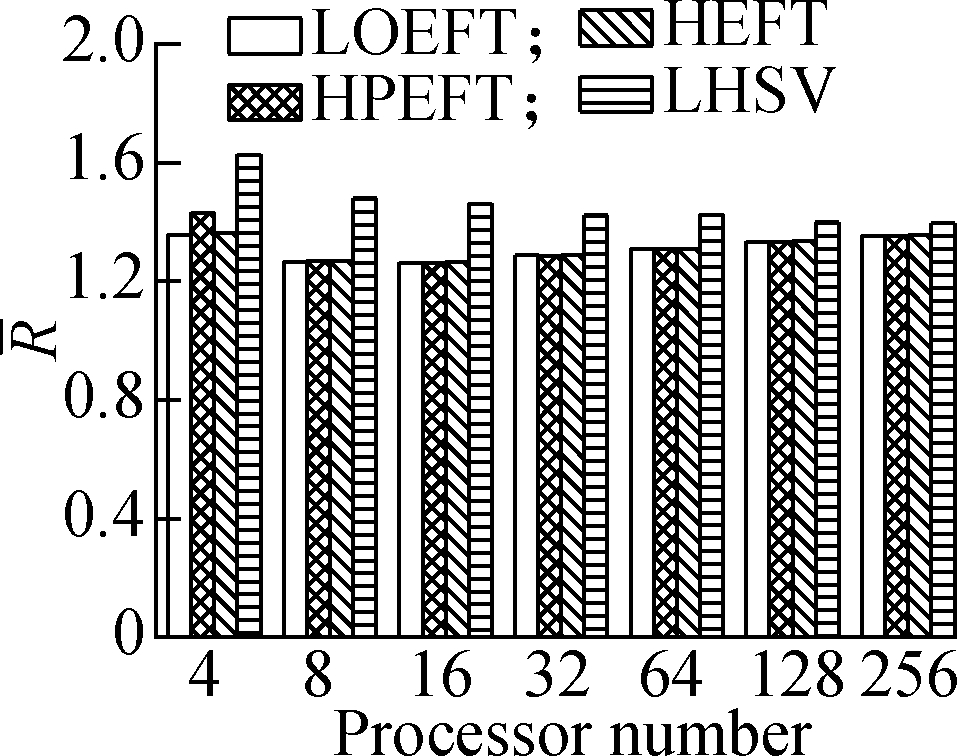
Experiment 3 This compares the change trend of the R value of each algorithm under the four different DAG workflows when the number of processors changes. The specific steps are as follows: fixing other parameters (n, r, ε, and ρ) and changing the number of processors. The obtained results are shown in Fig.4. According to the experimental analysis, in the process of increasing the number of processors, the increasing order of the average R value is as follows: LOEFT, HEFT, HPEFT, and LHSV. The R value of the LOEFT algorithm is 4.7% lower than that of the HEFT algorithm, and the R values of the HPEFT and LHSV algorithms are 0.7% and 4% higher than that of the HEFT algorithm, respectively. This is caused by the task prioritization obtained by the LOEFT algorithm that achieves precise positioning of the processor on the basis of more accurate task prioritization. In addition, the HSV value, which is the selection criterion of the LHSV algorithm processor, misjudges the exit task, thereby extending the completion time of the workflow.
(a)
(b)

(c)
(d)
Fig.4 Average R under different processor numbers. (a) Random DAG; (b) GE; (c) FFT; (d) Laplace
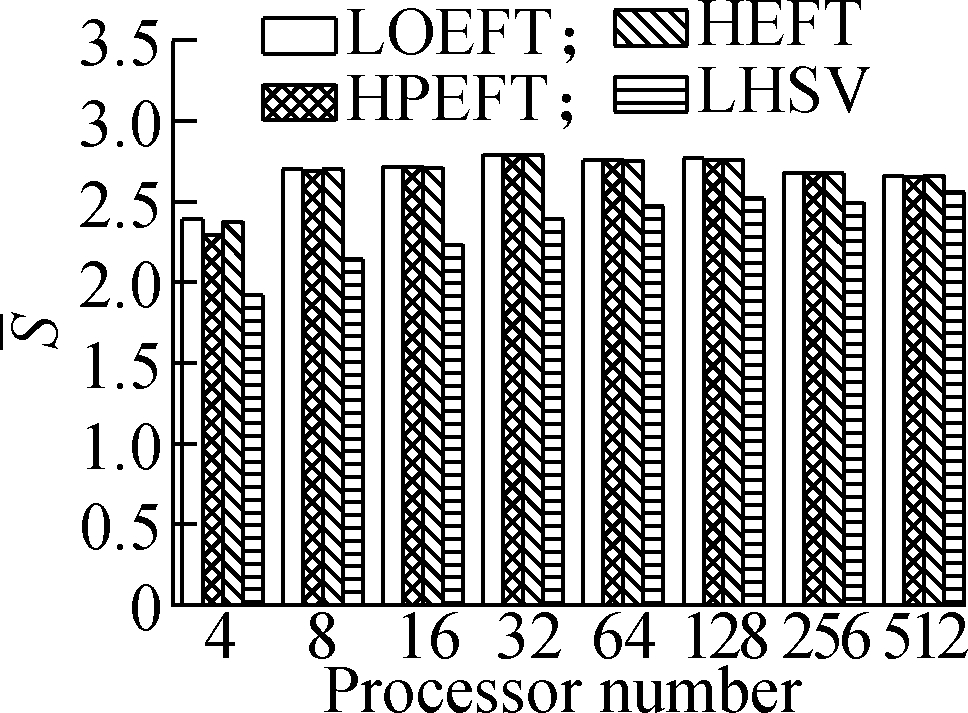
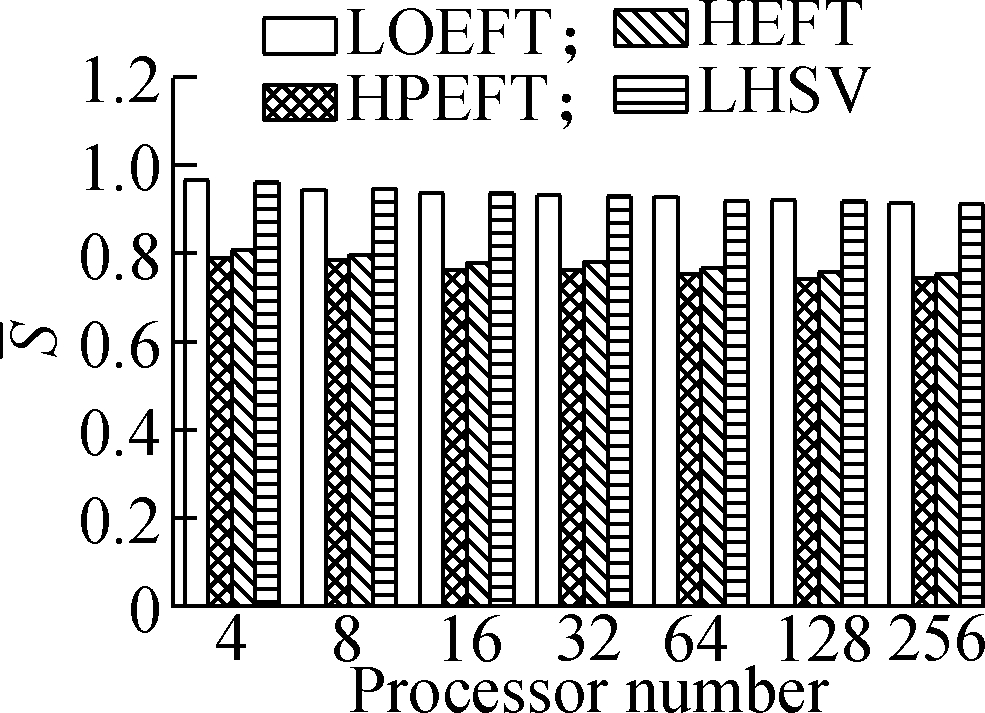
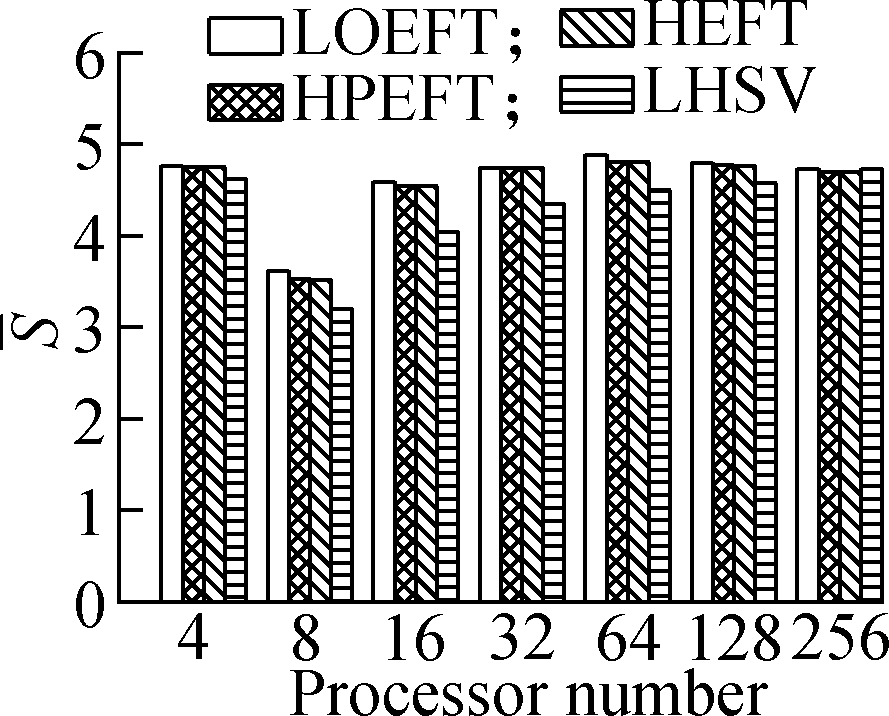
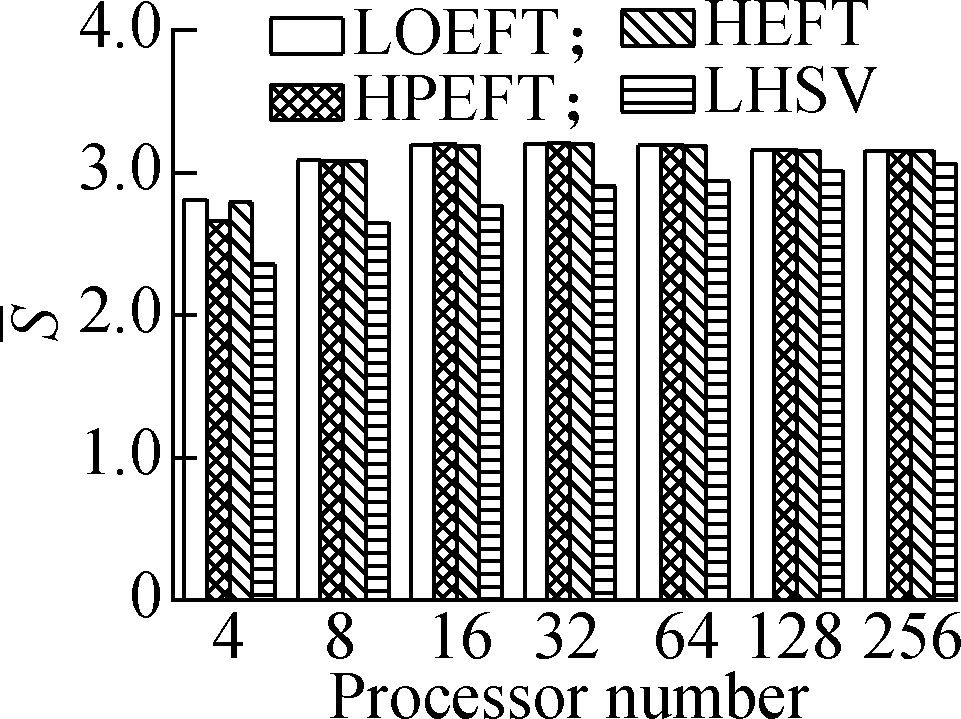
Experiment 4 It compares each algorithm’s S value under the four different DAG workflows when the number of processors changes. The specific steps are the same as experiment 3. The results are shown in Fig.5. According to the experimental analysis, with the increase in processor number, the decreasing order of the average S value is as follows: LOEFT, HEFT, HPEFT, and LHSV. Compared with the HEFT algorithm, the change trend of the LOEFT algorithm positively increases, the change trend of the HPEFT algorithm is the closest, and the change trend of the LHSV algorithm negatively increases. This result also confirms the conclusion drawn from the previous experiments that the LOEFT algorithm has a clear advantage over the three algorithms in terms of time optimization.
(a)
(b)
(c)
(d)
Fig.5 Average S under different processor numbers. (a) Random DAG; (b) GE; (c) FFT; (d) Laplace
5 Conclusions
1)As application completion time has a profound impact on users, systems, and the environment, optimizing it is an ongoing research topic in computing systems.
2)As a special application, workflow is commonly used in scientific research. Aiming at the scheduling time optimization problem of the static workflow under the heterogeneous distributed computing system, three algorithms are proposed, namely, LOEFT, LHSV, and HPEFT. In particular, task depth is incorporated into task out-degree, thus enabling the proposed algorithms to minimize workflow completion time in a simple and efficient manner. Among them, the LOEFT algorithm has achieved excellent scheduling results.
3)The model studied in this paper is relatively simple, and the proposed equation is coarse in granularity. Thus, there is a possibility for further improvement. Next, we will highlight the difficulty of the problem and consider imposing a duplication strategy for tasks with a large out-degree, and simultaneously optimize the time and reliability of workflow scheduling.
[1]Li K L, Tang X Y, Li K Q. Energy-efficient stochastic task scheduling on heterogeneous computing systems[J].IEEE Transactions on Parallel and Distributed Systems, 2014, 25(11): 2867-2876. DOI:10.1109/TPDS.2013.270.
[2]Jiang J, Lin Y, Xie G, et al. Energy optimization heuristic for deadline-constrained workflows in heterogeneous distributed systems[J].Journal of Computer Research and Development, 2016, 53(7): 1503-1516. (in Chinese)
[3]Tanenbaum A. Modern operating systems[M]. Beijing: China Machine Press, 2009.
[4]Yang G W, Jin H, Li M L, et al. Grid computing in China[J].Journal of Grid Computing, 2004, 2(2): 193-206. DOI:10.1007/s10723-004-4201-2.
[5]To W M, Lai L S L, Chung A W L. Cloud computing in China: Barriers and potential[J].IT Professional, 2013, 15(3): 48-53. DOI:10.1109/mitp.2012.64.
[6]Shi W S, Cao J, Zhang Q, et al. Edge computing: Vision and challenges[J]. IEEE Internet of Things Journal, 2016, 3(5): 637-646. DOI:10.1109/jiot.2016.2579198.
[7]Huang B, Xia W, Zhang Y, et al. Dependent task assignment algorithm based on particle swarm optimization and simulated annealing in ad-hoc mobile cloud[J]. Journal of Southeast University (English Edition),2018, 34(4):430-438.
[8]Deelman E, Gannon D, Shields M, et al. Workflows and e-Science: An overview of workflow system features and capabilities[J].Future Generation Computer Systems, 2009, 25(5): 528-540. DOI:10.1016/j.future.2008.06.012.
[9]Bharathi S, Chervenak A, Deelman E, et al. Characterization of scientific workflows[C]// Third Workshop on Workflows in Support of Large-Scale Science. Austin, TX, USA, 2008: 1-10.
[10] Jiang J Q, Lin Y P, Xie G Q, et al. Time and energy optimization algorithms for the static scheduling of multiple workflows in heterogeneous computing system[J].Journal of Grid Computing, 2017, 15(4): 435-456. DOI:10.1007/s10723-017-9391-5.
[11] Oliveira D, Brinkmann A, Rosa N, et al. Performability evaluation and optimization of workflow applications in cloud environments[J].Journal of Grid Computing, 2019, 17(4): 749-770. DOI:10.1007/s10723-019-09476-0.
[12] Jia Y H, Chen W N, Yuan H Q, et al. An intelligent cloud workflow scheduling system with time estimation and adaptive ant colony optimization[J].IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019,pp(99): 1-16. DOI:10.1109/tsmc.2018.2881018.
[13] Zhou J L, Wang T, Cong P J, et al. Cost and makespan-aware workflow scheduling in hybrid clouds[J].Journal of Systems Architecture, 2019, 100: 101631. DOI:10.1016/j.sysarc.2019.08.004.
[14] Zhao L P, Ren Y Z, Sakurai K. Reliable workflow scheduling with less resource redundancy[J].Parallel Computing, 2013, 39(10): 567-585. DOI:10.1016/j.parco.2013.06.003.
[15] Garg R, Mittal M, Son L H. Reliability and energy efficient workflow scheduling in cloud environment[J].Cluster Computing, 2019, 22(4): 1283-1297. DOI:10.1007/s10586-019-02911-7.
[16] Zhou J L, Zhang M, Sun J, et al. DRHEFT: Deadline-constrained reliability-aware HEFT algorithm for real-time heterogeneous MPSoC systems[J/OL]. IEEE Transactions on Reliability, 2020.http://ieeexplore.ieee.org/abstract/document/9063674. DOI: 10.1109/TR.2020.2981419.
[17] Topcuoglu H, Hariri S, Wu M Y. Performance-effective and low-complexity task scheduling for heterogeneous computing[J]. IEEE Transactions on Parallel and Distributed Systems, 2002, 13(3): 260-274. DOI:10.1109/71.993206.
[18] Bittencourt L F, Sakellariou R, Madeira E R M. DAG scheduling using a lookahead variant of the heterogeneous earliest finish time algorithm[C]// Proceedings of the 2010 18th Euromicro Conference on Parallel, Distributed and Network-Based Processing. IEEE Computer Society, 2010: 27-34.
[19] Wang X L, Huang H B, Deng S. List scheduling algorithm for static task with precedence constraints for cyber-physical systems[J]. Acta Automatica Sinica, 2012, 38(11): 1870. DOI:10.3724/sp.j.1004.2012.01870.
[20] Xie G Q, Li R F, Li K Q. Heterogeneity-driven end-to-end synchronized scheduling for precedence constrained tasks and messages on networked embedded systems[J]. Journal of Parallel and Distributed Computing, 2015, 83: 1-12. DOI:10.1016/j.jpdc.2015.04.005.
[21] Canon L C, Jeannot E, Sakellariou R, et al. Comparative evaluation of the robustness of DAG scheduling heuristics[M]//Grid Computing. Boston, MA,USA: Springer US, 2008: 73-84. DOI:10.1007/978-0-387-09457-1_7.
[22] Sih G C, Lee E A. A compile-time scheduling heuristic for interconnection-constrained heterogeneous processor architectures[J]. IEEE Transactions on Parallel and Distributed Systems, 1993, 4(2): 175-187. DOI:10.1109/71.207593.
[23] Daoud M I, Kharma N. A high performance algorithm for static task scheduling in heterogeneous distributed computing systems[J]. Journal of Parallel and Distributed Computing, 2008, 68(4): 399-409. DOI:10.1016/j.jpdc.2007.05.015.
[24] Sun J, Yin L, Zou M H, et al. Makespan-minimization workflow scheduling for complex networks with social groups in edge computing[J]. Journal of Systems Architecture, 2020, 108: 101799. DOI:10.1016/j.sysarc.2020.101799.
[25] Huang K C, Gu D S, Liu H C, et al. Task clustering heuristics for efficient execution time reduction in workflow scheduling[J]. Journal of Computers, 2017, 28(1): 43-56.
[26] Gupta I, Kumar M S, Jana P K. Task duplication-based workflow scheduling for heterogeneous cloud environment[C]// 2016 Ninth International Conference on Contemporary Computing (IC3). Noida, India, 2016: 1-7. DOI: 10.1109/IC3.2016.7880207.
[27] TGGTCE. Task graph generator[EB/OL]. (2020-05-28)[2020-08-10]. http://sourceforge.net/projects/taskgraphgen/.
[28] Tang Z, Qi L, Cheng Z Z, et al. An energy-efficient task scheduling algorithm in DVFS-enabled cloud environment[J]. Journal of Grid Computing, 2016, 14(1): 55-74. DOI:10.1007/s10723-015-9334-y.
[29] Mei J, Li K L, Zhou X, et al. Fault-tolerant dynamic rescheduling for heterogeneous computing systems[J]. Journal of Grid Computing, 2015, 13(4): 507-525. DOI:10.1007/s10723-015-9331-1.