Severe illumination variation is considered to be one of the serious issues for the face image in the outdoor environment, such as the driver face image in the intelligent transportation systems[1]. Hence, it is important to address illumination variations in face recognition, especially for severe illumination variation. The face illumination invariant measures[2-4] were developed based on the lambertian reflectance model[5].
Due to the commonly-used assumption that illumination intensities of neighborhood pixels are approximately equal in the face local region, the illumination invariant measure constructed the reflectance-based pattern by eliminating illumination of the pixel face. The Weber-face[2] proposed a simple reflectance-based pattern that the difference between the center pixel and its neighbor pixel was divided by the center pixel in the 3×3 block region. The multiscale logarithm difference edgemaps (MSLDE)[3] was obtained from the multi local edge regions of the logarithm face. The local near neighbor face (LNN-face)[4] was attained from the multi local block regions of the logarithm face. In MSLDE and LNN-face, different weights were assigned to different local edge or block regions, whereas the edge-region-based generalized illumination robust face (EGIR-face) and the block-region-based generalized illumination robust face (EGIR-face) removed the weights associated with multi edge and block regions, respectively[1]. The EGIR-face and BGIR-face were obtained by combining the positive and negative illumination invariant units in the logarithm face local region.
The local binary pattern (LBP)-based approach was an efficient hand-crafted facial descriptor, and was robust to various facial variations. The centre symmetric local binary pattern (CSLBP)[6] employed the symmetric pixel pairs around the centre pixel in the 3×3 block region to code the facial feature. Recently, the centre symmetric quadruple pattern (CSQP)[7]extended the centre symmetric pattern to quadruple space, which can effectively recognize the face image with variations of illumination, pose and expression.
Nowadays, the deep learning feature is the best for face recognition, which requires massive available face images to train. VGG[8] was trained by 2.6 M internet face images (2 622 persons and 1 000 images per person). ArcFace[9] was trained by 85 742 persons and 5.8 M internet face images. As large-scale face images for training the deep learning model are collected via internet, the deep learning feature performed very well on internet face images. However, the internet face images are without severe illumination variations, and thus the deep learning feature performed unsatisfactorily under severe illumination variations[10].
In this paper,the centre symmetric quadruple pattern based illumination invariant measure (CSQPIM) is proposed to tackle severe illumination variations. The CSQPIM model is obtained by combining the positive and negative CSQPIM units, and then the CSQPIM model is used to generate several CSQPIM images of the single image. The single CSQPIM image with the arctangent function develops the CSQPIM-face. Multi CSQPIM images employ the extended sparse representation classification (ESRC) to form the CSQPIM image-based classification (CSQPIMC). Furthermore, the CSQPIM model is integrated with the pre-trained deep learning model (PDL), which is termed as CSQPIM-PDL for brevity.
1 Centre Symmetric Quadruple Pattern
The centre symmetric pattern was widely used in the LBP-based approach, and the most recent one is CSQP[7] which extended the centre symmetric pattern to quadruple space. The quadruple space is based on a 4×4 block region, which means that the CSQP codes the LBP-based facial feature in a face local region with the size of 4×4 pixels. The CSQP divided the local kernel of the size 4×4 into 4 sub-blocks of the size 2×2. Fig.1 shows the centre symmetric quadruple pattern. Suppose that m≥n, the pixel image I has m rows and n columns. In Fig.1, I(i,j) denotes the pixel intensity at location (i,j), where location (i,j) denotes the image point of the i-th row and the j-th column.

Fig.1 The centre symmetric quadruple pattern
The CSQP code[7] is calculated as
A(i,j)=27×C(I(i,j),I(i+2,j+2))+
26×C(I(i,j+1),I(i+2,j+3))+
25×C(I(i+1,j),I(i+3,j+2))+
24×C(I(i+1,j+1),I(i+3,j+3))+
23×C(I(i,j+2),I(i+2,j))+
22×C(I(i,j+3),I(i+2,j+1))+
21×C(I(i+1,j+2),I(i+3,j)+
20×C(I(i+1,j+3),I(i+3,j+1)))
(1)
(2)
where I1 and I2 are two pixels in the CSQP. From Eqs.(1) and (2), the CSQP code A(i,j) is a decimal number. The CSQP[7] can efficiently capture diagonal asymmetry and vertical symmetry in a facial image.
2 CSQP-Based Illumination Invariant Measure
One of the major contribution of the CSQP[7] is that the 4×4 face local region is employed. The even×even block region such as the 4×4 block has no centre pixel in the face local region, whereas the odd×odd block region such as the 3×3 block or the 5×5 block has a centre pixel. The current illumination invariant measure usually used the odd×odd block region. The even×even block region has never been used in the illumination invariant measure. In this paper, the 4×4 block region CSQP is extended to the illumination invariant measure.
From the lambertian reflectance model[5], the logarithm image can be presented as I(i,j) = lnR(i,j) + lnL(i,j), where R and L are the reflectance and illumination, respectively. Fig.2 shows the proposed CSQPIM pattern, which is a logarithm version of the CSQP in Fig.1. According to the commonly-used assumption of the illumination invariant measure that illumination intensities are approximately equal in the face local region, the CSQPIM units are defined as
U1=ln(I(i,j))-ln(I(i+2,j+2))=
ln(R(i,j))-ln(R(i+2,j+2))
(3)
U2=ln(I(i,j+1))-ln(I(i+2,j+3))=
ln(R(i,j+1))-ln(R(i+2,j+3))
(4)
U3=ln(I(i+1,j))-ln(I(i+3,j+2))=
ln(R(i+1,j))-ln(R(i+3,j+2))
(5)
U4=ln(I(i+1,j+1))-ln(I(i+3,j+3))=
ln(R(i+1,j+1))-ln(R(i+3,j+3))
(6)
U5=ln(I(i,j+2))-ln(I(i+2,j))=
ln(R(i,j+2))-ln(R(i+2,j))
(7)
U6=ln(I(i,j+3))-ln(I(i+2,j+1))=
ln(R(i,j+3))-ln(R(i+2,j+1))
(8)
U7=ln(I(i+1,j+2))-ln(I(i+3,j))=
ln(R(i+1,j+2))-ln(R(i+3,j))
(9)
U8=ln(I(i+1,j+3))-ln(I(i+3,j+1))=
ln(R(i+1,j+3))-ln(R(i+3,j+1))
(10)
The CSQPIM unit Uk (k=1,2,…,8) is the subtraction of the pixel pairs of the CSQPIM pattern. As illumination intensities are approximately equal in the CSQPIM pattern,the CSQPIM unit Uk can be represented by the logarithm reflectance subtraction of the CSQPIM pixel pairs, which is independent of the illumination. Hence, Uk (k=1,2,…,8) can be used to develop the illumination invariant measure.

Fig.2 The CSQPIM pattern
As Uk=0 contributes nothing to the illumination invariant measure, we divide Uk (k=1, 2,…,8) into positive CSQPIM uints (CSQPIM+) and negative CSQPIM units (CSQPIM-) in the CSQPIM pattern, where ![]() denote the positive CSQPIM unit and the negative CSQPIM unit, respectively. The CSQPIM model can be obtained as
denote the positive CSQPIM unit and the negative CSQPIM unit, respectively. The CSQPIM model can be obtained as
(11)
From Eq.(3), the CSQPIM image can be written as
(12)
where α is the weight to control the balance of positive and the negative CSQPIM units, and 0≤α≤2. From Eq.(12), the CSQPIM-face is obtained by the CSQPIM image with the arctangent function,
CSQPIM-face(i,j)=![]()
(13)
where parameter 4 is the same as that recommended in Ref.[3]. Some CSQPIM images and CSQPIM-faces are shown in Fig.3. In the first row, 5 original images with different illumination variations are from one single face. The second row contains the logarithm images of the 5 original images in the first row. Each of the third rows to the seventh row contains CSQPIM images of the 5 original images in the first row. Each of the eighth rows to the twelfth row contains CSQPIM-faces of the 5 original images in the first row. Compared with Refs.[1, 3-4], the CSQPIM image and CSQPIM-face are quite different from previous illumination invariant measures.

Fig.3 Some CSQPIM images and CSQPIM-faces under different parameters
3 Classification of the CSQPIM image
3.1 Single CSQPIM image classification
According to Refs.[1-4], the high-frequency interference seriously impacts the performance of the illumination invariant measure under the template matching classification method, which can be tackled by the saturation function well. Hence, the illumination invariant measure with the saturation function (i.e. CSQPIM-face) is more efficient than the illumination invariant measure without the saturation function (i.e. CSQPIM image) for the single image recognition by the template matching classification method, such as the nearest neighbor classifier. In this paper, The CSQPIM-face is employed to tackle the single CSQPIM image recognition under the nearest neighbor classifier, and parameter α=0.4 in Eq.(13) is adopted under severe illumination variations, which is the same as that recommended in Ref.[1].
3.2 Multi CSQPIM images classification
In many practical applications, such as the driver face recognition in the intelligent transportation systems[1], the severe illumination variation and single sample problem coexist. Similar to Ref.[1], Eq.(12) is used to generate multi training CSQPIM images of the single training image by different parameter α. Multi CSQPIM images employ the noise robust ESRC[11] to tackle severe illumination variation face recognition with a single sample problem. Multi training CSQPIM images contain more intra class variations of the single training image as shown in Fig.3, which can improve the representation ability of ESRC. In this paper, we select three CSQPIM images with α=0.4, 1, and 1.6 to form multi training CSQPIM images of each single training image, which is the same as that recommended in Ref.[1]. Accordingly, the CSQPIM image of the test image is also generated by α=1, and the CSQPIM image of each generic image is also generated by α=1.
In this paper, ESRC with multi CSQPIM images is termed as multi CSQPIM images-based classification (CSQPIMC). The homotopy method[12] is used to solve the L1-minimization problem in the CSQPIMC.
3.3 Multi CSQPIM images and the pre-trained deep learning model based classification
Similar to Ref.[1], the proposed CSQPIM model can be integrated with the pre-trained deep learning model. The ESRC can be used to classify the state-of-the-art deep learning feature. The representation residual of the CSQPIMC can be integrated with the representation residual of the ESRC of the deep learning feature to conduct the final classification, which is termed as multi CSQPIM images and the pre-trained deep learning model-based classification (CSQPIM-PDL).
In this paper, the pre-trained deep learning models VGG[8] and ArcFace[9]are adopted. Multi CSQPIM images and VGG (or ArcFace)-based classification is briefly termed as CSQPIM-VGG (or CSQPIM-ArcFace).
4 Experiments
The CSQPIM model is proposed to tackle severe illumination variations. The performances of the proposed methods are validated on the benchmark Extended Yale B[13], CMU PIE[14] and Driver[4] face databases. In this paper, all cropped face images and experimental settings are the same as those in Ref.[1]. The recognition rates of Tabs.1 and 2 are the same as those in Ref.[1] (i.e. Tabs.Ⅲ, Ⅳ and Ⅴ in Ref.[1]) except for the proposed method. Tabs.1 and 2 list average recognition rates of the compared methods on the Extended Yale B, CMU PIE and Driver. Fig.4 shows some used images from Extended Yale B, CMU PIE and Driver face databases.
The Extended Yale B face database[13] contains grayscale images of 28 persons. 64 frontal face images of each person are divided into subsets 1 to 5 with illumination variations from slight to severe. Subsets 1 to 5 consist of 7,12,12,14 and 19 images per person, respectively. As the deep learning feature requires a color face image, three RGB channels use the same grayscale image for the experiments on the Extended Yale B.
The CMU PIE[14] face database incorporates color images of 68 persons. 21 images of each person from each of C27 (frontal camera), C29 (horizontal 22.5° camera) and C09 (above camera) in CMU PIE illum set are selected. CMU PIE face images show slight, moderate, and severe illumination variations. According to Ref.[14], the pose variation of C29 is larger than that of C09.
The simulative Driver database[4] was built to research the identity recognition problem for drivers in intelligent transportation systems and can be regarded as a practical scenarios-based face database. This database incorporates 28 people with each containing 22 images (12 images indoors and 10 images in cars).
Table.1 The average recognition rates of the compared methods on the Extended Yale B face database %

MethodSubsets 1 to 3Subset 4Subset 5Subsets 4 and 5Subsets 1 to 5Weber-face[2]87.0758.6692.5277.6674.21MSLDE[3]81.3053.3581.4566.7960.27LNN-face[4]84.8361.5992.0277.9870.32CSQP[7]83.1359.0487.6774.5565.53EGIR-face[1]77.2061.6988.1274.5466.74BGIR-face[1]77.9970.1593.2782.1772.75CSQPIM-face83.3662.0394.9279.8775.80VGG[8]86.3147.1427.6730.9045.32ArcFace[9]85.5653.2830.9335.4949.71EGIRC[1]95.8875.6296.3186.8483.59BGIRC[1]96.3178.5397.3089.2786.69CSQPIMC92.8778.3797.3589.8388.66EGIR-VGG[1]98.3381.7984.3080.6982.28BGIR-VGG[1]98.4282.4582.8480.1983.53CSQPIM-VGG97.5681.5888.4383.0387.48EGIR-ArcFace[1]97.9279.4983.1379.1978.24BGIR-ArcFace[1]97.9579.1981.7378.3078.97CSQPIM-ArcFace97.1679.9289.2782.4784.58
Table.2 Average recognition rates of the compared methods on the CMU PIE and Driver face databases %
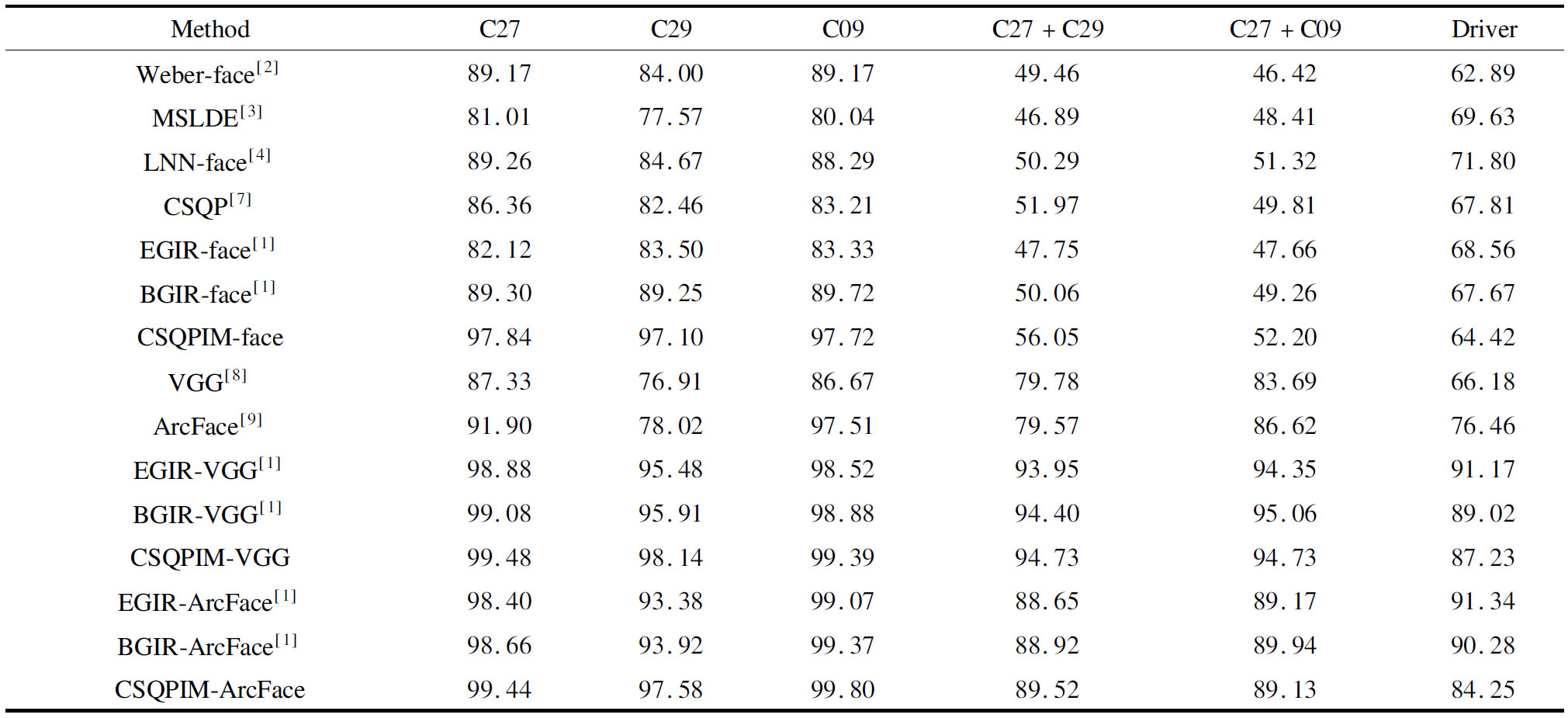
MethodC27C29C09C27+C29C27+C09DriverWeber-face[2]89.1784.0089.1749.4646.4262.89MSLDE[3]81.0177.5780.0446.8948.4169.63LNN-face[4]89.2684.6788.2950.2951.3271.80CSQP[7]86.3682.4683.2151.9749.8167.81EGIR-face[1]82.1283.5083.3347.7547.6668.56BGIR-face[1]89.3089.2589.7250.0649.2667.67CSQPIM-face97.8497.1097.7256.0552.2064.42VGG[8]87.3376.9186.6779.7883.6966.18ArcFace[9]91.9078.0297.5179.5786.6276.46EGIR-VGG[1]98.8895.4898.5293.9594.3591.17BGIR-VGG[1]99.0895.9198.8894.4095.0689.02CSQPIM-VGG99.4898.1499.3994.7394.7387.23EGIR-ArcFace[1]98.4093.3899.0788.6589.1791.34BGIR-ArcFace[1]98.6693.9299.3788.9289.9490.28CSQPIM-ArcFace99.4497.5899.8089.5289.1384.25

Fig.4 Some images from Extended Yale B, CMU PIE, and Driver face databases
4.1 Experiments on the Extended Yale B face database
The Extended Yale B face database is has extremely challenging illumination variations. Face images in subsets 1 to 3 have slight and moderate illumination variations, where subsets 1 and 2 face images have slight illumination variations, and subset 3 face images have small scale cast shadows. Face images in subsets 4 and 5 have severe illumination variations, where subset 4 face images have moderate scale cast shadows, and subset 5 face images have large scale cast shadows (or severe holistic illumination variations).
From Tab.1, CSQPIM-face outperforms EGIR-face, BGIR-face, MSLDE and LNN-face on all Extended Yale B datasets, except that CSQPIM-face lags behind BGIR-face on subset 4 and subsets 4-5, and LNN-face on subsets 1-3. Although moderate scale cast shadows of subset 4 images are not as severe as the large-scale cast shadows of subset 5 images, moderate scale cast shadows incorporate more edges of cast shadows than large scale cast shadows as shown in Fig.4. Edges of cast shadows of face images violate the assumption of the illumination invariant measure that illumination intensities are approximately equal in the local face block region.
CSQPIMC performs better than CSQPIM-face. There may be two main reasons. One is that multi CSQPIM images contain more intra class variation information than the single CSQPIM image, and the other one is that ESRC is more robust than NN under illumination variations. CSQPIMC outperforms EGIRC and BGIRC under severe illumination variations such as on subset 5, subsets 4-5 and subsets 1 to 5, whereas CSQPIMC slightly lags behind BGIRC on subset 4.
VGG/ArcFace was trained by large scale light internet face images, without considering severe illumination variations, and it performs well on subsets 1 to 3, but is unsatisfactory under severe illumination variations such as those on subsets 4 and 5. CSQPIM-VGG performs better than EGIR/BGIR-VGG on subset 5, subsets 4 and 5 and subsets 1 to 5. CSQPIM-ArcFace outperforms EGIR/BGIR-ArcFace on all Extended Yale B datasets except on subsets 1 to 5. Despite CSQPIM-VGG/ArcFace being unable to attain the highest recognition rates on all datasets, CSQPIM-VGG/ArcFace achieves very high recognition rates on all Extended Yale B datasets. Hence, the proposed CSQPIM-PDL model has the advantages of both the CSQPIM model and the pre-trained deep learning model to tackle face recognition.
4.2 Experiments on the CMU PIE face database
Some CMU PIE face images are bright (i.e. slight illumination variations), and others are partially dark (i.e. with moderate and severe illumination variations). Illumination variations of CMU PIE are not as extreme as those of Extended Yale B. From Fig.4, images in each of C27, C29 and C09 have the same pose (i.e.,frontal, 22.5° profile and downward, respectively), whereas images in each of C27+C29 and C27+C09 incorporate two face poses (i.e.,frontal pose and non-frontal pose).
From Tab.2, CSQPIM-face achieves very high recognition rates on C27, C29 and C09, and performs much better than EGIR-face, BGIR-face, MSLDE and LNN-face on all CMU PIE datasets. However, CSQPIM-face lags behind VGG/ArcFace on C27+C29 and C27+C09. It can be seen that CSQPIM-face is very robust to severe illumination variations under a fixed pose, whereas it is sensitive to pose variations. Although CSQPIM-face outperforms EGIR-face, BGIR-face, MSLDE and LNN-face under pose variations, these shallow illumination invariant approaches perform unsatisfactorily under pose variations.
However,CSQPIM-VGG/ArcFace performs very well on all CMU PIE datasets, which illustrates that the CSQPIM-PDL model can achieve satisfactory results under both severe illumination variations and pose variations. Hence, the CSQPIM-PDL model is robust to both illumination variations and pose variations. As CSQPIM-face is superior to EGIR-face and BGIR-face under severe illumination variations, CSQPIM-VGG/ArcFace is slightly better than EGIR-VGG/ArcFace and BGIR-VGG/ArcFace on C27, C29 and C09, whereas they achieve a similar performance on C27+C29 and C27+C09, since VGG/ArcFace is the dominant feature under pose variations.
4.3 Experiments on the Driver face database
The Driver face images were taken under manually controlled lighting. From Fig.4, illumination variations of Driver face images are slight and moderate, and not as severe as those of Extended Yale B and CMU PIE. From Tab.2, CSQPIM-face achieves rational recognition rates on Driver, whereas it lags behind other illumination invariant measures such as EGIR-face, BGIR-face, LNN-face, and MSLDE. Moreover, the CSQPIM-face even lags behind CSQP, which means that the CSQPIM-face cannot tackle slight and moderate illumination variations well. Hence, CSQPIM-VGG and CSQPIM-ArcFace lag behind EGIR/BGIR-VGG and EGIR/BGIR-ArcFace on Driver.
5 Conclusion
This paper proposes a CSQPIM model to address severe illumination variation face recognition. CSQPIM-face achieves higher recognition rates compared to the previous illumination invariant approaches EGIR-face, BGIR-face, LNN-face and MSLDE under severe illumination variations. CSQPIMC is effective for severe illumination variations due to the fact that multi CSQPIM images cover more discriminative information of the face image. Furthermore, the proposed CSQPIM model is integrated with the pre-trained deep learning model to have the advantages of both the CSQPIM model and the pre-trained deep learning model.
[1]Hu C H, Zhang Y, Wu F,et al. Toward driver face recognition in the intelligent traffic monitoring systems[J]. IEEE Transactions on Intelligent Transportation Systems, 2019: 1-14. to be published. DOI:10.1109/tits.2019.2945923.
[2]Wang B, Li W F, Yang W M, et al. Illumination normalization based on weber’s law with application to face recognition[J]. IEEE Signal Processing Letters, 2011, 18(8): 462-465. DOI:10.1109/lsp.2011.2158998.
[3]Lai Z R, Dai D Q, Ren C X, et al. Multiscale logarithm difference edgemaps for face recognition against varying lighting conditions[J]. IEEE Transactions on Image Processing, 2015, 24(6): 1735-1747. DOI:10.1109/tip.2015.2409988.
[4]Hu C H, Lu X B, Ye M J, et al. Singular value decomposition and local near neighbors for face recognition under varying illumination[J]. Pattern Recognition, 2017, 64: 60-83. DOI:10.1016/j.patcog.2016.10.029.
[5]Horn B K P. Robot vision [M]. Cambridge, MA,USA:MIT Press, 1997.
[6]Heikkilä M, Pietikäinen M, Schmid C. Description of interest regions with local binary patterns[J]. Pattern Recognition, 2009, 42(3): 425-436. DOI:10.1016/j.patcog.2008.08.014.
[7]Chakraborty S, Singh S K, Chakraborty P. Centre symmetric quadruple pattern:A novel descriptor for facial image recognition and retrieval[J]. Pattern Recognition Letters, 2018, 115: 50-58. DOI:10.1016/j.patrec.2017.10.015.
[8]Parkhi O M, Vedaldi A, Zisserman A. Deep face recognition[C]//Proceedings of the British Machine Vision Conference. Swansea, UK: British Machine Vision Association, 2015: 1-12. DOI:10.5244/c.29.41.
[9]Deng J K, Guo J, Xue N N, et al. ArcFace: Additive angular margin loss for deep face recognition[C]//2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Long Beach, CA, USA, 2019: 4690-4699. DOI:10.1109/cvpr.2019.00482.
[10]Hu C H, Lu X B, Liu P,et al. Single sample face recognition under varying illumination via QRCP decomposition[J]. IEEE Transactions on Image Processing, 2019, 28(5): 2624-2638. DOI:10.1109/tip.2018.2887346.
[11]Deng W H, Hu J N, Guo J. Extended SRC: Undersampled face recognition via intraclass variant dictionary[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(9): 1864-1870. DOI:10.1109/tpami.2012.30.
[12]Donoho D L, Tsaig Y. Fast solution of L1-norm minimization problems when the solution may be sparse[J]. IEEE Transactions on Information Theory, 2008, 54(11): 4789-4812. DOI:10.1109/tit.2008.929958.
[13]Georghiades A S, Belhumeur P N, Kriegman D J. From few to many: Illumination cone models for face recognition under variable lighting and pose[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2001, 23(6): 643-660. DOI:10.1109/34.927464.
[14]Sim T, Baker S,Bsat M. The CMU pose, illumination, and expression database[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2003, 25(12): 1615-1618. DOI:10.1109/tpami.2003.1251154.