Black cotton soil abounds in Kenya and is characterized by its high expansive potential when exposured to water[1-2]. The water losing shrinkage and the following soil cracking are the most commonly encountered engineering problems in light construction on such clays[3-4]. Similarly, the highway embankment constructed on expansive clays maybe cracks due to the water losing shrinkage of the foundation soil. The initial cracking behavior of the highway embankment on the expansive soil is influenced by the hydraulic and geological conditions, seasonal weather change, embankment height, burial depth of expansive soil and more. The soil movement due to water content changes in the expansive soil will result in the deformations of the upper highway embankment, and additional stress occurs in those embankment soils if their deformations are restricted. The additional tensile stress will cause cracks in the highway embankment if it exceeds the ultimate tensile strength of the soil. The cracking reduces the strength of the embankment soil, and provides a passage for rainfall infiltration[5]. In consequence, the decline of the shear strength of the soil mass leads to the slope failure of the highway embankment.
Much research on the initial cracking of the expansive soil has been performed by the laboratory test, theoretical analysis and numerical simulation to investigate the geometric shape, propagating path and depth of the crack[6-8]. Tang et al.[9] observed the water losing process of thin clay specimens and the evolution law of the soil crack. The soil crack increased slowly in the early stage of the evaporation following the fast extension, and the crack distribution on the soil surface tended to be stable when the moisture content was close to the shrinkage limit of the clays. The crack extension was obviously influenced by the air temperature, and there was a high crack development at the high air temperature than the low air temperature. With the help of the discrete element code, Jun et al. [10] researched the cracking mechanisms and development. Wu et al. [11] calculated the change in the moisture content of clays and the initial cracking depth of the soil surface using the humidity stress field theory. Unfortunately, the focus of the research is on the water losing shrinkage and cracking of the clays, but the embankment soil cracking due to water losing shrinkage of the expansive soil foundation attracts less attention. Therefore, it is necessary to investigate the initial cracking of highway embankment to determine the replacement depth of the BCS foundation.
This paper presents the results of numerical research to investigate the influence of the embankment height, BCS thickness and replacement depth of BCS on the initial cracking behavior of the highway embankment based on the coupled consolidation theory for unsaturated soils, using Abaqus 6.11 codes. As same as the highway embankment of the Southern Bypass in Nairobi, the numerical model was established to investigate the initial cracking depth of the highway embankment through the change in the maximum principal stress due to the water losing shrinkage of the BCS foundation. For proposing the rational replacement depth of the BCS foundation, the tensile stress distribution within the low embankment on deep BCS was analyzed.
1 Modelling the Water Losing Shrinkage of Clays
1.1 The coupled consolidation theory for unsaturated soils
Fredlund et al.[12]proposed the constitutive relationships for volume change in unsaturated soils by using the following two stress state variables:
(1)
(2)
where dεv is the volumetric strain of the clays; dθ is the change in volumetric moisture content; σm is the mean net normal stress; ua is the pore air pressure; uw is the pore water pressure; σm-ua is the mean normal stress; ua-uw is the matric suction; ![]() is the coefficient of water change related to the matric suction.
is the coefficient of water change related to the matric suction.
Using the mean normal stress and matric suction, the void ratio and moisture content can be defined as
e=f(σm-ua, ua-uw)
(3)
(4)
where e is the void ratio of the clays; w is the gravimetric moisture content; Gs is the specific gravity of the clays; f and g are the arbitrary functions.
The volumetric strain and change in the moisture content of the unsaturated soils can be written as
(5)
(6)
The compression coefficients can be calculated by Eqs. (1), (2), (5) and (6) and written as
(7)
(8)
(9)
(10)
The water continuity equation of the unsaturated soil can be obtained by soil water mass conversation if the water is assumed to be incompressible.
(11)
where ρw is the density of water; ρd is the dry density of the soils; g is the acceleration of gravity; k is the hydraulic conductivity; Cw is the specific water capacity of the soils.
1.2 Constitutive surface for unsaturated soils of BCS
1.2.1 Properties of BCS
The BCSs were sampled from a site at a depth of 1.0 m below the organic matter located at the Southern Bypass in Nairobi. The properties of BCS measured in accordance with JTG 3430—2020[13] are presented in Tab.1. BCS was characterized by the high clay content, plasticity index and water swelling potentiality.
Tab.1 Engineering properties of BCS
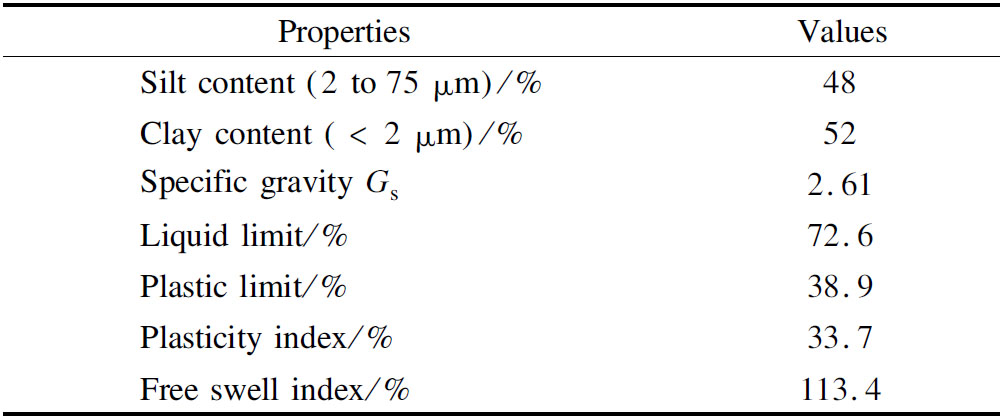
PropertiesValuesSilt content (2 to 75 μm)/%48Clay content (< 2 μm)/%52Specific gravity Gs2.61Liquid limit/%72.6Plastic limit/%38.9Plasticity index/%33.7Free swell index/%113.4
1.2.2 Test methods
The specific gravity of soils was measured in accordance with T0112—1993 (JTG 3430—2020) [13], and the test results are presented in Tab.1.
The swell-consolidation test was performed by following the Chinese standard[13]. The specimens (61.8 mm diameter and 20 mm length) were firstly prepared at a natural moisture content and dry density. Then, the specimens were placed in a consolidator. After soaking in water, the specimens would expand vertically under the pre pressure of 1 kPa. After expansion was stabilized, the specimens were loaded. The load grade and stability standard under each level of load met the requirements of T0125—1993 (JTG 3430—2020).
The free shrink test was performed on the cylindrical specimens (61.8 mm diameter and 20 mm length) in accordance with the method proposed by Briaud et al[14]. The specimens were prepared at optimum moisture content and maximum dry density. After vacuum saturation, the specimens were pressed out from the ring-knife with a permeable stone, and the size and mass of the specimens were measured. The thickness and diameter were measured every 120 ℃ along the specimen surface. Then, the specimens were placed vertically on the test bench for free shrinkage. The changes in the mass, thickness and diameter of the specimen with time were recorded. Finally, the specimens were oven-dried to measure the weight.
The suction of soils was measured by using the Whatman Grade 42 quantitative filter paper according to the existing research[15]. The specimens (61.8 mm diameter and 20 mm length) with different moisture contents were firstly prepared. Three pieces of filter paper (55 mm diameter) were overlapped on the upper surface of the lower specimen, and then the upper specimen was placed above the filter paper and pressed lightly to make the filter paper and the specimens in close contact. The upper and lower specimens were tightly wrapped with plastic film and then sealed with wax, and placed in a constant temperature environment for 12 d. After the water exchange between the filter paper and the sample was balanced, the filter paper was taken out and weighed before and after drying. The test procedure of the measuring suction of BCS using filter paper is shown in Fig.1. The matric suction of BCS under different moisture contents can be calculated by the calibration relationship between the equilibrium moisture content of the filter paper and the corresponding matric suction.
1.2.3 Boundary curves and constitutive surfaces
Six boundary curves are needed to construct the constitutive surface for the unsaturated soils of BCS. The void ratio versus the mean normal stress curve (e vs. (σm-ua)), moisture content versus the matric suction curve (w vs. (ua-uw)) and free shrinkage curves (e/S vs. w) were obtained by the swell-consolidation test, suction test and free shrinkage test, respectively. Here, S is the degree of saturation. The test results and the regression curves are presented in Fig.2. During the one-dimensional consolidation test, for any mechanical stress level, S=100%. Hence, the moisture content versus the mean normal stress curve (w vs. (σm-ua)) can be obtained by applying the relationship Se=wGs. The w vs. (ua-uw) curve and e vs. w curve are combined together to obtain the void ratio versus matric suction curve (e vs. (ua-uw)). Once e vs. (ua-uw) curve is obtained, the degree of saturation versus the matric suction curve (S vs. (ua-uw)) can be established by combining the w vs. (ua-uw) curve and the relationship Se=wGs. So far, six boundary curves, namely e vs. (σm-ua), w vs. (σm-ua), S vs. (σm-ua), e vs. (ua-uw), w vs. (ua-uw) and S vs. (ua-uw) curves, have been established completely.

(a)

(b)

(c)
Fig.1 Test procedure of measuring suction of BCS by filter paper.(a) Specimens and filter paper; (b) Wrapped with plastic film; (c) Sealed with wax
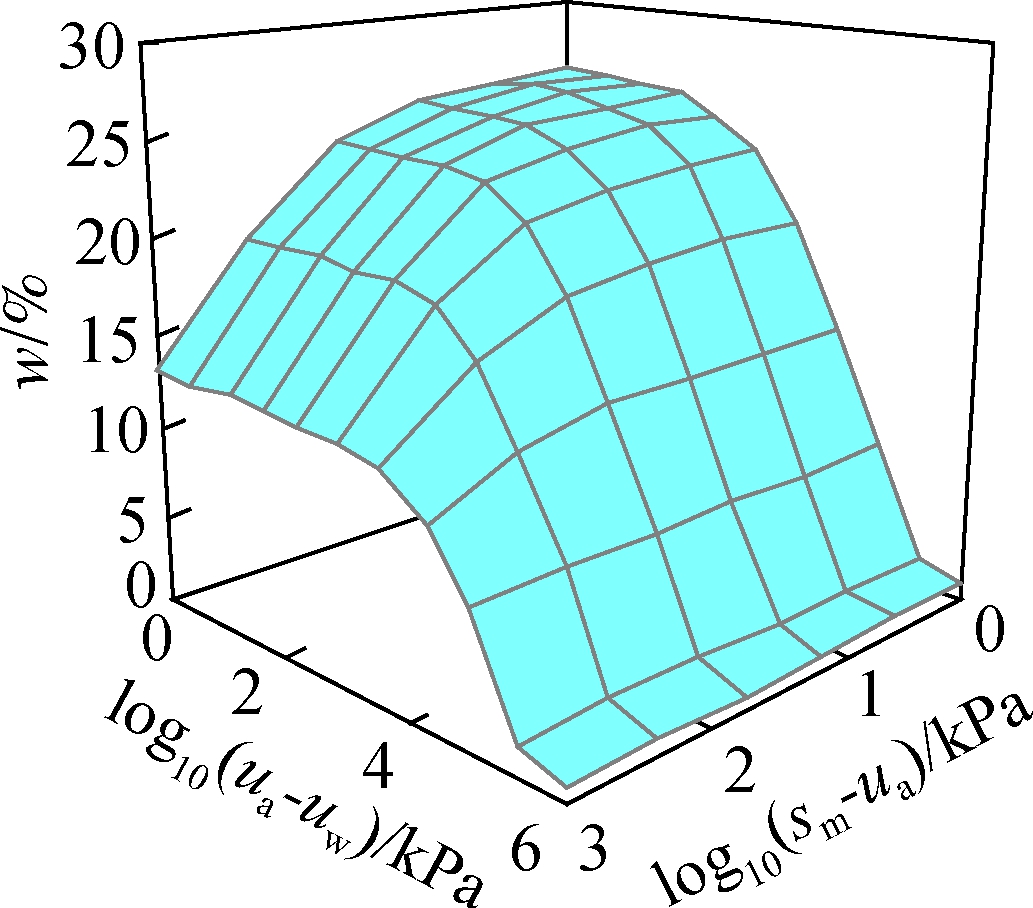
The straight-line interpolation was performed to construct the constitutive surface for the unsaturated soils of BCS using those curves as the boundary curves. The constitutive surface for the unsaturated soils of BCS is presented in Fig.3.

(a)

(b)

(c)
Fig.2 Experimental results for BCS and regression curves. (a) e vs. (σm-ua); (b) w vs. (ua-uw); (c) e/S vs. w

(a)
(b)

(c)
Fig.3 Constitutive surface of BCS. (a) Void ratio constitutive surface;(b) Degree of saturation constitutive surface;(c) Water content constitutive surface
1.3 Unsaturated hydraulic conductivity
The direct measurement of the hydraulic conductivity of the unsaturated soil is very difficult. Many indirect predictive methods of unsaturated hydraulic conductivity were proposed based on the size and shape distribution of soil porosity. The hydraulic conductivity of the unsaturated soil can be predicted by the soil-water characteristic curve (w vs.(ua-uw)) if the saturated hydraulic conductivity of the clays is known.
Three methods such as Green R E model, van Genuchten M model and Fredlund and Xing model have been widely employed in the prediction of the unsaturated hydraulic conductivity. Here, the van Genuchten M model was employed to predict the unsaturated hydraulic conductivity of BCS, which can be written as[16]
(12)
where K(ua-uw) is the unsaturated hydraulic conductivity of the clays related to the matric suction; Ks is the saturated hydraulic conductivity of the clays; a,m and n are regression parameters, m=1-1/n.
The unsaturated hydraulic conductivity of BCS is presented in Fig.4. Here, Ks,a,m,and n are 2.95×10-9 m/s,0.002,0.206, and 1.26, respectively.
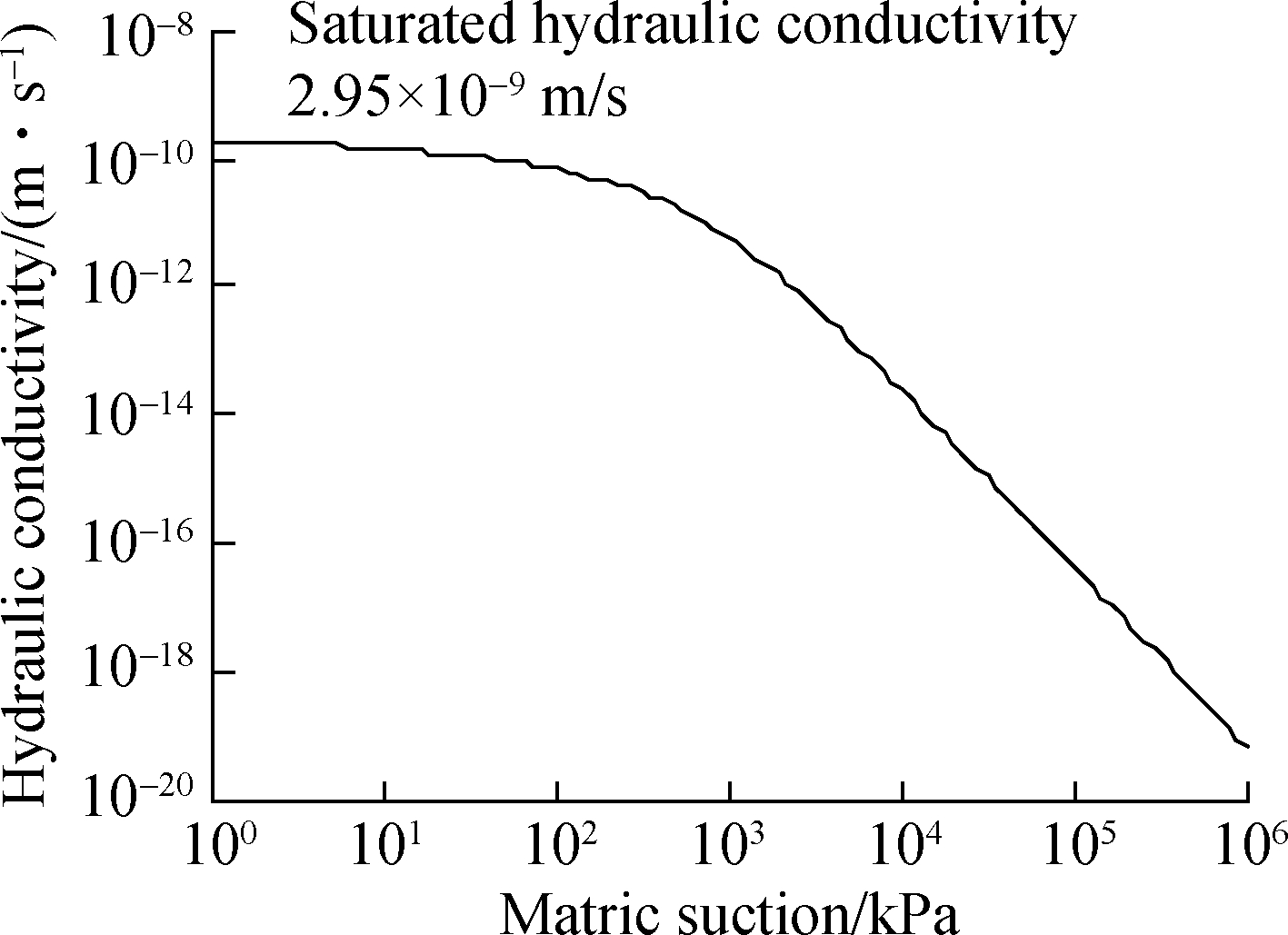
Fig.4 Variation of hydraulic conductivity with matric suction for BCS
2 Numerical Simulation of Highway Embankment on BCS
The unsaturated seepage and stress changes in the highway embankment constructed on the BCS foundation were simulated based on the coupled consolidation theory for unsaturated soils, using the coupled thermal stress method since it is similar to the coupled hydro-mechanical stress problem. For the validation of the coupled consolidation theory for unsaturated soils, the numerical model of the BCS specimen used in the free shrinkage test was developed to simulate the free shrinkage of BCS by Abaqus 6.11 codes.
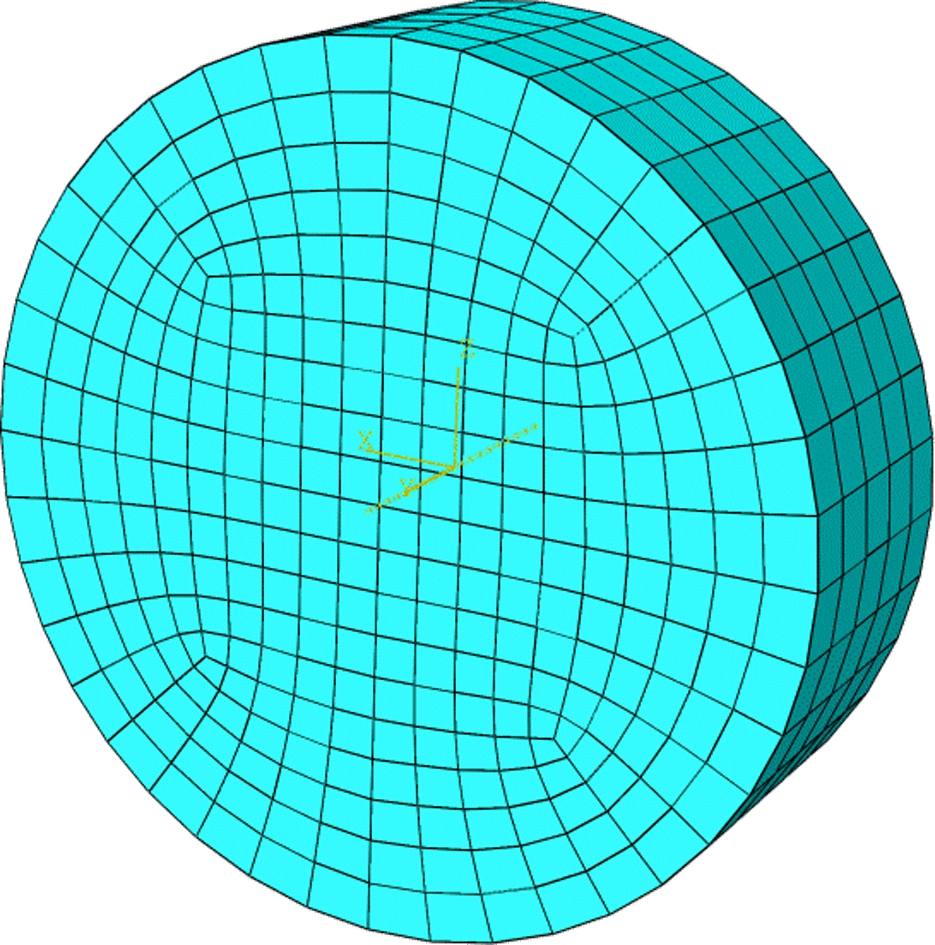
The size of the numerical model was the same as the laboratory specimen (61.8 mm diameter and 20 mm height). The material properties were calculated by the constitutive surfaces for BCS presented in Fig.3. The meshes of the model and boundary conditions are presented in Fig.5. The element types C3D8R, which are continuum stress/displacement, three-dimensional, linear hexahedron element types with heat flux being allowed, were used to simulate the free shrinkage of the BCS specimen. The same conditions as the laboratory test on the test table were considered. The nodes on the contact surface of the BCS specimen with the platform were fixed in all directions. The other nodes on the side face and curved surface can be free to move in all directions, and were influenced by the evaporation. The evaporation intensity was fixed at 2×10-8 m/s due to the lack of the aerodynamic effect. The free shrinkage test was performed after the vacuum saturation of BCS specimen, so the initial matric suction was assumed to be 10 kPa. Fig.6 presents the simulated results and test data of the free shrinkage of BCS. The void ratio and degree of saturation versus moisture content curves are roughly identical to the test results.
(a)
(b)
Fig.5 Numerical model for free shrinkage test. (a) Meshes;(b) Boundary conditions
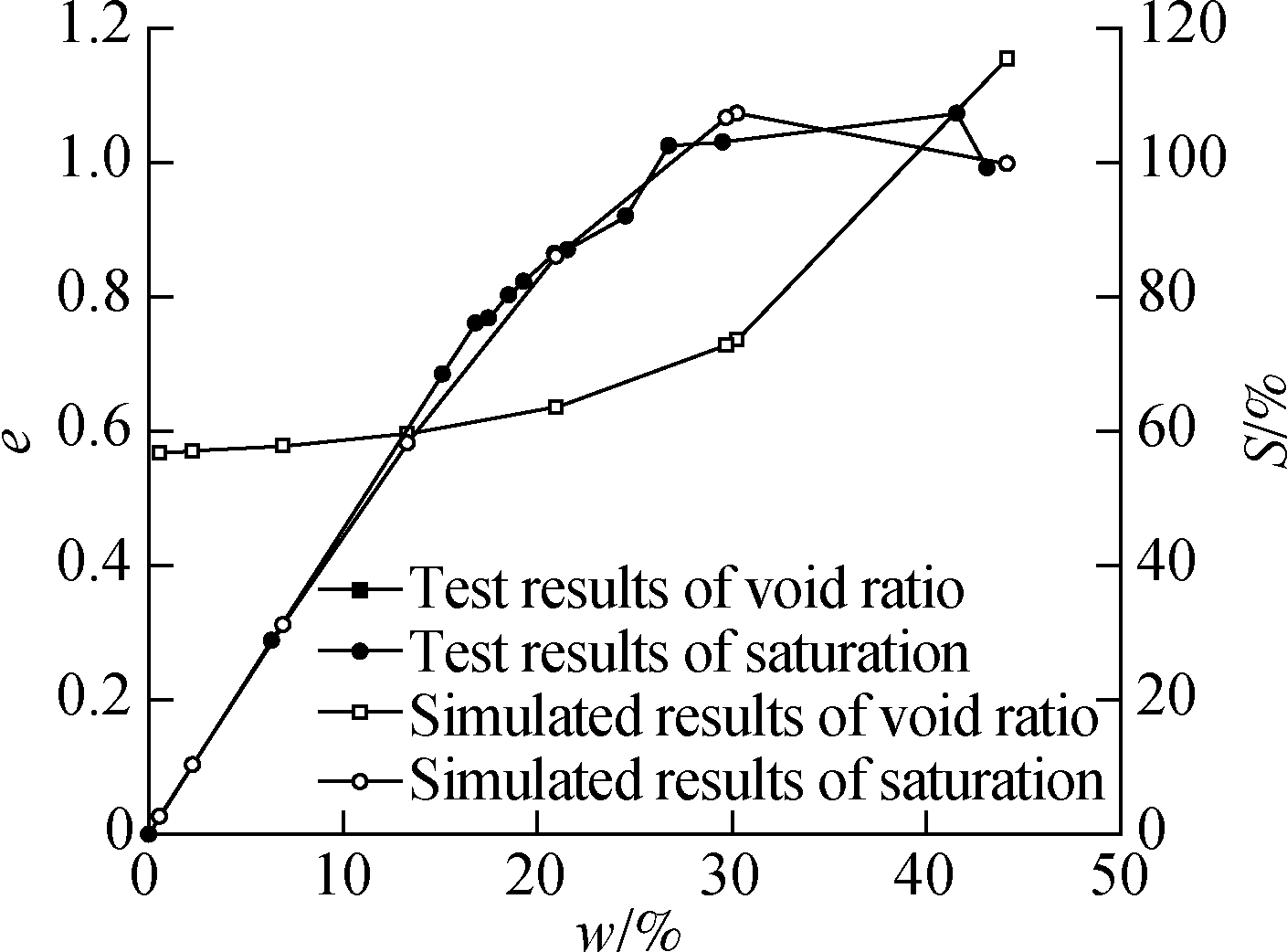
Fig.6 Comparison of numerical simulation of free shrinkage and test results
For investigating the initial cracking of the highway embankment on the BCS foundation, Abaqus/Standard was used to build the finite element model of a subgrade section in Nairobi to analyze the change in the maximum principal stress of embankment soil due to the water losing shrinkage of the BCS foundation. The simulation was performed by a main program and four user subroutines including USDFLD, UMAT, UMTHT and UEXPAN. With the help of FORTRAN, USDFLD was used to read the net normal stress and matric suction of every node from the main program, and calculate the material parameters of the subgrade soils based on the constitutive relation for unsaturated soils. Those material parameters included the elasticity modulus, expansion coefficient, compression coefficient and unsaturated hydraulic conductivity. The unsaturated hydraulic conductivity, coefficient of water change related to the matric suction and the change in mean normal stress were inputted into UMTHT to calculate the unsaturated seepage. The elasticity modulus was inputted into UMAT to update the stiffness matrix. The expansion coefficient was inputted into UEXPAN to calculate the change in the thermal stress.
The finite element model was the same as the subgrade section of the Southern Bypass in Nairobi, the width and slope degree of which were 23 m and 1∶1.75, respectively. Fig.7 shows the meshes and boundary conditions of the highway embankment model. The element types CPE4T, which are continuum stress/displacement, two-dimensional, linear plane element types with heat flux being allowed, were employed in the simulation. All the nodes on the bottom surface were fixed in the x and y directions, and the nodes on the two sides of the BCS foundation were fixed in the x direction. The evaporation continued on the two slope surfaces and the exposed BCS foundation surface, and the evaporation intensity was fixed at 5×10-8 m/s, which was close to the value calculated by the FAO-56 Penman-Monteith method, using the temperature, dew point temperature, solar radiation and wind speed [17]. The initial suction of the subgrade was assumed to be 10 kPa since the simulation started after the long-term rainfall. For simplification of the model, the unsaturated properties of the filling soils were not considered, and the conventional material parameters were used. Elasticity modulus E was 10 MPa, Poisson’s ratio μ was 0.35, hydraulic conductivity K was 1×10-10 m/s, specific water capacity Cw was 1×10-5 m/s, and expansion coefficient a was 1×10-10 m/s.

Fig.7 Finite elements and boundary conditions for a typical embankment section(unit:m)
3 Results and Discussion
3.1 The influence of replacement depth of deep BCS on embankment cracking
The highway embankment on BCS will crack if the tension stress caused by the soil shrinkage of the foundation is larger than the stress threshold of the soil cracking. Therefore, the maximum principal stress at the peak and its location were analyzed to study the initial cracking of the highway embankment, and the stress threshold of the soil cracking was fixed at 10 kPa[18].
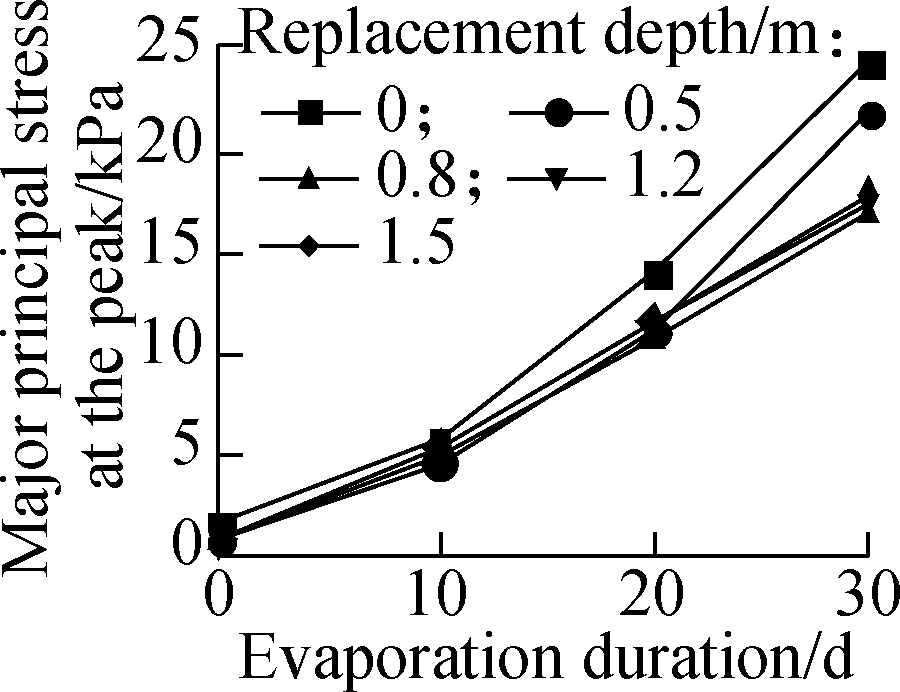
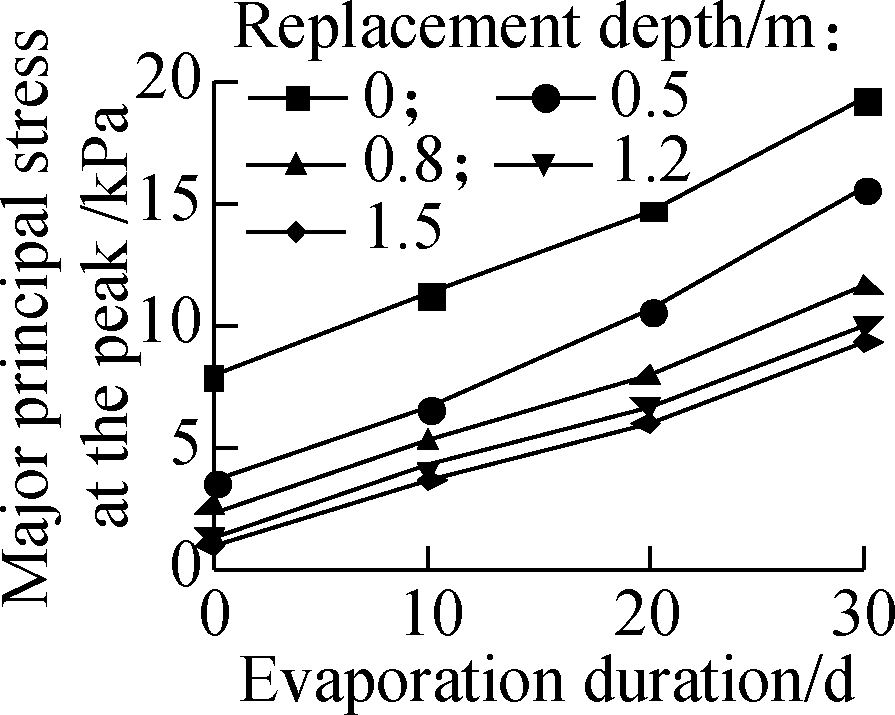
Fig.8 shows the effect of the replacement depth of deep BCS on the major principal stress at the peak on the top of the highway embankment at different heights. The evaporation intensity was fixed at 5×10-8 m/s, and the burial depth of BCS was fixed at 4 m in the simulation. The major principal stress at the peak decreases with the increase in highway embankment height and the replacement depth of BCS foundation. For 1 and 2 m high highway embankment, the increase in the replacement depth of BCS foundation has little effect on the major principal stress at the peak after the replacement depth reaches 0.8 m. For 3 and 4 m high highway embankment, the key replacement depth of the BCS foundation which controls the major principal stress at the peak is found to be 1.2 m.
(a)
(b)

(c)
(d)
Fig.8 Effect of replacement depth of BCS on major principal stress at the peak of embankment at different heights.(a) 1 m;(b) 2 m;(c) 3 m;(d) 4 m
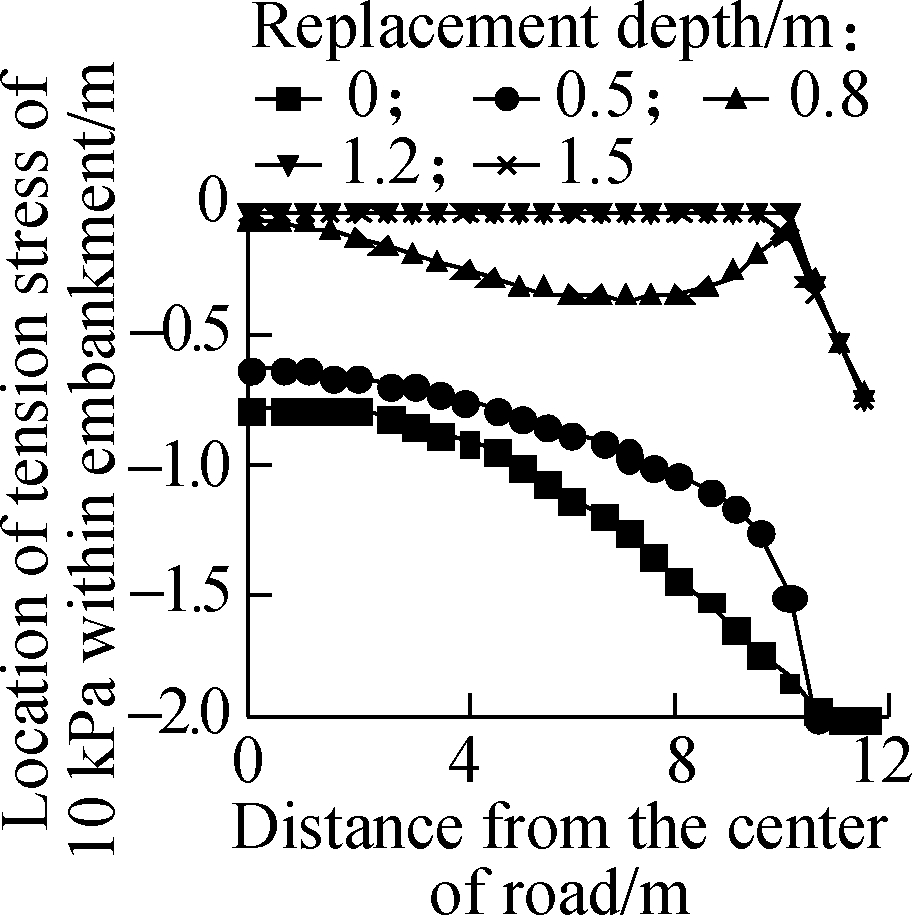
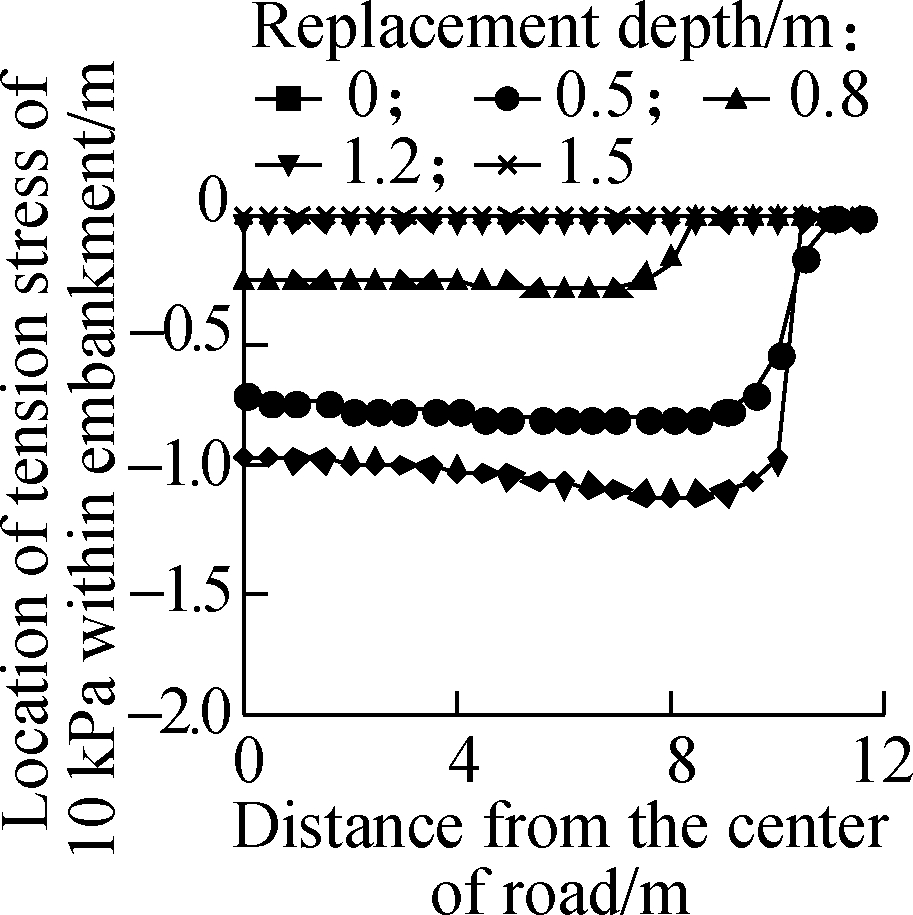
After 30 d of soil surface evaporation, the effect of the replacement depth of deep BCS on the initial cracking of the highway embankment at different heights is shown in Fig.9. The crack area and depth of the highway embankment decrease with the increase in the replacement depth of the BCS foundation. For 1 m high highway embankment, the crack which penetrates the embankment also occurs even if the replacement depth of the BCS foundation reaches 1.5 m. Therefore, when the height of the highway embankment is less than 1 m, more replacement measures should be employed except those for replacing the BCS with the non-expansive filling to further help reduce the effect of BCS shrinkage on the initial cracking of the highway embankment. For 2 m high highway embankment, after the replacement depth reaches 1.2 m, only the shallow cracking occurs at the road shoulder site, and cannot severely damage the whole highway embankment. The initial cracking has not occurred on the 2 and 3 m high highway embankment after the replacement depth of the BCS foundation reached 1.2 m.

(a)
(b)
(c)

(d)
Fig.9 Effect of replacement depth of BCS on initial cracking of the embankment at different heights. (a) 1 m;(b) 2 m;(c) 3 m;(d) 4 m
3.2 The influence of the replacement depth on the initial cracking of low embankment
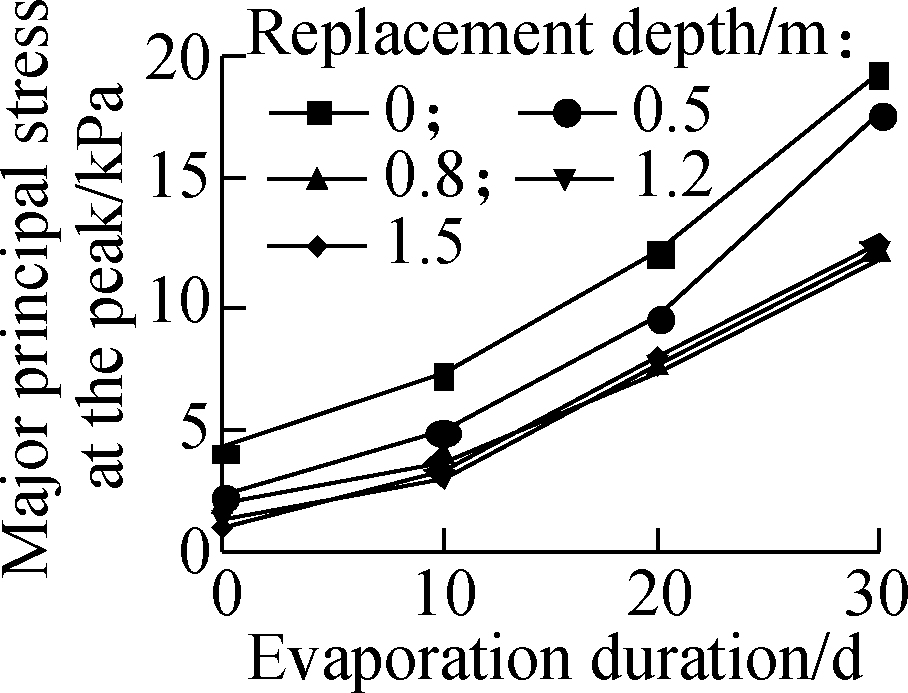
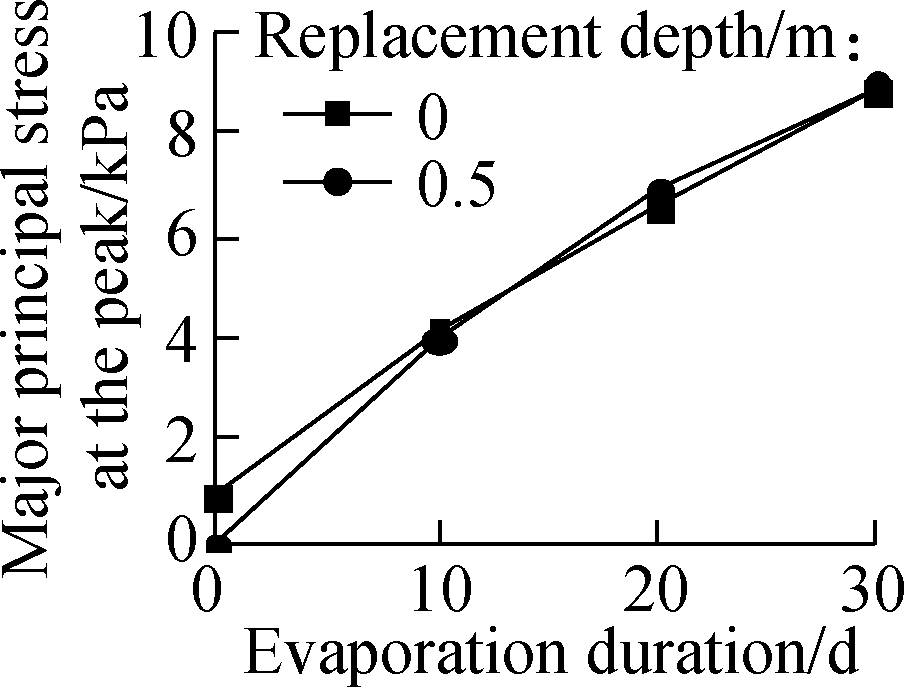
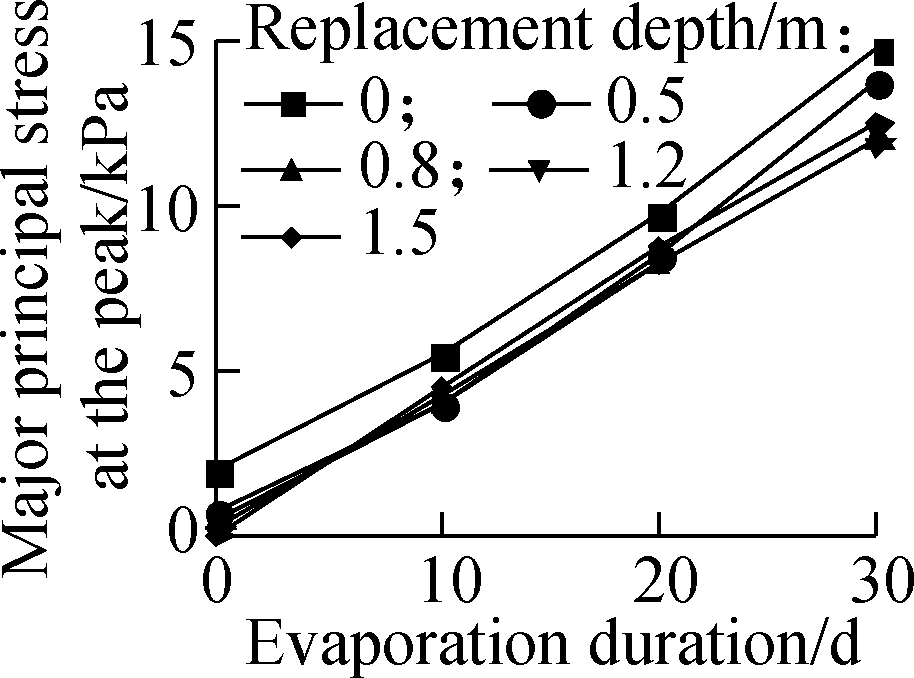
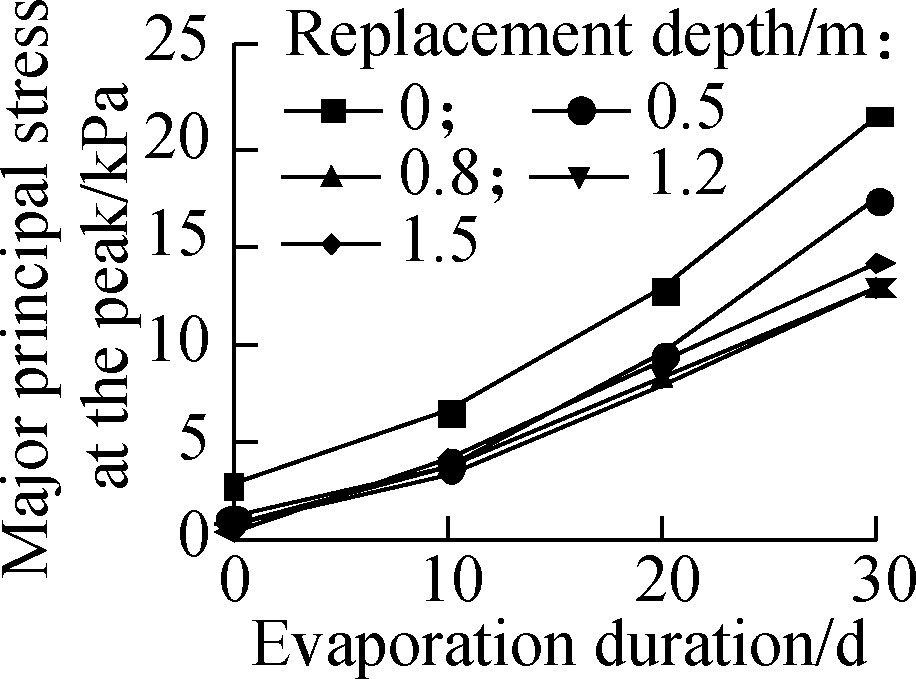
Fig.10 shows the influence of BCS replacement depth on the major principal stress at the peak on the top of the highway embankment at different burial depths of BCS. The evaporation intensity was fixed at 5×10-8 m/s, and the highway embankment height was fixed at 2 m in the simulation. The major principal stress at the peak on the top of the highway embankment increases with the increase in the burial depth of BCS, and decreases with the increase in the replacement depth of the BCS foundation. For 1 m thick BCS, the major principal stress at the peak on the top of the highway embankment is less than the stress threshold of the soil cracking after 30 d of soil surface evaporation even if the BCS foundation has not been treated. After the burial depth of BCS be comes larger than 2 m, the increase in the replacement depth has a small effect on the major principal stress at the peak of the highway embankment after the BCS replacement depth reaches 0.8 m. This behavior is attributed to the active zone of BCS in the range of 1.5 to 2.0 m under atmospheric effect.
(a)
(b)
(c)

(d)
Fig.10 Effect of BCS thickness and its replacement depth on major principal stress at the peak of embankment. (a) 1 m;(b) 2 m;(c) 3 m;(d) 4 m
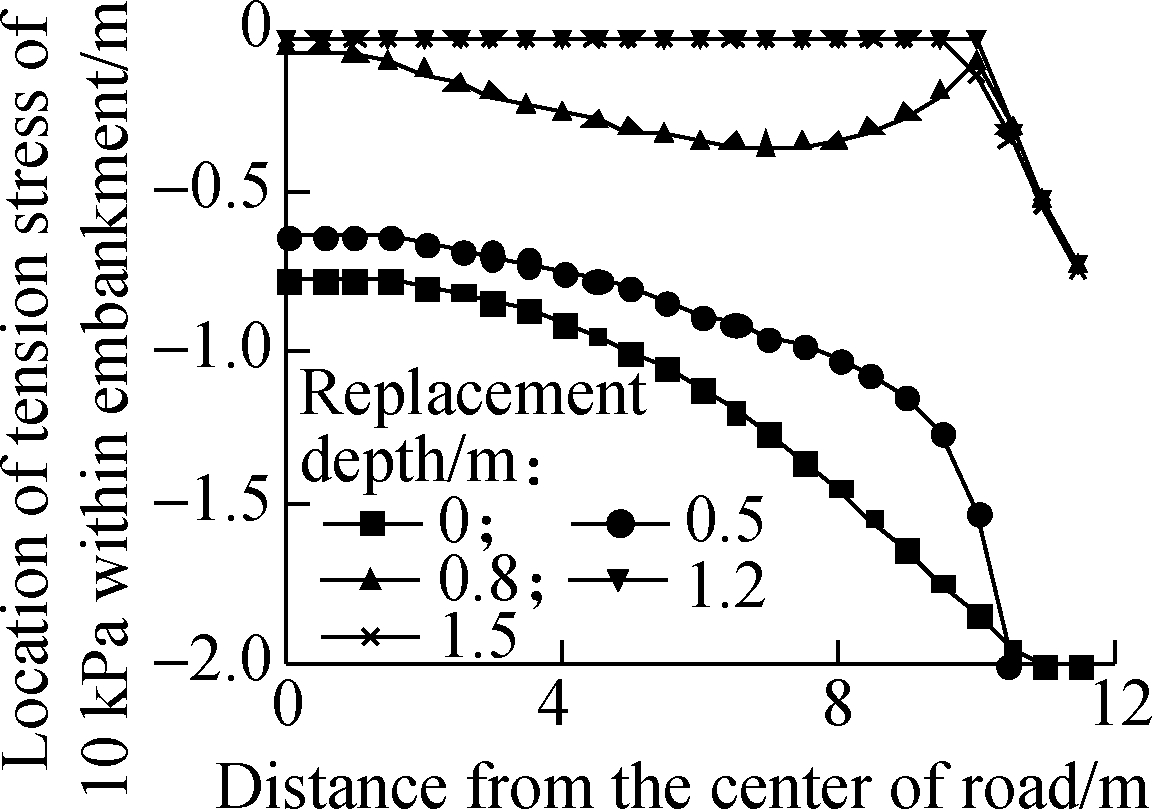
After 30 d of soil surface evaporation, the effect of the replacement depth of BCS on the initial cracking of the low highway embankment at different burial depths of the BCS is shown in Fig.11. The crack area and depth of the highway embankment tend to decrease with the increase in the replacement depth of the BCS foundation. The highway embankment cannot crack even if the BCS replacement has not been performed when the burial depth of the BCS is 1 m. After the replacement depth of 2 m thick BCS is larger than 0.8 m, only a small area located at the road shoulder cracks shallowly, and the increase in the BCS replacement depth has small effect on the initial cracking of the highway embankment. For the low highway embankment on 3 and 4 m thick BCS, the crack area and depth show a further increase, and considerable decrease after the BCS replacement depth reaches 1.2 m.

(a)

(b)
(c)
Fig.11 Effect of BCS thickness and its replacement depth on the initial cracking of the embankment. (a) 2 m;(b) 3 m;(c) 4 m
3.3 Rational replacement depth of BCS foundation
The effect of the BCS replacement depth on the initial cracking of the highway embankment varies greatly when the embankment height and the burial depth of BCS are different, and there is a key BCS replacement depth at which the cracking position and depth of the highway embankment on BCS can be controlled. For the highway embankment in the height range of 1 to 4 m on the deep BCS, the key values of the BCS replacement depth are 1.2 and 1.5 m, respectively. For the low highway embankment on the BCS with a burial depth of 2, 3 and 4 m, the key values of the BCS replacement depth are 0.8 and 1.2 m, respectively. On the basis of those key values of the BCS replacement depth, the rational BCS replacement depth presented in Tab.2 can be obtained from the perspective of controlling the initial cracking of the highway embankment and construction cost.
Tab.2 Rational replacement depth of the BCS foundation

Deep BCS layerLow embankmentEmbankmentheight/mReplacementdepth/mBCSthickness/mReplacementdepth/m≤1.0≥1.5≤1.0Surface cleaning1 to 3≥1.21 to 3≥0.8≥3.01.2≥3.0≥1.2
4 Conclusions
1) For the highway embankment on the deep BCS, the major principal stress and the cracking depth of the highway embankment decrease with the increase in the BCS replacement depth, and the key values of the BCS replacement depth for controlling the cracking position and depth of the highway embankment on deep BCS are 1.2 and 1.5 m.
2) For the low highway embankment on the BCS at different burial depths, the major principal stress and the cracking depth of the highway embankment increase with the increase in the BCS thickness, and decrease with the increase in the replacement depth of the BCS foundation. The key values of BCS replacement depth of the low highway embankment on 2, 3 and 4 m thick BCS are 0.8, 1.2 and 1.2 m, respectively.
3) The rational replacement depth of the BCS foundation was proposed from the perspective of controlling the cracking position and depth of the highway embankment on BCS.
[1]Miao S D, Shen Z P, Wang X L, et al. Stabilization of highly expansive black cotton soils by means of geopolymerization[J].Journal of Materials in Civil Engineering, 2017, 29(10): 04017170. DOI:10.1061/(ASCE)MT.1943-5533.0002023.
[2]Miao S D, Shi J Z, Sun Y B, et al. Mineral abundances quantification to reveal the swelling property of the black cotton soil in Kenya[J].Applied Clay Science, 2018, 161: 524-532. DOI:10.1016/j.clay.2018.02.003.
[3]Cheng Y Z, Huang X M, Li C, et al. Soil-atmosphere interaction as triggering factors of openings between embankment and pavement[J].KSCE Journal of Civil Engineering, 2018, 22(5): 1642-1650. DOI:10.1007/s12205-017-0679-6.
[4]Wang X Y, Yu X L, Song H, et al. Research on the replacement depth and treatment method of black cotton soil in Ethiopia[J]. Highway, 2017, 62(3): 7-12.(in Chinese)
[5]Galeandro A, Doglioni A, Simeone V, et al. Analysis of infiltration processes into fractured and swelling soils as triggering factors of landslides[J].Environmental Earth Sciences, 2014, 71(6): 2911-2923. DOI:10.1007/s12665-013-2666-7.
[6]Li G W, Li Y S, Yuan J P, et al. Crack development rule of expensive soil and its influence factors in river slope of Project of Leasing Water from Yangtze to Huai River[J]. Transactions of the Chinese Society of Agricultural Engineering, 2018, 34(12): 154-161. (in Chinese)
[7]Mao X, Wang S J, Cheng M S, et al. Mechanical behavior of expansive soil under initial damage and wetting-drying cycles[J]. Rock and Soil Mechanics, 2018, 39(2): 571-579. DOI:10.16285/j.rsm.2017.1136. (in Chinese)
[8]Nan C P, Tian J Y, Zhang J, et al. Analysis of crack characteristics of fiber-reinforced expansive soil under wetting-drying cycle[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(2): 392-400. (in Chinese)
[9]Tang C S, Cui Y J, Tang A M, et al. Shrinkage and desiccation cracking process of expansive soil and its temperature-dependent behavior[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(12): 2181-2187. (in Chinese)
[10]Jun S M, Jiang M J, Zhou C B. Numerical simulation of desiccation cracking in a thin clay layer using 3D discrete element modeling[J].Computers and Geotechnics, 2014, 56: 168-180. DOI:10.1016/j.compgeo.2013.12.003.
[11]Wu J H, Yuan J P, Lu T H. Analysis of initial cracking behavior of expansive soil due to moisture change stress[J]. Rock and Soil Mechanics, 2011, 32(6): 1631-1637. DOI:10.16285/j.rsm.2011.06.048. (in Chinese)
[12]Fredlund D G, Rahardjo H. Soil mechanics for unsaturated soils[M]. New York: John Wiley & Sons, 1993.
[13]Ministry of Transport of the People’s Republic of China. JTG 3430—2020 Test methods of soils for highway engineering[S]. Beijing: China Communications Press, 2020. (in Chinese)
[14]Briaud J L, Zhang X, Moon S. Shrink test-water content method for shrink and swell predictions[J].Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(7): 590-600. DOI:10.1061/(asce)1090-0241(2003)129:7(590).
[15]Huang Z Q, Yue K X, Li H, et al. Determination of soil-water characteristic curve of unsaturated expansive soils using filter paper method[J]. South-to-North Water Transfers and Water Science & Technology, 2015, 13(3): 82-486. (in Chinese)
[16]van Genuchten M T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal, 1980, 44(5): 892-898. DOI:10.2136/sssaj1980.03615995004400050002x.
[17]Cheng Y Z, Huang X M, Li C, et al. Field and numerical investigation of soil-atmosphere interaction at Nairobi, Kenya[J].European Journal of Environmental and Civil Engineering, 2017, 21(11): 1326-1340. DOI:10.1080/19648189.2016.1169224.
[18]Zheng J L, Yang H P. Expansive soil engineering of highway[M]. Beijing: China Communications Press, 2009. (in Chinese)