Joint replenishment is an important method to reduce purchasing costs, which has been adopted by many enterprises. For example, Suning and Tmall first jointly purchased some goods in 2016 to save procurement and management costs. Baiyun Mountain and other six pharmaceutical enterprises plan to set up a joint procurement platform to introduce agents and strategic products for each member enterprise and reduce enterprises’ purchasing costs. The General Motors and Peugeot Citroen Group (PSA Peugeot Citroen Group) announced a global purchasing company with estimated annual savings of two billion dollars through joint procurement of raw materials and standardized components[1]. In 2019, the Beijing, Tianjin and Hebei Medical Insurance Bureau jointly issued Beijing-Tianjin-Hebei medical consumables combined with the procurement work opinion, which is expected to be included in the pilot scope of medical consumables varieties, and the reduction of price was more than 50%. Due to the inconsistency of lead time and replenishment cycle, the same product has the same replenishment cycle when the enterprise carries out joint replenishment. The fixed cost of replenishment is shared among the enterprises. Therefore, it is necessary to minimize the cost of joint replenishment per unit time and solve the cost allocation problem.
The research on joint replenishment has been mainly devoted to optimizing total costs and searching for the replenishment cycle of the cooperative alliance. Joint replenishment can be defined as reducing procurement costs by coordinating orders for multiple products to achieve economies of scale[2-3]. It can also be defined as retailers placing joint orders with one supplier to reduce purchase prices and save ordering costs[4]. Therefore, joint replenishment is regarded as a joint order of one or more items to reduce replenishment costs. It includes the joint replenishment of a single item[5] and the joint replenishment of multi-items[6]. The joint replenishment of a single item usually considers multiple periods in the research, and products of all retailers are ordered together. Multi-items joint replenishment strategies include the direct grouping strategy and the indirect grouping strategy. The direct grouping strategy means that products are randomly divided into the set group; the restocking cycle of the same group of products is the same; and the replenishment cycle of each group needs to be decided[7]. The indirect grouping strategy is to set a basic replenishment cycle. The replenishment cycle of all products is the integer times of the basic replenishment cycle, and the decision maker needs to make decisions on the basic replenishment cycle and each product cycle[8]. From the point of view of replenishment costs, van Eijs et al.[9-10] considered that the indirect grouping strategy is better than the direct grouping strategy.
Cost allocation is another research direction on joint replenishment, and the rationality of the cost allocation scheme will directly affect whether joint replenishment can be carried out and implemented. Meca et al.[11] designed the cost allocation scheme based on the cooperative game theory for joint replenishment with deterministic demand, no major setup cost, and zero lead time. Anily et al.[12] proposed a cost allocation scheme of joint replenishment with deterministic demand and zero lead time. Dror et al.[13] put forward the concept of product aggregation and pointed out that the core of the corresponding cooperative game is non-empty. Dror et al.[14] further analyzed the sensitivity of the parameters of the joint replenishment problem of the inseparable product set, and concluded that the game’s indivisibility occurs more likely than the concave. Ye et al.[15-16] presented the EOQ model of joint replenishment interval value and put forward the allocation scheme of proportion surplus allocation value. They also proposed the EOQ model of joint replenishment interval-value considering shortage cost and the cost allocation method of the variable-weight Shapley value. Chen et al.[17-18] constructed the linear programming model of joint replenishment and gave the allocation scheme of dual solution. Although some cost allocation rules are given in the above literature, cost allocation rules are generally not universally applied owing to some flaws. For example, the Shapley value with the large scale of the cooperative alliance is obtained after a long time and it may not be in the core of the corresponding cooperative game. Also, only by constructing a linear programming model, can the dual solution be guaranteed to be in the core of the cooperative game. Furthermore, there is a limitation in the literature on the cost allocation scheme of joint replenishment. The lead time is assumed to be zero in those studies, which is an ideal situation but is rare in practice. Most of the literature on joint replenishment considers deterministic lead time [19-20] or zero lead time, and only a few papers on joint replenishment consider random lead time [21-22], since the random lead time makes the joint replenishment model more complex.
In recent years, some scholars have paid attention to the joint replenishment problem with a controllable lead time. Braglia et al.[23] pointed out that how to control the lead time and ordering cost was an important problem in random inventory replenishment. Shortening lead time can reduce safety inventory and improve customer service[24]. Tersine[25] pointed out that the lead time include the cycle time of multiple processes, such as order processing, product processing, transportation and delivery, which can be accelerated by investing more costs. Therefore, the lead time, to a certain extent, can be shortened. In other words, it is controllable. Marcello et al.[26-27] studied the joint replenishment problem with a controllable lead time, in which the lead time can be shortened by crashing costs. More crashing costs of investment will lead to a shorter lead time. Those papers aim to minimize the cooperative coalition’s cost, which means that the joint replenishment is formed through cooperation.
To the best of our knowledge, there is no literature on the study of the cost allocation scheme of the joint replenishment problem with a controllable lead time. It is necessary to design corresponding allocation scheme that satisfies fairness and feasibility. Therefore, this paper will construct a model of the joint replenishment problem with a controllable lead time, make decisions on the joint replenishment cycle and replenishment quantity, and design the cost allocation scheme for the corresponding joint replenishment. The crashing cost function adopts the function used by Chen et al.[28-29]. Moreover, this paper also considers the quantity discount[30], which is very common in the inventory replenishment problem. The fixed cost independent of the product type and the replenishment quantity are considered, and the fixed cost related to the product type and independent of the replenishment quantity is assumed to be 0. Therefore, the problem considered in this paper is actually an extension of the cost allocation problem of Meca et al.[11], and this paper considers the flexible lead time and multi-items in the joint replenishment problem.
In this paper, first, the long-run average cost model and the corresponding joint replenishment model of multiple retailers ordering periodically under the condition of nonlinear quantity discount and controllable lead time are established. Then, an approximate algorithm is given to solve the model. Finally, the cost allocation rule in the core of the joint replenishment game is presented.
1 Problem and Model
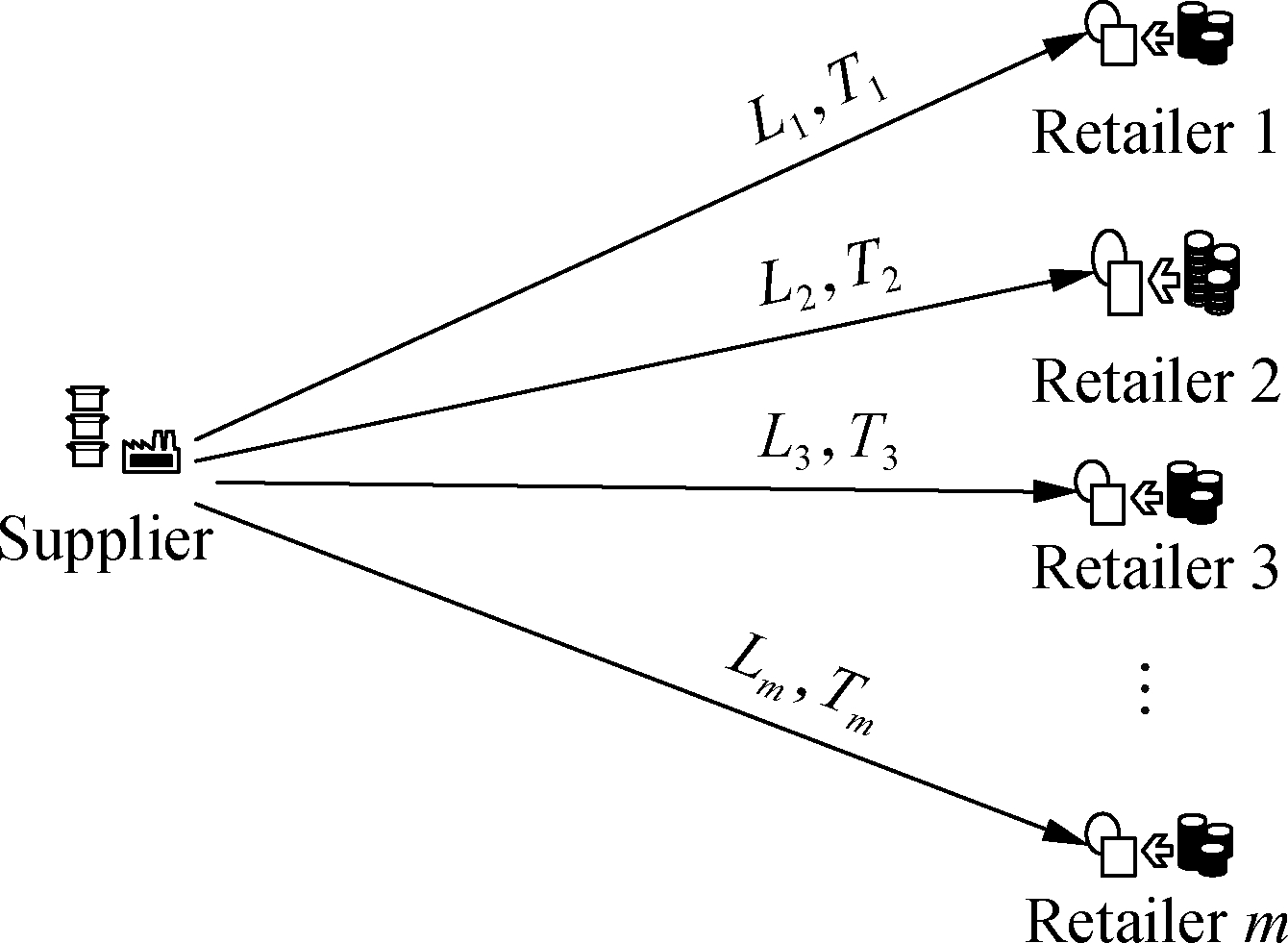
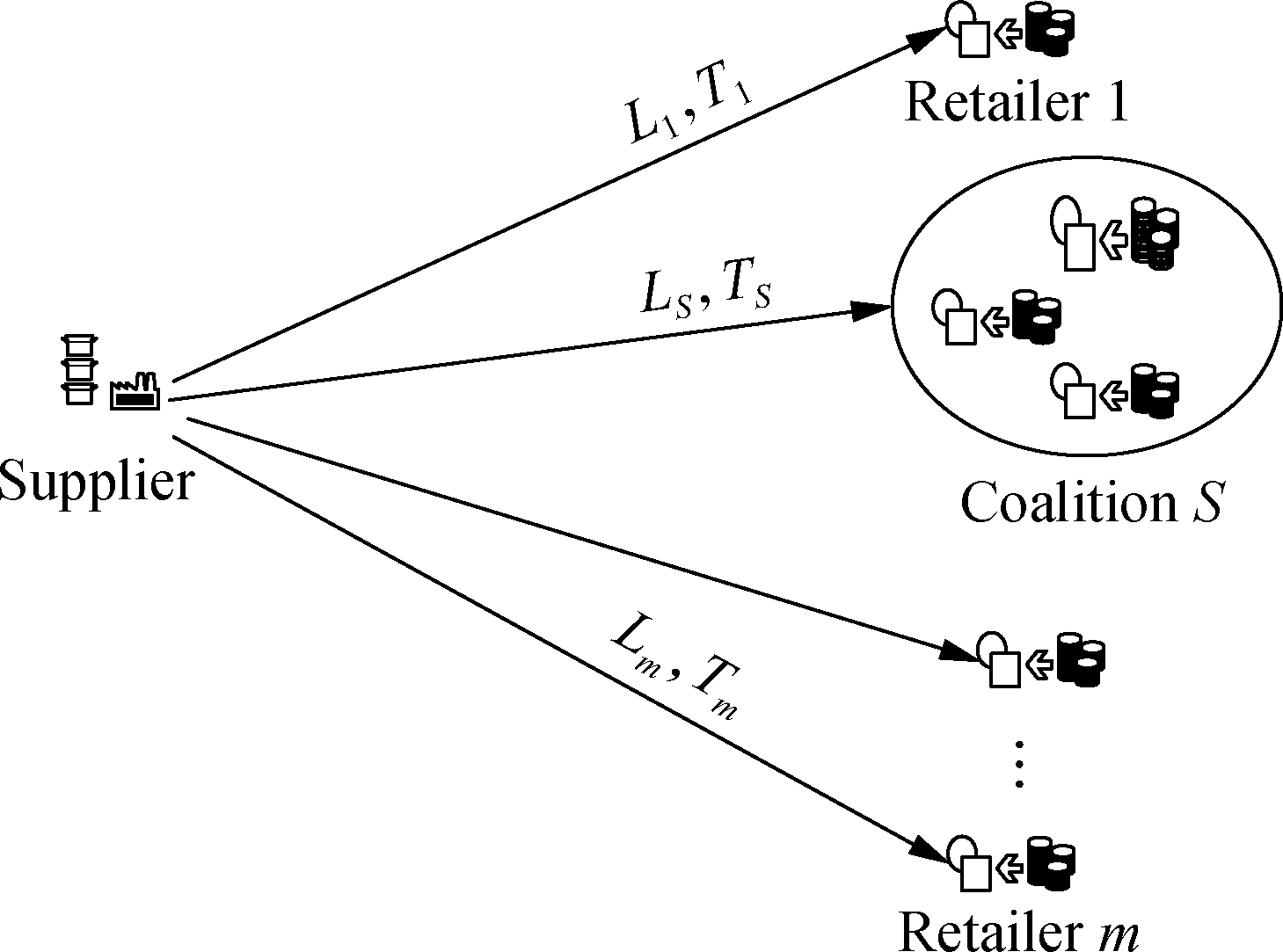
A supplier supplies n items to m retailers located in the same area. Let N={1,2,…,n}, M=1,2,…,m. The supplier provides a flexible lead time for retailers, and charges retailers a fee for the corresponding lead time. The fee is called the crashing cost, which is used for expediting order processing, production and shipping. Let Lj be the lead time of retailer j where j∈M and Lj∈[lmin,lmax],lmax>lmin>0. The corresponding crashing cost is C(Lj)-θ, θ>0. The orders of retailer j are placed together, and retailer j makes decisions on the lead time and replenishment cycle length to minimize the average total cost per unit time cost when he/she replenishes inventory separately. When some retailers form a coalition for joint replenishment, they make joint decisions on the uniform replenishment cycle length and lead time to minimize the average total cost per unit time cost of the cooperative coalition, as shown in Fig.1.
Joint replenishment not only helps retailers share the fixed cost but also helps them obtain a greater discount from the supplier. Assume that there is a trusted leader to help retailers form a cooperative coalition to jointly replenish inventory. To form a cooperative coalition for reducing their total cost, the following two problems need to be solved: 1) How to make decisions on the lead time and replenishment cycle length to minimize their total cost?
(a)
(b)
Fig.1 Replenishment individually and jointly. (a) Replenishment separately; (b) Joint replenishment of retailers in coalition S
and 2) How to allocate the total cost incurred by joint replenishment in fairness and rationality?
The inventory replenishment model of retailer j is proposed first, where j∈M. Considering that the supplier bears the transportation cost and provides the quantity discount to retailers, retailer j replenishes inventory periodically in an infinite horizon. A nonlinear all-unit quantity discount is adopted, and the price function of item i is expressed as ![]() where qi is the order quantity and Qi is the constant, which is large enough to be always greater than qi. To ensure that the price of item i decreases with the increase in the order quantity and it cannot be less than ci, we set Qi>qi in this paper. There is no limitation of storage capacity, and the related inventory cost is assumed to be time-invariant, unit item i storing unit time in the warehouse will incur the holding cost hi. The fixed cost A, which includes telephone charges, delivery costs and the labor cost incurred in processing the order, is incurred in each order. Retailer j places an order of all items he/she wants to purchase for the supplier. The average demand arrival rate of retailer j’s item i is λji where λji>0 represents retailer j does not purchase item i, and there is no more information on demand. To maintain a high service level, let the inventory level of item i be always not less than
where qi is the order quantity and Qi is the constant, which is large enough to be always greater than qi. To ensure that the price of item i decreases with the increase in the order quantity and it cannot be less than ci, we set Qi>qi in this paper. There is no limitation of storage capacity, and the related inventory cost is assumed to be time-invariant, unit item i storing unit time in the warehouse will incur the holding cost hi. The fixed cost A, which includes telephone charges, delivery costs and the labor cost incurred in processing the order, is incurred in each order. Retailer j places an order of all items he/she wants to purchase for the supplier. The average demand arrival rate of retailer j’s item i is λji where λji>0 represents retailer j does not purchase item i, and there is no more information on demand. To maintain a high service level, let the inventory level of item i be always not less than ![]() where ρ>0 is predetermined. The objective of retailer j is to minimize the average total cost per unit time incurred by inventory replenishment.
where ρ>0 is predetermined. The objective of retailer j is to minimize the average total cost per unit time incurred by inventory replenishment.
Without considering the shortage cost, the total costs incurred in a replenishment cycle includes the fixed cost, the purchase cost, the crashing cost and the holding cost. In a replenishment cycle Tj, the order quantity of retailer j’s item i is Tjλji, so the average inventory level of item i is ![]() The price of item i is
The price of item i is ![]() Therefore, the total cost incurred in a replenishment cycle is
Therefore, the total cost incurred in a replenishment cycle is
Let TCj(Lj,Tj) be the average total cost per unit time of retailer j, and it can be expressed as
Then, the objective of retailer j is
In the above expression, the range of lead time is limited since the lead time is usually larger than 0 and cannot be infinite even if there is no crashing cost. Lj and Tj are the decision variables of retailer j.
Joint replenishment without considering the consolidation cost does not change their cost structure, but it requires retailers to share the lead time and replenishment cycle length. Therefore, if retailers form coalition S where S⊆M to jointly replenish inventory, coalition S makes decisions on the uniform lead time LS and replenishment cycle length TS. The average cost per unit time of coalition S is
and the minimum of the average total cost per unit time is expressed as
(1)
Joint replenishment forces retailers to share the fixed cost A and the price of item i reduces ![]() which is as expected due to a larger order quantity.
which is as expected due to a larger order quantity.
2 Decision on Lead Time and Replenishment Cycle Length of Joint Replenishment
The previous section presents the inventory replenishment model of retailer j and the joint replenishment model of coalition S. The solution method of those models will be presented in this section.
Observing the joint replenishment model of coalition S, S⊆M, it is easy to see that ![]() Let LS,TS be the optimal lead time and the optimal replenishment cycle length of coalition S.
Let LS,TS be the optimal lead time and the optimal replenishment cycle length of coalition S.
![]()
where
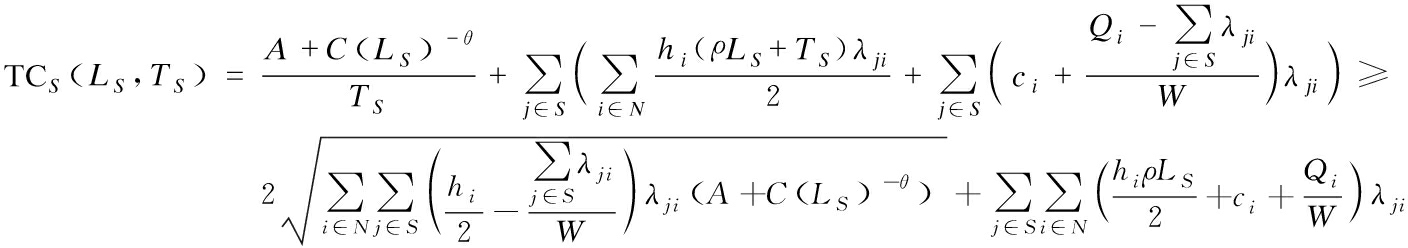
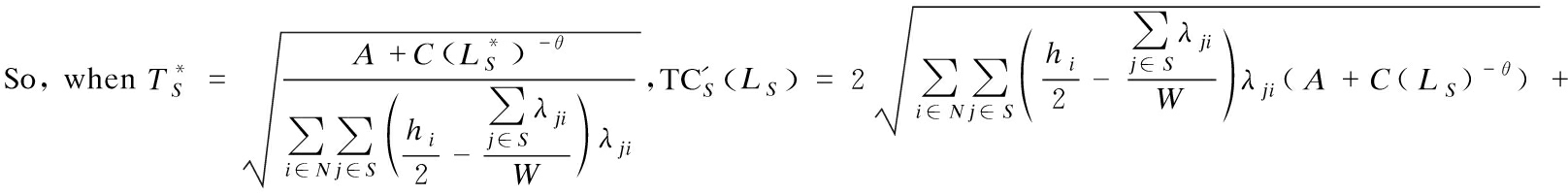
Note that if  always holds, and then the optimal replenishment cycle length of coalition S is
always holds, and then the optimal replenishment cycle length of coalition S is 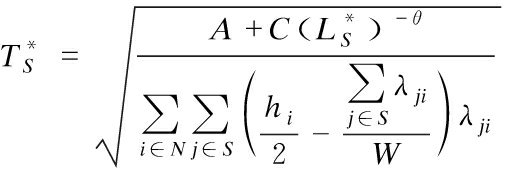 by the proof of Lemma 1.
by the proof of Lemma 1.
Let ![]() where S⊆M, then we have the following proposition.
where S⊆M, then we have the following proposition.
Proposition 1 There is an optimal lead time ![]() decreases with the increase in the fixed cost A and increases with the increase in W or C.
decreases with the increase in the fixed cost A and increases with the increase in W or C.
Proof
![]() is continuous and different-
is continuous and different-
iable in [0,+∞), and then
![]() =
=
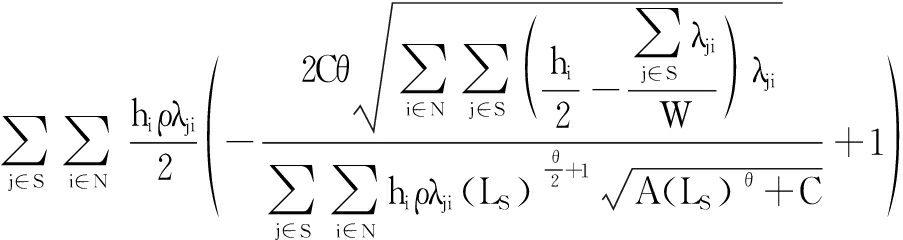
If ![]() =0, then
=0, then 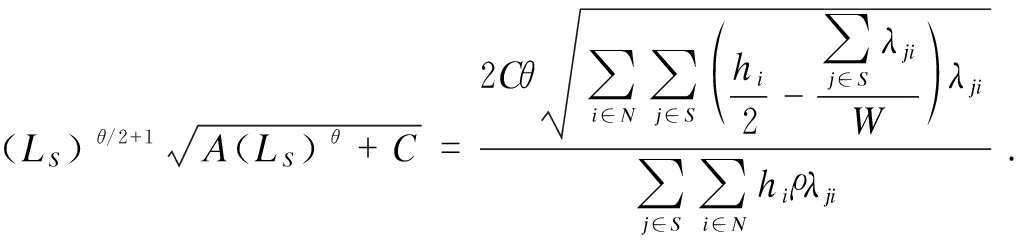 Furthermore,
Furthermore, ![]() increases with the increase in LS in [0,+∞), the solution to
increases with the increase in LS in [0,+∞), the solution to ![]() =0 is unique, and then it is clear that there is a unique solution to
=0 is unique, and then it is clear that there is a unique solution to ![]()
Again, if there exists a solution ![]() to
to ![]() =0, then it is obvious that
=0, then it is obvious that 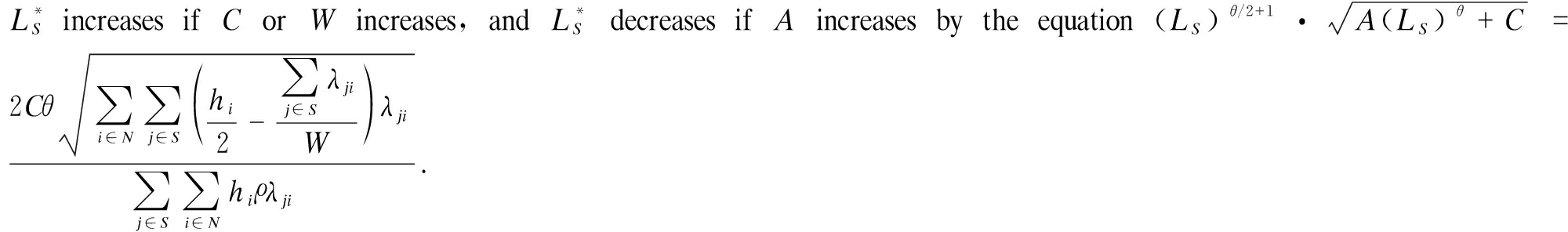
If ![]() we know that
we know that  is non-decreasing with the increase in W. The quantity discount reduces if W increases. In other words, the replenishment cycle length may be reduced due to the reduced quantity discount.
is non-decreasing with the increase in W. The quantity discount reduces if W increases. In other words, the replenishment cycle length may be reduced due to the reduced quantity discount.
Lemma 1 simplifies the objective function and Proposition 1 proves the existence and uniqueness of the optimal lead time. Though it still cannot help us find its optimal solution expression, it may help us search for a relatively close approximate solution to the optimal solution more easily. For searching for an approximate solution to meet the precision requirement, Proposition 2 is proposed to estimate the error caused by the approximate solution. The percentage error is defined as the ratio of the difference between the approximation and the optimal value to the optimal value. If ![]() then
then
the percentage error is ![]()
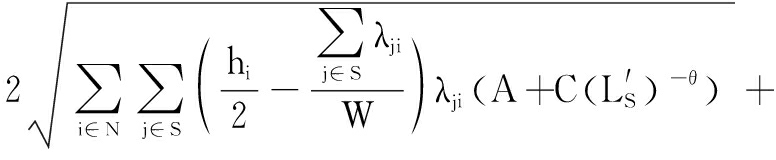
Hence,
Then, we have
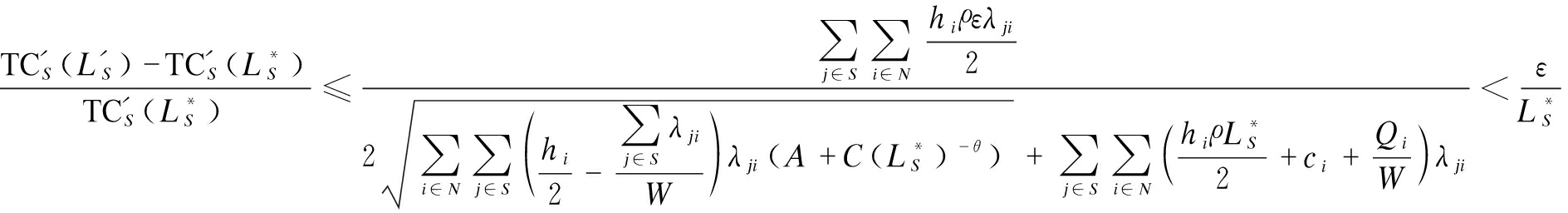
According to Proposition 2, the error can be estimated by the difference between the optimal lead time and the approximate optimal lead time. Then, Algorithm 1 is proposed to search the approximate optimal solution. Let [x] be the smallest positive integer that is not less than x where x>0.
Algorithm 1
Input:M,N,hi,A,ρ,λji,ci,Qi,W,lmin,lmax, and the percentage error η.
While (k≤K)
![]()
end
k←k+1
end
Return results.
Proposition 3 The percentage error of the lead time obtained by Algorithm 1 does not exceed η.
Proof According to Algorithm 1, ∃k′ satisfies ![]() According to Proposition 2, then
According to Proposition 2, then
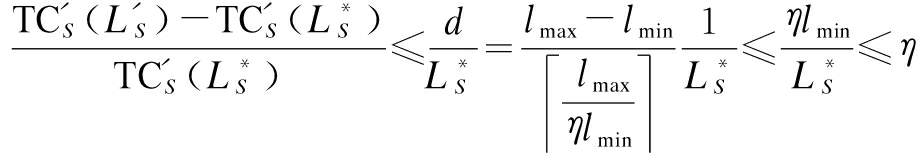
![]()
Therefore, the approximate solution of any specified accuracy η can be obtained theoretically by Algorithm 1, and then we can call it an η-approximate algorithm. Algorithm 1 can search the lead time of coalition S and then the replenishment cycle of coalition S can be obtained by  As Algorithm 1 can solve the approximate solution with arbitrary accuracy, we can regard it as the optimal solution.
As Algorithm 1 can solve the approximate solution with arbitrary accuracy, we can regard it as the optimal solution.
3 Cost Allocation for Joint Replenishment
The joint replenishment model and the solution to the joint replenishment model are presented in the above sections, but they are based on a cooperative coalition that has been formed. Retailers can choose cooperation and non-cooperation before an action, and retailers will not participate in cooperation without sufficient motivation. Generally speaking, retailers’ actions are driven by their interest, and cost savings is the motivation for retailers to participate in cooperation. On the other hand, retailers also pay attention to the fairness of cost allocation when choosing whether to cooperate. The cost allocation rule ensures that the cost savings for retailers is fair and reasonable, and it will also be the motivation for retailers to participate in the cooperation. The cost allocation in the core of the cooperative game is a relatively fair and reasonable allocation scheme, so the cost allocation scheme is designed based on the cooperative game theory. The replenishment game is a cooperative cost game[31] and the cooperative cost game is introduced before designing the allocation rule.
The replenishment game is a cooperative cost game. A cooperative cost game is defined as (P,v) where P is a set of players and v is a real-valued set function (characteristic function) which maps the subsets S of the set P into the set of real numbers. v(S) expresses the total cost of coalition S, so does v(φ).
The cooperative game’s core is an important concept in the cooperative game theory since it is the set of solutions satisfying efficiency, individual rationality and coalition rationality. Efficiency means that the whole cost of the coalition is allocated to just the retailers. Individual rationality is that retailers have reduced their cost after cooperation. Coalition rationality is defined as a no sub-coalition which can save more costs after departing from the grand coalition where the grand coalition means that all retailers participate in the joint replenishment. Let ξ=(ξ1,ξ2,…,ξ|P|) be an allocation of cooperative game (P,v), where |P| is the number of elements of set P. Then, we have the following formulae if it is in the core of cooperative game (P,v):
(2)
(3)
Since S includes the singleton set {j}, j∈P, the inequation (3) includes individual rationality and coalition rationality. The allocation rule ξ is called the core allocation rule.
Only when the cost allocation rule is known before cooperation, then the retailer decides whether to participate. Improper cost allocation rules may cost retailers more than they want, and it is an obstacle for forming the coalition. Therefore, this section works on the design of cost allocation based on the total cost that has been incurred.
Assume that 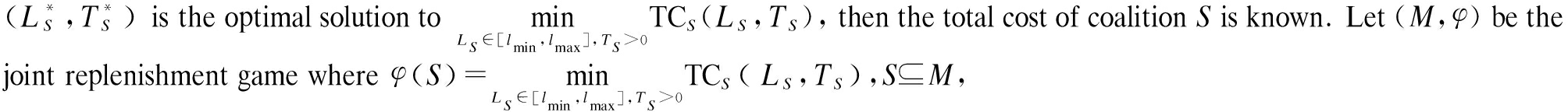 then we have following proposition.
then we have following proposition.
Proposition 4 The joint replenishment game (M,φ) is subadditive.
Proof Subadditivity in the cooperative cost game is defined as φ(U∪V)≤φ(U)+φ(V), where U∩V=∅, and U,V⊆M. We will prove the inequality φ(U∪V)≤φ(U)+φ(V) in the following. Let ![]() and
and ![]() be the optimal solutions of
be the optimal solutions of ![]() and
and ![]() respectively. Then, we have
respectively. Then, we have

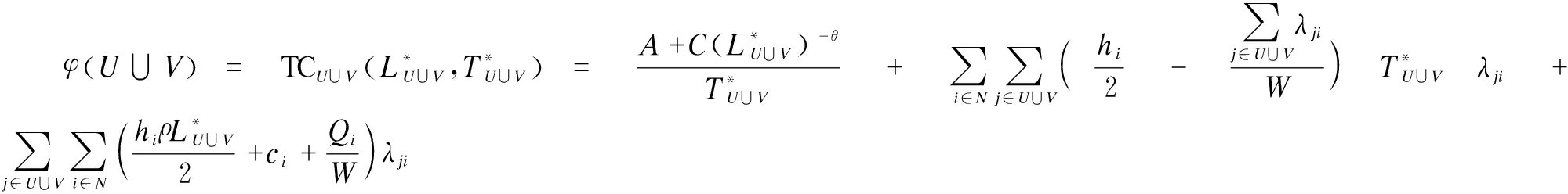
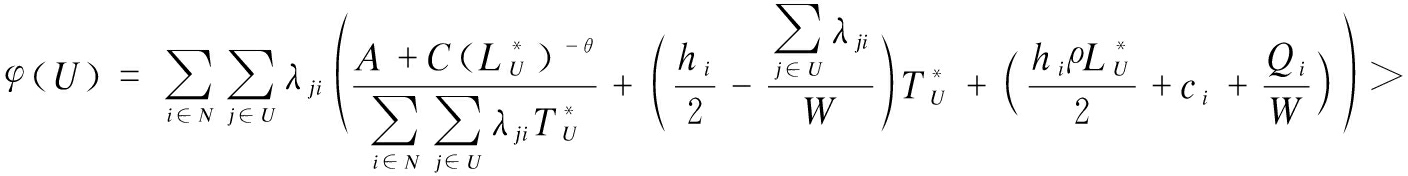
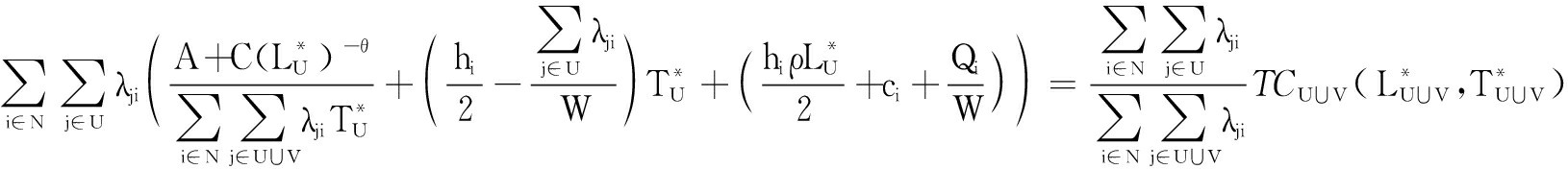
The following inequality can be obtained in the same way.
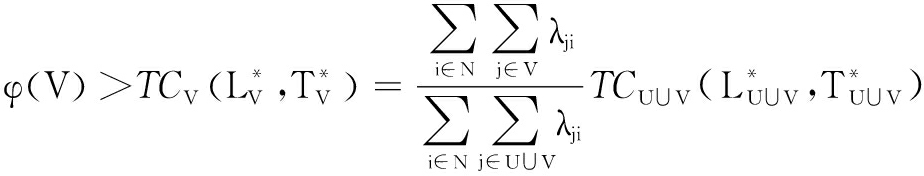
So, φ(U)+φ(V)>TCU∪V(L*U∪V,T*U∪V)=φ(U∪V).
By Proposition 4, we have φ(U∪{i})<φ(U)+φ({i}), so there are no dummy players who have made no contribution to the coalition because everyone in the coalition is helpful for reducing the cost of coalition. It implies that the more retailers take part in the coalition, the more cost savings incurred. Therefore, we aim to encourage all retailers to participate in joint replenishment for maximizing the cost savings of the joint replenishment. It requires fair and reasonable allocation rules to motivate retailers to participate in joint replenishment.
First, the allocation rule ensures that retailers’ costs are reduced after cooperation, and all the costs incurred by the coalition should be allocated to retailers. Secondly, under the same rule, no smaller coalition can cost less than that they are allocated from the grand coalition; otherwise, they will leave the large coalition and form a smaller coalition. Such a rule can be considered as fair and reasonable, and the solution in the core of the joint replenishment game satisfies such conditions. So, we try to find a solution for the core of the joint replenishment game.
Let ζ={ζ1,ζ2,…,ζm} be an allocation vector where ζj is the total cost allocated to retailer j in joint replenishment game (M,φ).
Theorem 1 The allocation vector ζ={ζ1,ζ2,…,ζm} is in the core of joint replenishment game (M,φ) where
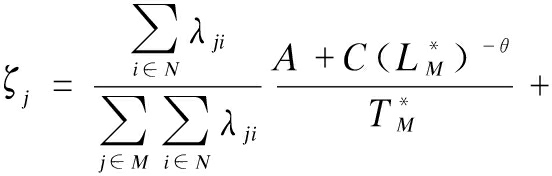
![]()
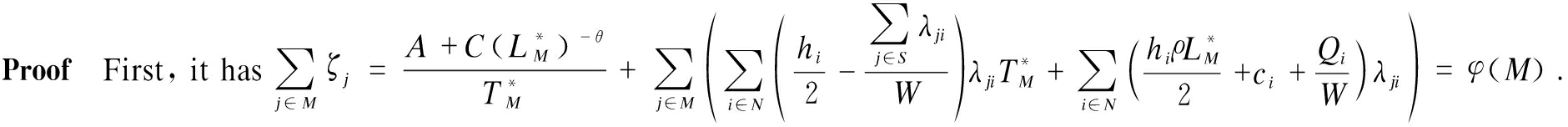
So, the allocation rule satisfies efficiency. Then,
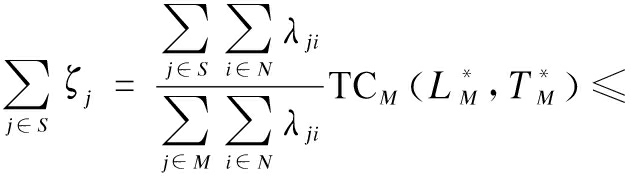
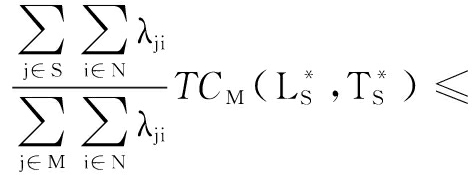

![]()
So, the allocation ζ={ζ1,ζ2,…,ζm} satisfies individual rationality and coalition rationality.
In summary, the allocation is in the core of the joint replenishment game (M,φ). Proof is complete.
 is the cost per unit time of retailer j, then the total cost in a replenishment cycle is
is the cost per unit time of retailer j, then the total cost in a replenishment cycle is 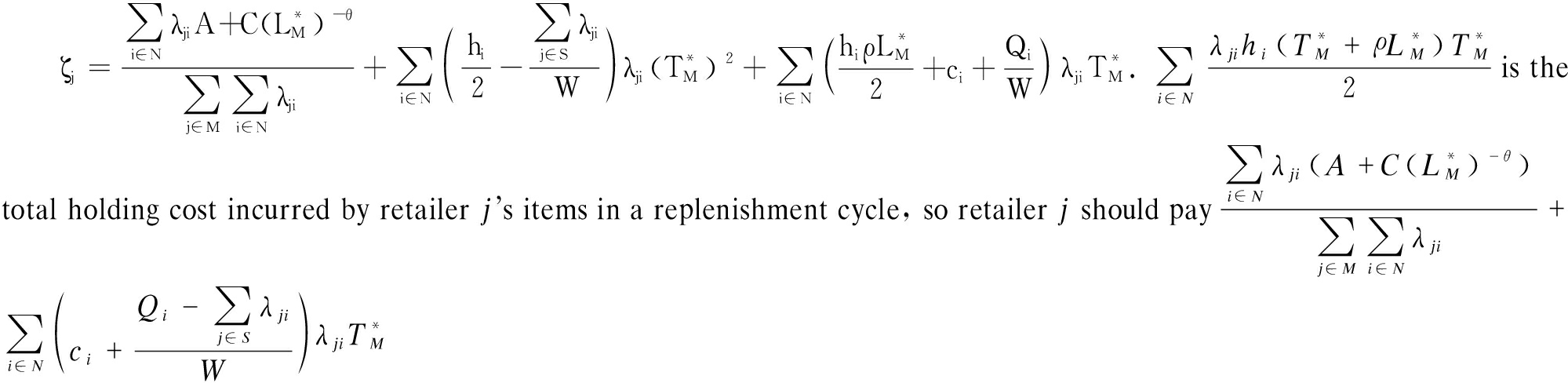 in each joint replenishment cycle, where the fixed cost and the crashing cost are allocated in proportion to the total demand of the grand coalition and retailer j bears the purchasing cost of his/her own products. Such a cost allocation rule is clear and easy to understand, and also more convenient to implement.
in each joint replenishment cycle, where the fixed cost and the crashing cost are allocated in proportion to the total demand of the grand coalition and retailer j bears the purchasing cost of his/her own products. Such a cost allocation rule is clear and easy to understand, and also more convenient to implement.
4 Numerical Experiments
This section verifies the effectiveness of the solution method and the cost allocation rule through some numerical experiments.
4.1 The computational time of solution
Computational time is a measure of the solution method. Too long a computational time may render the solution method infeasible. Therefore, it is necessary to test the computational time of different product types and their accuracy to observe the solution method’s feasibility. Since the method for solving the joint replenishment problem is the same as that of the replenishment model without cooperation, we only do the test of the computational time for the replenishment model without cooperation, i.e., only one retailer. The number of items is 10, 20, 40, 80, 160, 320, 640, and the accuracy of the solution is 0.1, 0.01, 0.001, and 0.000 1, respectively. Since those parameters except lmin and lmax do not affect the computational time of the algorithm, those parameters’ value for this section can be set as follows: A=100,C=100,W=10 000,ρ=1,θ=2. The computational time increases with the increase in the value lmax-lmin. We set the value lmax-lmin large enough so that the optimal lead time is in [lmin,lmax], and then let lmin=1,lmax=100. Other parameters’ values are generated randomly by the Matlab random function. The demand arrival rate λji is randomly generated in [0,10]; hi is randomly generated in [1,2]; and Qi are randomly generated in [5 000,5 500]. Tab.1 shows the computational time for a different number of items and percentage error.
The computational time is the time that it takes to search for the approximate value. After fixing the items’ number, retailers’ number and percentage error, each test was carried out 10 times, and we took the average computational time. Tab.1 shows that the solution time increases rapidly with the increase in the number of items and it increases with the decrease in the percentage error. However, it also shows that when the number of items is 640, the percentage error is 0.000 1, and the solution time is about 627 s, which means that the problems with no more than 640 kinds of items and no less than 1×10-6 error can be solved quickly. It can run faster if we narrow down the search length of lead time since we find that the search area is relatively large, and all the lead times we obtain are not greater than 5, which means that lmax=100. Therefore, lmax=10 is a more appropriate parameter value.
Tab.1 Computational time s

ηn102040801603206400.10.001 7530.018 1400.001 9620.012 2860.038 4990.131 3000.819 0890.010.016 0000.025 1600.026 6320.051 8760.232 8530.813 8305.874 2290.0010.044 6220.056 0030.146 6880.493 9201.529 4657.234 9987.234 9980.000 10.393 8060.526 8961.189 1023.564 06214.260 76071.288 220627.673 831
4.2 The computational time of solution
This section mainly analyzes the impact of ordering cost, safety inventory level and quantity discount on retailer cooperation income. Take five retailers and five products as an example, and the main parameters of the example are set as follows: A=100, C=100, W=10 000,ρ=1, θ=2,lmin=1, lmax=10. Q=[5 298, 5 148, 5 062, 5 194, 5 408], h={1.38, 1.63, 1.36, 1.41, 1.37}, c={7.68, 2.33, 5.87, 4.59, 8.61}. The average demand arrival rate of five retailers are {2.98, 5.34, 5.07, 2.04, 7.75},{4.97, 5.74, 3.81, 8.14, 1.65}, {8.99, 4.13, 0.65, 3.93, 9.12}, {5.01, 0.15, 3.59, 0.54, 3.19}, {2.77, 7.03, 2.35, 3.75, 3.30}, respectively. We observe the trend of cost savings and cost saving rate when parameter values change in this section. The cost savings is the total cost generated by non-cooperation minus the cost to be borne after cooperation. The cost saving rate is the ratio of cost savings to the total cost generated by non-cooperation. The higher cost saving rate leads to a better cooperation effect.
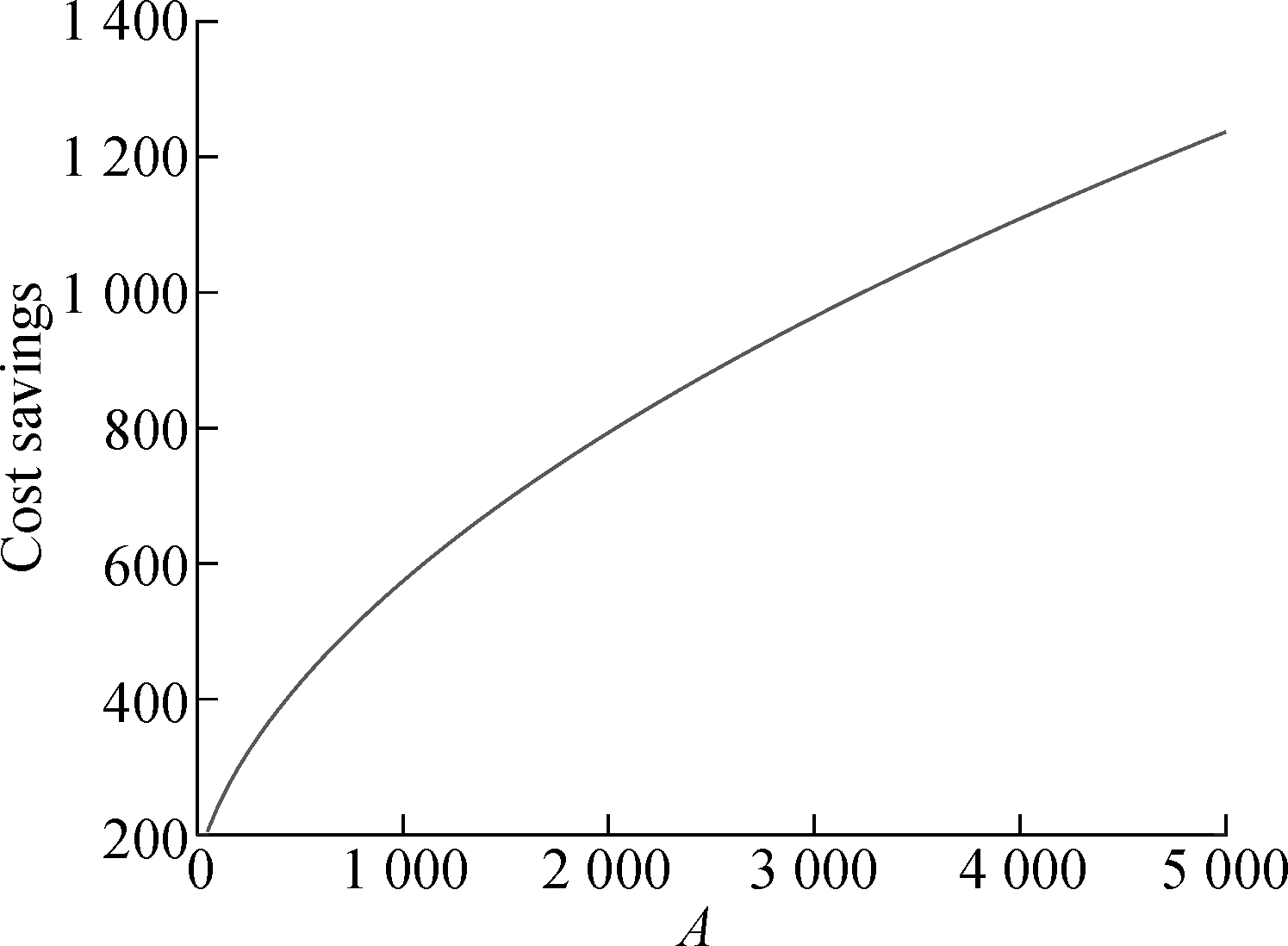
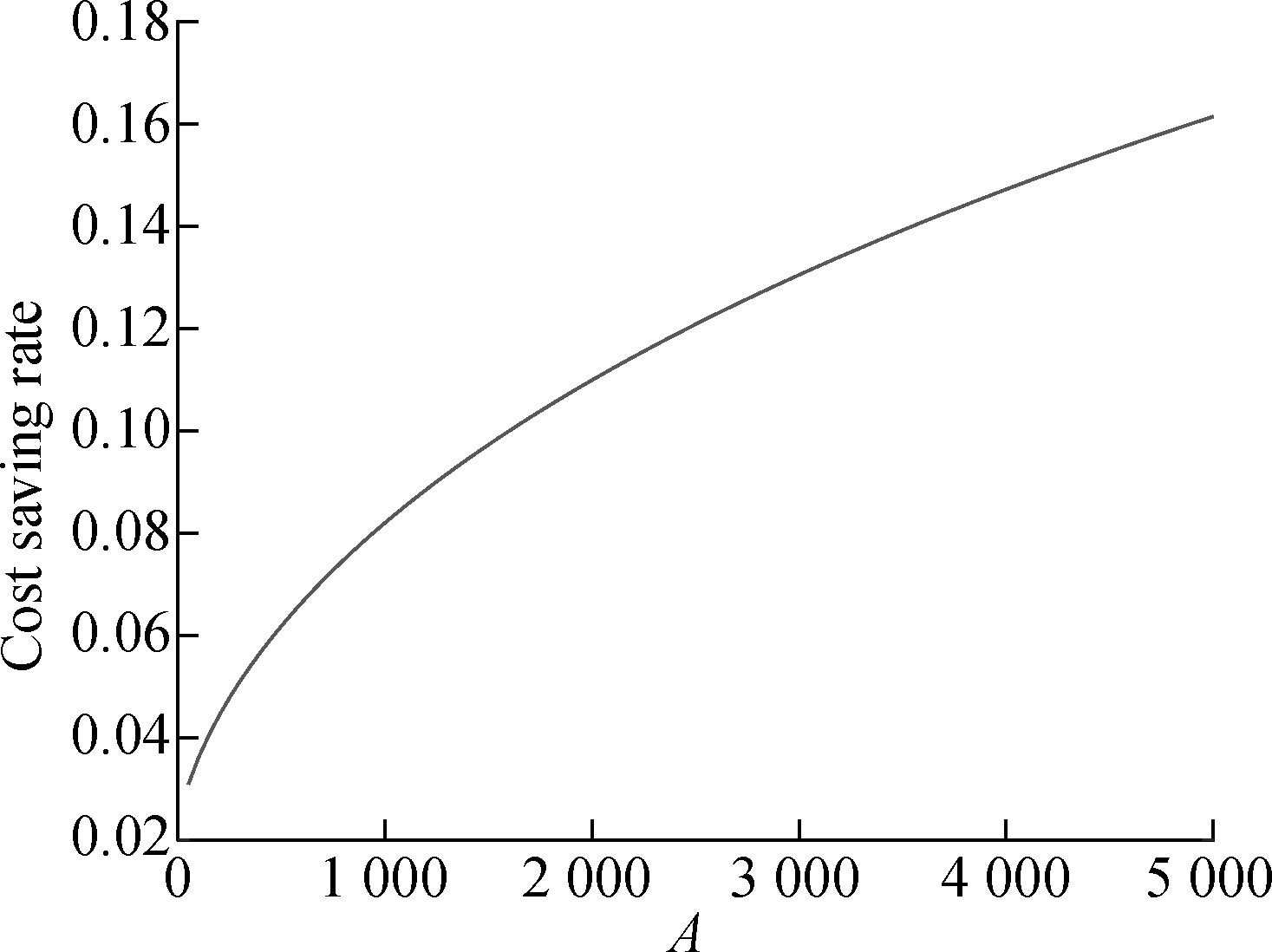
First, we observe the effect of increasing fixed cost A on the cost of retailer 1. From Fig.2, it can be observed that the cost savings increases gradually with the increase in the fixed cost, but the increment decreases gradually. Fig.2 also shows that the cost saving rate is also increasing but stabilizing faster. When the fixed cost exceeds 5 000, the cost saving rate is greater than 30. It implies that the higher fixed cost may lead to retailers’ increased willingness to participate in joint replenishment in the view of cost.
(a)
(b)
Fig.2 Fixed cost effect on cost of retailer 1. (a) Effect on cost savings; (b) Effect on cost saving rate
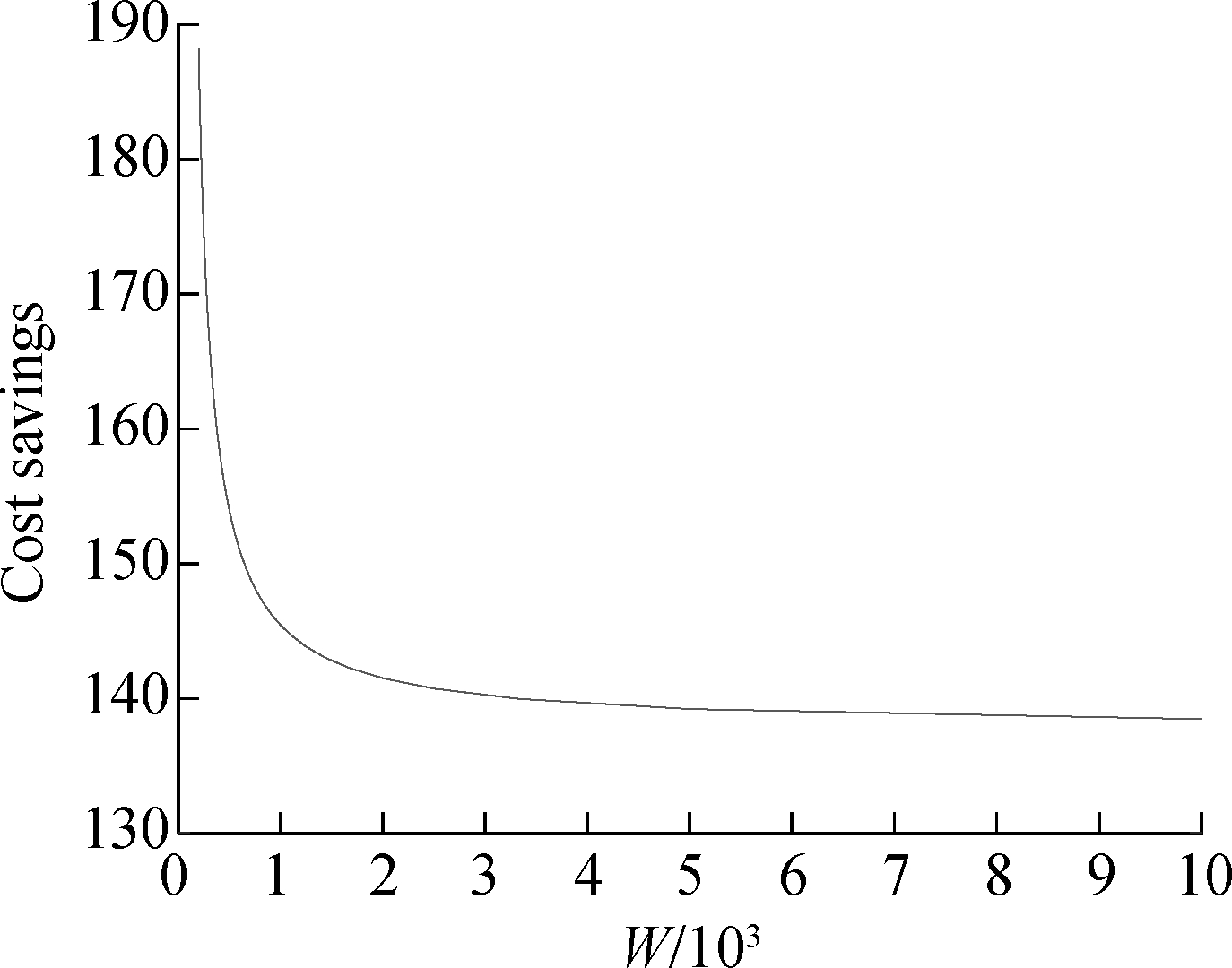
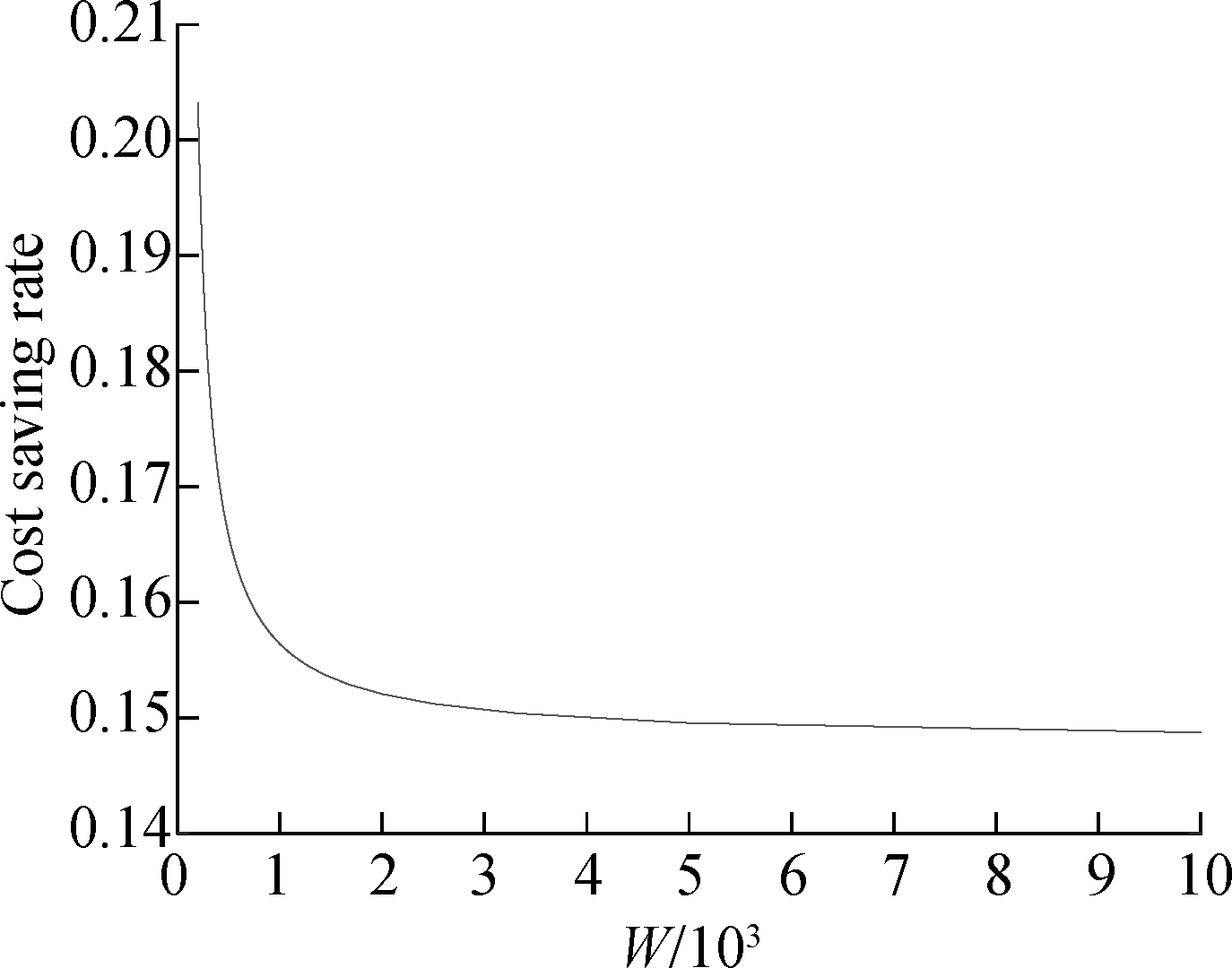
Then, we observe the effect of quantity discount on the cost of retailer 1, and also observe the change of cost saving rate and cost savings. Fig.3 shows that the cost savings and the cost saving rate vary with the increase in W, where Q and W magnify or reduce the same multiple simultaneously. Then the quantity discount can be decreased by increasing Q and W in proportion since ![]()
![]() if k>1, which means that the larger W will lead to a smaller quantity discount in Fig.3. We can conclude that the cost savings and cost saving rate of retailer 1 decreases with the decrease in quantity discount from Fig.2, respectively. It implies that the greater quantity discount leads to a better cooperation effect and the increased willingness of retailers to cooperate from the perspective of cost. The cost savings and the saving rate stabilize because the quantity discount has also stabilized when W>2 000.
if k>1, which means that the larger W will lead to a smaller quantity discount in Fig.3. We can conclude that the cost savings and cost saving rate of retailer 1 decreases with the decrease in quantity discount from Fig.2, respectively. It implies that the greater quantity discount leads to a better cooperation effect and the increased willingness of retailers to cooperate from the perspective of cost. The cost savings and the saving rate stabilize because the quantity discount has also stabilized when W>2 000.
(a)
(b)
Fig.3 Quantity discount effect on cost of retailer 1. (a) Effect on cost savings; (b) Effect on cost saving rate
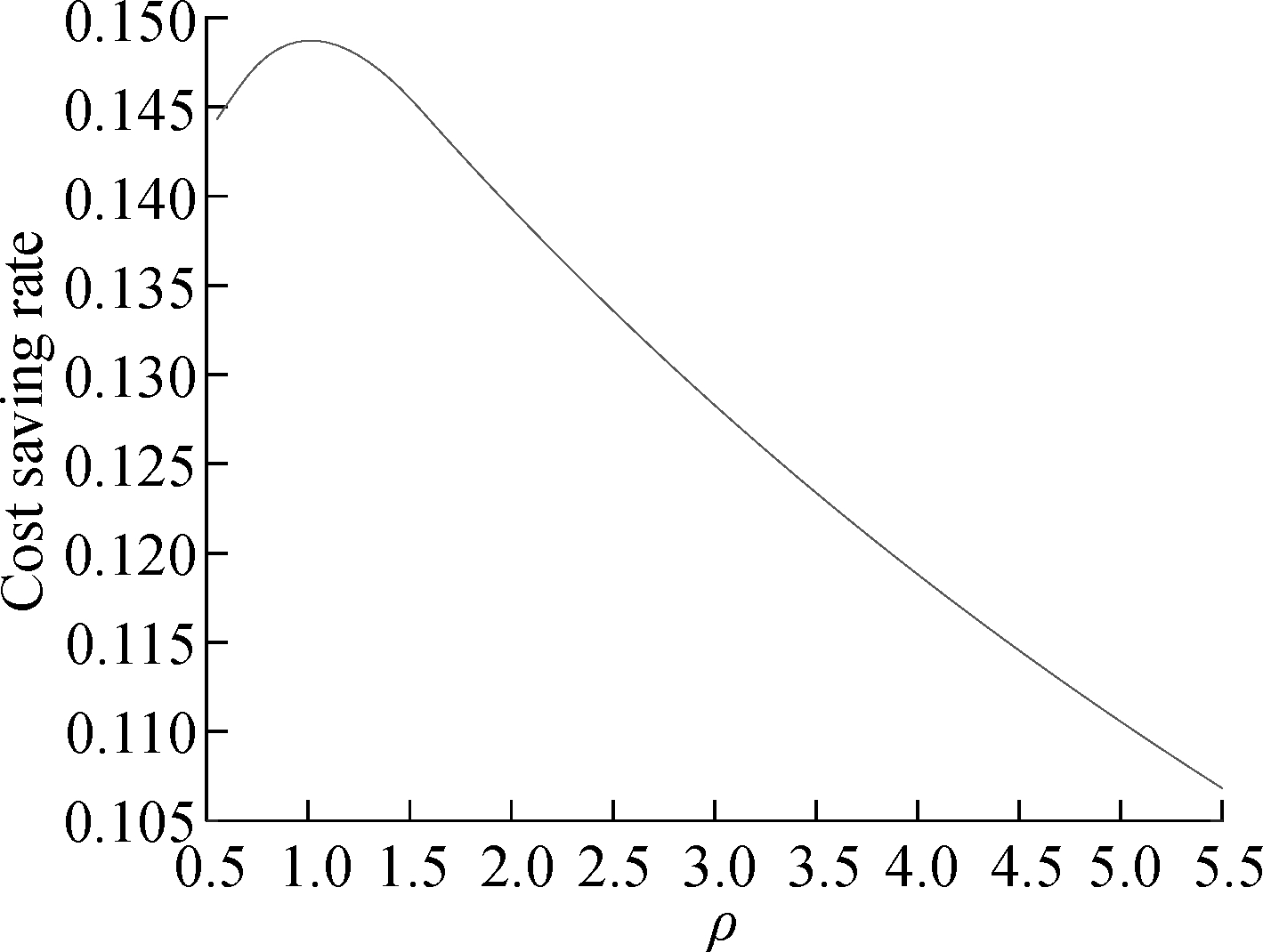
Finally, we investigate the impact of safety inventory level on the cost of retailer 1, and Fig.4 shows the cost savings and the cost saving rate varies with the increase in ρ. It can be seen that both cost savings and cost saving rate rise first and then fall. The cost savings is the highest when ρ=1 and the cost saving rate is the highest when ρ=1.5. Therefore, ρ=1.5 is best if retailers are more inclined to higher service levels, and the cost saving rate of retailers is the highest, and the cooperation effect is the best when ρ=1.

(a)
(b)
Fig.4 Safety inventory level effect on cost of retailer 1. (a) Effect on cost savings; (b) Effect on cost saving rate
4.3 The coalition size and number of items’ effect on cooperation
We have proved that the joint replenishment game is sub-additive in Section 3, which means that cooperation is always fruitful. However, it is unknown how the cooperation is affected by the coalition size and the number of items, so the investigation of cost savings and cost savings with different coalition sizes and the number of items is presented in Tab.2. The demand arrival rate and the holding cost rate are generated randomly by Matlab. Other parameters are kept as formerly described in Subsection 4.1 except for lmax. Based on the experience of Subsection 4.1, let lmax=10. Then, we test the cost savings and the cost saving rate with the increase in the number of retailers and the number of items. The cost savings is the total cost of all retailers before cooperation minus the total cost after cooperation. The cost saving rate is the ratio of the cost savings to the total cost generated in non-cooperation. The number of retailers represents the coalition size, and it takes the value of 5, 10, 20, 40, 80, 160, 320. The number of items n in Tabs. 2,3 and 4 takes 10, 20, 40, 80,160, 320, respectively.
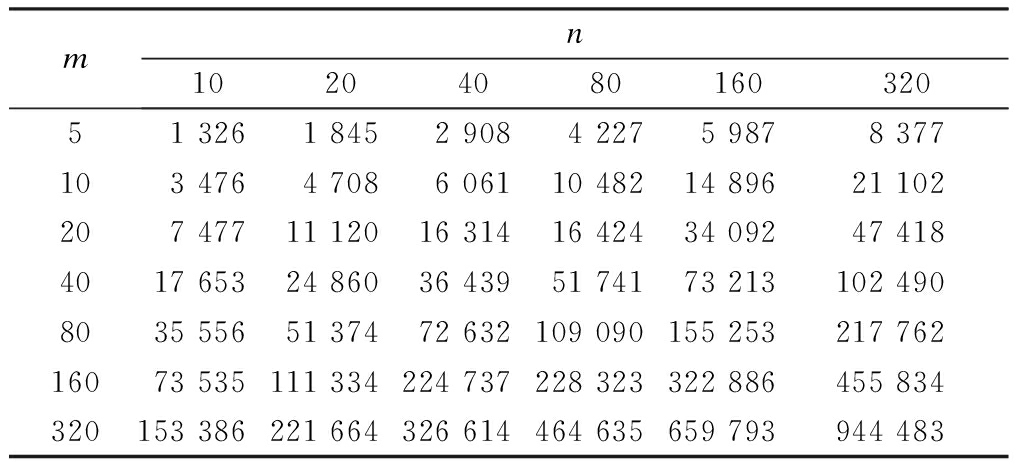
Tab.2 Cost savings of coalition
mn1020408016032051 3261 8452 9084 2275 9878 377103 4764 7086 06110 48214 89621 102207 47711 12016 31416 42434 09247 4184017 65324 86036 43951 74173 213102 4908035 55651 37472 632109 090155 253217 76216073 535111 334224 737228 323322 886455 834320153 386221 664326 614464 635659 793944 483
Tab.3 Cost saving rate of coalition

mn1020408016032050.219 30.201 70.168 80.127 80.098 80.074 0100.284 00.248 70.208 00.157 80.123 80.088 9200.329 30.296 90.229 70.233 60.140 80.101 6400.394 70.289 10.257 50.212 10.152 90.110 9800.363 60.347 50.251 20.213 80.163 60.114 81600.407 70.381 00.222 10.231 20.161 70.116 83200.422 00.372 50.262 80.225 10.162 80.127 6
Observing the data of each row in Tabs.2, 3 and 4, it can be seen that the data for each row in Tab.2 is an upward trend, which indicates that cost savings increase with the increase in the number of items, meaning that cooperative coalition benefit from the joint replenishment of these products. The data in each row in Tab.3 is declining with the increase in the number of items, which indicates that the total cost savings of the cooperative coalition decrease and the effect of cooperation decreases with the increase in the number of items. When we calculate the cost savings of retailer 1, we find that it decreases when the items number increases from 40 to 80, which may lead to the dissatisfaction of the retailer. Therefore, when the number of items is greater than 40, it is recommended to carry out batch replenishment.
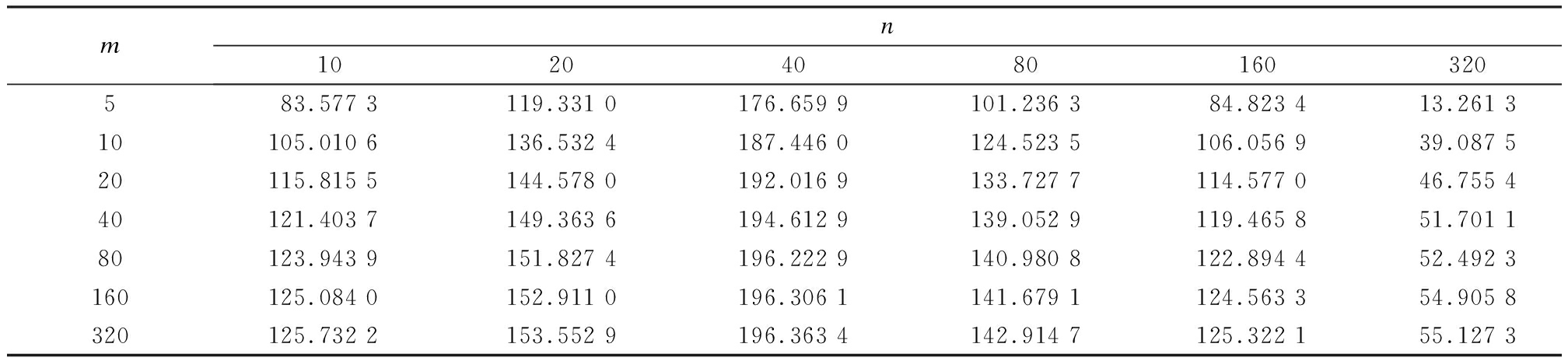
Tab.4 Cost savings of retailer 1
mn10204080160320583.577 3119.331 0176.659 9101.236 384.823 413.261 310105.010 6136.532 4187.446 0124.523 5106.056 939.087 520115.815 5144.578 0192.016 9133.727 7114.577 046.755 440121.403 7149.363 6194.612 9139.052 9119.465 851.701 180123.943 9151.827 4196.222 9140.980 8122.894 452.492 3160125.084 0152.911 0196.306 1141.679 1124.563 354.905 8320125.732 2153.552 9196.363 4142.914 7125.322 155.127 3
Observing the data of each column in Tabs.2, 3 and 4, it can be seen that each column of data in Tab.3 is generally on the rise as the item’s number increases, although individual data suddenly decreases. When the item number is small, the cooperative coalition’s cost saving rate can be maintained at a high level. The data in each column in Tab.2 is strictly incremental, and each set of data is more than double that of the previous data, which also verifies the subadditivity of the joint replenishment game. Each column of data in Tab.4 shows an increasing trend, but the increasing amplitude is gradually decreasing. It shows that the cost savings of a retailer after cooperation increases with the increase in the coalition’s size, but the cost saving rate decreases with the increase in the coalition’s size.
5 Conclusions
1) Considering that multiple retailers jointly replenish inventory from one supplier where the supplier offers a quantity discount and the flexible lead time to retailers, the problem is modeled as the optimization of binary functions. This paper proves that joint replenishment is beneficial to the coalition and it reduces the coalition’s total costs. The grand coalition can achieve the most significant benefit.
2) Based on cooperative game theory, a cost allocation rule of joint replenishment is designed to ensure that all participating retailers can benefit from the cooperation. It suggests the costs each retailer should bear in the joint replenishment.
3) This paper presents an η-algorithm, and the percentage error is introduced to control the approximate solution. The approximate solution can be regarded as an optimal solution if the percentage error η is agreed by all retailers who take part in the cooperation.
4)Numerical experiments show that our solution method can quickly solve the joint replenishment problem with a large number of items. Numerical experiments also show that it can save more costs when the fixed cost and quantity discount are high, and retailers will have an increased willingness to cooperate in view of the cost. Joint replenishment may help retailers save more than 20% of their cost. The numerical experiments suggest the proposal of a safety stock level and the number of items to be joint ordered.
[1]Qu H, Ai X Y, Wang L. Optimizing an integrated inventory-routing system for multi-item joint replenishment and coordinated outbound delivery using differential evolution algorithm[J]. Applied Soft Computing, 2020, 86: 105863. DOI:10.1016/j.asoc.2019.105863.
[2]Chen Y R, Yang L, Jiang Y S, et al. Joint replenishment decision considering shortages, partial demand substitution, and defective items[J]. Computers & Industrial Engineering, 2019, 127: 420-435. DOI:10.1016/j.cie.2018.10.031.
[3]Körpeo lu E,
lu E,  en A, Güler K. Non-cooperative joint replenishment under asymmetric information[J]. European Journal of Operational Research, 2013, 227(3): 434-443. DOI:10.1016/j.ejor.2013.01.004.
en A, Güler K. Non-cooperative joint replenishment under asymmetric information[J]. European Journal of Operational Research, 2013, 227(3): 434-443. DOI:10.1016/j.ejor.2013.01.004.
[4]He S M, Sethuraman J, Wang X, et al. A noncooperative approach to cost allocation in joint replenishment[J]. Operations Research, 2017, 65(6): 1562-1573. DOI:10.1287/opre.2017.1645.
[5]Levi R, Roundy R,Shmoys D, et al. A constant approximation algorithm for the one-warehouse multiretailer problem[J]. Management Science, 2008, 54(4): 763-776. DOI:10.1287/mnsc.1070.0781.
[6]Cui L G, Deng J, Wang L, et al. A novel locust swarm algorithm for the joint replenishment problem considering multiple discounts simultaneously[J]. Knowledge-Based Systems, 2016, 111: 51-62. DOI:10.1016/j.knosys.2016.08.007.
[7]Sindhuchao S, Romeijn H E, Akçali E, et al. An integrated inventory-routing system for multi-item joint replenishment with limited vehicle capacity[J]. Journal of Global Optimization, 2005, 32(1): 93-118. DOI:10.1007/s10898-004-5908-0.
[8]Wang L, Dun C X, Bi W J,et al. An effective and efficient differential evolution algorithm for the integrated stochastic joint replenishment and delivery model[J]. Knowledge-Based Systems, 2012, 36: 104-114. DOI:10.1016/j.knosys.2012.06.007.
[9]van Eijs M J G, Heuts R M J, Kleijnen J P C. Analysis and comparison of two strategies for multi-item inventory systems with joint replenishment costs[J]. European Journal of Operational Research, 1992, 59(3): 405-412. DOI:10.1016/0377-2217(92)90197-H.
[10]Olsen A L. An evolutionary algorithm to solve the joint replenishment problem using direct grouping[J].Computers & Industrial Engineering, 2005, 48(2): 223-235. DOI:10.1016/j.cie.2005.01.010.
[11]Meca A, Timmer J, García-Jurado I, et al. Inventory games[J]. European Journal of Operational Research, 2004, 156(1): 127-139. DOI:10.1016/S0377-2217(02)00913-X.
[12]Anily S, Haviv M. The cost allocation problem for the first order interaction joint replenishment model[J]. Operations Research, 2007, 55(2): 292-302. DOI:10.1287/opre.1060.0346.
[13]Dror M, Hartman B C. Shipment consolidation: Who pays for it and how much?[J]. Management Science, 2007, 53(1): 78-87. DOI:10.1287/mnsc.1060.0607.
[14]Dror M, Hartman B C, Chang W. The cost allocation issue in joint replenishment[J]. International Journal of Production Economics, 2012, 135(1): 242-254. DOI:10.1016/j.ijpe.2011.07.015.
[15]Ye Y, Li D. Joint replenishment interval-value EOQ model and cooperative game method of the cost allocation [J]. Systems Engineering-Theory & Practice, 2018, 38(7): 1819-1829. (in Chinese)
[16]Ye Y, Li D, Yu G. Joint replenishment interval-value EOQ model and cost allocation method based on variable weight price [J]. Chinese Journal of Management Science, 2019, 27(10): 90-99. (in Chinese)
[17]Chen X, Zhang J W. A stochastic programming duality approach to inventory centralization games[J]. Operations Research, 2009, 57(4): 840-851. DOI:10.1287/opre.1090.0699.
[18]Chen X, Zhang J W. Duality approaches to economic lot-sizing games[J]. Production and Operations Management, 2016, 25(7): 1203-1215. DOI:10.1111/poms.12542.
[19]Qu H, Ai X Y, Wang L. Optimizing an integrated inventory-routing system for multi-item joint replenishment and coordinated outbound delivery using differential evolution algorithm[J]. Applied Soft Computing, 2020, 86: 105863. DOI:10.1016/j.asoc.2019.105863.
[20]Cui L G, Deng J, Zhang Y J, et al. The bare-bones differential evolutionary for stochastic joint replenishment with random number of imperfect items[J]. Knowledge-Based Systems, 2020, 193: 105416. DOI:10.1016/j.knosys.2019.105416.
[21]Ai X Y, Zhang J L, Song D P, et al. Modelling and optimising the multi-item stochastic joint replenishment problem with uncertain lead-time and controllable major ordering cost [J]. European Journal of Industrial Engineering, 2019, 13(6): 746-774.DOI:10.1504/ejie.2019.104280.
[22]Cui L G, Deng J, Zhang Y J, et al. Hybrid differential artificial bee colony algorithm for multi-item replenishment-distribution problem with stochastic lead-time and demands[J]. Journal of Cleaner Production, 2020, 254: 119873. DOI:10.1016/j.jclepro.2019.119873.
[23]Braglia M, Castellano D, Frosolini M. Joint-replenishment problem under stochastic demands with backorders-lost sales mixtures, controllable lead times, and investment to reduce the major ordering cost[J]. Journal of the Operational Research Society, 2016, 67(8): 1108-1120. DOI:10.1057/jors.2016.13.
[24]Poole L W. Profiting from cycle time reductions[J]. Hospital Materiel Management Quarterly, 1997, 18(4): 67-70.
[25]Tersine R J. Principles of inventory and materials management [M]. New Jersey: Prentice-Hall, 1994.
[26]Marcello B, Davide C, Liberatina S, et al. Controlling lead times and minor ordering costs in the joint replenishment problem with stochastic demands under the class of cyclic policies [J]. International Transactions in Operational Research, 2018, 28(1):376-400. DOI:10.1111/itor.12571.
[27]Cui L G, Deng J, Liu R, et al. A stochastic multi-item replenishment and delivery problem with lead-time reduction initiatives and the solving methodologies[J]. Applied Mathematics and Computation, 2020, 374: 125055. DOI:10.1016/j.amc.2020.125055.
[28]Chen Z G, Xu Y, Gia T. Inventory model with nonlinear lead time crashing cost [J]. Forecasting, 2007, 26(1): 64-69. (in Chinese)
[29]Chen Z G, Xu Y, Gia T. Integrated vendor-buyer cooperative inventory model with nonlinear lead time crashing cost [J]. Systems Engineering—Theory & Practice, 2008, 28(3): 64-70. (in Chinese)
[30]Zhang Y, Wang Y, Gong B G. The level coordination for the ameliorating items supply chain considering ordering coordination cost and quantity discount [J]. Chinese Journal of Management Science, 2019, 27(12): 55-66. (in Chinese)
[31]Peters H. Game theory: A multi-leveled approach [M]. Berlin: Springer-Verlag, 2008.