Environmental sustainability is attracting more and more attention. Many governments encourage enterprises to produce green products, in order to develop the green economy and improve the ecological environment. For example, in the three decades from 1989 to 2019, the Chinese government has made great efforts in environmental protection, including setting energy consumption caps for dozens of products, implementing laws and regulations such as the environmental protection law and the water resources protection law[1]. For enterprises, Haier joined hands with Chinese home appliance retailers Gome and Suning to form the first “zero carbon conversion alliance” in China since 2010. Moreover, environmental protection has also been taken into consideration by more and more ordinary consumers. A survey conducted by Accenture shows 80% of consumers will consider green features before paying for a product[2].
The green supply chain management (GSCM) is a kind of modern management mode, which considers environmental impact and resource efficiency in the whole supply chain. Research on GSCM is growing rapidly. On the one hand, relevant research focused on government subsidy policies, such as different government subsidy models and green credit policies. On the other hand, the research focused on contract coordination, such as revenue sharing contracts and cost sharing contracts.
Enterprises play an key role in the construction and development of a sustainable supply chain, especially in monopoly enterprises, such as China Mobile, China Unicom, and China Telecom in the communication industry, Gome and Suning in the home appliance field. The existing research on the market mainly focuses on the general market, while the green monopoly market is neglected. In the field of green supply chains, how the decisions are affected by the behavior between the two echelon retailers in the green supply chain (GSC) is also neglected. This paper considers a two-echelon GSC consisting of an environment-friendly manufacturer and two oligopolistic retailers, and analyzes the behavior between retailers.
A green supply chain aims to transform products and processes to make products more environmentally friendly. It is often said that the industry’s unplanned and irresponsible behavior is a potential threat to sustainability. Researchers, scholars, practitioners and scientists from different fields have jointly proposed ways to maintain environmental sustainability.Sheu et al. [3]introduced the concepts of sustainability and environmental thinking into GSCM, and found that the environmental pollution problems accompanying industrial development should be solved simultaneously during the operating process of supply chain management.Zhao et al. [4]found that the economic benefits of companies can be increased by improving the company’s environmental performance (from production to sales).
On the macro level, the literature focused on government subsidies and green credit. Xu et al. [5] studied the subsidy problem under the duopoly competition environment, discussed how to select the subsidy object and formulate the corresponding unit subsidy amount to minimize the total amount of subsidy.Yang et al.[6]considered a two-echelon GSC with one manufacturer and two capital constrained retailers, analyzed the impact of credit strategy on the performance of a green supply chain. In the micro aspect, most of the literature focused on contract coordination.Song et al.[7] established a GSC game model with two revenue sharing contracts. The results showed that the products’ green level and the whole product can be effectively improved by a revenue sharing contract.Li et al.[8] studied the impact of revenue sharing and cost sharing contracts provided by retailers on emission reduction and corporate profitability.
The existing research on the monopoly market mainly focused on the general market. There is pricing competition between duopolistic retailers, and each retailer can optimize its retail price to improve its own demand[9].Modak et al. [10] studied a three-level supply chain in which the manufacturer supplies batch products with random incomplete quality products. The influence of incomplete quality products on the optimal decision was analyzed.Hosseini-Motlagh et al. [11]analyzed the performance of a supply chain consisting of a monopolistic manufacturer and two competing retailers under a promotional-effort credit-period dependent demand. Xu et al. [12] introduced overconfidence into duopoly supply chain and analyzed the effect of retailer overconfidence on supply chain performance.
Existing research on the green monopoly market is rare. Qi et al. [13] considered a make-to-order supply chain with one supplier and two retailers under carbon cap regulation, and analyzed optimal pricing decisions for the decentralized and centralized models.
Yang et al. [14] considered a two-echelon supply chain with one supplier and two capital constrained retailers. The impact of external financing on the best decision of participants and supply chain performance was discussed. Wang et al. [1] studied a duopoly market, and analyzed the influence of consumers’ green preference on members’ optimal decision. However, the research on the competitive strategies among retailers in the green monopoly market was scarce.
In this paper, how the strategic behavior between two echelons influence decision-making in an oligopoly market is discussed. Firstly, the influence of a manufacturer’s green production on the decision-making and green level is analyzed. Secondly, four kinds of strategic behaviors among two duopolistic retailers are discussed. Particularly, the impacts of competition intensity among retailers on the profitability and decisions of supply chain members are assessed.
1 Problem Description and Assumptions
Fig.1 depicts a two-echelon green supply chain competitive model. This model consists of a monopolistic manufacturer investing in green production and two competing retailers. The manufacturer sells products to “green” sensitive consumer markets through duopolistic retailers. The manufacturer acts as the Stackelberg leader, determining the green level of product θ and setting the wholesale price of product ω to the retailers. Then, two duopolistic retailers sharing a common market respond by setting sale price p and the corresponding order quantity q.
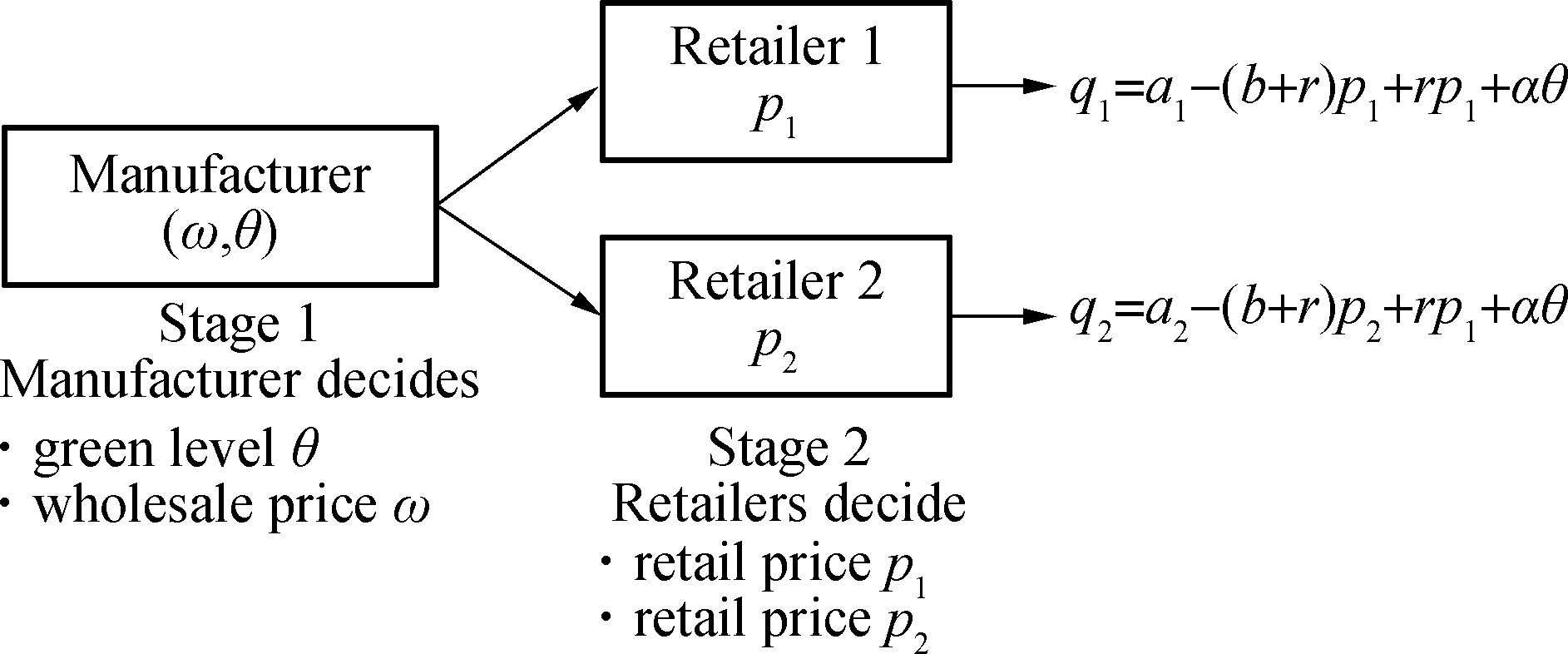
Fig.1 Two-echelon GSC competitive model
The linear market demand model is widely used in supply chain research. In this model, market demand D is expressed as a linear function of retail price and the product green level. The actual demand of the market changes with the green level of the manufacturer and the retail price of the two duopolistic retailers.
The demand function of this paper is
Di(p,θ)=ai-bpi+r(pj-pi)+αθ i=1,2;j=3-i
(1)
where ai represents the potential market size; b represents the consumers’ sensitivity to the retail price of the products decided by the retailers, which indicates how strongly consumers respond to retail prices;parameter r is the consumers’ sensitivity to the retail price difference of the products; α is the marginal consumer demand coefficient of green level. Parameter α must be nonnegative, and the larger the α, the stronger the consumer’s preference for green products. In other words, a lower retail price and higher green level of products will lead to higher market demand. In a similar model, r represents a “leakage” of the demand from one retailer to another, corresponding to switching customers. r is also used as an alternative for retailers. The demand function is arranged as
Di(p,θ)=ai-(b+r)pi+rpj+αθ i=1,2;j=3-i
(2)
Competition is common in the duopoly market. The competitive intensity is defined as the degree of substitution between competing products. The competition in this model is interpreted as the customer transfer caused by the retail price set by both retailers to the market demand of the other party. On the influence ratio of retail price to competitor’s demand between two retailers, t=t/(r+b). Here, parameter t is the demand substitutability of retail price between two retailers, representing the competition intensity between duopolistic retailers in this paper. When t=0, the demand is completely independent. Each retailer is a monopolist in its own region.
In the demand function, the price competition between retailers leads to the transfer of consumers between two retailers. The total demand of the market will not change due to the competition in this model. Similar demand functions include Anderson and Bao[15], Zhang et al.[16], Huang et al.[17], Chen et al.[18].
In this model,the following assumptions are made:
1) The manufacturer and retailers are risk-neutral and pursue the maximum profit.
2) To improve the green level of the product, manufacturers need to invest funds for new product research and development (R&D).The R&D investment has a quadratic relationship with its results and the cost of green product R&D is entirely borne by the manufacturers.
3) The improvement of the products’ green level will not affect the marginal production cost. The product greenness θ is transparent to consumers. Information between supply chains can be well transferred.
4) The order quantity of manufacturer and retailer is equal to the market demand.
2 Competitive Behaviors Model
There are different competitive behavior models between two duopolistic retailers, i.e. Cournot, collusion, and Stackelberg. Particularly, in the collusion model, in different market environments, two retailers choose to set the same or different retail price. Therefore, two cases of collusion, co-pricing and unified pricing, have been discussed in detail.
2.1 Cournot competitive behavior model
Fig.2 presents the structure of the Cournot model. The duopolistic retailers independently respond to the retail price p1 and p2. In this behavior, there is no collusion between retailers, and each retailer knows how the other party acts. Therefore, retailers can make the best decision independently to maximize profitability.
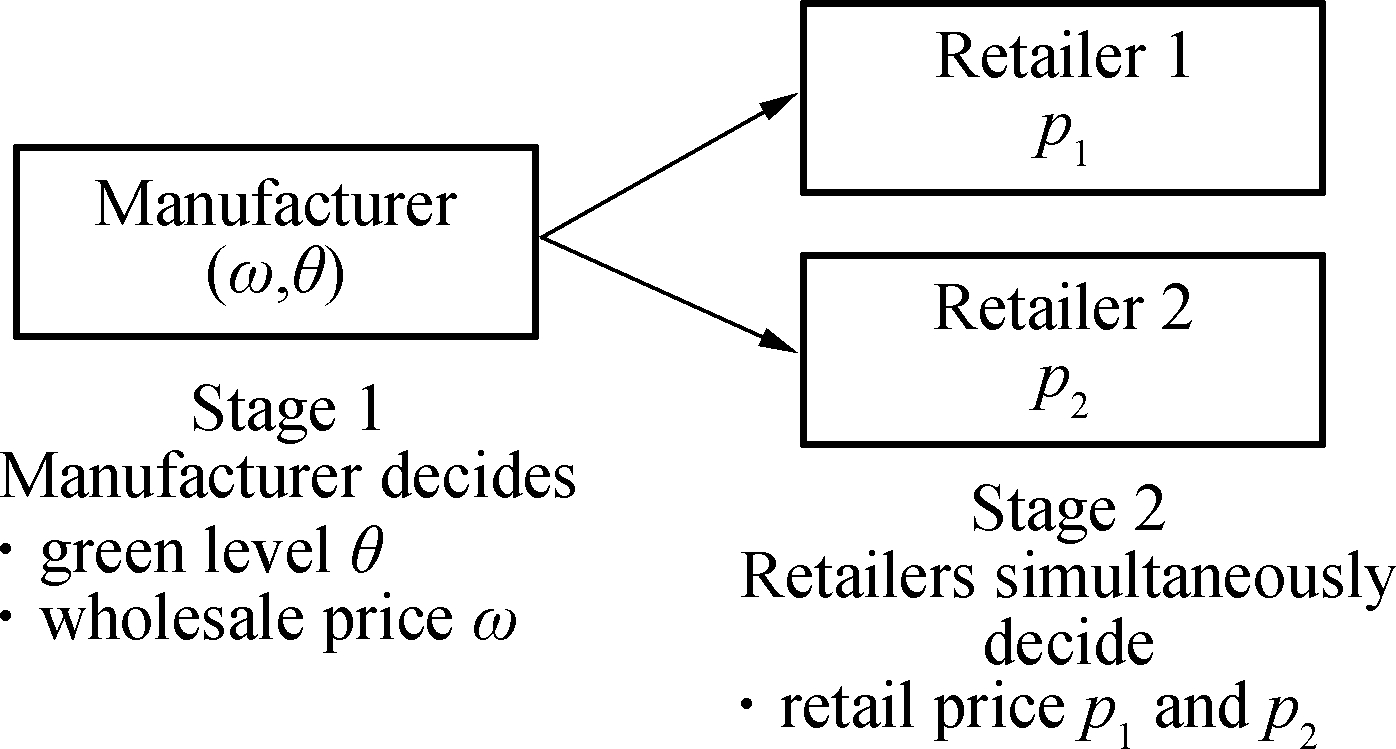
Fig.2 Cournot model
As analyzed in the market demand function, the order quantity of duopolistic retailers is
q1=a1-(b+r)p1+rp2+αθ
(3a)
(3b)
The manufacturer’s profitability function is
(4)
Parameter c represents the unit manufacturing cost, and parameter I represents the investment coefficient of green products.
Solving the retailer’s profit function first, we obtain
(5a)
(5b)
As for the duopolistic retailers, the optimal order quantities and retail price need to be determined. Meanwhile, consumer demand is the function of retail price p and green level θ. Therefore, the retailers pursue profitability maximization with retail price as a parameter. The optimal retail price p1 and p2 can be obtained by solving ![]()
(6a)
(6b)
Substituting the expression of retail price (6a) and (6b) into the expression of the order quantity (3a) and (3b), the optimal order quantities of the retailers can be obtained as below:
(7a)
(7b)
Furthermore, the manufacturer’s profit function can be written as
(8)
The profitability of the manufacturer is a concave function of ω and θ.
Taking the second-order partial derivatives of ![]() with respect to ω and θ, the Hessian matrix of the manufacturer’s profit function is
with respect to ω and θ, the Hessian matrix of the manufacturer’s profit function is

The manufacturer has the optimal profit. It is required that the first-order principal minor determinant H1=bI(2b+r)-(b+r)α2>0. The corresponding constraint is
s.t.
bI(2b+r)-(b+r)α2>0
The optimal wholesale price ωc* and the optimal green degree θc* can be obtained by solving ![]()
(9)
(10)
Substituting ωc* and θc* into the corresponding expression, the optimal pricing policies and the corresponding maximum profitability can be obtained.
2.2 Collusion behaviors model
Fig.3 presents the structure of the collusion model. Two scenarios of the collusion strategic behaviors are discussed. Fig.3(a) is the co-pricing model. The two retailers jointly design retail price p1 and p2 with the goal of maximizing the downstream profitability of the supply chain. Fig.3(b) is the unified pricing model. The two retailers set a uniform retail price p in the downstream market. Unified pricing aims at controlling the market and gaining monopoly profitability. In particular, it is a non-competitive collusion.
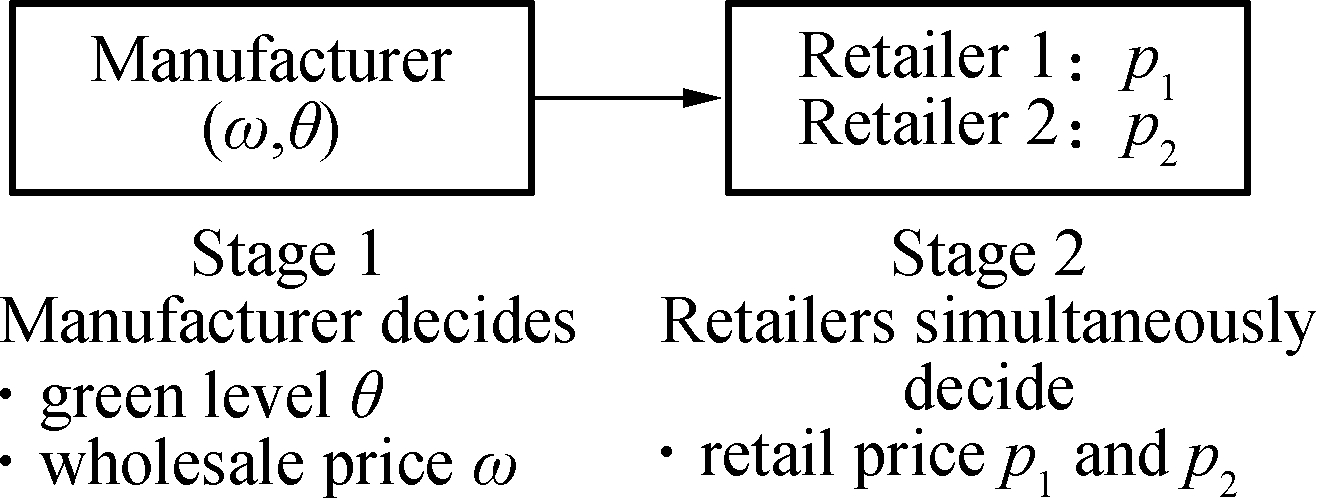
(a)
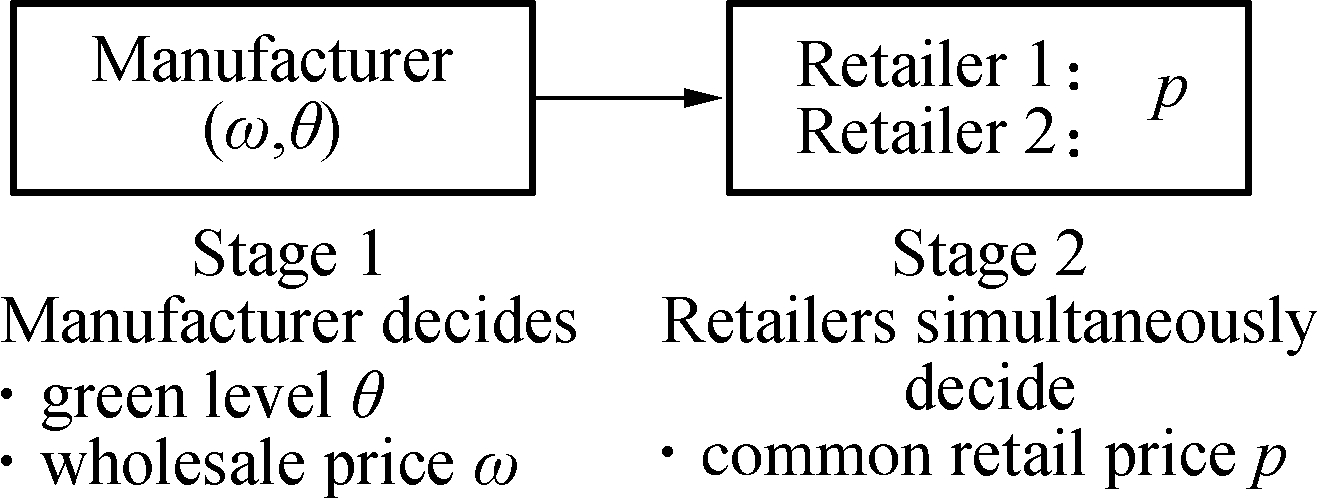
(b)
Fig.3 Collusion behaviors model.(a) Co-pricing model;(b) Unified pricing model
2.2.1 Co-pricing model
The two duopolistic retailers jointly design retail price p1 and p2 to achieve maximum profitability. The total profitability of the downstream retail market is given as
![]()
[a2-(b+r)p2+rp1+αθ](p2-ω)
(11)
The total profitability of the downstream retail market is a concave function of p1 and p2.
Solving the equations of ![]() gives the optimal retail price of the duopolistic retailers as
gives the optimal retail price of the duopolistic retailers as
(12a)
(12b)
Substituting (8a) and (8b) into the demand function of the retailers, the optimal order quantities of the retailers are
(13a)
(13b)
Being a leader, the manufacturer knows the retailers’ reaction to the wholesale prices and green degree, and thus substituting (13a) and (13b), the manufacturer’s profitability is
(14)
The profitability of the manufacturer is a concave function of ω and θ, and the corresponding constraint is
![]()
s.t.
2bI-a2>0
Solving the equations of ![]()
(15)
(16)
Similarly, the optimal pricing policies and the maximum profitability can be obtained by substituting ![]() into the corresponding expression.
into the corresponding expression.
2.2.2 Unified pricing model
In this model,two duopolistic retailers set a unified downstream market price, resulting in an eliminating price competition among retailers.Two retailers are equivalent to an exclusive retailer downstream functionally.
In this way, the price difference of two retailers will no longer affect the purchase demand of consumers.The demand function is simplified as
q=a-bp+αθ
(17)
The total profit function of the corresponding downstream market is
(18)
The total profitability of the downstream retail market is a non-negative concave function of the unified price p, and the corresponding constraint is
The optimal unified downstream market price can be obtained by setting the first derivative of downstream market profitability with respect to retail price equal to zero:
(19)
The manufacturer’s profit function is
(20)
The profit function of the manufacturer is a concave function of ω and θ, and the corresponding constraint is
![]()
s.t.
2bI-α2>0
Similarly, the optimal policies of the manufacturer can be obtained:
(21)
(22)
It can be found that under the condition of retailers acting in collusion, the decision-making of the manufacturer will not be affected by the collusion strategic behavior of downstream retailers, where
ωu1*=ωu2*, θu1*=θu2*
Substituting (15) and (16) into the manufacturer’s profit function (14), we can obtain
The two retailers set a unified downstream market price, aiming at controlling the market and gaining monopoly profits. However, comparing the calculation results of the two scenarios of the collusion strategic behaviors, the result is counter-intuitive.
With a unified pricing method, retail prices do not relatively increase, and the profitability of retailers declines. It indicates that cooperation without competition is undesirable, and moderate competition is beneficial to both sides of the retailers. It can be explained by the lack of enthusiasm when there is no competition among retailers, leading to the failure to achieve an ideal purpose of cooperation.
2.3 Stackelberg behavior model
Fig.4 presents the structure of the Stackelberg model. The duopolistic retailers play a sequential game. An assumption is made that retailer 1 acts as a Stackelberg leader, setting the retail price first. Then, the follower retailer 2 adjusts its retail price to maximize the profitability based on retail price p1.

Fig.4 Stackelberg model
The profit function of retailer 2 is
(23)
Solving the equation of ![]() gives retailer 2’s reaction function about retailer 1.
gives retailer 2’s reaction function about retailer 1.
(24)
Retailer 1 maximizes profitability. Substituting retailer 2’s reaction function into profit function and solving ![]() gives the optimal retail price for retailer 1:
gives the optimal retail price for retailer 1:
(25a)
Then by substituting (25a) into (24), the optimal retail price for retailer 2 can be easily obtained.
(25b)
Similarly, the optimal order quantities of ![]() for retailers are
for retailers are
![]()
(26a)
(26b)
Consequently, the manufacturer’s profit function of wholesale price and green degree is
(27)
The profitability of the manufacturer is a concave function of ω and θ, and the corresponding constraint is
s.t. 8bI(b+r)(2b2+4br+r2)-(8b3+28b2r+29br2+8r3)α2>0
Solving the equations of ![]() gives the manufacturer’s optimal wholesale price ωs* and the optimal green degree θs*.
gives the manufacturer’s optimal wholesale price ωs* and the optimal green degree θs*.
(28)
(29)
where
F=2b2+4br+r2, G=8b3+28b2r+29br2+8r3
Substituting ωs* and θs* into the corresponding expression, the optimal pricing policies and profitability of the manufacturer can be obtained:
(30a)
(30b)
(31)
where
H=20b4+76b3r+91b2r2+36br3+4r4
J=8b5+64b4r+164b3r2+169b2r3+66br4+8r5
M=80b6+464b5r+1044b4r2+1 148b3r3+
639b2r4+168br5+16r6
2.4 Corollaries of model analysis
Corollary 1 One retailer with a larger market share will set a higher retail price than another retailer.
Take the Cournot model as an example. Comparing the optimal retail price among two duopolistic retailers,there is ![]() if a1>a2, then
if a1>a2, then ![]()
Meanwhile, the competition between duopolistic retailers will result in quite a close retail price.Setting t=r/b+r, where t∈(0,1), r=bt/(1-t) can be obtained. Substituting r can give
It can be found that when consumers’ price sensitivity remains stable, with the increase in the competition intensity t, the value of ![]() approaches 0.
approaches 0.
Corollary 2 For the Stackelberg game between retailers, the game leader tends to be the retailer with the bigger market, who meanwhile obtains a higher profitability.
As the game leader, the retailer can respond to the market quickly and adjust its strategy, resulting in better profitability. According to the retailers’ profit expression ![]() it can be found that when a1>a2,
it can be found that when a1>a2, ![]()
When retailers have the same market share a1=a2, there is
It can be found that only if the market factor satisfies the condition 2bc-a≥0, there will be a game leader.
Corollary 3 The manufacturer’s marginal profitability is no less than the sum of the two duopolistic retailers’ marginal profitability. However, owing to the green cost of manufacturers, the profitability of downstream market may exceed the upstream manufacturer’s profitability when satisfying certain conditions:
when bI<α2<2bI![]()
Proof Taking Cournot as an example, ![]() downstream profitability minus upstream manufacturer’s profit function is
downstream profitability minus upstream manufacturer’s profit function is
![]()
![]()
After simplification,
Combining the constraint of Eq.(8) and the non-negativity of green degree, when α2-bI>0 , ![]() can be obtained.
can be obtained.
With the manufacturer as the initiator of green supply chain, the original intention is varied, such as adapting to the market demand for more profitability, shouldering social responsibility, or just ensuring compliance with the requirements of laws and policies. However, due to the manufacturer’s green investment, the downstream profitability may exceed the manufacturer’s profit. It is showed that the green supply chain can be better implemented if the manufacturer can obtain some help. For instance, the government can set an appropriate policy or economic support to manufacturers. The retailers can shoulder part of the green cost and promote green products in the downstream market.
3 Numerical Analysis
Due to the complexity of the case analysis and display results of the Stackelberg model, the calculation results have been analyzed using numerical values. The main purpose is to compare and analyze the strategic behaviors among retailers. The impact of manufacturer’s green production is discussed. The effect of competition intensity among retailers on the supply chain members’ profitability is also analyzed.
In this study, assumptions are made that the related parameters are a=1 200, b=7, c=30, α=5, I=6.
3.1 The impact of manufacturer’s profitability and decision
Tab.1 presents a comparison of manufacturers’ decision-making and profitability under different strategy scenarios. From Tab.1, when a market factor changes during a certain period, no matter what the market factor is, the duopolistic retailers’ action in Cournot results in the highest wholesale price, the green degree and the highest profitability, middle in the Stackelberg behaviors scenario, the lowest in the collusion behaviors scenario.
In numerical experiments, the initial market size ratio set for retailers is 5.5∶4.5, a1=660, a2=540. Meanwhile, considering the non-negativity of profit function and decision variables, the upper limit of α is 8.13. In particular, the changes in the market factors are considered. The comparison uses a certain range for each parameter, not just a single value.
The comparison results enlighten that manufacturer prefers the Cournot competitive behavior among the retailers. This is because it provides not only the maximum profitability, but also more environmentally friendly products.
Tab.1 The comparison of the manufacturers’ decision-making and profitability under different strategy scenarios

The variation range of the parametersThe comparison of variablesbrcIαθωπM(4,10)53065θc>θs>θuωc>ωs>ωuπcM>πsM>πuM7(0,20)3065θc>θs>θuωc>ωs>ωuπcM>πsM>πuM75(20, 40)65θc>θs>θuωc>ωs>ωuπcM>πsM>πuM7530(3,15)5θc>θs>θuωc>ωs>ωuπcM>πsM>πuM75306(0, 8.13)θc>θs>θuωc>ωs>ωuπcM>πsM>πuM
Due to the manufacturer’s green investment, the downstream profitability may exceed the upstream manufacturer’s profitability. Next, the impact of the consumers’ green sensitivity on manufacturers’ profitability is analyzed.
Fig.5 presents the impact of consumers’ green sensitivity on manufacturers’ profitability. It can be found that among the three scenarios, the retailers’ action in Cournot causes the manufacturer to charge the highest profitability. The collusion behavior results in the minimum profitability. Moreover, the manufacturer’s profitability under Cournot and Stackelberg behavior is significantly higher than that of collusion behavior. Furthermore, the green sensitivity of consumers is conducive to the manufacturer’s profitability. With the increase in the consumers’ green sensitivity coefficient α, the profitability of the manufacturer will gradually increase.
Note that, the manufacturer’s profitability does not always increase with the increase in α. In this numerical analysis, when α exceeds a certain threshold (8.13 in this experiment), the manufacturer will have a negative profitability. This is because the green level cannot be set particularly high. A higher green level requires a higher green cost.
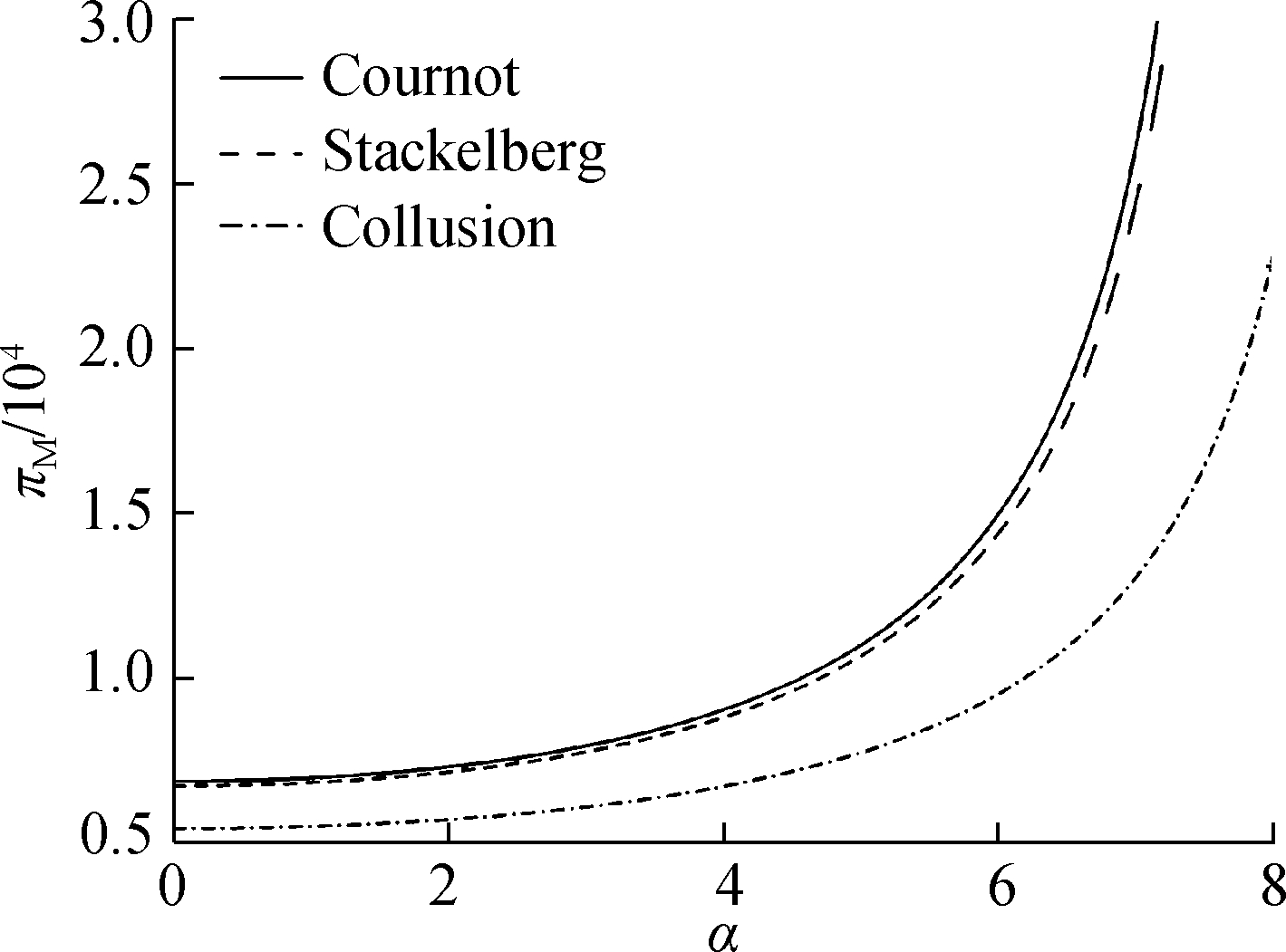
Fig.5 The impact of consumers’ green sensitivity on manufacturers’ profitability
3.2 Analysis on the competitive behaviors among duopolistic retailers
The duopolistic retailers’ competitive behaviors selection is to obtain a higher market profitability. The manufacturer set in this paper is a clean manufacturer. It is found that the retailers’ action in collusion are not always able to achieve the goal of cooperation. The collusion depends on some market factors, such as the sensitivity of consumers to products. In this analysis, the sum of retailers’ profitability is chosen for studying the choice of the competition strategy.In order to study the competitive behaviors, it is made assumptions that r=5, α=3.
Figs.6 to 8 present the impact of consumer product sensitivity on the sum of retailers’ profitability. Fig.6 presents the impact of consumers’ green sensitivity α on downstream market profitability πR. It can be found that the Cournot behavior and the Stackelberg behavior are very similar. When α is higher than 4.4,the downstream market profitability of the Cournot behavior begins to exceed that of the Stackelberg behavior. For collusion behavior, there is the critical point α=3.0. When α<3.0, the downstream market profitability will exceed the other two behaviors. In other words, the retailers will choose to cooperate only when the consumers’ green sensitivity α<3.0. The improvement of consumer’s green sensitivity will increase retailers’ profitability.
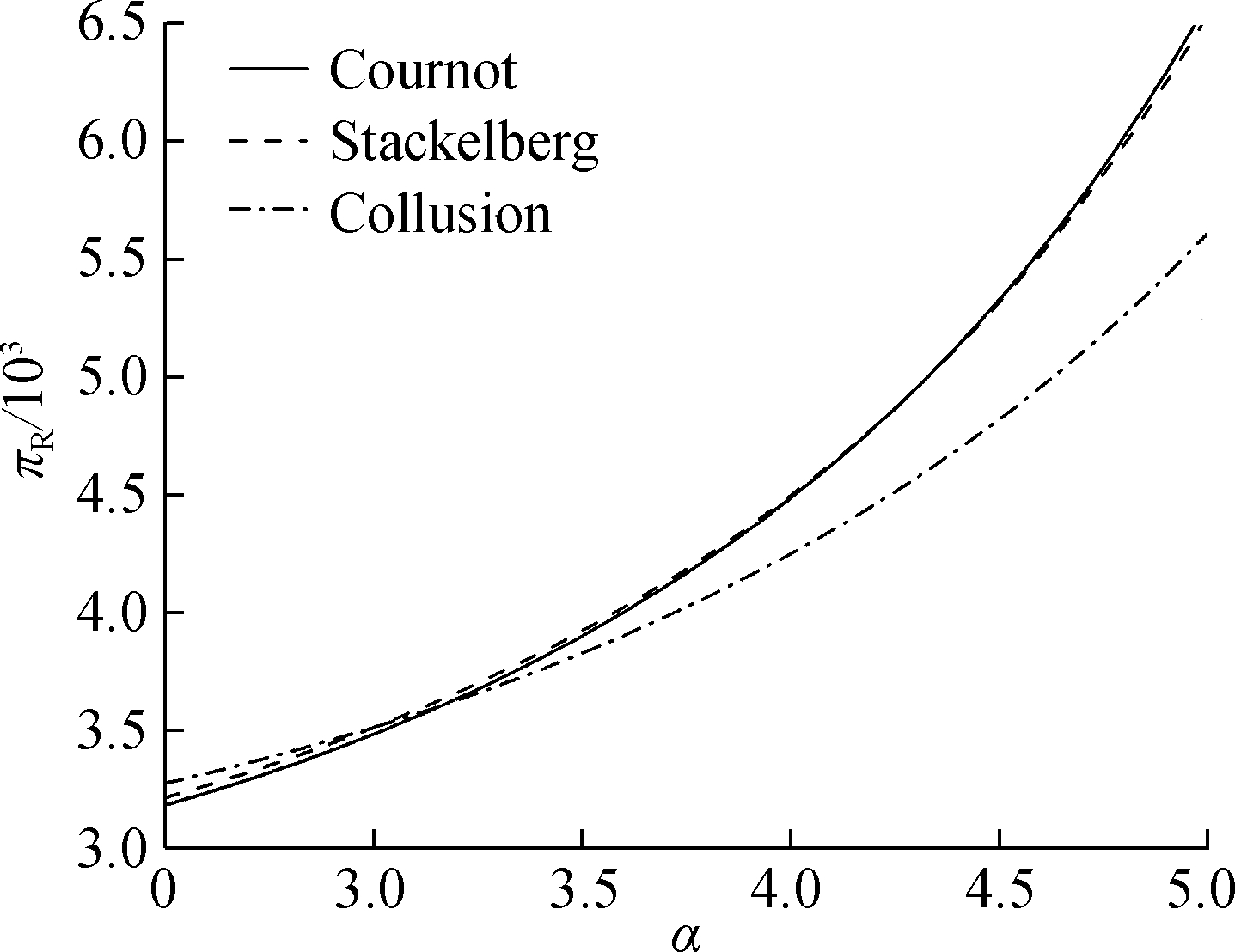
Fig.6 The impact of consumers’ green sensitivity on downstream market profitability
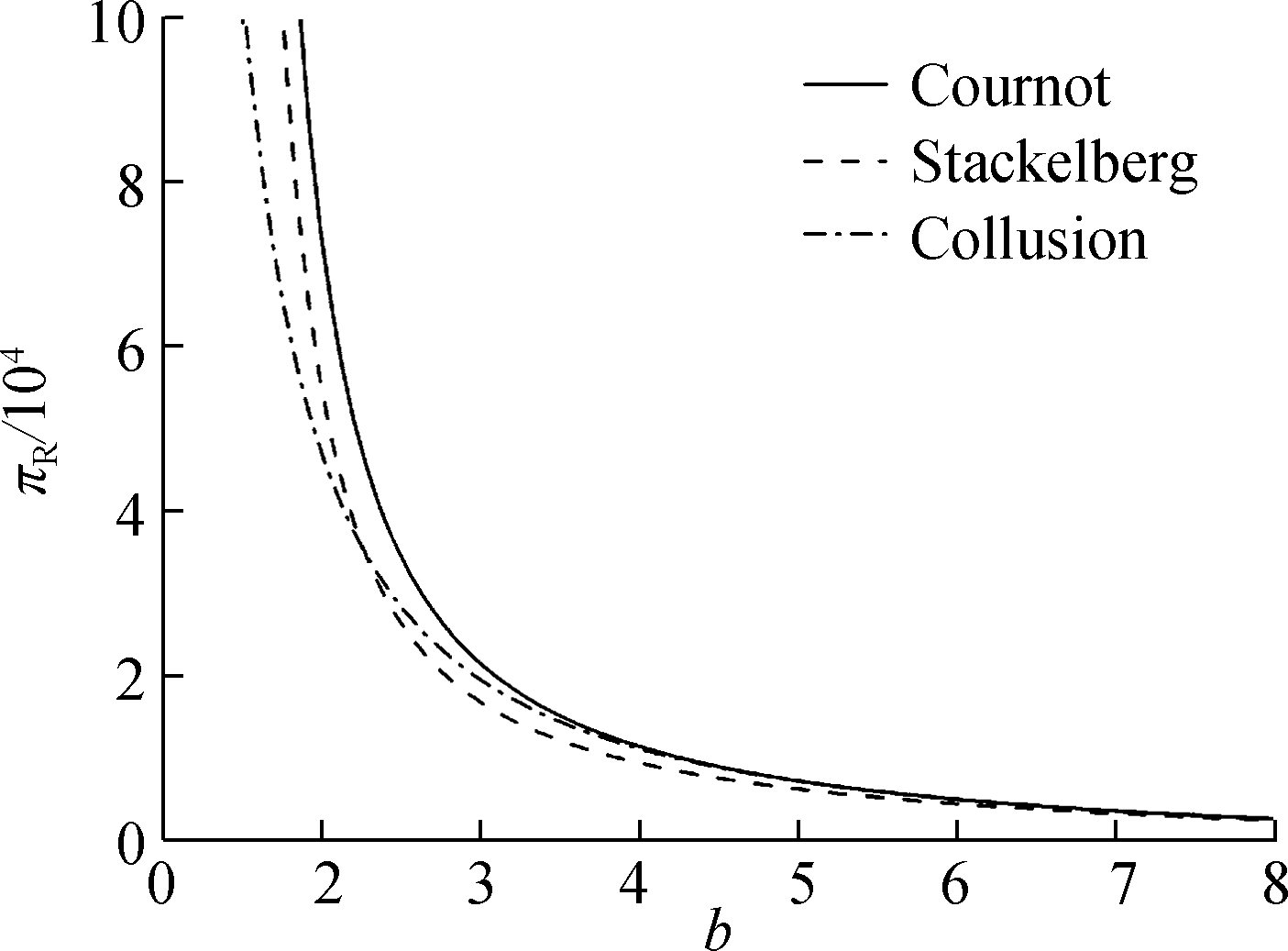
Fig.7 The impact of consumers’ price sensitivity on downstream market profitability

Fig.8 The impact of consumers’ price difference sensitivity on downstream market profitability
Fig.7 presents the impact of consumers’ price sensitivity b on downstream market profitability πR. It can be found that the downstream market profitability is negatively correlated with coefficient b. When b is less than 5.21, the downstream market profitability of collusion behavior is significantly lower than that of the Cournot behavior and Stackelberg behavior. That is to say, other market factors remain in a stable period, and when b is less than 5.21, the duopolistic retailers will choose either the Cournot or the Stackelberg strategic behavior.
Fig.8 presents the impact of consumers’ price difference sensitivity coefficient r on downstream market profitability πR. It can be found that the collusion behavior can significantly reduce the profitability loss caused by the increased price difference sensitivity.
When consumers are more sensitive to the price difference of products, the collusion behavior results in better profitability. There is the obvious inflection point r=5.1. When r>5.1, the retailers are keen on collusion behavior. It can also be seen that when r>2, the Stackelberg behavior is a better choice when retailers cannot cooperate.
3.3 The impact of competition intensity
In order to study the impact of competition intensity t, assumptions are made that b=7, c=30, I=6. The initial market size ratio in this section is 5.5∶4.5.
Fig.9 presents the impact of retailers’ competition intensity on manufacturers’ profitability. The consumers’ green sensitivity is set to be α=3. It can be found that the competition between duopolistic retailers is beneficial for the manufacturer’s profitability. The duopolistic retailers’ action in Cournot causes the manufacturer to acquire the highest profitability, while the collusion behavior results in the lowest profitability. Furthermore, the manufacturer’s profitability is positively related to the competition intensity t.It can be inferred that manufacturers hate the collusion between retailers. Manufacturers prefer fierce competition among retailers.
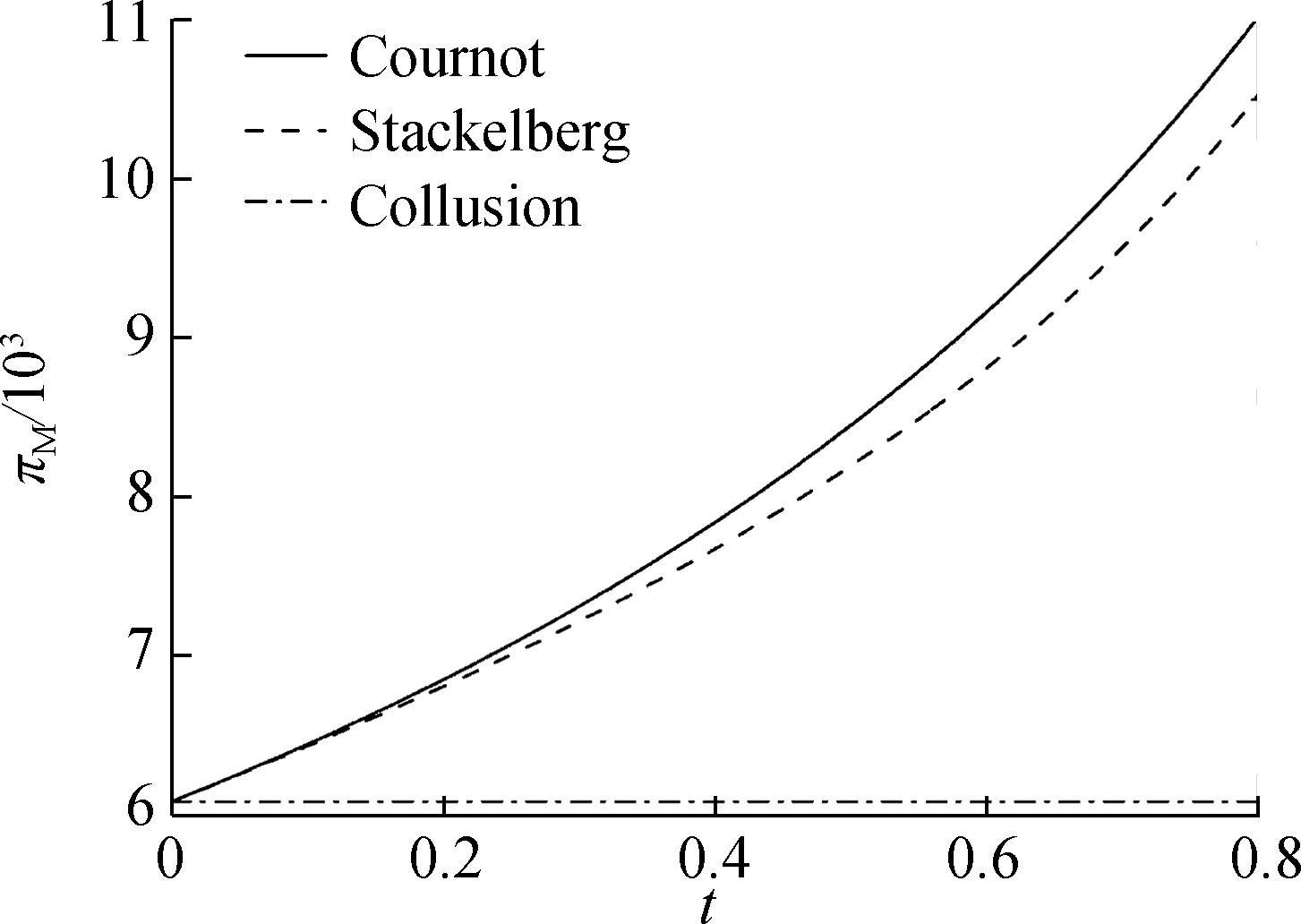
Fig.9 The impact of retailers’ competition intensity on manufacturers’ profitability
Fig.10 presents the relationship between the downstream profitability and the competition strength t. The consumers’ green sensitivity is set to be α=3 in Fig.10(a), α=5 in Fig.10(b). When the consumers’ green sensitivity is high, just as in Fig.10(a), the retailers will not like to choose collusion. With the increase in competition intensity, the downstream market’s profitability shows a trend of rising first and then declining. It indicates that for the Cournot behavior and Stackelberg behavior, certain competition is beneficial for the total profitability. However, it is necessary to avoid excessive competition. When the consumers’ green sensitivity is low, as shown in Fig.10(b), the more drastically the duopolistic retail market competes, the smaller the downstream market’s profitability is made. There is the critical point t=0.41.
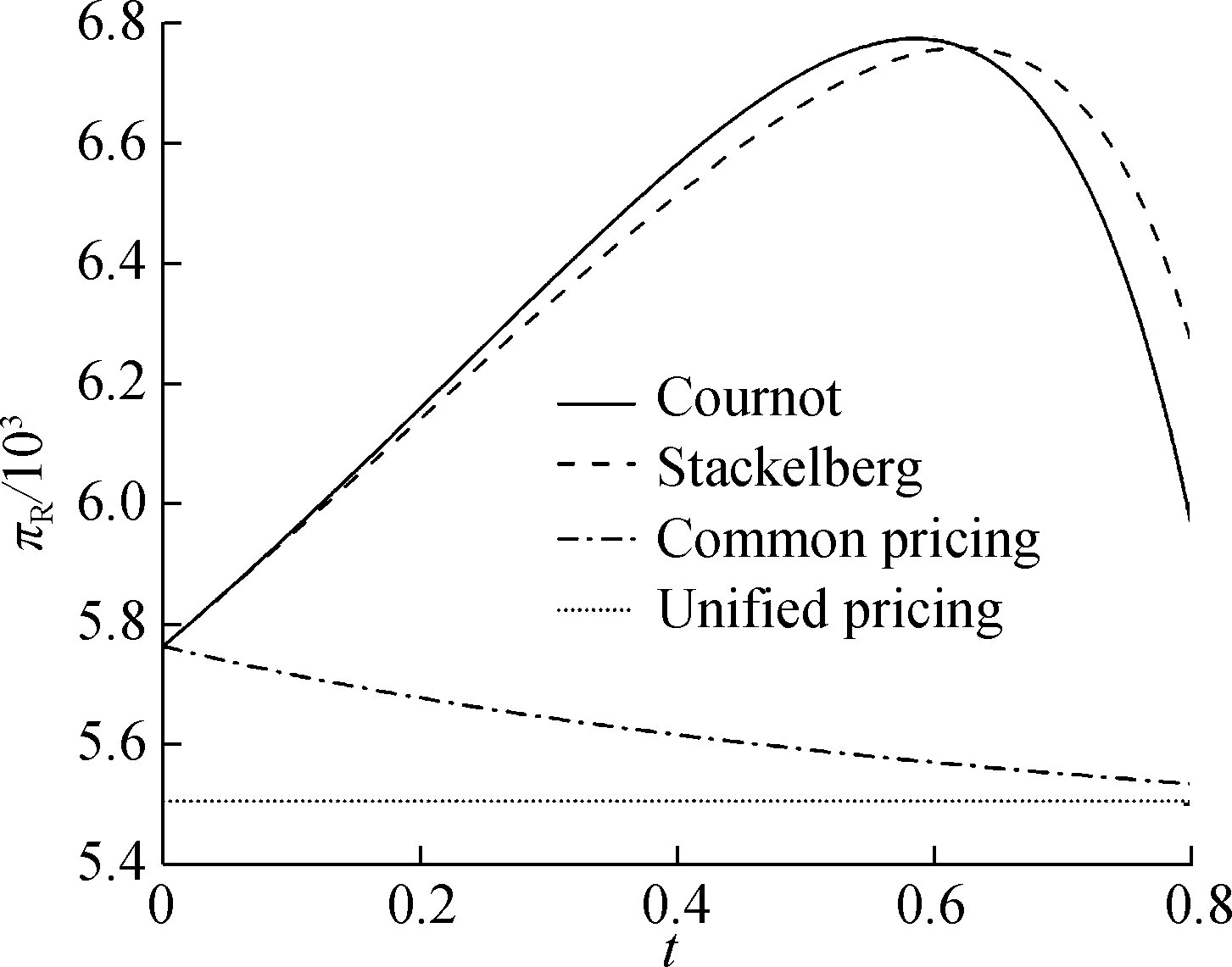
(a)
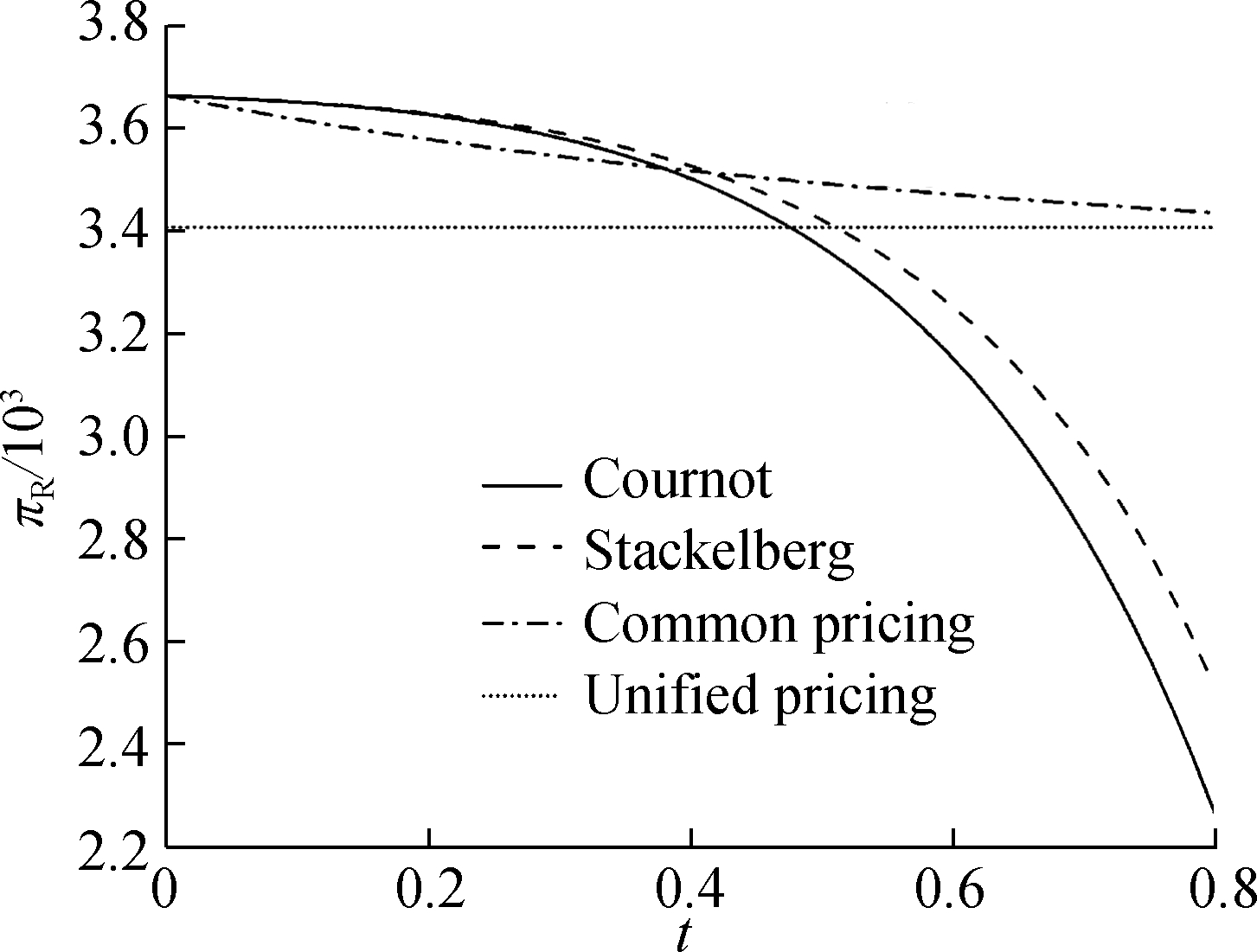
(b)
Fig.10 The impact of competition intensity on downstream market profitability.(a) α=5;(b) α=3
When t<0.41, the behavior of Cournot and Stackelberg has higher downstream market profitability. When the competition is drastic, the collusion behavior will bring a higher profitability.
4 Conclusions
1) The marginal profitability of the manufacturer is no less than the total profitability of the duopolistic retailers. However, due to the manufacturer’s green investment, the downstream profitability of the supply chain may exceed the manufacturer’s profitability.Meanwhile, with the improvement of consumers’ green sensitivity, the profitability of the manufacturers and downstream retailers will increase.
2) The duopolistic retailers’ action in Cournot causes the manufacturer to acquire the highest profitability and set the highest degree of the green level. However, there is an opposite result in collusion.
3) Manufacturers’ profitability will increase as competition among retailers intensifies. Appropriate competition will benefit both retailers’ profitability.
4) Retailers will not choose collusion when the consumer’s green sensitivity is higher than a threshold.When the consumers are more sensitive to price difference, retailers prefer collusion, and then the Stackelberg behavior is chosen. In particular, with the increase in consumers’ sensitivity to price difference, the retailers’ profitability will drop dramatically with the Stackelberg or Cournot behavior.
[1]Wang Y, Hou G S. A duopoly game with heterogeneous green supply chains in optimal price and market stability with consumer green preference[J].Journal of Cleaner Production, 2020, 255: 120161. DOI:10.1016/j.jclepro.2020.120161.
[2]Hong Z F, Guo X L. Green product supply chain contracts considering environmental responsibilities[J].Omega, 2019, 83: 155-166. DOI:10.1016/j.omega.2018.02.010.
[3]Sheu J B, Chou Y H, Hu C C. An integrated logistics operational model for green-supply chain management[J].Transportation Research Part E: Logistics and Transportation Review, 2005, 41(4): 287-313. DOI:10.1016/j.tre.2004.07.001.
[4]Zhao R, Neighbour G, Han J J, et al. Using game theory to describe strategy selection for environmental risk and carbon emissions reduction in the green supply chain[J].Journal of Loss Prevention in the Process Industries, 2012, 25(6): 927-936. DOI:10.1016/j.jlp.2012.05.004.
[5]Xu L, Dong M, Chen J. The selection of subsidy objects in duopoly competition [J]. Journal of Systems Management, 2018, 27(5): 961-70. (in Chinese)
[6]Yang H X, Miao L Y, Zhao C. The credit strategy of a green supply chain based on capital constraints[J].Journal of Cleaner Production, 2019, 224: 930-939. DOI:10.1016/j.jclepro.2019.03.214.
[7]Song H H, Gao X X. Green supply chain game model and analysis under revenue-sharing contract[J].Journal of Cleaner Production, 2018, 170: 183-192. DOI:10.1016/j.jclepro.2017.09.138.
[8]Li T, Zhang R, Zhao S L, et al. Low carbon strategy analysis under revenue-sharing and cost-sharing contracts[J].Journal of Cleaner Production, 2019, 212: 1462-1477. DOI:10.1016/j.jclepro.2018.11.282.
[9]Seyedhosseini S M, Hosseini-Motlagh S M, Johari M, et al. Social price-sensitivity of demand for competitive supply chain coordination[J]. Computers & Industrial Engineering, 2019, 135: 1103-1126. DOI:10.1016/j.cie.2019.05.019.
[10]Modak N M, Panda S, Sana S S. Three-echelon supply chain coordination considering duopolistic retailers with perfect quality products[J]. International Journal of Production Economics, 2016, 182: 564-578. DOI:10.1016/j.ijpe.2015.05.021.
[11]Hosseini-Motlagh S M, Nematollahi M, Johari M, et al. A collaborative model for coordination of monopolistic manufacturer’s promotional efforts and competing duopolistic retailers’ trade credits[J]. International Journal of Production Economics, 2018, 204: 108-122. DOI:10.1016/j.ijpe.2018.07.027.
[12]Xu L, Shi X R, Du P, et al. Optimization on pricing and overconfidence problem in a duopolistic supply chain[J]. Computers & Operations Research, 2019, 101: 162-172. DOI:10.1016/j.cor.2018.04.003.
[13]Qi Q, Wang J, Bai Q G. Pricing decision of a two-echelon supply chain with one supplier and two retailers under a carbon cap regulation[J]. Journal of Cleaner Production, 2017, 151: 286-302. DOI:10.1016/j.jclepro.2017.03.011.
[14]Yang H L, Zhuo W Y, Shao L S. Equilibrium evolution in a two-echelon supply chain with financially constrained retailers: The impact of equity financing[J]. International Journal of Production Economics, 2017, 185: 139-149. DOI:10.1016/j.ijpe.2016.12.027.
[15]Anderson E J, Bao Y. Price competition with integrated and decentralized supply chains[J]. European Journal of Operational Research, 2010, 200(1): 227-234. DOI:10.1016/j.ejor.2008.11.049.
[16]Zhang L H, Wang J G, You J X. Consumer environmental awareness and channel coordination with two substitutable products[J]. European Journal of Operational Research, 2015, 241(1): 63-73. DOI:10.1016/j.ejor.2014.07.043.
[17]Huang H, Ke H, Wang L. Equilibrium analysis of pricing competition and cooperation in supply chain with one common manufacturer and duopoly retailers[J]. International Journal of Production Economics, 2016, 178: 12-21. DOI:10.1016/j.ijpe.2016.04.022.
[18]Chen X, Luo Z, Wang X J. Compete or cooperate: Intensity, dynamics, and optimal strategies[J]. Omega, 2019, 86: 76-86. DOI:10.1016/j.omega.2018.07.002.