The study of Gorenstein projective modules can be traced back to Ref.[1], where the G-dimension of a finitely generated module over a two-sided Noetherian ring was introduced. Furthermore, the definition of Gorenstein projective modules was given in Ref.[2]. We knew already that a module of G-dimension zero is actually a Gorenstein projective module. Gorenstein projective modules play an important role in many areas. For example, they are widely used in the representation theory of Artin algebras, the theory of stable and singularity categories, and the cohomology theory of commutative rings, and so on.
Weak bialgebras and weak Hopf algebras introduced in Ref.[3] generalized the ordinary bialgebras and Hopf algebras by weakening the comultiplication of unit and the multiplication of counit. Comultiplication is allowed to be non-unital, but it is still coassociative. In exchange for coassociativity, the multiplicativity of the counit is replaced by a weaker condition, implying that the unit representation is not necessarily one-dimensional and irreducible. Weak Hopf algebras can provide us with a good framework for studying the symmetries of certain quantum field theories. Groupoid algebras, face algebras and generalized Kac algebras are examples of weak Hopf algebras.
The main purpose of this paper is to study the representation of weak Hopf algebras by investigating the Gorenstein dimensions of weak Hopf algebras and weak Hopf-Galois extensions. Let H be a weak Hopf algebra with a bijective antipode, A a weak right H-comodule algebra and B the H-coinvariant subalgebra of A. After recalling some basic definitions and giving a summary of the fundamental properties concerned with weak Hopf algebras, we study some properties of Gorenstein projective H-modules in representation category, and find that the Gorenstein global dimension of H is the same as the Gorenstein projective dimension of its left unital subalgebra. By applying the integral theory of weak Hopf algebras, on the one hand, we give a sufficient and necessary condition that a projective A-module is a projective B-module; on the other hand, we describe the separability of the functor A⊗B- and that of the restriction of scalar function B(-). Consequently, we investigate the Gorenstein global dimension of a weak Hopf-Galois extension.
1 Preliminaries
Throughout this article, k denotes a fixed field, and we will always work over k. The tensor product ⊗:=⊗k and Hom-functor are always assumed to be over k. We also use Sweedler’s notations for the terminologies on coalgebras and comodules. For a coalgebra C, we write the comultiplication Δ(c)=∑c1⊗c2 for any c∈C. For a right C-comodule M, we denote its coaction by ρ(m)=∑m(0)⊗m(1) for any m∈M. For any unexplained definitions and notations, one may refer to Ref.[4] or Ref.[5].
Definition 1[3] A weak Hopf algebra H is an algebra (H,μ,η) and a coalgebra (H,Δ,ε) such that
Δ(xy)=Δ(x)Δ(y)
(1)
ε(xyz)=∑ε(xy1)ε(y2z)=∑ε(xy2)ε(y1z) (2)
Δ2(1H)=(Δ(1H)⊗1H)(1H⊗Δ(1H))=
(1H⊗Δ(1H))(Δ(1H)⊗1H)
(3)
and there exists a linear map S: H→H, called an antipode, satisfying
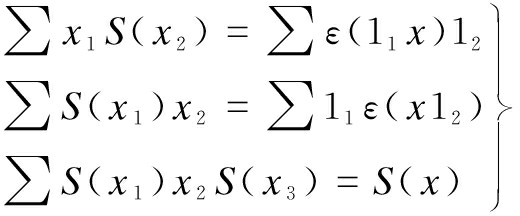
(4)
for all x, y, z∈H, where Δ(1H)=∑11⊗12, ![]()
Let H be a weak Hopf algebra. The images Ht=εt(h) and Hs=εs(h) of the projections εt,εs: H→H defined by
εt(h)=∑ε(11h)12, εs(h)=∑11ε(h12)
are both separable subalgebras of H and commute with each other[3]. Ht and Hs are called left and right unital subalgebras, respectively.
Definition 2[3] A left integral in H is an element l∈H satisfying hl=εt(h)lfor all h∈H. Furthermore, if εt(l)=1H, then it is said to be normalized. A normalized right integral is defined similarly. A left or right integral in H is called non-degenerate if it defines a non-degenerate functional on H*, the dual space of H.
The spaces of left and right integrals in H are denoted as ![]() and
and ![]() respectively.
respectively.
∑S(hl1)⊗l 2=∑l1⊗hl 2
(5)
for all h∈H. Meanwhile, according to Ref.[6], the left integral λ∈![]() satisfies the following invariant properties for all h,g∈H,
satisfies the following invariant properties for all h,g∈H,
∑h1λ(gh2)=∑λ(g2h)S(g1)
(6)
If a weak Hopf algebra H is finite dimensional, then it has a bijective antipode S[6], in which inverse is denoted as S-1 in the following, and there exist non-degenerate left integrals ![]() such that ∑l1λ(l 2)=1H[7]. Furthermore, the quasi-basis of λ is ∑l2⊗S-1(l1)[3]. Therefore, for all h∈H,
such that ∑l1λ(l 2)=1H[7]. Furthermore, the quasi-basis of λ is ∑l2⊗S-1(l1)[3]. Therefore, for all h∈H,
∑λ(S-1(l)h)=ε(h)
(7)
Let H be a weak Hopf algebra with an antipode S. According to Refs.[8-9], we have
(8)
(9)
(10)
(11)
Definition 3[10] Let H be a weak Hopf algebra, and A a right H-comodule, which is also an associative algebra. We call A a weak right H-comodule algebra if
ρ(ab)=ρ(a)ρ(b)
(12)
∑a1(0)⊗1(1)=∑a(0)⊗εt(a(1))
(13)
for all a,b∈A.
Let H be a weak Hopf algebra, and A a weak right H-comodule algebra. Then, according to Ref.[8], we obtain that
∑a1(0)⊗εs(1(1))
(14)
Define the H-coinvariant subalgebra of A as
Then, we know from Ref.[11] that
Definition 4[12] Let A be a weak right H-comodule algebra and B the H-coinvariant subalgebra of A. The extension A/B is said to be weak Hopf-Galois, if the canonical map
β:A⊗BA→A⊗sH, β(a⊗Bb)=∑ab(0)⊗sb(1)
is an isomorphism, where ⊗s:=⊗Hs is the relative tensor product over Hs![]() is a right Hs-module via y·a=∑ε(ya(1))a(0) for all y∈Hs, a∈A, and H is a left Hs-module via its multiplication).
is a right Hs-module via y·a=∑ε(ya(1))a(0) for all y∈Hs, a∈A, and H is a left Hs-module via its multiplication).
2 Gorenstein Global Dimensions for Weak Hopf Algebras
For a ring R, we denote the class of projective left R-modules by P, and for an object M in RM, the category of left R-modules, we denote the projective and injective dimension of M by p.dimRM and i.dimRM, respectively.
Definition 5[13] A left R-module M is Gorenstein projective if there exists an RHom(-,P)-exact sequence
…→P1→P0→P0→P1→…
such that M=Ker(P0→P1), where every Pi and Pi are projective.
Dually, Gorenstein injective left R-modules can be defined.
Definition 6 For a left R-module M, the Gorenstein projective dimension G.p.dimRM is at most n if there is an exact sequence
0→Gn→Gn-1→…→G1→G0→M→0
where every Gi is Gorenstein projective.
Dually, the Gorenstein injective dimension G.i.dimRM can be defined.
For any ring R, Ref.[14] shows us that
sup{G.p.dimRM|M∈RM}=sup{G.i.dimRM|M∈RM}
The common value is called the left Gorenstein global dimension of R and denoted as G.gl.dim(R).
We know that G.gl.dim(R)=0 if and only if the ring R is quasi-Frobenius[15]. In addition, R is left Gorenstein hereditary if every submodule of a projective left R-module is Gorenstein projective[16], i.e., G.gl.dim(R)≤1.
In what follows, we always assume that H is a weak Hopf algebra with a bijective antipode S. Then, the left H-module category HM, called the representation category, is an abelian monoidal category[17-18] such that
• Ht is the unit object with a left H-action via h·x=εt(hx) for all h∈H and x∈Ht;
• For M,N∈HM, the tensor product is M⊗tN:=M⊗HtN, where the right Ht-module structure on M is defined by m·x=S-1(x)·m for all m∈M and x∈Ht;
• The left H-module structure on M⊗tN is defined by the following diagnosing action h·(m⊗tn)=h1·m⊗th2·n, for all h∈H, m∈M, n∈N;
• For M,N∈HM, a homomorphism between M and N is left H-linear.
Proposition 1 If P is a Gorenstein projective left H-module, then so is P⊗tX for any left H-module X.
Proof If P is a Gorenstein projective left H-module, then there is an HHom(-,P)-exact sequence
P:…→P1→P0→P0→P1→…
such that M=Ker(P0→P1), where every Pi and Pi are projective. As Ht is separable, we can obtain an exact sequence
P⊗tX:…→P⊗tX→P0⊗tX→P0⊗tX→P1⊗tX→…
such that M⊗tX=Ker(P0⊗tX→P1⊗tX). Meanwhile, every Pi⊗tX and Pi⊗tX are projective left H-modules[19]. For any projective left H-module Q,
HHom(P⊗tX,Q)≅HtHom(X,HHom(P,Q))
Hence, HHom(P⊗tX,Q) is exact, as desired.
Theorem 1 Let H be a weak Hopf algebra with a bijective antipode S. Then, G.gl.dim(H)=G.p.dimHHt.
Proof Obviously, G.gl.dim(H)≥G.p.dimHHt. Hence, we shall prove the reverse inequality. Assume that G.p.dimHHt=n<+∞. Then, there is an exact sequence
0→Gn→Gn-1→…→G1→G0→Ht→0
where every Gi is Gorenstein projective. For any left H-module X, we obtain an exact sequence
0→Gn⊗tX→Gn-1⊗tX→…→G1⊗tX→
G0⊗tX→Ht⊗tX→0
As Ht⊗tX≅X, and every Gi⊗tX is Gorenstein projective by Proposition 1, we obtain G.gl.dim(H)≤n. This shows that G.gl.dim(H)≤G.p.dimHHt.
3 Gorenstein Global Dimensions for Weak Hopf-Galois Extensions
Throughout this section,H is always assumed to be a weak Hopf algebra with a bijective antipode S, unless otherwise stated. Then, let ![]() be two non-degenerate left integrals such that ∑l1λ(l2)=1H, and we fix a weak Hopf-Galois extension A/B and use the following formal notation for the inverse of β for all h∈H,
be two non-degenerate left integrals such that ∑l1λ(l2)=1H, and we fix a weak Hopf-Galois extension A/B and use the following formal notation for the inverse of β for all h∈H,
β-1(1A⊗sh)=∑ili(h)⊗Bri(h)∈A⊗BA
such that
∑∑ili(h)ri(h)(0)⊗sri(h)(1)=1A⊗sh (15)
by definition. Such elements enjoy the following properties.
Lemma 1[20] For all a∈A and h∈H, we have
∑ili(h)ri(h)=∑ε(h1(1))1(0)
∑∑ili(h)⊗Bri(h)(0)⊗sri(h)(1)=
∑∑ili(h1)⊗Bri(h1)⊗sh2
∑∑ili(h)(0)⊗Bri(h)⊗sli(h)(1)=
∑∑ili(h2)⊗Bri(h2)⊗sS(h1)
Consider the two functors:
A⊗B-:BM→AM, N A⊗BN
A⊗BN
B(-):AM→BM, M BM
BM
where B(-) is the restriction of the scalars functor.
Lemma 2 (A⊗B-,B(-)) and (B(-),A⊗B-) are double adjunctions.
Proof Note that the element ∑λ(a(1))a(0)∈B[21] for a∈A. Then, for all N∈BM, we have a well-defined map φ:A⊗BN→BHom(A,N) given by
φ(a⊗Bn)(b)=∑λ(b(1)a(1))b(1)a(0)·n
a,b∈A, n∈N
Then, it is easy to check that φ is a morphism of left A-modules, where BHom(A,N)∈AM via (a·f)(b)=f(ba) for all a,b∈A and f∈BHom(A,N). Meanwhile, we claim that φ is a bijection with the inverse given by
φ:BHom(A,N)→A⊗BN
φ(f)=∑li(S-1(l ))⊗Bf(ri(S-1(l )))
Indeed, on the one hand, for all a,b∈A and n∈N, by Lemma 1, we have
φφ(a⊗Bn)=
∑∑ili(S-1(l ))⊗Bλ(ri(S-1a(1))ri(S-1a(0)·n=
∑∑ili(S-1(l ))ri(S-1a(0)λ(ri(S-1a(1))⊗Bn=
∑∑ili(S-1(l 2))ri(S-1(12))a(0)λ(S-1(l 1)a(1))⊗Bn=
∑1(0)a(0)λ(S-1(l )1(1)a(1))⊗Bn
On the other hand, for all b∈A and f∈BHom(A,N), by Lemma 1, we have
φφ(f)(b)=
∑∑iλ(b(1)li(S-1(l ))(1))b(0)li(S-1(l ))(0)·
f(ri(S-1(l )))n=
∑∑iλ(b(1)l 2)f(b(0)li(S-1(l 1))ri(S-1(l 1)))=
∑λ(l 2)ε(S-1(l 1)b(1)1(1))f(b(0)1(0))=
∑λ(l 2)ε(S-1(l 1)b(1))f(b(0))n=f(b)
Hence, the adjoint isomorphism theorem, (A⊗B-,B(-)) and (B(-),A⊗B-) are double adjunctions[12].
By Lemma 2, we have the following assertion.
Corollary 1 If P∈BM is projective, then A⊗BP∈AM is projective.
Lemma 3 If H is semisimple and P∈AM, then P is projective as a left A-module if and only if P is projective as a left B-module.
Proof As H is semisimple, we know that H is finite dimensional and there is ![]() which is normalized[3], i.e., εs(J)=1H. Then, for all a∈A,
which is normalized[3], i.e., εs(J)=1H. Then, for all a∈A,
∑iali(J)⊗Bri(J)=∑ili(J)⊗Bri(J)a
(16)
In fact, by Lemma 1, we have
∑∑iali(J)ri(J)(0)⊗sri(J)(1)=
∑∑iali(J1)ri(J1)⊗s2J2=
as needed.
Consider that P is a projective left B-module and let M,N∈AM. Suppose that δ:M→N and ξ:P→N are left A-module morphisms such that δ is surjective. Since P is projective as a left B-module, there is a left B-module morphism f:P→M such that ![]() Define
Define
![]() ·f(ri(J)·p)
·f(ri(J)·p)
for all p∈P.
Obviously, ![]() is a morphism of left A-modules by (16). Moreover,
is a morphism of left A-modules by (16). Moreover,
∑ili(J)ri(J)·ξ(p)=∑ε(J1(1))1(0)·ξ(p)=
∑ε(εs(J)1(1))1(0)·ξ(p)=∑ε(1(1))1(0)·ξ(p)=
1A·ξ(p)=ξ(p)
where the third equality follows[8]. Hence, ![]() Thus, P is projective as a left A-module.
Thus, P is projective as a left A-module.
Conversely, suppose that P is projective as a left A-module. It follows from Lemma 2 that (A⊗B-,B(-)) is an adjoint pair. Since A is projective as a right B-module[22], we obtain that the functor A⊗B- is exact. Hence, B(-) preserves projective objects. Therefore, P is projective as B-module.
Definition 7[23] Let C and D be categories. A covariant functor F:C→D is separable if for all objects M,N∈C, there are maps ![]() satisfying the following conditions:
satisfying the following conditions:
1) For α∈HomC(M,N), we have ![]()
2) Given M′,N′∈C, f∈HomD(F(M),F(N)),g∈HomD(F(M′),F(N′)), α∈HomC(M,M′), β∈HomC(N,N′), we have ![]()
Lemma 4 1) If H is semisimple, then B(-) is separable.
2) If H* is semisimple, then A⊗B- is separable.
Proof 1) Let J∈![]() such that εs(J)=1H. By the proof of Lemma 3, we can know that the element ∑ili(J)⊗Bri(J) is exactly the separability idempotent, i.e., the extension A/B is separable. Hence, the restriction of scalars functor B(-) is separable[23].
such that εs(J)=1H. By the proof of Lemma 3, we can know that the element ∑ili(J)⊗Bri(J) is exactly the separability idempotent, i.e., the extension A/B is separable. Hence, the restriction of scalars functor B(-) is separable[23].
2) Note that A is a weak left H*-module algebra under the action φ⇀a=∑φ(a(1))a(0) for a∈A, φ∈H*[24]. As H* is semisimple, there exists a normalized left integral ![]() Then, λ⇀1A=1A, and the map F:A→B defined by F(a)=λ⇀a is a B-bimodule projection[21]. This assumes that B is a direct summand of A as a B-bimodule. Hence, the unit
Then, λ⇀1A=1A, and the map F:A→B defined by F(a)=λ⇀a is a B-bimodule projection[21]. This assumes that B is a direct summand of A as a B-bimodule. Hence, the unit ![]() of the adjunction (A⊗B-,B(-)) is a split monomorphism[25]. So, the induction function A⊗B- is separable[11].
of the adjunction (A⊗B-,B(-)) is a split monomorphism[25]. So, the induction function A⊗B- is separable[11].
Corollary 2 1) If H is semisimple, then M is a left A-module direct summand of A⊗BM for all M∈AM.
2) If H* is semisimple, then N is a left B-module direct summand of A⊗BN for all N∈BM.
Proof 1) As H is semisimple, we know from Lemma 4 that B(-) is separable. Hence, the counit  :
:![]() of the adjunction (A⊗B-,B(-)) is a cosplit epimorphism[11], that is, there is a natural transformation
of the adjunction (A⊗B-,B(-)) is a cosplit epimorphism[11], that is, there is a natural transformation ![]() for all M∈AM. Thus, M is a left A-module direct summand of A⊗BM.
for all M∈AM. Thus, M is a left A-module direct summand of A⊗BM.
2) As H* is semisimple, we have that A⊗B- is separable by Lemma 4. Hence, we also know that the counit ![]() of the adjunction (B(-),A⊗B-) is a cosplit epimorphism[11]. Thus, N is a left B-module direct summand of A⊗BN for all N∈BM.
of the adjunction (B(-),A⊗B-) is a cosplit epimorphism[11]. Thus, N is a left B-module direct summand of A⊗BN for all N∈BM.
Lemma 5 If N∈BM is Gorenstein projective, then A⊗BN∈AM is Gorenstein projective.
Proof Suppose that N is a Gorenstein projective left B-module. Then, there is a BHom(-,P)-exact sequence
P:…→P1→P0→P0→P1→…
such that N=Ker(P0→P1), where every Pi and Pi are projective. Since A is projective as a right B-module, we obtain that A⊗BP is exact and A⊗BN=Ker(A⊗BP0→A⊗BP1). We also obtain that A⊗BPi is projective for every i because of the assertion that B(-) is exact and A⊗B- is a left adjoint[12].
Let us suppose finally that Q∈AM is Gorenstein projective. Then,
AHom(A⊗BP,Q)≅BHom(P,Q)
However, BQ is projective since B(-) is a left adjoint of A⊗B- which is exact. Thus, BHom(P,Q) is exact since N is Gorenstein projective, and so, AHom(A⊗BP,Q) is also exact, which implies that A⊗BN is Gorenstein projective.
Theorem 2 If H is a semisimple and cosemisimple weak Hopf algebra, then G.gl.dim(A)=G.gl.dimB.
Proof Assume that G.gl.dimB=n<+∞. For any M∈AM, as a left B-module, there is a Gorenstein projective resolution:
0→Gn→Gn-1→…→G1→G0→M→0
where every Gi is Gorenstein projective. Since the functor A⊗B- is exact, it induces a left A-module exact sequence
0→A⊗BGn→A⊗BGn-1→…→
A⊗BG1→A⊗BG0→A⊗BM→0
From Lemma 5, we know that every A⊗BGi is Gorenstein projective, and thus, G.gl.dimA(A⊗BM)≤n. Since M is a direct summand of A⊗BM as left A-modules by Corollary 2, G.gl.dimAM≤n[26]. Hence, G.gl.dim(A)≤n.
Suppose that G.gl.dim(A)=q≤n=G.gl.dimB. Then, G.gl.dimB(A⊗BN)≤q for any N∈BM. Therefore, BExti(A⊗BN,U)=0 for all i>q and all projective left B-module U[26]. Since N is a left B-module direct summand of A⊗BN and the functor BExt(-,U) preserves finite direct sums, BExt(N,U)=0 for all i>q and all projective left B-module U, and, hence, G.gl.dimBN≤q. This implies that G.gl.dim(A)≤G.gl.dimB. Therefore, in view of the above discussion, we have G.gl.dim(A)=G.gl.dimB.
Corollary 3 Let H be a semisimple and cosemisimple weak Hopf algebra. Then, A is quasi-Frobenius (rep. left Gorenstein hereditary) if and only if so is B.
In particular, if R#H is a weak smash product of a weak left H-module algebra R (see Ref.[24] for the definitions), then R#H is quasi-Frobenius (rep. left Gorenstein hereditary) if and only if so is R.
[1]Auslander M, Bridger M. Stable module theory [M]. New York: American Mathematical Society, 1969.
[2]Enochs E E, Jenda O M G. Gorenstein injective and projective modules[J]. Mathematische Zeitschrift, 1995, 220(1): 611-633. DOI:10.1007/bf02572634.
[3]Böhm G, Nill F, Szlach nyi K. Weak Hopf algebras: Ⅰ. Integral theory and C*-structure[J]. Journal of Algebra, 1999, 221(2): 385-438. DOI:10.1006/jabr.1999.7984.
nyi K. Weak Hopf algebras: Ⅰ. Integral theory and C*-structure[J]. Journal of Algebra, 1999, 221(2): 385-438. DOI:10.1006/jabr.1999.7984.
[4]Montgomery S. Hopf algebras and their actions on rings[M]. Providence, Rhode Island: American Mathematical Society, 1993. DOI:10.1090/cbms/082
[5]Sweedler M. Hopf algebras [M]. New York: Benjamin, 1969.
[6]Nikshych D. On the structure of weak Hopf algebras[J]. Advances in Mathematics, 2002, 170(2): 257-286. DOI:10.1016/s0001-8708(02)92081-5.
[7]Vecsernyés P. Larson-Sweedler theorem and the role of grouplike elements in weak Hopf algebras[J]. Journal of Algebra, 2003, 270(2): 471-520. DOI:10.1016/j.jalgebra.2003.02.001.
[8]Wang Z W, Chen C, Zhang L Y. Morita equivalence for weak Hopf-Galois extensions[J]. Communications in Algebra, 2017, 45(1): 162-182. DOI:10.1080/00927872.2016.1175572.
[9]Wang Z W, Chen Y Y, Zhang L Y. Total integrals for weak Doi-Koppinen data[J]. Algebras and Representation Theory, 2013, 16(4): 931-953. DOI:10.1007/s10468-012-9340-8.
[10]Caenepeel S, Groot E. Modules over weak entwining structures [J]. Contemporary Mathematics, 2000, 267: 31-54.
[11]Raposo A B R. Crossed products for weak Hopf algebras[J]. Communications in Algebra, 2009, 37(7): 2274-2289. DOI:10.1080/00927870802620274.
[12]Caenepeel S, Groot E. Galois theory for weak Hopf algebras [J]. Revue Roumaine de Mathématiques Pures et Appliquées, 2007, 52(2): 151-176.
[13]Enochs E E, Jenda O M G. Relative homological algebra[M]. Berlin, New York: De Gruyter, 2000. DOI:10.1515/9783110803662.
[14]Bennis D, Mahdou N. Global Gorenstein dimensions[J]. Proceedings of the American Mathematical Society, 2010, 138(2): 461-465. DOI:10.1090/s0002-9939-09-10099-0.
[15]Bennis D, Mahdoua N, Ouarghi K. Rings over which all modules are strongly Gorenstein projective[J]. Rocky Mountain Journal of Mathematics, 2010, 40(3): 749-759. DOI:10.1216/rmj-2010-40-3-749.
[16]Mahdou N, Tamekkante M. On (strongly) Gorenstein (semi)hereditary rings[J]. Arabian Journal for Science and Engineering, 2011, 36(3): 431-440. DOI:10.1007/s13369-011-0047-7.
[17]Böhm G, Caenepeel S, Janssen K. Weak bialgebras and monoidal categories[J]. Communications in Algebra, 2011, 39(12): 4584-4607. DOI:10.1080/00927872.2011.616438.
[18]Nikshych D, Turaev V, Vainerman L. Quantum groupoids and invariants of knots and 3-manifolds [J]. Topology and Its Applications, 2003, 127: 91-123.
[19]Wang D G, Yang S L. Representations of weak Hopf algebras associated to cyclic quivers[J]. Communications in Algebra, 2005, 33(11): 4321-4335. DOI:10.1080/00927870500243106.
[20]Niu R F, Wang Y, Zhang L Y. The structure theorem of endomorphism algebras for weak Doi-Hopf modules[J]. Acta Mathematica Hungarica, 2010, 127(3): 273-290. DOI:10.1007/s10474-010-9134-6.
[21]Wang Z W, Chen Y Y, Zhang L Y. Extensions of the endomorphism algebra of weak comodule algebras[J]. Mathematical Notes, 2014, 96(3/4): 342-352. DOI:10.1134/S0001434614090065.
[22]Bohm G. Galois theory for Hopf algebroids[J]. Annali dell’Universita di Ferrara, 2005, 51(1): 233-262. DOI:10.1007/BF02824833.
[23]Năstăsescu C, van den Bergh M, van Oystaeyen F. Separable functors applied to graded rings[J]. Journal of Algebra, 1989, 123(2): 397-413. DOI:10.1016/0021-8693(89)90053-7.
[24]Nikshych D. A duality theorem for quantum groupoids [J]. Contemporary Mathematics, 2000, 267: 237-243.
[25]Reiten I, Riedtmann C. Skew group algebras in the representation theory of Artin algebras[J]. Journal of Algebra, 1985, 92(1): 224-282. DOI:10.1016/0021-8693(85)90156-5.
[26]Holm H.Gorenstein homological dimensions[J]. Journal of Pure and Applied Algebra, 2004, 189(1/2/3): 167-193. DOI:10.1016/j.jpaa.2003.11.007.