With the development of modern industry, gearboxes have been widely used in various mechanical equipment due to their fixed transmission ratios, large driving torque and compact structures. Gearboxes usually work under harsh conditions and are prone to failure[1]. By analyzing the vibration signals of mechanical equipment, the health of gears can be diagnosed and predicted[2]. However, the vibration signals measured in actual engineering are doped with strong background noise and interference source signals. Therefore, how to effectively extract gearbox fault feature information under strong background noise and interference source signals is worthy of further study.
In recent years, various non-linear and non-stationary signal decomposition and analysis methods have been proposed. Empirical mode decomposition (EMD) [3] as a typical adaptive time-frequency analysis method, has good time-frequency aggregation and does not need to construct any basis function for matching signal components. However, EMD has defects such as mode mixing and endpoint effects. In order to solve the EMD mode mixing problem, ensemble empirical mode decomposition (EEMD) [4] and other methods have been proposed one after another. Non-parametric time-frequency analysis methods based on the EMD decomposition theory such as the local mean decomposition (LMD) [5], ensemble local mean decomposition (ELMD)[6], empirical wavelet transform (EWT)[7] and variational mode decomposition (VMD) have been proposed successively, but these methods also have certain shortcomings[8].
FDM is a non-linear and non-stationary data processing method based on the Fourier theory and zero-phase filter proposed by Singh et al.[9], and has been successfully applied to EEG. The time-frequency analysis of the signal was later introduced into the field of mechanical vibration signal processing. Currently, many scholars have carried out much research work on FDM algorithm analysis and made some progress[10-12]. For instance, Liu et al.[10] proposed a fault diagnosis method for rotor rubbing based on FDM. Deng et al.[11] proposed a new optimized Fourier spectrum decomposition method, called the bandwidth Fourier decomposition (BFD) for the early fault detection of rolling bearings. Dou et al.[12] proposed a novel method for machinery fault feature extraction based on FDM. FDM provides a new idea for the analysis of nonlinear and non-stationary time series. In 2018, Singh[13] proposed a new formulation of the FDM using the discrete cosine transform, but mode mixing exists. Therefore, a new method of selecting the cut-off frequency to overcome modal aliasing is proposed in this paper.
FDM is as sensitive to noise as other signal decomposition algorithms[9]. The actual vibration signal contains much noise, and it also participates in FDM decomposition. Therefore, the noise causes the FDM decomposition component to increase and aggravates the boundary effect. It can be seen from the above that in order to achieve better decomposition effect when FDM is decomposed, the signal needs to be pre-processed for noise reduction.
The signal sparseness shows successful application in the fields of image processing and compressed sensing[14]. Dictionaries are the key to success in sparse representation. The design of the dictionary mainly includes the analytical method and learning method[15]. The analytic method is based on commonly used fast transformations and their variations such as the Fourier dictionary, wavelet dictionary, Gabor dictionary and discrete cosine dictionary[15-16]. They have the advantage of a fast calculation speed, but there are many restrictions or assumptions, and the actual application effect is not good[17]. The learning method is based on the machine learning techniques to construct sparse dictionaries such as sparse K-SVD[18] and multi-scale dictionary learning [19]. This kind of dictionary has a slow calculation speed and poor anti-noise performance. When processing mechanical vibration signals, the physical meaning of learning a dictionary is not clear. For instance, Medina et al.[20] proposed a sparse representation method of vibration signals for gear fault detection and classification based on dictionary learning. Nagaraj et al.[21] proposed a novel dictionary that was used to analyze EEG signals by improving the linear frequency modulation function (LFMF). Moreover, Lü et al. [22] introduced the dictionary into the processing of mechanical fault signals. Therefore, the design of the dictionary has a great effect on the diagnosis results. Based on the idea of the sparse signal representation, this paper proposes a compound dictionary using prior knowledge of gearbox faults. It includes the gear steady-state modulation (SSM) dictionary and impact modulation (IM) dictionary. The SSM-IM dictionary combined with the OMP algorithm is used to preprocess the vibration signal for noise reduction.
In this paper, a fault feature extraction method of the gearbox based on the SSM-IM dictionary noise reduction and OFDM is proposed. Firstly, the SSM-IM dictionary combined with the OMP algorithm is used to pre-process the original vibration signal. Secondly, OFDM is used to decompose the signal. Finally, the correlation coefficient between each AFIBF component and the source signal is calculated, and the AFIBF component with the largest correlation coefficient is selected for the Hilbert envelope spectrum. Through the envelope spectrum analysis, the fault feature of the gearbox can be accurately extracted. Simulation and experimental analysis verify the effectiveness of the method proposed in this paper.
1 OMP and Compound Dictionary Design
1.1 The OMP algorithm
The basic idea of the OMP algorithm[23] is to iteratively decompose the signal. The specific steps of the OMP algorithm are as follows:
Step 1 Project a given signal x(t) in the Hilbert space to each atom of the overcomplete atomic library D={gk,k=1,2,…,n}, where each vector g1,g2,…,gn can be called an atom, and its length is the same as the length of signal x(t). These vectors have been treated as normalization, that is ‖xi‖=1, the unit vector length is 1, and Schmidt orthogonalization is guaranteed.
Step 2 Calculate the inner product of the signal and each column (atom) in the over-complete atomic dictionary matrix. Firstly, it finds the atom with the largest inner product of the original signal, i.e., the best atom, in the dictionary:
(1)
where Γ is the set of parameter groups Υ. |〈x,grk〉| is the inner product of signal x and atom grk.
Based on the law of conservation of energy, the signal can be decomposed into the optimal reconstruction component and the residual component:
x=〈x,grk〉grk+Rk+1x
(2)
where 〈x,grk〉grk is the projection of the signal on the atom grk after the k-th iteration; Rk+1x is the remaining amount of the (k+1)-th best match for the signal.〈Rk+1x,grk〉=0 indicates that in the k-th iteration, an atom grkbest matching the current residual signal Rk+1x will be found:
‖x‖2=|〈x,grk〉|2+‖Rk+1x‖2
(3)
To minimize the energy ‖Rx‖ for approaching errors, grk∈D is necessary to maximize |〈x,grk〉|.
|〈x,grk〉|=αsup|〈x,gr〉| 0<α<1
(4)
Rkx=〈Rkx,grk〉grk+Rk+1x
(5)
The value of the participation signal is the termination condition of the iteration. The basic idea of matching pursuit is to express the basic characteristics of a signal by a linear combination of fewer atoms.
(6)
1.2 Design of compound dictionary
In sparse decomposition, the construction of the dictionary directly affects the sparse expression of the signals to be analyzed[18]. Dictionary has a great impact on the performance of the OMP algorithms. If the dictionary is not selected correctly, the sparse representation of the signal may have a large deviation.
Most scholars extract the fault feature of gears in the gearbox by constructing a single dictionary, and do not make full use of the structural parameters of the gearbox. This paper constructs a composite dictionary based on the mathematical model of the fault signal when the gearbox fails, which includes a steady-state modulation (SSM) dictionary and an impact modulation (IM) dictionary, which makes it more physical.
1.2.1 Constructing an SSM sub-dictionary
When gears have distributed faults, the vibration signals of most gear faults are expressed as amplitude modulation (AM) and frequency modulation (FM) signals. The mathematical model of the distributed fault is[24]
x(t)=[1+an(t)]cos(2πkfzt+φm+bm(t))
(7)
where an(t)=sin(2πnfnt),bm(t)=sin(2πmfnt);fz is the meshing frequency;fn is the rotational frequency.
When an(t)=0, Eq.(7) becomes the frequency modulation model:
x1(t)=cos(2πkfzt+φm+bm(t))
(8)
When bm(t)=0, Eq.(7) becomes the amplitude modulation model:
x2(t)=[1+an(t)]cos(2πkfzt+φn)
(9)
Let m,n∈{1,2,3,…},and k is chosen so that the atomic frequency covers the highest order of the meshing frequency of the vibration signal. To better match the actual vibration signal, the atomic frequency is expanded by±2Δf(Δf is the frequency resolution,Δf=fs/N, fs is the sampling frequency).
It can be seen that the characteristics of the gearbox operating parameters and vibration signals are fully considered in the constructed SSM sub-dictionary.
1.2.2 Constructing an IM sub-dictionary
The vibration signal caused by local gear failure (such as pitting and broken teeth) is a series of periodic impulse response functions, so a single impulse response is used to construct the IM sub-dictionary.
x3(t)=exp(-lt1)cos(2πfzt+μ), t1=mod(t,1/fn)
(10)
where ![]() l∈[0,100] is the attenuation index. When l=0, Eq.(10) degenerates into a cosine dictionary.
l∈[0,100] is the attenuation index. When l=0, Eq.(10) degenerates into a cosine dictionary.
Since the parameters of the atom are determined based on the actual vibration signal, the true state of the faulty gearbox can be better represented by the IM sub-dictionary.
Therefore, the constructed compound dictionary atomic library is expressed as
d(t)={x1(t),x2(t),x3(t)} ‖d(t)‖2=1
(11)
1.3 Simulation evaluation index
In order to test the effectiveness and accuracy of a complete compound dictionary (i.e. SSM-IM dictionary), the following evaluation indicators are introduced [22]:
Mean square error Em
(12)
Comparability index Cm
(13)
Signal to noise ratio Rm

(14)
where N is the length of the signal; x and ![]() is the source signal and the reconstruction signal after the m-th iteration, respectively.
is the source signal and the reconstruction signal after the m-th iteration, respectively.
1.4 Simulation analysis of SSM-IM dictionary
In order to comprehensively analyze the performance of the SSM-IM dictionary, the Fourier dictionary, DCT dictionary and LFMF dictionary[21] combined with the OMP algorithm are used to decompose and reconstruct the simulation signal. Corresponding conclusions are drawn through analysis and comparison.
When the gear suffers local damage, its vibration signal is a modulation signal. Assuming that the gearbox is a first-level reducer, its parameters are as follows:
The rotation frequency of the input shaft is 15 Hz, the number of the teeth of the small gear is 25, and the number of the teeth of the large gear is 75. The meshing frequency is 375 Hz, and the rotation frequency of the output shaft is 5 Hz. Assuming that one of the gears is locally worn, the vibration signal can be approximated by
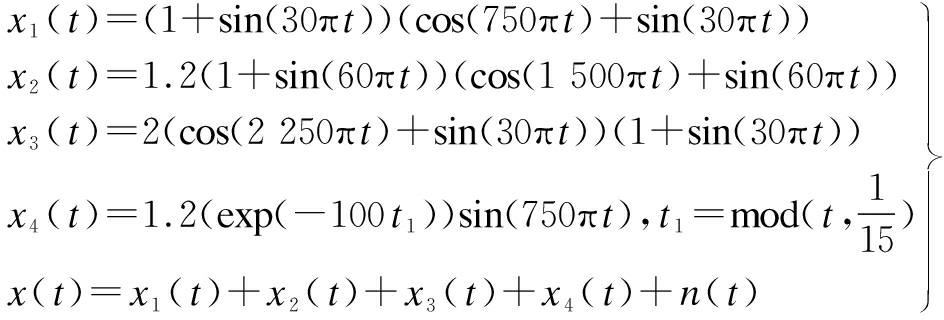
(15)
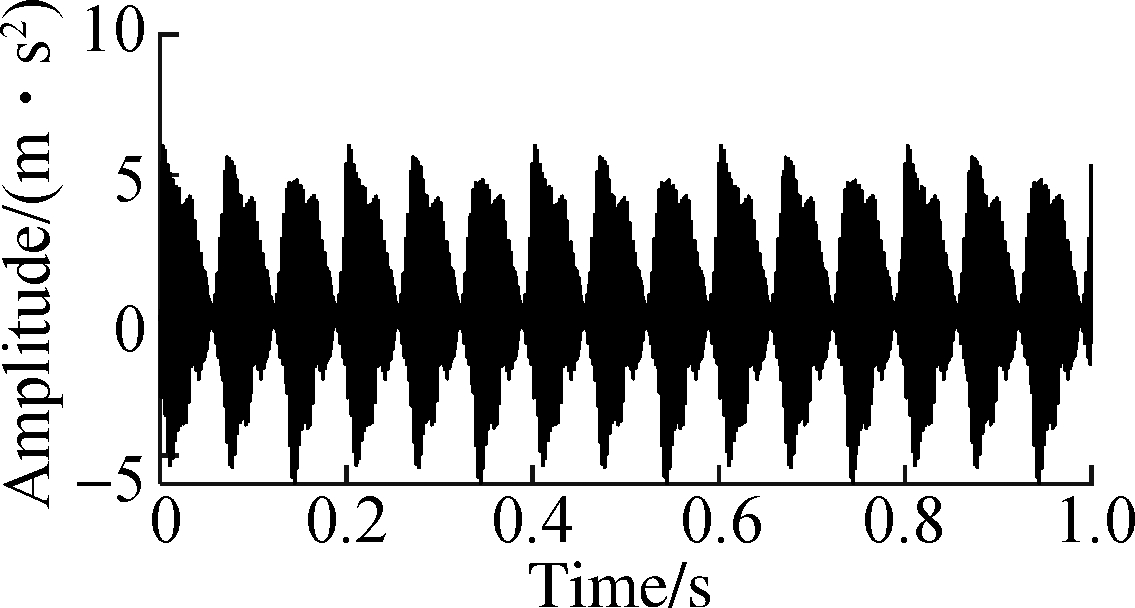
where x1(t),x2(t) and x3(t) are AM and FM signals; x4(t) is an impulse signal; and n(t) is random noise with a signal to noise ratio (SNR) of -5 dB. The number of the sampling points is 4 096 and the sampling frequency is 3 kHz. The time-domain waveform diagram of the simulation signal constructed according to the above parameters is shown in Fig.1.
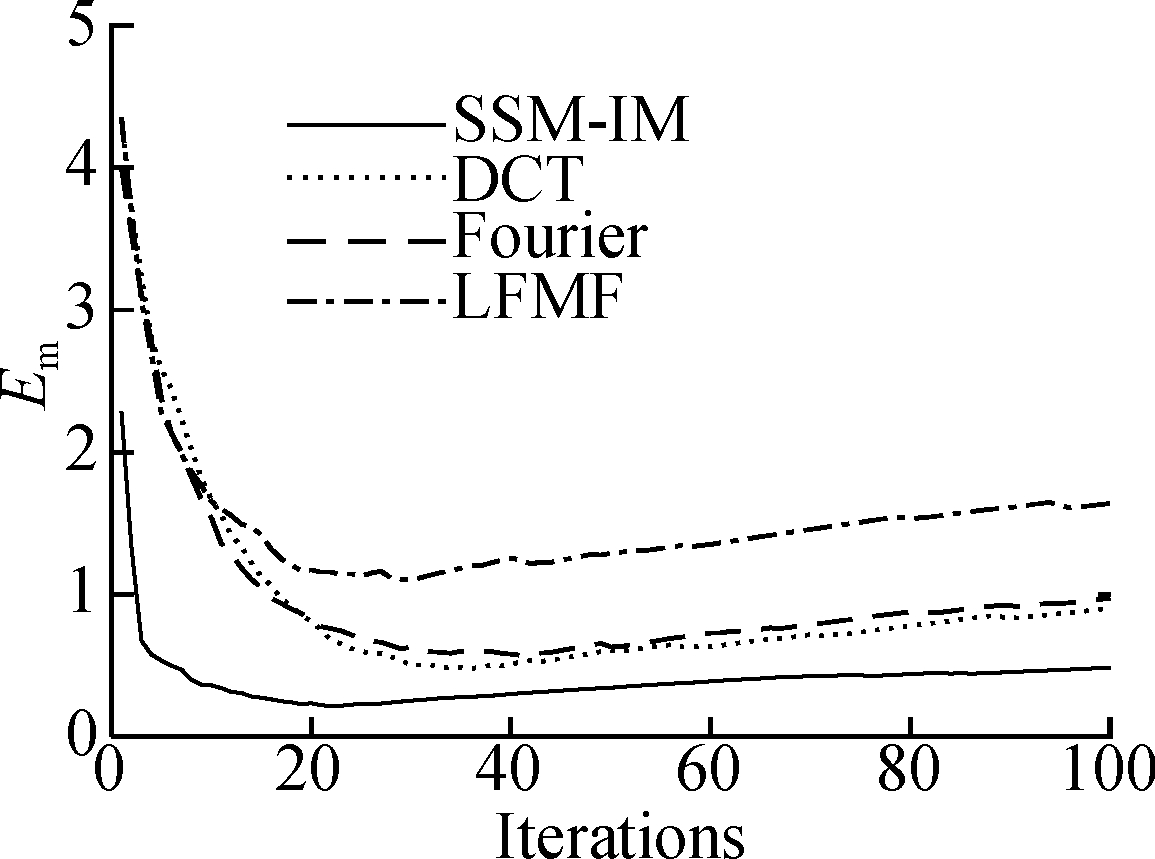
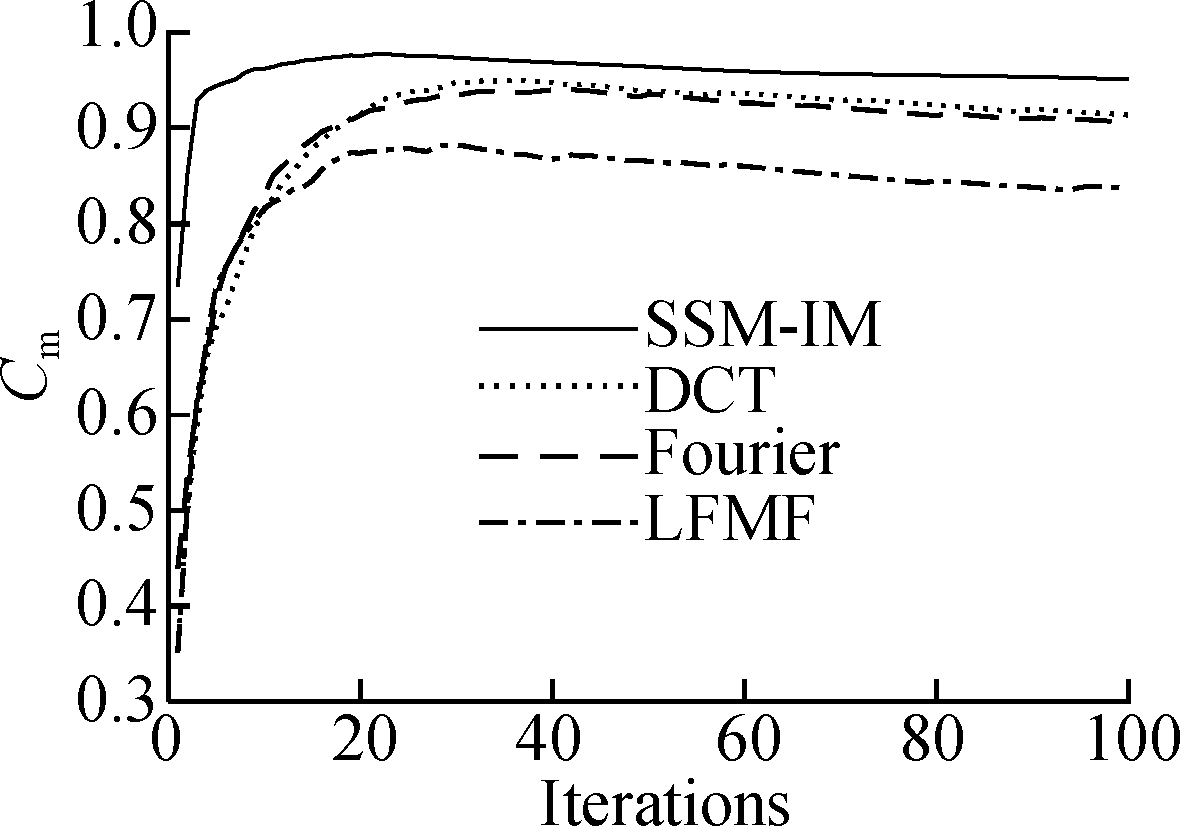
In Fig.2, it can be seen that the SSM-IM dictionary can more effectively reconstruct the simulation signal compared with the DCT dictionary, Fourier dictionary, and LFMF dictionary. Moreover, Figs.2(a), (b) and (c) show that the signal reconstruction of the SSM-IM dictionary has the lowest residual error, the best correlation and the smallest Emcompared with the DCT dictionary, Fourier dictionary, and LFMF dictionary.
(a)

(b)
Fig.1 Simulation signal waveform. (a) The pure signal waveform; (b) The noise signal waveform
The results show that the SSM-IM dictionary has better signal reconstruction accuracy and higher reconstruction stability for extracting the gearbox fault feature.
(a)
(b)

(c)
Fig.2 Simulation signal analysis results. (a) Em; (b) Cm; (c) Rm
1.5 Analysis of the influence of noise on the SSM-IM dictionary
The simulation results above show that the SSM-IM dictionary has high accuracy in signal reconstruction. In order to further explore the performance of the dictionary, it is used to reconstruct the signal of noise with different intensities, that is, the influence of noise. The simulation signal of Eq.(15) is used to decompose and reconstruct the noise signals with different SNR, which are -1, -3, -5 and -7 dB respectively. In this part, the simulated pure signal of Eq.(15) is regarded as a useful signal.
Fig.3(a) and Fig.3(b) are the trends of Em and Cm with the number of iterations, respectively. From Fig.3(a), the following conclusions can be drawn. First, for noise signals with different strengths, the Em value tends to decrease first and then increase as the number of iterations increase. Secondly, when the signal-to-noise ratio is -1 dB, the smallest Em is 0.182 12. When the SNR is -3, -5 and -7 dB, the minimum Em that can be achieved is 0.182 12, 0.216 07 and 0.272 65, respectively. It can be seen that signals with the SNR of -3, -5 and -7 dB can also achieve better noise reduction with fewer iterations. It shows that the performance of the SSM-IM dictionary is more robust.
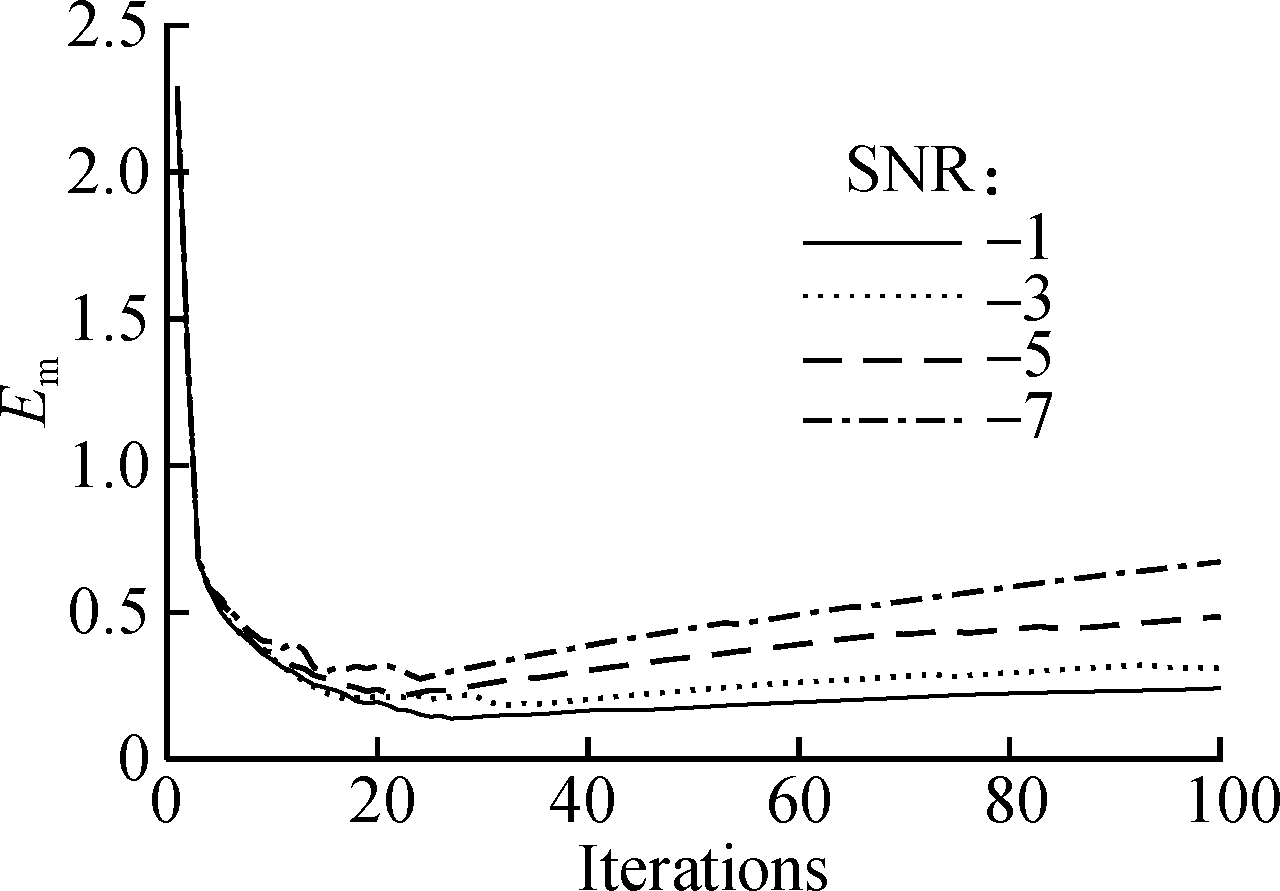
(a)

(b)
Fig.3 Simulated signal analysis results. (a) Em; (b) Cm
The following conclusions can be drawn from Fig.3(b). First, for signals containing different SNRs, the value of Cm increases first and then decreases with the increase in the number of iterations. Secondly, compared with the SNR of -3, -5 and -7 dB, the change trend of Cm with the SNR of -1 dB can reach the maximum value faster than that with the SNR of -3, -5 and -7 dB. In contrast, when the SNR is -3, -5 and -7 dB, signals can also achieve a higher extraction accuracy with fewer iterations.
In summary, after optimal matching, the correlation between useful signals and reconstructed signals decreases and Em increases with the increase in iteration times. The result shows that with the increase in iteration times, the noise signal is introduced into the reconstructed signal again. Therefore, the useful signal can be obtained after the appropriate number of iterations, while the residual signal is noise.
2 The Optimized FDM (OFDM)
Singh[13] proposed a new formulation of the FDM using the discrete cosine transform (DCT). The block diagram of the algorithm is shown in Fig.4.
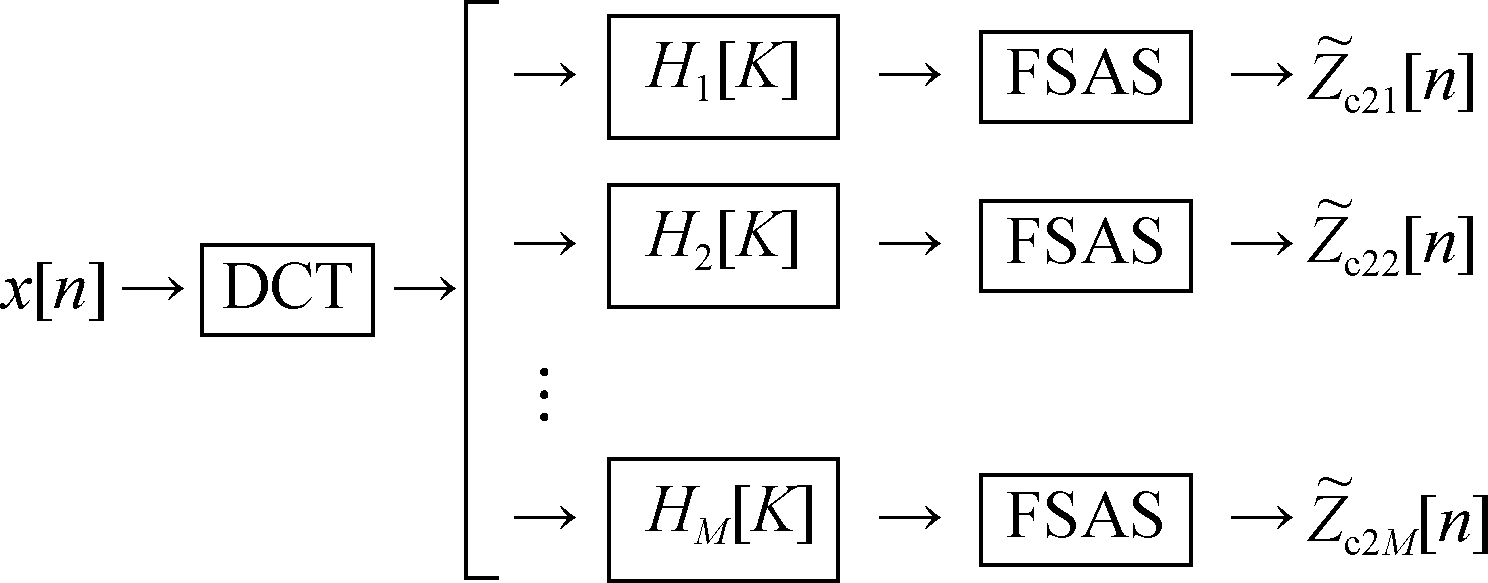
Fig.4 The block diagram of FDM
For each i, i∈[1,M],
(16)
1≤i≤M, N0=0, NM=N-1
(17)
FDM is a signal decomposition algorithm based on a zero-phase filter. A cut-off frequency is required when the signal is decomposed. The question is how to obtain cut-off frequencies (CFs). The binary method is adopted to select CFs in the FDM algorithm(fc1=fmax/2,fc2=fmax/22,…,fcl=fmax/2l), where fmax is the maximum frequency of a signal x(t) and for the sampled signal, the maximum frequency is half of the sampling frequency (fs/2).
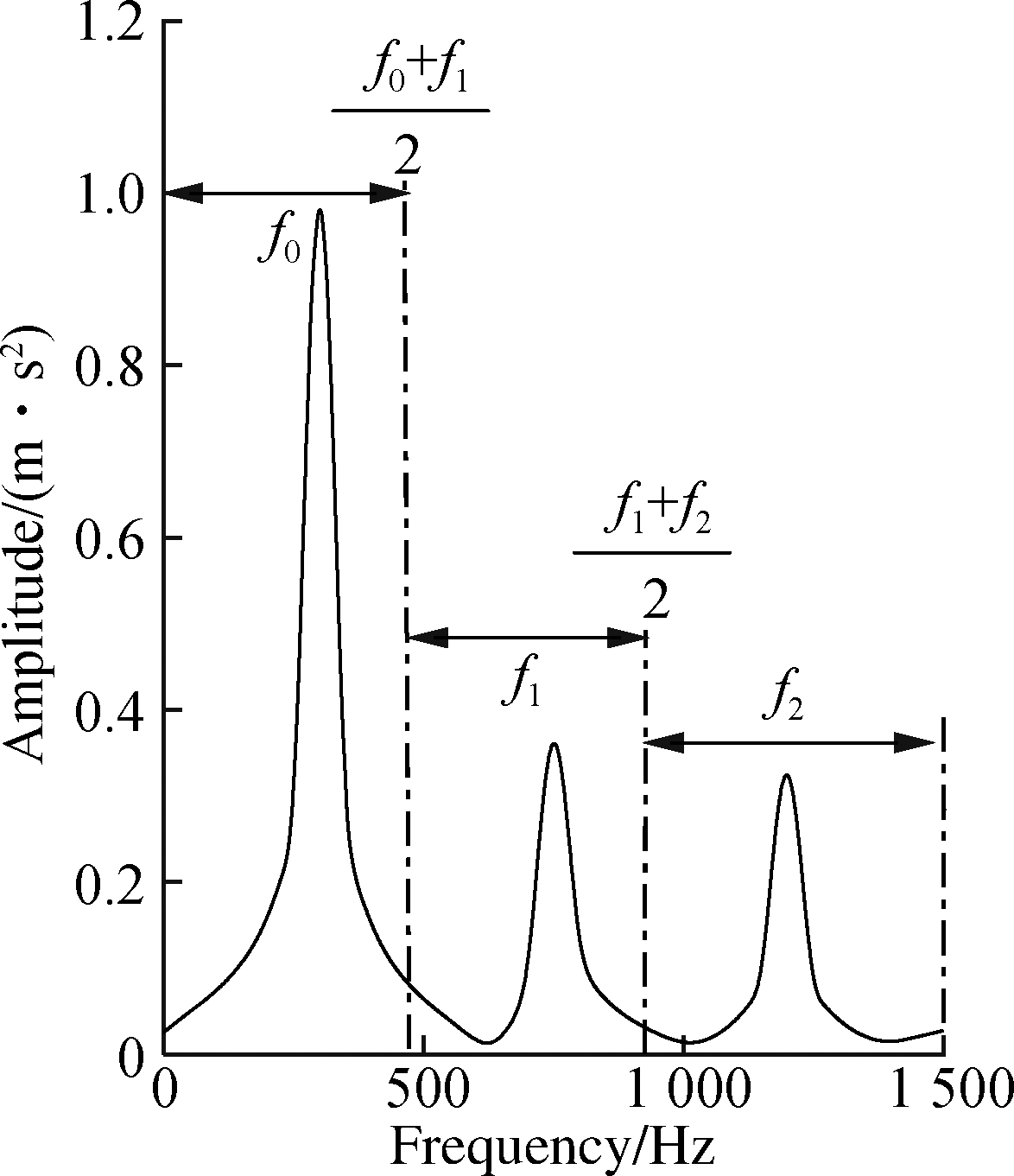
Most of the fault signals of a gear are AM and FM signals, and the analytic Fourier intrinsic band functions (AFIBF) obtained by using the binary cut-off frequency selection method for FDM generate mode aliasing easily. Therefore, this paper proposes a new method for selecting the cut-off frequency to overcome the shortcomings of the above method. The specific steps of the algorithm are as follows:
Step 1 Perform FFT on the collected vibration signal x[t], that is X[k]=FFT{x[t]}, as shown in Fig.5(a).
Step 2 Envelope the FFT spectrum obtained in Step 1 to obtain the envelope spectrum of the FFT spectrum, as shown in Fig.5(b).
Step 3 Extract the frequency value corresponding to the main peak of the waveform in Step 2, such as (f0,f1,f2,…,fn).
Step 4 Obtain the CFs of each band component using the following formula:
(18)
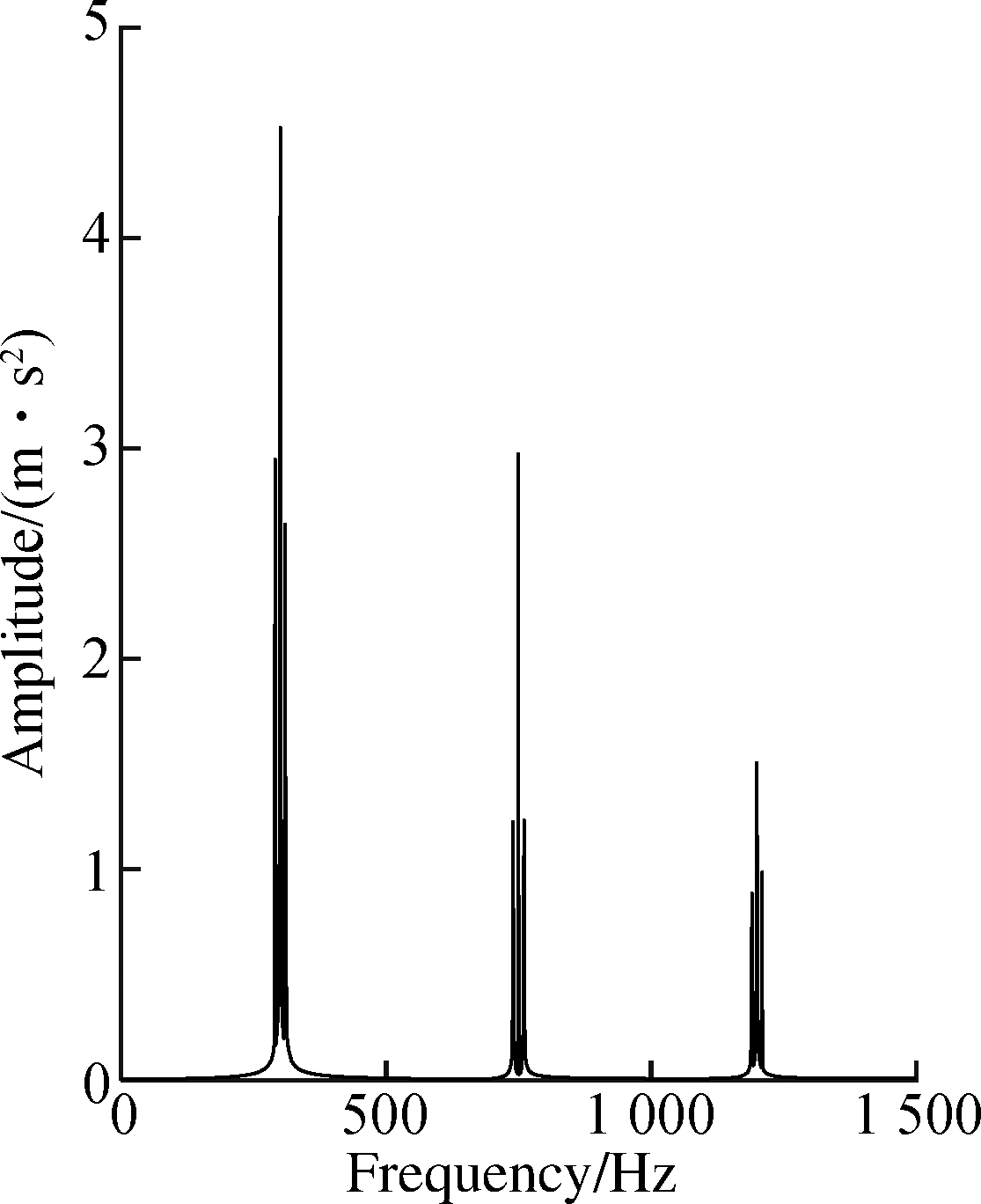
(a)
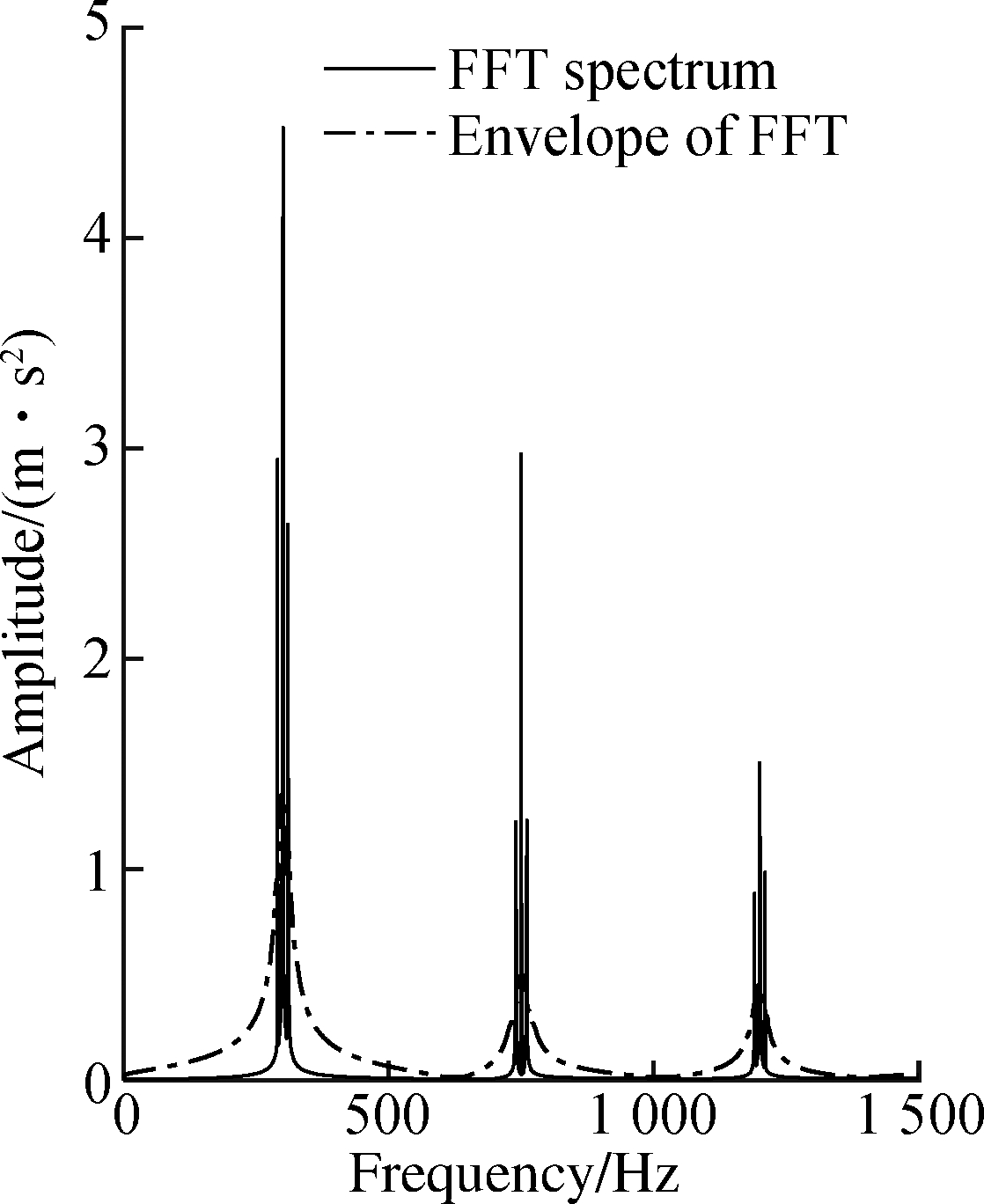
(b)
(c)
Fig.5 Spectrum envelope analysis. (a) FFT spectrum; (b) Envelope of FFT spectrum; (c) Envelope
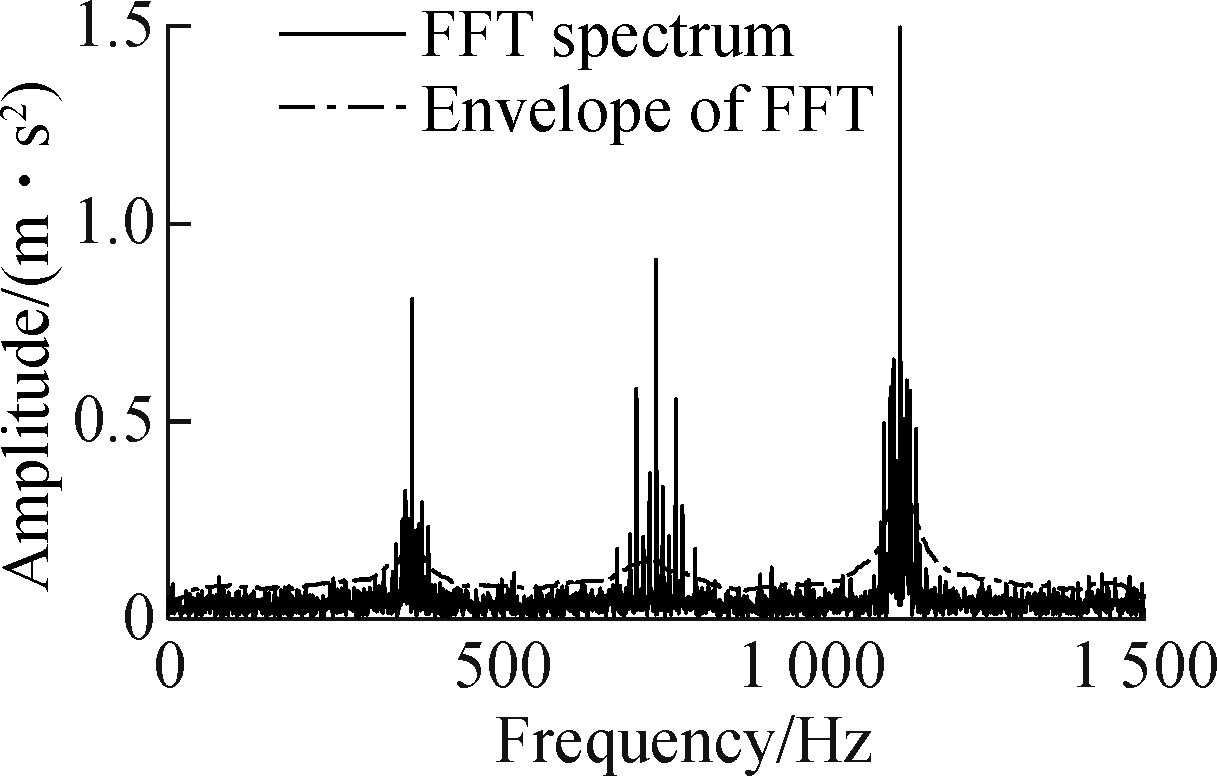
In order to analyze the noise sensitivity of the cut-off frequency method proposed above, -1, -3, -5, -7 dB noises are added to Eq.(15), respectively. Then this method is used to perform a fast FFT spectrum envelope, and the result is shown in Fig.6. It can be seen that the envelope of the spectrum can clearly envelope the main peak points of the spectrum. Therefore, the method is also applicable to signals with a certain intensity of noise, thus verifying the effectiveness of the method.

(a)
(b)

(c)

(d)
Fig.6 FFT envelope after adding different intensities of noise. (a) -1 dB; (b) -3 dB; (c) -5 dB; (d) -7 dB
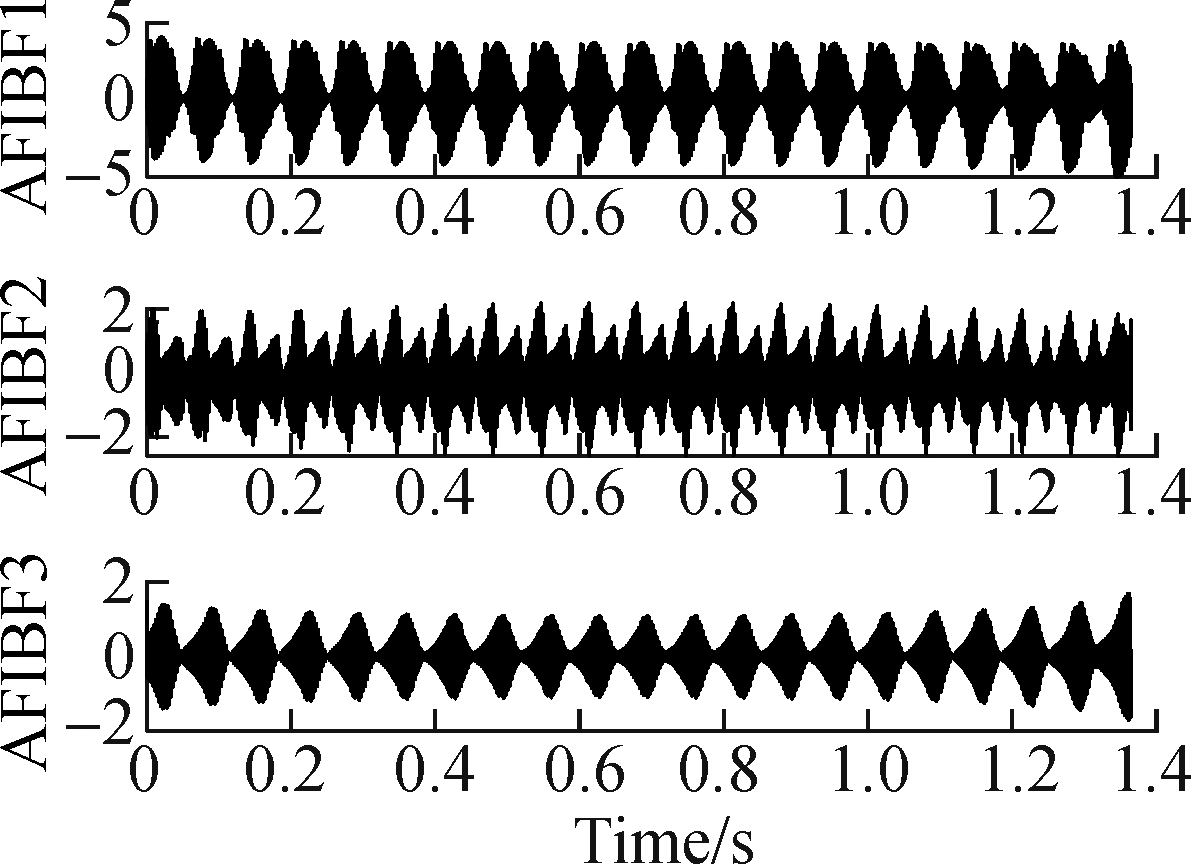
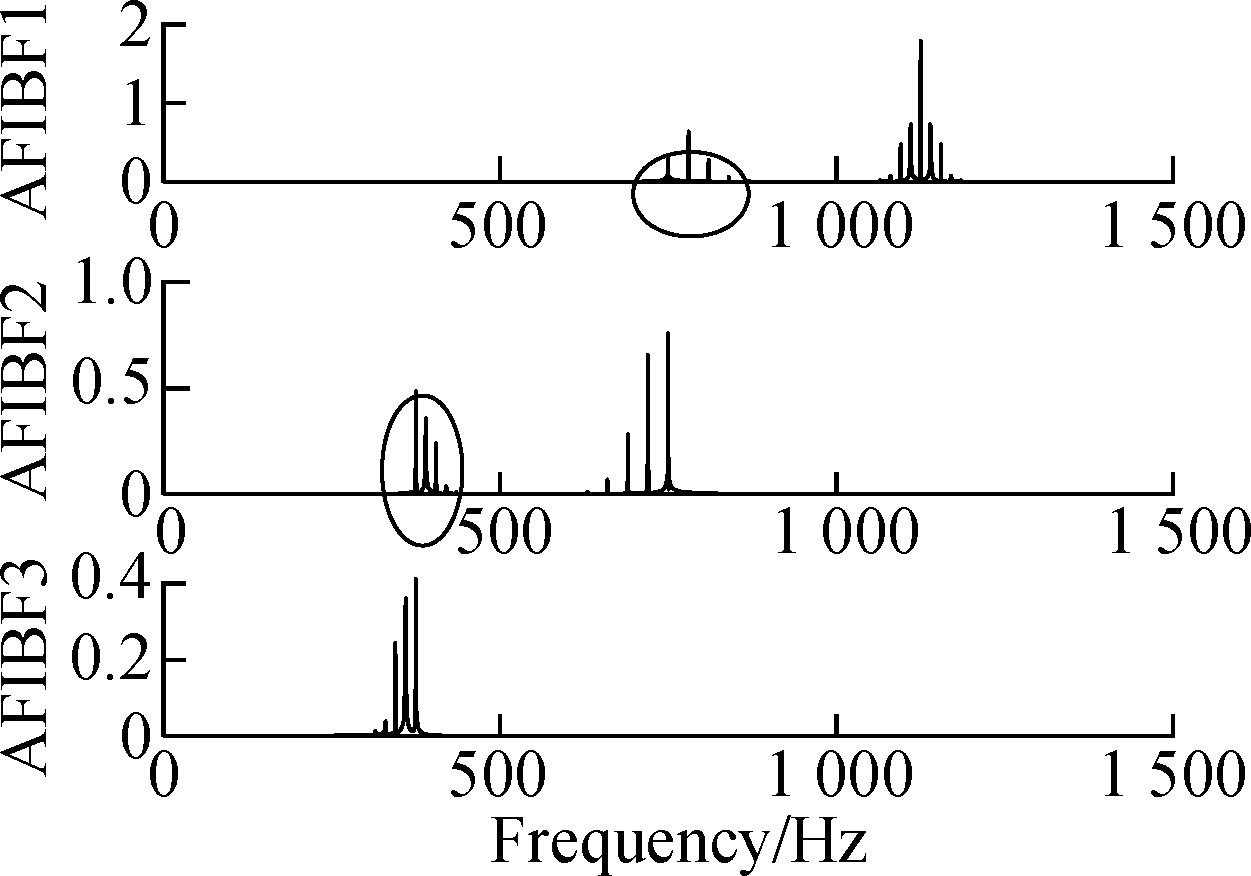
In order to verify the effectiveness of the CFs selection method proposed, the pure signal without noise in Eq.(15) is taken as the simulation signal and compared with the binary CFs selection method.
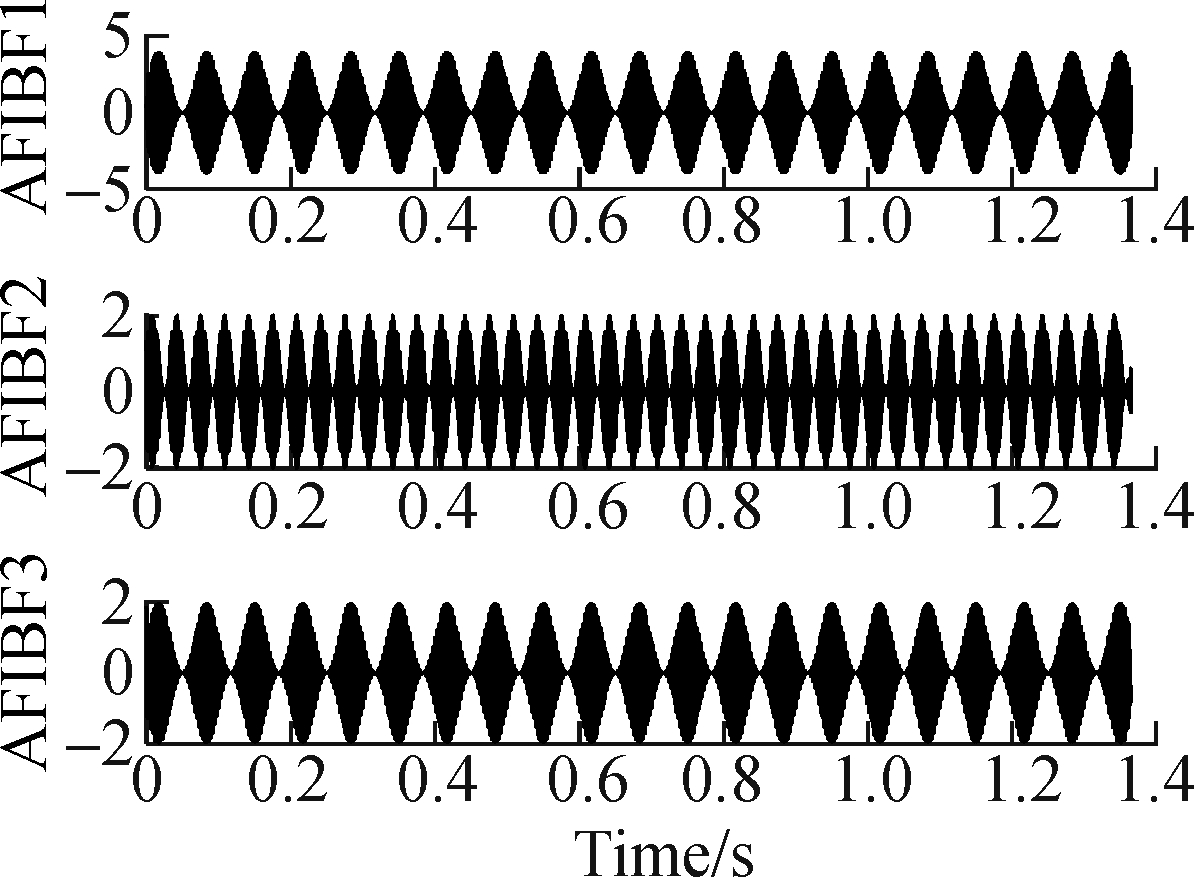
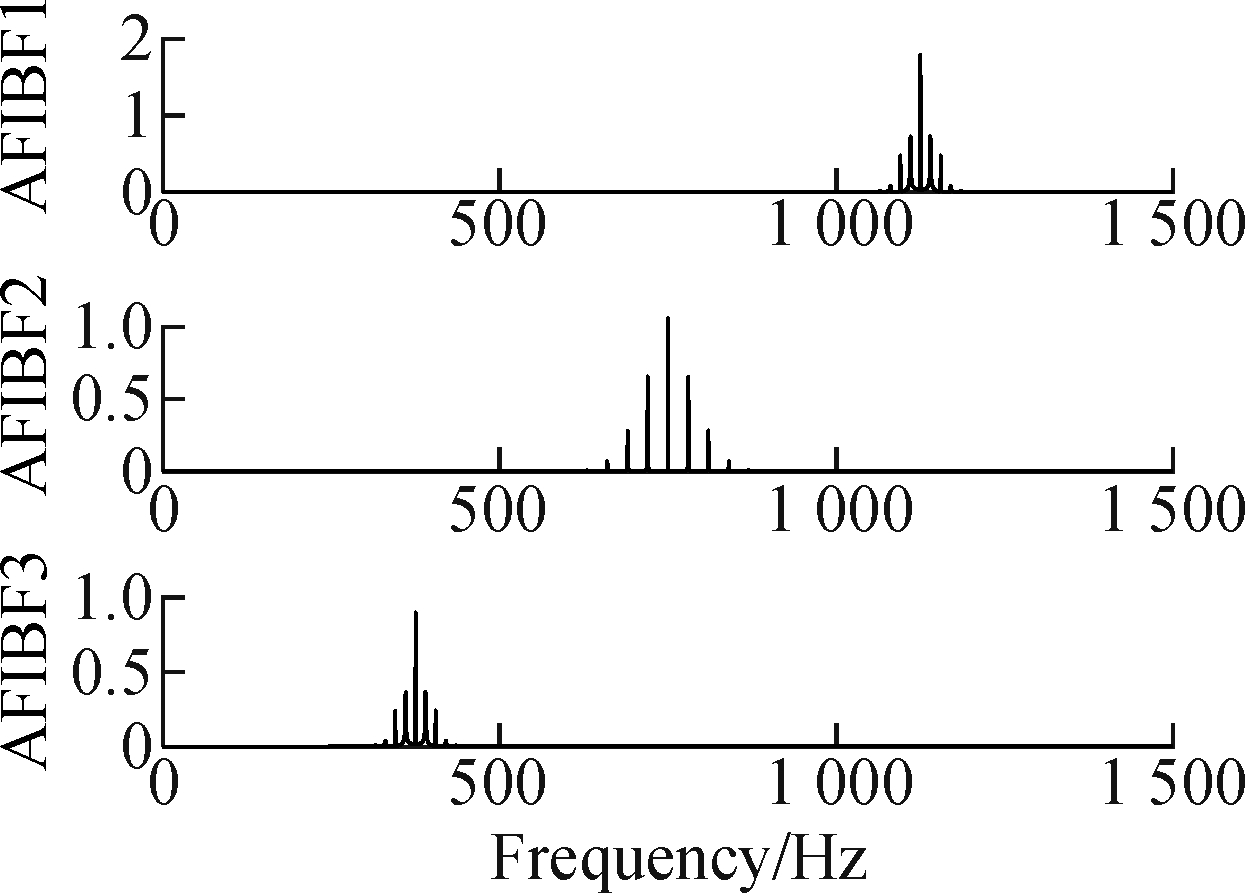
It can be seen from Fig.7(b) that mode mixing will occur among AFIBF1, AFIBF2 and AFIBF3 after signal decomposition with unoptimized FDM, which causes errors in subsequent signal processing and leads to the incorrect identification of fault types.
It can be seen from Fig.7(d) that the OFDM effectively overcomes the problem of mode mixing among various components caused by the frequency division of FDM with binary CFs, and verifies the validity of the proposed frequency band division.
(a)
(b)
(c)
(d)
Fig.7 Comparison of FDM before optimization and FDM after optimization. (a) AFIBFs of FDM before optimization; (b) The FFT of AFIBFs of FDM before optimization; (c) AFIBFs of FDM after optimization; (d) The FFT of AFIBFs of FDM after optimization
3 Procedure of SSM-IM-OFDM
In order to solve the problem of the gearbox fault feature extraction under the influence of the strong background noise and interference source signal, this paper proposes a method based on the combination of the SSM-IM dictionary and OFDM. The detailed process description is as follows:
1) The measurement signal is obtained from the gearbox with a partial faulty gear.
2) The SSM-IM dictionary and OMP method proposed in this paper are used to perform noise reduction preprocessing on the gearbox fault signal.
3) The OFDM is used to decompose the gear fault signal after noise reduction and preprocessing to obtain several AFIBFs.
4) The cross-correlation criterion is used to select the AFIBF component with the largest correlation coefficient between each component and the denoised signal, and then the Hilbert envelope spectrum demodulation is carried out on the component. The frequency spectrum characteristic of the demodulation result is analyzed to achieve the accurate extraction of the gearbox fault feature.
4 Experimental Verification
4.1 Public data verification
In order to verify the effectiveness of SSM-IM-OFDM, this section uses the prognostics and health management (PHM) 2009 Challenge Data to verify the fault data of helical gears on small and medium-sized test benches. PHM 2009 Challenge Data is a complete set of gearbox data from the 2009 International Competition of the PHM Association, including the faults of gears, bearings and shafts. The experimental platform structure is shown in Fig.8. There are three shafts (input shaft, idler shaft, and output shaft) inside. The two sets of the meshing gears used in the experiment are the spur gear mode and helical gear mode. Vibration sensors are installed on both sides of the box to collect data. The input speed of the gear is 50 Hz, the sampling frequency is 66.67 kHz, the number of sampling points is 67 000.

(a)  (b)
(b)
Fig.8 Schematic diagram of PHM 2009 Challenge Data installation and example of gear fault. (a) Schematic diagram of PHM 2009 Challenge Data installation; (b) Example of gear fault
This paper takes helical gear fault as an example. Combined with the relevant parameters of speed and gearbox, the two-stage meshing frequency and fault feature frequency of each gear can be obtained, as shown in Tab.1.
Tab.1 Feature frequency of the gearbox

Meshing frequency/HzFeature frequency/HzHigh speedLow speedfG1fG2fG3fG41 6008005016.6716.6710
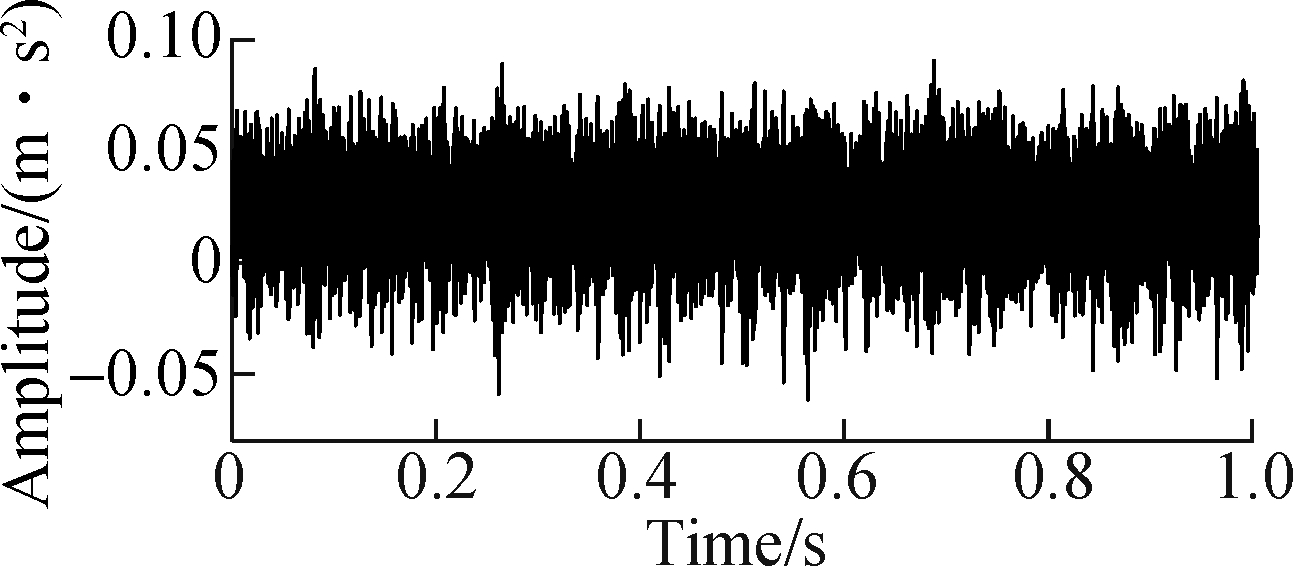
Fig.9 shows the time domain waveform and Hilbert envelope spectrum obtained by OFDM. As shown in Fig.9(a), the signal waveform contains a large amount of noise and is affected by multiple interference sources between the transmission members, so there is no obvious periodic impact. In Fig.9(b), the harmonic 2f3 and 6f3 of the fault feature frequency can be found, but the fault feature frequency f3 and its harmonic 3f3, 4f3,… are interfered with by other frequencies and cannot be clearly identified.
The SSM-IM-OFDM proposed in this paper is used for analysis. Feature extraction and noise reduction are performed on the signal through the SSM-IM dictionary and OMP algorithm. The result after the 50th iteration is selected as the reconstructed signal and decomposed by the OFDM and calculate the correlation coefficient between each AFIBF and the original vibration signal. The results are shown in Tab.2. The AFIBF9 component with the largest number of correlations was selected for the Hilbert envelope spectrum as shown in Fig.10. The fault feature frequency f3 and harmonics 2f3,3f3,…,8f3 of G3 can be clearly identified in Fig.10. With the SSM-IM-OFDM, more feature frequency information can be obtained, which effectively reduces the effect of background noise and irrelevant frequencies.
(a)

(b)
Fig.9 Gearbox fault signal. (a)Time-domain waveform; (b) Hilbert envelope spectrum by OFDM
Tab.2 Correlation coefficient of each AFIBF with the original signal
Correlation coefficientC1C2C3C4C5C6C7C8C9C10C11Values0.0010.0240.0090.0870.0600.1170.3960.3560.5800.5160.296
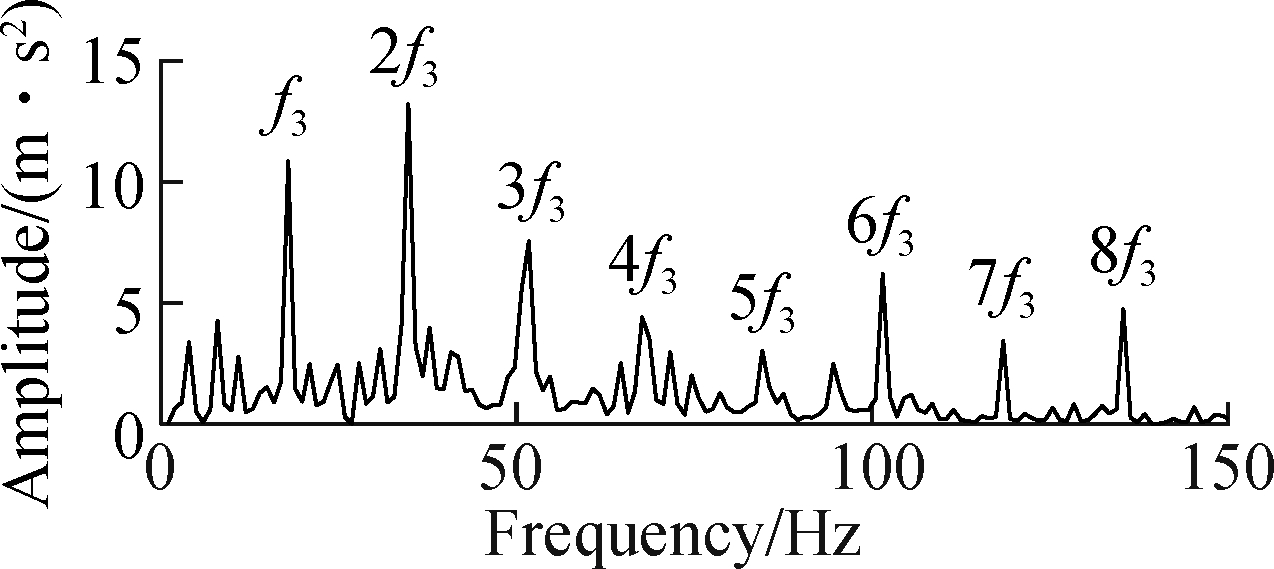
Fig.10 Hilbert envelope spectrum of AFIBF9 component
4.2 Methods contrast Ⅰ
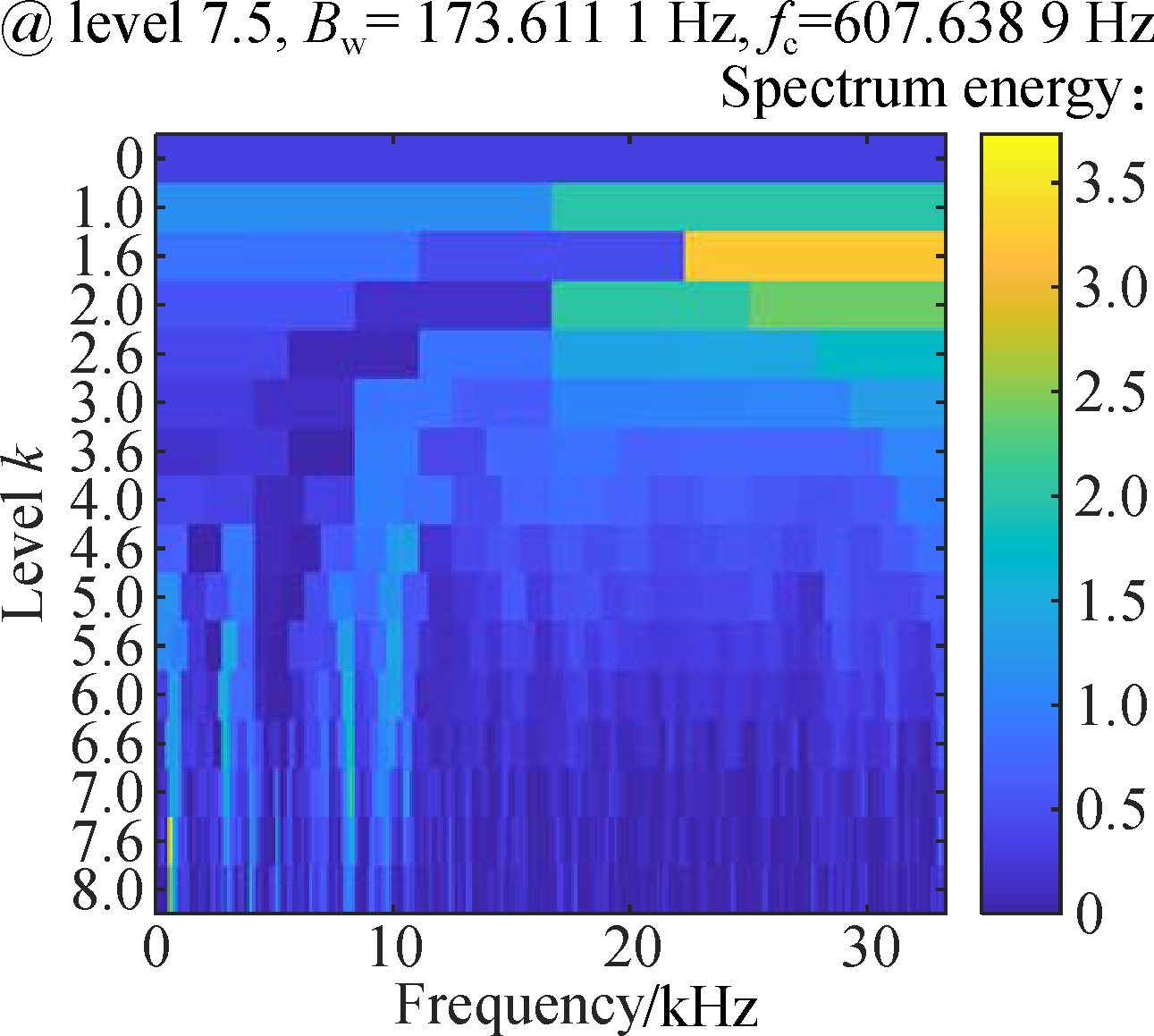
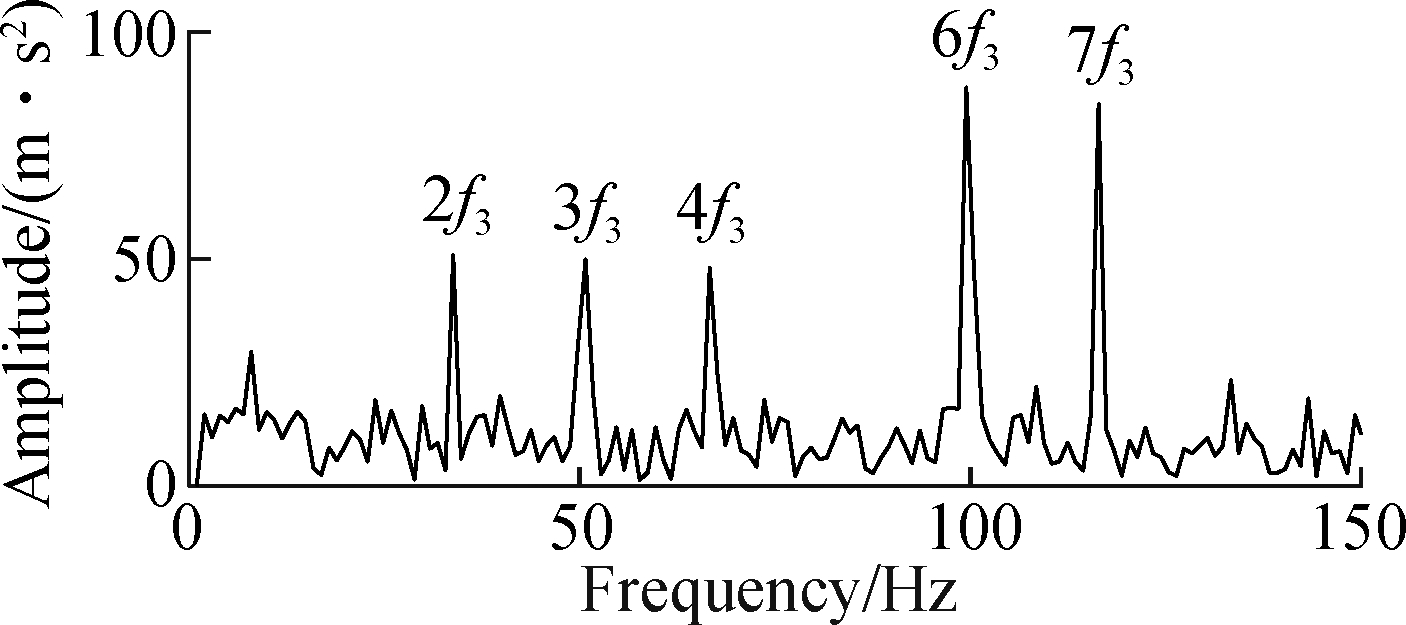
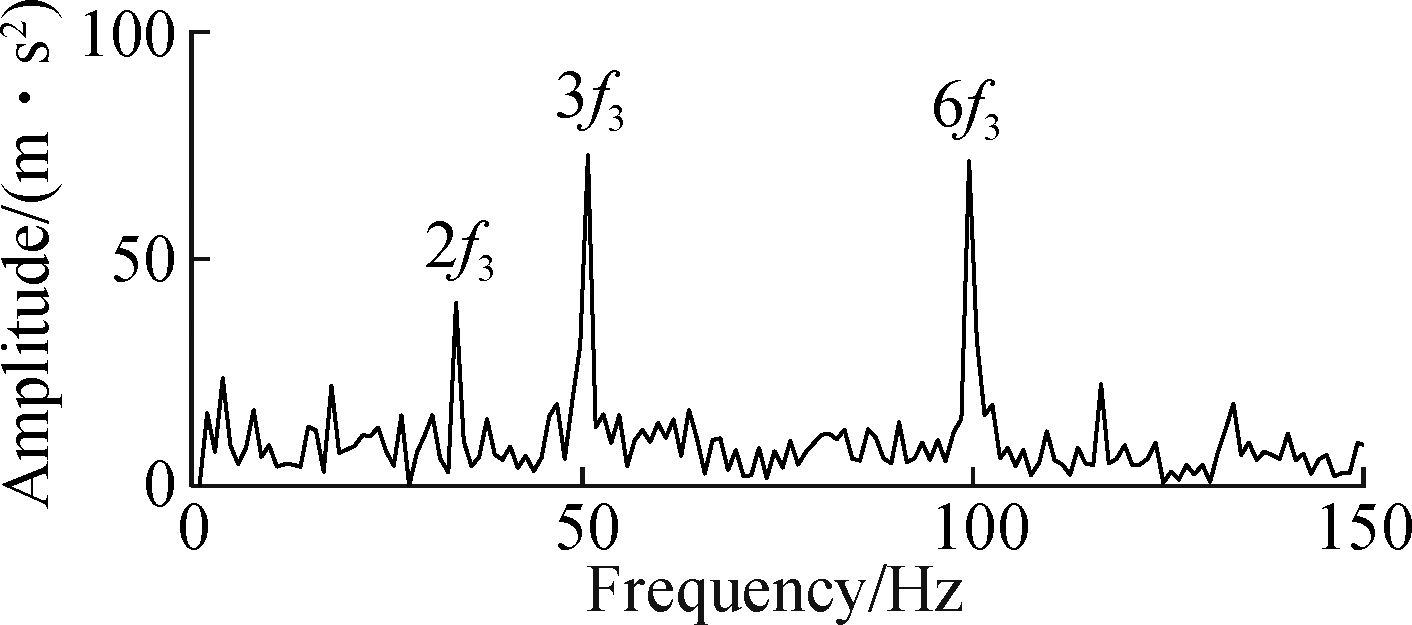
The fast kurtogram method (FK) [25] and EMD are effective fault diagnosis methods, so they are used as a benchmark for evaluating the performance of SSM-IM-OFDM. Fig.11 shows the analysis results of the FK. As shown in Fig.11 (b), the fault feature frequency 2f3 and harmonics 3f3,4f3,5f3,6f3 are also identified. However, this method greatly weakens the signal strength, and the corresponding spectral amplitude is much smaller than the SSM-IM-OFDM. In Fig.12, after EMD decomposition, the Hilbert envelope spectrum processing is performed on the IMF1 and IMF2 components. Whether it is the envelope spectrum of IMF1 or IMF2, the extracted fault characteristic frequency can be used for fault diagnosis, but some harmonics are missing.
By comparing the results, the advantages of the SSM-IM-OFDM are proved. In the gearbox fault diagnosis, its performance is better than that of the FK and EMD. In order to verify the above analysis conclusion, further research will be carried out in the next section.
(a)

(b)
Fig.11 The PHM data analysis results obtained by FK. (a) Kurtogram of the signal; (b) The Hilbert envelope spectrum
(a)
(b)
Fig.12 The PHM data analysis results obtained by EMD. (a) The Hilbert envelope spectrum of IMF1; (b) The Hilbert envelope spectrum of IMF2
4.3 Laboratory data verification
In order to further verify the effectiveness of the SSM-IM-OFDM, laboratory data is used for verification. The gearbox test bench in the laboratory is shown in Fig.13. The gearbox input shaft is connected to the motor through a coupling, and the acceleration sensor is installed in the gearbox’s shaft end. The data collection is completed by the MFD310 system developed by our laboratory. The vibration data unit of the gearbox test bench is mm/s2. The gearbox consists of 2 shafts, the gear ratio is 46∶31, the data sampling length is 4 096 points, and the sampling frequency is 3 838.77 Hz. The gear meshing frequency is 307 Hz, the frequency of shaft Ⅰ is fⅠ=10 Hz, and the frequency of shaft Ⅱ is fⅡ=7 Hz.

Fig.13 Gearbox test bench
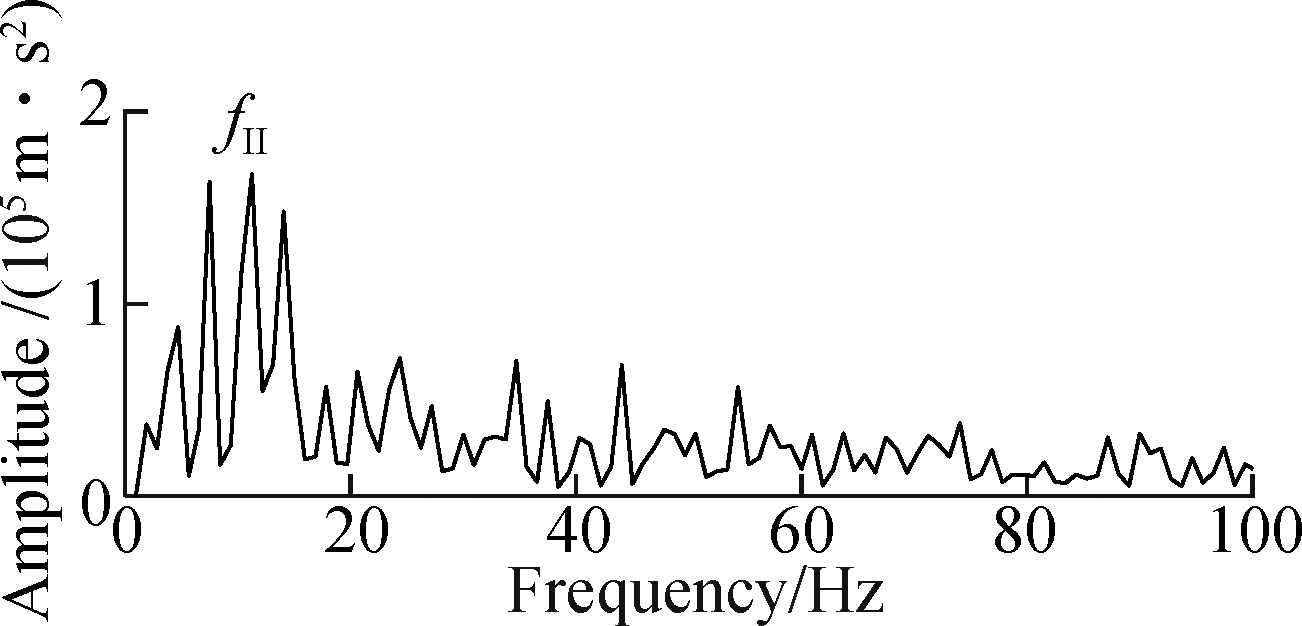
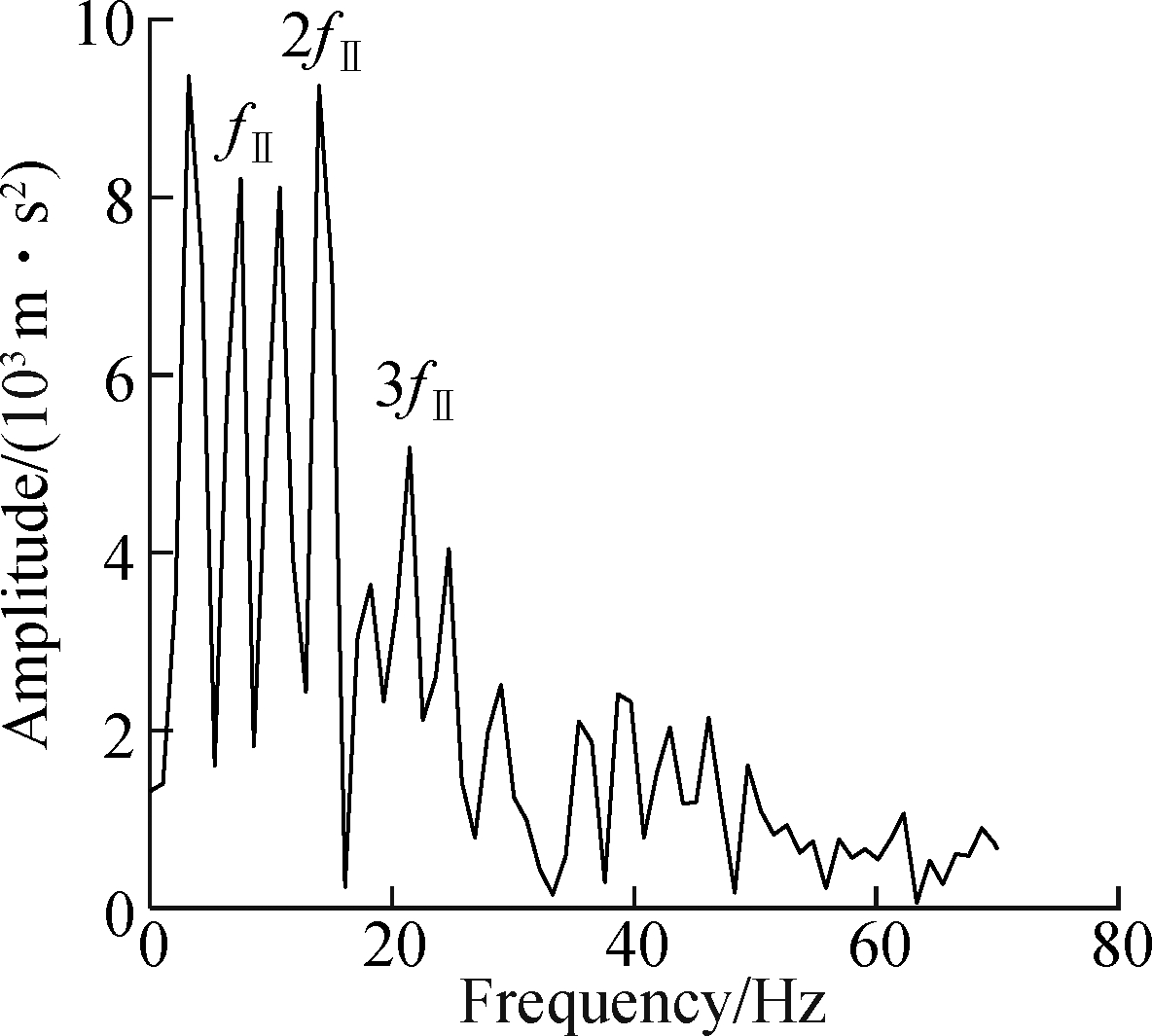
Figs.14(a) and (b) are the time-domain waveform and Hilbert envelope spectrum by OFDM, respectively. In Fig.14(b), the fault feature frequency fⅡ can be found, but its harmonic 2fⅡ,3fⅡ,… is interfered with by other frequencies and cannot be clearly identified.
The SSM-IM-OFDM is used to analyze the gearbox fault signal actually measured in Fig.14(a). The SSM-IM dictionary is combined with the OMP algorithm for feature extraction and noise reduction of the measured signals, and the signal after the 20th iteration is selected as the reconstructed signal, which is decomposed by OFDM. Then the correlation coefficient between each AFIBF and the original vibration signal is calculated, and the results are shown in Tab.3. The AFIBF3 component with the largest correlation number was selected for Hil-bert envelope spectrum analysis, and the results are shown in Fig.15. It clearly shows the fault feature frequency and its harmonic components of 7 Hz on shaft Ⅱ. Based on this, it is judged that the large gear in the gearbox is faulty, and the analysis result is consistent with the actual situation. Using the SSM-IM-OFDM can obtain more feature frequency information, and effectively reduce the effect of background noise and irrelevant frequencies.

(a)
(b)
Fig.14 Time-frequency diagram of the gearbox fault signal. (a) Time domain diagram; (b) Hilbert envelope spectrum by OFDM
Tab.3 Correlation coefficient of each AFIBF with the original signal
Correlation coefficientC1C2C3C4C5Values0.010 00.011 70.118 90.234 10.036 8
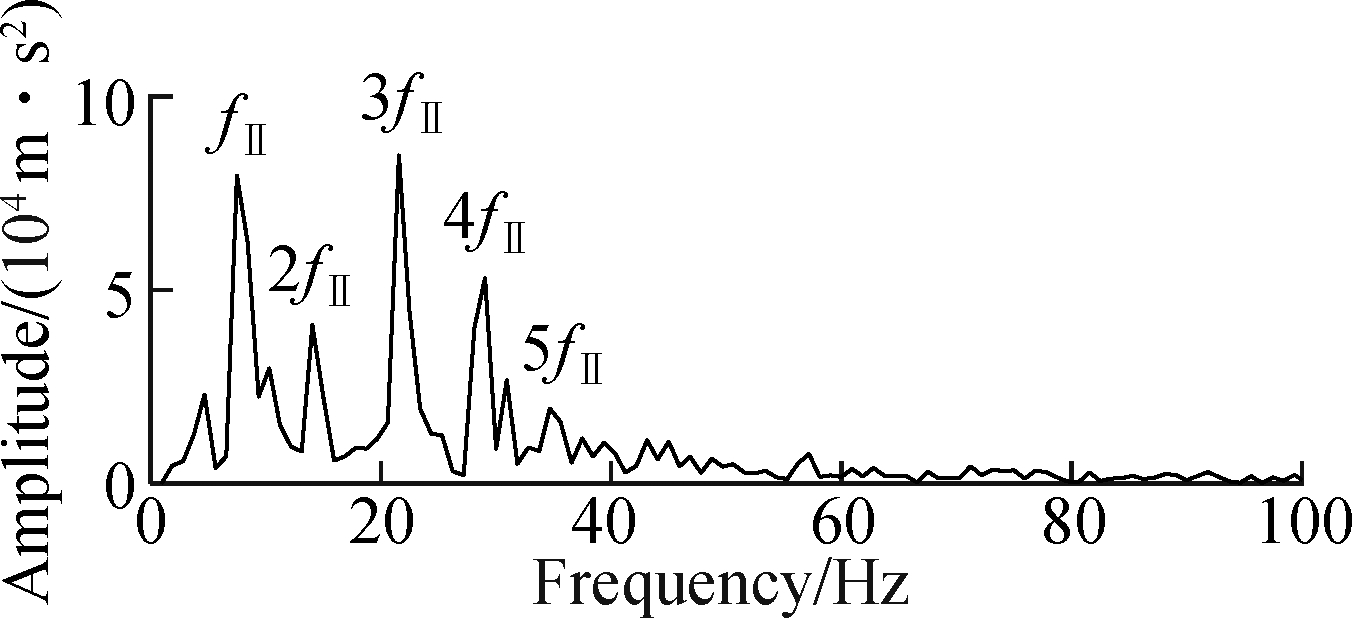
Fig.15 Hilbert envelope spectrum of AFIBF4 component
4.4 Methods contrast Ⅱ
This part also uses FK and EMD as comparison methods. Fig.16 shows the analysis results. In Fig.16(b), the fault feature frequency 7 Hz and its harmonic frequency 14 Hz are also identified, but many interfering frequency components around them will affect the accuracy of fault diagnosis. In addition, this method greatly weakens the signal strength, and the corresponding spectral amplitude is much smaller than that of the SSM-IM-OFDM. In Fig.17, after EMD decomposition, Hilbert envelope spectrum processing is performed on the IMF1 and IMF2 components. After Hilbert envelope spectrum processing on IMF1, the fault feature frequency is not clear, and therefore, fault diagnosis cannot be performed. Similarly, after IMF2 is processed by the Hilbert envelope spectrum, although it can extract the fault feature frequency, it is smaller than the fault feature frequency component extracted by the method proposed in this paper.
The research of laboratory data further verifies the effectiveness of the proposed method for gearbox vibration signal analysis and fault diagnosis. In addition, the advantages of the SSM-IM-OFDM are highlighted by comparison with the FK and EMD.
(a)
(b)
Fig.16 The laboratory data analysis results obtained by FK. (a) Kurtogram of the signal; (b) The Hilbert envelope spectrum

(a)

(b)
Fig.17 The laboratory data analysis results obtained by EMD. (a) The Hilbert envelope spectrum of IMF1; (b) The Hilbert envelope spectrum of IMF2
5 Conclusions
1) In most cases, the gearbox distributed fault can be modeled by a stable modulation signal, while local faults can be modeled by a impact modulation signal. Therefore, a compound dictionary (SSM-IM) based on the modulation signals of distributed faults and local faults is established, and the dictionary design has a clear physical meaning and wide versatility. The performance is better than that of the DCT dictionary, Fourier dictionary and IFMF dictionary.
2) FDM is an algorithm based on the Fourier theory and a zero-phase filter, which decomposes non-linear and non-stationary signals into a series of single-component signals with physical significance at instantaneous frequencies. In order to suppress the mode aliasing effect caused by the binary cut-off frequency selection method in the FDM decomposition process, a new cut-off frequency selection method is proposed to optimize the Fourier decomposition algorithm, which improves the frequency band division accuracy and decomposition quality of FDM.
3) In order to solve the problem of difficult extraction of the gearbox fault feature information under strong background noise and interference frequency, a gearbox fault diagnosis method based on the combination of the SSM-IM dictionary and OFDM is proposed. The validity of the proposed method is verified by the analysis of PHM data and laboratory gearbox failure data.
[1] Lu S L, He Q B, Wang J. A review of stochastic resonance in rotating machine fault detection[J].Mechanical Systems and Signal Processing, 2019, 116: 230-260. DOI:10.1016/j.ymssp.2018.06.032.
[2] Li N, Huang W G, Guo W J, et al. Multiple enhanced sparse decomposition for gearbox compound fault diagnosis[J].IEEE Transactions on Instrumentation and Measurement, 2020, 69(3): 770-781. DOI:10.1109/TIM.2019.2905043.
[3] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193.
[4] Wu Z H, Huang N E. Ensemble empirical mode decomposition: A noise-assisted data analysis method[J].Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. DOI:10.1142/s1793536909000047.
[5] Smith J S. The local mean decomposition and its application to EEG perception data[J].Journal of the Royal Society, Interface, 2005, 2(5): 443-454. DOI:10.1098/rsif.2005.0058.
[6] Yang Y, Cheng J S, Zhang K. An ensemble local means decomposition method and its application to local rub-impact fault diagnosis of the rotor systems[J].Measurement, 2012, 45(3): 561-570. DOI:10.1016/j.measurement.2011.10.010.
[7] Gilles J. Empirical wavelet transform[J].IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010. DOI:10.1109/TSP.2013.2265222.
[8] Dragomiretskiy K, Zosso D. Variational mode decomposition[J].IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675.
[9] Singh P, Singh P, Joshi S D, et al. The Fourier decomposition method for nonlinear and non-stationary time series analysis[J].Proceedings Mathematical, Physical, and Engineering Sciences, 2017, 473(2199): 20160871. DOI:10.1098/rspa.2016.0871.
[10] Liu Y, Liu X B, Liang S, et al. Aeroengine rotor fault diagnosis based on Fourier decomposition method [J]. China Mechanical Engineering, 2019, 30(18): 2156-2163. DOI: 10.3969/j.issn.1004-132X.2019.018.003. (in Chinese)
[11] Deng M Q, Deng A D, Zhu J, et al. Bandwidth Fourier decomposition and its application in incipient fault identification of rolling bearings[J].Measurement Science and Technology, 2020, 31(1): 015012. DOI:10.1088/1361-6501/ab4069.
[12] Dou C H, Lin J S. Extraction of fault features of machinery based on Fourier decomposition method[J].IEEE Access, 2019, 7: 183468-183478. DOI:10.1109/ACCESS.2019.2960548.
[13] Singh P. Novel Fourier quadrature transforms and analytic signal representations for nonlinear and non-stationary time-series analysis[J]. Royal Society Open Science, 2018, 5(11): 181131. DOI: 10.1098/rsos.181131.
[14] Duarte M F, Davenport M A, Takhar D, et al. Single-pixel imaging via compressive sampling[J].IEEE Signal Processing Magazine, 2008, 25(2): 83-91. DOI:10.1109/MSP.2007.914730.
[15] Feng Z P, Zhou Y K, Zuo M J, et al. Atomic decomposition and sparse representation for complex signal analysis in machinery fault diagnosis: A review with examples[J].Measurement, 2017, 103: 106-132. DOI:10.1016/j.measurement.2017.02.031.
[16] Yan R Q, Gao R X, Chen X F. Wavelets for fault diagnosis of rotary machines: A review with applications[J].Signal Processing, 2014, 96: 1-15. DOI:10.1016/j.sigpro.2013.04.015.
[17] Chen X F, Du Z H, Li J M, et al. Compressed sensing based on dictionary learning for extracting impulse components[J].Signal Processing, 2014, 96: 94-109. DOI:10.1016/j.sigpro.2013.04.018.
[18] Aharon M, Elad M, Bruckstein A. K-SVD: An algorithm for designing overcomplete dictionaries for sparse representation[J].IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322. DOI:10.1109/TSP.2006.881199.
[19] Ophir B, Lustig M, Elad M. Multi-scale dictionary learning using wavelets[J].IEEE Journal of Selected Topics in Signal Processing, 2011, 5(5): 1014-1024. DOI:10.1109/JSTSP.2011.2155032.
[20] Medina R, Alvarez X, Jadán D, et al. Gearbox fault classification using dictionary sparse based representations of vibration signals[J].Journal of Intelligent & Fuzzy Systems, 2018, 34(6): 3605-3618. DOI:10.3233/jifs-169537.
[21] Nagaraj S B, Stevenson N, Marnane W, et al. A novel dictionary for neonatal EEG seizure detection using atomic decomposition[C]//2012 Annual International Conference of the IEEE Engineering in Medicine and Biology Society. San Diego, CA, USA, 2012: 1073-1076. DOI:10.1109/EMBC.2012.6346120.
[22] Lü Y, Luo J, Yi C C. Enhanced orthogonal matching pursuit algorithm and its application in mechanical equipment fault diagnosis[J].Shock and Vibration, 2017, 2017: 1-13. DOI:10.1155/2017/4896056.
[23] Pati Y C, Rezaiifar R, Krishnaprasad P S. Orthogonal matching pursuit: Recursive function approximation with applications to wavelet decomposition[C]//Proceedings of 27th Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA, 1993: 40-44. DOI:10.1109/ACSSC.1993.342465.
[24] Ding K, Li W, Zhu X. The useful technique of gear and gear faults diagnosis [M]. Beijing: China Machine Press, 2005: 35-38. (in Chinese)
[25] Antoni J. Fast computation of the kurtogram for the detection of transient faults[J]. Mechanical Systems and Signal Processing, 2007, 21(1): 108-124. DOI:10.1016/j.ymssp.2005.12.002.