The massive consumption of fossil fuels and environmental degradation motivated many researchers to find more efficient ways to save energy and reduce gas emissions and pollutants. Ultra-supercritical (USC) thermal power units have significant energy saving and environmental improvement effects. Compared with supercritical units, USC units have a thermal efficiency increase of 1.2%-4%, which is more obvious than in conventional coal-fired generating units. High-efficiency and low-emission USC thermal power units are the main direction of future thermal power construction.
However, the problem of controlling it is extremely challenging because of the severe nonlinearity in the wide operation range, the coupling between multiple variables, the hard constraints on manipulated variables, and unknown disturbances[1-4]. Traditional proportional-integral-derivative (PID) control is difficult to meet the control objectives. To this end, it is of urgence to develop advanced control strategies to improve boiler-turbine systems’ operation performance.Model predictive control (MPC) is widely accepted as an optimal control method for industrial processes due to its inherent robustness, ability to handle constraints, and receding horizon implementation of optimal control inputs. Linear dynamic matrix control (DMC)[5] and generalized predictive control (GPC)[6]are used for boiler-turbine systems. Simulation results verify that linear MPCs can achieve better control effects than PID controllers. However, the control quality of linear MPCs deteriorates due to system nonlinearity during the wide-range operation of units. Collocation method-based nonlinear model predictive control (NMPC)[7] and fuzzy neural network and input-output feedback linearization-based NMPC[8] are proposed for boiler-turbine systems. Although control performance is improved, nonlinear optimization is time-consuming. Besides, it is often difficult to obtain accurate nonlinear models of NMPC for complex industrial processes.
An alternative method is to use fuzzy model predictive control (FMPC) based on the T-S model to solve these problems. The T-S fuzzy dynamic models have been widely accepted to represent nonlinear dynamics in the control community. Many state feedback FMPC[9-10] and output feedback FMPC methods[11-12]have been developed. These FMPC methods adopt the min-max strategy, which is first proposed in Ref.[13]. Unfortunately, most of the above min-max FMPC methods are derived from state adjustment and stability problems. For stepwise track reference signals, especially in plant parameter variations or uncertainties, their output tracking performance cannot always be guaranteed.In industrial applications, it is more necessary to study tracking control methods, which are more complicated than the stabilization control design[14]. In Refs.[15-16], fuzzy model predictive tracking control (FMPTC) methods are developed through a state and disturbance observer, a steady-state target calculator, and a stable predictive controller. However, they need to assume that the corresponding input of desired output trajectories is known. An extended state observer-based FMPC[17] and generalized discrete-time nonlinear disturbance observer-based FMPC[18] are proposed to overcome nonlinearity and disturbances simultaneously. However, its compensation operation is added directly to the input, causing the overall optimality to be destroyed. In Ref.[19], min-max state feedback model predictive tracking control based on the extended state-space model is proposed to improve output tracking performance. However, the controller needs the state of processes to be measurable. To this end, in Ref.[20], the input and output variables of processes are selected as the state of the comprehensive model to solve the problem of the unmeasurable state, but it leads to a large increase in the order of the comprehensive model and online computing burden for multi-variable systems. Moreover, for nonlinear constrained systems, the design separation principle between the controller and the observer does not exist. Therefore, to ensure the stability of the entire closed-loop control system, the MPC needs to consider the observer’s estimation error.
Motivated by the analysis above, an improved min-max FMPTC controller is developed to improve the control performance of multi-variable nonlinear USC boiler-turbine systems while ensuring the closed-loop system stability and the inputs in their given constraints.The merit and novelty of the proposed controller in this paper lie in that:
1) Unlike the traditional FMPTC scheme, which is designed directly based on the T-S model, the proposed control method first amplifies the T-S model and then designs the subsequent controller based on the extended T-S model. The design facilitates the subsequent tracking controller design and allows the controller to use a new state- and output-based objective function.
2) A new state- and output-based objective function instead of the output-based objective function is employed for the controller design. The resulting controller can also control state variables during output tracking processes and offer a higher degree of freedom to tune the closed-loop system behavior.
3) In the MPC design, the observer estimation error is regarded as a bounded disturbance, ensuring that the entire closed-loop control system is stable.
1 USC Boiler-Turbine Dynamics
The model used in this paper represents the behavior of a 1 000 MW USC power plant in Taizhou, China[21]. This model is developed from the first-principles, and its parameters are identified using real plant operating data. It is well approximated to the real plant dynamics and is widely used to verify the effectiveness of controllers[2,17]. The nonlinear time-delay model is given by
(1)
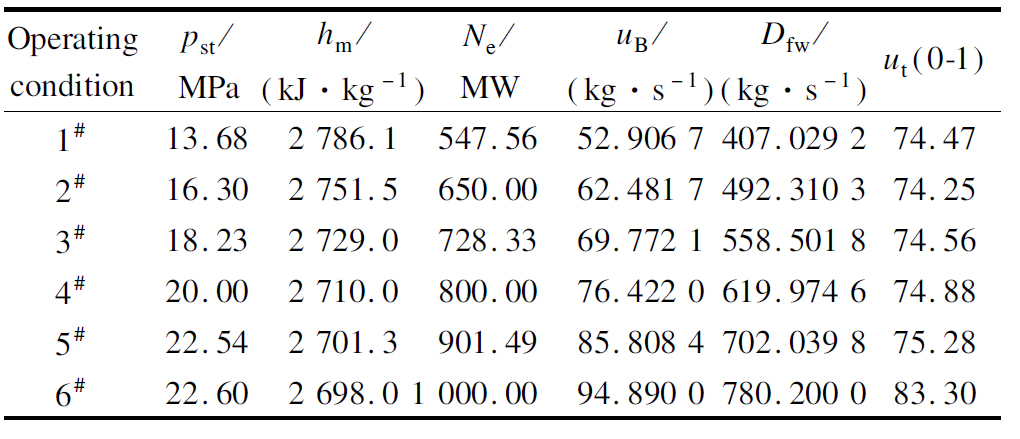
where state variables rB, pm and hm represent the pulverized coal flow rate that enters the boiler (kg/s), separator steam pressure (MPa), and the separator steam enthalpy (kJ/kg), respectively; τd=17 s represents the delay of the milling system; the controlled variables pst, hm and Ne represent the throttle steam pressure (MPa), the separator steam enthalpy (kJ/kg), and the active power (MW), respectively; manipulated variables uB, Dfw and ut represent the pulverized coal flow rate (kg/s), the feedwater flow rate (kg/s), and the turbine throttle opening, respectively. The manipulated variables are constrained by 40 kg/s≤uB≤100 kg/s, 350 kg/s≤Dfw≤800 kg/s, 0≤ut≤1, -10 
The equilibrium operating points of the USC thermal power unit are shown in Tab.1.
Tab.1 Equilibrium operating points of the USC thermal power unit
2 T-S Fuzzy Modeling of the USC Boiler-Turbine System
The T-S fuzzy dynamic model is widely accepted as an excellent approximator to complex nonlinear plants. Since the dynamics of USC thermal power units depend on the load change, the output power Ne is selected as the only premise variable in fuzzy modeling.
According to the nonlinearity analysis, the unit’s nonlinearity increases with the increase of power[17]. Although increasing the number of local models can improve the accuracy of the T-S fuzzy model, it increases the computation burden of the subsequent predictive controller. For the sake of simplicity, three local models are developed around operation points 1# (547.56 MW),3 # (728.33 MW), and 5# (901.49 MW) by using the Taylor series expansion. The membership function of the fuzzy model is shown in Fig.1.
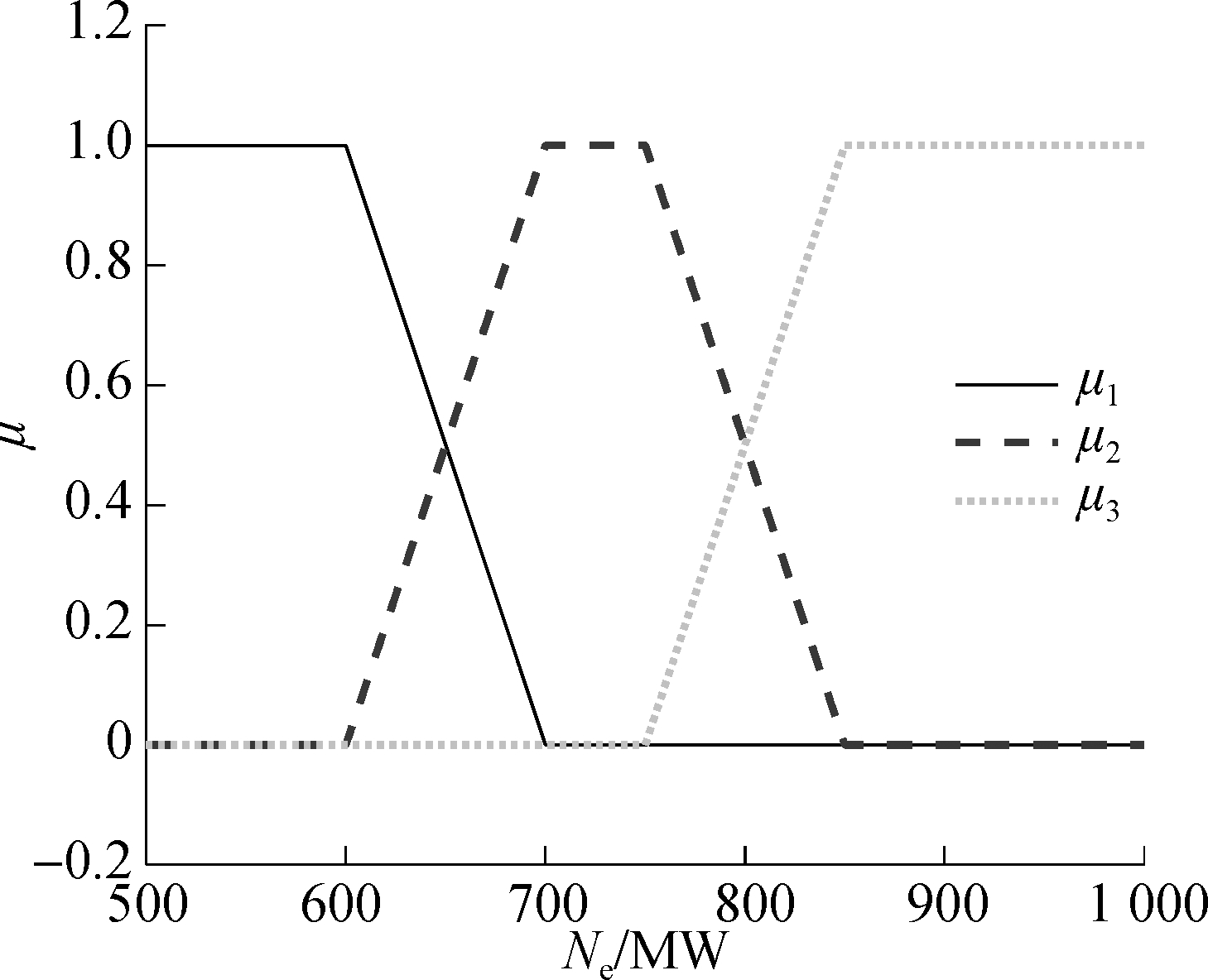
Fig.1 Membership function of active power Ne in a fuzzy model
Then the model (1) is expressed as the following fuzzy affine model with time delay:
Rl:if Ne(k) is Ml, then
l=1,2,…,L
(2)
where Rl denotes the l-th fuzzy inference rule, L=3 the number of inference rules, Ml the l-th fuzzy set of Ne(k), 
the l-th local model, τ the time delay step, and xm={rB,pm,hm}T, u={uB,Dfw,ut}T and y={pst,hm,Ne}T denote the state variable, the control variable, and output variable at time k, respectively.
By using a singleton fuzzifier, the product inference, and the center-average defuzzifier, the fuzzy model is expressed by the global model,
(3)
where
To obtain a model without time delay, the delay inputs are amplified into the model. The form of the extended model is as follows:
(4)
where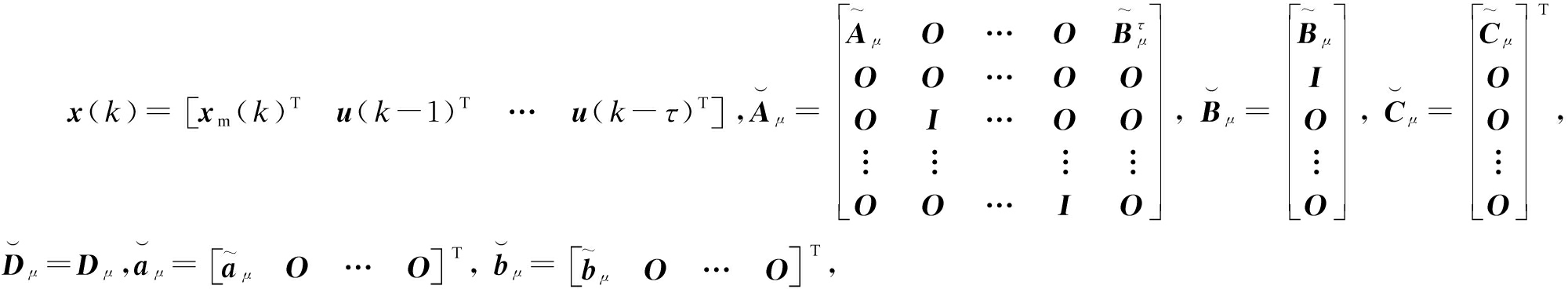 
O and I denote the zero matrix and unit matrix with appropriate dimensions, respectively.
The purpose of the subsequent controller design is to quickly track the load references under unknown uncertainties while ensuring the closed-loop system’s stability and meeting the input constraints.
3 Improved Min-max FMPTC for the USC Boiler-Turbine System
In conventional min-max FMPTC, the following predictive mode is employed to design subsequent controllers:
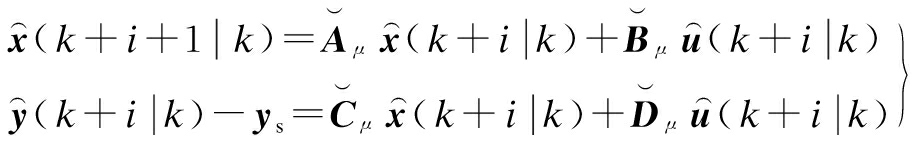
(5)
where 
denotes desired outputs, xs and us the corresponding state and input, respectively, x(k+i+1|k) the state of time k+i+1 calculated at time k.
The above traditional min-max control method is only suitable for plants without uncertainties because the corresponding xs and us of ys change when there are uncertainties. However, uncertainties, including modeling errors and various disturbances, are unavoidable in actual power plant operation.
The improved min-max FMPTC is based on the following extended model:
(6)
where z(k)=[Δx(k) y(k)]T,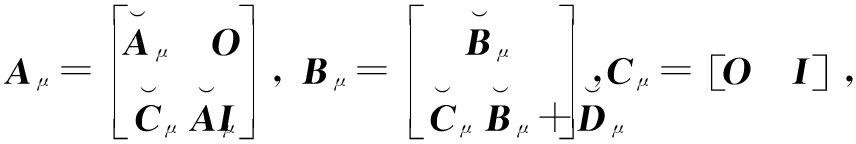 
Δx(k)=x(k)-x(k-1), Δu(k)=u(k)-u(k-1).
The following fuzzy observer is used to estimate the state of the extended model (6):
(7)
where 
the estimated output variable, y the real plant output, and Hμ the observer gain. 
The matrices M-1 and Ni are obtained by solving the following LMIs：
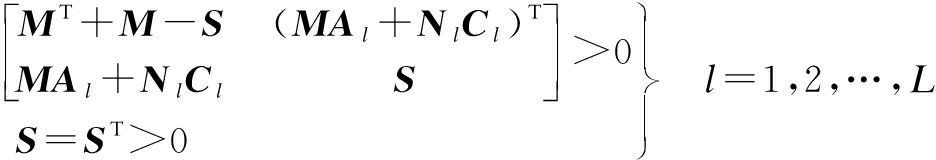
(8)
The observer (7) is equivalent to the state’s feedback correction based on the error between the model output and the actual output. It effectively overcomes the effect of the uncertainties of USC boiler-turbine units.
Then, the following prediction model is obtained:
(9)
where 
z(k+i+1|k) is the state of time k+i+1 calculated at time k.
In the conventional min-max FMPTC, the following output-based infinite-horizon min-max performance cost is considered:
(10)
where 
and R are the symmetric positive definite weighting matrices for output and control input, respectively.
By using a novel state- and output-based infinite-horizon quadratic performance cost,the following min-max optimization problem for USC boiler-turbine units is formulated as
(11)
s.t.
(12)
(13)
(14)
umin≤u(k+i|k)≤umax k,i≥0
(15)
Δumin≤Δu(k+i|k)≤Δumax k,i≥0
(16)
Remark 1
1) Eq.(11) is the form of state adjustment rather than output regulation because the extended state 
contains tracking errors and state variables. Therefore, we call it the state- and output-based performance cost.
2) 
qxi denotes the weighting parameter for states. The greater they are, the smoother the corresponding state changes. 0,0,…,0 denotes the weighting parameter for delay inputs. qyi denotes the weighting parameter for tracking errors. The larger they are, the faster the corresponding output tracking speed.
3) Based on the performance cost (11), the subsequent controller can adjust the state variables while implementing the tracking adjustment. It allows a higher degree of freedom to tune the closed-loop system behavior, and better control performance is expected.
Then the improved min-max FMPTC controller is determined by Theorem 1.
Theorem 1 Consider the fuzzy system (2) subject to the input constraints: umin≤u(k+i|k)≤umax,i≥0, Δumin≤Δu(k+i|k)≤Δumax,i≥0 with the fuzzy observer (7) determined by LMIs (8) at sampling time k. If there are N-step-free control increment sequence ΔU(k), matrix Y, and symmetric positive definite matrix S, the following dynamic optimization problem is feasible:
(17)
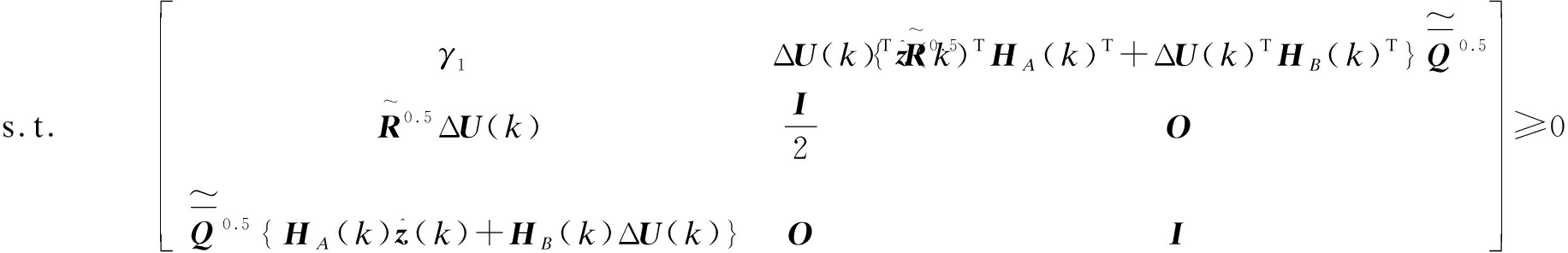
(18)
(19)
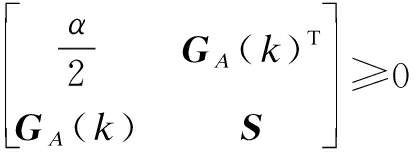
(20)
i=1,2,…,L
(21)
(22)
(23)
where 
⊗ denotes the Kronecker product.
Then, at each sampling time k, the free control sequence
u(k+i|k)=Δu(k+i|k)+u(k-1) 0≤i<N
(24)
and the feedback control law
(25)
can drive the system optimally to track the set-points while ensuring the input-to-state stability of the closed-loop system.
Proof To reduce conservation, following the method in Ref.[22], the objective function (11) is divided into two parts as follows:
(26)
(27)
Based on Eq.(9), we can explicitly derive multi-step-advance state prediction:
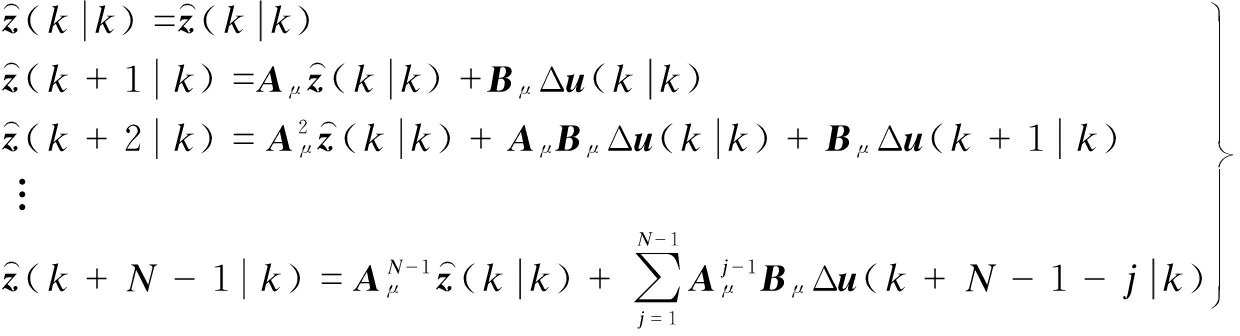
(28)
Then,Eq.(26) is rewritten as
(29)
where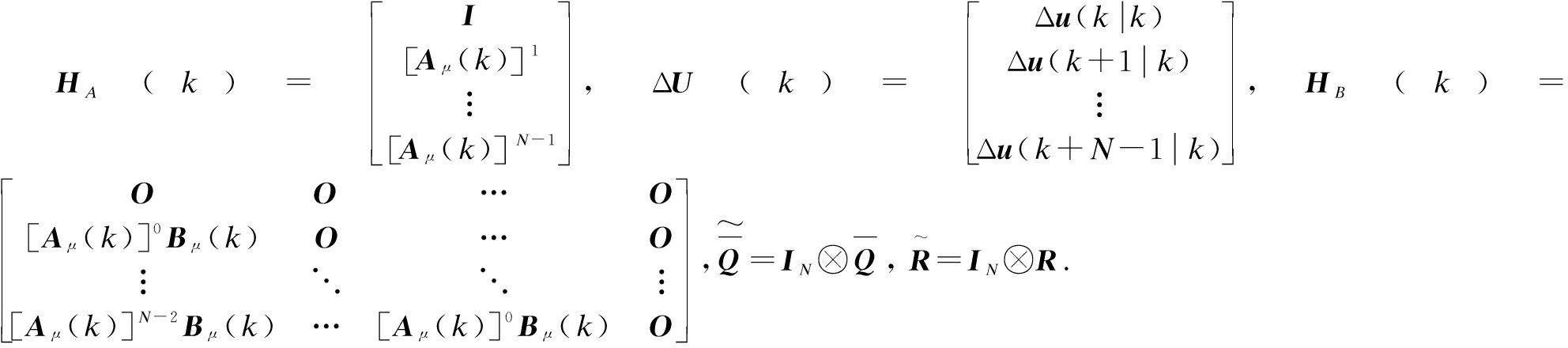 
Note that the separation principle between controller and observer designs may be lost for nonlinear constrained systems; therefore, the influence of the state estimation error on the stability of MPC systems cannot be ignored.
Then one has
(30)
where 
denotes the state estimation error; z(k) denotes the real state; 
Next, the controller derivation is divided into three parts. The first part is to derive the upper bound of the objective function (11). Control performance is ensured by minimizing the upper boundary. The second part is to derive the condition for guaranteeing the stability of the closed-loop system. The third part is to derive the condition that satisfies the input constraints (15) and (16).
Part 1 This part deduces the upper bounds of 
by the two upper bounds.
First, we can obtain the upper bound of 
+
(31)
Since 
is a constant, using the Schur complements, the last inequality of (31) gives (18).
Suppose a common Lyapunov function
(32)
satisfies
(33)
for all time, the system can be guaranteed to be stable.
Furthermore, summing (33) for i=N to i=∞, and with 
and V(∞|k)=0, we obtain
(34)
Then, substituting (28) into (34) yields
(35)
where GA(k)=[Aμ(k)]N-1,GB(k)=
Suppose
(36)
2GA(k)TPGA(k)≤αγ2I
(37)
where P=γ2S-1, and α is a given design parameter.
Then one has
(38)
By using the Schur complements, (36) and (37) can be converted to (19) and (20), respectively.Then we can obtain the upper bound of the total objective function 
(39)
Therefore, it can be concluded that the minimization of γ1+(1+αw2)γ2 means the minimum of the objective function 
Part 2 Consider the following state feedback control law:
(40)
The stability constraint (33) is satisfied if the following holds:
(41)
which can be expressed as (21).
Part 3 The control sequence is divided into free control inputs ΔU(k) and state feedback control law 
The free control inputs are similar to those in conventional MPC, so constraints (22) and (23) are used for amplitude and rate constraints. However, it is challenging for the state feedback law to derive amplitude and rate constraints while guaranteeing stability[15]. Since only the first step of the free control sequence is implemented on the system, we ignore future control constraints in the form of state feedback to ensure closed-loop stability.
The respective roles of LMIs are as follows: (18), (19) and (20) guarantee that φ is the upper boundary of the objective function (11), (21) guarantees the stability of the input-to-state of the closed-loop system, (22) and (23) ensure that the free control sequence u(k+i|k),0≤i<N satisfies the given magnitude and rate constraints, respectively.
4 Simulation Results and Analysis
In this section,three tests are implemented to evaluate the performance of the proposed FMPTC controller for the USC boiler-turbine unit.
The parameters of the proposed controller are set as follows:the sampling time Ts=10 s, state estimation error bound w=1.2, free control step N=6, α=4.0×105, time delay step τ=2, the extended state and input weight matrices 
and R=diag{0.1,0.1,0.1}，respectively. The input constraints are umin=
, umax=
,Δumin={-10,-40,-0.01}T, and Δumax={10,40,0.01}T. The parameters of the proposed algorithm are the same in the following tests.
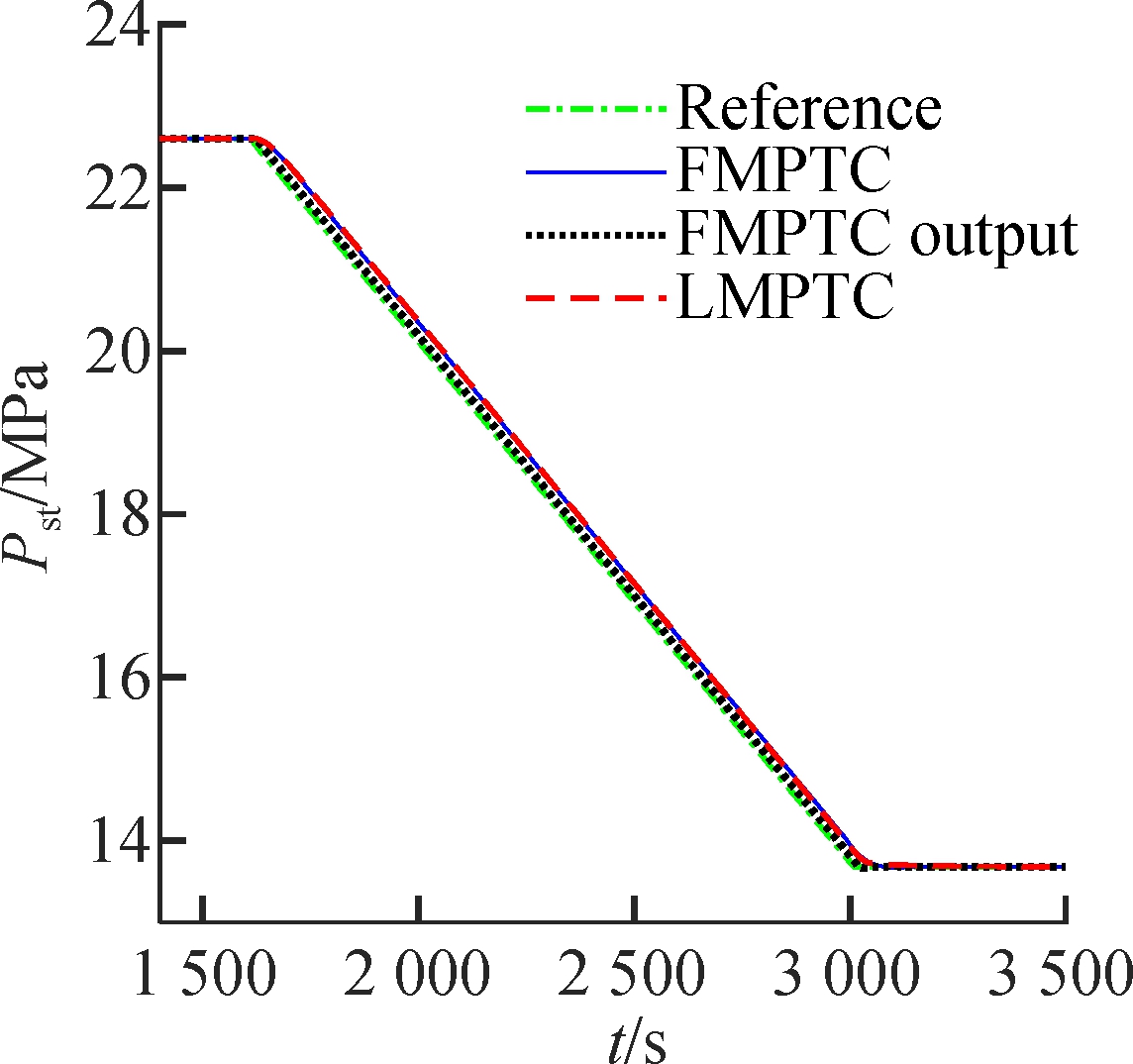
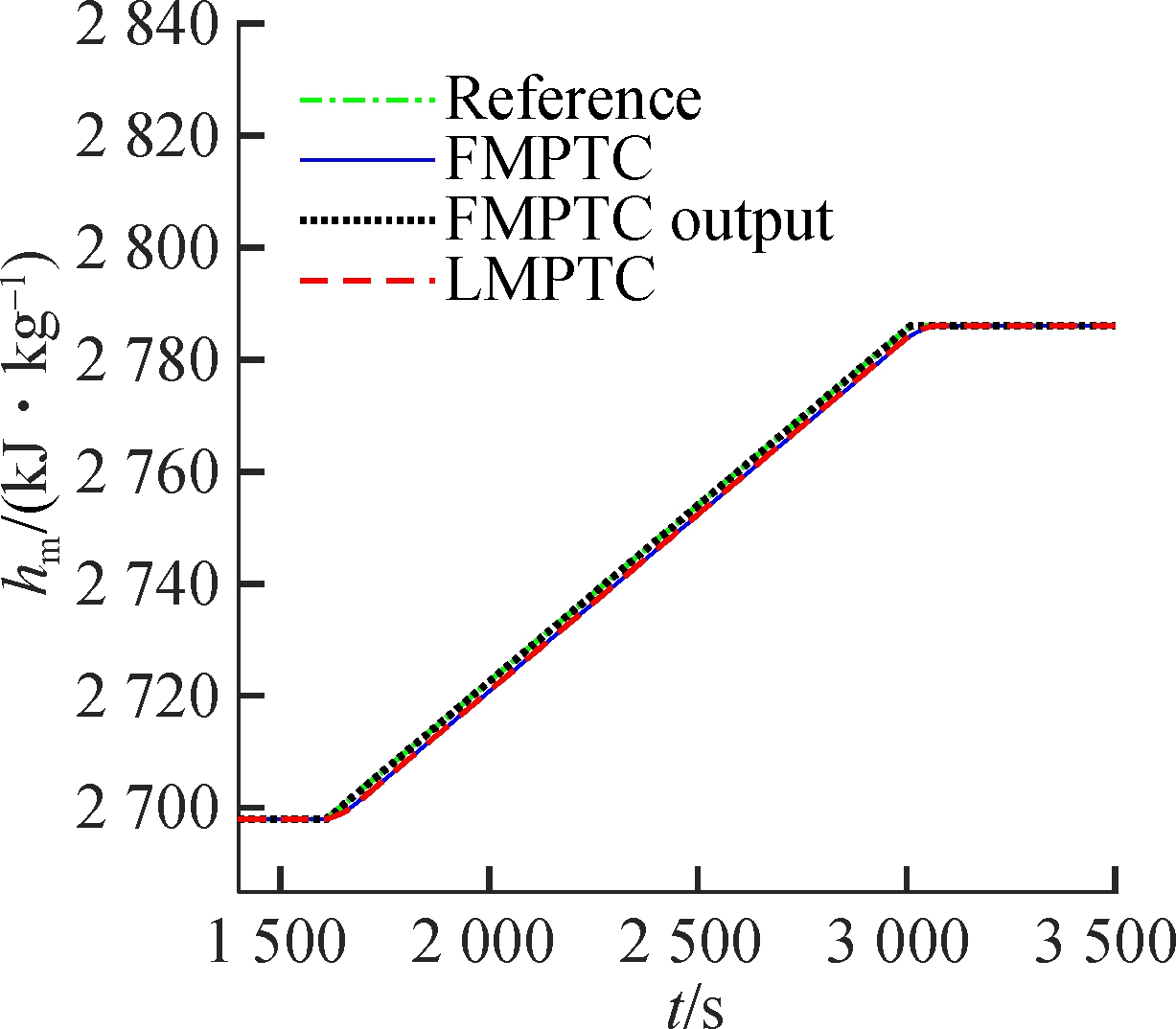
Case 1 is designed to test the load tracking capability of the FMPTC controller over a wide operating range. Suppose that the system changes from operating point 6# (22.6 MPa, 2 698 kJ/kg, 1 000 MW) to operating point 1# (13.68 MPa, 2 786.1 kJ/kg, 547.56 MW) at a speed of 20 MW/min at t=1 600 s.
The proposed FMPTC controller is compared with two other controllers.
1) To test the T-S model’s performance, the same MPTC based on the single linear model obtained at 901.49 MW point (LMPTC) is proposed. The controller parameters are the same as those of the proposed controller.
2) To test the effect of the state and output-based objective function, the same FMPTC based on the output-based performance cost (FMPTC-output) is proposed. For the control scheme, we set 
and other parameters are the same as those of the proposed controller.
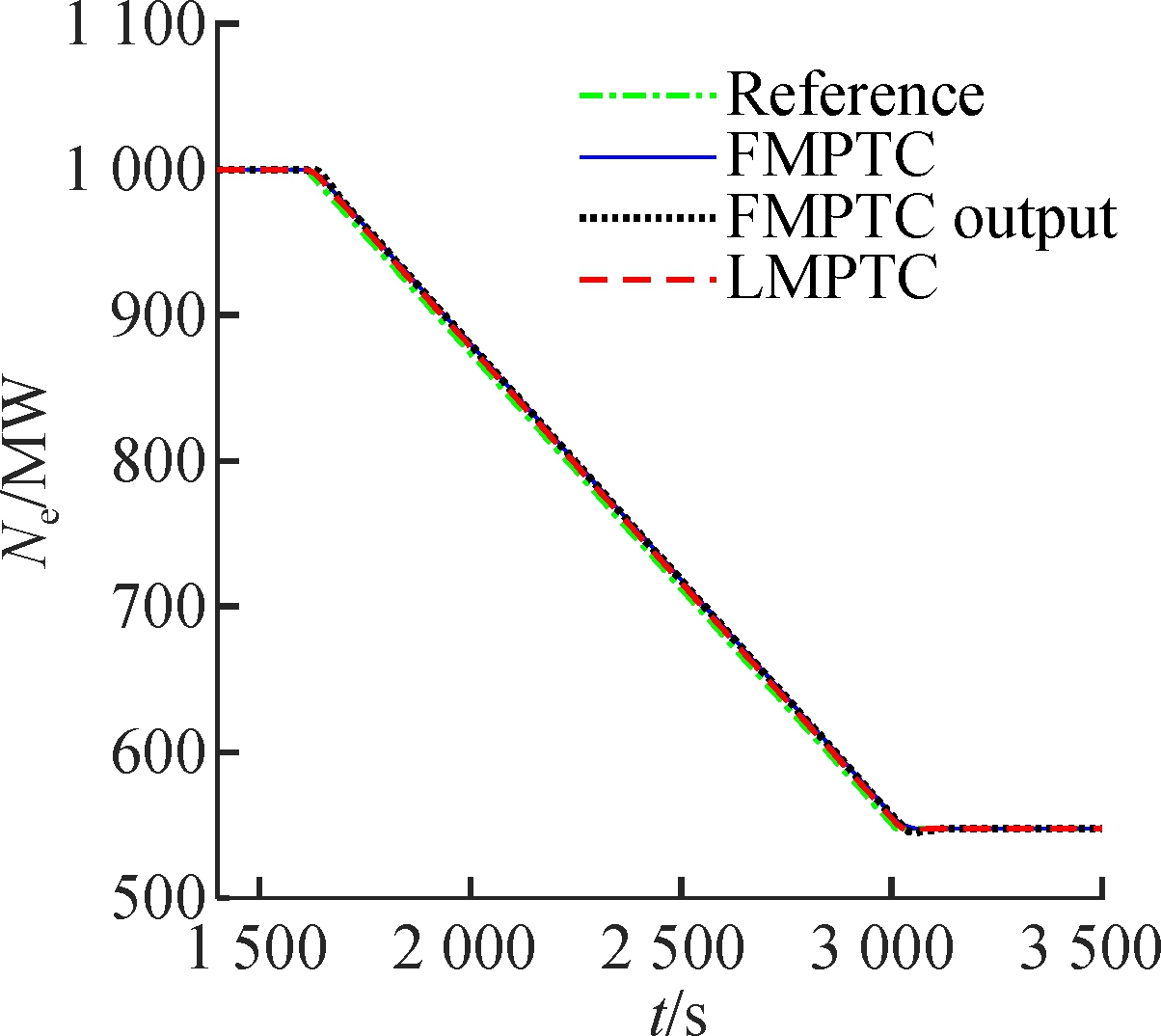
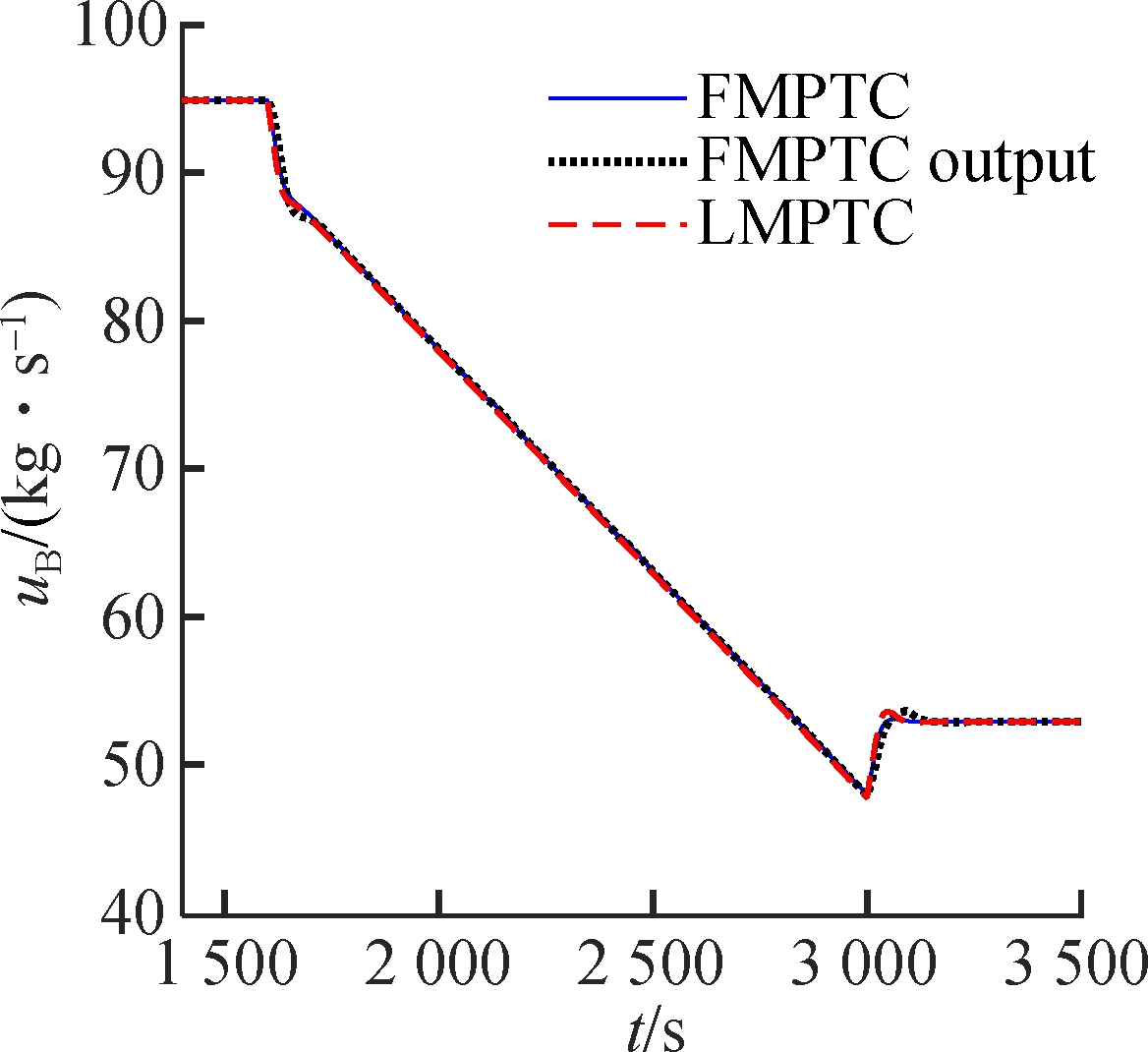
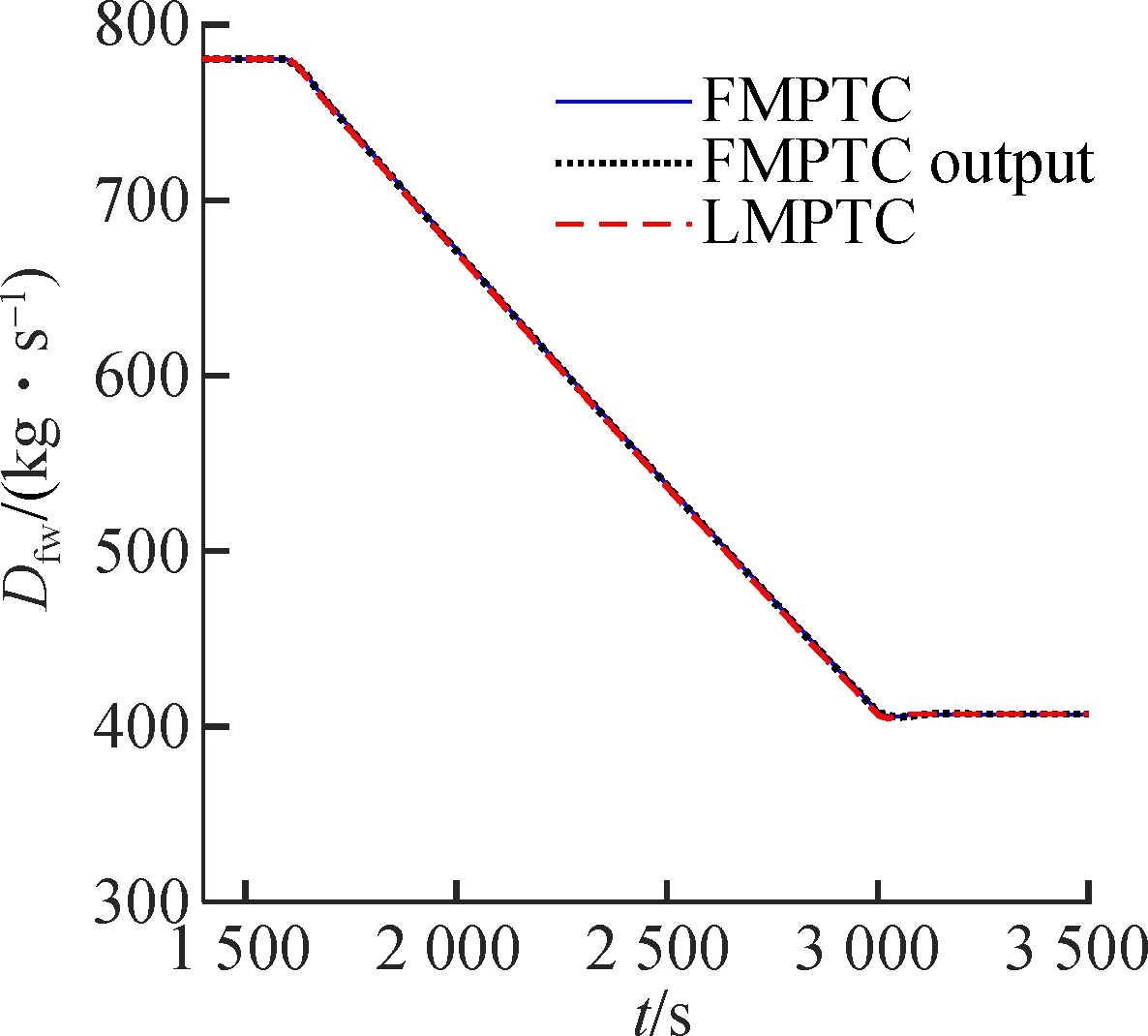
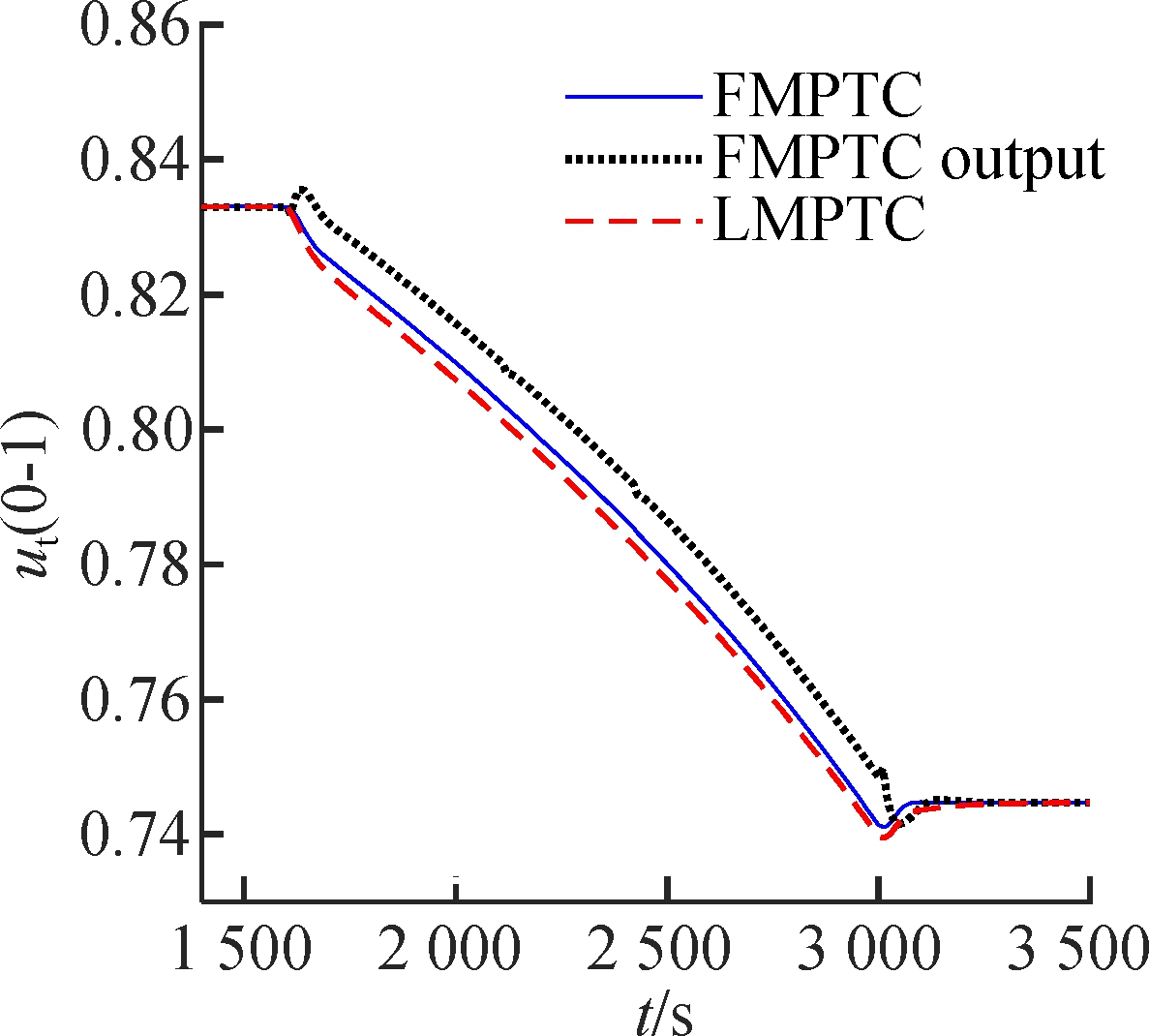
The simulation results are given in Fig.2. The LMPTC and the proposed controller have similar performance near the 901.49 MW load level because the model of the LMPTC is developed here. However, when the operating point deviates from 901.49 MW, the control performance of the LMPTC decreases due to the increase of modeling mismatch. Compared with the FMPTC output, the proposed method has a smaller overshoot and shorter settling time. The reason is that the proposed controller is devised using state and output-based objective function. This design allows the resulting controller to adjust the state, increase design freedom, and obtain a better performance.
(a)
(b)
(c)
(d)
(e)
(f)
Fig.2 Wide-range load tracking control of the USC boiler-turbine unit.(a) Throttle steam pressure; (b)Separator steam enthalpy; (c) Active power (d) Pulverized coal flow rate; (e) Feedwater flow rate; (f) Turbine throttle opening
The purpose of case 2 is to test the disturbance rejection capability of the proposed FMPTC controller. In real thermal power plants, there are various unknown disturbances, such as changes in coal quality and combustion conditions, which cause outputs to deviate from set-points and even affect the stability of the closed-loop systems. For comparison, the traditional min-max RMPC[13] is used to control the plant.
The parameters of the conventional min-max RMPC are set as follows: the sampling time Ts=10 s, the state and input weigh matrices Q=diag{30,100,0.1} and R=diag{0.1,0.1,0.1}，respectively, the input constraints umin={40,350,0}T, and umax={100,800,1}T.
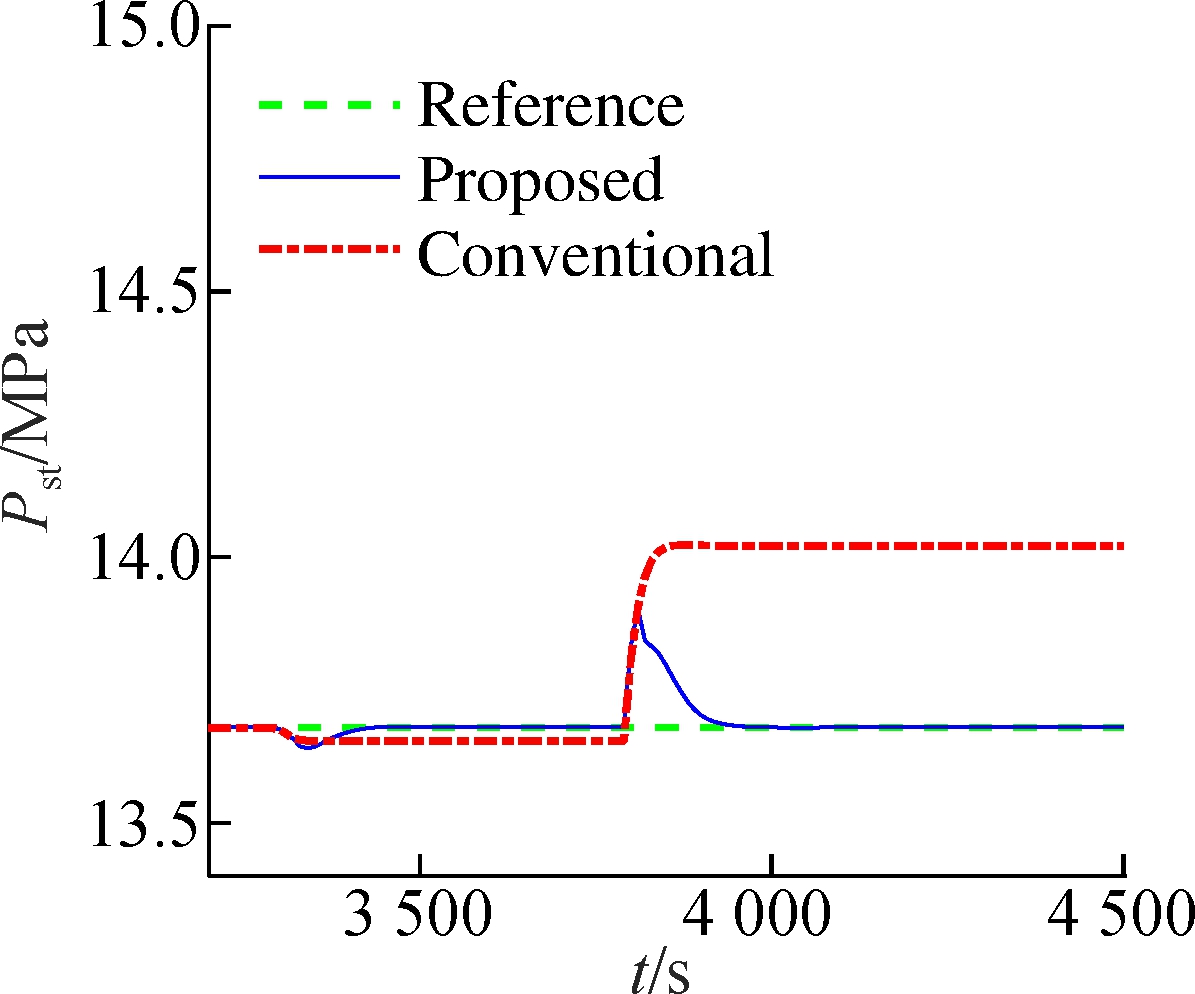
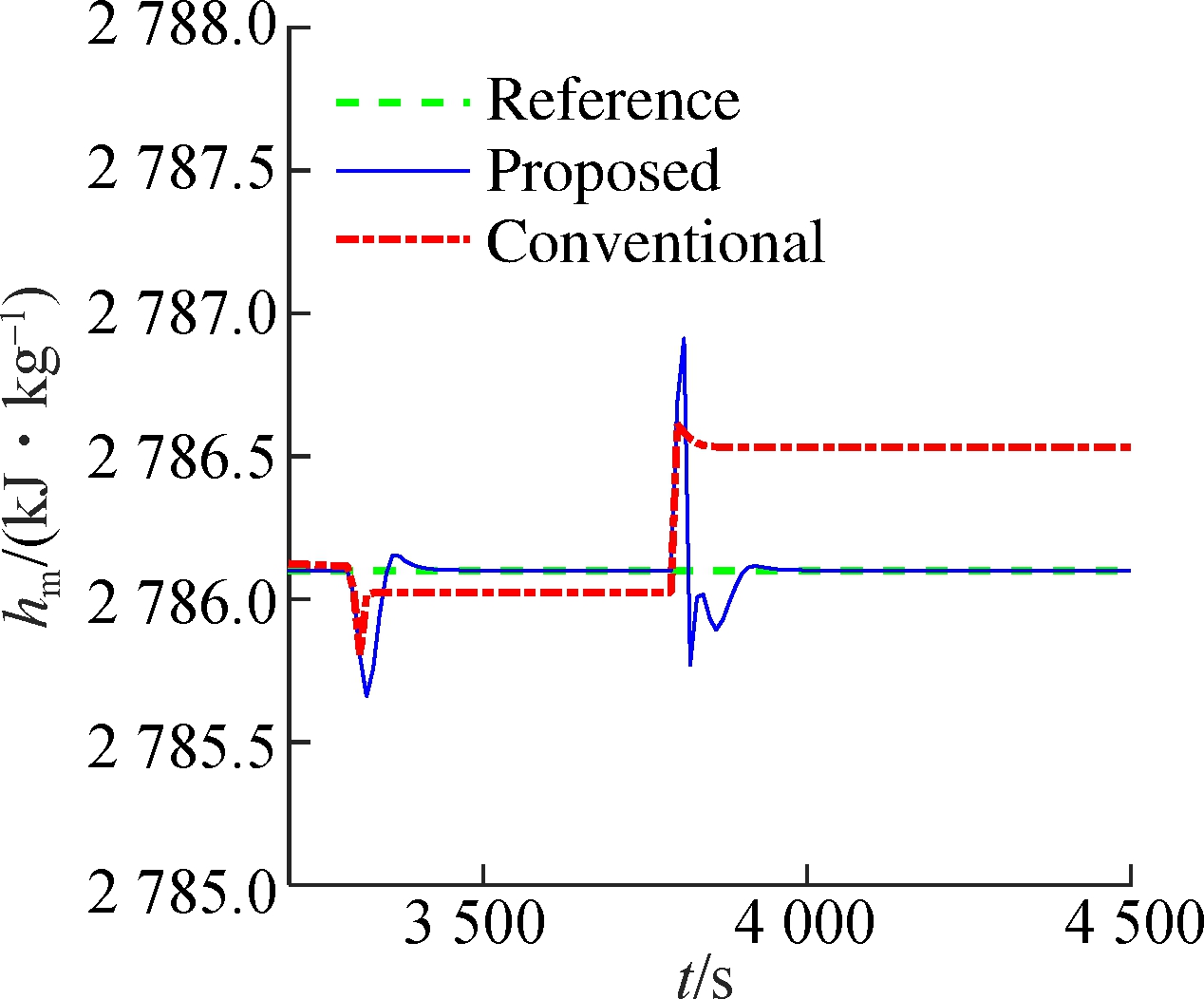
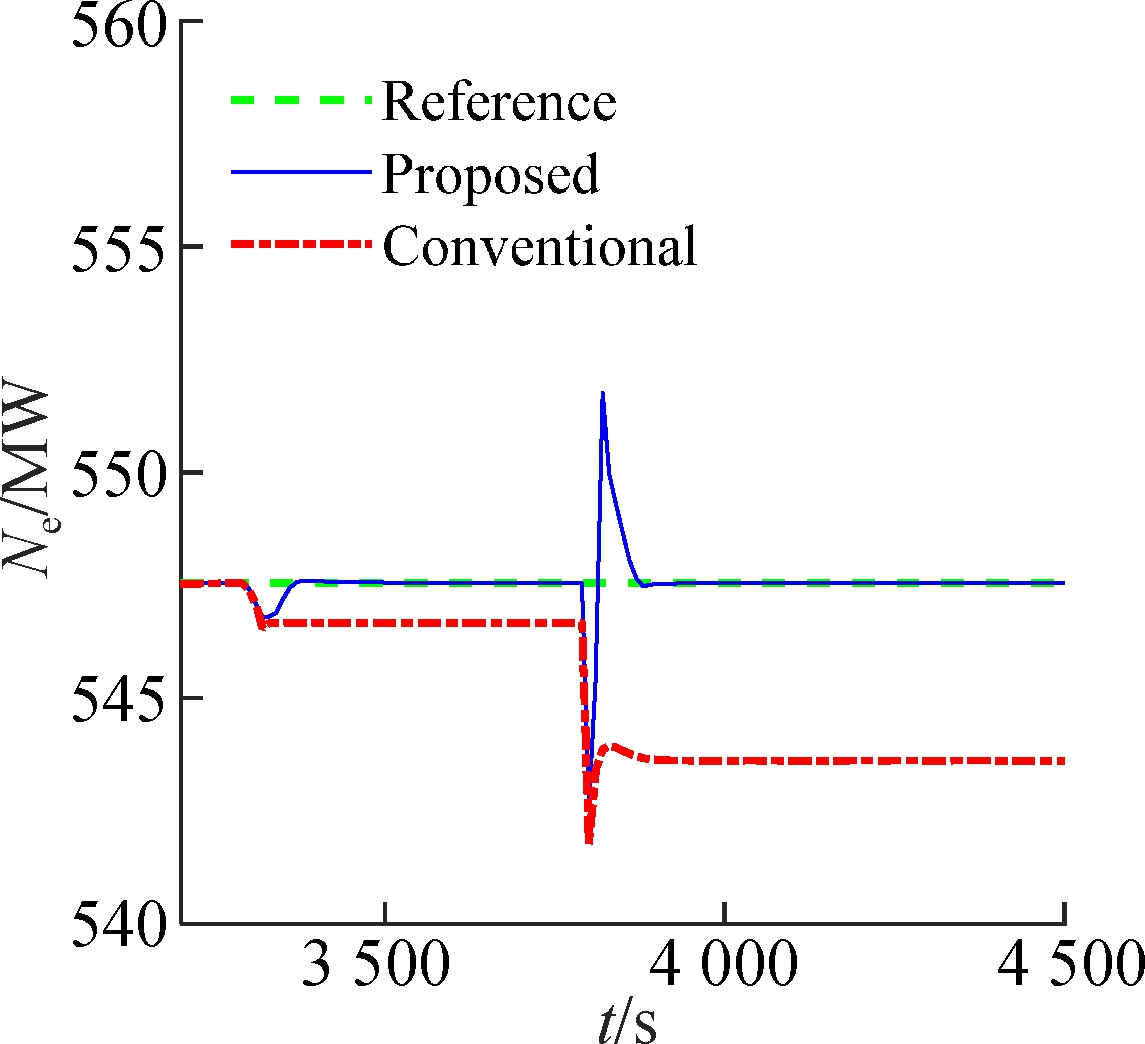
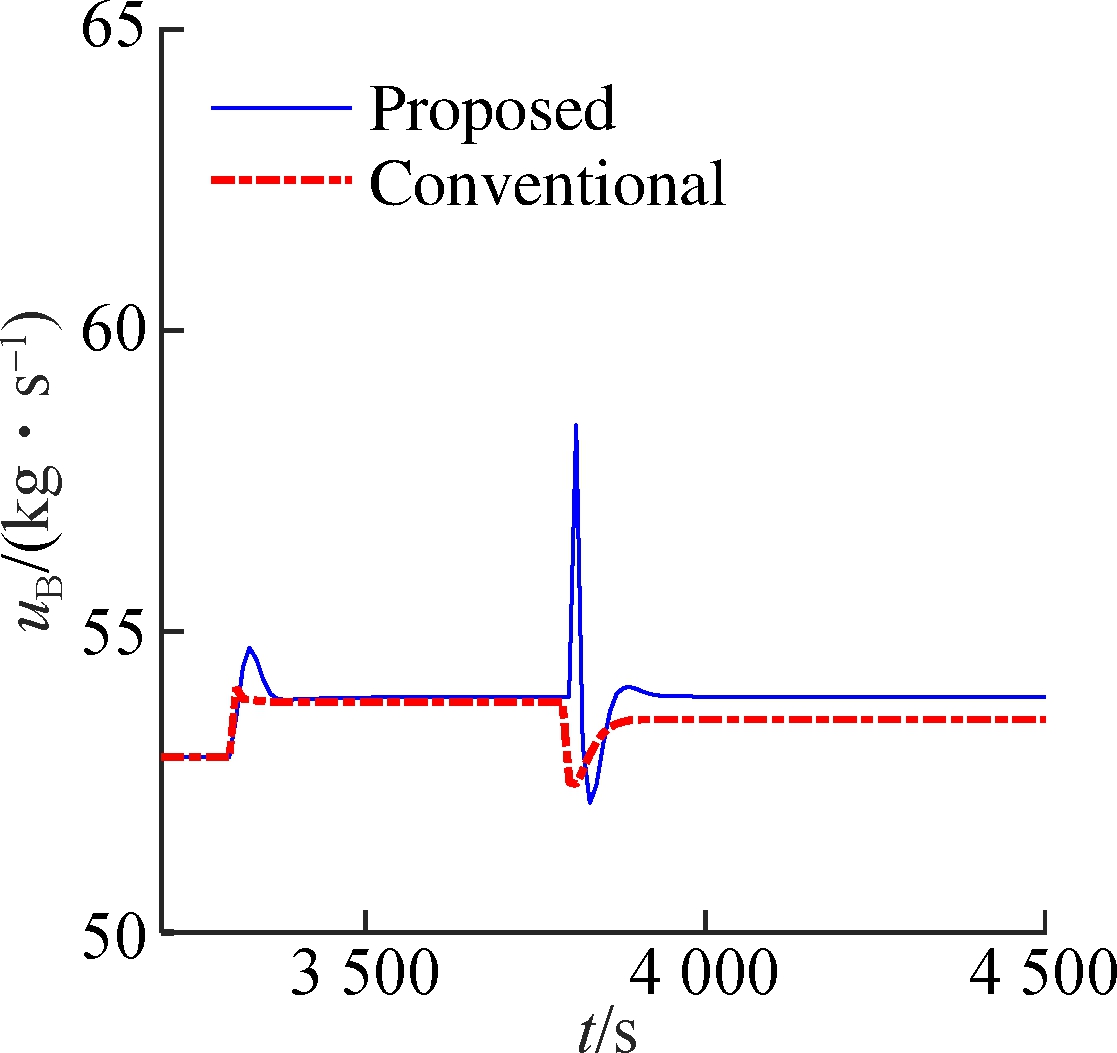
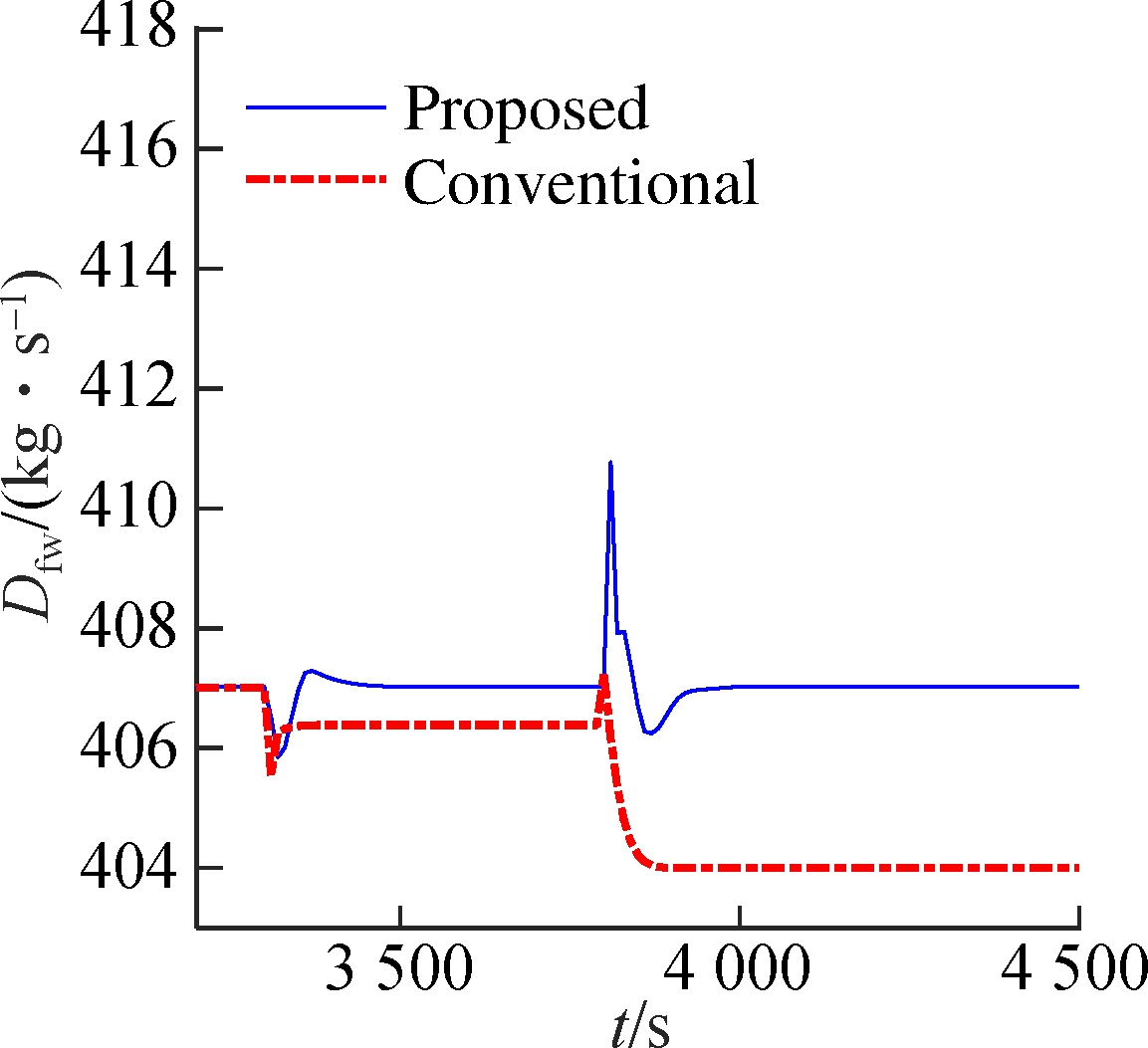
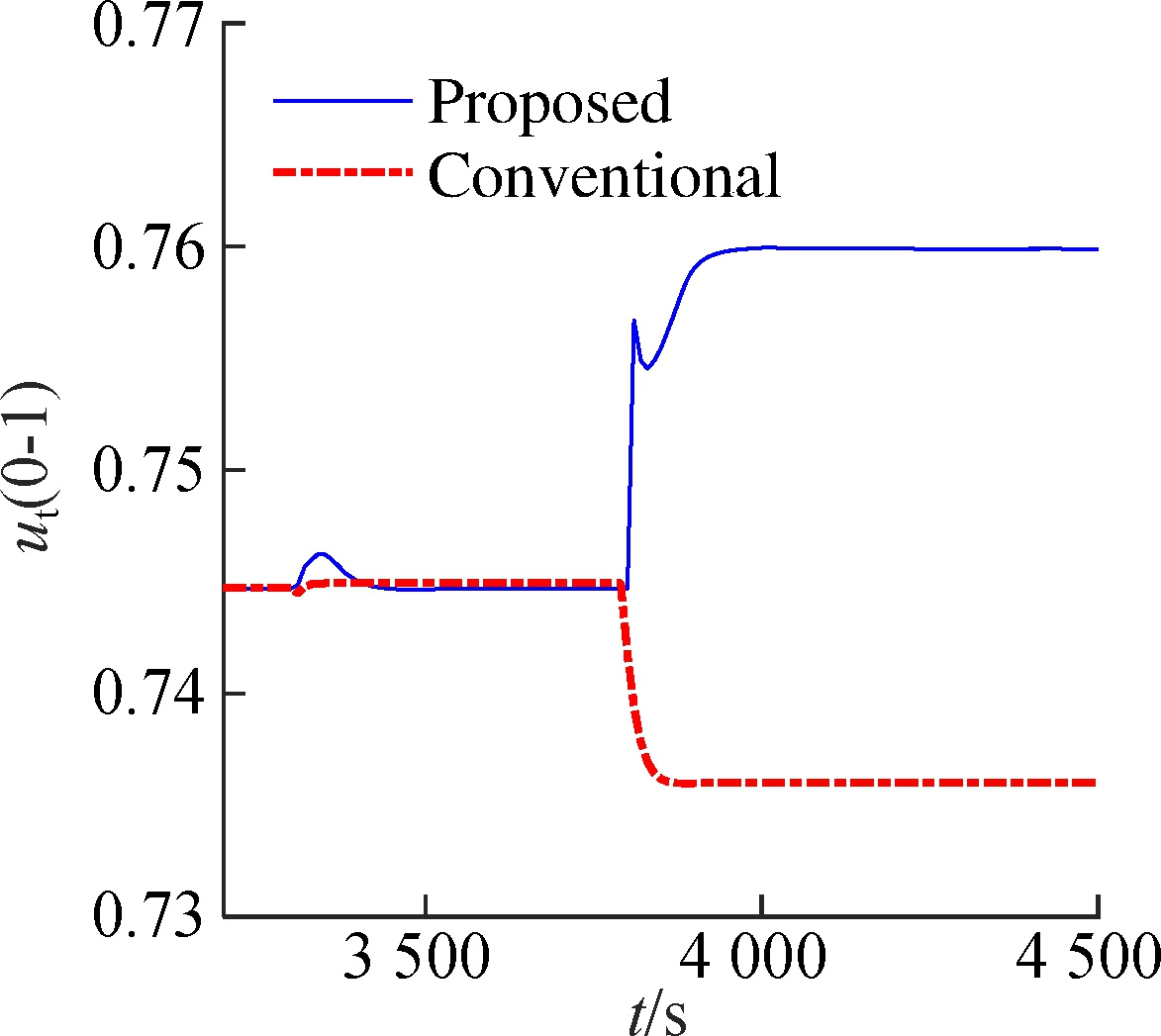
Assume that the system runs at operating point 1# (13.68 MPa, 2 786.1 kJ/kg, 547.56 MW). At 3 300 s, a step-type disturbance d=-1 kg/s is added to the input uB. At t=3 800 s, suppose that the valve has a partial failure ut=0.98ut. The simulation results are given in Fig.3. When disturbances occur, the traditional control method deviates from the set-points because the corresponding xs and us of ys have changed. The proposed method can effectively eliminate the effect of disturbances. The reason is that the observer (7) is equivalent to feedback correction of the state based on the error between the model output and the actual output.
(a)
(b)
(c)
(d)
(e)
(f)
Fig.3 Disturbance rejection performance of the USC boiler-turbine unit.(a) Throttle steam pressure; (b)Separator steam enthalpy; (c) Active power (d) Pulverized coal flow rate; (e) Feedwater flow rate; (f) Turbine throttle opening
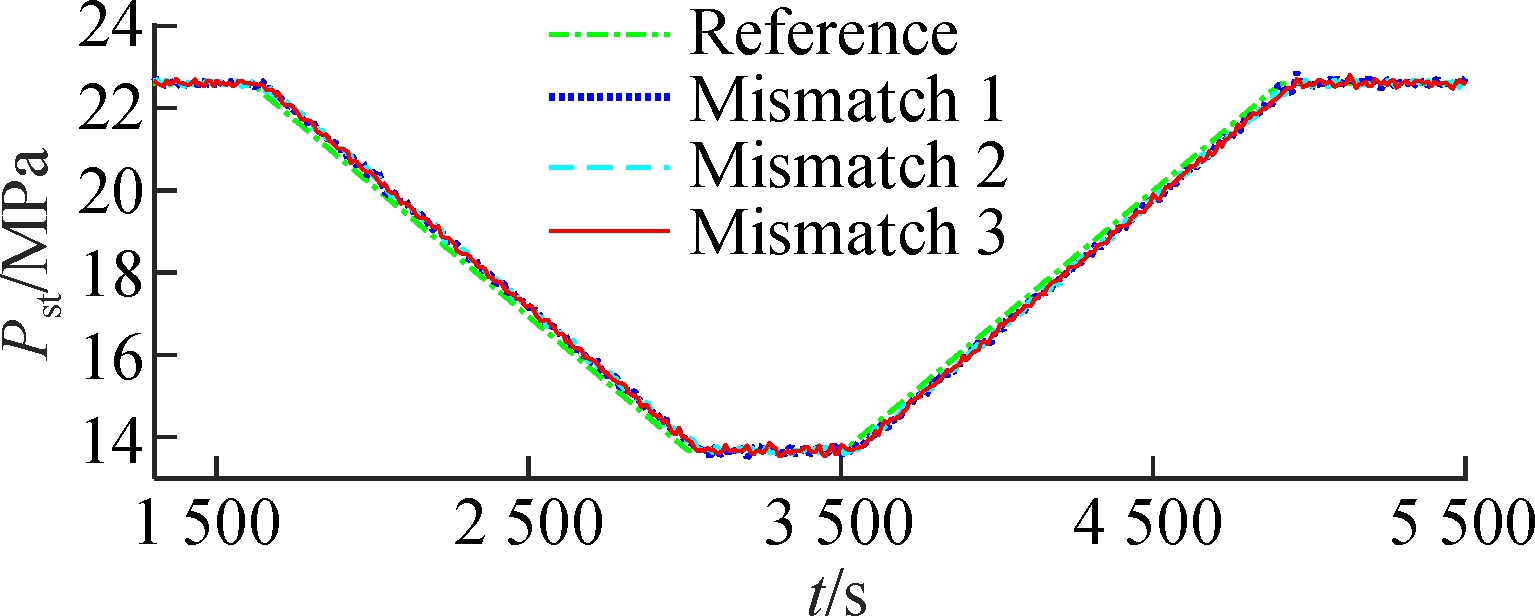
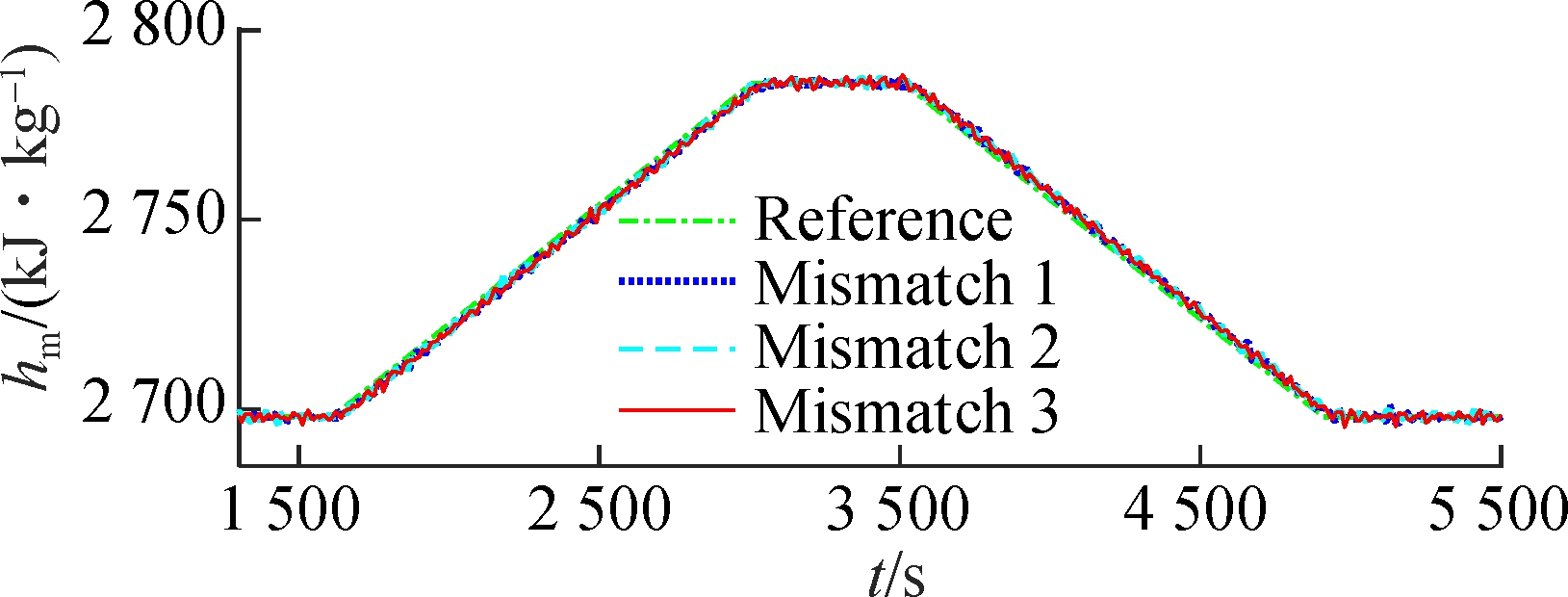
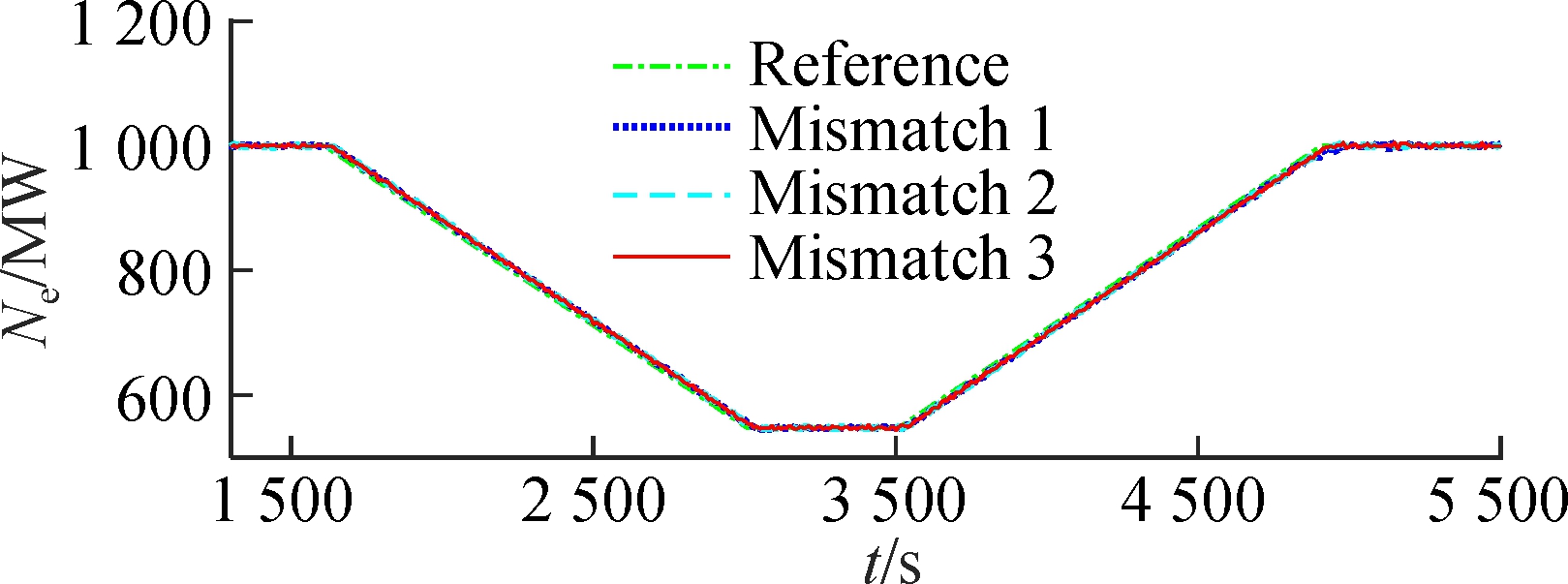
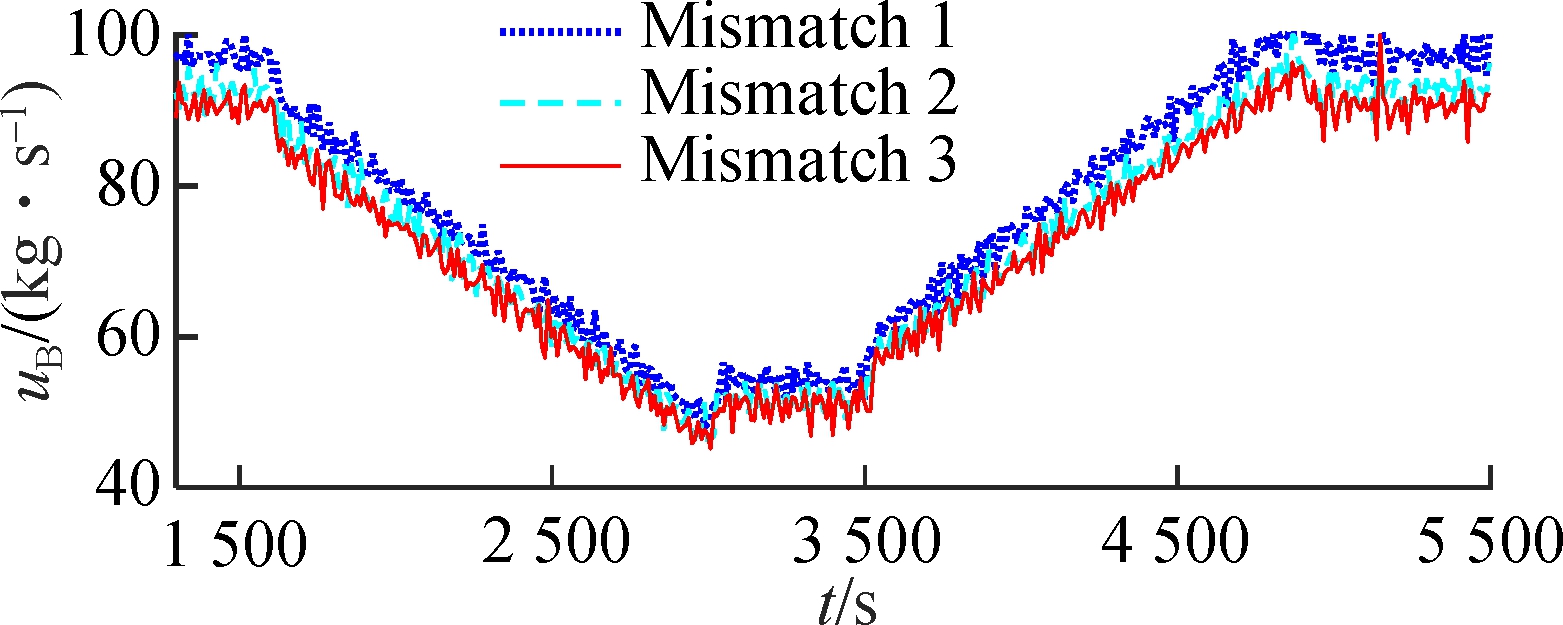
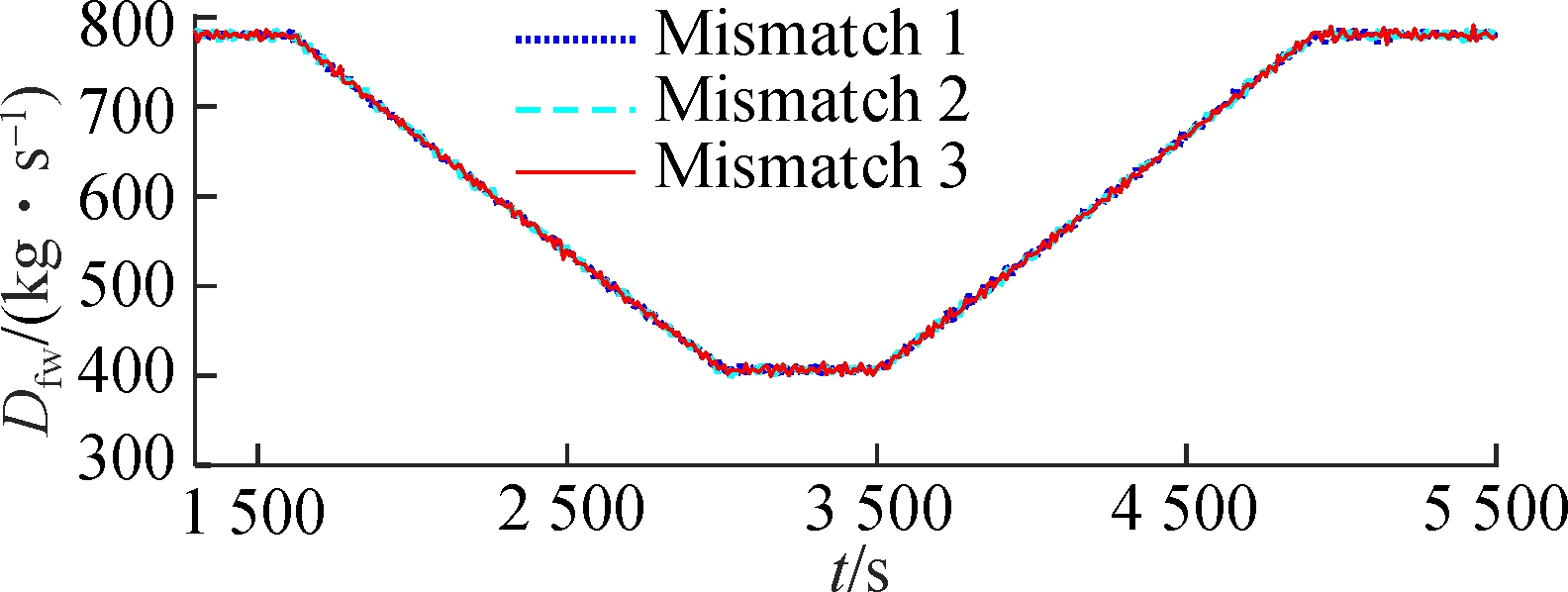
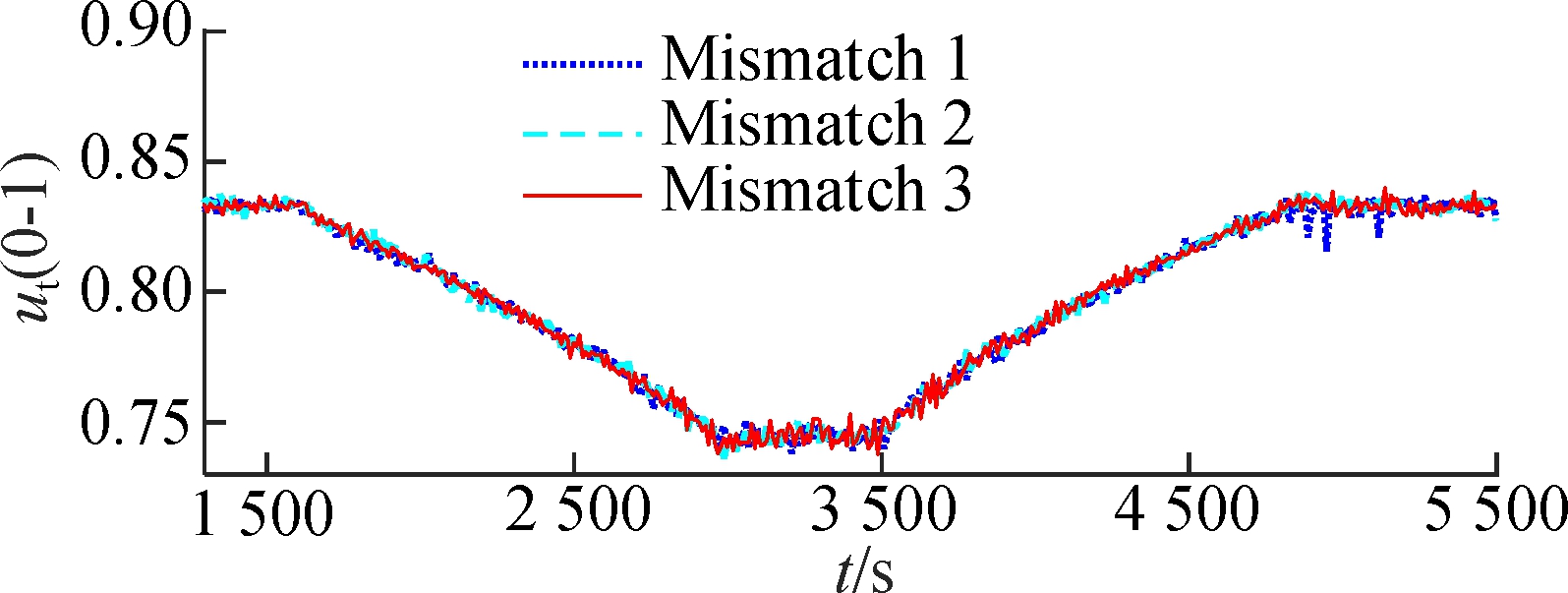
Case 3 is designed to test the robustness of the FMPTC. In the real control system of USC power plants, the mismatch between the model and plant is inevitable. Suppose that the nonlinear model (1) has mismatch 1, mismatch 2, and mismatch 3;that is, all parameters are changed to 99.5%, 100.5%, and 101%of their original values, respectively. Besides, Gaussian white noise with powers of 0.001, 0.14, and 0.1 W is added to the output pst, hm and Ne, respectively. The simulation results are shown in Fig.4. Under model-plant mismatch and Gaussian white noise, the system still maintains a good control performance.
(a)
(b)
(c)
(d)
(e)
(f)
Fig.4 Wide-range load tracking control of the USC boiler-turbine unit under model mismatches and measurement noises.(a) Throttle steam pressure; (b)Separator steam enthalpy; (c) Active power (d) Pulverized coal flow rate; (e) Feedwater flow rate; (f) Turbine throttle opening
The above three cases verify the effectiveness of the proposed control method. The proposed controller is also implemented by solving a set of linear matrix inequalities (LMIs), which is known to be a computationally efficient algorithm.For most sampling points, the controller’s calculation time is between 0.2 s and 0.3 s. The calculation time exceeds 0.4 s but less than 0.5 s during only a few sampling times. The results show that the controller’s calculation time is much shorter than its sampling time, indicating the potential of the controller’s highly good quality in practical applications. MATLAB R2016b is used on our PC(3.3 GHz, Core-i5 CPU, 16 GB memory).
5 Conclusions
1) An improved min-max stable fuzzy model predictive tracking control has been developed for constrained nonlinear ultra-supercritical boiler-turbine systems. The simulation results on the 1 000 MW ultra-supercritical boiler-turbine model verify the effectiveness of the method.
2) The controller that adopts the objective function based on the state and output obtains a higher degree of freedom to adjust the closed-loop system’s behavior and achieves a better control performance.
3) With the help of the extended model and observer, the effects of unknown uncertainties are eliminated because the extended model contains anintegral action and a state observer equivalent to feedback correction.
[1] Pan L, Shen J, Wu X, et al. Improved internal-model robust adaptive control with its application to coordinated control of USC boiler-turbine power units in flexible operations[J].International Journal of Systems Science, 2020, 51(4): 669-686. DOI:10.1080/00207721.2020.1737267.
[2] Chen C, Pan L, Liu S J, et al. A sustainable power plant control strategy based on fuzzy extended state observer and predictive control[J].Sustainability, 2018, 10(12): 4824. DOI:10.3390/su10124824.
[3] Pan L, Luo J, Cao C Y, et al. L1 adaptive control for improving load-following capability of nonlinear boiler-turbine units in the presence of unknown uncertainties[J].Simulation Modelling Practice and Theory, 2015, 57: 26-44. DOI:10.1016/j.simpat.2015.05.012.
[4] Kong X B, Liu X J, Lee K Y. An effective nonlinear multi-variable HMPC for USC power plant incorporating NFN-based modeling[J]. IEEE Transactions on Industrial Informatics, 2016, 12(2): 555-566. DOI:10.1109/TII.2016.2520579.
[5] Moon U C, Lee K Y. Step-response model development for dynamic matrix control of a drum-type boiler-turbine system[J]. IEEE Transactions on Energy Conversion, 2009, 24(2): 423-430. DOI:10.1109/TEC.2009.2015986.
[6] Hou G L, Xi Y, Liu J B, et al. Simulation research of the multi-variable generalized predictive control in 500 MW unit plant coordinated control system[C]//The 2011 International Conference on Advanced Mechatronic Systems. Zhengzhou, China, 2011: 196-201.
[7] Zhang F, Shen J, Li Y G, et al. Nonlinear model predictive control of ultra-supercritical once through boiler-turbine unit[C]//2015 Chinese Automation Congress. Wuhan, China, 2015: 2194-2198. DOI:10.1109/CAC.2015.7382868.
[8] Liu X J, Guan P, Chan C W. Nonlinear multi-variable power plant coordinate control by constrained predictive scheme[J]. IEEE Transactions on Control Systems Technology, 2010, 18(5): 1116-1125. DOI:10.1109/TCST.2009.2034640.
[9] Liu X J, Jiang D, Lee K Y. Quasi-min-max fuzzy MPC of UTSG water level based on off-line invariant set[J]. IEEE Transactions on Nuclear Science, 2015, 62(5): 2266-2272. DOI:10.1109/TNS.2015.2466658.
[10] Cui J H, Chai T Y, Liu X J. Deep-neural-network-based economic model predictive control for ultrasupercritical power plant[J]. IEEE Transactions on Industrial Informatics, 2020, 16(9): 5905-5913. DOI:10.1109/TII.2020.2973721.
[11] Ding B C. Dynamic output feedback predictive control for nonlinear systems represented by a Takagi-Sugeno model[J]. IEEE Transactions on Fuzzy Systems, 2011, 19(5): 831-843. DOI:10.1109/TFUZZ.2011.2147320.
[12] Ding B C, Ping X B. Output feedback predictive control with one free control move for nonlinear systems represented by a Takagi-Sugeno model[J]. IEEE Transactions on Fuzzy Systems, 2014, 22(2): 249-263. DOI:10.1109/TFUZZ.2013.2251637.
[13] Kothare M V, Balakrishnan V, Morari M. Robust constrained model predictive control using linear matrix inequalities[J]. Automatica, 1996, 32(10): 1361-1379. DOI:10.1016/0005-1098(96)00063-5.
[14] Tseng C S, Chen B S, Uang H J. Fuzzy tracking control design for nonlinear dynamic systems via T-S fuzzy model[J]. IEEE Transactions on Fuzzy Systems, 2001, 9(3): 381-392. DOI:10.1109/91.928735.
[15] Wu X, Shen J, Li Y G, et al. Fuzzy modeling and stable model predictive tracking control of large-scale power plants[J]. Journal of Process Control, 2014, 24(10): 1609-1626. DOI:10.1016/j.jprocont.2014.08.007.
[16] Zhang T J, Feng G, Zeng X J. Output tracking of constrained nonlinear processes with offset-free input-to-state stable fuzzy predictive control[J]. Automatica, 2009, 45(4): 900-909. DOI:10.1016/j.automatica.2008.11.016.
[17] Zhang F, Wu X, Shen J. Extended state observer based fuzzy model predictive control for ultra-supercritical boiler-turbine unit[J]. Applied Thermal Engineering, 2017, 118: 90-100. DOI:10.1016/j.applthermaleng.2017.01.111.
[18] Kong L, Yuan J Q. Generalized discrete-time nonlinear disturbance observer based fuzzy model predictive control for boiler-turbine systems[J]. ISA Transactions, 2019, 90: 89-106. DOI:10.1016/j.isatra.2019.01.003.
[19] Wu S, Jin Q B, Zhang R D, et al. Improved design of constrained model predictive tracking control for batch processes against unknown uncertainties[J]. ISA Transactions, 2017, 69: 273-280. DOI:10.1016/j.isatra.2017.04.006.
[20] Zhang R D, Wu S, Cao Z X, et al. A systematic min-max optimization design of constrained model predictive tracking control for industrial processes against uncertainty[J]. IEEE Transactions on Control Systems Technology, 2018, 26(6): 2157-2164. DOI:10.1109/TCST.2017.2748059.
[21] Liu J Z, Yan S, Zeng D L, et al. A dynamic model used for controller design of a coal fired once-through boiler-turbine unit[J]. Energy, 2015, 93: 2069-2078. DOI:10.1016/j.energy.2015.10.077.
[22] Ding B C, Xi Y G, Li S Y. A synthesis approach of on-line constrained robust model predictive control[J]. Automatica, 2004, 40(1): 163-167. DOI:10.1016/j.automatica.2003.07.007.