拟群Hopf群余代数基本原理

In 2000, Turaev[1] introduced, for group π, the notion of a modular crossed π-category and showed that such a category gives rise to a three-dimensional homotopy quantum field theory with target space K(π,1). Examples of π-categories can be constructed from the so-called Hopf π-coalgebras also introduced in Ref.[1]. The notion of a Hopf π-coalgebra generalizes that of a Hopf algebra. Some mathematicians have contributed to the subject[1-7]. The subject of Hopf π-coalgebras continues to grow in some directions. More recent considerations have led to generalizations of the notion of Hopf π-coalgebras.

The authors in Refs.[8-10] proved that, for every Malcev algebra L, there is an algebra U(L) and a monomorphism ι:L→U(L) of L into the commutator algebra U(L) such that the image of L lies into the alternative center of U(L), and U(L) is a universal object with respect to such homomorphisms.

The algebra U(L), in general, is not alternative, but it has a basis of Poincaré-Birkhoff-Witt type over L and inherits some good properties of universal enveloping algebras of Lie algebras. If G is a smooth Moufang loop with Malcev algebra (L,[,]) not of characteristic 2, 3, as tangent spaces of G, then the authors in Ref.[11] showed that the enveloping algebra U(L) is a Moufang Hopf quasigroup with the structure maps Δ:U(L)→U(L)⊗U(L),ε:U(L)→k defined by Δ(x)→x⊗1+1⊗x and ε(x)=0 for all x∈L extended to U(L) as algebra homomorphisms, and S:U(L)→U(L) defined by S(x)=-x extended as an antialgebra homomorphism. Let G act on U(L) by Hopf quasigroup endomorphisms induced by the quasigroup conjugation. Let U(L)G={U(L)α}α∈G, where the algebra U(L)α is a copy of U(L) for each α∈G. Fix an identification isomorphism of algebras iα:U(L)→U(L).

For any α,β∈G, one defines a comultiplication Δα,β:U(L)αβ→U(L)α⊗U(L)β by Δα,β(iαβ(h))=∑iα(h1)⊗iα(h2) for any h∈U(L). The counit ε:U(L)1→k is defined by ε(i1(h))=ε(h) for h∈U(L). For any α∈G, the antipode Sα:U(L)α→U(L)α-1 is given by Sα(iα(h))=iα-1(S(h)). The constructions above give a so-called quasigroup Hopf G-coalgebra in this paper.

The aim of the present paper is to establish the existence of integrals for a quasigroup Hopf π-coalgebras.

Throughout the paper, we let π be a discrete group (with neutral element 1) and k be a field (although much of what we do is valid over any commutative ring). We use the Sweedler notation to express the coproduct of a coalgebra C as Δ(c)=∑c1⊗c2[12]. We set k*=k{0}. All algebras are supposed to be over k and unitary, but not necessarily associative. The tensor product ⊗=⊗k is always assumed to be over k. If U and V are k-spaces, σU,V:U⊗V→V⊗U will denote the flip map defined by σU,V(u⊗v)=v⊗u.

1 Preliminaries

1.1 Group-coalgebras

We recall from Ref.[2] that a π-coalgebra (over k) is a family C={Cα}α∈π of k-spaces endowed with a family Δ={Δα,β:Cαβ→Cα⊗Cβ}α,β∈π of k-linear maps (the comultiplication) and a k-linear map ε:C1→k(the counit) such that Δ is coassociative in the following sense that, for any α,β,γ∈π,

The coassociativity axiom

Note that (C1,Δ1,1,ε) is the usual coalgebra.

We extend the Sweedler notation for a comultiplication in the following way: for any α,β∈π and c∈Cαβ, we write

or shortly, if we leave the summation implicit, Δα,β(c)=c(1,α)⊗c(2,β). The coassociativity axiom gives that, for any α,β,γ∈π, and c∈Cαβγ,

c(1,αβ)(1,α)⊗c(1,αβ)(2,β)⊗c(2,γ)=c(1,α)⊗c(2,βγ)(1,β)⊗c(2,βγ)(2,γ)

The element of Cα⊗Cβ⊗Cγ is written as c(1,α)⊗c(2,β)⊗c(3,γ). By iterating the procedure, we define inductively c(1,α1)⊗…⊗c(n,αn), for any c∈Cα1…αn.

1.2 Convolution algebras

Let C=({Cα},Δ,ε)α∈π be a π-coalgebra and (A,m,1A) be an (not necessarily associative) algebra with multiplication m and unit element 1A. For any f∈Homk(Cα,A) and g∈Homk(Cβ,A), we define their convolution product by

Using the coassociativity axiom and counit axiom, one verifies that the k-space

endowed with the convolution product * and the unit element ε1A, is a not necessarily associative π-graded algebra, called convolution algebra.

In particular, for A=k, the associative π-graded algebra

is called dual to C and is denoted by C*.

1.3 Hopf quasigroups

Recall from Definition 4.1 in Ref.[11] that a Hopf quasigroup is a unital algebra H(possibly nonassociative) equipped with algebra homomorphisms Δ:H→H⊗H,ε:H→k forming a coassociative coalgebra and a map S:H→H such that

Remark 1 A Hopf quasigroup is a Hopf algebra iff its product is associative.

2 Quasigroup Hopf Group-Coalgebras

Definition 1 A quasigroup Hopf group-coalgebra over π is a π-coalgebra H=({Hα}α∈π,Δ={Δα,β:Hαβ→Hα⊗Hβ}α,β∈π,ε), endowed with a family S={Sα:Hα→Hα-1}α∈π of k-linear maps (the antipode) such that the following conditions hold:

Axiom 1 Each (Hα,mα,1α) is not a necessarily associative algebra with multiplication mα and unit element 1α∈Hα.

Axiom 2 For all α,β∈π, Δα,β and ε are algebra homomorphisms .

Axiom 3 For all α∈π,

mα(idHα⊗mα)(Sα-1⊗idHα⊗idHα)(Δα-1,α⊗idHα)=

Axiom 4 For all α∈π,

mα(mα⊗idHα)(idHα⊗Sα-1⊗idHα)(idHα⊗Δα-1,α)=

In this paper, a quasigroup Hopf group-coalgebra over π is called a quasigroup Hopf π-coalgebra. We note that the notion of a quasigroup Hopf π-coalgebra is not self-dual and that (H1,m1,11,Δ1,1,ε,S1) is a (classical) Hopf quasigroup. One can easily verify that a quasigroup Hopf π-coalgebra is a Hopf π-coalgebra if and only if its product is associative.

Definition 2 1) A quasigroup Hopf π-coalgebra H is commutative if each mα is commutative.

2) A quasigroup Hopf π-coalgebra H=({Hα},Δ,ε)α∈π is cocommutative if, for any α∈π,Δα,α-1=σHα-1,HαΔα-1,α, i.e. for any h∈H1, h(1,α)⊗h(2,α-1)=h(2,α)⊗h(1,α-1).

3) A quasigroup Hopf π-coalgebra H=({Hα},Δ,ε)α∈π is the first flexible if

and the second flexible if

4) A quasigroup Hopf π-coalgebra H=({Hα},Δ,ε)α∈π is the first alternative if, for any α∈π,h∈H1,g∈Hα,

and the second alternative if, for any α∈π,h∈H1,g∈Hα,

5) A quasigroup Hopf π-coalgebra H=({Hα},Δ,ε)α∈π is called the first Moufang if, for any α∈π,h∈H1,g,f∈Hα,

and the second Moufang if, for any α∈π,h∈H1,g,f∈Hα,

A quasigroup Hopf π-coalgebra H=({Hα},Δ,ε)α∈π is said to be of finite type if, for all α∈π,Hαis finite dimensional (over k). Note that it does not mean that

is finite-dimensional (unless Hα≠0, for all but a finite number of α∈π).

The antipode S={Sα}α∈π of H is said to be bijective if each Sα is bijective. We will later show that it is bijective whenever H is of finite type [12].

Example 1 Let (H,m,Δ,ε,S) be a Hopf quasigroup and the group π act on H by Hopf quasigroup endomorphisms.

1) Set Hπ={Hα}α∈π where the algebra Hα is a copy of H for each α∈π. Fix an identification isomorphism of algebras iα:H→Hα. For α,β∈π, one defines a comultiplication Δα,β:Hαβ→Hα⊗Hβ by Δα,β(iαβ(h))=∑iα(h1)⊗iβ(h2) for any h∈H. The counit ε:H1→k is defined by ε(i1(h))=ε(h) for h∈H. For any α∈π, the antipode Sα:Hα→Hα-1 is given by Sα(iα(h))=iα-1(S(h)). All the axioms of a quasigroup Hopf π-coalgebra for Hπ follow directly from definitions. Let

be the same family of algebras {Hα=H}α∈π with the same counit, the comultiplication

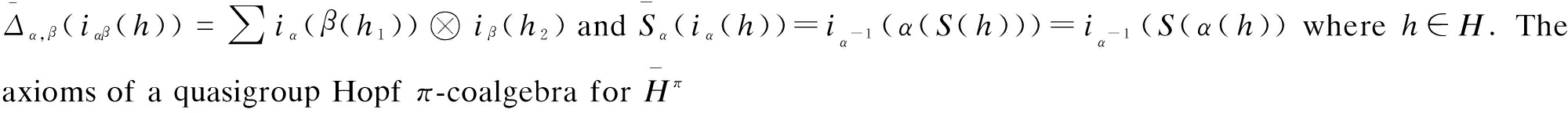and the antipode Sα:Hα→Hα-1 defined by width=733,height=52,dpi=110

follow from definitions. Both Hπ and

as Hopf quasigroups.

2) In particular, if G is a smooth Moufang loop with Malcev algebra (L,[,]) not of characteristic 2, 3, as tangent spaces of G, then the enveloping algebra U(L) in Ref.[12] is a Moufang Hopf quasigroup with the structure maps Δ:U(L)→U(L)⊗U(L),ε:U(L)→k defined by Δ(x)=x⊗1+1⊗x and ε(x)=0 for all x∈L extended to U(L) as algebra homomorphisms, and S:U(L)→U(L) defined by S(x)=-x extended as an antialgebra homomorphism. Let G act on U(L) by Hopf algebra endomorphisms induced by the quasigroup conjugation. The constructions above give a quasigroup Hopf G-coalgebras (U(L))G={U(L)α}α∈G and

where each U(L)α is a copy of U(L) sitting at α∈G.

Theorem 1 Let H be a quasigroup Hopf π-coalgebra. Then

①mα(Sα-1⊗idHα)Δα-1,α=1αε=mα(idHα⊗Sα-1)Δα,α-1, ∀α∈π.

②Sα(ab)=Sα(b)Sα(a),∀α∈π,a,b∈Hα.

③Sα(1α)=1α-1,∀α∈π.

④Δβ-1,α-1Sαβ=σHα-1,Hβ-1(Sα⊗Sβ)Δα,β,∀α,β∈π.

Proof ① is obtained by applying Axiom 3 in the definition of a quasigroup Hopf π-coalgebra to h⊗1α,∀α∈π,h∈H1. We now show 4) as follows:

Δβ-1,α-1Sαβ*Δβ-1,α-1(h)=mβ-1⊗α-1(Δβ-1,α-1Sαβ⊗

Δβ-1,α-1)Δαβ,β-1α-1(h)=Δβ-1,α-1(Sαβ(h(1,αβ)))Δβ-1,α-1·

(h(2,β-1α-1))=Δβ-1,α-1(Sαβ(h(1,αβ))h(2,β-1α-1))=

Δβ-1,α-1(Sαβ*idβ-1α-1(h))=ε(h)Δβ-1,α-1(1β-1α-1)=

ε(h)(1β-1⊗1α-1)

Δβ-1,α-1*σHα-1,Hβ-1(Sα⊗Sβ)Δα,β(h)=

mβ-1⊗α-1(Δβ-1,α-1⊗σHα-1,Hβ-1(Sα⊗Sβ)Δα,β)Δβ-1α-1,αβ(h)=

h(1,β-1)Sβ(h(4,β))⊗h(2,α-1)Sα(h(3,α))=h(1,β-1)Sβ(h(3,β))⊗

ε(h(2,1))1α-1=h(1,β-1)Sβ(h(2,β))⊗1α-1=ε(h)(1β-1⊗1α-1)

Furthermore, for any h∈Hαβ,

σHα-1,Hβ-1(Sα⊗Sβ)Δα,β(h)=ε(1β-1⊗1α-1)*σHα-1,Hβ-1(Sα⊗

Sβ)Δα,β(h)=(Δβ-1,α-1Sαβ*Δβ-1,α-1)*σHα-1,Hβ-1(Sα⊗Sβ)·

Δα,β(h)=(Sαβ(h(1,αβ))(1,β-1)h(2,β-1))Sβ(h(5,β))⊗

(Sαβ(h(1,αβ))(2,α-1)h(3,α-1))Sα(h(4,α))=

(Sαβ(h(1,αβ))(1,β-1)h(2,β-1))Sβ(h(4,β))⊗(Sαβ(h(1,αβ))(2,α-1)ε(h(3,1))) (by Axiom 4)=

(Sαβ(h(1,αβ))(1,β-1)h(2,β-1))Sβ(h(3,β))⊗Sαβ(h(1,αβ))(2,α-1)=

ε(h(2,1))(Sαβ(h(1,αβ))(1,β-1)⊗Sαβ(h(1,αβ))(2,α-1))=

ε(h(2,1))Δβ-1,α-1Sαβ(h(1,αβ))=Δβ-1,α-1Sαβ(h)

Thus,Δβ-1,α-1Sαβ=σHα-1,Hβ-1(Sα⊗Sβ)Δα,β,∀α,β∈π.

To show ②, we observe that

Sα(ab)=ε(b(1,1))Sα(ab(2,α))=

Sα(b(1,1)(1,α))(b(1,1)(2,α-1)Sα(ab(2,α)))=

Sα(b(1,1)(1,α))(ε(a(1,1))(b(1,1)(2,α-1))Sα((a(2,α))b(2,α)))=

Sα(b(1,1)(1,α))((Sα(a(1,1)(1,α))(a(1,1)(2,α-1)b(1,1)(2,α-1)))Sα·

Sα(b(1,α))((Sα(a(1,α))(a(2,α-1)b(2,α-1)))Sα(a(3,α)b(3,α)))=

Sα(b(1,α))((Sα(a(1,α))(a(2,1)b(2,1))(1,α-1))Sα·

((a(2,1)b(2,1))(2,α))=

Sα(b(1,α))(Sα(a(1,α))ε(a(2,1)b(2,1)))=

Sα(b(1,α))Sα(a(1,α))ε(a(2,1))ε(b(2,1))=Sα(b)Sα(a)

Thus, Sα

mα=mα

σHα,Hα

(Sα⊗Sα),∀α∈π,a,b∈Hα.

Finally, it is easy to obtain ③ and ⑤ by ①.

This completes the proof.

Corollary 1 Let H=({Hα}α∈π,Δ,ε) be a quasigroup Hopf π-coalgebra with the antipode S={Sα}α∈π. Then, Sα is the unique convolution inverse of idHα-1 in the convolution algebra Conv(H,Hα-1), for all α∈π.

Proof Theorem 1① says that Sα is a convolution inverse of idHα-1 in the convolution algebra Conv(H,Hα-1), for all α∈π.

Fix α∈π. Let Tα be a right convolution inverse of idHα-1 in the convolution algebra Conv(H,Hα-1). For all h∈Hα,

Sα(h)=Sα*(idHα-1*Tα)(h)=

Sα(h(1,α))(idHα-1*Tα)(h(2,1))=

Sα(h(1,α))(h(2,α-1)Tα(h(3,α)))=ε(h(1,1))Tα(h(2,α)))=

Tα(ε(h(1,1))h(2,α)))=Tα(h)

Fix α∈π. Let Tα now be a left convolution inverse of idHα-1 in the convolution algebra Conv(H,Hα-1). For all h∈Hα, similarly we have,

Sα(h)=(Tα*idHα-1)*Sα(h)=

(Tα*idHα-1)(h(1,1))Sα(h(2,α))=

(Tα(h(1,α))h(2,α-1))Sα(h(3,α))=Tα(h(1,α))ε(h(2,1))=

Tα(h(1,α)ε(h(2,1)))=Tα(h)

and thus, Tα=Sα. Therefore, Sα is the unique convolution inverse of idHα-1 in the convolution algebra Conv(H,Hα-1), for all α∈π. This completes the proof.

Corollary 2 Let H be a quasigroup Hopf π-coalgebra with the antipode S={Sα}α∈π. Then, Δβ-1,α-1Sαβ is the unique convolution inverse of Δβ-1,α-1 in the convolution algebra Conv(H,Hβ-1⊗Hα-1), for all α,β∈π.

Proof One can see directly from the proof of Theorem 1(4) that Δβ-1,α-1Sαβ is a convolution inverse of Δβ-1,α-1 in the convolution algebra Conv(H,Hβ-1⊗Hα-1), for all α,β∈π. Fix α,β∈π. Let Tβ-1,α-1 be a right convolution inverse of Δβ-1,α-1 in the convolution algebra Conv(H,Hβ-1⊗Hα-1).

We write Tβ-1,α-1(h):=Tβ-1(h)1⊗Tα-1(h)2. For all h∈Hαβ, we have

Δβ-1,α-1Sαβ(h)=Δβ-1,α-1Sαβ*(Δβ-1,α-1*Tβ-1,α-1)(h)=

(Sβ(h(2,β))⊗Sα(h(1,α)))((h(3,β-1)⊗h(4,α-1))Tβ-1,α-1

(h(5,αβ)))=(Sβ(h(2,β))⊗

Sα(h(1,α)))((h(3,β-1)⊗h(4,α-1))(Tβ-1(h(5,αβ))1⊗

Tα-1(h(5,αβ))2))=Sβ(h(2,β))(h(3,β-1)Tβ-1(h(5,αβ))1)⊗

Sα(h(1,α))(h(4,α-1)Tα-1(h(5,αβ))2)=

ε(h(2,1))Tβ-1(h(4,αβ))1⊗Sα(h(1,α))(h(3,α-1)Tα-1(h(4,αβ))2)

Tβ-1(h(3,αβ))1⊗Sα(h(1,α))(h(2,α-1)Tα-1(h(3,αβ))2)=

Tβ-1(h(2,αβ))1⊗ε(h(1,1))Tα-1(h(2,αβ))2=

ε(h(1,1))Tβ-1,α-1(h(2,αβ))=Tβ-1,α-1(h)

which implies that Δβ-1,α-1Sαβ=Tβ-1,α-1. Fix α,β∈π. Let Tβ-1,α-1 be a left convolution inverse of Δβ-1,α-1 in the convolution algebra Conv(H,Hβ-1⊗Hα-1). In a similar manner, we can deduce by Axiom 4 that Δβ-1,α-1Sαβ=Tβ-1,α-1.

Δβ-1,α-1Sαβ is thus the unique convolution inverse of Δβ-1,α-1 in the convolution algebra Conv(H,Hβ-1⊗Hα-1), for all α,β∈π. This completes the proof.

Corollary 3 According to Theorem 1①, each quasigroup Hopf π-coalgebra is both the first alternative and the second alternative.

Corollary 4 Let H={Hα}α∈π be a quasigroup Hopf π-coalgebra. Then, {α∈π|Hα≠0} is a subgroup of π.

Proof Set G={α∈π|Hα≠0}. Since ε(11)=1k≠0, we first have 11≠0,i.e.H1≠0, and so 1∈G. Then, let α,β∈G. Using Axiom 2, one can also see that Δα,β(1αβ)=1α⊗1β≠0. Then, 1αβ≠0 and so αβ∈G. Finally, let α∈G. By Theorem 1③, Sα-1(1α-1)=1α≠0. Thus, 1α-1≠0 and hence, α-1∈G. This completes the proof.

Theorem 2 Let H be a quasigroup Hopf π-coalgebra. Then, for any α∈π, Sα-1Sα=idHα if H is commutative or cocommutative.

Proof For any α∈π. Let h∈Hα. If H is commutative, we have

Sα-1Sα(h(1,α))(Sα-1(h(2,α-1))h(3,α))=

Sα-1(Sα(h(1,1)(1,α)))(Sα-1(h(1,1)(2,α-1))h(2,α))=

Sα-1(S1(h(1,1))(2,α-1))(S1(h(1,1))(1,α)h(2,α))=

(h(2,α)S1(h(1,1))(1,α))Sα-1(S1 (h(1,1))(2,α-1))=

ε(S1(h(1,1)))h(2,α)=ε(h(1,1))h(2,α)=h

It follows that Sα-1Sα=idHα.

If H is cocommutative, we find that

Sα-1Sα(h(1,α))ε(h(2,1))=

Sα-1Sα(h(1,α))(Sα-1(h(2,α-1))h(3,α))=

Sα-1(Sα(h(1,1)(1,α)))(Sα-1(h(1,1)(2,α-1))h(2,α))=

Sα-1(S1(h(1,1))(2,α-1))(S1(h(1,1))(1,α)h(2,α))=

Sα-1(S1(h(1,1))(1,α-1))(S1(h(1,1))(2,α)h(2,α))=

ε(S1(h(1,1)))h(2,α)=ε(h(1,1))h(2,α)=h

It also follows that Sα-1Sα=idHα. This completes the proof.

[1] Turaev V. Homotopy field theory in dimension 3 and crossed group-categories[J/OL]. arXiv: math/0005291.2000. https: //arxiv.org/abs/math/0005291.

[2] Virelizier A. Hopf group-coalgebras[J].Journal of Pure and Applied Algebra, 2002, 171(1): 75-122. DOI:10.1016/S0022-4049(01)00125-6.

[3] Wang S H. Group twisted smash products and doi-Hopf modules for T-coalgebras[J].Communications in Algebra, 2004, 32(9): 3417-3436. DOI:10.1081/AGB-120039402.

[4] Wang S H. Group entwining structures and group coalgebra Galois extensions[J].Communications in Algebra, 2004, 32(9): 3437-3457. DOI:10.1081/AGB-120039403.

[5] Wang S H. A Maschke type theorem for Hopf π-comodules[J]. Tsukuba Journal of Mathematics, 2004, 28(2): 377-388. DOI:10.21099/tkbjm/1496164806.

[6] Zunino M. Double construction for crossed Hopf coalgebras[J].Journal of Algebra, 2004, 278(1): 43-75. DOI:10.1016/j.jalgebra.2004.03.019.

[7] Zunino M. Yetter-Drinfeld modules for crossed structures[J].Journal of Pure and Applied Algebra, 2004, 193(1/2/3): 313-343. DOI:10.1016/j.jpaa.2004.02.014.

[8] Pérez-Izquierdo J M, Shestakov I P. An envelope for Malcev algebras[J].Journal of Algebra, 2004, 272(1): 379-393. DOI:10.1016/S0021-8693(03)00389-2.

[9] Pérez-Izquierdo J M. An envelope for Bol algebras[J].Journal of Algebra, 2005, 284(2): 480-493. DOI:10.1016/j.jalgebra.2004.09.038.

[10] Pérez-Izquierdo J M. Algebras, hyperalgebras, nonassociative bialgebras and loops[J].Advances in Mathematics, 2007, 208(2): 834-876. DOI:10.1016/j.aim.2006.04.001.