Given greater demands for fuel economy, energy conservation, and emission reduction in oil-fueled automobiles, technologies that can reduce friction power losses (FPLs) to improve the power of internal combustion engines (ICE) is a major concern for designers. The main causes of engine power loss include the friction between the piston skirt and the ring against the cylinder bore during motion and the friction between moving surface pairs of joints in the slider-crank mechanism (SCM) [1-3].
Studies on the influence of various SCM design parameters, the inertial mass of the piston, and the eccentricity between the crankshaft and cylinder centers on the horizontal impact force of the piston in the cylinder bore have been carried out over the last few decades[4-6]. Friction and noise vibration between the piston skirt and ring around the cylinder bore could significantly be reduced by optimizing the structure of the SCM. Optimization studies have also investigated the characteristics of lubrication factors, such as the friction force F and friction coefficient μ, between the moving surfaces of a piston and cylinder[1-2,6-7]. Researchers have found that FPLs are significantly reduced when a stable oil film exists on the lubricating surfaces.
The lubrication model of crankpin bearings (CBs) under an external load acting on the shaft moving at high speed was previously studied to illustrate the stability of the lubricating oil film thickness h on the friction surface pairs of the engine[8-10] according to the evaluation indices of load bearing capacity (LBC) and F. Results showed that the stability of h greatly depends on the pressure generated by the oil film. The effects of several factors, such as the temperature[11], radial clearance[7, 12-13], and load and speed of the shaft, on the oil film pressure have also been discussed [9-11,14]. Previous studies mainly assessed the lubrication efficiency (LE) of the CB under the condition of a static load on a shaft moving at high speed. In actual applications, the shear stress of the oil film generated under various speeds and the dimensions of the CB could affect the resistance of the oil film. Moreover, in the working cycle of an ICE, the dynamic load acting on the CB changes very quickly under various engine speeds ω in terms of direction and intensity. Therefore, the effects of ω and CB dimensions should be taken into account during analyses of the LE-FPL of an engine. However, investigations on the LE-FPL of engines considering ω and CB dimensions together have rarely been reported.
The current study establishes a new numerical method by coupling the SCM dynamic and CB lubrication models to investigate their effect on the LE-FPL of an engine. An algorithm program based on the hybrid model was developed in MATLAB, and numerical simulations were performed to solve the hydrodynamic equations of the SCM and CB. The LBC, F, μ, and eccentricity ratio ε between the shaft and bearing were then selected as objective functions. Finally, the influence of ω, bearing radius rb, and bearing width B on the LE-FPL was clarified.
1 SCM Dynamic and CB Lubrication Models
1.1 SCM dynamic model
Assuming that the center of a crankshaft coincides with the cylinder center, the SCM dynamic model can be established as shown in Fig.1. Here, L and R are the connecting rod length and rotation radius of the crankshaft, respectively; P is the combustion gas pressure acting on the piston peak; N and Fc are the piston forces impacting on the cylinder wall and connecting rod, respectively; F is the total force of the piston; Fic, Fc1, and Fc2 are the respective centrifugal inertial, radial, and tangent forces of the large-rod-end mass of the connecting rod impacting on the CB; Fip is the inertial force of the small-rod-end and piston; W0 is the impacting force on the CB; and φ and ω are the respective angle and angular velocity of the crankshaft.
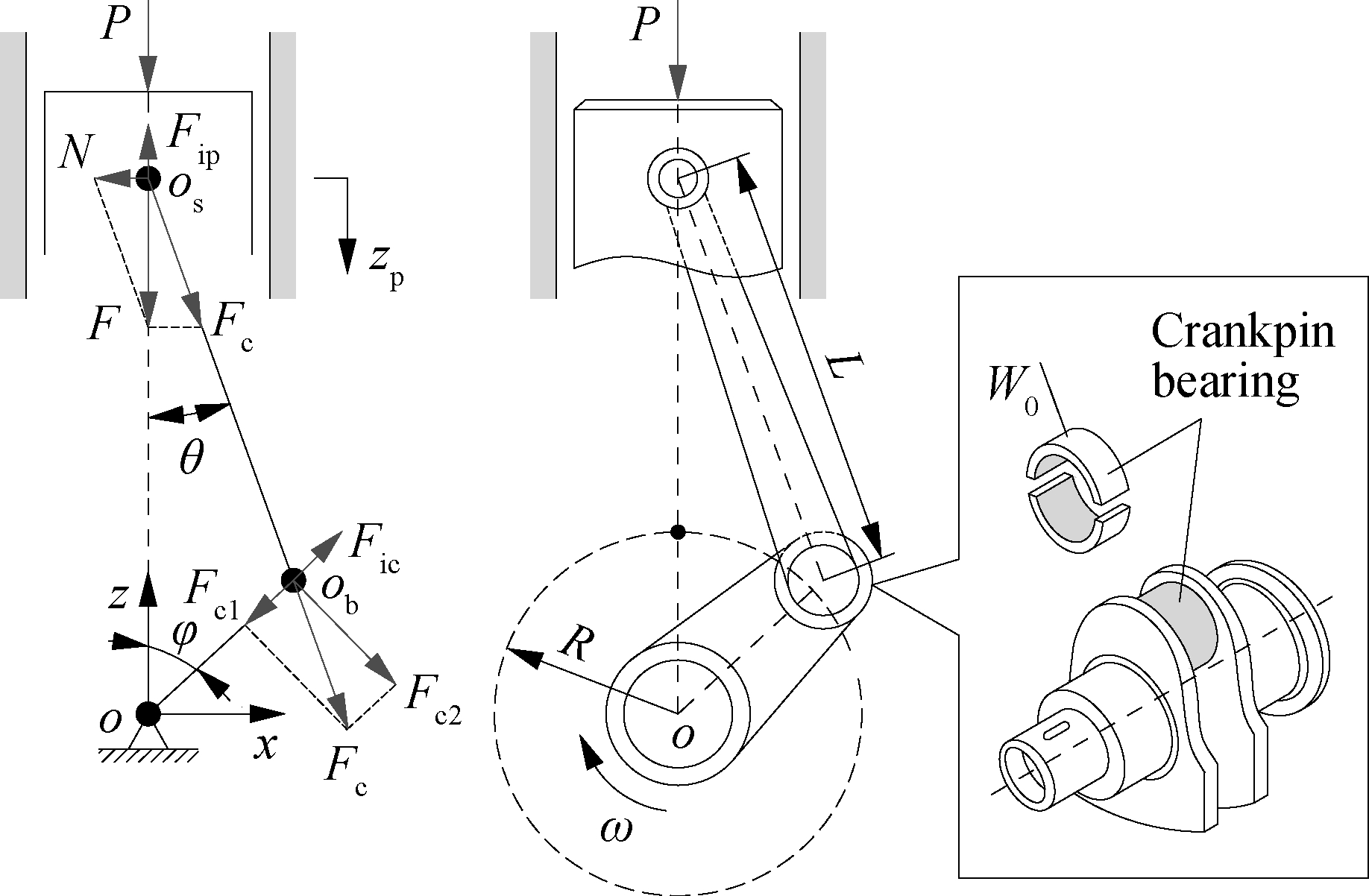
(a)(b)
Fig.1 SCM model and its lubrication joints. (a) SCM dynamic system; (b) Lubrication joints
The piston’s motion can be determined as
zp=L+R-Rcosφ-Lcosθ
(1)
The kinematic relation of SCM can be determined by
(2)
where λ=R/L is the ratio between the rotation radius of the crankshaft and the length of the connecting rod.
Substituting Eq.(2) into Eq.(1), the piston’s motion and acceleration can be rewritten as
(3)
(4)
msc and mbc are assumed to be the lumped masses of the small- and large-rod-ends of the connecting rod at os and ob, respectively. Thus, the Fip of the small-rod-end and piston is written as
Fip=-(msc+mp)Rω2(cosφ+λcos2φ)
(5)
where mp is the piston mass.
Under the impact of P on the piston peak, the dynamic forces impacting the cylinder wall and connecting rod can be determined by
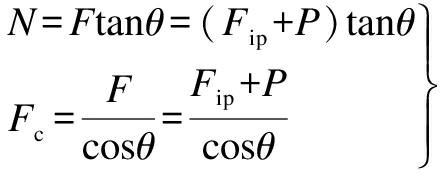
(6)
The impact of Fc, which has two components of tangential and radial forces, on the CB is determined by
(7)
The large-rod-end mass of the connecting rod is rotated with ω, and its Fic can be defined as
Fic=-mbcRω2
(8)
The bearing of the connecting rod provides a rotating motion and transmits loads between the large-rod-end and crankpin. Thus, the dynamic load W0 of the connecting rod impacting on the CB is determined by
(9)
Changes in W0 in both direction and intensity could be applied to analyze the LE-FPL of the CB.
1.2 CB lubrication model
1.2.1 Lubrication model in the computational region
In the working cycle of the engine, the crankpin is impacted by W0 and rotated with an angular velocity ω inside the bearing of the connecting rod, as shown in Fig.1. Therefore, the LE-FPL of the CB could be evaluated by modeling the crankpin under the impact of W0 and rotated at ω inside the bearing as shown in Fig.2.
In Fig.2, B and rb are the bearing width and radius, respectively; rs is the shaft radius and rs<rb; e and ε=e/c (0<ε<1) are the eccentricity and eccentricity ratio between the center of the bearing and shaft, respectively; c=rb-rs is the radial clearance between the shaft and bearing fully filled with the lubricant to create the hydrodynamic pressure p; u0=ωrb is the relative velocity between the CB surfaces; and ψ is the attitude angle. Then, h can be determined from the CB lubrication model as
h=rb-rs+ecosφ=c(1+εcosφ)
(10)
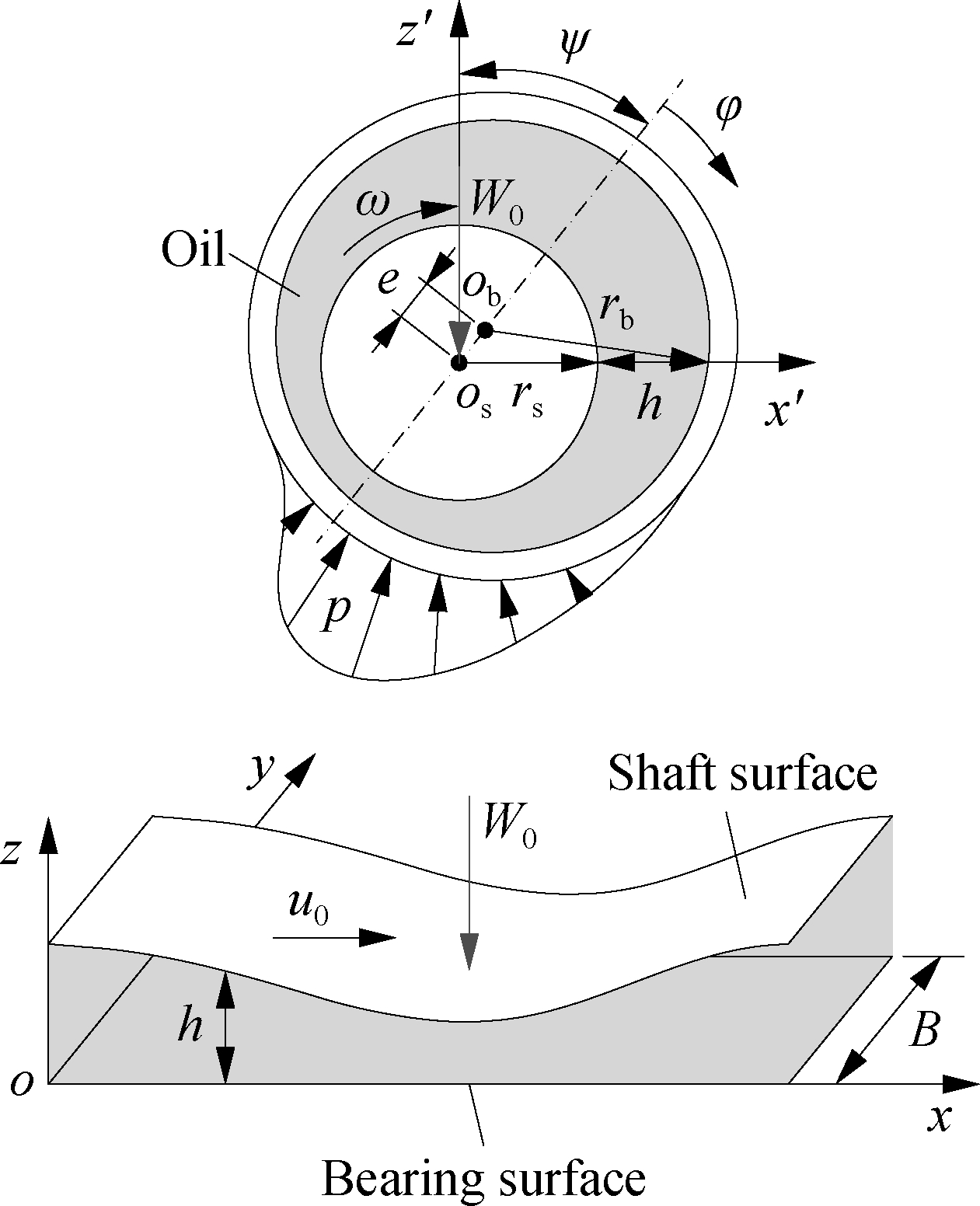
Fig.2 The CB hydrodynamic model
1.2.2 Application of the Reynolds equations
Assume that the bearing surface is fixed in the x- and y-directions and that the shaft surface only moves with a constant velocity u0 in the x-direction, as seen in Fig.2. The boundary conditions of the fluid velocity on the CB surface in the x- and y-directions are determined by
(11)
The lubricant density and viscosity are also assumed to be constant, and the influence of the inertia of the lubricant flow on the working process is negligible. Therefore, the pressure distribution of the lubrication film can be described as [11, 15]
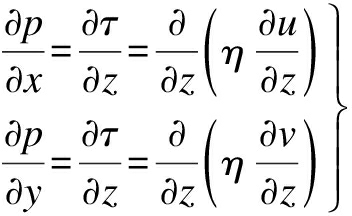
(12)
Taking the second integral of Eq.(12) with respect to z and considering the initial conditions in Eq.(11), the velocity fluid equations are written as

(13)
where η is the dynamic viscosity of the oil film.
The volumetric flows of qx and qy in the x- and y-directions are calculated by integrating Eq.(13) over the z-direction and written as

The equation of the fluid continuity condition is given by
(15)
where ρ is the fluid density; u and v are the fluid velocities in the x- and y-directions, respectively, as determined in Eq.(13); ![]() is the fluid velocity in the z-direction.
is the fluid velocity in the z-direction.
![]() 0 and ρ is a constant. Thus, the integral of Eq.(14) in the z-direction is
0 and ρ is a constant. Thus, the integral of Eq.(14) in the z-direction is
(16)
In Eq.(10), the oil film thickness h is constantly changing according to the rotation angle φ. Thus, the substitution of Eq.(14) into (16) and mathematical transformation lead to a new form of Eq.(16) [16-17],
(17)
The dimensionless form of the Reynolds equation in Eq.(17) can be expressed as
(18)
where β=B/rb, H=h/c, φ=x/rb, Y=y/B, P=p/p0, T=t/t0, Π=6ηωB2/(c2p0), Λ=12ηB2/(c2p0t0), and p0=101.325 kPa.
The boundary conditions must be determined to obtain the pressure distribution of the oil film over the computational domain of Eq.(17). In this study, we assume that h exists over the CB surfaces and that the inlet and outlet lubricants are at the maximum position of h. The ambient pressure around the CB and the inlet and outlet pressures are equal to the atmospheric pressure p0. The computational region Γ of the CB is plotted in Fig.3. Here, i and f are the respective boundary lines of the initial and final pressures at the maximum position of h corresponding to φ = 0° and 360°, and r and l are the respective boundary lines of the right and left pressures of the bearing at y=0 and B.
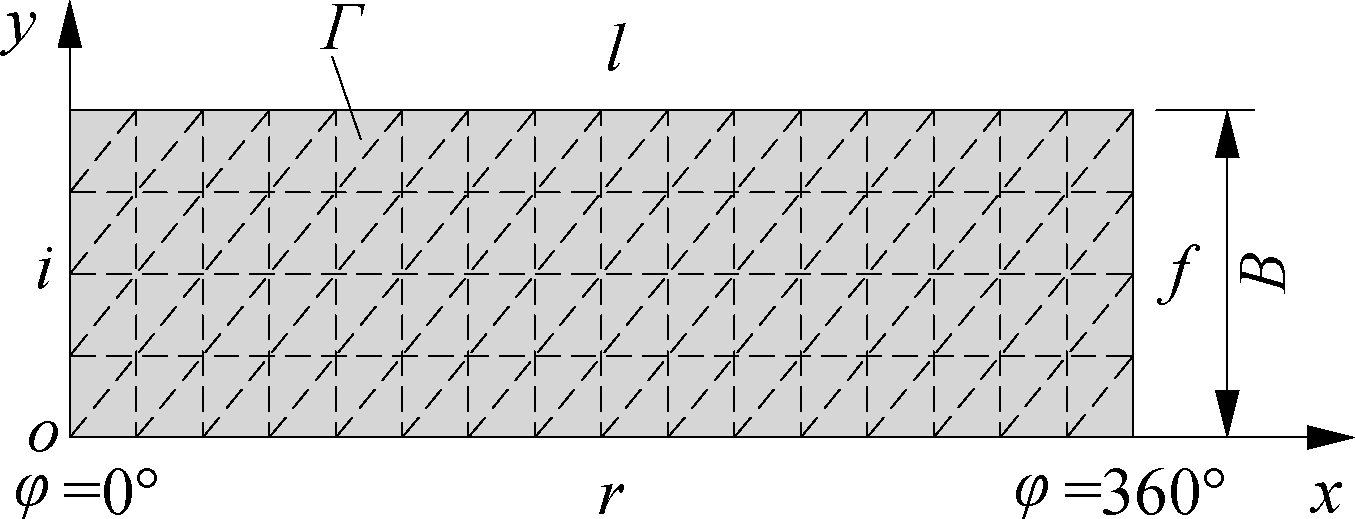
Fig.3 CB computational region and meshing diagram
The boundary conditions of the oil film pressure can be written as
(19)
In general, the oil film in the small gap of the CB can usually be divided into the liquid and cavitation zones when the oil film is ruptured[11]. Because negative pressure due to gas dissolution and cavitation effects exists, Eq.(17) above cannot be used to calculate the cavitation region [18-19]. Thus, instead of ignoring negative pressures in the cavitation zone, only pressures below the saturation pressure ps are varied to achieve the effective pressure pe [15]. The oil film pressure in the cavitation zone can then be expressed as
(20)
1.2.3 Lubrication forces of mixed hydrodynamics
Under the impact of W0 on the CB, the LBC of the oil film pressure generated in Γ can be determined by [16]
(21)
where load bearing capacity W equals the dynamic load W0 on the CB.
F generated from the interfacial shear stress τ acting on the shaft in Γ can be calculated by[17]
(22)
When W and F are obtained, the μ of the CB can be given by [15]
(23)
In this study, the W, F, μ, and ε between the shaft and bearing are selected as indices to evaluate the LE-FPL of the engine.
2 Algorithm
An algorithm written in MATLAB was used to estimate the objective functions and solve the equations of the system models. The simulation process includes three main steps as follows.
Step 1 The initial parameters that must be set include the dimensions of the SCM and CB, the combustion pressure on the piston peak, the zero matrices of the oil film pressure and shear stress (a×b), and the zero matrices of the force vectors (1×b). The W0 and coefficients of Eq.(18) are then calculated, and the initial pressure and shear stress matrices are also determined. Herein, the number of grid nodes is a=b=120.
Step 2 When the pressure and shear stress have been determined, the initial LE-FPL can be obtained. In theory, W equals W0. However, in actual conditions, W is not in equilibrium with W0; thus, the computational algorithm cannot give the stopping condition for the computational process. This issue is addressed by setting a stopping condition of W0-W0 ≤ζ with a very small value of ζ. Reaching the stop condition means that the difference between Wb and W0 is very small. In this case, the distribution of the oil film pressure and shear stress in Γ and ε between the journal and bearing are considered acceptable, and the computational algorithm is stopped. The computational algorithm is continuously performed until the stopping condition is satisfied.
Step 3 The time required to complete a cycle of the engine corresponding to a crankshaft rotation angle of 720° is t0. Parameter t0 is divided into 120 equal parts, and t refers to each time node corresponding to a crankshaft rotational angle of t′=6°. The oil film pressure and shear stress are calculated at each time t, and the computational algorithm is continued for the next loop at t=t+t′ until t≥t0. The complete computational algorithm and objective functions of the LE-FPL are finally obtained. A schematic of the calculation process is provided in Fig.4.

Fig.4 Flowchart of the algorithm of the computational model
3 Simulation Results and Analysis
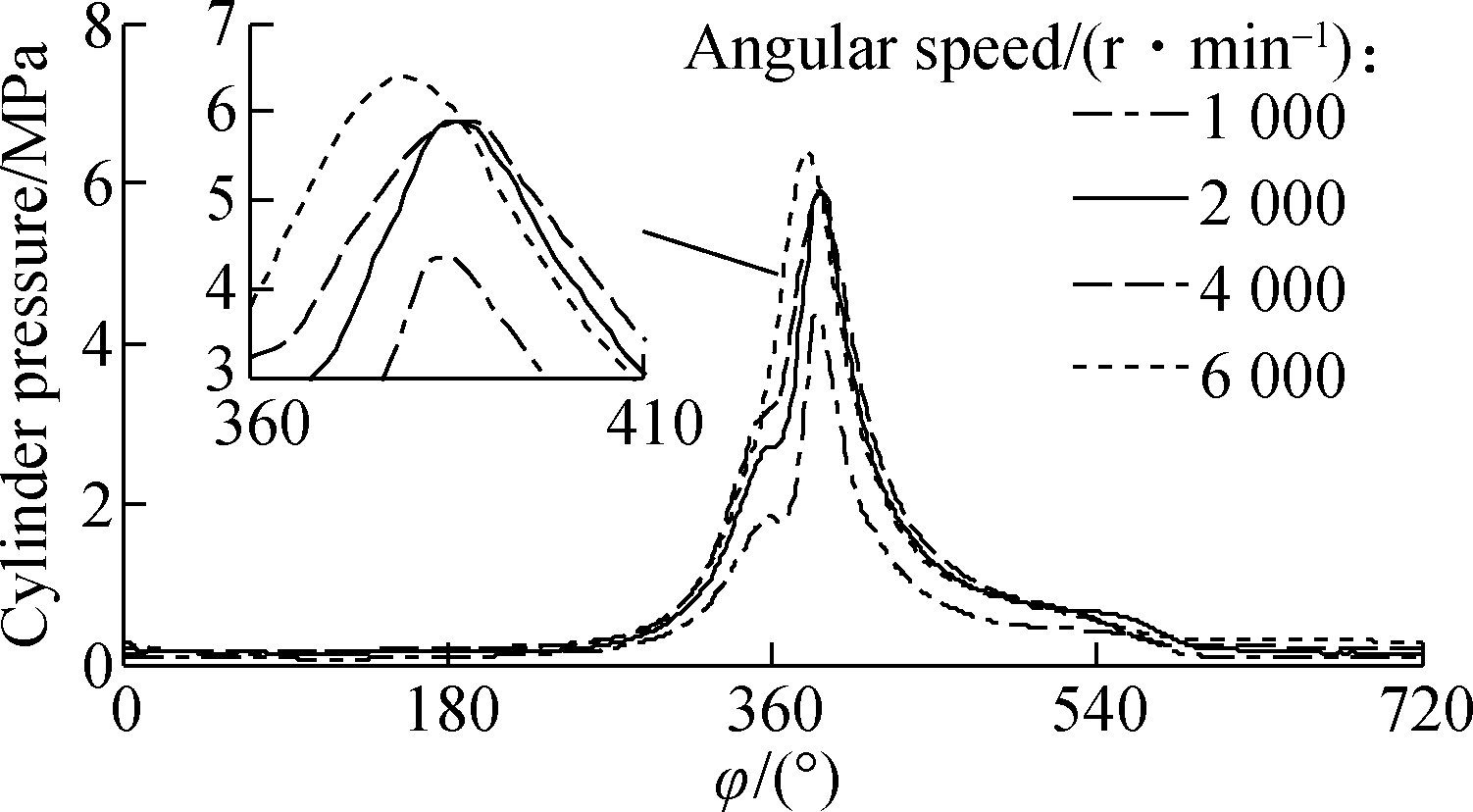
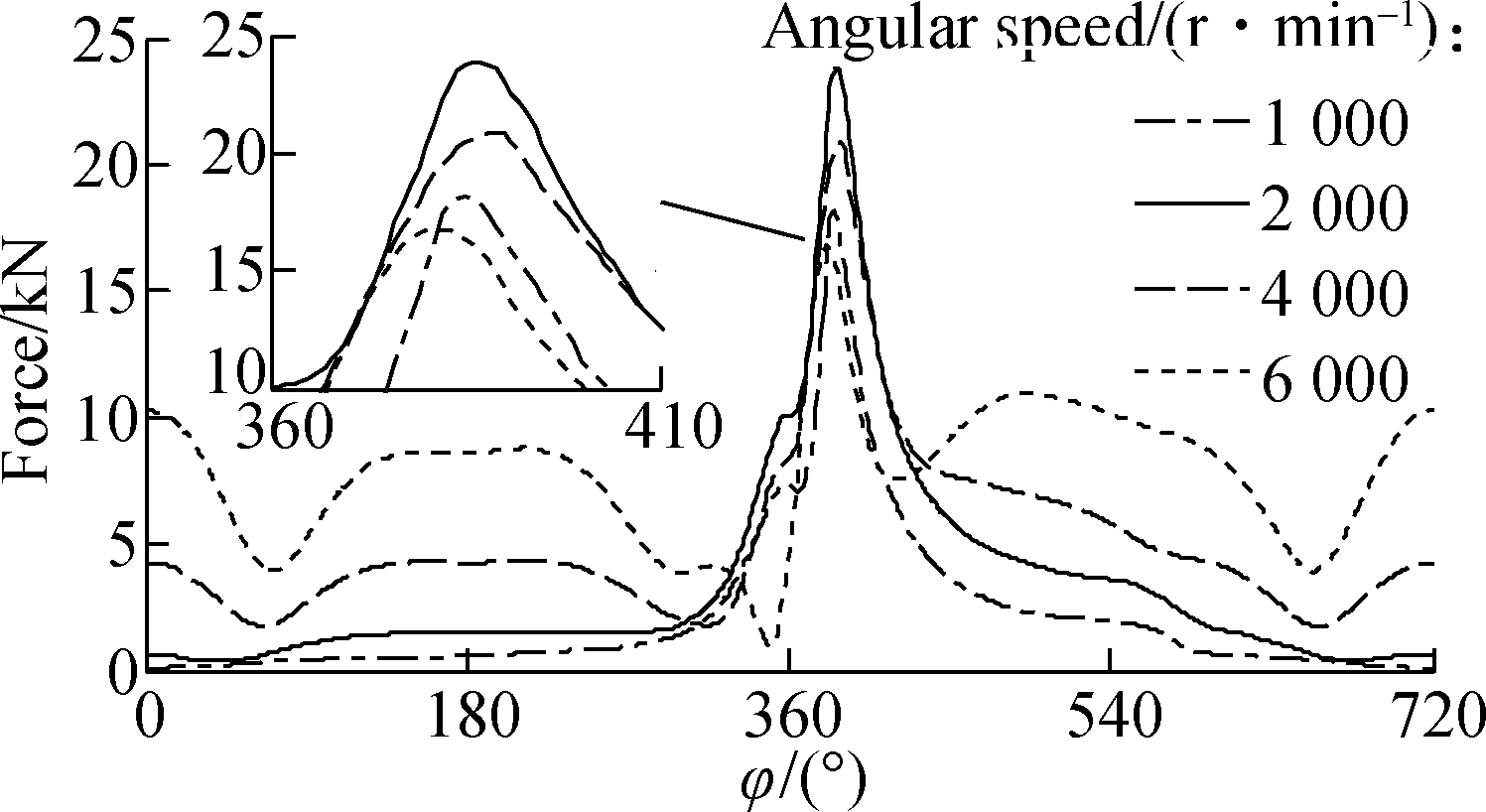
The necessary parameters for simulation listed in Tab.1 and the combustion gas pressure acting on the piston peak, which is obtained from the experimental data in Ref.[14], as shown in Fig.5(a), were applied to calculate W0 under various ω and analyze the LE-FPL. The W0 results are plotted in Fig.5(b).
As shown in Fig.5(b), the impact load is constantly varied under different ω and rotation angles. As the crankshaft rotational angle moves from 360° to 410°, corresponding to the combustion stroke of the engine, the maximum and minimum values of W0 are 2 000 and 6 000 r/min, respectively. However, outside the rotational angles of 360°- 410°, the maximum W0 is 6 000 r/min. This finding may be attributed to the effect of the Fic of the large-rod-end of the connecting rod and ω in Eq.(8). Thus, the LE-FPL of the CB is affected by the operating parameters of the CB. The effect of ω, rb, and B of the CB are investigated in the next subsections.
Tab.1 Parameters of the SCM and CB
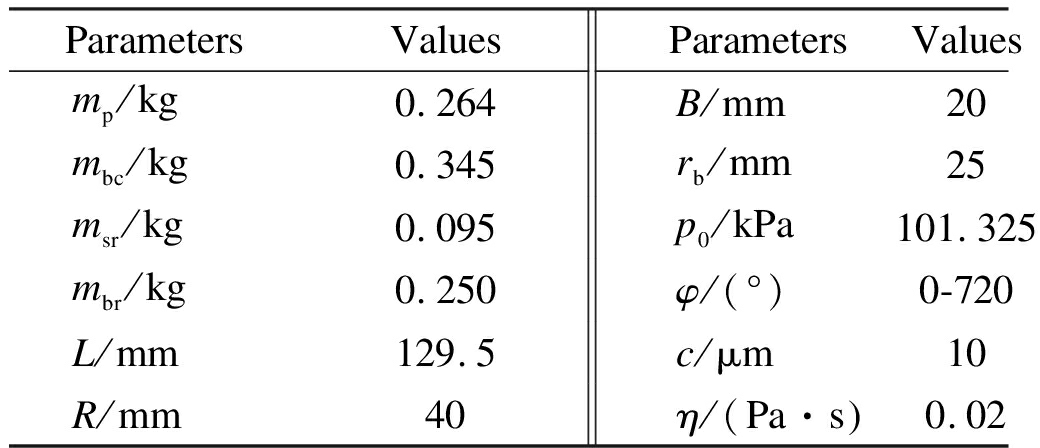
ParametersValuesParametersValues mp/kg0.264 B/mm20 mbc/kg0.345 rb/mm25 msr/kg0.095 p0/kPa101.325 mbr/kg0.250 φ/(°)0-720 L/mm129.5 c/μm10 R/mm40 η/(Pa·s 0.02
(a)
(b)
Fig.5 Impact forces on the CB under various angular speeds. (a) Experimental combustion gas pressures; (b) Impacting forces of W0 on the CB
3.1 Effect of engine speed
The relative speed between the shaft and bearing surfaces is u0=ωrb; thus, ω of 1 000, 2 000, 4 000, and 6 000 r/min with the corresponding W0 are applied to study their effects on the LE-FPL of the CB, as shown in Fig.5(b).
The simulation results of the oil film pressure and shear stress distributions on the CB surfaces under different W0 at 2 000 r/min are shown in Fig.6. The p values are mainly distributed over the range of 90°-180° with B, and the maximum p at 158° is 88.8 MPa. This finding is identical to the results presented in Refs.[1,14-15]. The shear stress is also uniformly distributed along B.

(a)
(b)
Fig.6 Oil film pressure and shear stress on the CB surface at an angular speed of 2 000 r/min. (a) Pressure distribution; (b) Shear stress distribution
However, in the circumferential direction, the shear stress remarkably varies and peaks at 178°.
The oil film pressure and shear stress distributions at a bearing width of B/2 with various ω are illustrated in Fig.7. Fig.7(a) shows that the oil film pressure strongly depends on W0 and ω. The maximum and minimum pressures corresponding to W0 are also obtained at 2 000 and 6 000 r/min, and the results are shown in Fig.5(b). The oil film shear stress mainly depends on ω, and the shear stress increases with increasing ω and vice versa.

(a)
(b)
Fig.7 Oil film pressure and shear stress at a bearing width of B/2 under different angular speeds. (a) Pressure distribution; (b) Shear stress distribution
The CB’s load bearing capacity W and F are calculated from the results in Fig.7 and plotted in Figs.8(a) and (b). The W shown in Fig.8(a) is similar to the W0 in Fig.5(b) under different ω because the oil film pressure varies to satisfy the condition that W is equivalent to W0. Fig.8(b) reveals that F increases sharply with increasing ω. Moreover, F peaks at a high ω of 6 000 r/min, which means that the F acting on the CB is greatest at this point. This result may be due to the increase in relative velocity between the shaft and the bearing surface, which increases the shear stress and friction resistance of the oil film.
(a)

(b)
(c)

(d)
Fig.8 Effect of angular speed on the LE-FPL. (a) CB’s load bearing capacity; (b) Friction force; (c) Friction coefficient; (d) Eccentricity ratio between the journal and bearing
Fig.8(c) presents the μ of the CB. The values of μ change with the variation of W and F and decrease with increasing ω. Comprehensive comparative analysis shows that, in the combustion stroke of the engine (i.e., a crankpin angle of 360°-410°), the maximum W0 affects not only the CB’s LE but also its engine power. In particular, when ω is maintained at 2 000 r/min, W0 peaks, but F and μ remain relatively small. Thus, this is also a reason that most engines should work at this speed[1, 6].
The effect of ε between the journal and bearing is also investigated to analyze the stability of the CB under various ω, as shown in Fig.8(d). The results indicate that increasing ω can reduce ε and vice versa. Moreover, ε peaks at a low ω of 1 000 r/min, and its minimum value occurs at a high ω of 6 000 r/min. Therefore, ε could also affect the LE and stability of the CB. ε shows less variation when ω is 6 000 r/min than at other speeds, which means that the lubrication capacity and the rotation of the journal are fairly stable at this point.
3.2 Effect of bearing radius
Considering the analysis above, the maximum W0 at ω of 2 000 r/min is selected to investigate the effect of rb and B on the LE-FPL of the engine.
The simulation results of oil film pressure and shear stress distributions at a bearing width of B/2 and rb=15, 20, 25, 30, 35 mm are plotted in Figs.9(a) and (b). The results show that the oil film pressure decreases, whereas the shear stress increases as rb gradually increases from 15 to 35 mm.
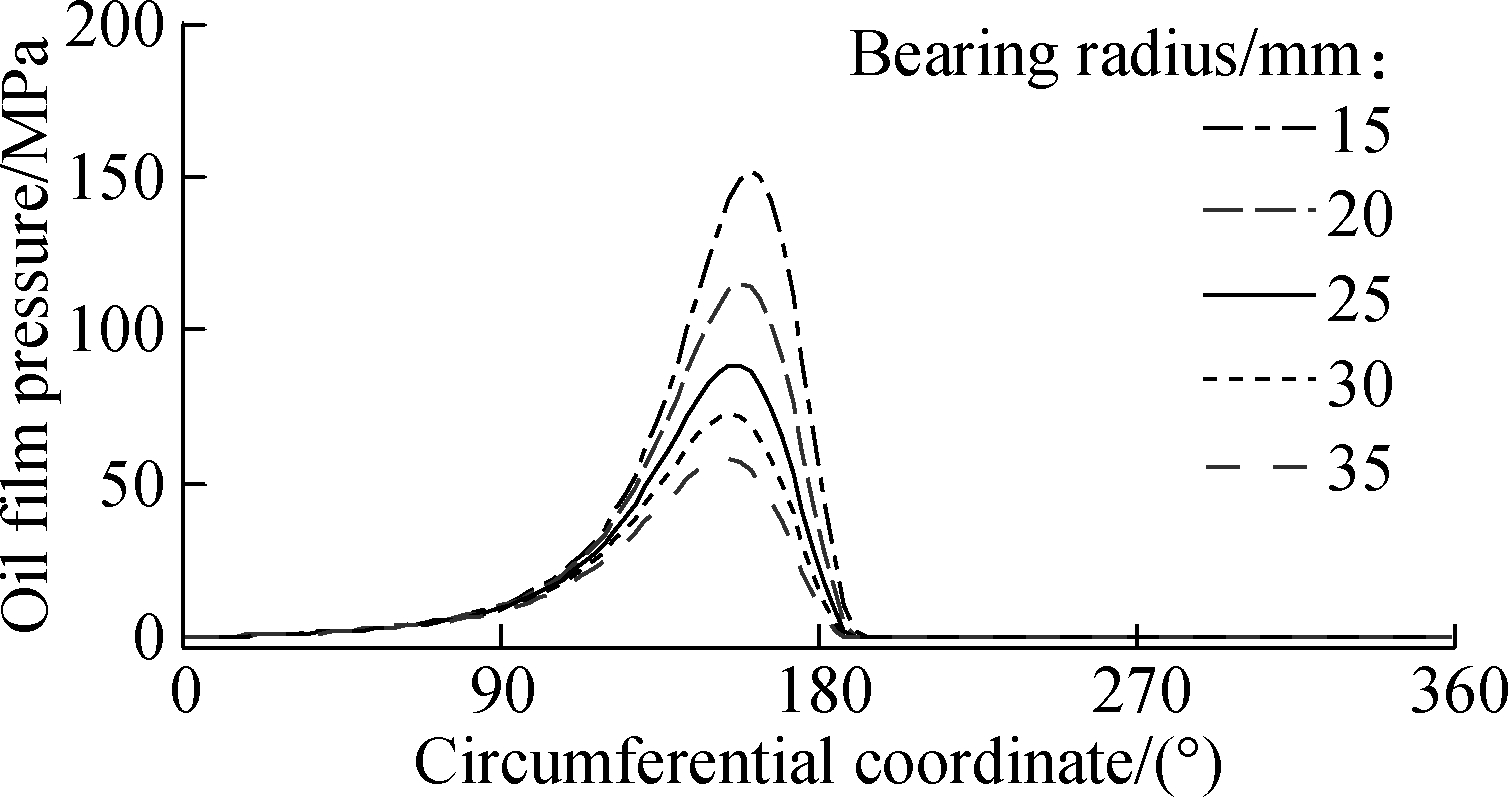
(a)
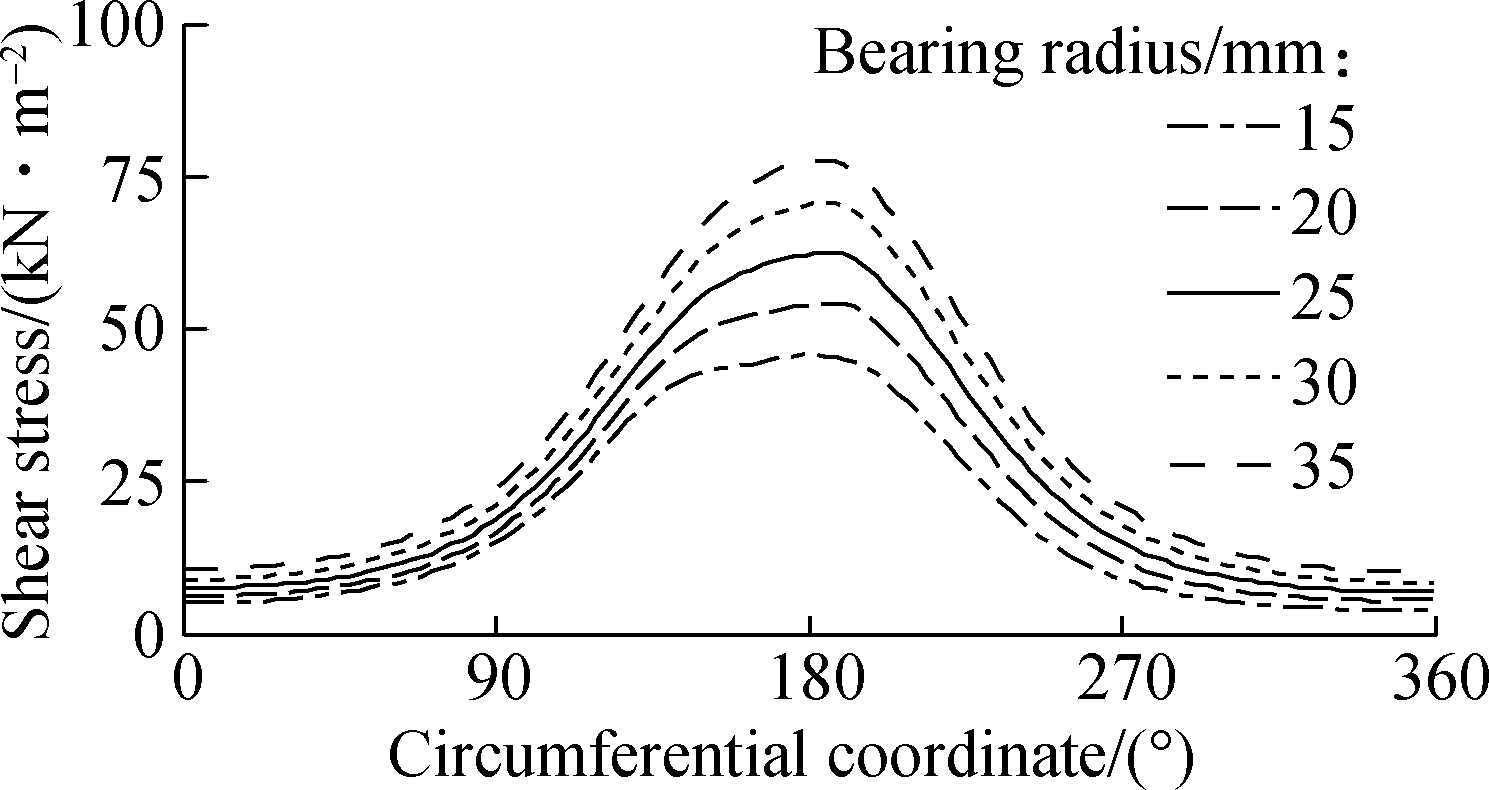
(b)
Fig.9 Oil film pressure and shear stress at a bearing width of B/2 with different bearing radii. (a) Pressure distribution; (b) Shear stress distribution
Figs.10(a) and (b), respectively, reflect changes in W and F under different rb. Changes in rb appear to have less effect on W in comparison with that on W0 under the condition of equivalent W and W0, as illustrated in Fig.10(a). This result may be attributed to an increase in Γ due to the increase in rb, which leads to a decrease in oil film pressure, as shown in Fig.9(a), to stabilize W and vice versa. This finding also verifies the accuracy and robustness of the mathematical model and algorithm developed in this study.
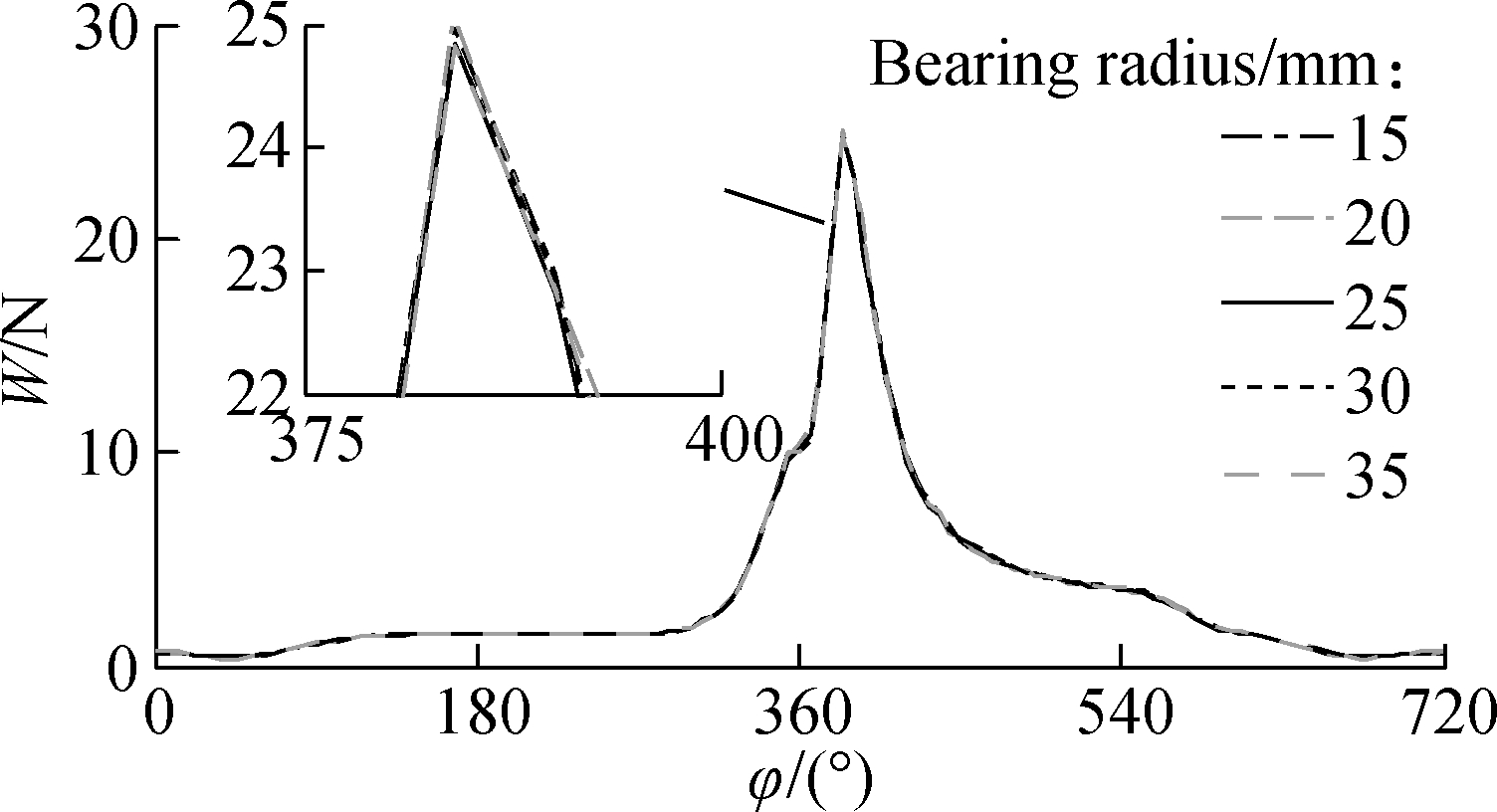
(a)
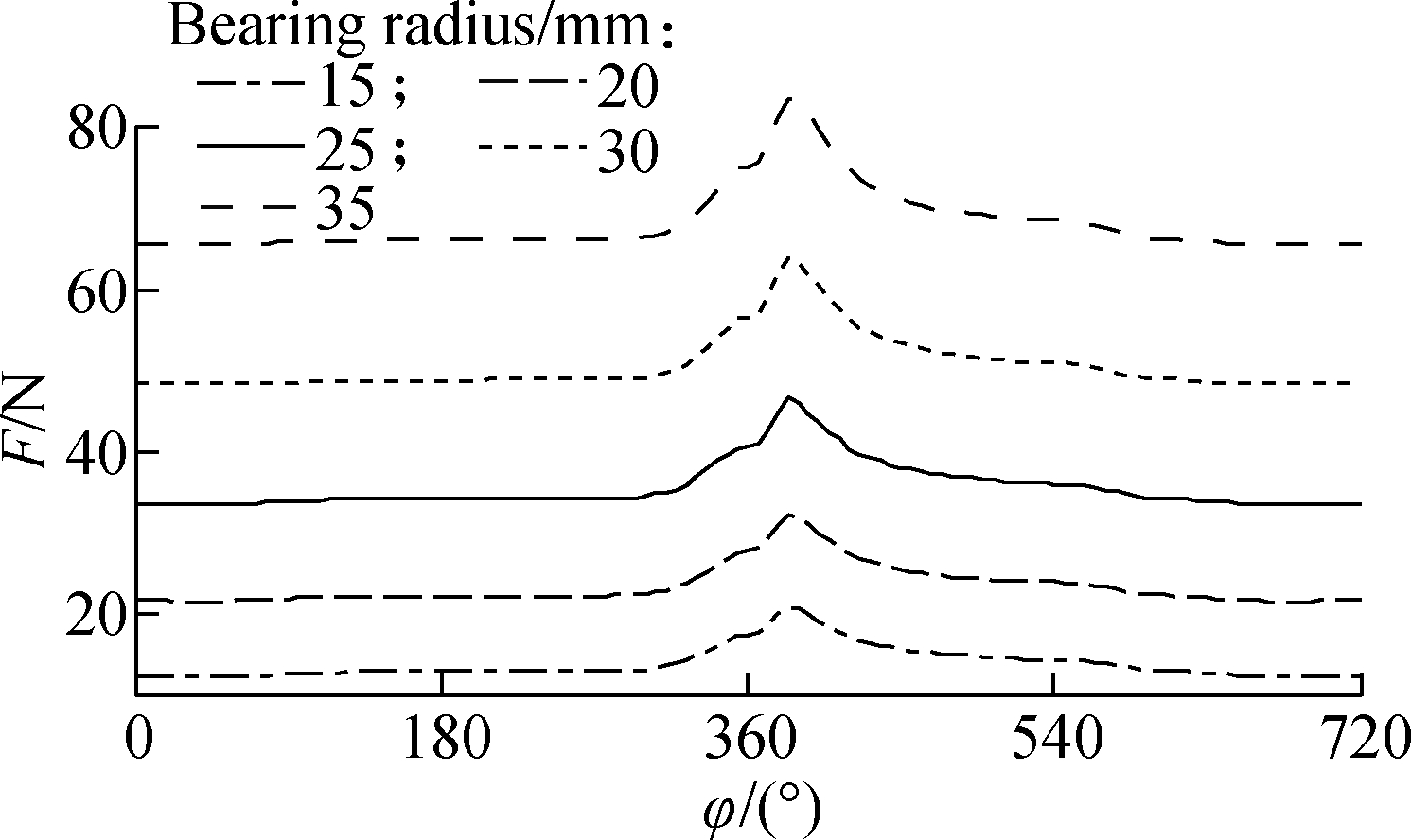
(b)

(c)
(d)
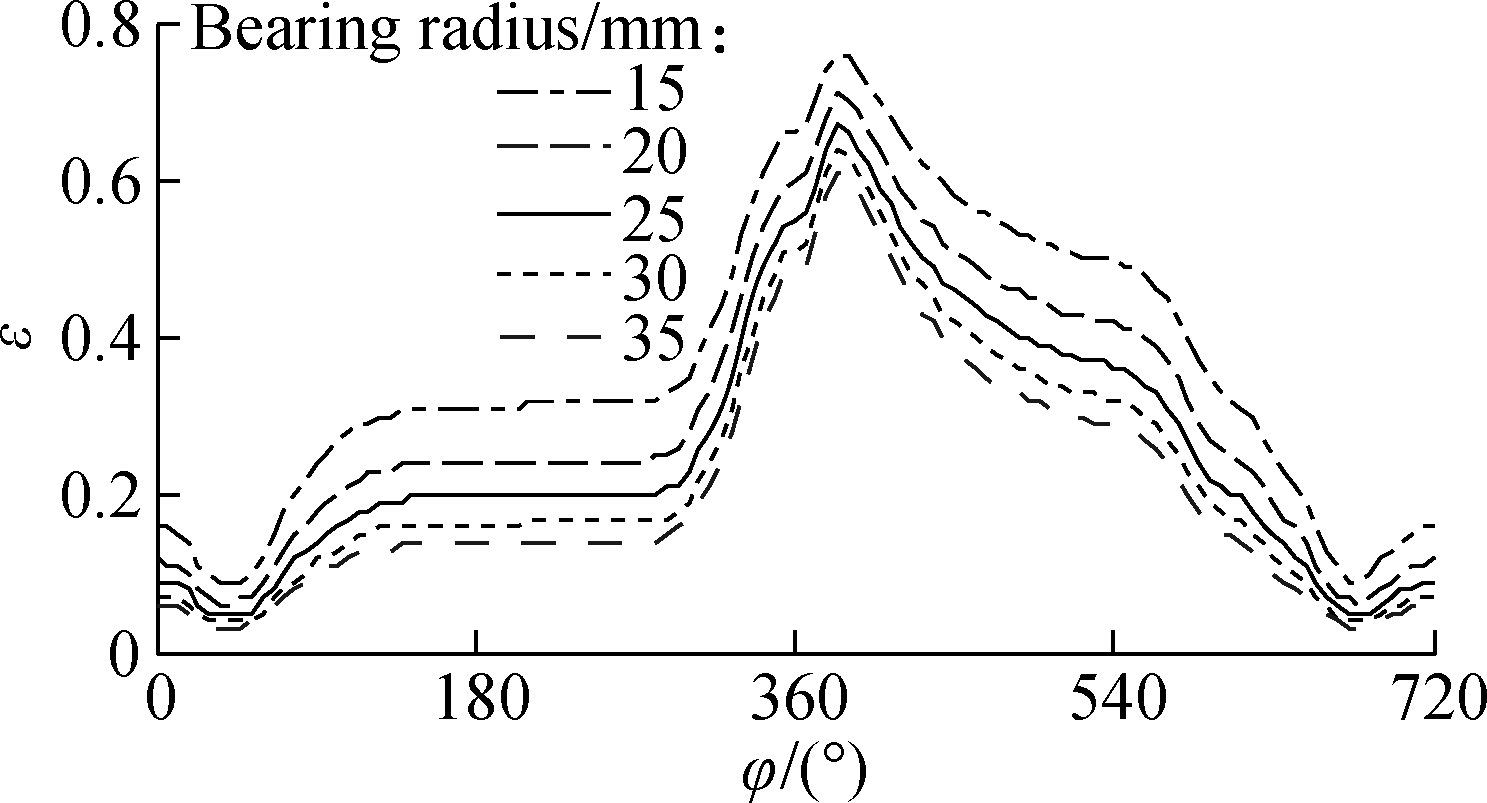
Fig.10 Effect of bearing radius on the LE-FPL. (a) CB’s load bearing capacity; (b) Friction force; (c) Friction coefficient; (d) Eccentricity ratio between the journal and bearing
Fig.10(b) reveals that F tends to increase with increasing rb. This finding may be attributed to increases in the relative speed of the oil film (u0=ωrb) and Γ affecting the oil film shear stress and friction resistance. Because W does not vary with different rb, μ increases because of the increase in F of the CB, as shown in Fig.10(c). Moreover, as seen in Fig.10(d), the influence of rb on ε is not significant, and the gap between the shaft and bearing of the CB shows an obvious tendency to decrease with increasing rb.
3.3 Effect of bearing width
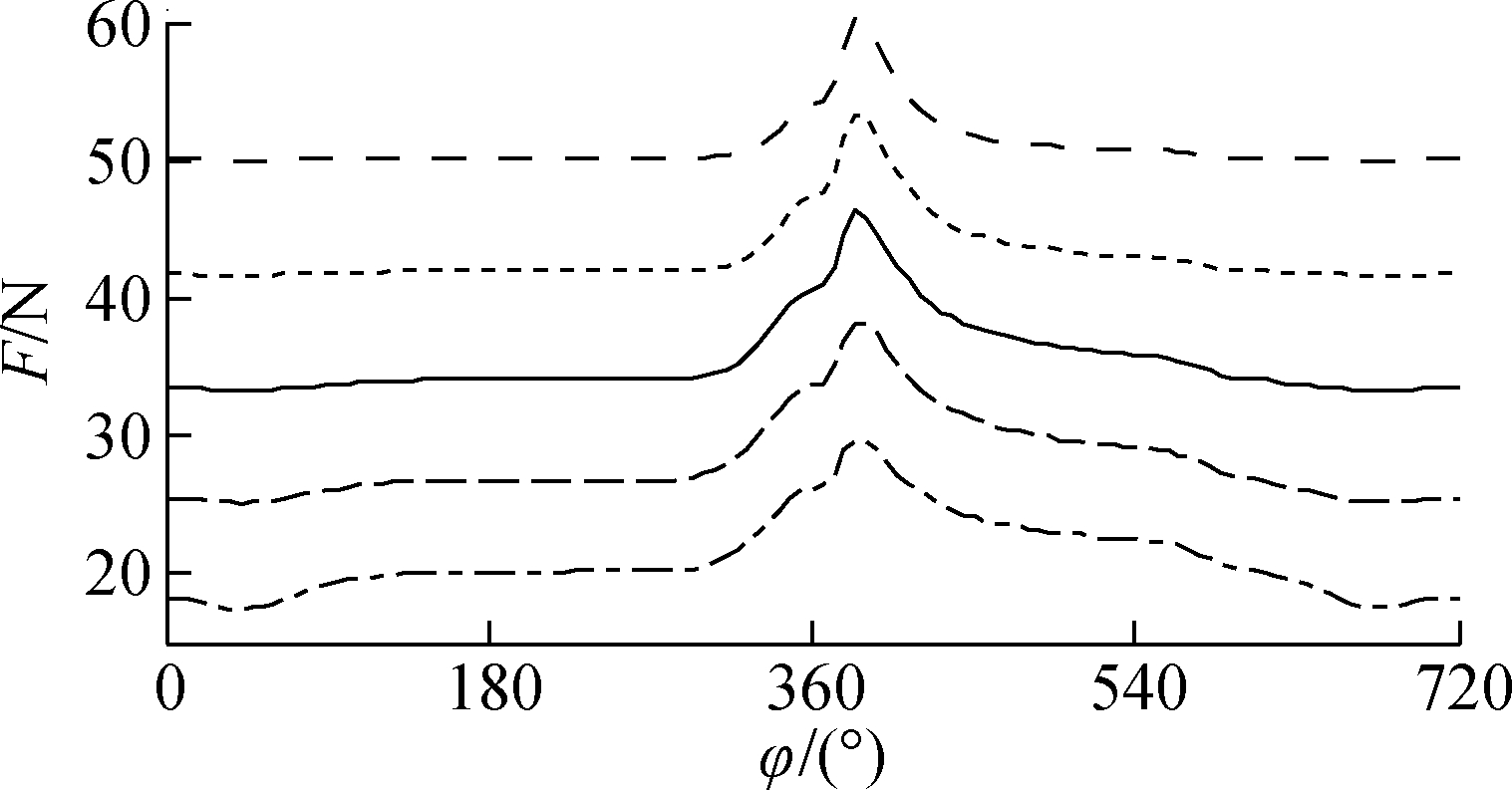
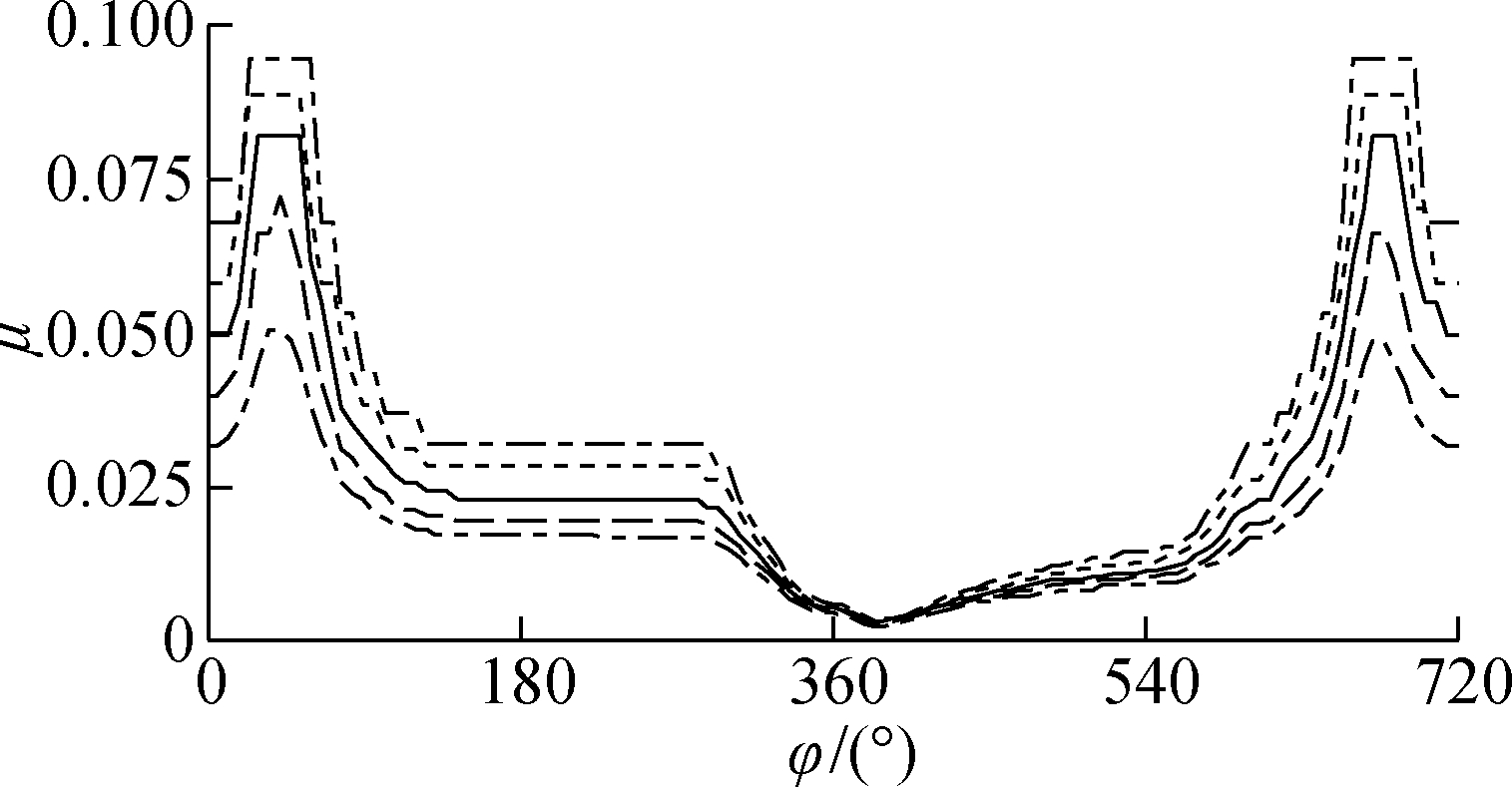
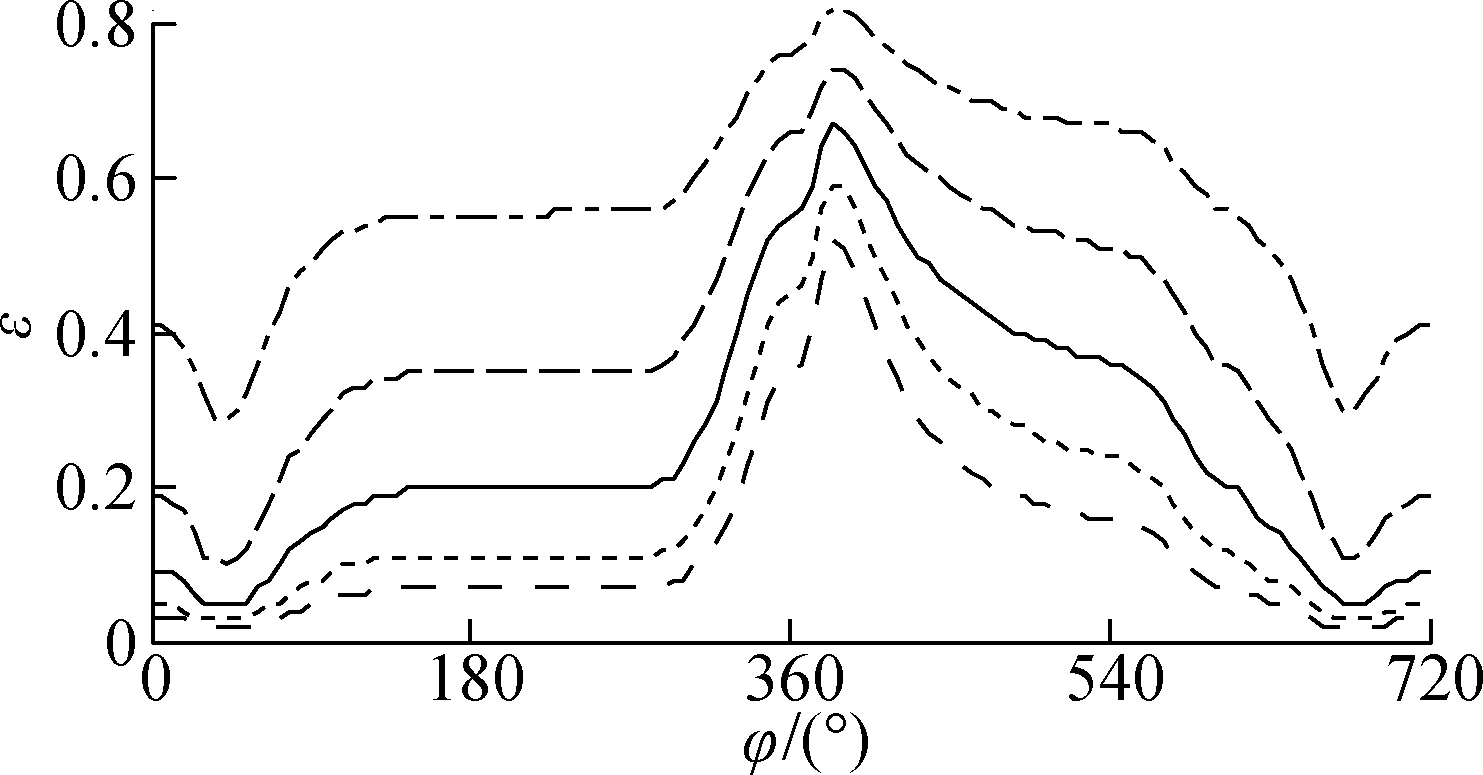
Fig.11 demonstrates the influence of B=10, 15, 20, 25, 30 mm on the LE-FPL under a constant W0 at 2 000 r/min. Fig.11(a) shows that the W generated from the oil film pressure does not change significantly in comparison with W0 as B is gradually increased from 10 to 30 mm, likely because the oil film pressure changes to stabilize W. F and μ also tend to increase, as shown in Figs.

(a)
(b)
(c)
(d)
![]()
Fig.11 Effect of bearing width on the LE-FPL. (a) CB load bearing capacity; (b) Friction force; (c) Friction coefficient; (d) Eccentricity ratio between the journal and bearing
11(b) and (c), which directly causes greater FPL. However, B variations have little effect on the ε between the journal and bearing [6, 16-17], as indicated in Fig.11(d).
4 Conclusions
1) Increasing ω not only effectively reduces the ε between the journal and bearing but also increases the minimum h, thereby directly improving the CB LE. However, increases in ω also increase F, thereby increasing the FPL of the engine. The simulation results show that the engine’s LE-FPL can be improved better when ω is maintained at 2 000 r/min.
2) Increasing the rb or B of the CB can help decrease ε, thereby improving the LE. In addition, the dimensional change of the CB has a great influence on F and μ, which, in turn, increase the FPL of the engine.
3) Improving LE while reducing FPL is a challenging issue. Therefore, the present study not only contributes to the existing body of knowledge on the LE-FPL of automotive engines but also provides an important reference for optimal SCM design parameters to improve this engine property further.
[1]Zhao B, Dai X D, Zhang Z N, et al. A new numerical method for piston dynamics and lubrication analysis[J].Tribology International, 2016, 94: 395-408. DOI:10.1016/j.triboint.2015.09.037.
[2]Meng X H, Ning L P, Xie Y B, et al. Effects of the connecting-rod-related design parameters on the piston dynamics and the skirt-liner lubrication[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2013, 227(6): 885-898. DOI:10.1177/0954407012464025.
[3]Li Y Y, Chen G P, Sun D Y, et al. Dynamic analysis and optimization design of a planar slider-crank mechanism with flexible components and two clearance joints[J]. Mechanism and Machine Theory, 2016, 99: 37-57. DOI:10.1016/j.mechmachtheory.2015.11.018.
[4]Cho S H,Ahn S T, Kim Y H. A simple model to estimate the impact force induced by piston slap[J]. Journal of Sound and Vibration, 2002, 255(2): 229-242. DOI:10.1006/jsvi.2001.4152.
[5]Liu K,Xie Y B, Gui C L. A comprehensive study of the friction and dynamic motion of the piston assembly[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 1998, 212(3): 221-226. DOI:10.1243/1350650981542038.
[6]Mansouri S H, Wong V W. Effects of piston design parameters on piston secondary motion and skirt-liner friction[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2005, 219(6): 435-449. DOI:10.1243/135065005x34026.
[7]Patir N, Cheng H S. Application of average flow model to lubrication between rough sliding surfaces[J]. Journal of Lubrication Technology, 1979, 101(2): 220-229. DOI:10.1115/1.3453329.
[8]Daniel G B,Cavalca K L. Analysis of the dynamics of a slider-crank mechanism with hydrodynamic lubrication in the connecting rod-slider joint clearance[J]. Mechanism and Machine Theory, 2011, 46(10): 1434-1452. DOI:10.1016/j.mechmachtheory.2011.05.007.
[9]Wang X L, Zhang J Y, Dong H. Analysis of bearing lubrication under dynamic loading consideringmicropolar and cavitating effects[J]. Tribology International, 2011, 44(9): 1071-1075. DOI:10.1016/j.triboint.2011.05.002.
[10] Raj A,Sinha P. Transverse roughness in short journal bearing under dynamic loading[J]. Tribology International, 1983, 16(5): 245-251. DOI:10.1016/0301-679X(83)90081-6.
[11] Zhang H,Hua M, Dong G N, et al. Boundary slip surface design for high speed water lubricated journal bearings[J]. Tribology International, 2014, 79: 32-41. DOI:10.1016/j.triboint.2014.05.022.
[12] Patir N, Cheng H S. An average flow model for determining effects of three-dimensional roughness on partial hydrodynamic lubrication[J]. Journal of Lubrication Technology, 1978, 100(1): 12-17. DOI:10.1115/1.3453103.
[13] Greenwood J A, Tripp J H. The contact of two nominally flat rough surfaces[J]. Proceedings of the Institution of Mechanical Engineers, 1970, 185(1): 625-633. DOI:10.1243/pime_proc_1970_185_069_02.
[14] Zhao B, Zhang Z N, Fang C C, et al. Modeling and analysis of planar multibody system with mixed lubricated revolute joint[J]. Tribology International, 2016, 98: 229-241. DOI:10.1016/j.triboint.2016.02.024.
[15] Nguyen V, Wu Z P, Le V. Optimization of crankpin bearing lubrication under dynamic loading considering effect of micro asperity contact[J]. Industrial Lubrication and Tribology, 2020, 72(10): 1173-1179. DOI:10.1108/ilt-02-2020-0072.
[16] Wu Z P, Nguyen V, Zhang Z H, et al. Study on curved surface design of sliding pair based on stepped topography model[J]. Industrial Lubrication and Tribology, 2019, 72(1): 86-92. DOI:10.1108/ilt-04-2019-0121.
[17] Wang P L, Nguyen V, Wu X Y, et al. Research on different structures of dimpled textures on improving the LE-FPL of engine[J]. Industrial Lubrication and Tribology, 2021. DOI:10.1108/ilt-07-2020-0286.
[18] Christiansen C K, Walther J H,Klit P, et al. Investigation of journal orbit and flow pattern in a dynamically loaded journal bearing[J]. Tribology International, 2017, 114: 450-457. DOI:10.1016/j.triboint.2017.04.013.
[19] Braun M J, Hannon W M.Cavitation formation and modelling for fluid film bearings: A review[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2010, 224(9): 839-863. DOI:10.1243/13506501jet772.