In recent years, with the continuous improvement of road traffic, more attention has been paid to the ride comfort and humanized design of vehicle seats. In construction machinery vehicles, cab seats are vibrated to various degrees during the vehicle operation[1]. Traditional studies mainly focus on the vibration isolation of engines and vehicle-mounted equipment of construction machinery[2-4]. However, long periods of forced vibration in the working environment will cause driver fatigue and lead to frequent accidents. The driver’s mental and physical health will also be seriously damaged. Cervical, spinal, and pelvis injuries of the human body frequently occur[5-6]. Thus, the research and development design of seat suspension systems are closely related to people’s life. Advocating people-orientedness, fully considering the driver’s physical feelings and strengthening their protection, and improving the working environment are important development directions of vehicle seat suspension systems.
The vibration-isolation mechanism of parallel springs with a negative stiffness structure is a new type of nonlinear vibration-isolation device, and it can significantly improve the vibration-isolation effect, especially the low-frequency ones. van Eijk et al.[7] first used negative stiffness in the mechanical design of leaf springs to reduce the total stiffness of the system. Lee et al.[8] developed the seat vibration-isolation mechanism with the negative stiffness based on the thin-shell theory and offered theoretical derivation and experimental verification, which achieved good results. Yang et al.[9] studied the dynamics and power flow behavior of a nonlinear vibration-isolation system with a negative stiffness mechanism and derived the nonlinear dynamic equations of the system; they obtained the frequency response function of the system under harmonic excitation by using the average method. Han et al.[10] used a kind of bending mounted spring-roller mechanism as a negative stiffness calibrator in parallel with a vertical linear spring and developed and designed a passive nonlinear isolator; they also analyzed the dynamic characteristics of the isolator. Fan et al.[11] developed a vibration absorber of positive and negative stiffness elastic elements in parallel by the principle of counteraction of the elements. Its stiffness can be arbitrarily low. Zhang et al.[12] studied a new type of vibration-isolation system with positive and negative stiffnesses in parallel. This system had a high support stiffness and a low motion stiffness. The natural frequency can be reduced by adjusting the magnitude of force at both ends of the negative stiffness mechanism. The vibration-isolation effect was improved significantly. Ji et al.[13] proposed a new type of vibration-isolation system with a negative stiffness damping device (NSD) attached to the ordinary vibration isolation layer and discussed the effect of NSD on the performance of the vibration isolation system. In recent years, numerous scholars have carried out a series of studies on the negative stiffness structure[14-20]. However, little literature focused on the in-depth research of negative stiffness structure for cab seats of construction machinery vehicles. Therefore, it is necessary to establish an accurate seat suspension system with the characteristics of a negative stiffness suspension structure (NSS) and analyze its dynamic features; the ideal parameters of the system need to be designed based on the space size of the cab seat.
In this paper, the nonlinear dynamic model of the cab seat suspension system based on the negative stiffness structure is first established, and the Runge-Kutta method is used to discuss the different structural parameters and their influence on dynamic stiffness to determine the ideal configuration parameter range of the suspension system. Based on the initial results, the optimization model of the seat suspension structure of construction machinery cabs is put forward, and a nonlinear simulation analysis is carried out to study the vibration transfer characteristics of this suspension system. In accordance with the ISO 2631 standard, different methods are used to evaluate the ride comfort of the seat to improve the working environment of drivers and reduce vibration.
1 Model Description
The vehicle cab seat model consists of three parts:the seat suspension system, seat structure frame, and driver (see Fig.1). In the analysis of the dynamic characteristics of seat suspension specifically, the weights of the seat and the human body are simplified into a rigid mass block M, and the elasticity of the cushion, the damping inside the human body, and the weight of the connecting rod and joint are neglected. The simplified model contains two symmetrical negative stiffness structures, dampers, a mass block, and a supporting spring in the vertical direction (see Fig.2).
Fig.1 Simplified vehicle seat model
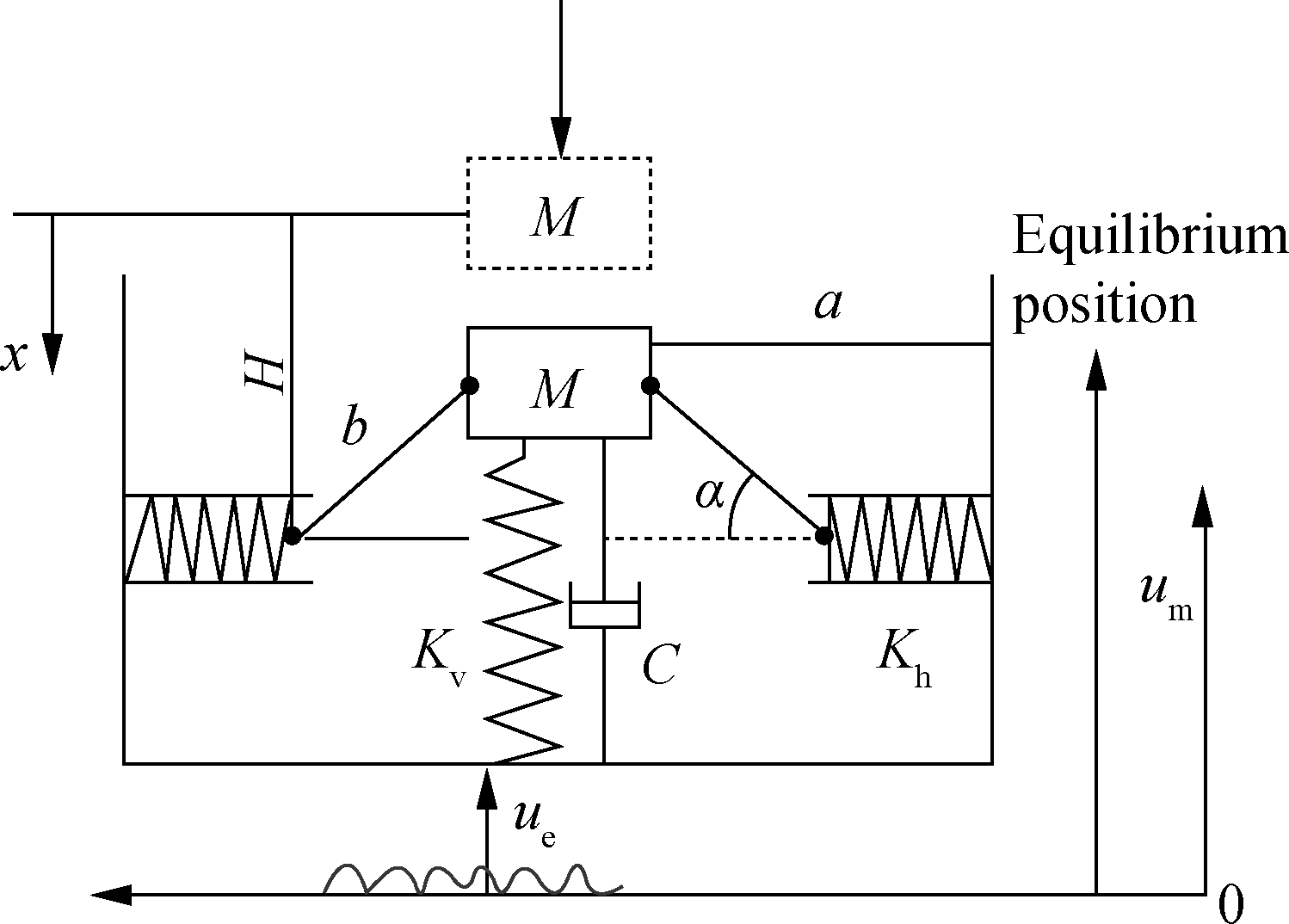
Fig.2 Mathematical model of seat isolation system
The variables in Fig.2 are described as follows: x, displacement in the vertical direction relative to the static equilibrium position of the vibration-isolated objects; Kv and Kh, vertical and horizontal spring stiffnesses, respectively; b, length of the connecting rod between the horizontal spring and mass block; a, distance from mass block M to the fixed end of the horizontal spring. The initial state of the mass block is the position of the dashed frame, and each spring of the suspension system is in a compression state during vehicle operation. The dynamic stiffness of the suspension system can be adjusted by changing the above parameters.
The rotation freedom of the seat structure is limited, and the seat can only move in the vertical direction. The vibration reduction amount of the suspension system is affected by different parameters, such as spring stiffness, damping coefficient, length of connecting rod, and the angle between the rod and horizontal plane.
2 Dynamic Model of Seat Suspension
When the system drops x from its initial position, its kinetic energy T, potential energy V, and dissipation function D are respectively computed as
(1)
(2)
(3)
where C is the damping coefficient, N/(m·s); k is the spring stiffness,N/m; Δ is the variation of the spring length; ![]() is the relative velocity at both ends of the spring, m/s; and subscripts l, r, and v represent the left, right, and vertical directions of the suspension system, respectively. Given the symmetrical structure of the system, kl=kr=Kh, Cl=Cr, and Δl=Δr. Using the Lagrangian equation, the equation of motion can be expressed as
is the relative velocity at both ends of the spring, m/s; and subscripts l, r, and v represent the left, right, and vertical directions of the suspension system, respectively. Given the symmetrical structure of the system, kl=kr=Kh, Cl=Cr, and Δl=Δr. Using the Lagrangian equation, the equation of motion can be expressed as
(4)
Assuming that the spring in Fig.2 is in equilibrium, the deformation length of the horizontal spring is as
(5)
where L0 is the original length of the horizontal spring.
Then, the horizontal force produced by the horizontal spring is computed as
(6)
Next, the horizontal force is converted to the force Fhv in the vertical direction:
(7)
where α is the angle between the rod and horizontal plane.
(8)
The force produced by the vertical spring in the vertical direction is as
Fv=Kvx
(9)
At this point, in accordance with the principle of virtual work, the vertical-direction restoring force F of the system is obtained with the following equation:
(10)
Eq.(10) deals with dimensionless variables, where the structural parameters of the system are calculated as
where F′ is the dimensionless restoring force, and x′ is the dimensionless displacement. Thus, the dimensionless force-displacement relation of the system is obtained as
(11)
Then, the derivation of x′ is acquired, and the dimensionless dynamic stiffness K′ of the system is obtained.
(12)
With respect to the seat suspension system, a vertical upward external excitation ue is applied at the bottom. u is the displacement of the suspension system relative to the base. um is the absolute displacement of the suspension system in space. The dynamic equation of the system is obtained by the Lagrangian equation.
![]() ·
·![]()
(13)
The relative displacement, velocity, and acceleration of the isolated equipment relative to the equilibrium position are respectively defined as
z=H-x
(14)
(15)
(16)
where
Mg=KvH
(17)
Substituting Eq.(13) into Eqs.(14)-(17), the new dynamic equation is rewritten as
(18)
3 Analysis of Seat Suspension System
3.1 Parameter analysis of seat suspension system
Different parameters will have different effects on the suspension system. The design parameters need to be further determined to evaluate the mechanical properties of the system. Eq. (12) shows that the dimensionless dynamic stiffness K′ is determined by three-parameter variables, i.e., α, γ1, and γ2. According to the principle of the single-factor variable method, the structural parameters are discussed as follows (see Tab.1).
Tab.1 Structural parameters of the model
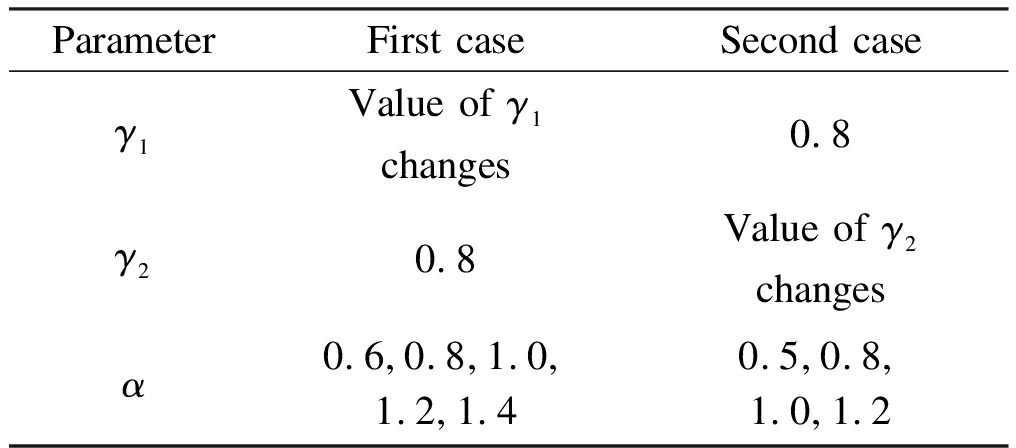
ParameterFirst caseSecond caseThird caseγ1Value of γ1 changes0.80.8γ20.8Value of γ2 changes1.2α0.6 0.8 1.0 1.2 1.40.5 0.8 1.0 1.2Value of α changes
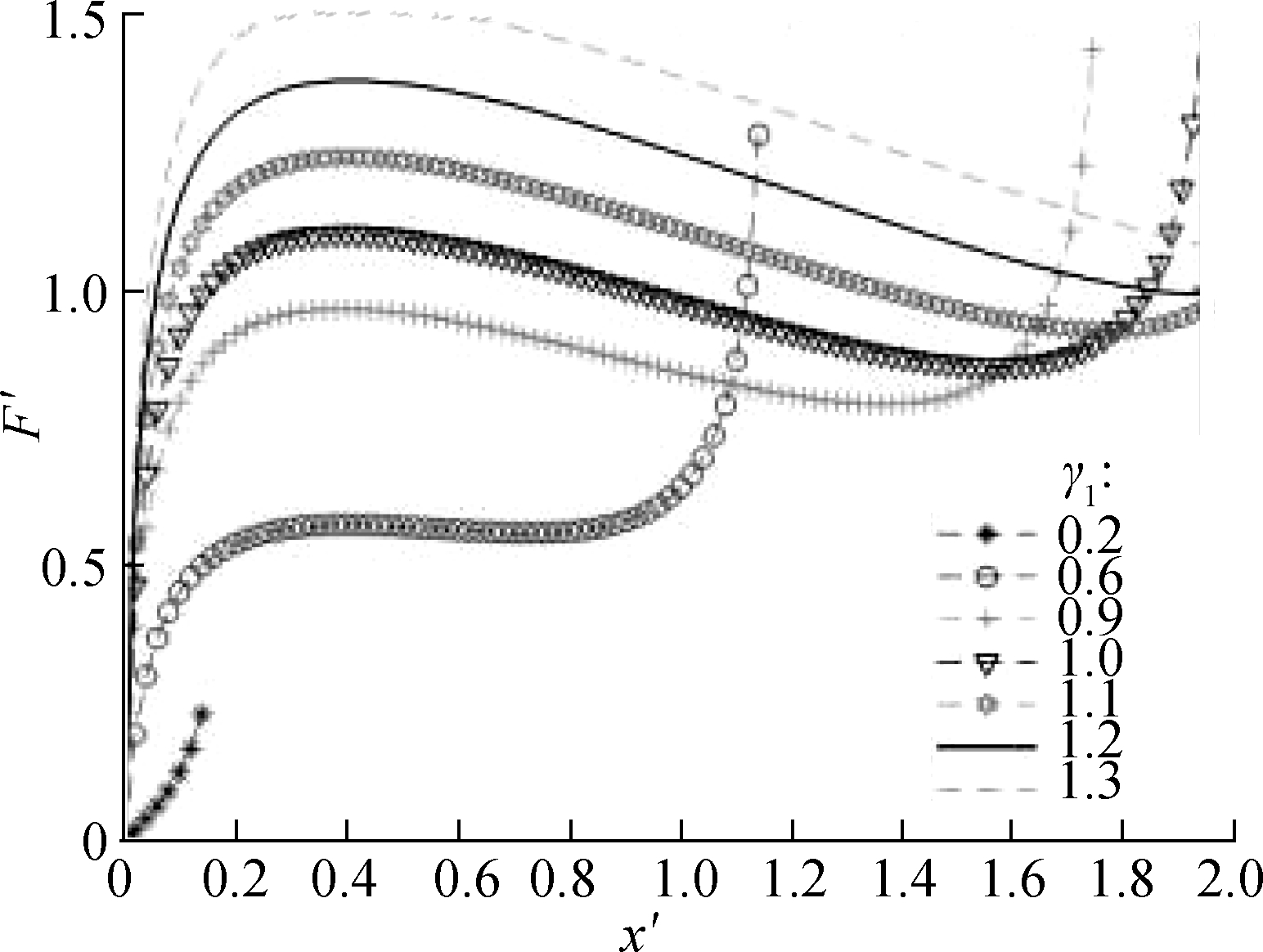
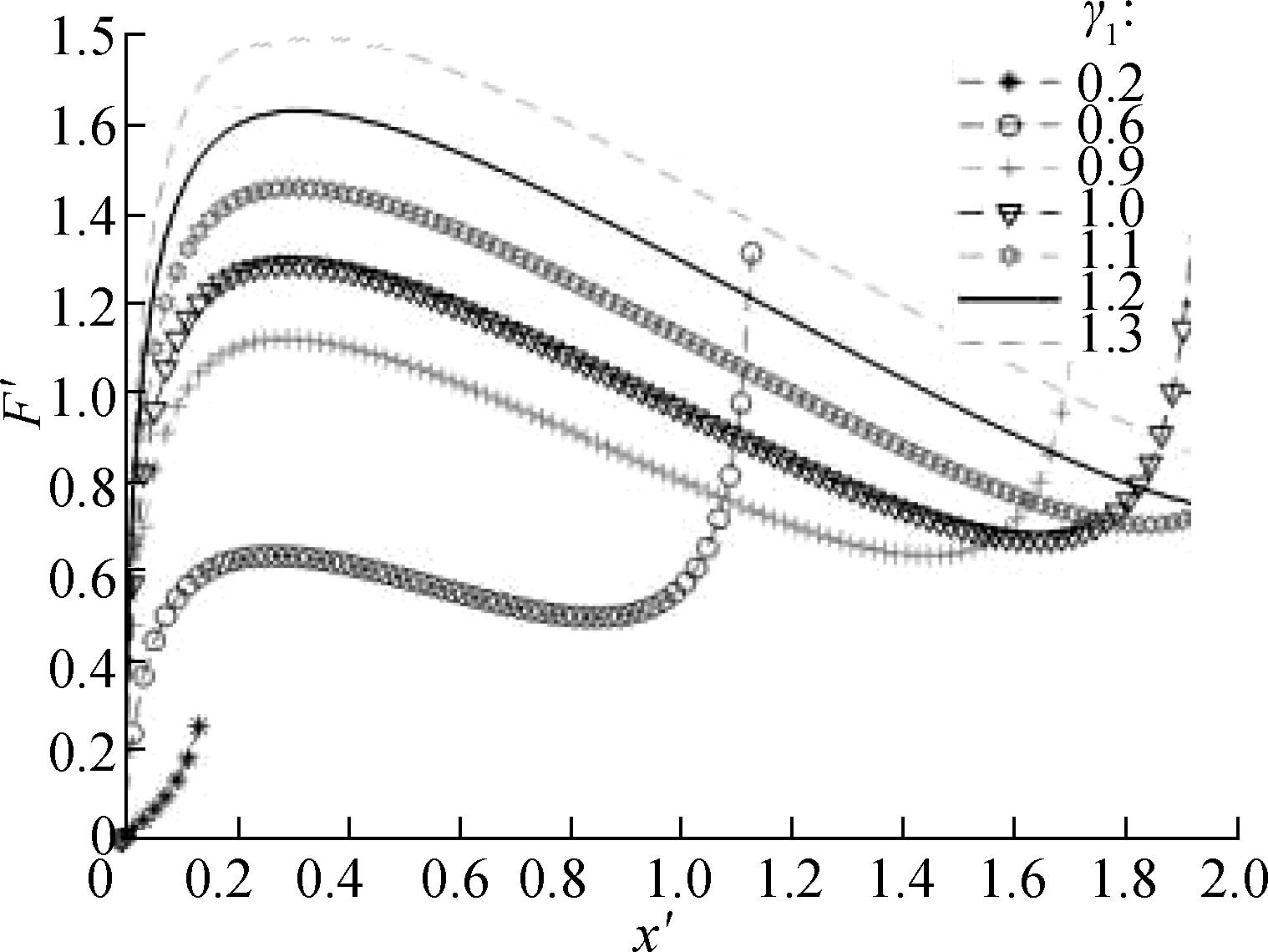
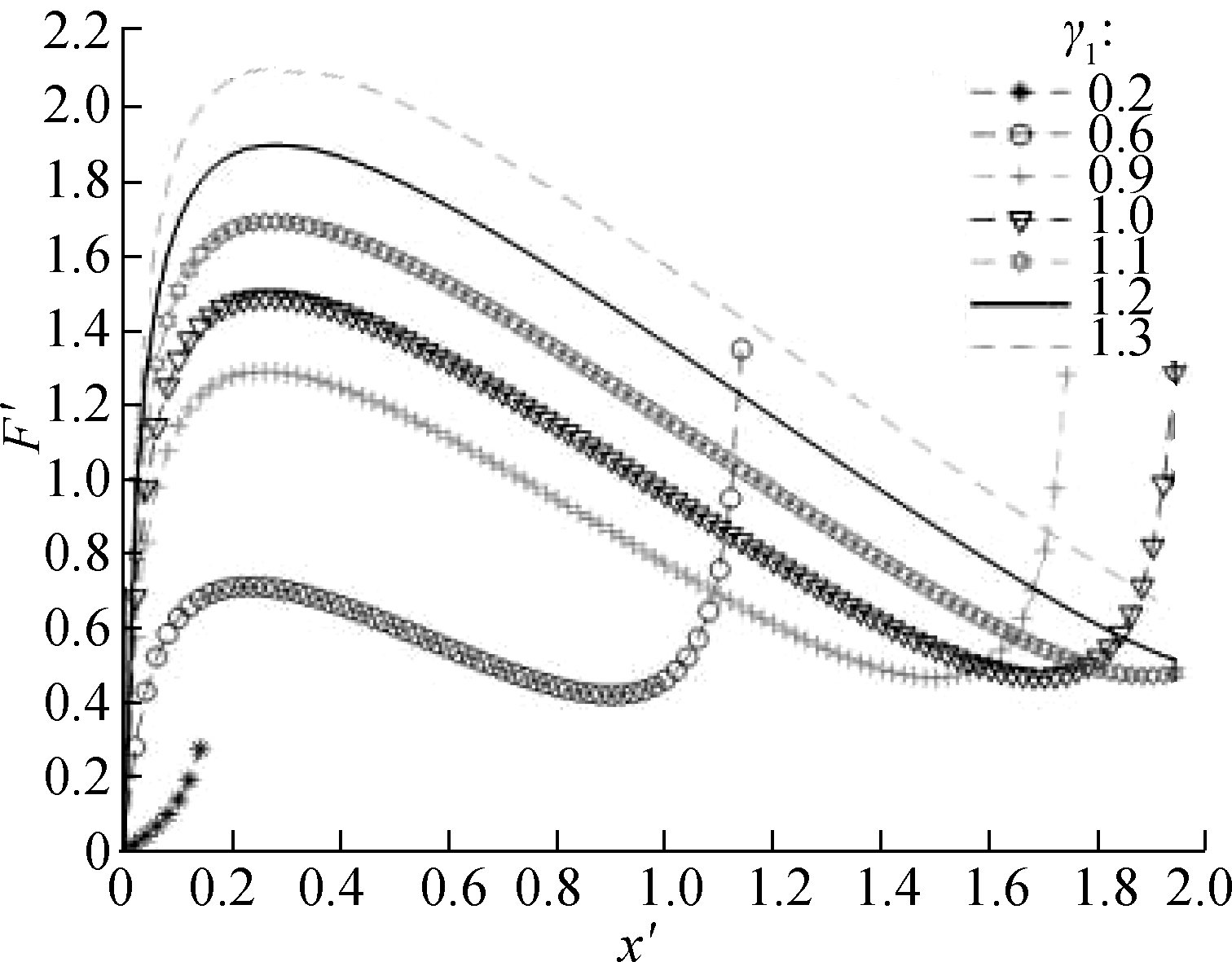
By MATLAB numerical calculation, the force characteristic curve of the system is obtained (see Fig.3). With the increase in displacement, the restoring force curve of the system presents a downward trend, and the structure exhibits negative stiffness characteristics. When γ1<1, the occurrence time of the first peak of the curve is short, and the change in the corresponding displacement is small. When γ1≥1, the force change trend of the system
(a)
(b)
(c)
Fig.3 Dimensionless force-deflection curves with various values of γ1. (a) α=0.8,γ2=1.2; (b) α=1.0,γ2=1.2; (c) α=1.2,γ2=1.2
in the vertical direction is smooth, which indicates the improved performance of the seat vibration-isolation system and ideal selection of the NSS parameters. The dimensionless force F′ of the system will peak in a short time when the value of γ1 is especially small. Therefore, this situation should be avoided when designing parameters to prevent affecting the dynamic characteristics of the suspension system. In addition, by contrasting and analysis, the results show that the change in α will affect the trend of the overall force change of the system. With the increase in α, the trend of the system bearing the force change will accelerate, indicating the increased vibration amplitude of the seat in the vertical direction and the reduced ride comfort of the driver. As a result, the use of a large-value α is discouraged, and the stiffness of the horizontal spring should be smaller than that of the vertical spring.
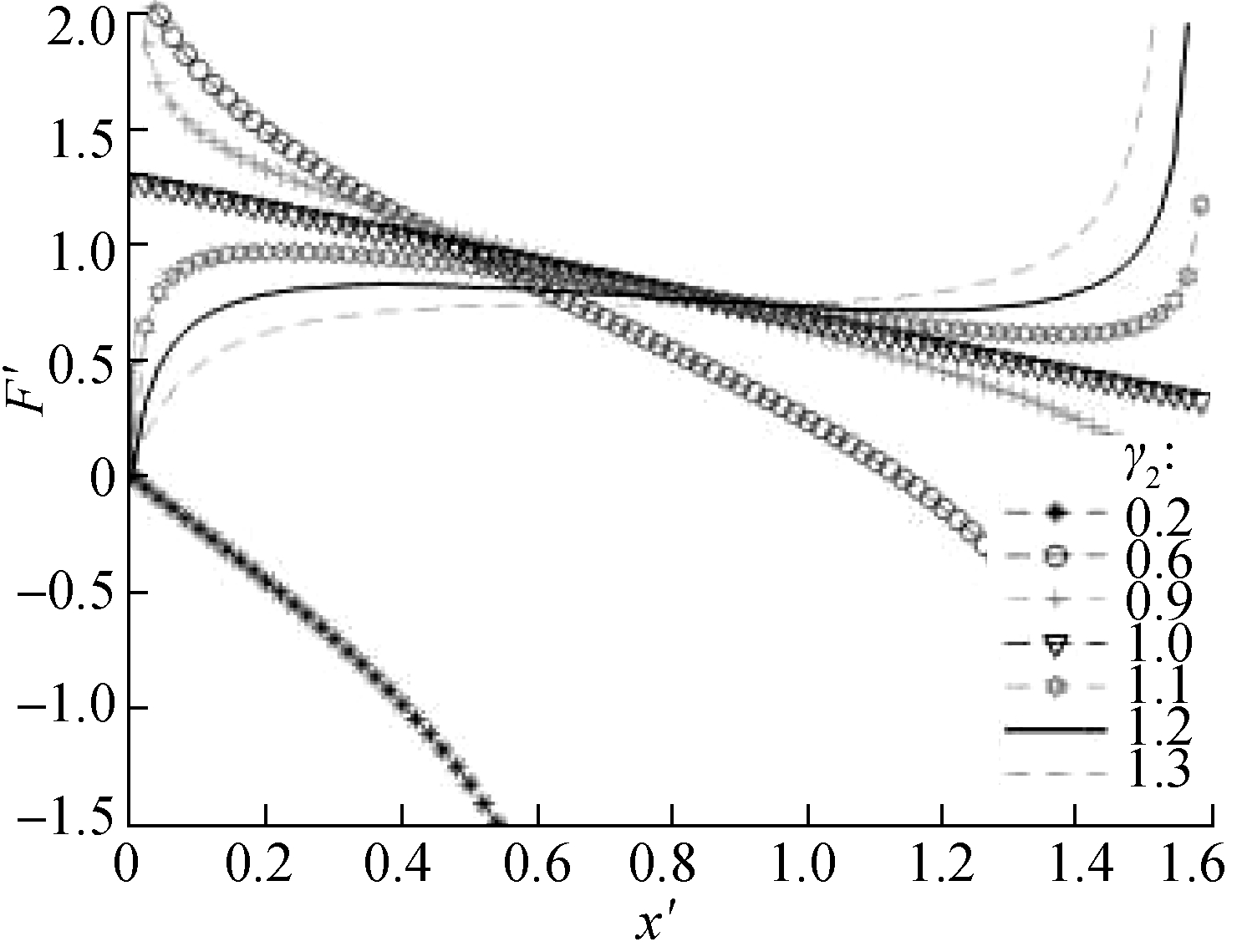
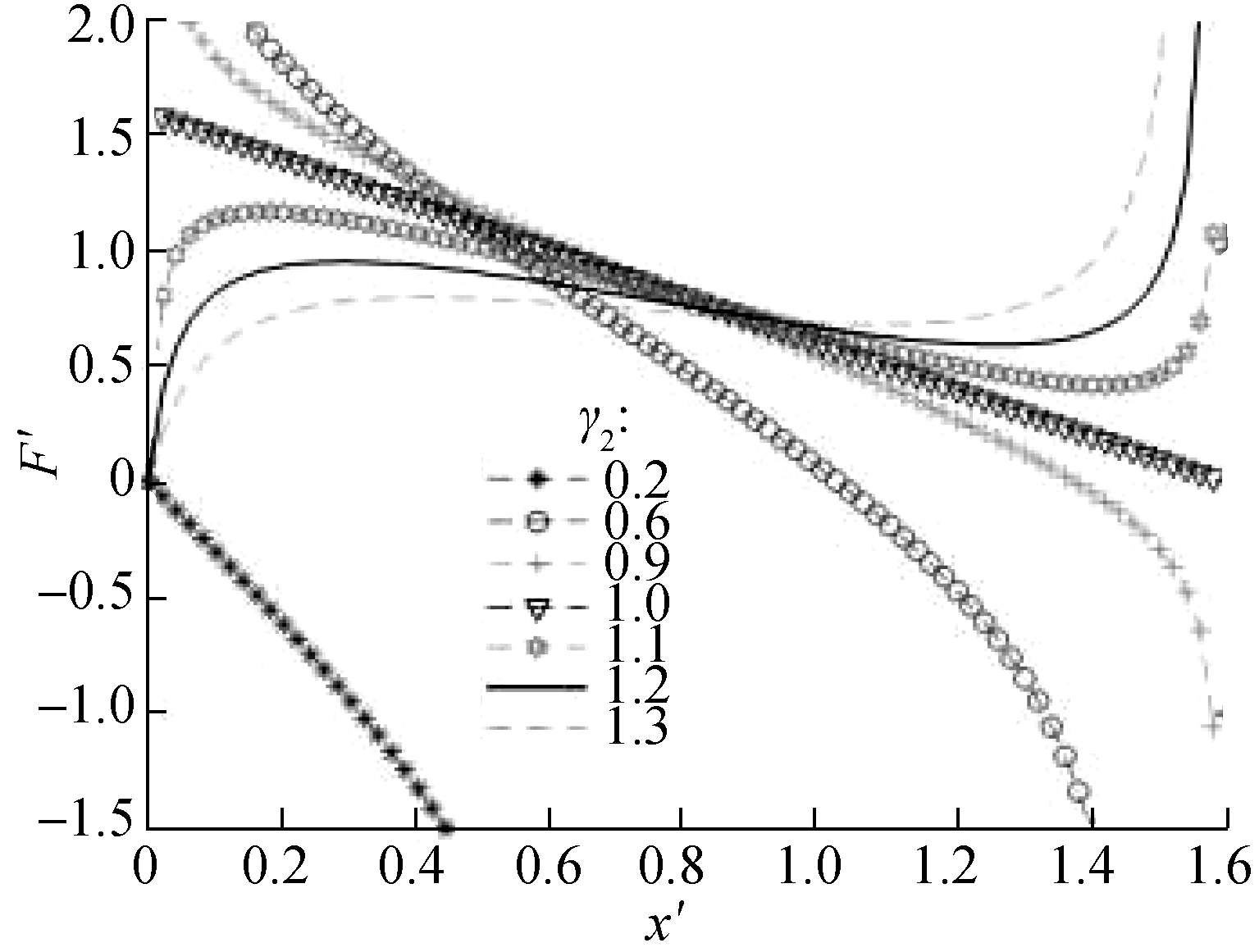
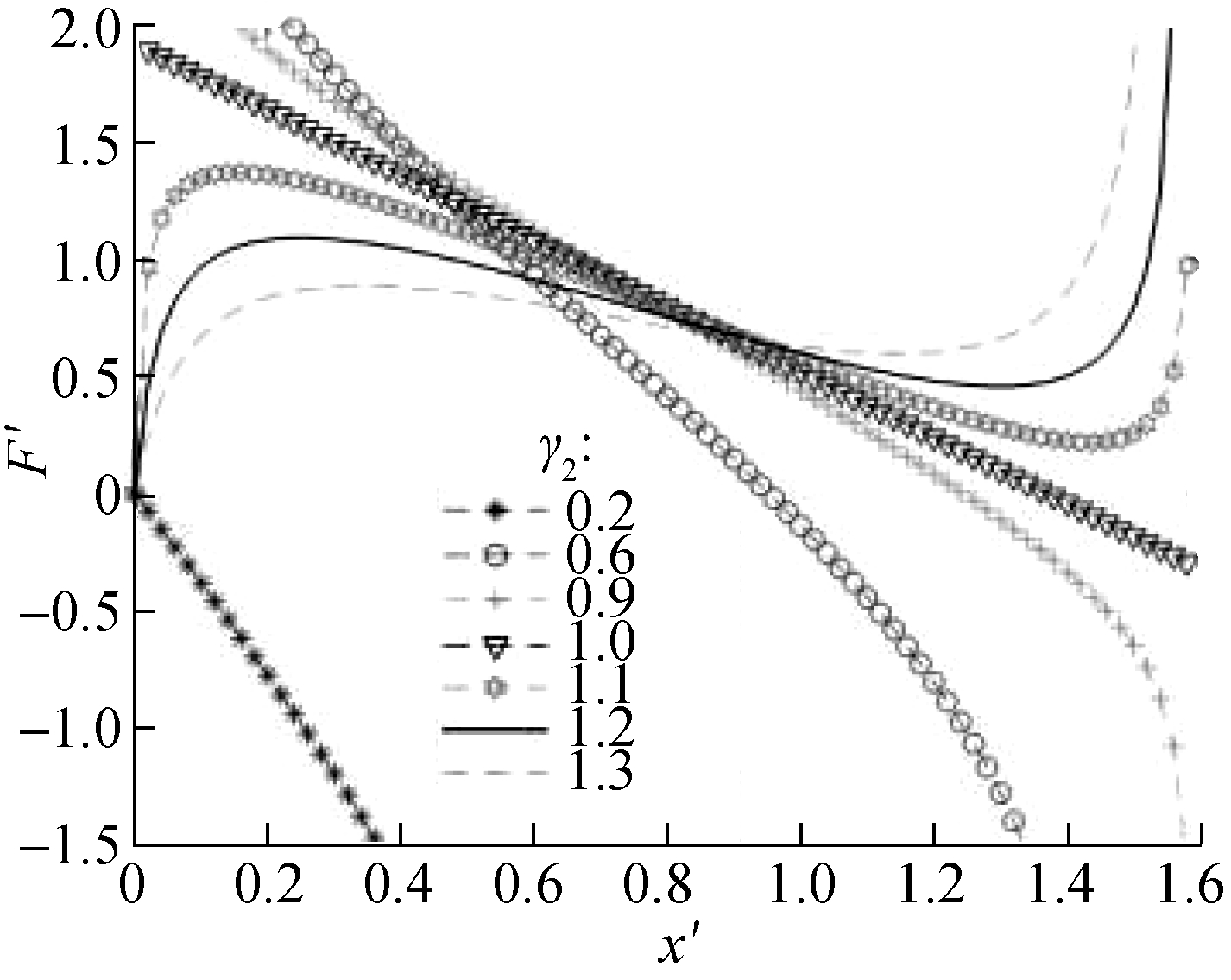
Fig.4 shows the dimensionless force-deflection characteristic curves with different values of γ2. The results show that when γ2>1, the curve changes regularly, similar to an elongated sinusoidal curve, along with the existing maximum and minimum peak values. Thus, the dimensionless force F′ between the two peaks decreases with the increase in displacement, and inversely, in the other positions, the value of F′ increases with the increase in displacement. However, when γ2<1, the initial value of the dimensionless force F′ fluctuates, and the value of F′ decreases with the increase in displacement.
(a)
(b)
(c)
Fig.4 Dimensionless force-deflection curves with various values of γ2. (a) α=0.8,γ1=0.8; (b) α=1.0,γ1=0.8; (c) α=1.2,γ1=0.8
In this case, although the stiffness of the suspension system is negative stiffness, it is unsuitable for the design of the above negative stiffness model structure. When γ2<1, the shape of the stiffness curve is a convex parabola, and the stiffness reaches the maximum peak value in the static equilibrium position. However, at a far enough distance away from the static equilibrium position, the stiffness of the system is always negative, and the vibration-isolation system is in an unstable state. Fig.5 shows the dimensionless force-deflection characteristic curves under different values of α. With the increase in the value of α, the flatness of the curve also changes.
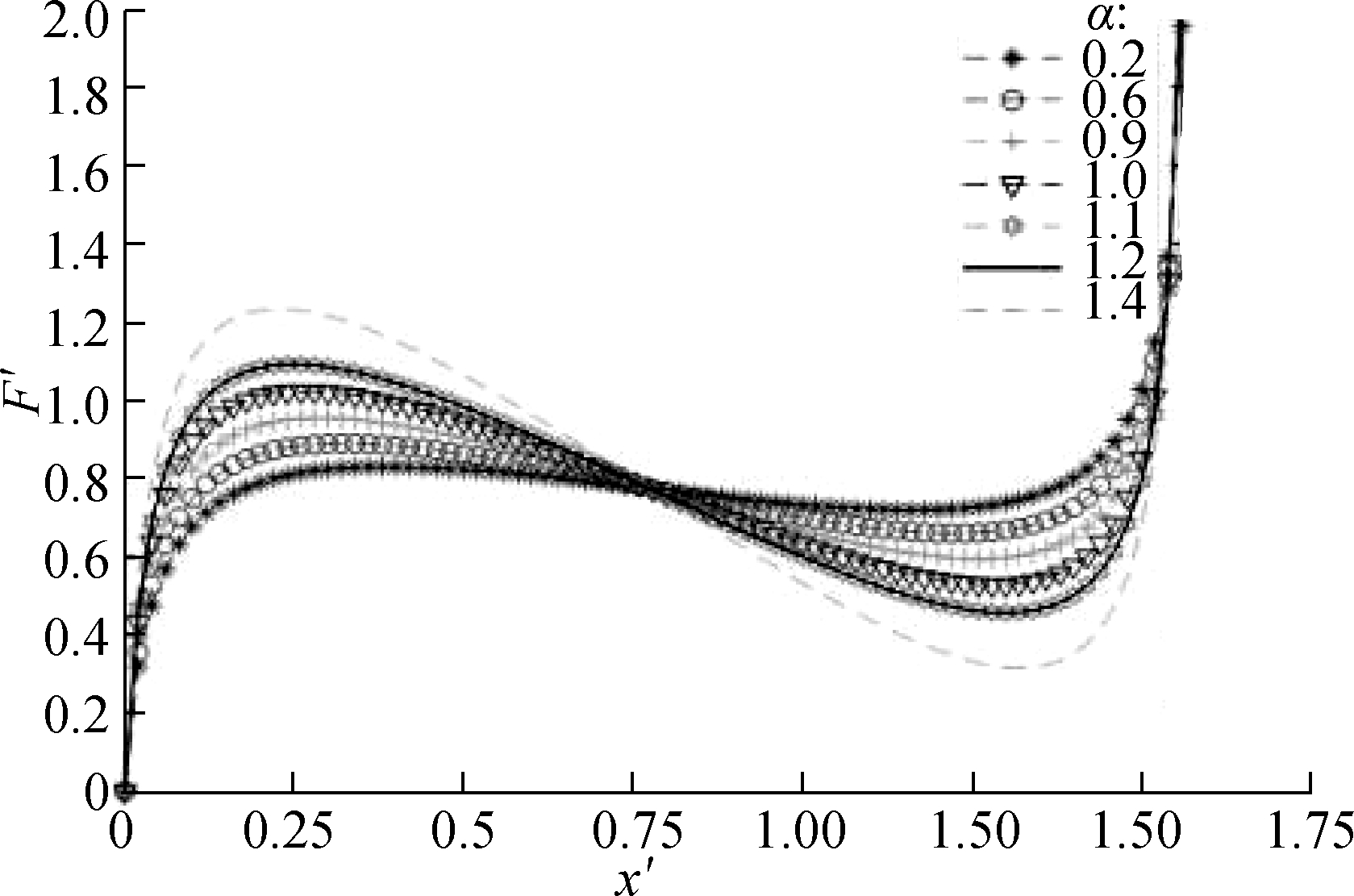
Fig.5 Dimensionless force-deflection curves with various values of α
3.2 Dynamic stiffness analysis of the seat suspension system
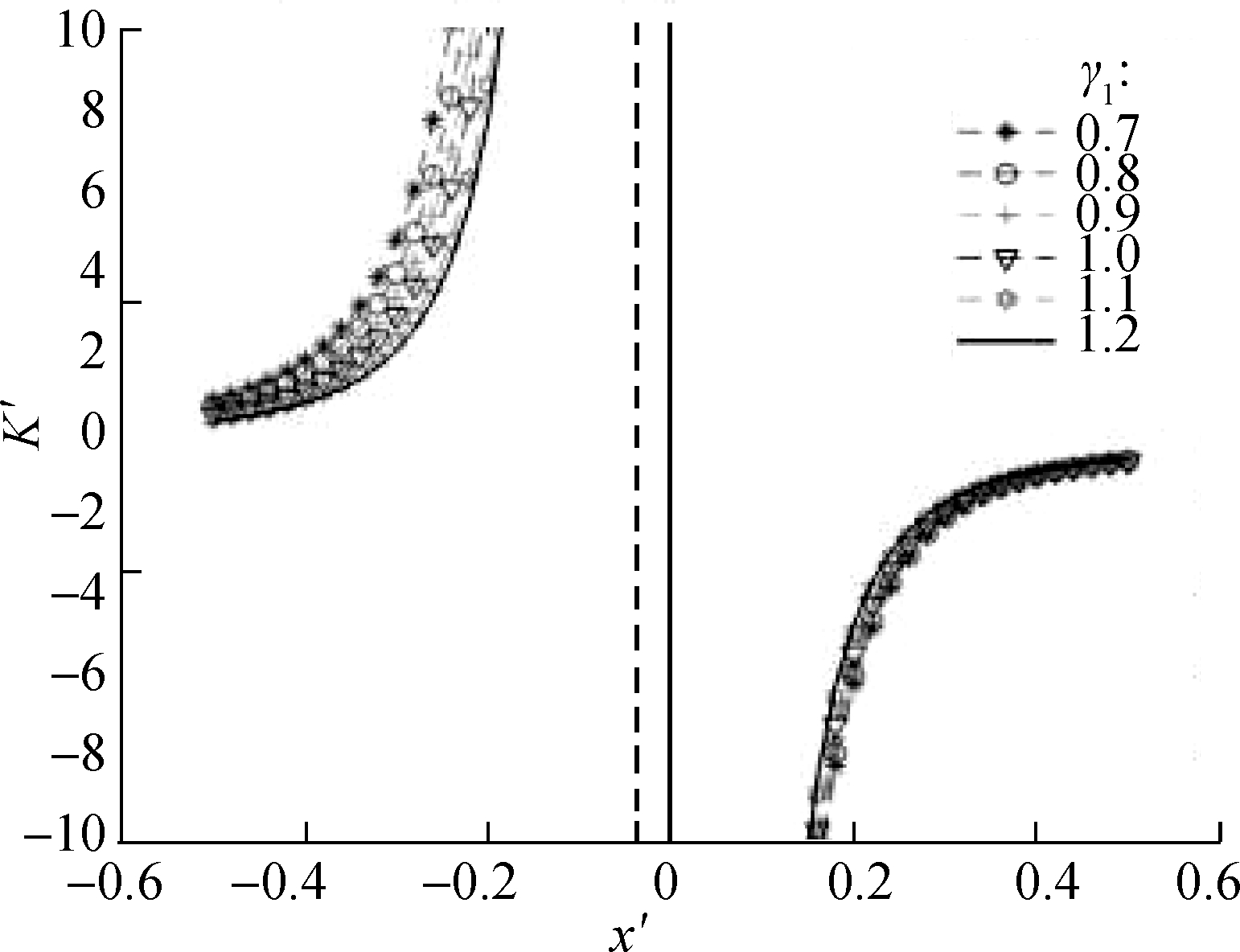
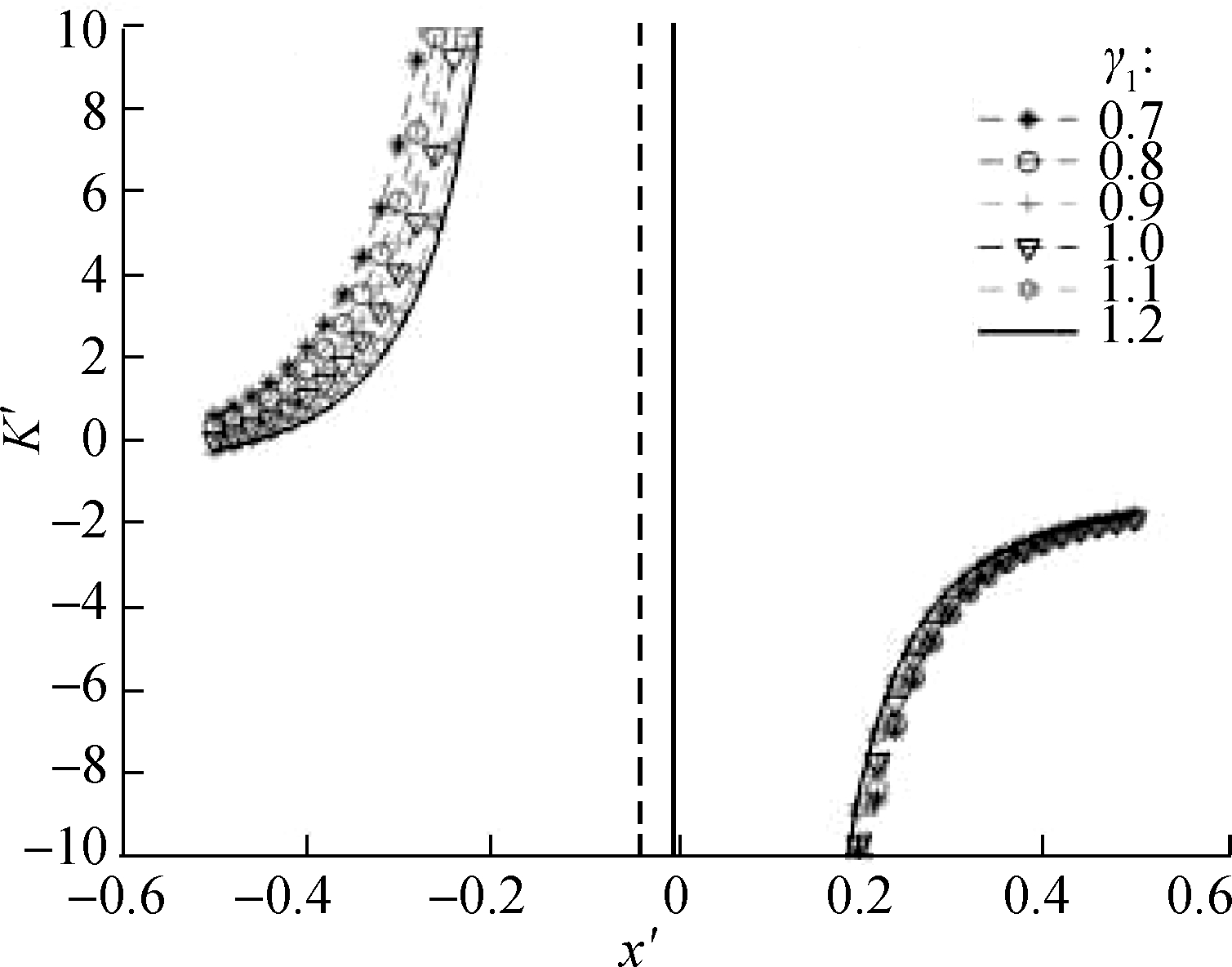
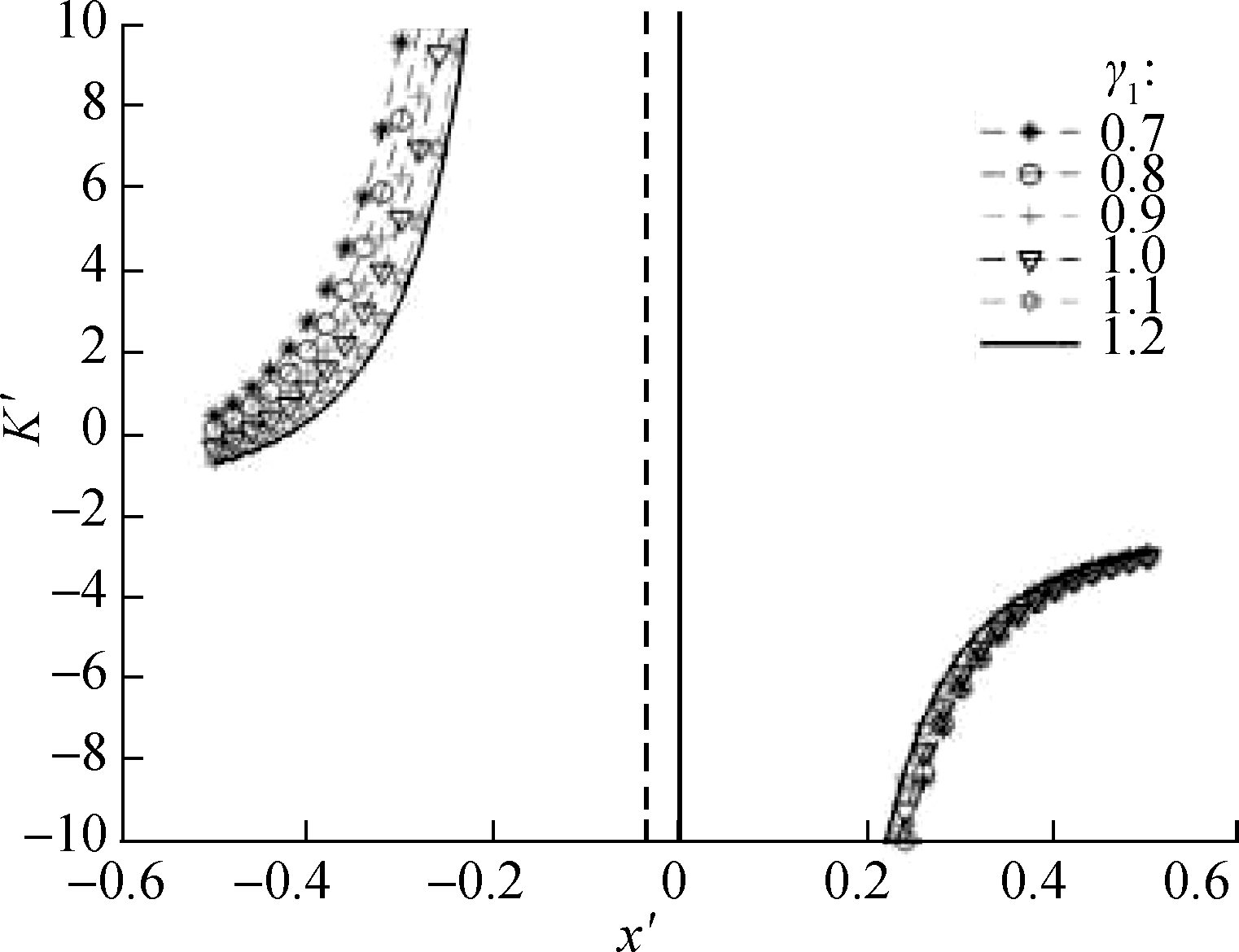
Considering the nonlinear characteristics of the suspension system and multiple design parameters, the dimensionless dynamic stiffness of the system should be used to evaluate the vibration-isolation system to select the appropriate suspension configuration parameters. According to Fig.6, as the value of γ1 increases, the basic outline of the stiffness characteristic curves of the system shows no evident change, whereas changes occur in the curvature of the stiffness characteristic curve. For dimensionless displacement x′<0, when the value of α increases, the absolute values of stiffness of the suspension system also increases. For dimensionless displacement x′>0, when the value of α increases, the curve moves to the right overall, and the suspension system increasingly deviates from the quasi-zero stiffness. Notably, the value of parameter α should not be extremely large.
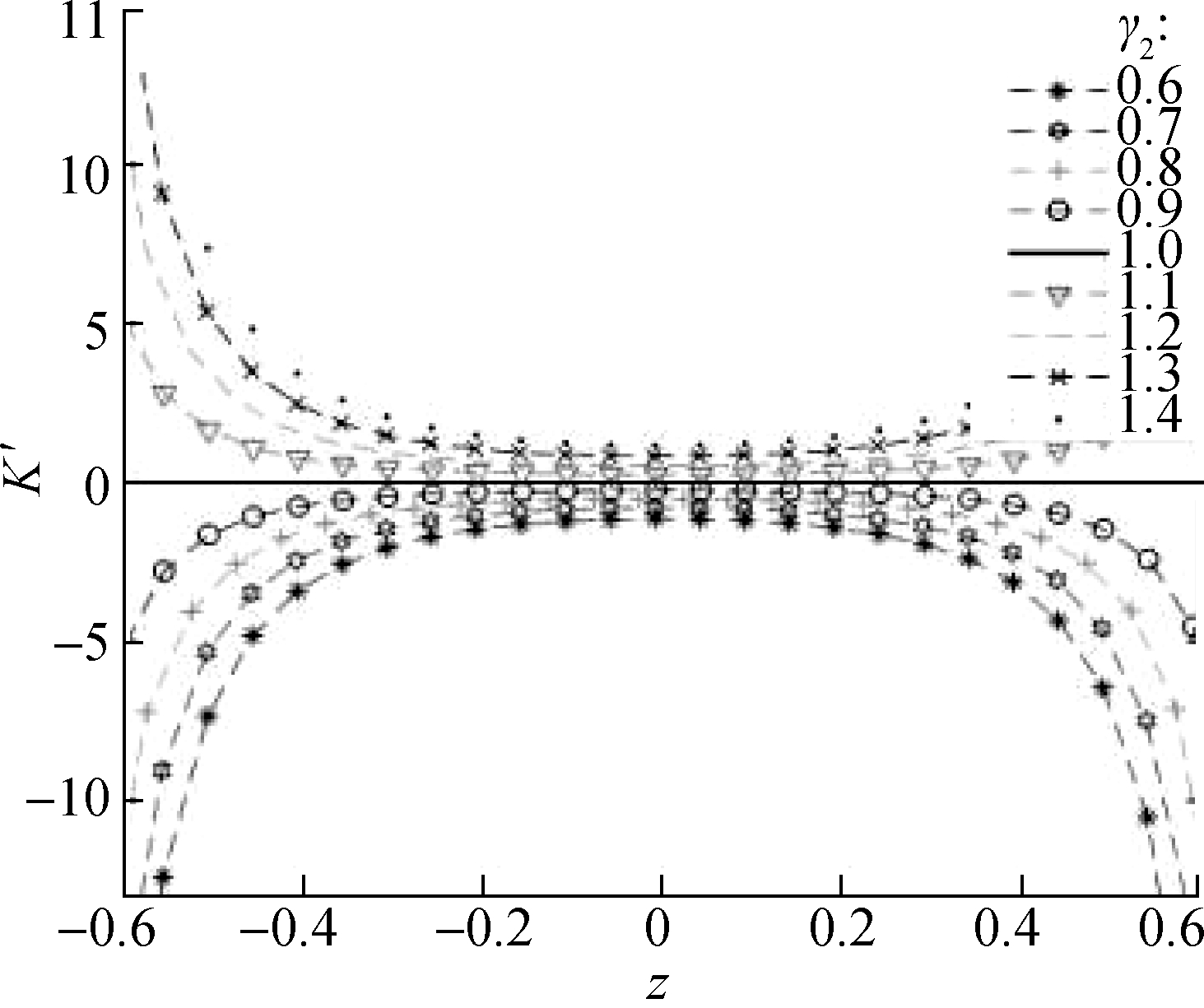
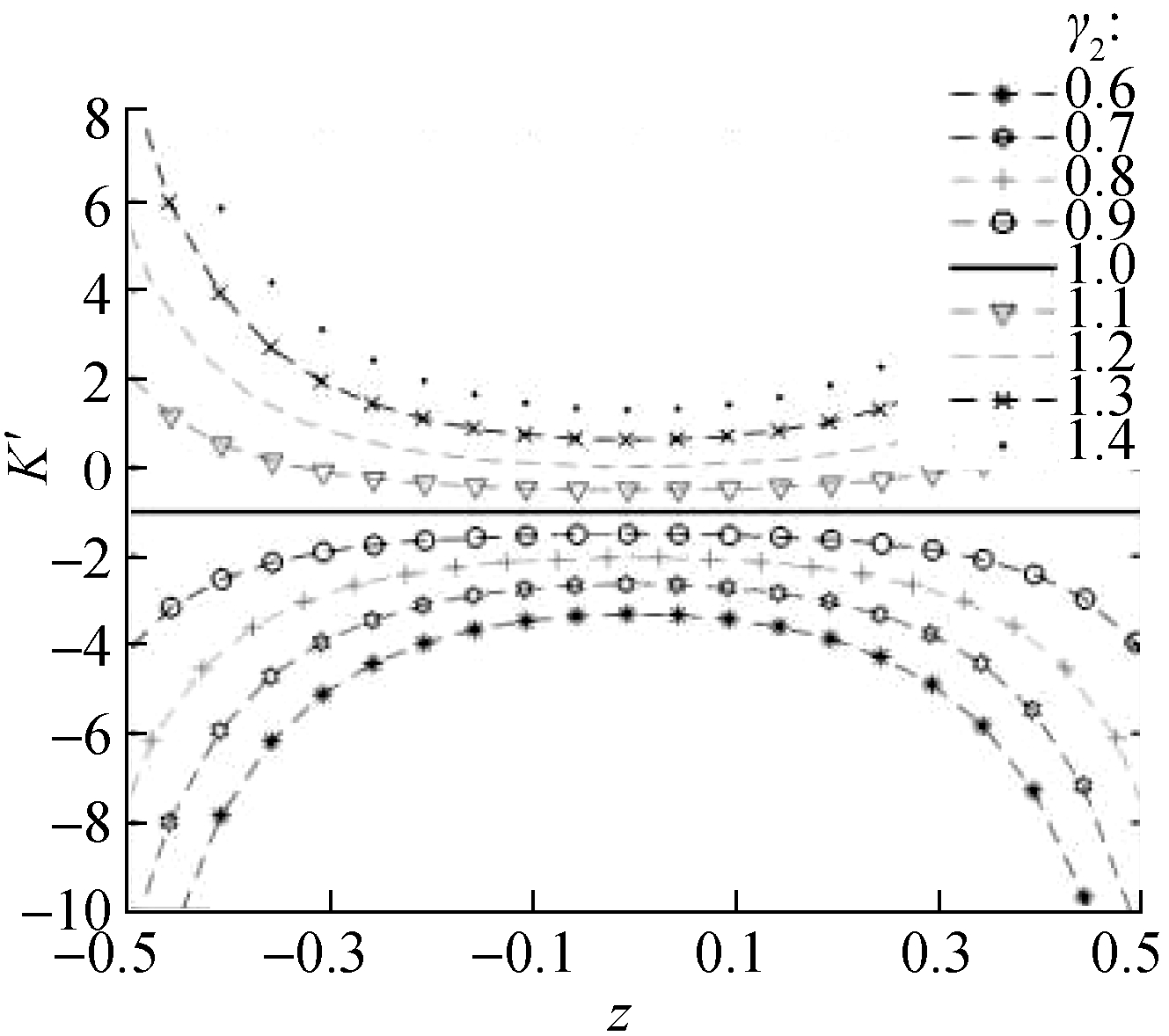
From Fig.7, the corresponding stiffness curves under different values are symmetric at about z=0. When γ2>1, the dynamic stiffness curve has a concave parabola shape, and the stiffness value at the static equilibrium position is the smallest. When α≤1, the stiffness value is always greater than -1. Therefore, the configuration of structural parameters needs to be reasonably selected to ensure that the dynamic stiffness of the static equilibrium position is zero or greater than zero. Additionally, when
(a)
(b)
(c)
Fig.6 Dynamic stiffness curves of systems with various values of γ1. (a) α=0.6,γ2=0.8; (b) α=1.0,γ2=0.8; (c) α=1.4,γ2=0.8
γ2=1 and α=1, the dynamic stiffness curve becomes a straight line, and the stiffness value is always equal to -1. This situation shows that the distance from the mass block to the static equilibrium position can be infinite, and the dynamic stiffness of the region above the line K′=-1 is always less than the static stiffness. However, in the case of γ2>1, the infinite range from the mass block to the static equilibrium position decreases with the increase in γ2.
Fig.7 also shows several sets of stiffness curves corresponding to different values of α. When α=0.5 and γ2>1, the dynamic stiffness of the system around the static equilibrium position is very close to zero, that is, near quasi-zero stiffness. This condition illustrates that the selection of parameters α and γ2 has a certain effect on the stiffness characteristics of the system.
(a)

(b)
(c)
(d)
Fig.7 Dynamic stiffness curves of systems with various values of γ2(z=H-x′).(a) α=0.5,γ1=0.8; (b) α=0.8,γ1=0.8; (c) α=1,γ1=0.8; (d) α=1.2,γ1=0.8
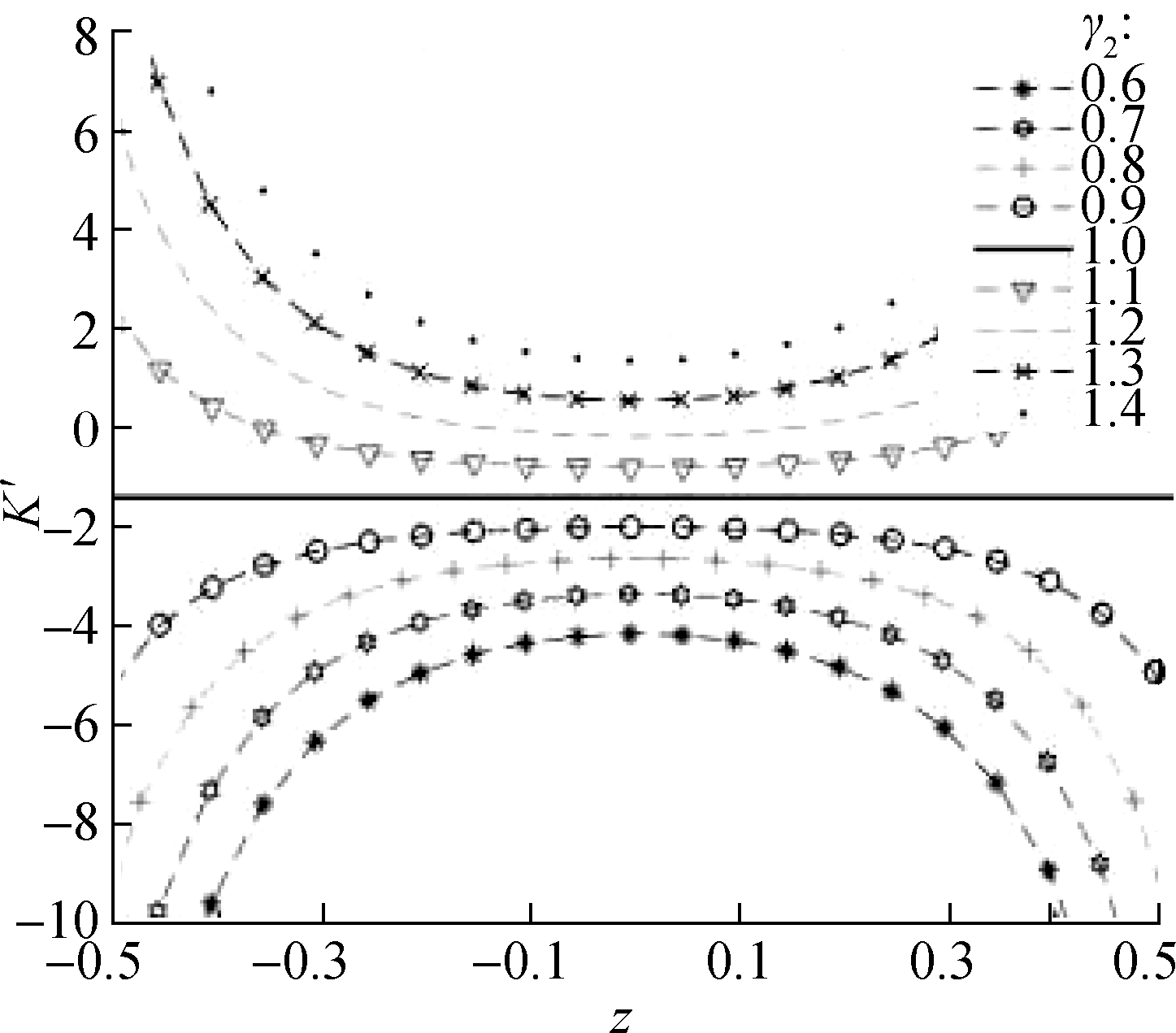
Fig.8 shows the dynamic stiffness curves of the system under different values of α. As the value of α increases, the minimum value of the dimensionless stiffness curve decreases. When α=1, 1.2, the system is close to quasi-zero stiffness, but the concave parabola is closer to the center axis. The correctness of the above γ2>1 analysis results is verified again. The larger the range of displacement changes in the suspension system, the better the vibration-isolation effect. To sum up, the design parameters of the suspension system 1≤γ2≤1.3 and α=0.5 are the ideal configuration parameters of the system. However, in the actual design process, obtaining these accurate values is difficult because of the errors in manufacturing and assembly, and γ2<1 may appear. Thus, the quasi-zero stiffness should be satisfied as much as possible during the design.
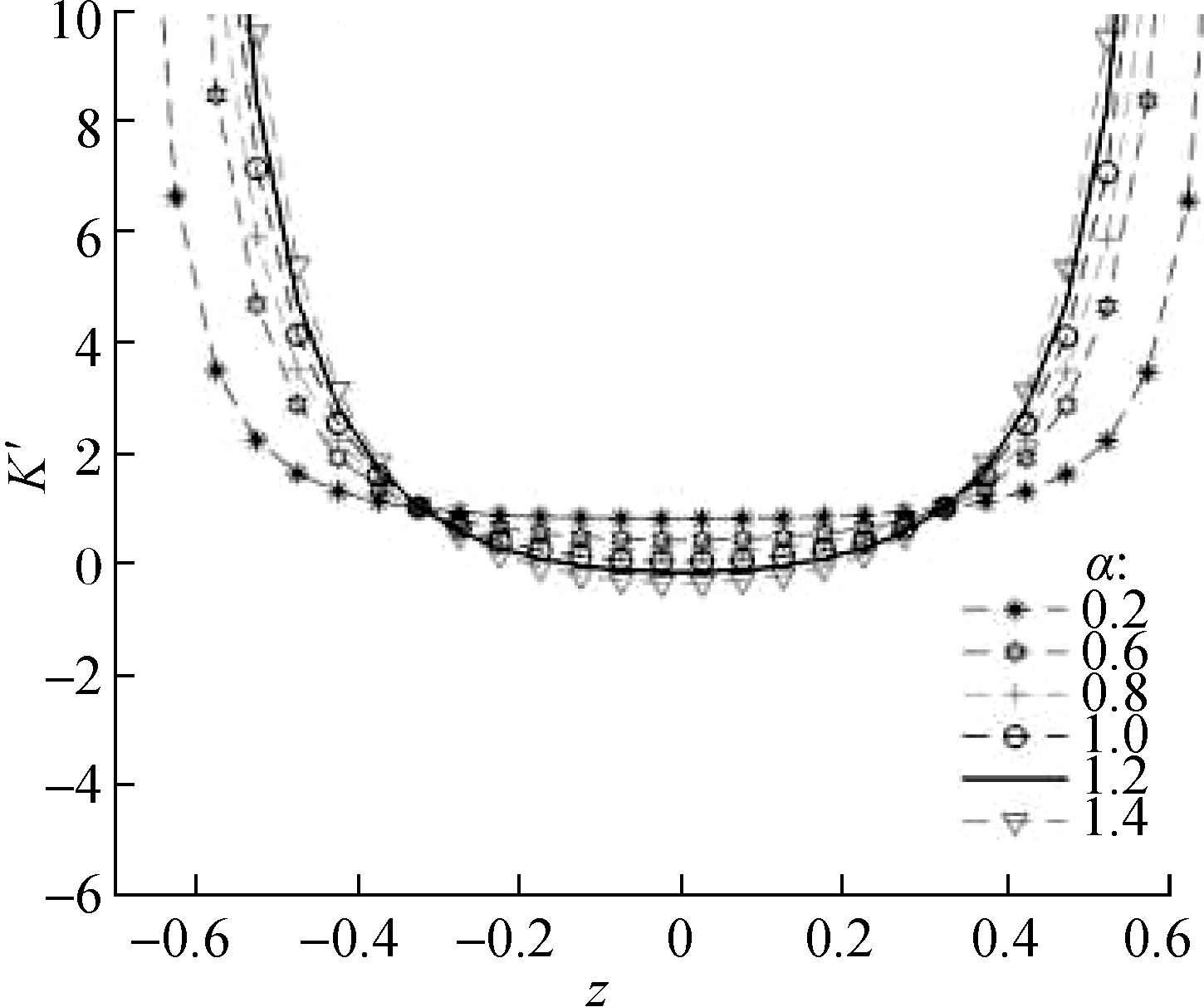
Fig.8 Dynamic stiffness curves of systems with various values of α(z=H-x′)
4 Design Optimization of Cab Seat Suspension System
With a medium loader as an example, the weight of the cab seat is set to 12 kg. The mass range of the human body is 50-85 kg, and the weight range of the mass block in the model is 62-97 kg. Therefore, the fluctuation difference of the mass accepted for the suspension system is 35 kg. According to the design requirements of NSS, the horizontal spring should be forcibly kept horizontally under the static balance. In addition, when keeping the stiffness of the supporting spring unchanged, the maximum floating range is 80 mm in the vertical direction of the designed seat. According to the calculation of the vertical spring stiffness, an additional displacement should be required for the no-load condition as 12.25-20.83 mm, which describes the distance required when the system reaches the equilibrium position at the moment the driver first takes his seat. In this paper, the selected value is a little large, and the stiffness of the support spring is increased moderately to reduce the displacement deviation caused by the input of different system masses.
4.1 Cab floor vibration
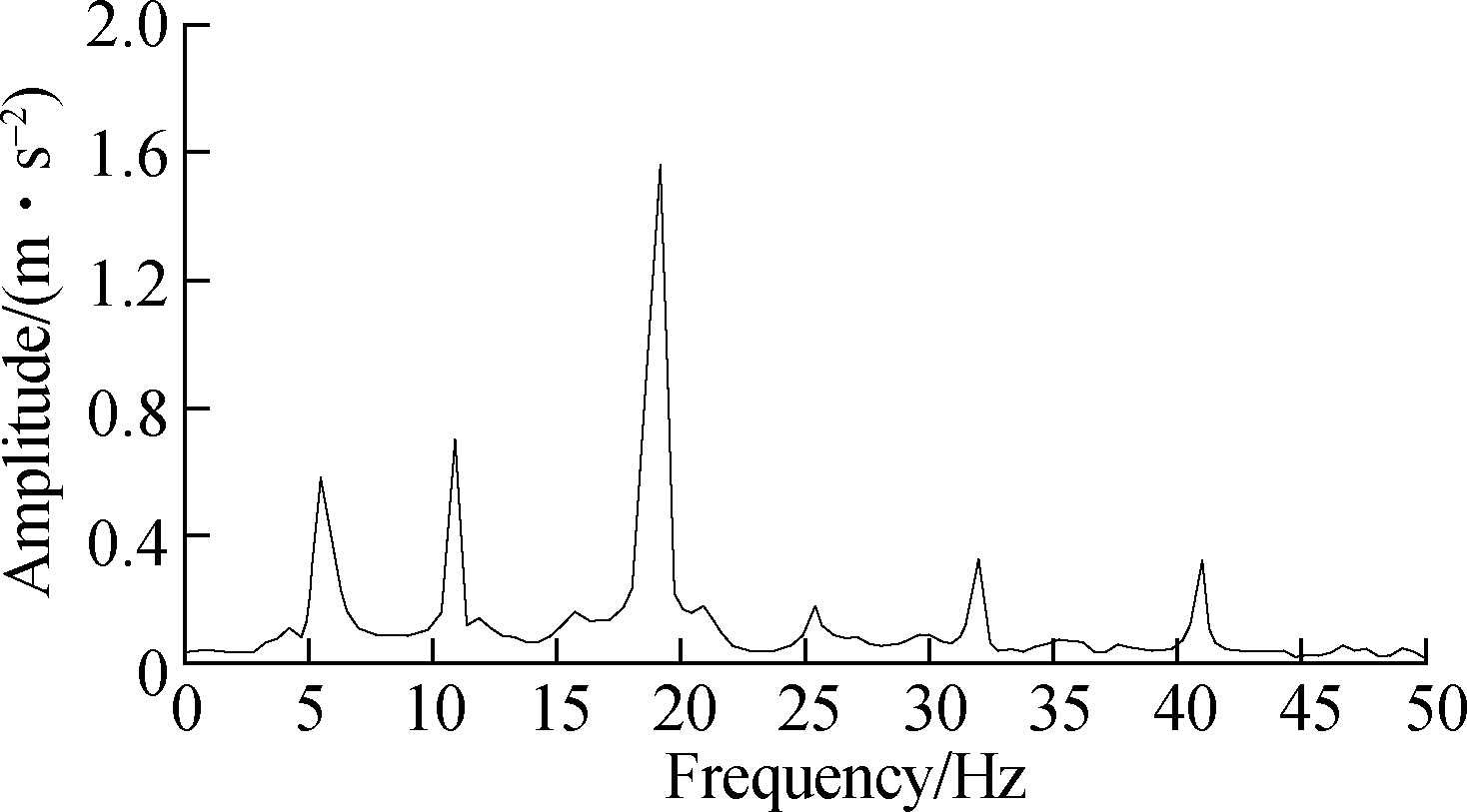
Cab floor vibration is a common phenomenon in construction machinery operations. The vibration source is one of the prerequisites for the simulation of the seat suspension system. The vibration of most construction machinery vehicles is produced by the engine, main/tail rotor, and transmission, which are mechanically connected together. The variable speed motion is carried out by the engine governor, and the vibration is finally passed through the seat to the driver, which results in the whole-body vibration of the driver[5]. In this paper, with the same type of loader as an example, the frequency of the vehicle generating the vibration source is extracted (see Tab.2). The data in the right side of the table can be used to identify the frequency component in the frequency domain diagram, that is, the vibration signal of the cab floor can be reproduced for simulation. In addition, the amplitude of the seat model depends on the external natural conditions during the operation of the construction machinery (such as the soft degree of the road surface, slope turning road, and other road conditions). The excitation source is changeable, and the vibration source propagation path is long, resulting in the external excitation at the connection between the cab floor and the very unstable seat connection. For this reason, the collection of vibration amplitude data is difficult, and thus, the data in other references are referred to[21]. Fast Fourier transform (FFT) is used, and the vibration signal is converted from the time domain to the frequency domain[22]. The amplitude of the frequency component of the vibration signal for the cab floor is reproduced (see Tab.3). Given that the effects of vibration frequencies above 50 Hz on the human body gradually decrease according to ISO 2631, the frequencies above 50 Hz are ignored when the vibration signal of the cab floor is reproduced.
Tab.2 Vibration sources and frequencies of the loader

Vibration sourceSpeed r·min-1 Frequency/HzMain rotor3365.2Tail rotor59112.7Hydraulic pump3 20019.5Rotor drive shaft3 70025.3Transmission input shaft5 50032.6Oil cooler5 80041.7Rotor brake6 30053.4
Tab.3 Vibration sources and frequencies of the loader

Frequency/Hz5.212.719.525.332.641.7Amplitude/g0.0520.0650.1360.0170.0410.043 Amplitude/ m·s-2 0.590.731.580.140.360.37
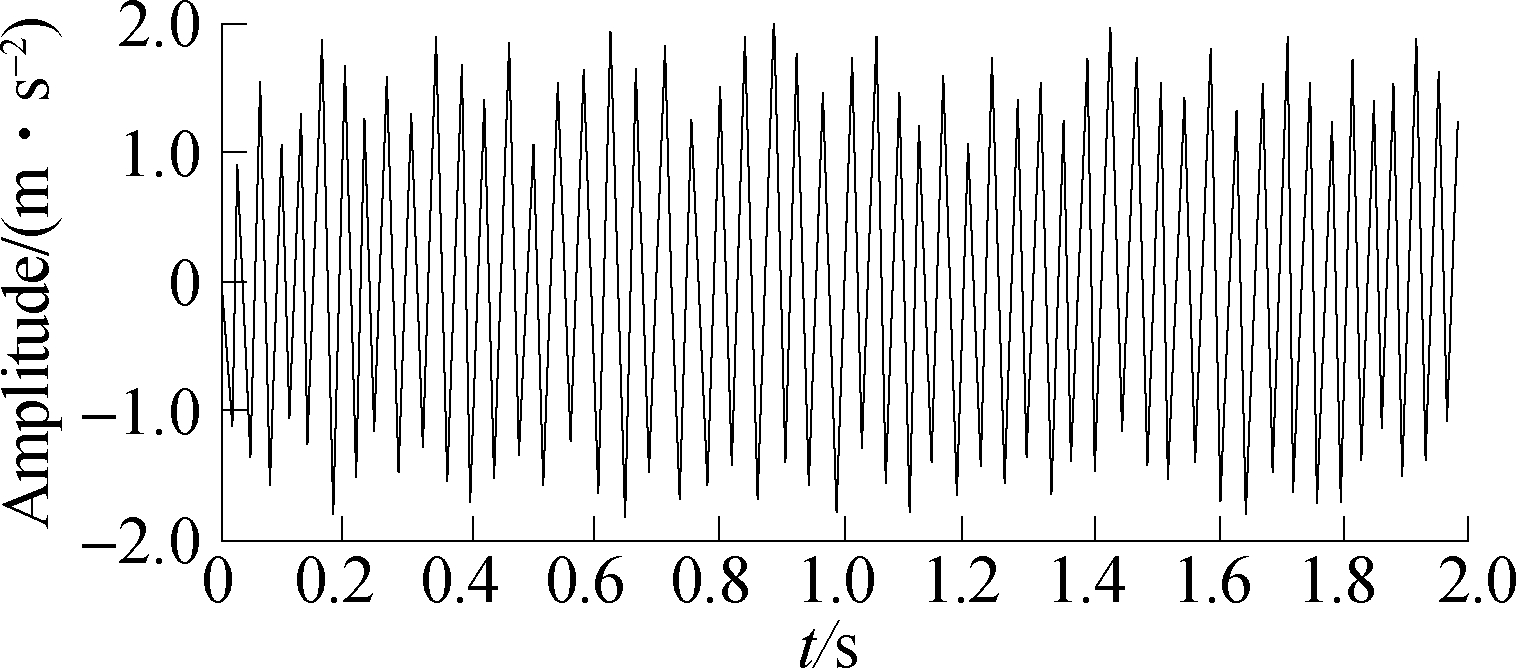
Fig.9 shows the time domain and frequency domain diagram of the vertical vibration signal of the cab floor. The reproduced signal is simulated as the excitation signal of the floor.
(a)
(b)
Fig.9 Reproduced vibration signal of the cab floor in the vertical direction. (a) Time domain map; (b) Frequency domain map
4.2 Evaluation criteria for suspension systems
Different methods are used to evaluate system vibrations. At present, the weighted root mean square (RMS) is widely used to evaluate suspension vibrations. However, the use of the RMS method will underestimate the effects of vibration characteristics with numerous peaks[23]. Therefore, the four-time power vibration dose value(VDV) method is used to evaluate the vibration characteristics of the suspension system, because the VDV method is sensitive to the peak value of vibration. Its expression is
(19)
where the unit of AVDV is m/s1.75 or rad/s1.75; aw(t) is the instantaneous frequency weighted acceleration; and T is the duration of the measurement.
To evaluate the effectiveness of the seat suspension system and reduce the vibration transfer amplitude, the frequency weighting function is considered based on the ISO 2631 standard, and seat effective amplitude transmissibility (SEAT), which is defined as follows, is adopted:

(20)
where ![]() is the weighted RMS acceleration for the cab floor.
is the weighted RMS acceleration for the cab floor.
To evaluate the vibration transmissibility characteristics of the NSS suspension system in the frequency domain, we use the following equation to calculate the vibration transmissibility ratio:
(21)
where GBX is the cross power of vibration signals of the cab floor and seat; and GBB is the auto power of vibration signals of the cab floor in the vertical direction. The calculation equation is as
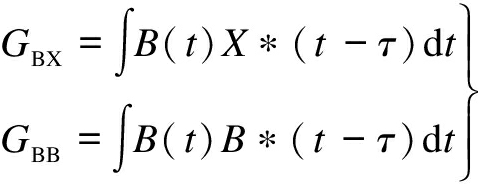
(22)
where B and X represent the floor and seat bottom vibrations, respectively; τ is the time delay between signals; and * is the conjugate signal. The frequency with a transmissibility ratio greater than 1 represents the amplified frequency through the vibration transfer path.
4.3 Optimization model of cab seat suspension system
The design variable refers to the stiffness of the seat suspension system, and the optimization model of low-frequency response for the cab suspension system is as
![]()
1≤γ2≤1.3, α=0.5![]()
![]()
![]()
where ωexc is the excitation frequency; ωn is the natural frequency of the system; and keq is the total vertical stiffness of the suspension structure. As shown in Figs. 6-8, the value of the dimensionless equivalent stiffness is k′=0.3. The established dynamic model is simulated and calculated by using MATLAB, and the constraint optimization method is used to solve the problem. The design domain contains discrete points, and the optimal solution is searched for. Given the actual engineering design, the parameter values are generally rounded off. Tab.4 shows the structural parameters of the designed seat suspension system.
Tab.4 Parameter setting of seat isolation system

ParameterValuesL0/mm200 220 230 240 250 260a/mm260 275 285 300 315 325b/mm180Kv/ N·mm-1 28 34 40 46 52 58Kh/ N·mm-1 14 17 20 23 26 29M/kg62-97
4.4 Simulation results
Based on the above NSS suspension system dynamics model, the displacement and acceleration response curves of the seat are obtained by optimization design (see Fig.10). The vibration signal of the floor is compared with the vibration signal transmitted to the seat. The results show that the response amplitude of the optimized system is remarkably reduced, which indicates that the suspension model based on the NSS effectively reduces the vibration transmitted to the seat through the cab floor. Tab.5 shows the comparison between the vibration characteristics of the cab floor after optimization and those transmitted to the seat. The VDV and RMS method calculation values of the seat in the vertical vibration direction are 0.192 7 and 0.150 6, respectively. Compared with the cab floor vibration, the vibration amplitude and peak amplitude decrease by 86% and 87%, respectively. The finding also illustrates the improved vibration-isolation performance of the seat suspension system. In addition, according to the ISO 2631 standard, the results in Tab.5 show that the driver’s ride comfort and vibration environment have been substantially improved.
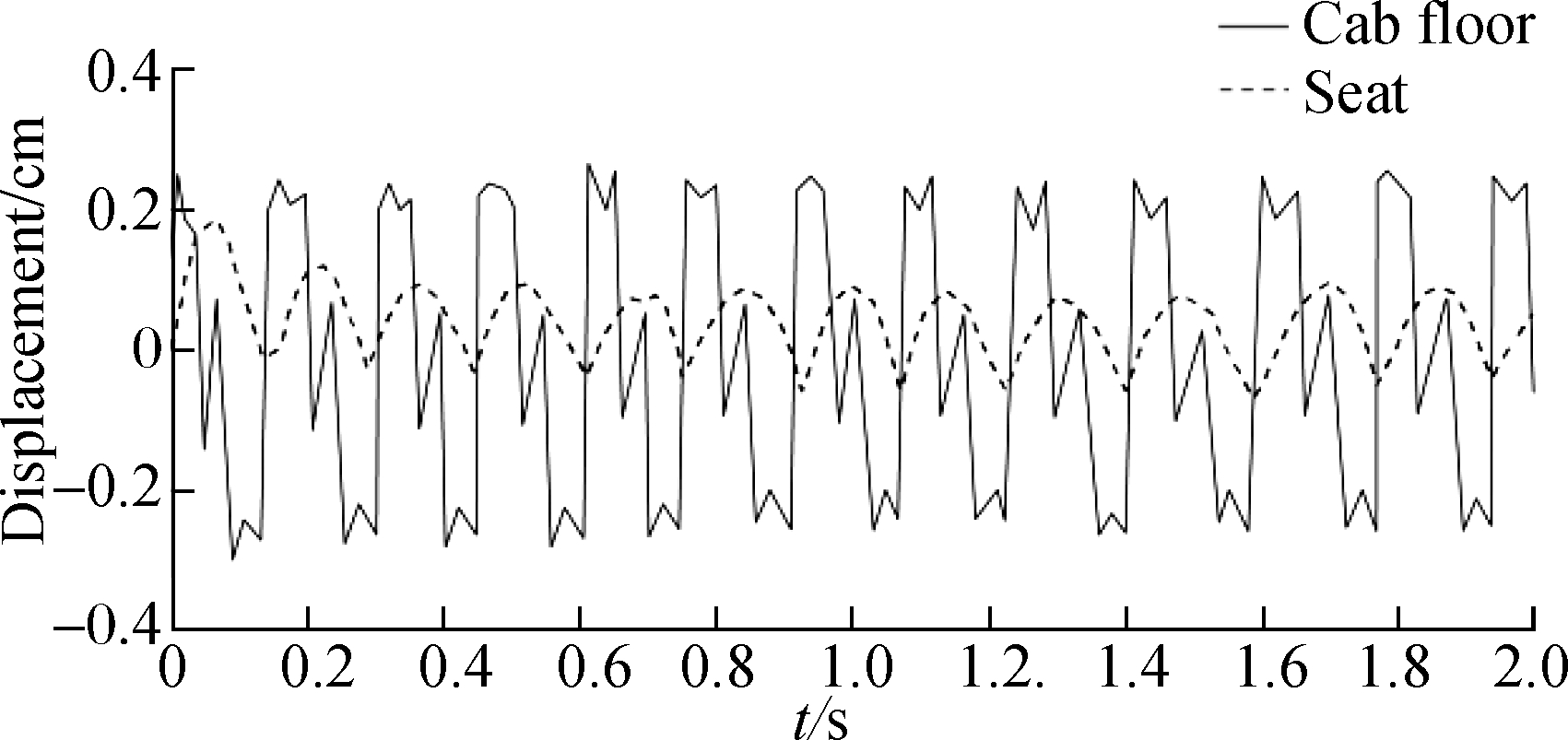
(a)
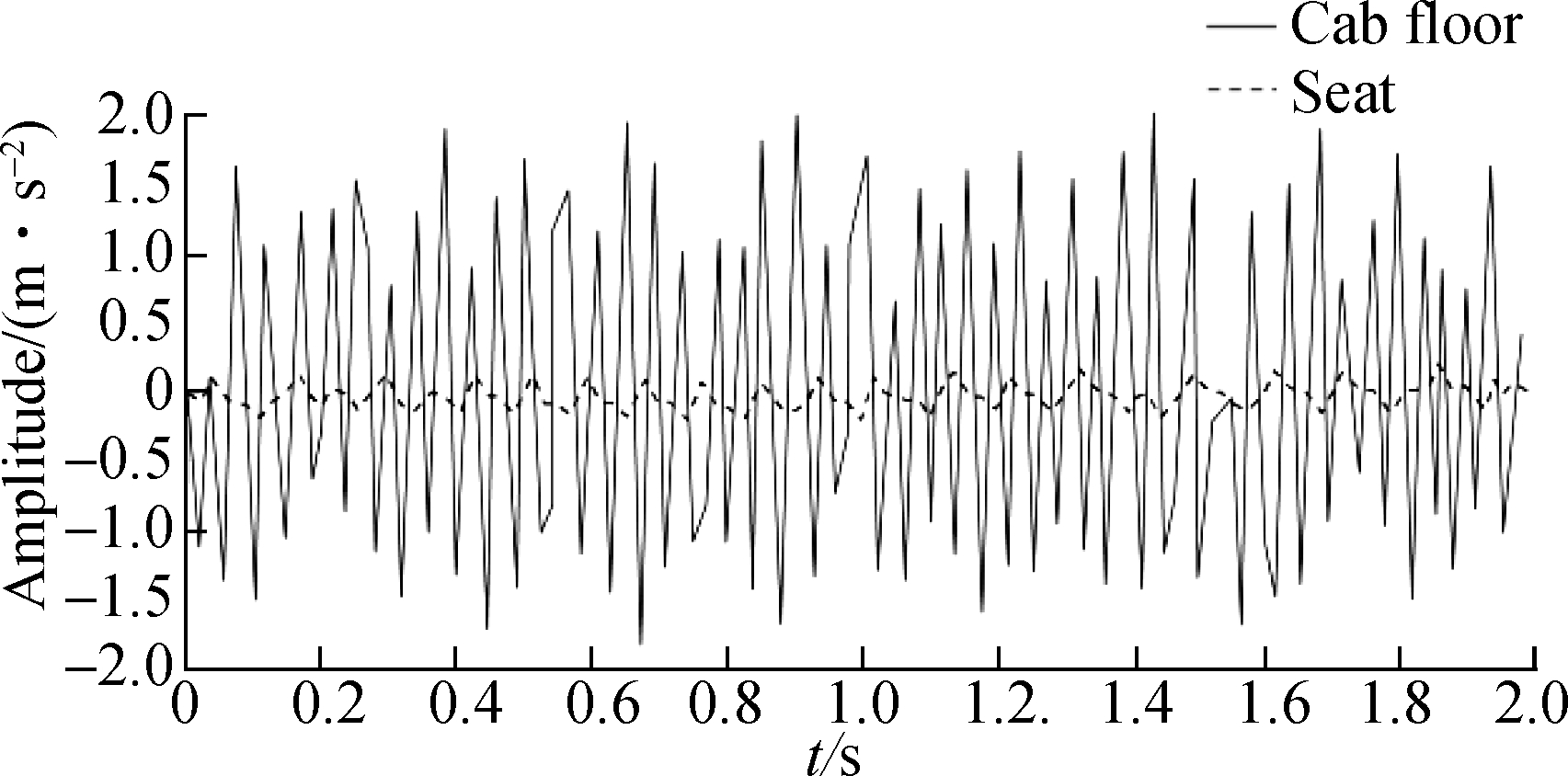
(b)
Fig.10 Amplitude contrast between the cab floor and vibration signal transmitted to the seat (i.e., driver) after optimization. (a) Displacement amplitude; (b) Acceleration amplitude
Tab.5 Vibration characteristics of cab floor and vibration characteristics transmitted to the seat after optimization

Vibration source positionCab floorSeat VDV/ m·s-1.75 1.482 60.192 7 RMS/ m·s-2 1.075 80.150 6 Drivers ride comfortPoor comfort and feelapparent discomfortGood comfort and not causing adverse disease
Given that VDV and RMS only reflect the main characteristics of vibration signals, the performance of the suspension system can be evaluated intuitively by calculating ASEAT and Ttrans. Tab.6 presents the evaluation results obtained after the optimal design. The values of ASEAT and Ttrans are 0.0874 and 0.0755, respectively. Compared with the suspension system with vertical spring stiffness only, the vibration transmissibility rate of the seat decreases, which illustrates that the NSS suspension system has good vibration-isolation performance.
Tab.6 Vibration sources and frequencies of loader after optimization
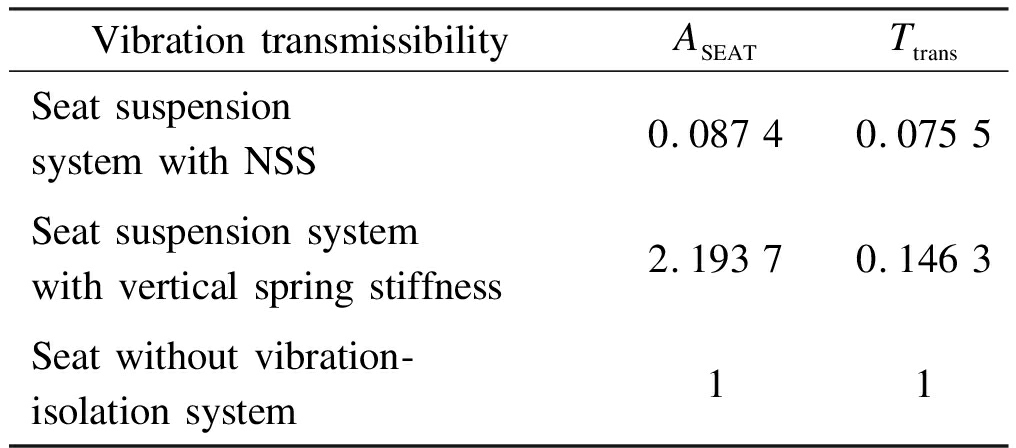
Vibration transmissibilityASEATTtransSeat suspension system with NSS0.087 40.075 5Seat suspension system with vertical spring stiffness2.193 70.146 3Seat without vibration-isolation system11
To analyze the difference between the vibration frequency transmitted to the driver and the resonance frequency of the human body, we analyze the vibration characteristics of the seat in the frequency domain in this paper. Fig.11 shows the vibration FFT spectrum transmitted to the driver through the suspension structure. The results show that for the optimization model, the vibration frequency transmitted to the driver changes is within 1-50 Hz, in which the minimum frequency value is 4.7 Hz. Given that the human body is sensitive to certain special frequencies, the driver or certain parts of their body will suffer from diseases when they are exposed to such vibrational frequencies for a long time. Human body vibration has a critical frequency of 4 Hz[11,24-25], and 4.7 Hz is very close to this critical frequency. Given the internal damping of the human body and the low amplitude transmitted to the seat, the frequency of 4.7 Hz will not cause physical discomfort to the driver. Moreover, none of the other frequency values in the spectrum approach the other critical frequency values of the human body. To sum up, the design of the seat suspension system has no adverse effect on the health of the driver after being vibrated. Fig.12 shows the vibration spectrum contrast of the cab floor and seat suspension system. The acceleration amplitude is evidently reduced, and the spectrum diagrams of the seat and the cab floor are notably similar. These findings illustrate that no frequency regulation occurs in the vibration transfer path.
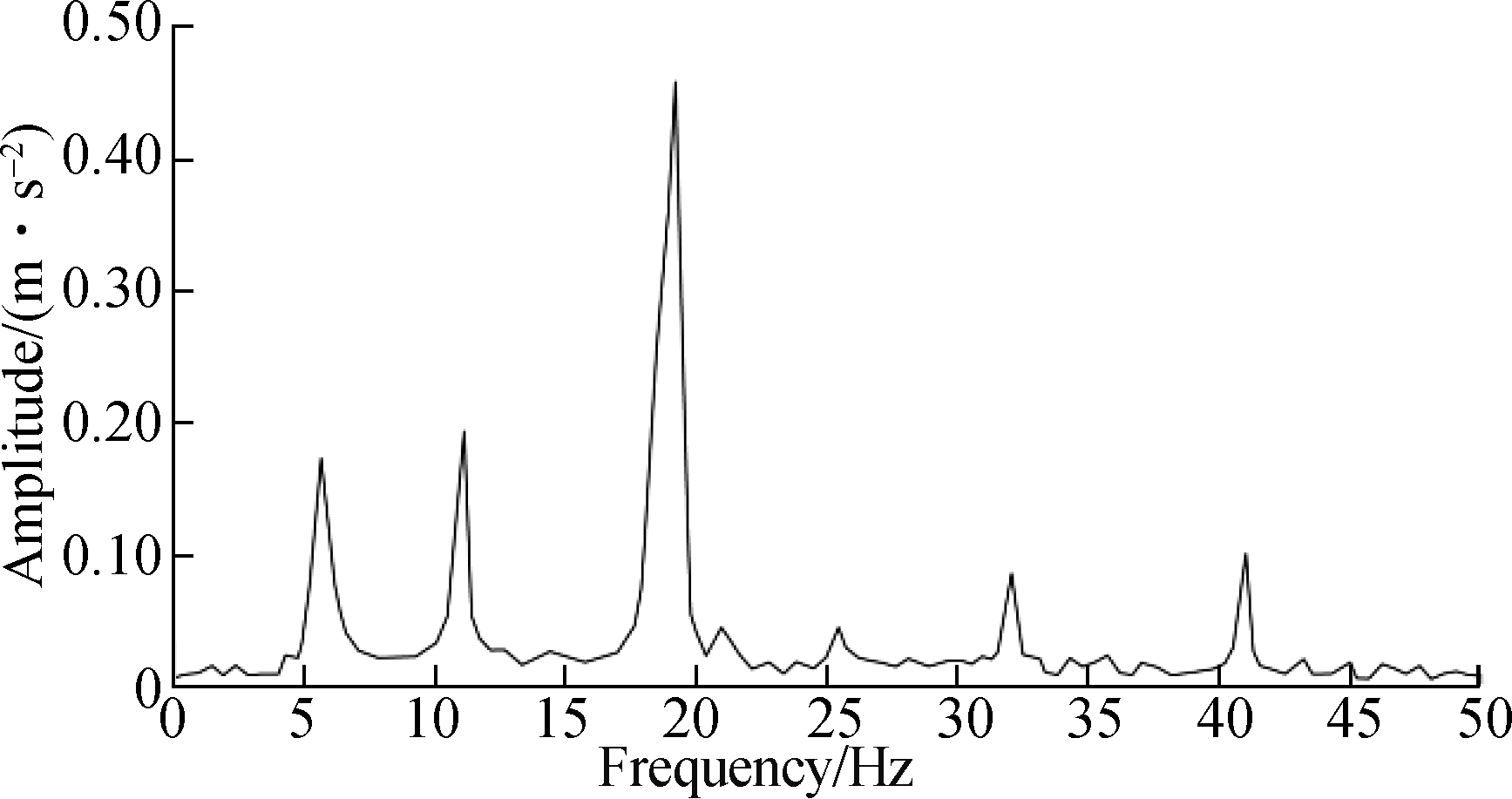
Fig.11 Vibration spectrum of the optimal model of the seat suspension system
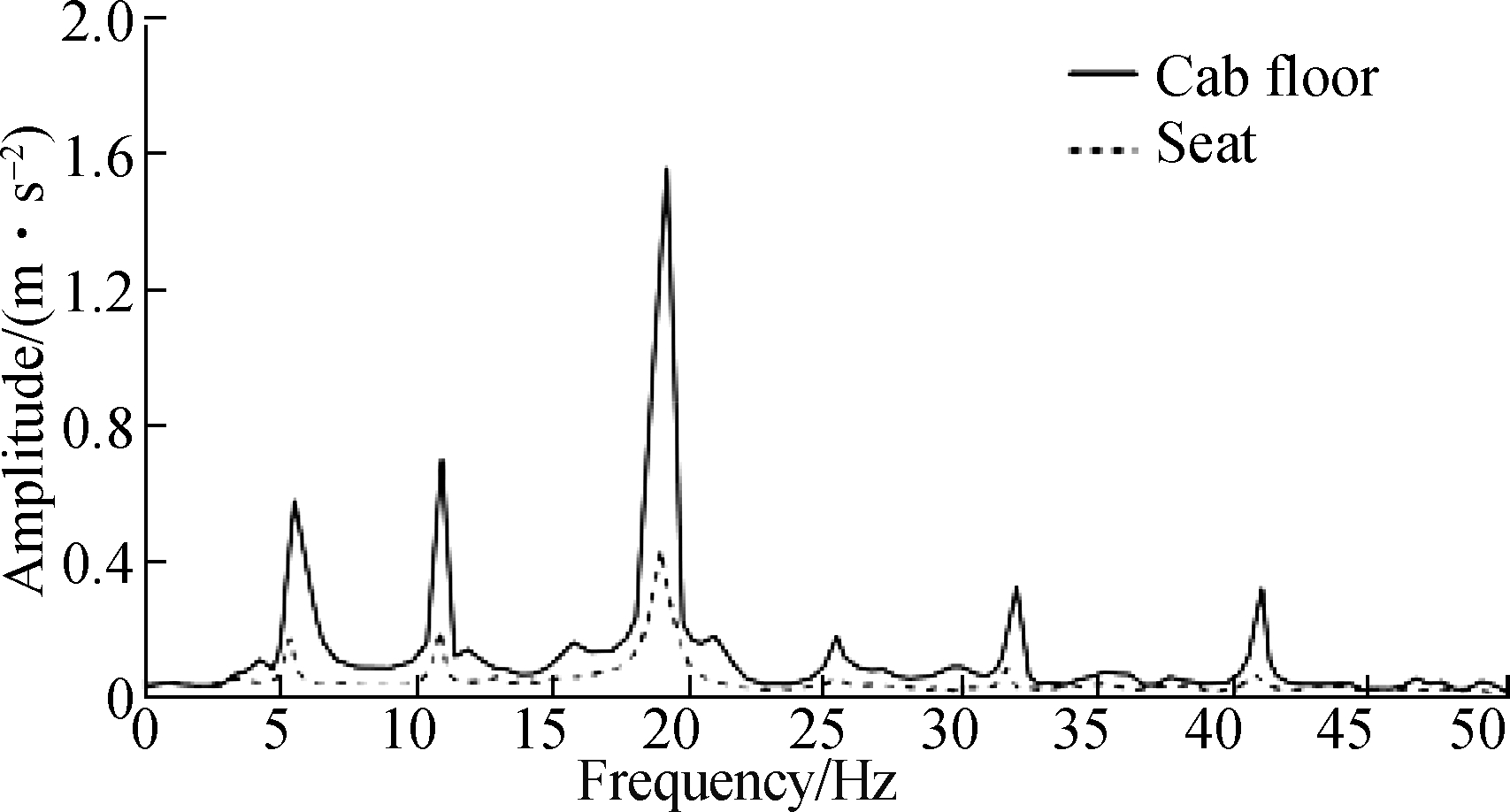
Fig.12 Comparison of vibration spectrum between the cab floor and seat (transmitted to driver)
To study the influence of different loads and uncertainty on the performance of the suspension system, based on the optimization model, we carry out simulations based on different driver weights and the uncertainty of stiffness coefficients. Tab.7 shows the comparative analysis results. The ASEAT values of the seat suspension system are given in the table. When the load P≥ 80 kg, the value of ASEAT increases with the increase in uncertainty of the spring stiffness coefficient. The vibration transmissibility rate also increases. When the load P<80 kg, an increase in the uncertainty of the spring stiffness factor first leads to a small ASEAT value. This finding indicates the improved performance of the suspension system. Then, the ASEAT value increases, and the vibration-isolation performance of the system decreases gradually.
Tab.7 ASEAT values of NSS suspension system under different uncertainties
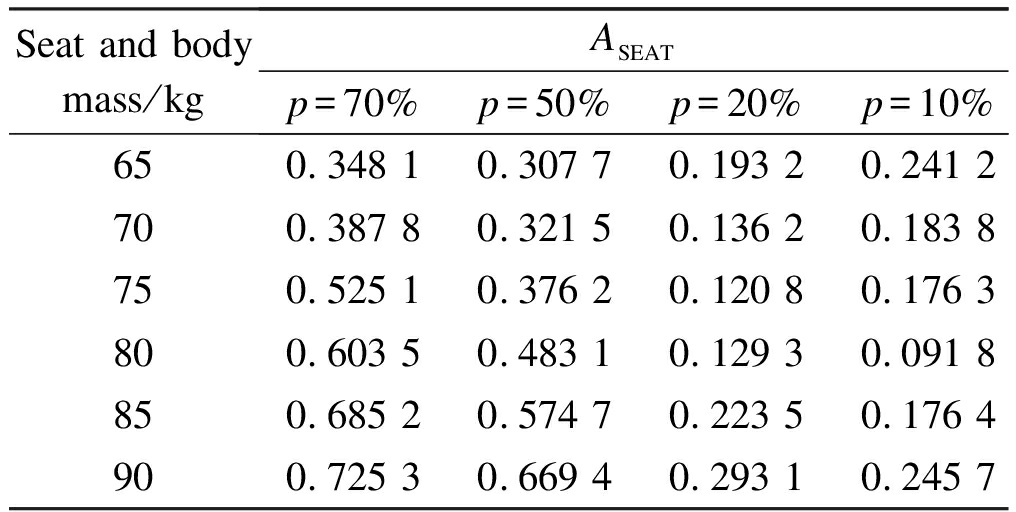
Seat and body mass/kg ASEATp=70%p=50%p=20%p=10%p=5%650.348 10.307 70.193 20.241 20.259 3700.387 80.321 50.136 20.183 80.197 6750.525 10.376 20.120 80.176 30.187 4800.603 50.483 10.129 30.091 80.081 5850.685 20.574 70.223 50.176 40.132 6900.725 30.669 40.293 10.245 70.231 9
Tab.8 shows the Ttrans values of the seat suspension system under different percentages of uncertainty p. The results show that as the uncertainty of the spring stiffness coefficient increases, the value of Ttrans increases gradually, and the vibration-isolation performance of the seat decreases. Different evaluation criteria are used between ASEAT and Ttrans values. The ASEAT calculation results express the reduction of the vibration amplitude itself, whereas the Ttrans values emphasize the relative dependence between the signals of excitation and seat vibration. Furthermore, the results from Tabs. 7 and 8 show that the performance of the suspension system exhibits no significant change with the variations in load mass, which indicates that any change in the driver’s weight in the range of 65-90 kg has no effect on the performance of the seat suspension system. To sum up, regardless of the uncertainty of the stiffness coefficient and changes in the load mass, the suspension structure still presents a good performance.
Tab.8 Ttrans values of NSS suspension systems under different uncertainties
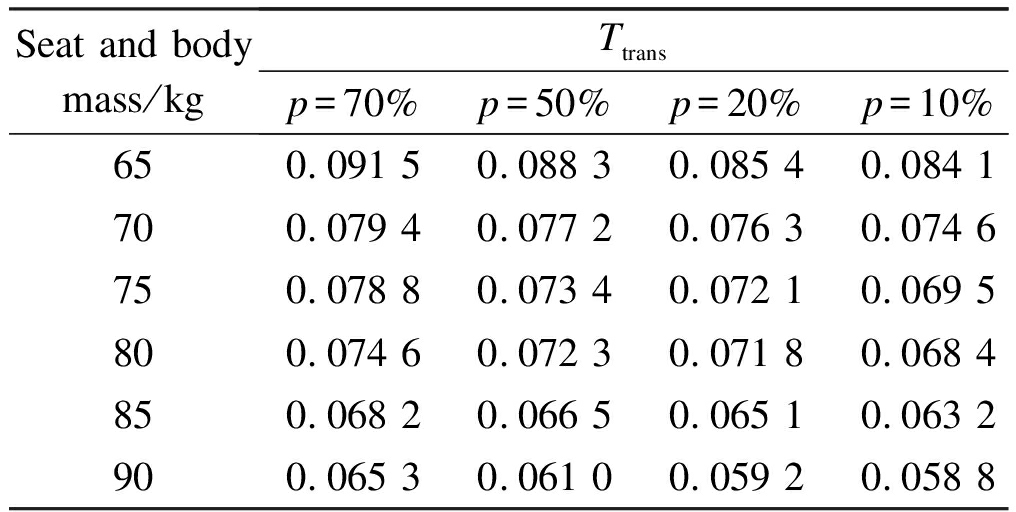
Seat and bodymass/kgTtransp=70%p=50%p=20%p=10%p=5%650.091 50.088 30.085 40.084 10.083 6700.079 40.077 20.076 30.074 60.072 5750.078 80.073 40.072 10.069 50.068 3800.074 60.072 30.071 80.068 40.064 9850.068 20.066 50.065 10.063 20.061 1900.065 30.061 00.059 20.058 80.057 3
5 Conclusions
1) A cab seat suspension system based on the NSS is designed in this paper, and its nonlinear dynamic model is established. The different structural parameters of the system and its influence on the dynamic stiffness characteristics are respectively analyzed. The ideal configuration parameter range and the final value of the suspension system are obtained.
2)The optimization model for the seat suspension structure of construction machinery cabs is put forward. By simulation and comparative analysis, the vibration transmissibility is studied. The results show that the acceleration and displacement amplitudes of the optimized seat suspension system are evidently reduced. According to the ISO 2631 standard, RMS and VDV method calculation values in the vertical vibration direction are reduced by 86% and 87%, respectively. The vibration transmissibility rate, ASEAT and Ttrans, are also reduced.
3) Through the analysis of the frequency domain response of the seat suspension system, the comparison results show that in accordance with the ISO 2631 standard, the peak frequency of the vibration transmitted to the driver avoids the key frequency, which can easily cause human resonance. The influences of the uncertainty of stiffness coefficients and different driver weights on the suspension system are discussed. The study results show that the change in a driver’s weight in the range of 65-90 kg has no effect on the performance of the seat suspension system. The seat suspension system with NSS exhibits good vibration-isolation performance, improving the working environment of the driver and the ride comfort of the seat.
[1]Nguyen S D, Nguyen Q H, Choi S B. A hybrid clustering based fuzzy structure for vibration control—Part 2: An application to semi-active vehicle seat-suspension system[J]. Mechanical Systems and Signal Processing, 2015, 56/57: 288-301. DOI:10.1016/j.ymssp.2014.10.019.
[2]Kulkarni S, Spencer S, Horton D J, et al. Isolation mount assembly: U.S. 11,001,306.[P]. 2021-05-11.
[3]Deshmukh S R, Balaji N S K, Saharabhudhe S, et al. Designing of control strategy for high voltage battery isolation in an electric vehicles[C]//2019 IEEE 5th International Conference for Convergence in Technology(I2CT). Bombay, India, 2019: 1-4. DOI:10.1109/I2CT45611.2019.9033891.
[4]Liu Z T, He H W. Sensor fault detection and isolation for a lithium-ion battery pack in electric vehicles using adaptive extended Kalman filter[J]. Applied Energy, 2017, 185: 2033-2044. DOI:10.1016/j.apenergy.2015.10.168.
[5]Griffin M J. Handbook of human vibration[M]. Cambridge: Academic Press, 2012: 25-80.
[6]Friesenbichler B, Nigg B M, Dunn J F. Local metabolic rate during whole body vibration[J]. Journal of Applied Physiology, 2013, 114(10): 1421-1425. DOI:10.1152/japplphysiol.01512.2012.
[7]van Eijk J, Dijksman J F. Plate spring mechanism with constant negative stiffness[J]. Mechanism and Machine Theory, 1979, 14(1): 1-9. DOI:10.1016/0094-114X(79)90036-3.
[8]Lee C M,Goverdovskiy V N, Temnikov A I. Design of springs with “negative” stiffness to improve vehicle driver vibration isolation[J]. Journal of Sound and Vibration, 2007, 302(4/5): 865-874. DOI:10.1016/j.jsv.2006.12.024.
[9]Yang J,Xiong Y P, Xing J T. Dynamics and power flow behaviour of a nonlinear vibration isolation system with a negative stiffness mechanism[J]. Journal of Sound and Vibration, 2013, 332(1): 167-183. DOI:10.1016/j.jsv.2012.08.010.
[10]Han J S,Meng L S, Sun J G. Design and characteristics analysis of a nonlinear isolator using a curved-mount-spring-roller mechanism as negative stiffness element[J]. Mathematical Problems in Engineering, 2018, 2018: 1-15. DOI:10.1155/2018/1359461.
[11]Fan Y Q, Gu P M. A vibration isolation device for elastic elements in parallel of positive and negative stiffness: China, CN8510917 [P].1985-11-01. (in Chinese)
[12]Zhang J Z, Li D, Dong S, et al. A study on ultra-low frequency nonlinear parallel vibration isolation system for precision instruments[J]. China Mechanical Engineering, 2004,15(1):69-71. (in Chinese)
[13]Ji H, Xiong S S, Yuan Y. Analysis of structural vibration isolation effect based on negative stiffness principle[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition),2010,38(2):76-79. DOI:10.13245/j.hust.2010.02.014. (in Chinese)
[14]Li D H, Zhao S G, et al. Dynamic analysis of a QZS vibration isolator with time delay control[J]. Vibration and Shock, 2018, 37(13): 49-55. DOI: 10.13465/j.cnki.jvs.2018.13.008. (in Chinese)
[15]Lu Z Q, Brennan M J, Chen L Q. On thetransmissibilities of nonlinear vibration isolation system[J]. Journal of Sound and Vibration, 2016, 375: 28-37. DOI:10.1016/j.jsv.2016.04.032.
[16]Sarlis A A, Pasala D T R, Constantinou M C, et al. Negative stiffness device for seismic protection of structures[J]. Journal of Structural Engineering, 2013, 139(7): 1124-1133. DOI:10.1061/(asce)st.1943-541x.0000616.
[17]Palomares E, Nieto A J, Morales A L, et al. Numerical and experimental analysis of a vibration isolator equipped with a negative stiffness system[J]. Journal of Sound and Vibration, 2018, 414: 31-42. DOI:10.1016/j.jsv.2017.11.006.
[18]Davoodi E, Safarpour P, Pourgholi M, et al. Design and evaluation of vibration reducing seat suspension based on negative stiffness structure[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2020, 234(21): 4171-4189. DOI:10.1177/0954406220921203.
[19]Dong G X, Zhang X N,Xie S L, et al. Simulated and experimental studies on a high-static-low-dynamic stiffness isolator using magnetic negative stiffness spring[J]. Mechanical Systems and Signal Processing, 2017, 86: 188-203. DOI:10.1016/j.ymssp.2016.09.040.
[20]Yao H L, Chen Z D, Wen B C. Dynamic vibration absorber with negative stiffness for rotor system[J].Shock and Vibration, 2016, 2016: 1-13. DOI:10.1155/2016/5231704.
[21]Carletti E, Pedrielli F. Tri-axial evaluation of the vibration transmitted to the operators of crawler compact loaders[J]. International Journal of Industrial Ergonomics, 2018, 68: 46-56. DOI:10.1016/j.ergon.2018.06.007.
[22]Wickramasinghe V K. Dynamics control approaches to improve vibratory environment of the helicopter aircrew[D]. Ottawa, Canada: Carleton University, 2013.
[23]ISO. Mechanical vibration and shock: evaluation of human exposure to whole-body vibration. Part 1, General requirements: International Standard ISO 2631-1: 1997 (E) [S]. Geneva: ISO, 1997.
[24]Knothe K, Stichel S. Human perception of vibrations-ride comfort[M]//Rail Vehicle Dynamics. Cham: Springer International Publishing, 2016: 141-157.
[25]Grabau P J. The simulation of vibrations experienced by patients during helicopter winching and retrieval[D]. Townsville, Australia: James Cook University, 2016.