With rapid economic development, geotechnical anchoring projects (e.g., foundation pit protection, underground engineering antifloating, railway tunnels, underground cave support, and slope reinforcement) are steadily expanding[1-3]. Anchor bolts are the core of anchoring projects as their quality plays a vital role in the stability of engineering structures; thus, testing the bearing capacity of anchor bolts is one of the most important links in quality inspection[4-5]. Given the complexity of geotechnical structures, the method for accurately determining the ultimate bearing capacity of anchor bolts still involves in situ pull-out tests. The P-s curve is determined according to the uplift load P and displacement s of the anchor bolt, and the maximum pull-out load is determined by the P-s curve[6]. Although this method is intuitive and reliable, testing the complete P-s curve requires the anchor bolts to be subjected to damage testing. The process also takes much time and money. Therefore, establishing a mathematical model that can predict the maximum pull-out load of anchor bolts before failure may help reduce testing time and costs.
A typical mathematical prediction model is generally established using partial measured data. On the basis of this model, the complete P-s curve of an anchor bold can then be obtained. Through this model, the maximum pull-out load of the anchor bolt can be predicted. Sun et al.[7-8] studied a prediction method for the pull-out load of anchor bolts that was based on the improved exponential-power mixed model and modified D-S evidence theory. By testing a dynamic mass measurement method for anchor bolts, Xu et al.[9] discussed the gray system prediction method for the uplift bearing capacity of anchor bolts. Liu[10] studied the method of predicting the pull-out load of anchor bolts by using gray system theory and then conducted engineering verification. Xue et al.[11] introduced a genetic algorithm to establish a genetic neural network model for predicting the maximum pull-out load of anchor bolts. Ying et al.[12] used hyperbolic and exponential models to simulate the P-s curve of an anchor bolt and analyzed their practicality. Zhao et al.[13] proposed an adjusted hyperbolic model to predict the maximum pull-out load of anchor bolts. These existing studies used single models to predict the P-s curve of anchor bolts. However, such models have some limitations, and they lack accuracy.
Meanwhile, the mixed model of improved exponential andpower function (MIEPF) and unequal interval gray GM(1,1) model (hereinafter referred to as the U-GM(1,1) model) have higher accuracy and more stable reliability than other single models for predicting the maximum pull-out load of anchor bolts. Specifically, the MIEPF has relatively high accuracy, whereas the U-GM(1,1) model has relatively poor accuracy. Considering the limitations of using a single model to predict the P-s curve, this study uses the minimum logarithmic error square sum as the objective function to solve the optimal weighting coefficient. An optimal weighted geometric mean combination prediction model is then proposed. Finally, the accuracy and stable reliability of every single model and the optimal combination model are verified in two engineering cases.
1 Existing Prediction Models
The mathematical models that can be used to predict the P-s curves of anchor bolts are the hyperbolic function model[14], adjustment hyperbolic (A-H) function model[13], modified hyperbolic (M-H) function model[15], power function model[16], exponential function model[12], exponential-power-linear (EPL) function model[17], improved exponential (I-E) function model)[8], MIEPF model[7], U-GM(1,1) model, and gray GM(1,1) model[18-19]. A brief introduction to each mathematical model is presented here. In the discussion, P, s, and Pu represent a certain level of uplift load, the displacement under load P, and the maximum pull-out load of the anchor bolt, respectively; a and b are two parameters to be solved.
1.1 Hyperbolic function model
Christon first proposed the hyperbolic function model. In using this model to predict the bearing capacity of anchor bolts, its mathematical equation is
(1)
1.2 A-H model
Zhao et al.[13] presented the A-H function model, which has stronger adaptability and adjustability than the hyperbolic function model. The A-H model is as
(2)
where sn-1 is the measured displacement of the anchor bolt under the last second-level uplift load.
1.3 M-H model
Jiang et al.[15] presented the M-H function model and verified it in practical engineering cases. The M-H model satisfies the following equation:
(3)
where c denotes the parameter to be solved.
1.4 Power function model
Bai et al.[16] described the power function model as
(4)
where k and n are the initial uplift stiffness and tangential stiffness index, respectively. If a=(n-1)k/Pu,b=1/(n-1), then Eq.(4) can be transformed into
(5)
For the slow P-s curve and steep P-s curve, the n values are 2.9 and 2.0, respectively.
1.5 Exponential function model
Ying et al.[12] assumed that the P-s curve of an anchor bolt conforms to the following exponential equation:
(6)
where a is the parameter to be solved. This model is simple and feasible, and it can be completed by a small computer program.
1.6 I-E model
Sun et al.[8] comprehensively analyzed Eqs. (1), (5), and (6) and discovered that they all have the same frame structure, which is
(7)
where f(s) and x are the function factor and parameter to be solved, respectively. Eq.(7) should satisfy the five characteristics (point of origin, non-negative and bounded, infinite convergence, convexity, and monotonous increase) of the P-s curve of a theoretical anchor bolt. A general function model framework is used to improve the exponential model under the assumption that the anchor bolt’s P-s curve satisfies the following improved exponential equation:
(8)
where a and k are the two parameters to be solved, a>0, k>-1.
1.7 MIEPF model
Sun et al.[7] presented the MIEPF and supposed that the anchor bolt’s P-s curve satisfies
(9)
where a, b, c, and k are the parameters to be solved.
1.8 EPL function model
Kuang et al.[17] established the EPL function model to describe the load-slip curves of anchor bolts; the model is given by
(10)
where α, β, and μ are undetermined parameters.
1.9 U-GM(1,1) model
The gray GM(1,1) model is mainly suitable for prediction problems with short time, small quantity, and low volatility[20]. Displacement is regarded as the generalized time when tracking the development trend of an anchor bolt’s P-s curve. The first-order dynamic differential equation-based GM(1,1) model of a load sequence is established. The actual anchor bolt displacement is an unequal interval, and in most cases, known displacement values are used to estimate load uplift values. Hence, the gray GM(1,1) model established should involve an unequal interval. The initial load sequence and settlement sequence can be obtained from the pull-out test as
(11)
The load and settlement series in Eq.(11) are reduced once, and a new series is obtained as
(12)
where
(13)
According to the modeling method of the gray system, the first-order differential equation GM(1,1) is established as
![]() +aP(1)=b
+aP(1)=b
(14)
where a is the development coefficient and b is the gray action quantity.
According to the least-squares method,
(15)
where
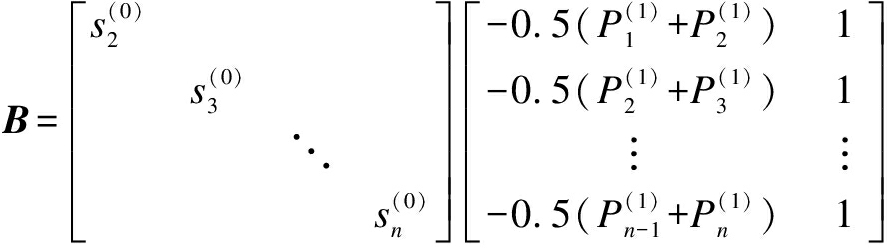
(16)
(17)
Therefore, the solution of differential equation (15) is as
(18)
where ![]() is the prediction value of the anchor bolt under the k+1 level uplift load. The maximum pull-out load of an anchor bolt can be obtained by
is the prediction value of the anchor bolt under the k+1 level uplift load. The maximum pull-out load of an anchor bolt can be obtained by
(19)
2 Optimal Weighted Average Geometric Prediction Model
Take for example m types of prediction models, such as ![]() is the weighted geometric average combination prediction model of the m types of prediction models and represents the prediction value of the t phase of the model.
is the weighted geometric average combination prediction model of the m types of prediction models and represents the prediction value of the t phase of the model.
(20)
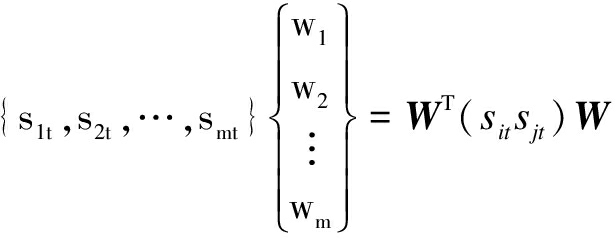
Suppose W={w1,w1,…,wm}T∈Rm, and ![]() wi≥0, i=1,2,…,m. If yt is the measured values of the displacement in the t period, then
wi≥0, i=1,2,…,m. If yt is the measured values of the displacement in the t period, then ![]() respectively. Subsequently,
respectively. Subsequently,

(21)
where W={w1,w2,…,wm}T and (sitsjt) is an m-order square matrix.
Thus, the logarithmic error square sum is
(22)
where ![]() is generally a positive definite matrix.
is generally a positive definite matrix.
1) As ![]() matrix A is a symmetric matrix.
matrix A is a symmetric matrix.
2) For random X={x1,x2,…,xm}T∈Rm-{0},
(23)
If XTAX=0 always holds, so ![]() t=1,2,…,m, that is, for any nonzero m-dimensional vector X, it is solved by
t=1,2,…,m, that is, for any nonzero m-dimensional vector X, it is solved by
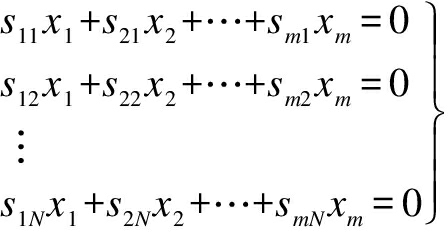
(24)
If xk=1, xi=0, i≠k, i,k=1,2,…,m, then skt=0, k=1,2,…,m, t=1,2,…,N, in t=1,2,…,N. In fact, ![]() is not always equal to zero. Thus,
is not always equal to zero. Thus,
XTAX≥0
(25)
From testimonies 1) and 2), matrix A is a positive definite matrix, so that A is invertible. For any nonzero vector W, the minimum logarithmic error square sum S2>0. If Q={1,1,…,1}T∈Rm, then the optimal weight coefficient W can be determined by minimizing the sum of the logarithmic error square S2=WTAW of the combined prediction model under the constraint conditions of WTQ=1, W≥0.
Based on the results of Ref.[21], the solution is
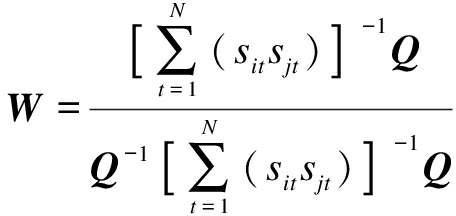
(26)
For the weighted geometric combination prediction model composed of the MIEPF and U-GM(1,1) model, the optimal weight coefficients are
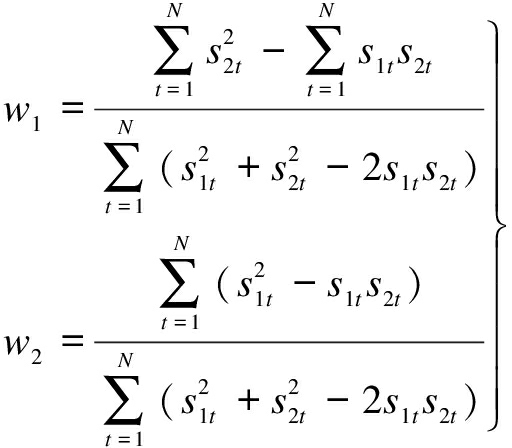
(27)
Given w1+w2=1, only one of w1, w2 is required in actual calculations.
3 Model Assessment
On the basis of the five parameters, namely, the sum of squares due to error (SSE), the sum of squares due to relative error (SSRE), standard error (SE), relative standard error (RSE), and mean absolute percentage error (MAPE), the accuracy of the proposed prediction model was used to quantify the estimation performance.
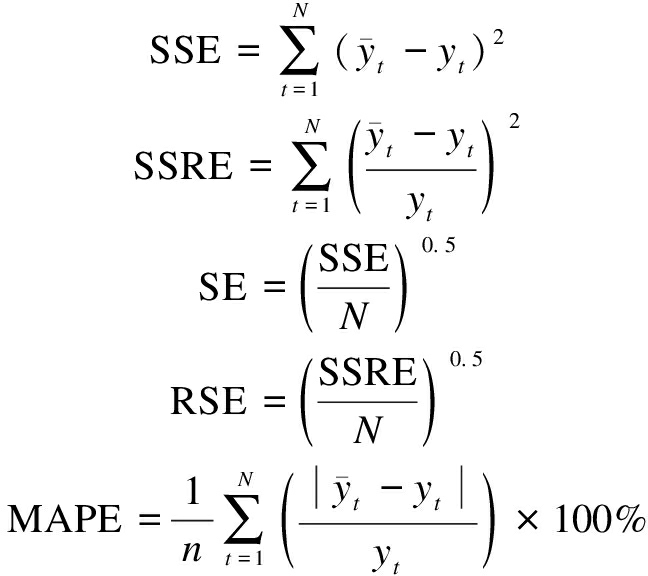
MAPE can be treated as the benchmark and is more stable than the commonly used mean absolute error and root mean square error[22] when used to evaluate the capability of the prediction model (see Tab.1).
Tab.1 Capability of the prediction model
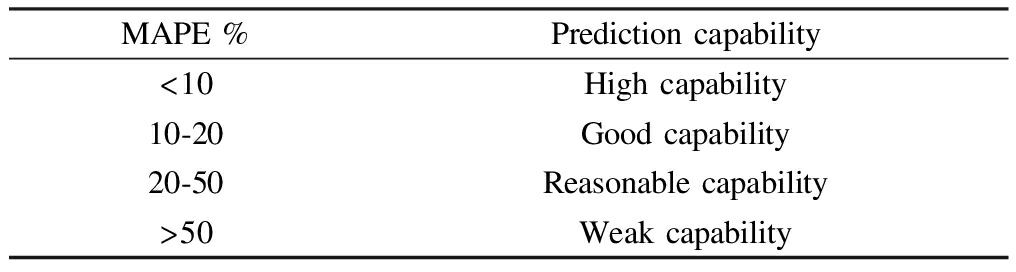
MAPE %Prediction capability<10High capability10-20Good capability20-50Reasonable capability>50Weak capability
4 Verification Based on Engineering Cases
An anchor bolt’s P-s curve obtained by the pull-out test is closely related to the mechanical characteristics of the anchor bolt itself and to multiple factors, such as side friction resistance, diameter, anchoring length, and mortar strength[23]. In general, the P-s curve can be roughly divided into two types: slow P-s curve and steep P-s curve. In this work, two typical engineering cases were selected to compare the accuracies and stabilities of the models, as well as the accuracies of the maximum pull-out loads predicted by the models. The P-s curve in case Ⅰ is the slow curve, while the P-s curve in case Ⅱ is the steep curve.
4.1 Case Ⅰ
The anchoring stratum of the antifloating anchor bolts in a swimming pool in Shenzhen, China, was granite residual soil[24]. During the loading process in which the “pressure cannot be increased and displacement does not converge,” the corresponding load was taken as the failure load, and 95% of it was taken as the maximum pull-out load. The anchor bolt lengths in test groups A and B were 12.0 and 15.0 m, respectively. The bolt-grouting body diameter was 180 mm, and the anchor bolts were all 2Φ32 mm threaded steel bars. The maximum pull-out load values of the anchor bolts in test groups A and B were 664 and 670 kN, respectively. The measured data are shown in Tab.2.
Tab.2 Measured data of pull-out test on anchor bolt (case Ⅰ)

P/kN70210350420490560595630665s/mmGroup A 0.602.194.866.828.8520.5523.8229.2446.03Group B 0.372.115.728.9913.6817.0719.6724.1339.19
4.2 Case Ⅱ
In an antifloating anchor bolt test at a construction site in Qingdao, China[25], a trench with a width of 1.2 m and a depth of 0.6 m was directly excavated. Reinforcing steel was set at the center of the trench, and the bottom plate was cast with C30 commercial concrete. The steel bar adopted a threaded anchor bolt with a tensile strength of 590 MPa, elastic modulus of 200 GPa, diameter of 28 mm, vertical anchoring length of 15d (d is the anchor bolt diameter), and horizontal bending lengths of 20d and 30d. The maximum pull-out load values of the anchor bolts were 360 and 381 kN, respectively. The measured data are shown in Tab.3.
Tab.3 Measured data of pull-out test on anchor bolt (case Ⅱ)

P/kN306090120150180210240270300330360s/mmWS-20d0.050.200.360.701.131.431.692.354.256.8411.8820.24WS-30d0.110.480.830.991.161.2819.6724.1339.196.2210.6318.94
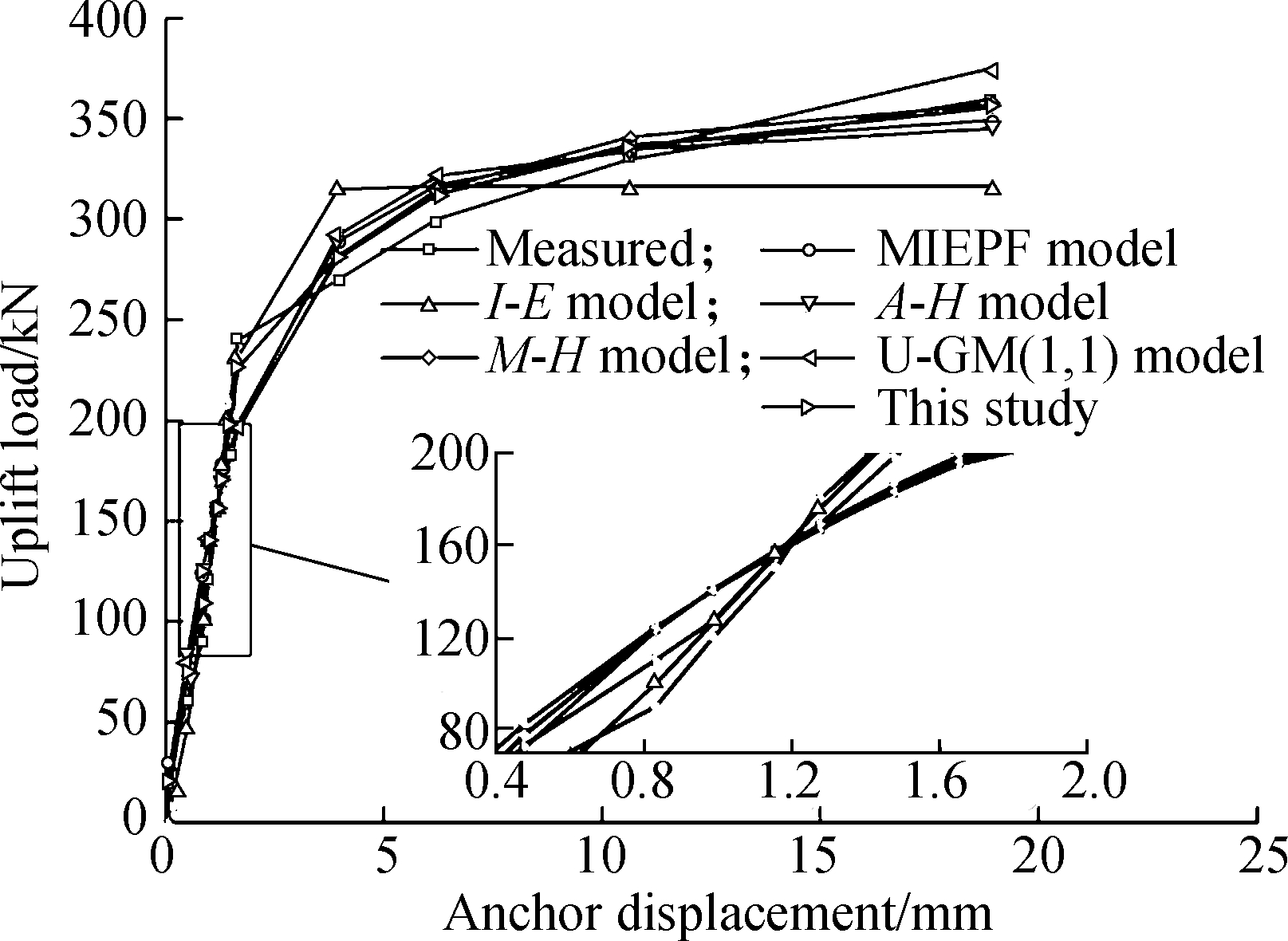
On the basis of the measured data in Tabs. 2 and 3, this study used MATLAB’s fmincon function based on the principle of minimum error square sum to obtain the prediction model parameters[8]. Among the existing models, the prediction accuracies of the exponential model, hyperbolic model, and power function model were very poor and could no longer be used to predict the bearing capacity of the anchor bolt. Apart from that of the U-GM(1,1) model, the maximum pull-out loads predicted with the MIEPE and I-E, A-H, and M-H models were all higher than the measured values (see Fig.1(a)). The predicted value of the maximum pull-out load in this study was relatively close to the measured value. As shown in Fig.1(b), for the tests WS-20d and WS-30d, the maximum pull-out loads predicted by the U-GM(1,1) model were less than the measured values, except for the I-E model in the test WS-30d. The predicted values from the MIEPE and I-E, A-H, and M-H models were all higher than the measured values. Meanwhile, the predicted values of the combined model were consistent with the measured values. Therefore, the optimal combination model proposed in this work can use the commonness and individuality of two single prediction models.

(a)

(b)
Fig.1 Maximum pull-out load of the anchor bolt. (a) Case Ⅰ; (b) Case Ⅱ
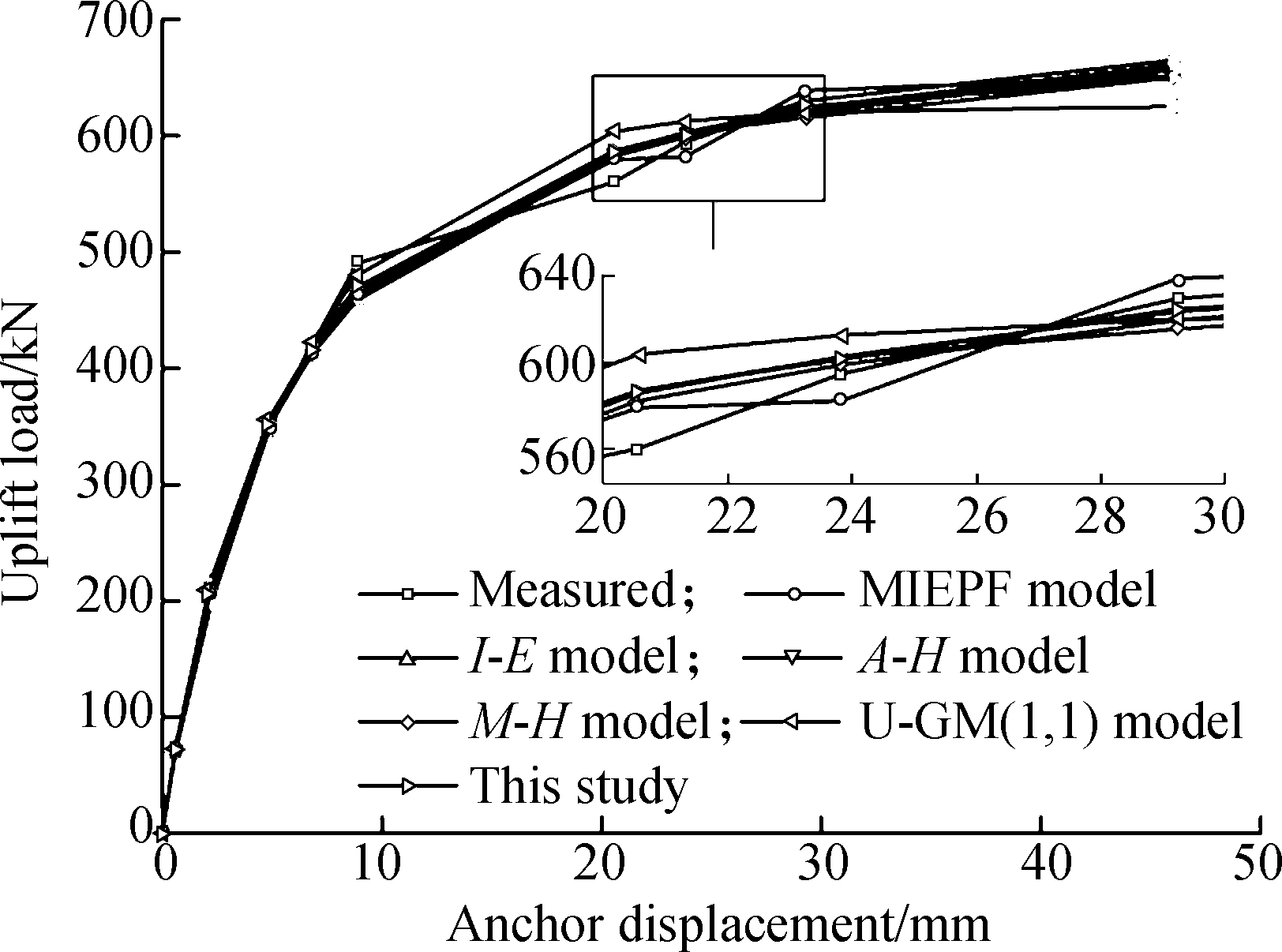
The anchor bolt’s P-s curves were all slow curves (see Fig.2), and the overall shape was convex. However, concave points were observed in the middle of the curves. The P-s curves simulated with the different prediction models showed the same trend. In the elastic phase, the predicted values of the test groups A and B were in good agreement with the measured values. In the elastoplastic phase, the predicted values were more discrete than the measured values, and the curve fit was poor. In both phases, the prediction accuracy of the proposed combined model was better than that of any single prediction model. Specifically, the P-s curve of the proposed model almost coincided with the measured curve.
(a)

(b)
Fig.2 P-s curves of different prediction models and the measured values (case Ⅰ). (a) Group A; (b) Group B
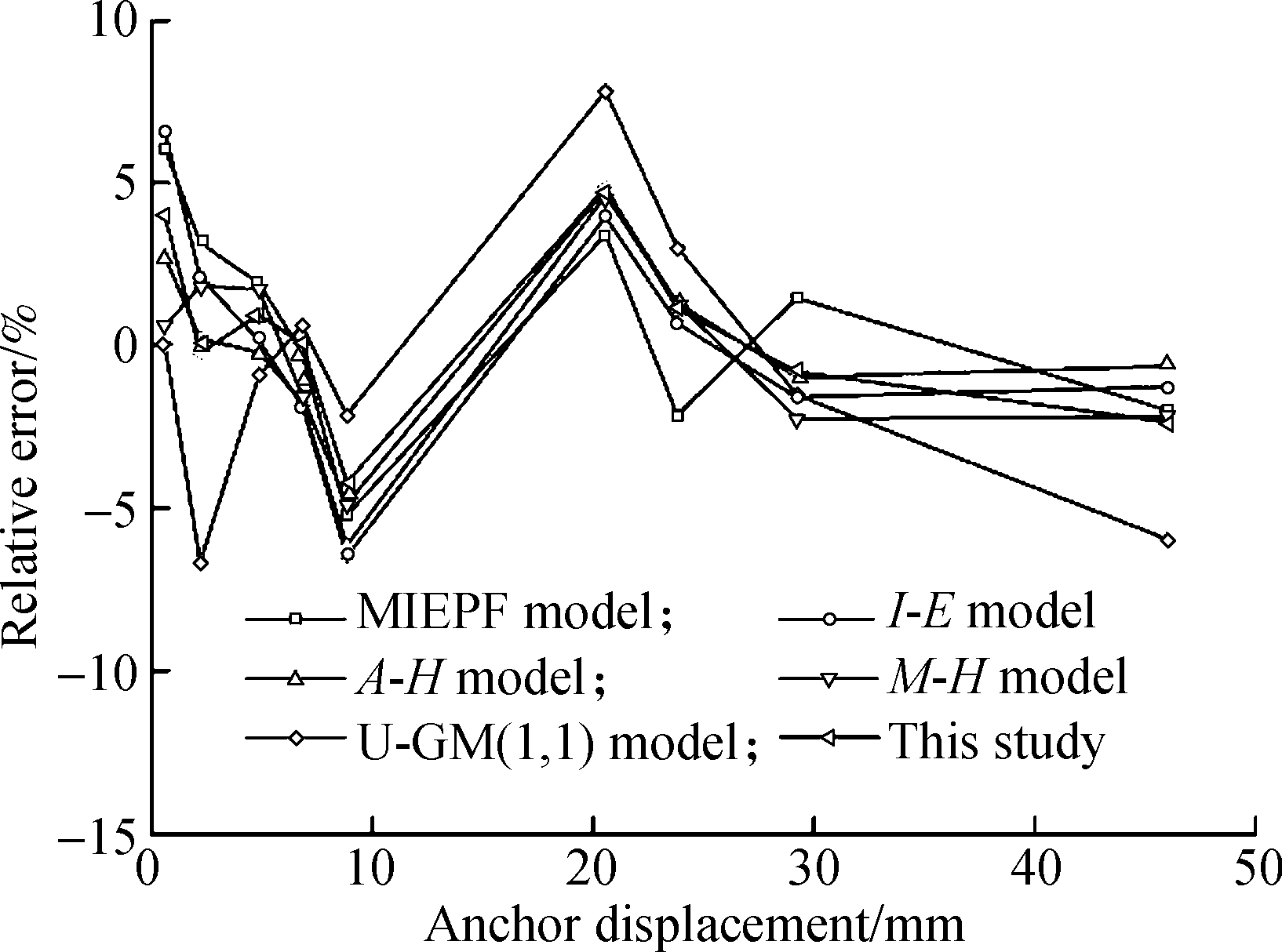
As shown in Fig.3, for the anchor bolt’s slow P-s curve, the relative error of the U-GM(1,1) model was large during the entire stage. When the anchor bolt displacement was small, the relative error of each prediction model was generally large, and the later fitting effect was satisfactory. For example, when the anchor bolt displacement of test group A was less than 8.85 mm, the relative error was between -6.47% and 6.57%. However, when the anchor bolt displacement was greater than 8.85 mm, the relative error of each prediction model was between -2.34% and 3.88%. For test group B, when the anchor bolt displacement was less than 13.68 mm, the relative error was between -18.66% and 6.24%. When the displacement was greater than 13.68 mm, the relative error of each prediction model was between -3.39% and 2.93%.
(a)
(b)
Fig.3 Relative error curves of different prediction models (case Ⅰ). (a) Group A; (b) Group B
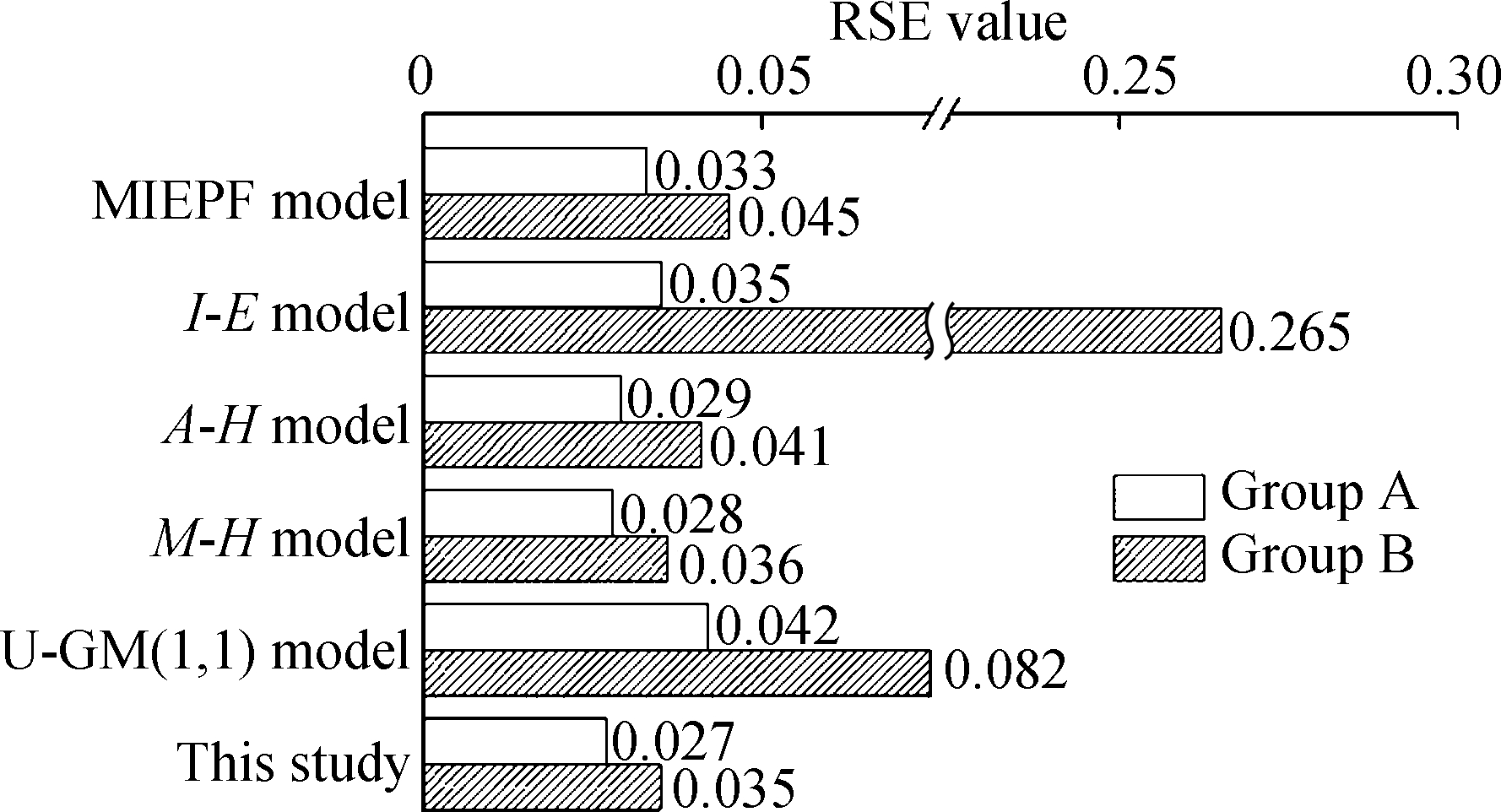
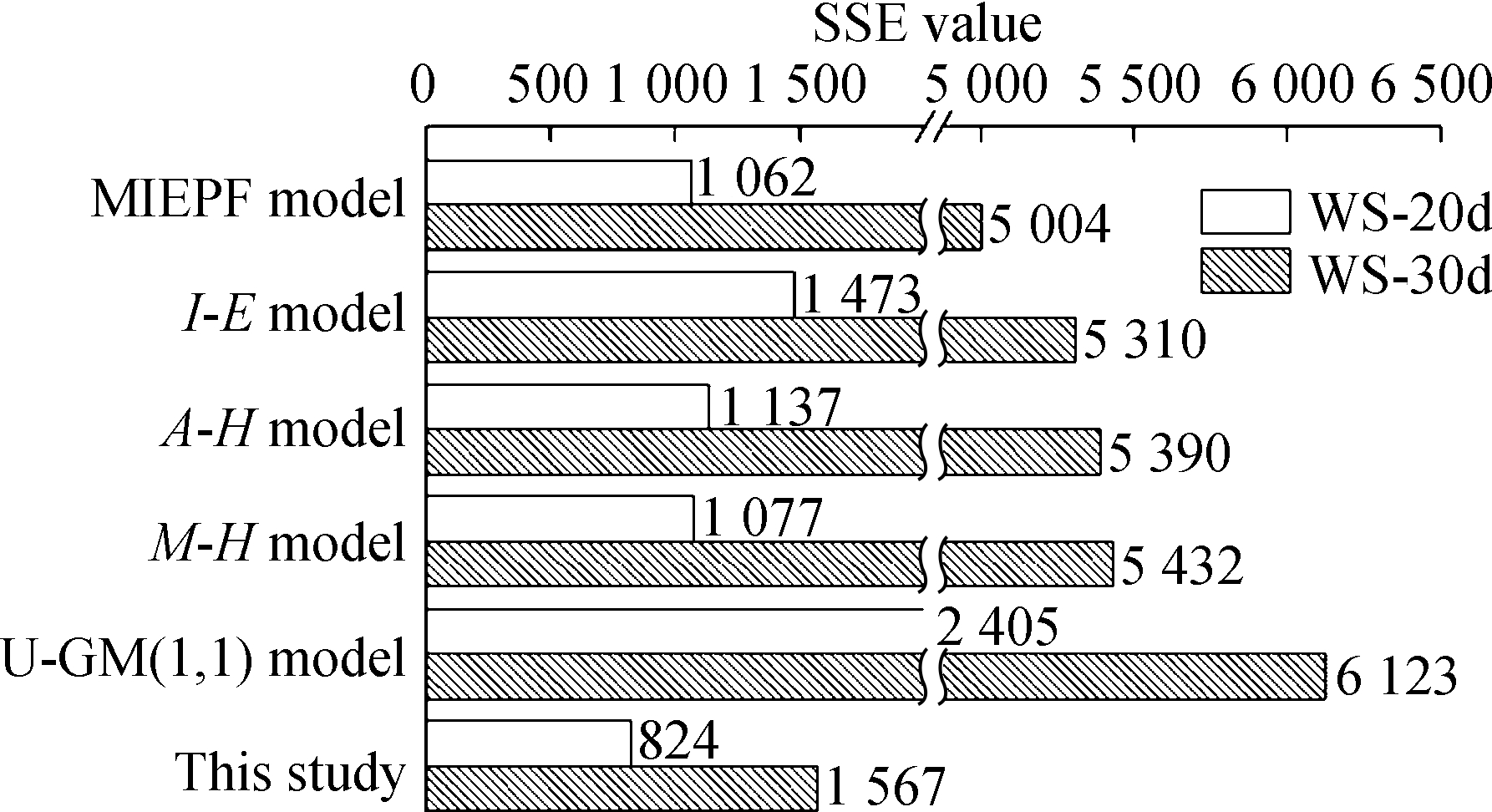
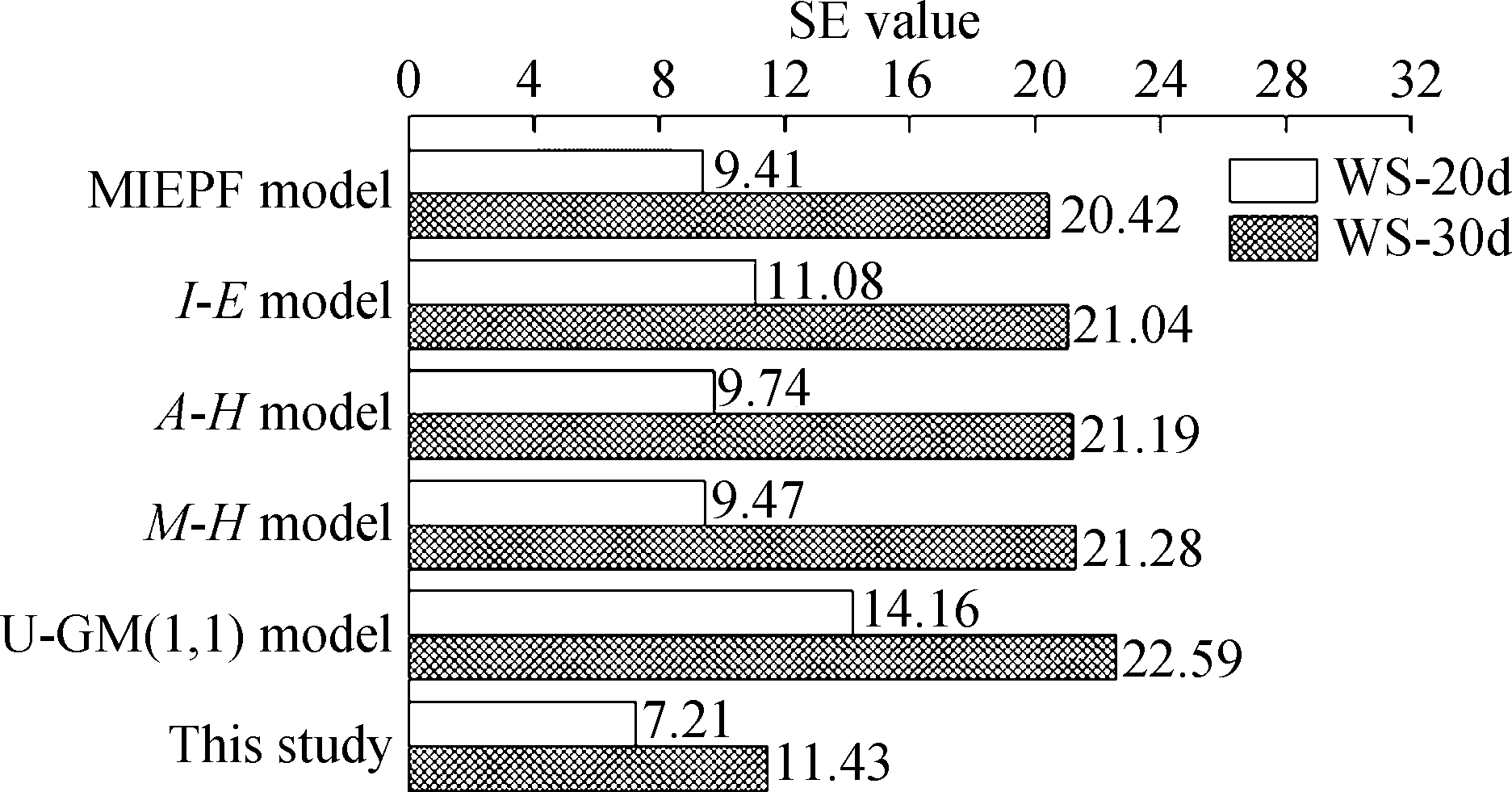
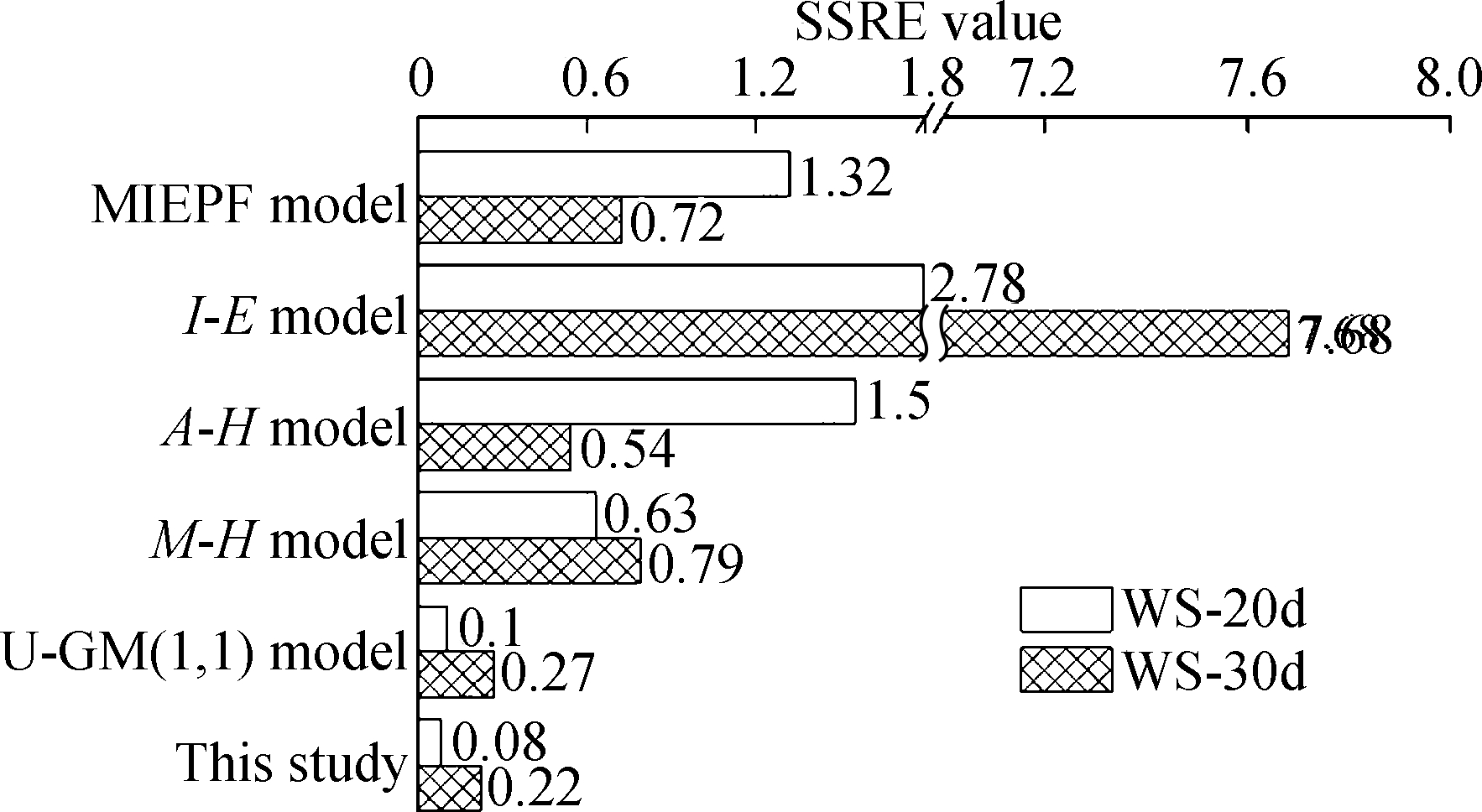
With regard to the SSE and SE for evaluating the accuracy of the prediction models (see Figs.4(a) and (b)), for the anchor bolt’s slow P-s curve, the I-E and U-GM(1,1) models showed the largest SSE and SE values, followed by the MIEPF and A-H and M-H models. The SSE and SE values calculated by the optimal combination model were the smallest. For the indexes SSRE and RSE, which reflected the stable reliability of the models (see Figs.4(c) and (d)), the optimal combination model also achieved the smallest values. This result revealed that the accuracy and reliability of the optimal combination model were higher than those of the other models.
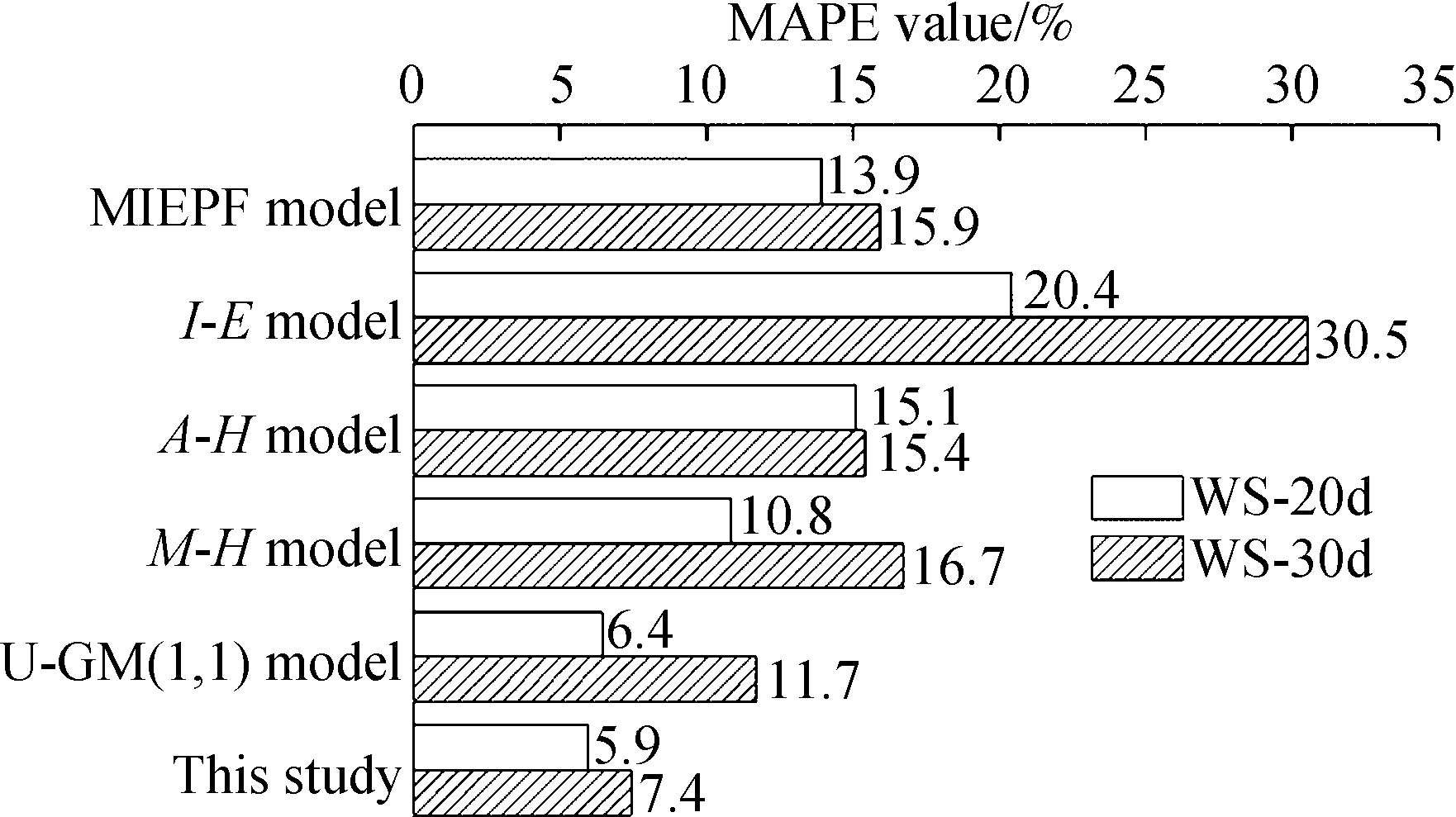
In terms of the capability classification of the prediction models (see Fig.5(a)), the I-E model (MAPE value of 12.4) that predicted the pull-out load showed good capability (10<12.4<20); all the other prediction models showed high capability (MAPE<10). Compared with the other single prediction models, the optimal combination model achieved better prediction effects for the anchor bolt’s slow P-s curve. From the perspective of the capability classification of the prediction models (see Fig.5(b)), the I-E model showed reasonable capability (20
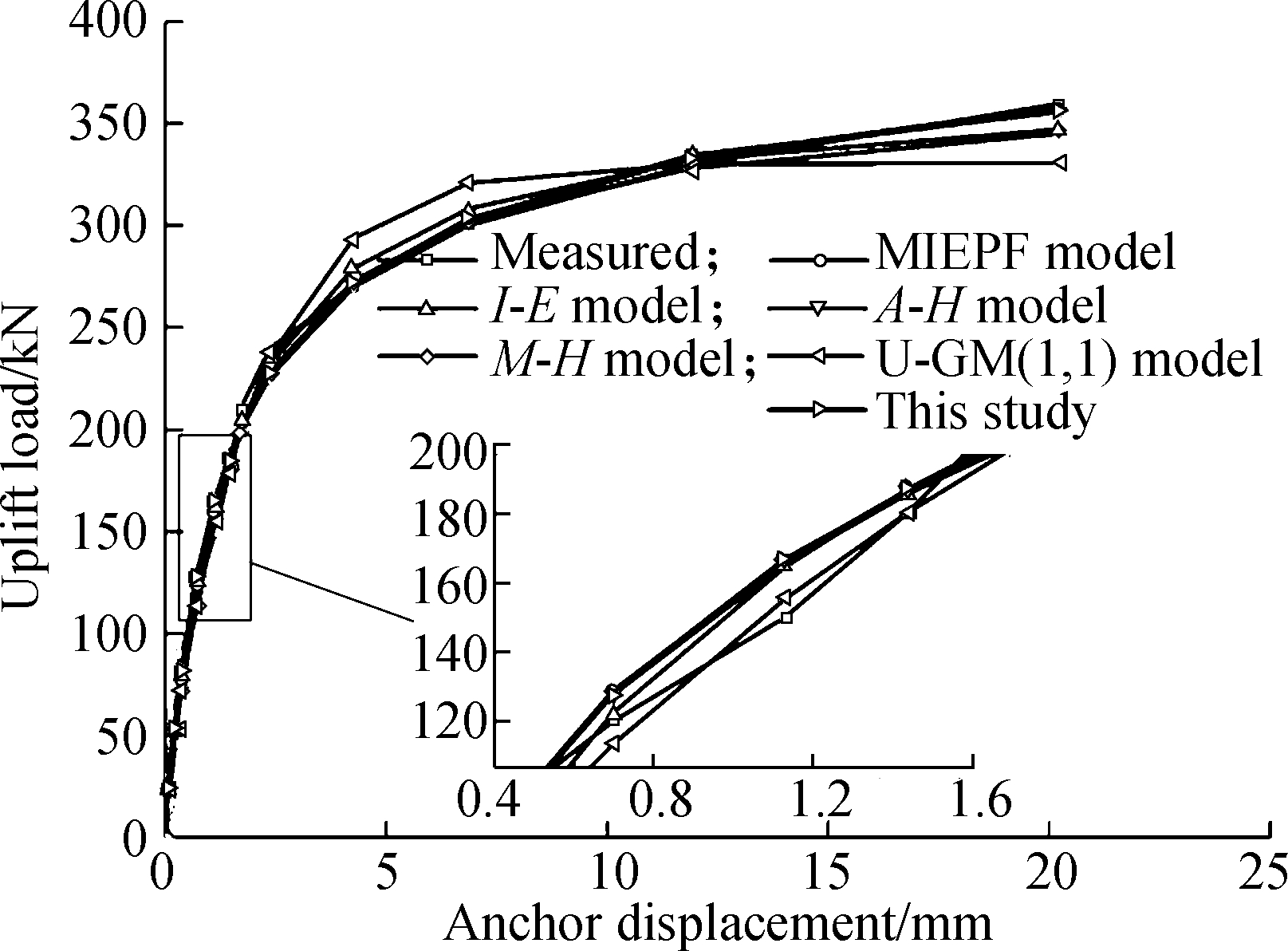
As shown in Fig.6, the P-s curves were all steep curves. When the anchor bolt displacement variation was small, the pull-out load changed greatly. The U-GM(1,1) model showed a poor simulation effect for the anchor bolt’s steep P-s curve, whereas the other models showed better simulation results. Meanwhile, the optimal combination model achieved the best outcome.

(a)

(b)

(c)
(d)
Fig.4 Accuracy and stable reliability indicators of different prediction models (case Ⅰ). (a) SSE value; (b) SE value; (c) SSRE value; (d) RSE value

(a)
(b)
Fig.5 Capability classification of prediction models. (a) Case Ⅰ; (b) Case Ⅱ
(a)
(b)
Fig.6 P-s curves of different prediction models and the measured values (case Ⅱ). (a) WS-20d; (b) WS-30d
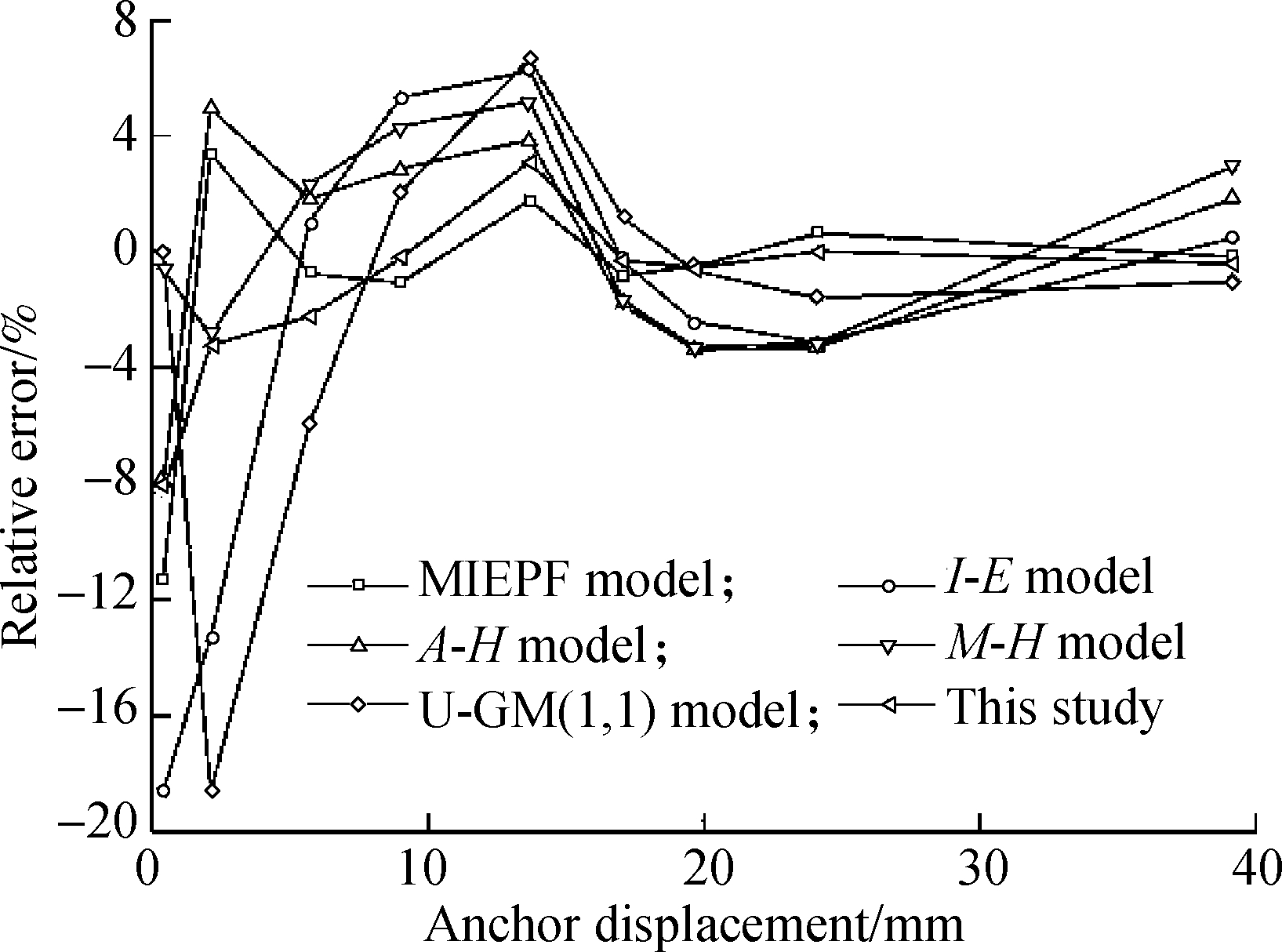
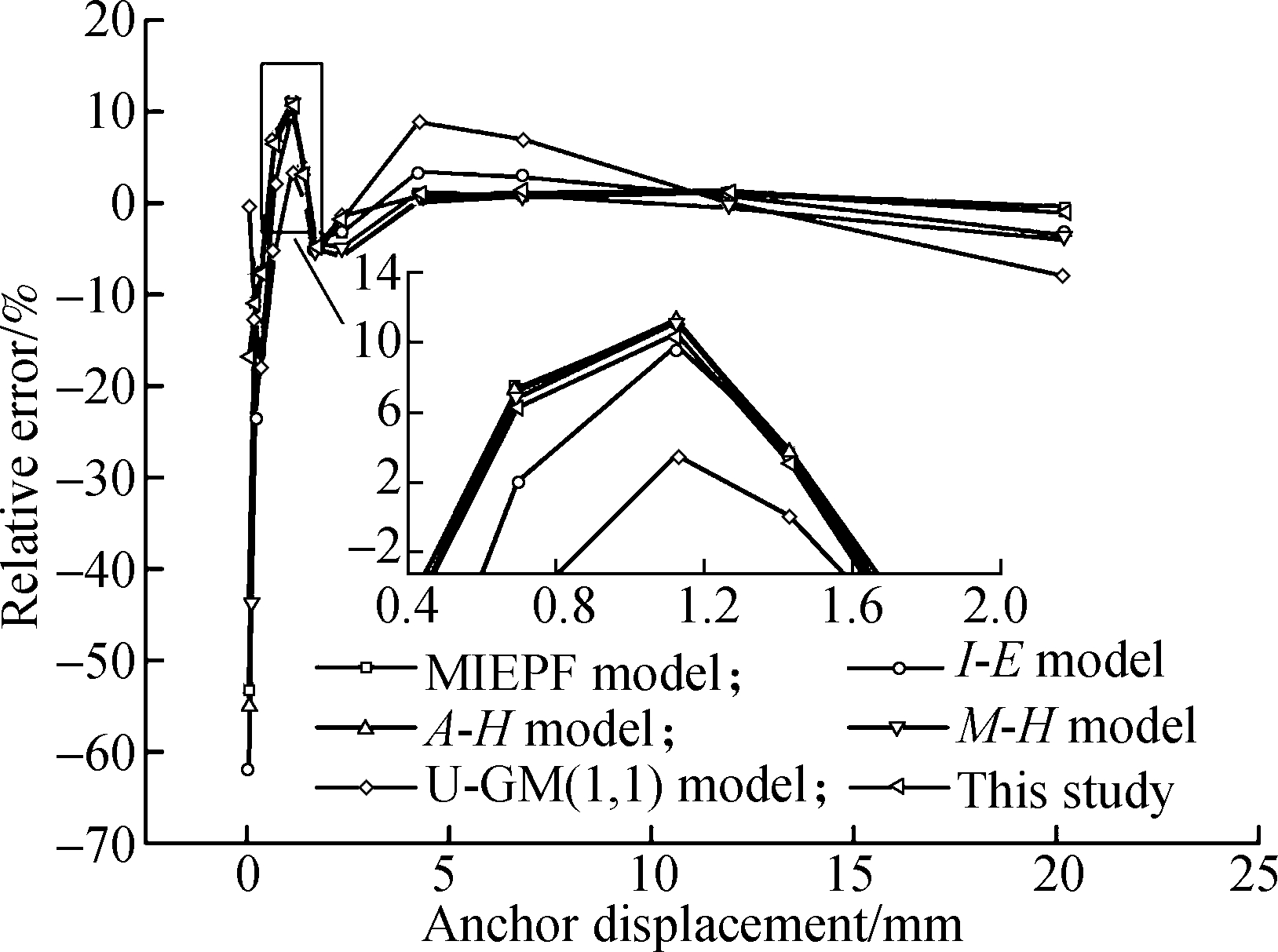
For the steep P-s curve (see Fig.7), similar to the slow P-s curve, the relative error of each prediction model was large when the anchor displacement was small. Furthermore, the relative error was larger than that for the slow P-s curve in the early stage. With an increase in displacement, the relative error of each prediction model gradually decreased. Thus, for the anchor bolt’s steep P-s curve, reducing the elastic phase data during processing should greatly improve the accuracy and stable reliability of each prediction model.
(a)

(b)
Fig.7 Relative error curves of different prediction models (case Ⅱ). (a) WS-20d; (b) WS-30d
As shown in Figs.8(a) and (b), for the steep P-s curve, the prediction accuracies of the MIEPE and I-E, A-H, M-H, and U-GM(1,1) models decreased. Meanwhile, the prediction accuracy of the optimal combination model was the highest. As for the SSPE and SPE values (see Figs.8(c) and (d)), the I-E model achieved the worst stable reliability, followed by the A-H model, MIEPE, M-H model, and U-GM(1,1) model. The optimal combination model had the best stable reliability.
(a)
(b)
(c)

(d)
Fig.8 Accuracy and stable reliability indicators of different prediction models (case Ⅱ). (a) SSE value; (b) SE value; (c) SSRE value; (d) RSE value
5 Conclusions
1) To accurately predict the maximum pull-out load of anchor bolts, this study optimally combined the MIEPE and U-GM(1,1) model. The minimum logarithmic error square sum of the proposed model was used as the objective function to solve the optimal weighting coefficient. The optimally weighted geometric average combination model for predicting the uplift bearing capacity of anchor bolts was then derived.
2) The analysis of cases Ⅰ and Ⅱ showed that regardless of the type of P-s curve of the anchor bolt (i.e., slow or steep curve), the relative error predicted by each model was large in the early stage and then greatly reduced in the later stage. The optimal combination model was not only suitable for steep P-s curves but also for slow curves. Its accuracy (SSE and SE) and stable reliability (SSRE and RSE), as well its prediction capability classification, were better than those of the other prediction models.
3) As an effective scientific modeling method, the proposed optimal combination model could be used to optimize the combination of multiple models and buffer the advantages and disadvantages of every single model. When the weight ratio does not appear negative, the accuracy of every single model can be improved through a scientific combination. Reducing the data at the elastic stage will also help to improve model accuracy in predicting the maximum pull-out load of anchor bolts.
[1]Ozhan H O, Guler E. Critical tendon bond length for prestressed ground anchors in pullout performance tests conducted in sand[J]. International Journal of Civil Engineering, 2018, 16(10): 1329-1340. DOI:10.1007/s40999-017-0261-0.
[2]Zhang N, Matthew Evans T, Zhao S W, et al. Discrete element method simulations of offshore plate anchor keying behavior in granular soils[J].Marine Georesources & Geotechnology, 2020, 38(6): 716-729. DOI:10.1080/1064119X.2019.1614705.
[3]Su W Z,Fragaszy R J. Uplift testing of model anchors[J]. Journal of Geotechnical Engineering, 1988, 114(9): 961-983. DOI:10.1061/(asce)0733-9410(1988)114: 9(961).
[4]Littlejohn S,Mothersille D. Maintenance and monitoring of anchorages: Guidelines[J]. Proceedings of the Institution of Civil Engineers—Geotechnical Engineering, 2008, 161(2): 93-106. DOI:10.1680/geng.2008.161.2.93.
[5]Kono K, Nakahashi A, Fukagawa R. Calculation formula for pullout resistance[J]. International Journal of Geomate, 2019, 16(58): 110-115. DOI: 10.21660/2019. 58.8181.
[6]Hofmann J,Welz G. Load-bearing behaviour and characteristic load-bearing capacity of injection anchors in masonry[J]. Mauerwerk, 2017, 21(6): 369-384. DOI:10.1002/dama.201700019.
[7]Sun X Y, Zhang T, Wang M M, et al. A method for predicting bearing capacity of anchor bolt based on modified D-S evidence theory[J]. Rock and Soil Mechanics, 2015, 36(12): 3556-3566. DOI:10.16285/j.rsm.2015.12.028.(in Chinese)
[8]Sun X Y, Zhang T, Wang M M, et al. A revised model for predicting the bearing capacity of rock bolts based on mixed exponential and power function[J]. Journal of Rock Mechanics and Engineering, 2014, 34(8): 1641-1649. DOI: 10.13722/j.cnki.jrme.2014.1106. (in Chinese)
[9]Xu M, Zhang Y X, Yin K. Prediction of ultimate bearing capacity of anchor rod by artificial neural network[J]. Journal of Rock Mechanics and Engineering, 2002, 21(5): 755-758. DOI:10.3321/j.issn:1000-6915.2002.05.032. (in Chinese)
[10]Liu M G. The prediction method of ultimate resistance capacity of bolt base on gray theory[J]. Journal of Underground Space and Engineering, 2006, 2(6): 1044-1048. DOI: 10.3969/j.issn.1673-0836.2006.06.035. (in Chinese)
[11]Xue X H, Zhang W H, Liu H J. Estimation of bearing capacity of bolts based on genetic neural network[J]. Journal of Engineering Geology, 2006, 14(2): 249-252. DOI: 10.3969/j.issn.1004-9665.2006.02.019. (in Chinese)
[12]Ying Z M, Zhang J, Shang Y Q. Exponential model for simulating load-displacement curve of anchor rod[J]. Rock and Soil Mechanics, 2005, 26(8): 1331-1334. DOI: 10.3969/j.issn.1000-7598.2005.08.028. (in Chinese)
[13]Zhao M H, Zhang T X, Zou X J. Analysis of anti-pull-force for anchored bars in retaining structures[J]. Central South Highway Engineering, 2003, 28(4): 4-7. DOI: 10.3969 /j.issn.1674-0610.2003.04.002. (in Chinese)
[14]Gurung N. A theoretical model for anchored geosynthetics in pull-out tests[J]. Geosynthetics International, 2000, 7(3): 269-284. DOI:10.1680/gein.7.0175.
[15]Jiang J P, Gao G Y, Liu W B. Modified hyperbolic model describing Q-s curves of squeezed branch pile[J]. Journal of Basic Science and Engineering, 2010, 18(6): 999-1009. DOI: 10.3969/j.issn.1005-0930.2010.06.015. (in Chinese)
[16]Bai P, Wei Q, Wang N. Research on ultimate uplift capacity of tension piles of uniform section based on prediction of power function model[J]. Grain Distribution Technology, 2010(6): 9-13. DOI: 10.3969/j.issn.1007-3582.2010.06.003. (in Chinese)
[17]Kuang Z, Zhang M Y, Bai X Y. Load-bearing characteristics of fibreglass uplift anchors in weathered rock[J]. Proceedings of the Institution of Civil Engineers—Geotechnical Engineering, 2020, 173(1): 49-57. DOI:10.1680/jgeen.18.00195.
[18]Deng J L. Control problems of grey systems[J]. Systems and Control Letters, 1982, 1(5): 288-294. DOI:10.1016/S0167-6911(82)80025-X.
[19]Yin K D,Geng Y, Li X M. Improved grey prediction model based on exponential grey action quantity[J]. Journal of Systems Engineering and Electronics, 2018, 29(3): 560-570. DOI:10.21629/JSEE.2018.03.13.
[20]Li Y, Wang J Q, Wu J. Model calibration concerning risk coefficients of driving safety field model[J].Journal of Central South University, 2017, 24(6): 1494-1502. DOI:10.1007/s11771-017-3553-2.
[21]Tang X W. Optimal combination prediction method and its application[J]. Statistics and Management, 1992, 11(1): 31-35. DOI: 10.13860/j.cnki.sltj.1992.01.007. (in Chinese)
[22]Makridakis S. Accuracy measures: Theoretical and practical concerns[J]. International Journal of Forecasting, 1993, 9(4): 527-529. DOI:10.1016/0169-2070(93)90079-3.
[23]Niroumand H, Kassim K A. Pullout capacity of irregular shape anchor in sand[J]. Measurement, 2013, 46(10): 3876-3882. DOI:10.1016/j.measurement.2013.07.042.
[24]Wang X N, Ye R, Zhou F J. Proposals for the selection of failure criteria in soil float-resisting anchor rod test[J]. Geological hazards and Environmental Protection, 2001, 12(3): 73--77. DOI: 10.3969/j.issn.1006-4362.2001.03. 017. (in Chinese)
[25]Zhang M Y, Zheng C, Bai X Y, et al. Experimental study on anchorage characteristics of GFRP and steel anti-floating anchor embedded in foundation slab[J]. Journal of Basic Science and Engineering, 2019, 27(4): 931-946. DOI: 10.16058/j.issn.1005-0930.2019.04.020. (in Chinese)