Multimodal transport is a green and efficient mode of transport organization; relative to a single mode of transport, multimodal transport can reduce carbon dioxide emissions[1]. Container transport strategies in seaports and dry ports have been optimized to reduce transportation costs and carbon emissions[2]. During the 13th Five-Year Plan period in China, several policies for multimodal transport were formulated. These policies called for the strengthening of the construction of multimodal transport hubs, the connectivity between multimodal transport hubs, and the elimination of barriers to the connection of different transport modes. These policies were also aimed at realizing a “channel+hub+network” operation system and a national transportation network. Hence, China is seeking to build a multimodal transport network.
The research on multimodal transport has long been focused on network design[1-4] and path planning[5-8]. With the improvement of multimodal transport hubs, multimodal transport networks have become a hot research topic. Take for example the market structure of European multimodal transport networks; a relevant study defined the boundaries of the transshipment market by using actual data to analyze the transshipment and transport markets[9]. Multimodal transport can reduce overall transportation costs, integrate transportation resources, and reduce carbon emissions. To optimize the cost of the multimodal transport service chain with consideration of transportation, distribution, environment, time, capacity, and other factors, existing research established a mixed integer programming model and performed numerical analysis on the basis of actual case data[10]. Another work evaluated the efficiency of a multimodal transport service chain by using the improved data envelopment analysis method for ten lines of the European multimodal transport[11]. Complex networks have been widely used in traffic network analysis. By contrast, multimodal transport networks, which are freight transport networks, have been rarely investigated using complex networks.
Several studies have focused on the structure and node failure scenarios of multimodal transport networks. The application of complex network theory to network node failure is mainly observed in public transportation networks, social networks, civil aviation networks, etc. Therefore, the current study considers the application of complex network theory in freight multimodal transport networks to the failure of nodes in a multimodal transport network. The research into complex networks for node failure (node removal) is significant in most real complex networks, such as the Internet, social network, electrical power grids, and transportation networks. When network nodes are subjected to random and intentional attacks, the topology of the network changes. In a power system, power failure in one part may cause a large-scale cascading failure event. Therefore, on the basis of complex network theory, an improved power system evaluation model has been proposed to evaluate the risk of cascading failure of a power system and simulate a cascading failure event[12]. Complex network theory has been applied to the research of urban traffic road network structures, and models have been constructed to analyze the characteristics of urban road traffic networks. In urban traffic networks, the failure of nodes or edges disrupts traffic flow and thereby causes cascading failure in the network. Through the improvement of indicators, the road network characteristics of motor vehicle lanes can be analyzed. The distribution of lane degrees is in line with the power law distribution, and the nodes with small degrees are inclined to connect with the nodes with large degrees[13]. The method of complex network dual modeling is used to analyze urban road network structures. In a previous study, the topological structures of urban road networks in six cities were compared to find important similarities between clusters[14]. The theory of complex networks can be used to identify the important nodes in multimodal networks and analyze the properties of networks with node failures. A local attack on an empowered Beijing road network was previously carried out to identify important nodes[15]. In a multimodal network, hub cities serve as important nodes; when these nodes are damaged by natural disasters, transportation time and costs increase.
Given a network with nodes, an intentional attack or a random attack was carried out on a node with a large capacity. The network connectivity after the attack was then analyzed. The results show that the impact of random attacks is relatively minimal. Nodes with a large degree and large capacity are very destructive to the network, and the effect is likely to lead to cascading failures[16]. A new cascading failure model based on underload failure has been proposed[17]. The spatial network structure is related to node failure. Research reveals that self-organized cities share similar scale-free networks in a nonspatial network distribution[18]. The tolerance to cascading failures in small-world networks and the size of the largest connected components after attacks have been analyzed[19]. Attacks against multiple nodes and the dynamic robustness of networks have also been studied. The impact of redistribution parameters and the initial load distribution parameter on network robustness has been studied as well[20]. A method for evaluating the robustness of a network after an attack has been designed, and the network structure has been optimized. The effectiveness of the method has also been verified[21]. Multimodal transport has been proved to perform well in carbon emissions[22], while robustness is the obstacle to development.
Multimodal transport networks are different from other transport networks. In the former, more than one transport mode exists between two nodes. The current work applies complex network theory to the analysis of multimodal transport networks. The topology of a multimodal transport network is analyzed, and its characteristics are analyzed accordingly. When a city as a node is attacked by natural disasters, such as floods, earthquakes, and snowstorms, the node city fails. In this study, the connectivity of the network after sudden node failure is investigated, and the vulnerability of the multimodal transport network in natural disasters is discussed. At the same time, random attacks on nodes and intentional attacks on nodes with varying degrees are analyzed, and the network vulnerabilities in both cases are analyzed and compared.
This work proposes the application of complex network theory to multimodal transport networks. Thus, the results should fill the gap in the application of complex network theory to multimodal freight transport networks.
1 Methodology
A multimodal transport network consists of two parts: the hub node and the transport route. Transport hubs serve as nodes in the network. The transportation route between each node acts as an edge. Moreover, more than one transport mode exists between nodes in a multimodal transport network; thus, different transport modes should be considered when calculating the edge weights between nodes. Graph theory is introduced to construct the multimodal transport network model. In the solution for G, node vi is the multimodal transport hub; edge bij is the transport route between nodes; and weight wij is introduced as the distance and node traffic between transport hubs. Then, the network structure model G is expressed as
G=(V,B,W)
(1)
where V is the set of nodes vi, V={v1,v2,…,vn}; B is the set of transport routes, B={b12,b13,…,bij}; and W is the set of transport weights between nodes, W={w12,w13,…,wij}.
The path refers to the edge in the multimodal transport network. Thus, the average of the paths between any two nodes refers to the average number of edges between any two nodes. The characteristic path length L is defined as the average number of edges between two nodes in the multimodal transport network[14].
〈k〉![]()
(2)
(3)
where 〈k〉 is the average degree of the network; N is the total number of nodes; L is the characteristic path length; dij is the number of edges on the shortest path connecting two nodes (i and j), and 1/dij is called the efficiency between two nodes.
As the capacities and speeds in transport modes differ, the capabilities of transferring goods to other transport modes via hubs also vary. The differences determine the multimodal transport cost and efficiency. Relative to the transport of goods directly from the origin to the destination by one transport mode, multimodal transport can reduce carbon emissions (relative to roadway transportation) and travel time (relative to waterway transportation) by combining the advantages of different transport modes. In a multimodal transport network, edge weight wij is defined as a function of the transport time from node i to j; it is obtained by the weighted sum of the transport time between two nodes. It also indicates the importance of nodes in the network. α, β, and γ are the coefficients of the transport time of each mode of transport. The carbon emissions of different transportation modes are proposed to be used as coefficients from the perspective of energy conservation and environmental protection. Thus, the values of α, β, and γ are determined by the carbon emission coefficients of each transportation mode.
(4)
(5)
where wij is the weight of the edge connecting node vi and vj; ![]() is the time spent in waterway transportation; Si is the vertex strength of node vi, and it represents the sum of the edge weights associated with the node; Ni is a set of node neighbors.
is the time spent in waterway transportation; Si is the vertex strength of node vi, and it represents the sum of the edge weights associated with the node; Ni is a set of node neighbors.
In a multimodal transport network, each node is connected to several nodes, which thus offers many transport route choices. Ci and C are used to evaluate one node’s connection and the network nodes’ connection, respec-tively. The larger Ci and C are, the lower the level of vulnerability of multimodal transport will be.
(6)
(7)
where Bi is the connected number of edges of node vi; Ci is the clustering coefficient of node i and is the ratio of the number of connected edges between all nodes adjacent to node i and the maximum number of possible edges between the adjacent nodes; ![]() is the total number of possible edges; and C is the clustering coefficient of the entire network.
is the total number of possible edges; and C is the clustering coefficient of the entire network.
Coreness (k-core) refers to the remaining subgraphs after the repeated removal of nodes whose degree is less than k. If a node has a k-core and is removed in the k+1 core, then the coreness of the node is k. The maximum number of node cores in the network is the number of cores in the graph. After the node of the network is attacked, the characteristic path length and the largest connected subgraph of the network are analyzed to evaluate the network performance.
Complex network theory is widely applied to social and information networks, but it is rarely adopted in freight transport networks. The current study proposes to apply this theory to multimodal transport networks. Complex network theory is general in nature, but its application to multimodal transport networks is innovative. All the results can be used as indexes in the management of multimodal transport companies. Fig.1 shows the framework of the application of complex network theory to multimodal transport network management.
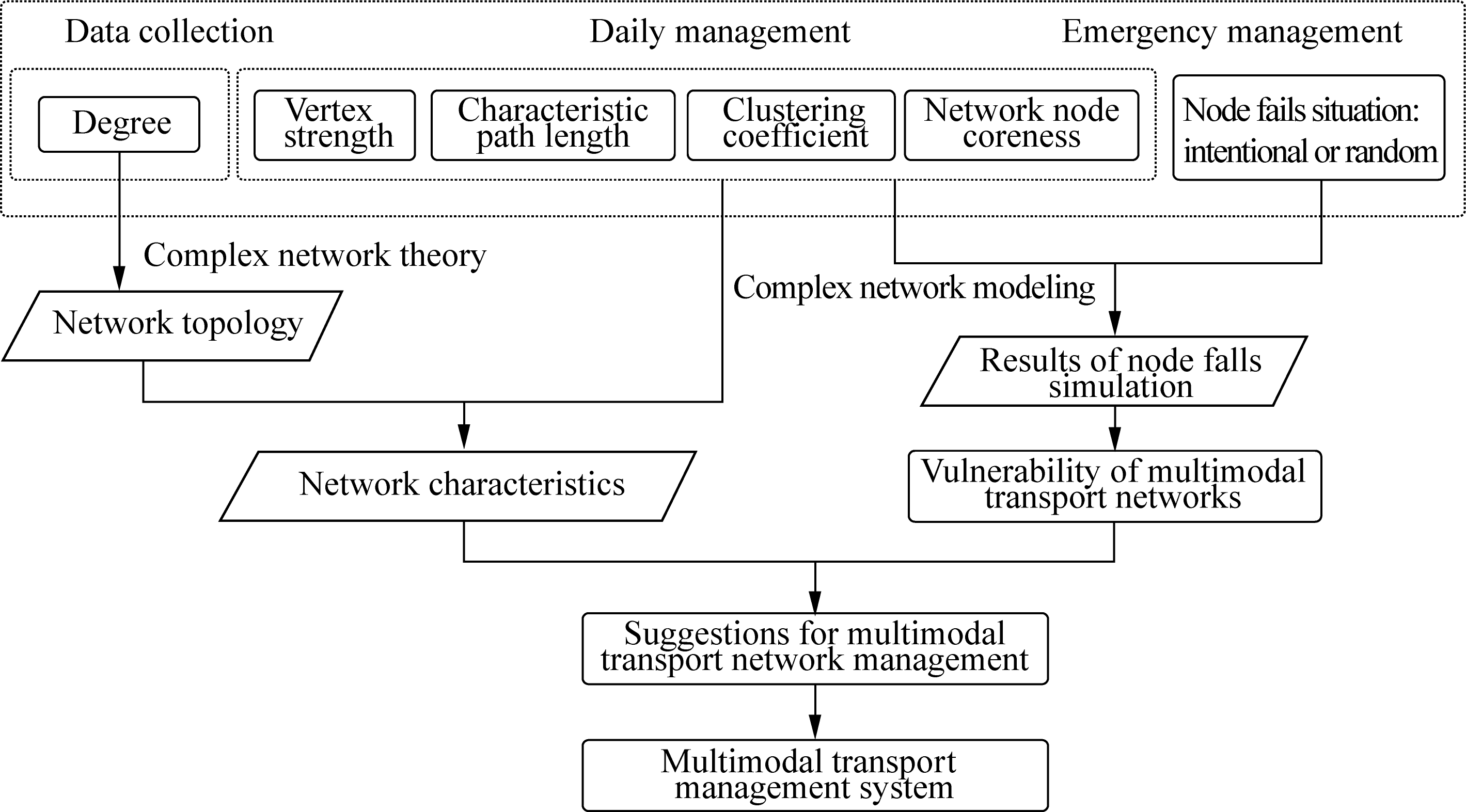
Fig.1 Framework of application of results to multimodal transport network management
2 Case Study
2.1 Data and background
For the multimodal transport network, this work considers CIMC Kaitong’s multimodal transport business in China. In the network, the name of the multimodal transport hub is replaced by the name of the city. Thus, the city name is used as the node name. Gephi provides support for network topology analysis. MATLAB is used for simulation analysis.
The network consists of 32 nodes and 140 edges. The degrees of each node city are shown in Fig.2. The depth of the node color in the graph indicates the size of the node degree. The deeper the color is, the higher the degree value of the node is. In Fig.3, each encircled number indicates the city number.
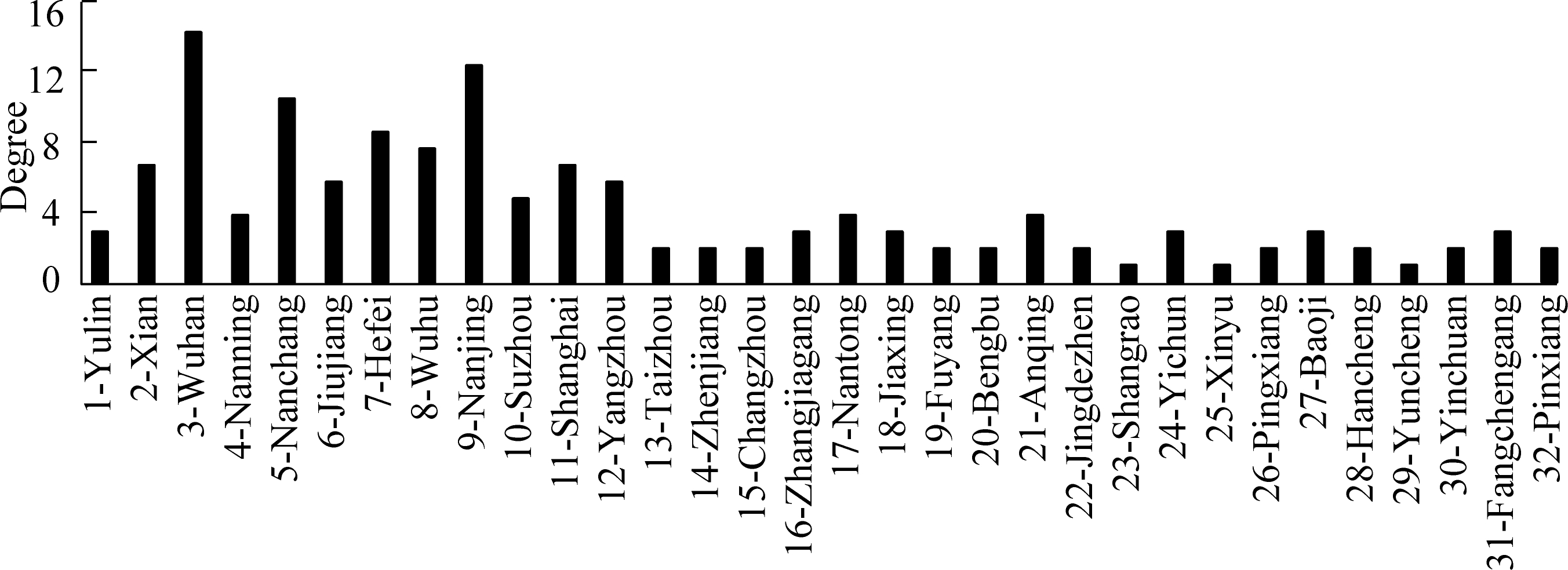
Fig.2 Node degree in multimodal transport network
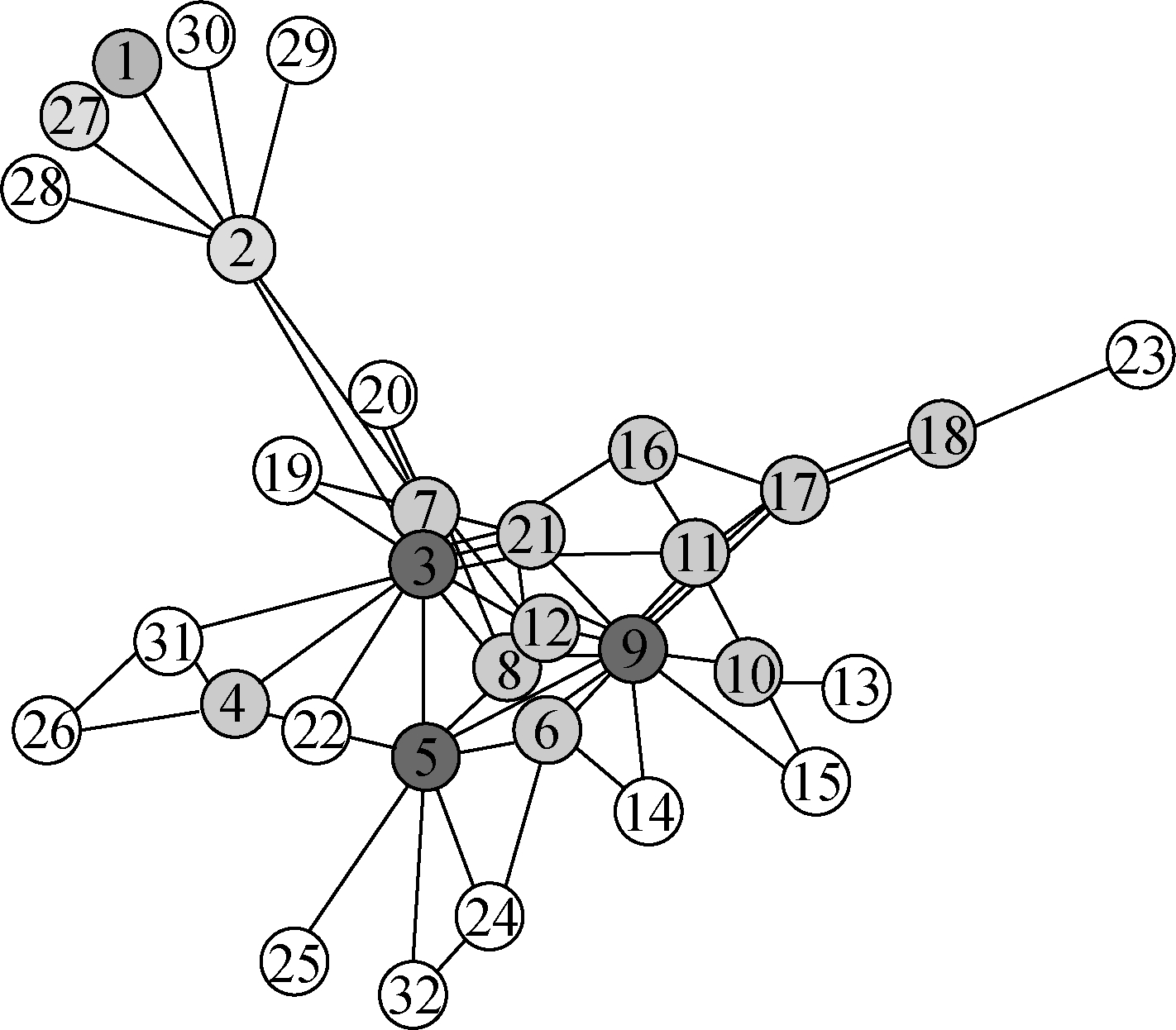
Fig.3 Multimodal transport network topology
2.2 Network characteristic analysis
According to the statistical data of the multimodal transport network, its topology, vertex strength, degree distribution, characteristic path length, clustering coefficient, and the number of cores can be obtained.
Most nodes have small degrees and a low level of vertex strength, while a few nodes may have high degrees, as shown in Figs.4 and 5. The nodes with high degrees have more connections with others and have more choices for transport routes than their counterparts with low degrees.
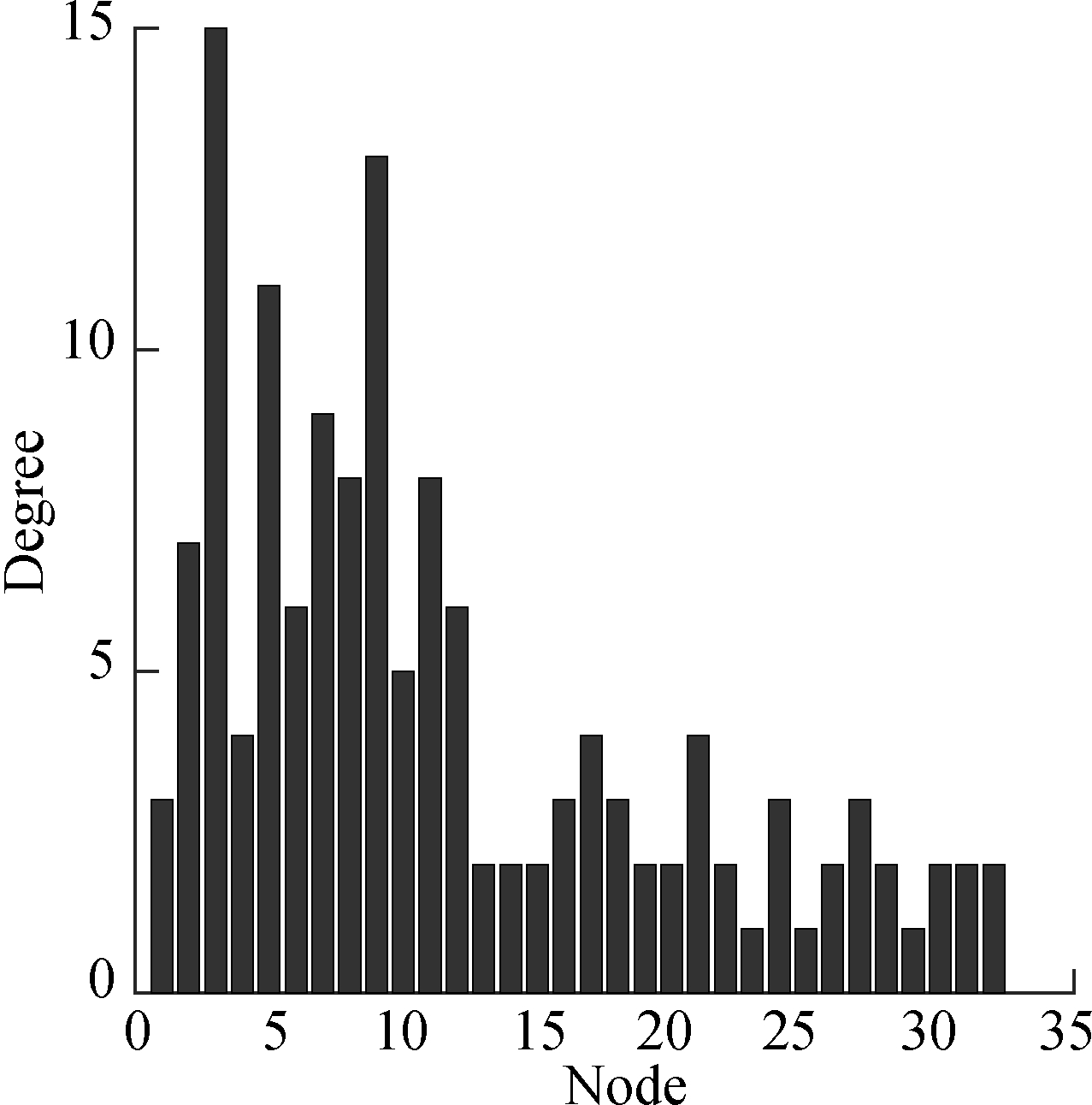
Fig.4 Distribution of node degrees in multimodal transport network
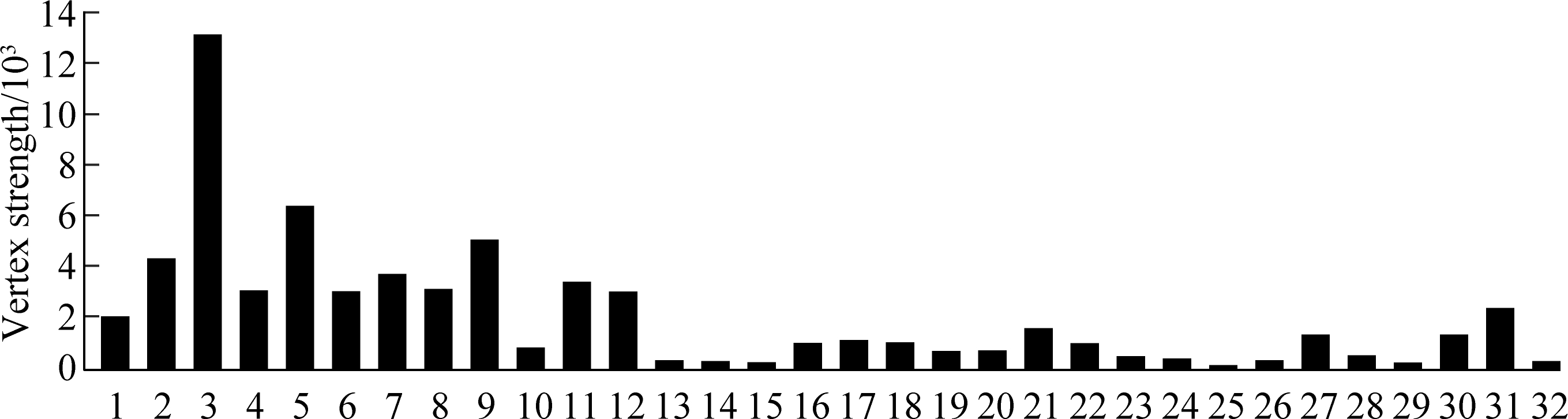
Fig.5 Vertex strength in the multimodal transport network
Meanwhile, the nodes with high weight values have more choices of transport modes and routes than the nodes with low weights. This characteristic is consistent with node degree. The nodes with particularly high degree values, such as Wuhan, Nanchang, and Nanjing, also have high vertex strength (see Fig.5). If these nodes fail, then the multimodal transport network would lose most of the edges, which are routes in actual scenarios. In such a case, network connectivity drops to a low level, and the vulnerability of the multimodal transport network increases.
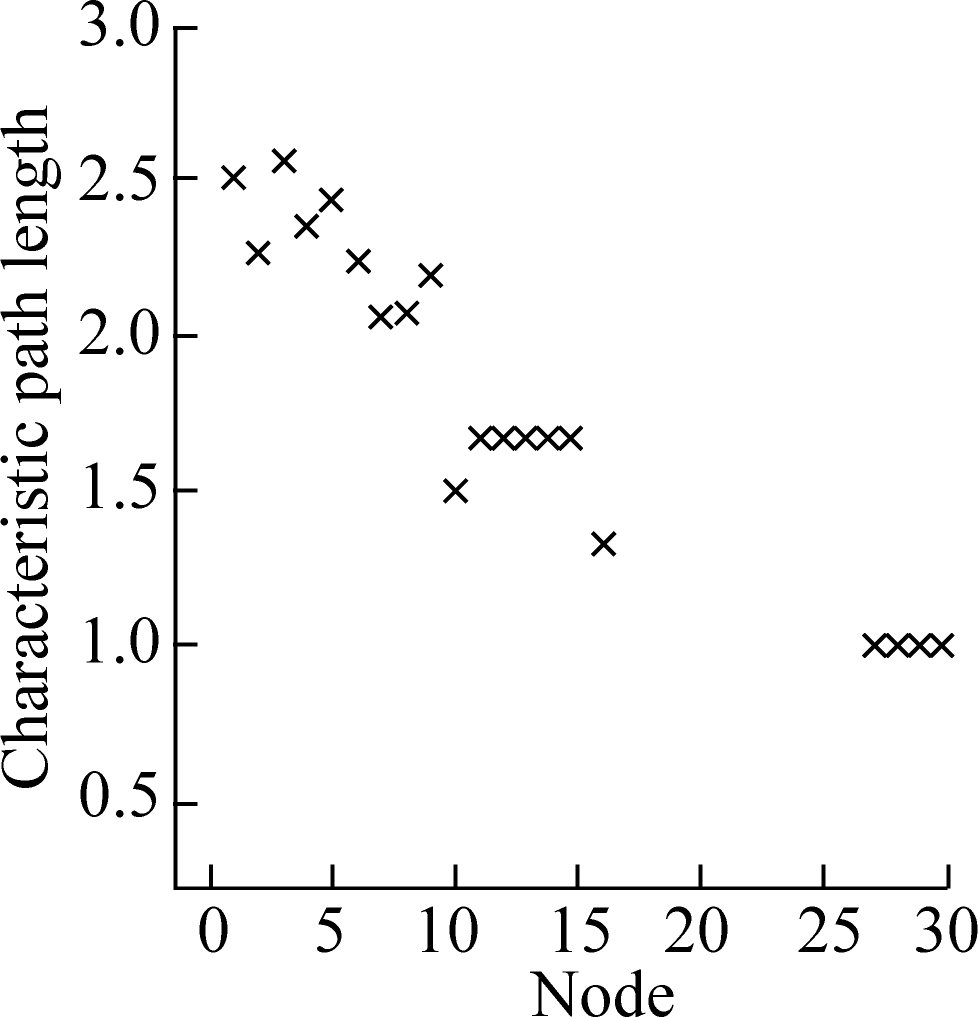
The characteristic path length of a multimodal transport network represents the average number of edges between the origin and destination of goods being transported. It is equal to 2.540 3 in this work. Each node’s path length is shown in Fig.6. Therefore, an average of 2.540 3 edges exist between the origin and the destination in the network. Moreover, an average of two transshipment hubs are utilized during transportation. The greater the number of transshipment hubs is, the higher the possibility of multimodal transport will be. When the characteristic path length is less than 2, the demand for multimodal transport declines to a low level. This condition is not conducive to the expansion of multimodal transport networks. The larger the characteristic path length is, the greater the potential of transshipment hubs will be, and the more likely multimodal transport will be adopted. The node with a large degree has a small characteristic path length, whereas a node with a large degree has more transport lines to choose from and is more connected to other nodes. However, the larger the characteristic path length is, the greater the impact of node failure will be. In such a case, the vulnerability of the network increases.

Fig.6 Characteristic path length in the multimodal transport network
The vulnerability of a multimodal transport network can also be reflected by the clustering coefficient, which is an indicator of network connectivity. In the case of a node failure, the larger the clustering coefficient is, the stronger the connectivity of the network will be. In the multimodal transport network, the clustering coefficient is 0.621 18, and clustering coefficient distribution is shown in Fig.7. When the clustering coefficient is 1, node failure exerts a minimal effect on the multimodal transport network.
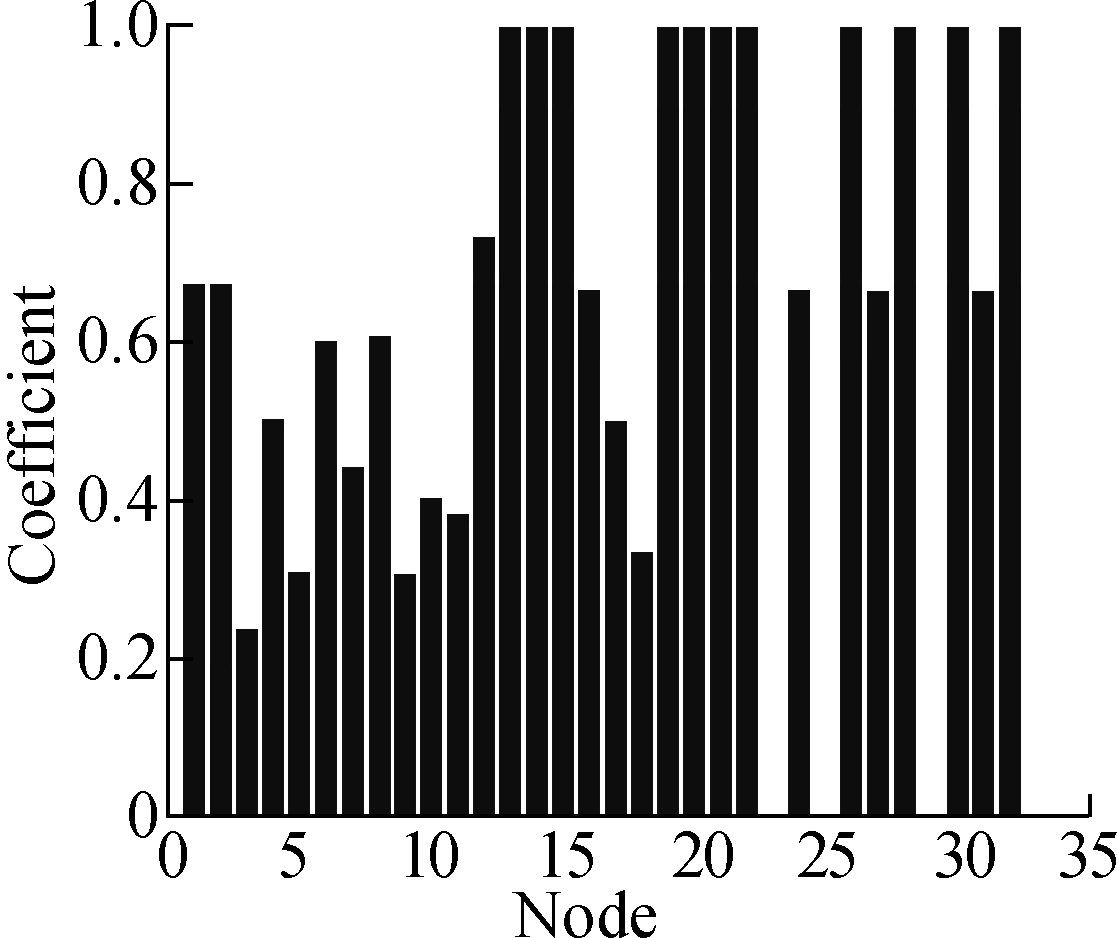
Fig.7 Clustering coefficient of the multimodal transport network
The number of node cores indicates the depth of the nodes in the network. The nodes with a large number of cores have great connectivity and strong propagation. Herein, the number of cores of the multimodal transport network is 5. In the multimodal transport network, the high-core nodes are the key nodes (see Fig.8). When these nodes fail, the connectivity of the network and its transportation efficiency are greatly affected.
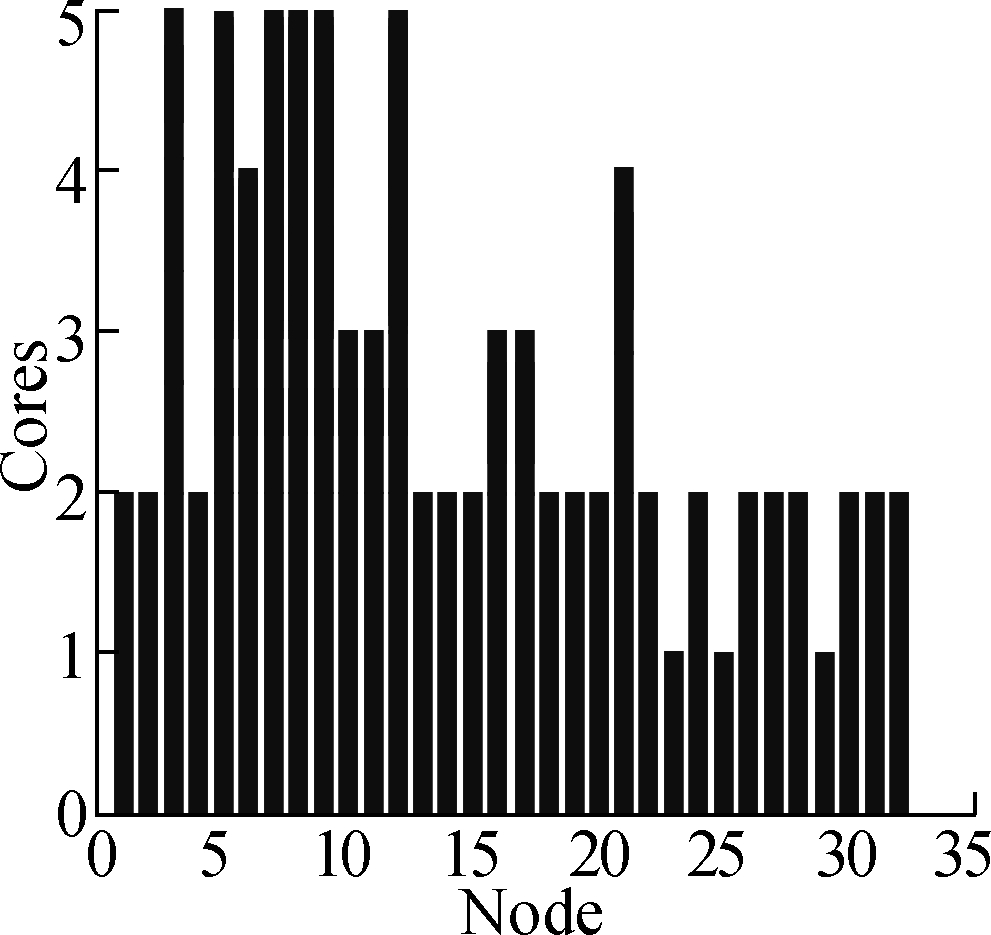
Fig.8 Multimodal network node cores
2.3 Network vulnerability analysis of node failures
When the node city of a multimodal transport network encounters natural disasters, such as floods, earthquakes, fire,and snowstorms, the node city cannot provide services for multimodal transshipment. As discussed in Section 2.2, when a node fails, all the characteristics change. Hence, the characteristics of a multimodal transport network after node failures should be investigated to establish a secure network at a low cost[15] and improve emergency response.
A failing node in a multimodal transport network is defined as a node under an intentional or random attack. Node failure occurs regularly at specific times and conditions. It is defined as an intentional attack on the network, such as floods in June and July in Wuhan City. When natural disasters occur randomly and cannot be predicted, the attack is defined as a random attack. Examples include earthquakes and fire. An experiment is conducted to analyze the multimodal transport network under intentional and random attacks.
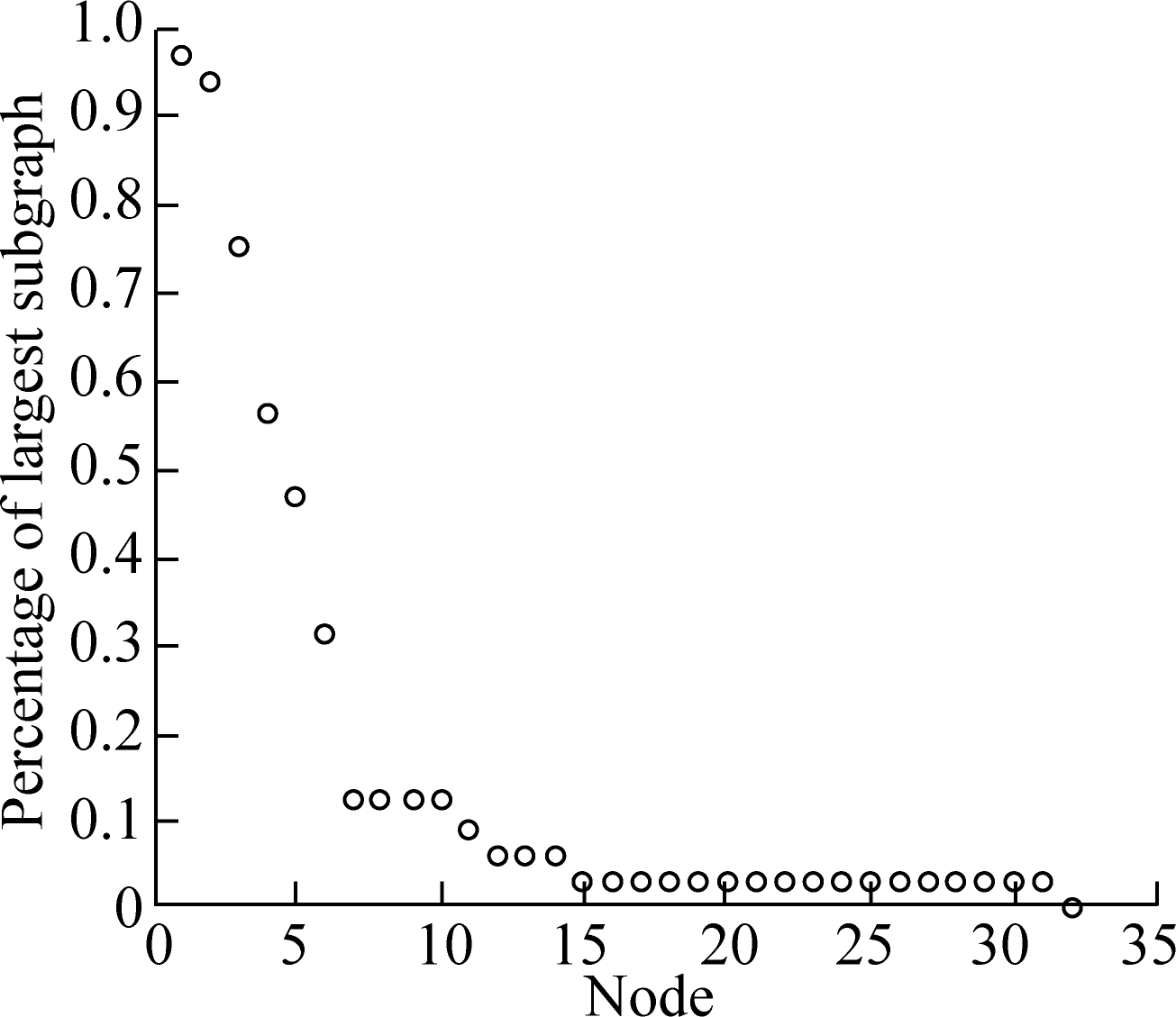
The characteristic path length and percentage of the largest connected subgraph are used to analyze the vulnerability of the multimodal transport network. The nodes with a large degree are the target of the intentional attack. The multimodal transport network is more vulnerable under an intentional attack than under a random attack. As shown in Fig.9, the characteristic path length and percentage of the largest connected subgraph decrease more sharply under an intentional attack than under a random attack. The characteristic path length is lower than 2, with ten nodes under random attack and seven nodes under intentional attack. The percentage of the largest connected subgraph is below 20%, with ten nodes failing
(a)

(b)

(c)
(d)
Fig.9 Vulnerability of multimodal transport network under random and intentional attacks.(a) Characteristic path length changes under random attack; (b) Percentage of largest subgraph changes under random attack; (c) Characteristic path length changes under intentional attack; (d) Percentage of largest subgraph changes under intentional attack
under random attack and seven nodes failing under intentional attack. In these situations, which may be caused by extremely heavy snow (e.g., the snow disaster in 2008) and the failure of several node cities, the network cannot operate effectively.
In the multimodal transport network, the nodes with a large degree are the key nodes that are critical to network security. Hence, one of the main assignments is to improve the operation and management of these nodes. When these nodes are unable to function because of a natural disaster, the efficiency of the whole multimodal transport network is greatly affected. Companies can consider setting some emergency node cities as key node alternatives in collaboration with other transport companies.
3 Conclusions
1) This study proposes to apply complex network theory to the analysis of the topology and vulnerability of a multimodal transport network. Data from CIMC Kaitong’s multimodal transport network are selected as a case study to implement the proposed method. All the results can support the company’s daily operations and emergency management.
2) The results of the multimodal transport network topology and characteristics can serve as indexes in network management. Specifically, the node degree and vertex strength are the indexes of the key node. The characteristic path length should be above 2, and the clustering coefficient and network node core should be high. The node with a large degree in the multimodal transport network has a small clustering coefficient and a large number of cores.
3) This work provides a method for analyzing the vulnerability of a multimodal transport network. The results should assist managers in preparing for cases of node failure.
[1]Zhang D, He R, Li S, et al. A multimodal logistics service network design with time windows and environmental concerns[J].PLoS One, 2017, 12(9): e0185001. DOI:10.1371/journal.pone.0185001.
[2]Tsao Y C, Linh V T. Seaport-dry port network design considering multimodal transport and carbon emissions[J]. Journal of Cleaner Production, 2018, 199: 481-492. DOI:10.1016/j.jclepro.2018.07.137.
[3]Jiang J H, Zhang D Z,Meng Q, et al. Regional multimodal logistics network design considering demand uncertainty and CO2 emission reduction target: A system-optimization approach[J]. Journal of Cleaner Production, 2020, 248: 119304. DOI:10.1016/j.jclepro.2019.119304.
[4]Resat H G, Turkay M. A bi-objective model for design and analysis of sustainable intermodal transportation systems: A case study of Turkey[J]. International Journal of Production Research, 2019, 57(19): 6146-6161. DOI:10.1080/00207543.2019.1587187.
[5]Fazayeli S, Eydi A, Kamalabadi I N. Location-routing problem in multimodal transportation network with time windows and fuzzy demands: Presenting a two-part genetic algorithm[J]. Computers & Industrial Engineering, 2018, 119: 233-246. DOI:10.1016/j.cie.2018.03.041.
[6]Wang Q Z, Chen J M, Tseng M L, et al.Modelling green multimodal transport route performance with witness simulation software[J]. Journal of Cleaner Production, 2020, 248: 119245. DOI:10.1016/j.jclepro.2019.119245.
[7]Li J, Yang B, Zhu X L. Path optimization of green multimodal transportation under mixed uncertainties[J].Journal of Transportation Systems Engineering and Information Technology, 2019, 19(4): 13-19,27. DOI:10.16097/j.cnki.1009-6744.2019.04.003.(in Chinese)
[8]Zhao Y R, Yang Z Z, Haralambides H. Optimizing the transport of export containers along China’s coronary artery: The Yangtze River[J]. Journal of Transport Geography, 2019, 77: 11-25. DOI:10.1016/j.jtrangeo.2019.04.005.
[9]Saeedi H, Wiegmans B, Behdani B, et al. European intermodal freight transport network: Market structure analysis[J]. Journal of Transport Geography, 2017, 60: 141-154. DOI:10.1016/j.jtrangeo.2017.03.002.
[10]Sitek P, Wikarek J. Cost optimization of supply chain with multimodal transport[C]//2012 Federated Conference on Computer Science and Information Systems (FedCSIS). Wroclaw, Poland, 2012: 1111-1118.
[11]Saeedi H, Behdani B, Wiegmans B, et al. Assessing the technical efficiency of intermodal freight transport chains using a modified network DEA approach[J]. Transportation Research Part E: Logistics and Transportation Review, 2019, 126: 66-86. DOI:10.1016/j.tre.2019.04.003.
[12]Wang Z Y, Hill D J, Chen G, et al. Power system cascading risk assessment based on complex network theory[J].Physica A: Statistical Mechanics and Its Applications, 2017, 482: 532-543. DOI:10.1016/j.physa.2017.04.031.
[13]Wang S G,Zheng L L, Yu D X. The improved degree of urban road traffic network: A case study of Xiamen, China[J]. Physica A: Statistical Mechanics and Its Applications, 2017, 469: 256-264. DOI:10.1016/j.physa.2016.11.090.
[14]Porta S, Crucitti P, Latora V. The network analysis of urban streets: A dual approach[J]. Physica A: Statistical Mechanics and Its Applications, 2006, 369(2): 853-866. DOI:10.1016/j.physa.2005.12.063.
[15]Bellingeri M, Bevacqua D, Scotognella F, et al. Efficacy of local attack strategies on the Beijing road complex weighted network[J]. Physica A: Statistical Mechanics and Its Applications, 2018, 510: 316-328. DOI:10.1016/j.physa.2018.06.127.
[16]Motter A E, Lai Y C. Cascade-based attacks on complex networks[J]. Physical Review E, 2002, 66(6): 065102. DOI:10.1103/physreve.66.065102.
[17]Wang Y C, Xiao R B. An ant colony based resilience approach to cascading failures in cluster supply network[J].Physica A: Statistical Mechanics and Its Applications, 2016, 462: 150-166. DOI:10.1016/j.physa.2016.06.058.
[18]Crucitti P, Latora V, Porta S. Centrality measures in spatial networks of urban streets[J]. Physical Review E, 2006, 73(3): 036125. DOI:10.1103/physreve.73.036125.
[19]Babaei M, Ghassemieh H, Jalili M. Cascading failure tolerance of modular small-world networks[J]. IEEE Transactions on Circuits and Systems Ⅱ: Express Briefs, 2011, 58(8): 527-531. DOI:10.1109/TCSII.2011.2158718.
[20]Lü C C, Si S B, Duan D L, et al. Dynamical robustness of networks against multi-node attacked[J]. Physica A: Statistical Mechanics and Its Applications, 2017, 471: 837-844. DOI:10.1016/j.physa.2016.12.066.
[21]Wang S, Liu J. Designing comprehensively robust networks against intentional attacks and cascading failures[J].Information Sciences, 2019, 478: 125-140. DOI:10.1016/j.ins.2018.11.005.
[22]Wang Q Z, Chen J M, Tseng M L, et al.Modelling green multimodal transport route performance with witness simulation software[J]. Journal of Cleaner Production, 2020, 248: 119245. DOI:10.1016/j.jclepro.2019.119245.