The fifth-generation mobile communication system (5G) and the long-term evolution (LTE) have similar procedures for establishing communication, both taking cell search as the first step in establishing communication between the user equipment (UE) and the base station. Therefore, the performance of the 5G cell search will affect the performance of the 5G physical broadcast channel (PBCH), which also has an impact on the subsequent communication process.
Compared with LTE[1], the 5G system adopts a large number of new technologies to achieve various key performance indicators proposed in the 5G system. In terms of spectrum management, the 5G system exploits not only the low-frequency band of 450 to 6 000 MHz, but also the millimeter-wave frequency band of 24 to 100 GHz, thus making the millimeter wave technology[2] a 5G key technology. When it comes to channel coding, the polar code[3] is used in the 5G control channel and the low-density parity-check code (LDPC) is used in the 5G data channel. Moreover, there are also many differences between the 5G system and the LTE system in terms of the frame structure, modulation mode, channel model, and so on. Therefore, it is of great significance to conduct research on the 5G cell search technology involving time-frequency synchronization and synchronization signal detection. This paper focuses on the downlink synchronization algorithm of the primary synchronization signal (PSS) in 5G, where an improved PSS block cross-correlation detection algorithm is developed to improve the detection performance under a low SNR. The impact of coarse frequency offset and residual frequency offset is also analyzed for better frequency offset estimation. The 5G downlink simulation platform is built on the MATLAB simulation software to verify the improved algorithm.
1 Downlink Synchronization Algorithm
1.1 Downlink synchronization process
In the cell search process, the UE first tries to access the cell where it last resided. If there is no previous resident information, the UE will use a global synchronization channel number (GSCN) in the 5G working frequency band to search for the SS/PBCH block according to the supported subcarrier spacing. It will then complete the detection of PSS, SSS, and the PBCH decoding to obtain the master information block (MIB).
This paper mainly studies the detection process after the UE searches for the SS/PBCH block ergodically according to the GSCN and the supported subcarrier spacing. At the transmitting terminal, both the SS/PBCH block and the PDSCH are added to improve the degree of simulation reduction. The main processes at the receiving terminal include the PSS and SSS detection, timing and frequency synchronization, and PBCH demodulation. The entire simulation flow chart is shown in Fig.1.
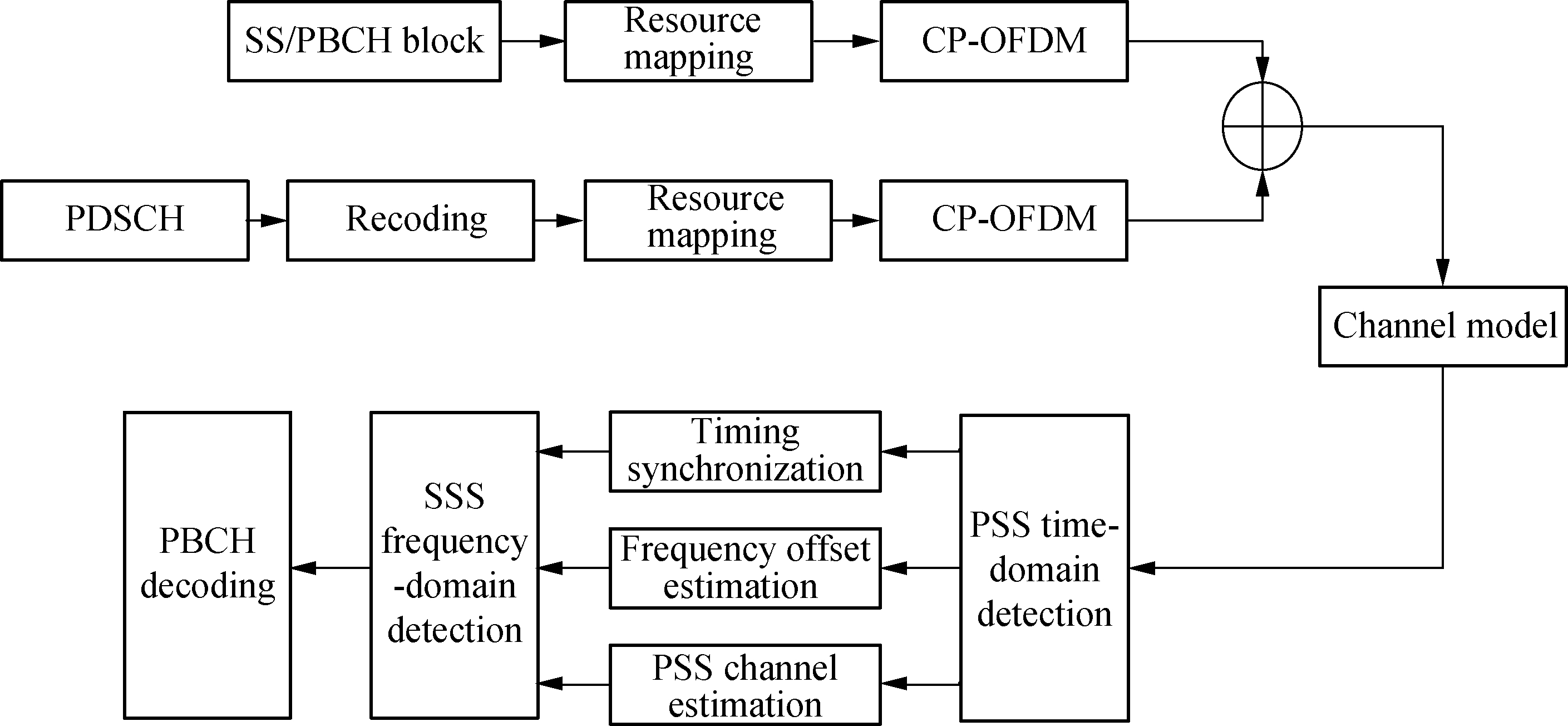
Fig.1 5G UE downlink synchronization simulation flowchart
The detection of the PSS sequence is the first step in parsing the entire SS/PBCH block. The identification within the cell group 
is obtained through the PSS sequence, which reduces the complexity of the SSS sequence detection. As the secondary synchronization signal (SSS) and part of PBCH are located on the same OFDM symbol, the accuracy of the timing position and frequency offset estimation has a great influence on separating the SSS and PBCH.
1.2 PSS sequence
Both the 5G and LTE physical layers define the PSS and the SSS. The UE completes the downlink synchronization by searching and analyzing the primary and secondary synchronization signals transmitted by the base station. Compared to the synchronization signal in LTE, which is always located on the 72 subcarriers in the center of the frequency band and is fixed on a specific symbol in the time domain, the time and frequency position of the 5G synchronization signal is more flexible.
The frequency-domain sequence of the PSS and SSS is only related to the physical layer ID of the cell where it currently resides. LTE supports 504 cell physical layer IDs, while 5G can support up to 1 008 cell physical layer IDs. The calculation formula is as follows[4-5]:
(1)
where 
represents the cell group identity, and 
represents the identity within the cell group.
5G systems choose an m-sequence with a length of 127. The PSS production formula of the m-sequence is as follows:
dPSS(n)=1-2x(m)
(2)
where dPSS(n) represents the PSS frequency domain sequence, and x(m) represents an m-sequence with a length of 127. The generator polynomial is as follows[6]:
x(i+7)=[x(i+4)+x(i)]mod 2
(3)
The initial state of the register is shown as follows:
[x(6) x(5) x(4) x(3) x(2) x(1) x(0)]=
[1 1 1 0 1 1 0]
(4)
2 Traditional PSS Block Cross-Correlation Detection Algorithm
The block cross-correlation algorithm reduces the cumulative influence of the normalized frequency offset ε in the calculation of the cross-correlation function value by block. Moreover, it can still complete an accurate coarse timing synchronization under a large frequency offset, which overcomes the weakness of the direct cross-correlation algorithm with poor anti-frequency offset performance[7]. The principal block diagram of the block cross-correlation algorithm is shown in Fig.2.
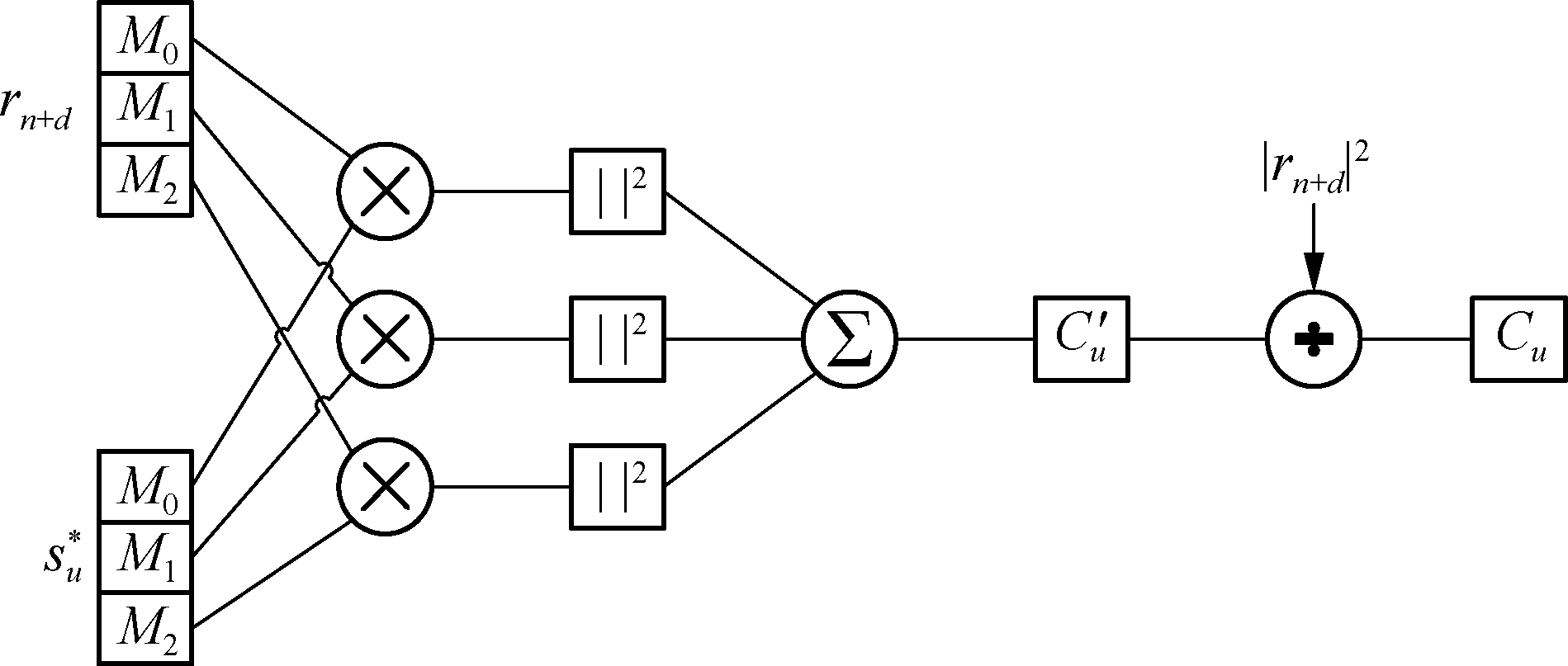
Fig.2 Block cross-correlation algorithm flowchart(M=3)
The block cross-correlation algorithm divides the received sequence and the local PSS sequence in the sliding window into M=3 blocks. Each sequence is operated separately and the modulus squared is superimposed. Similarly, to reduce the effect of the PAPR of the OFDM system, the block cross-correlation result set normalizes the signal energy in the sliding window[8]. The formula is described as follows:
u∈{0,1,2}
(5)
where L=N/M is the length of each sequence, and P(d) is the signal energy in the sliding window. It can be seen from Eq.(5) that the sequence block for the correlation operation allows the influence of the frequency offset to be accumulated only on the cross-correlation result of each sequence, which reduces the influence of the frequency offset on the entire cross-correlation result in the sliding window. In theory, the larger the number of blocks, the better the anti-frequency offset performance. However, an increase in the number of blocks will make the autocorrelation characteristics of the sequence worse under a low SNR. Consequently, the relative height of the correlation peaks will decrease and peak misalignment will appear[9].
3 Improved PSS Block Cross-Correlation Detection Algorithm
The traditional block cross-correlation algorithm has good detection performance and anti-frequency offset performance under a high SNR, but its performance under a low SNR cannot meet the needs of the 5G downlink synchronization. This paper is based on the traditional block cross-correlation algorithm and improves the traditional detection algorithm according to the new characteristics of the 5G SS/PBCH block[10].
3.1 Incoherent accumulation
Pulse accumulation is commonly used to improve the detection performance of radars[11]. Early radars used the afterglow effect of the display to achieve the accumulation effect. Presently, pulse accumulation is completed through special electronic equipment, and the accumulated signal is then judged. Pulse accumulation can be divided into coherent accumulation and incoherent accumulation. Although the effect of coherent accumulation can better improve the SNR, the use of coherent accumulation in PSS detection is more complicated and has strict coherence requirements for the transceiver equipment due to the time and frequency dispersion of the wireless channel. Thus, this study uses incoherent accumulation to improve the detection performance[12].
On the basis of the block cross-correlation algorithm, the cross-correlation modulus square of each sliding window is accumulated M times, and the coarse timing position estimation and cell group identification estimation are eventually obtained through the result set 
obtained by the i-th accumulated value are the same as the result obtained by the (i-1)-th accumulated value, the accumulation will end. 2) To avoid falling into infinite accumulation, the maximum value of M is set to Mmax=10, and the accumulation ends when the maximum value is reached.
3.2 Joint estimation of coarse frequency offset
Coarse frequency offset estimation is realized by a pre-compensation of the local PSS time series frequency offset.
To improve the detection performance of the algorithm, the coarse frequency offset estimation is not equal to the integer multiple frequency offset estimation, and the frequency offset detection granularity is set to 1/2 subcarrier spacing.
To reduce the influence of computational complexity caused by the fusion of coarse frequency offset estimation, the coarse frequency offset estimation does not use the optimal signal detection algorithm (such as the maximum likelihood detection algorithm) but uses the sub-optimal signal detection algorithm, namely the Monte Carlo (MC) detection algorithm.
The PSS cross-correlation detection algorithm fused with a coarse frequency offset estimation is described as follows: Monte Carlo’s normalized frequency offset candidate set is {-1,-0.5,0,0.5,1}. After the receiver generates the local PSS time sequence, it performs a frequency offset pre-compensation on these local sequences and generates a total of 15 types of PSS local time sequence (see Fig.3).
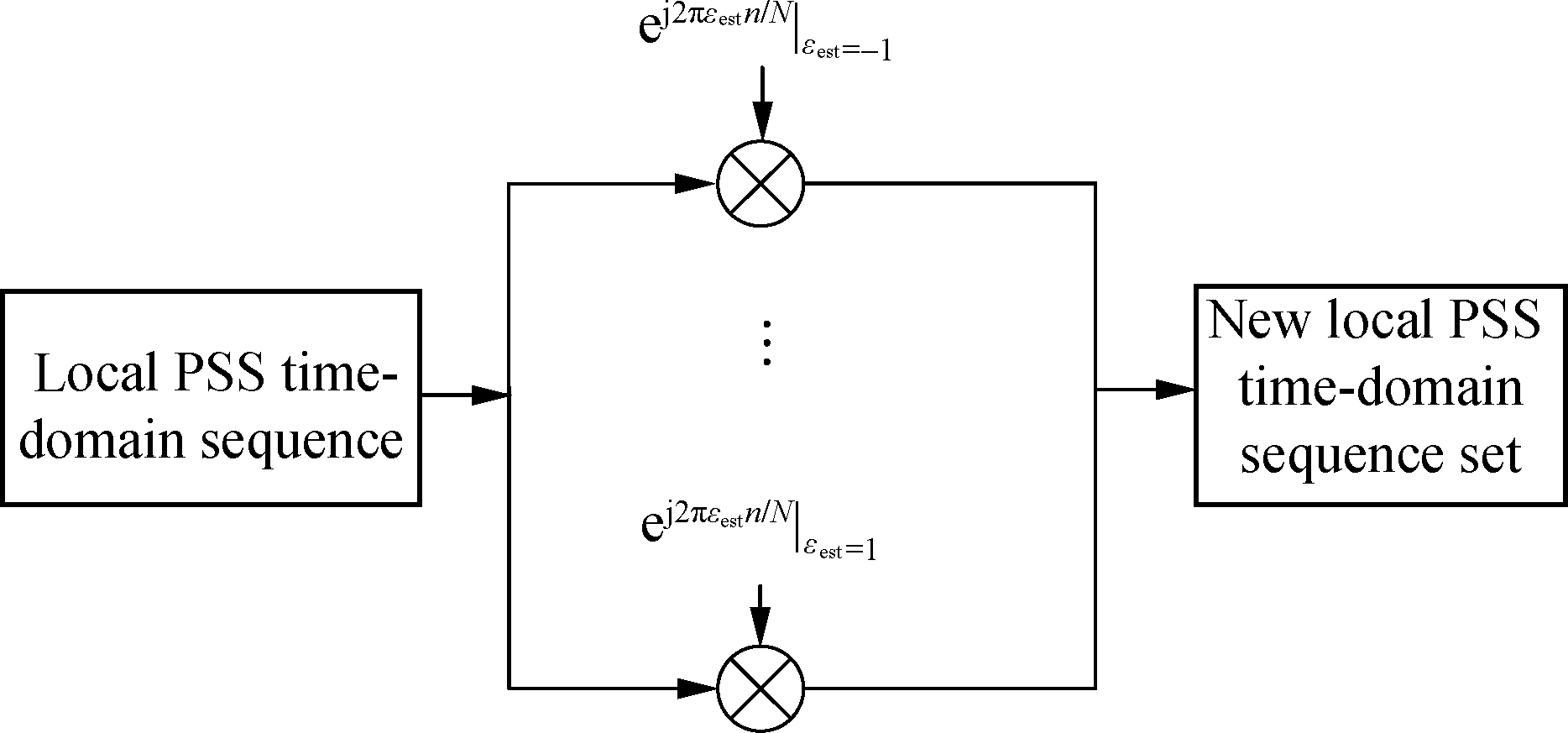
Fig.3 Pre-compensation for the frequency offset of the local PSS time sequence
The original local PSS time sequence is su(n) (u∈{0,1,2}), and the new sequence after coarse frequency offset compensation is:
su,εest(n)=su(n)ej2πεestn/N
u∈{0,1,2}, εest∈{-1,-0.5,0,0.5,1}
(6)
Based on the block cross-correlation detection algorithm, the estimation formulas of the coarse frequency offset estimation, coarse timing position and cell group identification are:
u∈{0,1,2}, εest∈{-1,-0.5,0,0.5,1}
(7)
Compared with the traditional cross-correlation detection algorithm, the cross-correlation detection algorithm fused with coarse frequency offset estimation can correctly detect the received signal whose frequency offset exceeds a subcarrier interval of 1 and avoid the repeated detection of PSS after frequency offset compensation.
4 Simulation Results and Analysis
In this section, a downlink simulation platform based on MATLAB simulation software is built to test the performance of the improved PSS block cross-correlation detection algorithm in different frequency offsets and different channels.
This paper selects the TDL-C channel model and configures the parameters of the TDL-C channel according to the 3GPP TS38.901 protocol[13]. In the simulation, the detection accuracy rate is used to measure the algorithm performance of the identity estimation in the cell group, and the coarse timing position and frequency offset estimation use the root mean square error (RMSE) of both to detect the algorithm performance. The RMSE calculation formula is as follows:
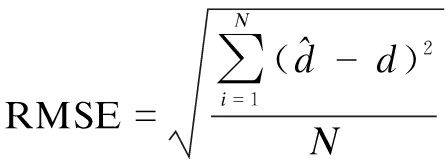
(8)
where N represents the number of times of estimation; 
represents the coarse timing position estimated by the algorithm; d represents the accurate timing position.
4.1 Comparison between direct and block cross-correlation
First, the performances of the block cross-correlation algorithm in the AWGN channel under different M values are compared.
Fig.4 shows the simulation results. When M=4,8, the frequency offset has less effect on the detection accuracy of PSS, which conforms to the theoretical derivation that states that the larger the value of M, the stronger is the anti-frequency offset performance. However, the detection accuracy is greatly affected by the SNR. The best detection accuracy is obtained when M=2, but the anti-frequency offset performance is slightly worse. Using the block cross-correlation algorithm with M=2, the performances of the direct cross-correlation algorithm and the block cross-correlation algorithm with M=2 under different channels and different frequency offsets are compared.
Fig.4 Comparison chart of the PSS detection accuracy rate under different numbers of blocks
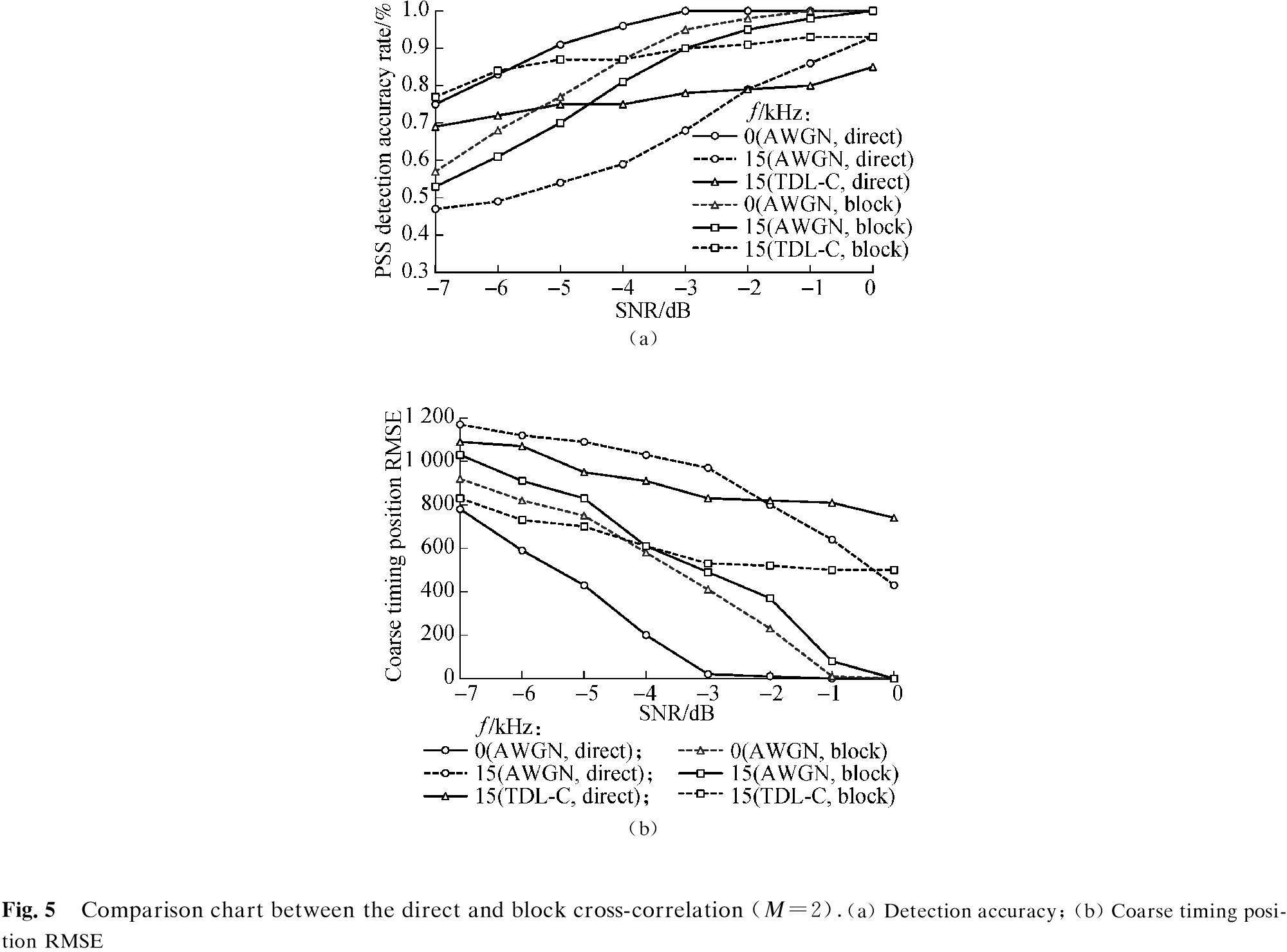
As shown in Figs.5 (a) and (b), when the AWGN channel has no frequency offset, the direct cross-correlation algorithm has better detection performance than the block cross-correlation algorithm under a low SNR. When the frequency offset is 15 kHz, i.e., the normalized frequency offset is 0.5, the detection accuracy and the coarse timing position RMSE of the block cross-correlation algorithm under the AWGN channel or the TDL-C channel are significantly better than those by the direct cross-correlation algorithm. Among them, in an AWGN channel with an SNR of -4 dB, the block cross-correlation algorithm can increase the detection accuracy by up to 22%, and the coarse timing RMSE is reduced by 39.2%.
4.2 Influence of incoherent accumulation on detection performance
Incoherent accumulation can improve the SNR of the cross-correlation result set Cu(d) and improve the detection performance of the PSS detection algorithm under a low SNR. Based on the block cross-correlation algorithm of M=2, the influence of incoherent accumulation on the detection performance under different channels is tested.
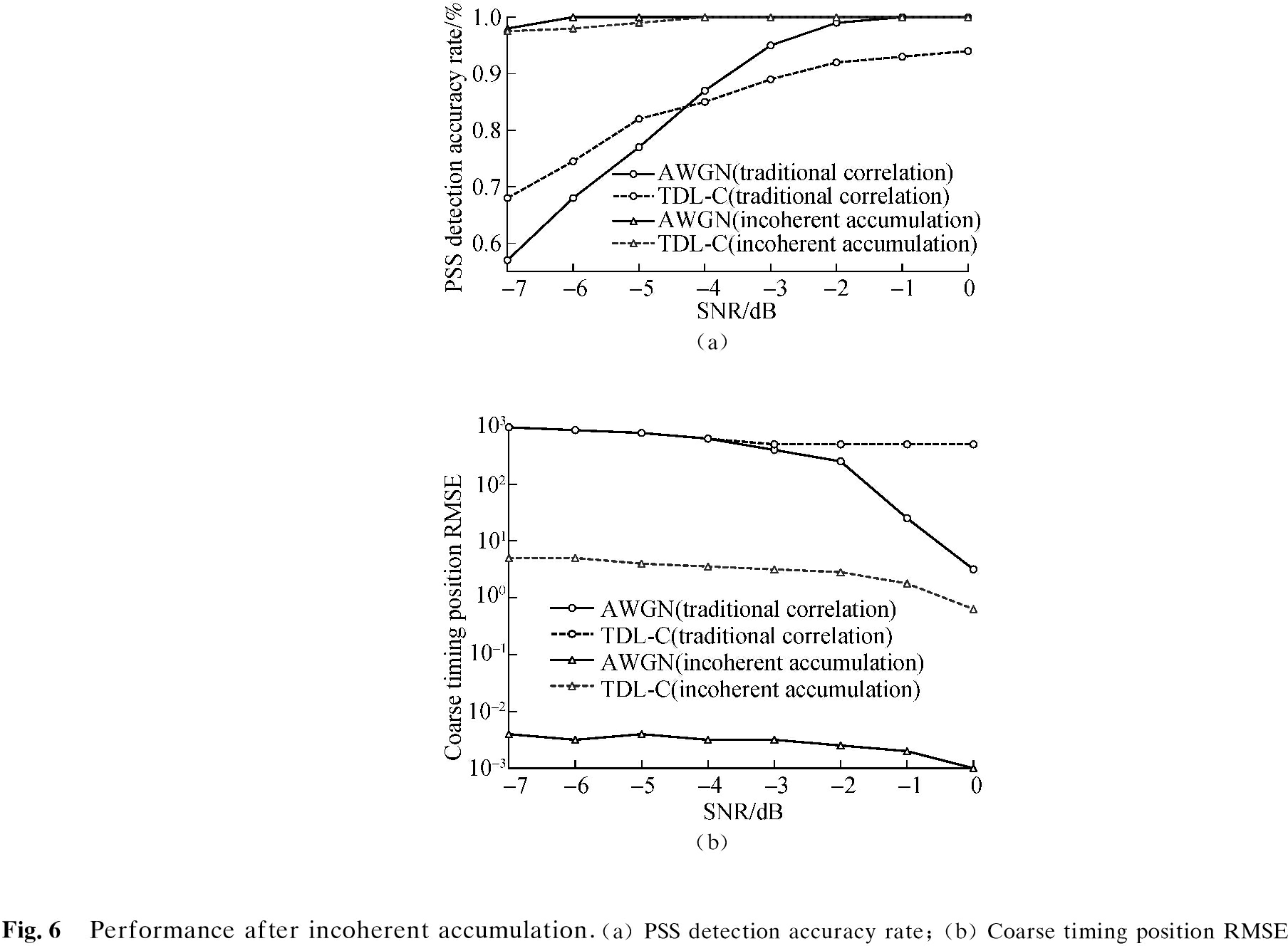
As shown in Fig.6 (a) and (b), in terms of detection accuracy, incoherent accumulation brings a 5-dB performance improvement in the AWGN channel and an 8.7-dB improvement in the TDL-C channel with an average accumulation of 3 times. In terms of coarse timing RMSE, the traditional algorithm is as high as 847.92 under the TDL-C channel and the SNR of -7 dB, and the improved algorithm is reduced to 4.71, meeting the actual symbol timing requirements. Therefore, incoherent accumulation can effectively improve the performance of the detection algorithm under a low SNR.
5 Conclusions
1) The improved block cross-correlation algorithm not only has good detection performance and anti-frequency offset performance under a high SNR, but it also can meet the needs of the downlink synchronization under a low SNR.
2) Introducing the incoherent accumulation method in radar signal processing and adapting the accumulation times resulted in a stable performance of the cross-correlation detection algorithm of PSS under the condition of a low SNR.
3) The new scheme of joint estimation of coarse frequency offset is used to replace the traditional scheme, which avoids the shortcomings of insufficient performance of the fractional frequency offset estimation algorithm. In addition, by introducing the incoherent accumulation method into the frequency offset estimation and configuring different weights in the accumulation process, the accumulation error is reduced and the defect of the traditional estimation algorithm where the RMSE is relatively high under the low signal-to-noise ratio is solved.
[1]Shafi M,Molisch A F,Smith P J,et al.5G:A tutorial overview of standards,trials,challenges,deployment and practice[J].IEEE Journal on Selected Areas in Communications,2017,35(6):1201-1221.DOI:10.1109/JSAC.2017.2692307.
[2]Shokri-Ghadikolaei H,Boccardi F,Fischione C,et al.Spectrum sharing in mmWave cellular networks via cell association,coordination,and beamforming[J].IEEE Journal on Selected Areas in Communications,2016,34(11):2902-2917.DOI:10.1007/978-3-030-47560-4_30.
[3]Arikan E.Channel polarization:A method for constructing capacity-achieving codes[C]// IEEE International Symposium on Information Theory (ISIT).Toronto,USA,2008:1173-1177.DOI:10.1109/TIT.2009.2021379.
[4]3GPP. Radio access network(NR); Physical channels and modulation:3GPP TS 38.211-V15.2.0-2018[S].Sophia-Antipolis,France:3GPP,2018.
[5]3GPP. Radio access network (NR); Base station (BS) radio transmission and reception:3GPP TS 38.104-V15.2.0-2018[S].Sophia-Antipolis,France:3GPP,2018.
[6]Kim J,Han J,Roh H,et al.SSS detection method for initial cell search in 3GPP LTE FDD/TDD dual mode receiver[C]//2009 9th International Symposium on Communications and Information Technology.Icheon,Korea,2009:199-203.DOI:10.1109/ISCIT.2009.5341260.
[7]Bai X J.Research and implementation of TD-LTE cell search and downlink synchronization technology[D].Chengdu:University of Electronic Science and Technology of China,2017.(in Chinese)
[8]K.Ota,A.Shimura,M.Sawahashi.Performance of Physical Cell ID Detection Probability Considering Frequency Offset for NR Radio Interface[C]//2019 IEEE 90th Vehicular Technology Conference.Honolulu,HI,USA,2019:1-6.DOI:10.1109/VTCFall.2019.8891182.
[9]Ota K,Sawahashi M,Nagata S.Physical cell ID detection probability using synchronization signals for NR radio interface in 28-GHz band[C]//2019 25th Asia-Pacific Conference on Communications.Ho Chi Minh City,Vietnam,2019:67-72.DOI:10.1109/VTS-APWCS.2019.8851626.
[10]Jeon Y,Park H,Choi E.Synchronization and cell search procedure in 3GPP 5G NR systems[C]//2019 21st International Conference on Advanced Communication Technology.Pyeongchang Kwangwoon Do,Korea,2019:475-478.DOI:10.23919/ICACT.2019.8701920.
[11]Ding L F,Geng F L,Chen J C.Radar principle[M].4th ed.Beijing:Publishing House of Electronics Industry,2009:28-31.(in Chinese)
[12]Koduru R,Budhiraja R.Algorithm design for 3GPP NR downlink cell search[C]// 2019 IEEE 20th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC).Cannes,France,2019:1-5.DOI:10.1109/SPAWC.2019.8815502.
[13]3GPP. Radio access network(NR); Study on channel model for frequencies from 0.5 to 100 GHz:3GPP TR 38.901-V15.1.0-2019[S].Sophia-Antipolis,France:3GPP,2019.
