The widespread application of the 5G mobile network greatly increases the amount of user equipment (UE), which brings much overhead to 5G base stations. Device-to-device (D2D) communication is considered a promising technology that releases the pressure on 5G base stations because the UE can communicate directly with each other without being directly involved in the 5G infrastructure. In addition, D2D communication can alleviate the mobile traffic explosion problem[1] and solve the problem of a spectrum resource shortage in a wireless communication system. However, data security is difficult to guarantee.
To realize data confidentiality protection in a data-sharing system, the data access control method is widely used.However, the traditional method of access control has multiple copies of ciphertext for different users with different keys, which may cause much storage overhead. Sahai et al.[2] proposed the concept of the attribute-based encryption (ABE) algorithm, which has two types: ciphertext policy attribute-based encryption (CP-ABE)[3] and key policy attribute-based encryption (KP-ABE)[4]. CP-ABE schemes[5-9] became promising for their efficient and fine-grained data access control. However, these schemes cannot realize attribute revocation. Yang et al.[10] proposed a cloud storage system based on CP-ABE to realize efficient data access control with attribute revocation. However, the users whose attributes were revoked may threaten the security of the scheme through a collusion attack.
The schemes [11-14] could achieve attribute revocation but could not realize dynamic user management. Wei et al. proposed an attribute-based access control scheme for multi-authority cloud storage[15] by adopting the binary tree to dynamically remove the user from the system. However, this algorithm incurred more computational overhead. Han et al. proposed a CP-ABE scheme that realized the application of hidden policy and white-box traceability[16]. However, although the illegal and invalidated users could be removed from the system in this scheme when new users joined the system, the proposed algorithm would become inapplicable. Thus, this scheme could only realize partial user management.
5G access and handover security, IoT security, D2D security, V2X security, and network slice security are five aspects of security for the current 3GPP 5G network[17]. 5G D2D communication provides efficient and low-latency service for the UE and should be designed to meet security requirements, such as low computational cost, secure and effective device discovery, confidentiality and integrity protection, secure group communication, and fine-grained access control of devices. To solve the problem of data confidentiality in D2D communication, Zhang et al.[18] proposed a secure data-sharing protocol, which merged the advantages of public-key cryptography and symmetric encryption to achieve data security in D2D communication. However, the protocol could not support fine-grained data access control. Yan et al.[19] proposed a flexible data access control scheme in D2D communications to realize secure data communication among UE, but the computational cost of the scheme was high. Li et al.[20] proposed a data access control scheme with multi-authority CP-ABE encryption in D2D communication. However, the multiple authorities may waste the network resources because the distributed authorities were not suitable for the D2D communication scenario.
1 Preliminaries
1.1 Bilinear mapping
Definition 1 (bilinear mapping) Let G1, G2 and G3 be three multiplicative cyclic groups of the same prime order p. Let e: G1×G2→G3 denote a bilinear map defined with the properties of bilinearity, non-degeneracy, and computability[21]. In bilinearity, e(ua,vb)=e(u,v)ab, ∀u∈G1, ∀v∈G2, and a,b∈Zp, where Zp denotes an integer group with prime order p. In non-degeneracy, ∃u∈G1, ∃v∈G2 such that e(u,v)≠I, where I is the identity element of G3. In computability, for any element u∈G1, v∈G2, there is a polynomial-time algorithm to calculate e(u,v).
1.2 Decisional bilinear Diffie-Hellman problem
Definition 2 (DBDH problem) Let g be a generator of group G with prime order p and a,b,c,d∈Zp be randomly chosen. Make ga,gb,gc∈Gp public. It is difficult to distinguish between (g,ga,gb,gc,e(g,g)abc) and (g,ga,gb,gc,e(g,g)d)[22].
Definition 3 The function Fu, which outputs z∈{0,1}, has advantage ε for solving the DBDH problem in group G, supposing that
Pr[Fu(e(g,g)abc)=0]-Pr[Fu(e(g,g)d)=0]≥ε
1.3 Linear secret sharing scheme
Definition 4 (linear secret sharing scheme) A secret sharing scheme over a set of parties P is called a linear secret sharing scheme (LSSS) if the shares for each party form a vector over Zp, and there is a matrix M called the share-generating matrix[23]. The matrix M has m rows and n columns. For i=1,2,…,l, the i-th row Mi of M is labeled as ρ(i), where ρ denotes the function from i=1,2,…,m to P. Given a column vector v={s,y2,…,yn}, where s∈Zp is the secret to be shared and y2,y3,…,yn∈Zp are randomly chosen; Mv is the vector of m shares of the secret s according to the scheme. The party ρ(i) obtains the share λi=(Mv)i of s from Mv.
2 NDA-CP-ABE Scheme
2.1 System model
Fig.1 presents the system architecture of the NDA-CP-ABE scheme in the 5G D2D environment. The system includes four kinds of entities: Trusted Authority, Core Server, Cloud, and UE, whose functions and characteristics are introduced as follows.
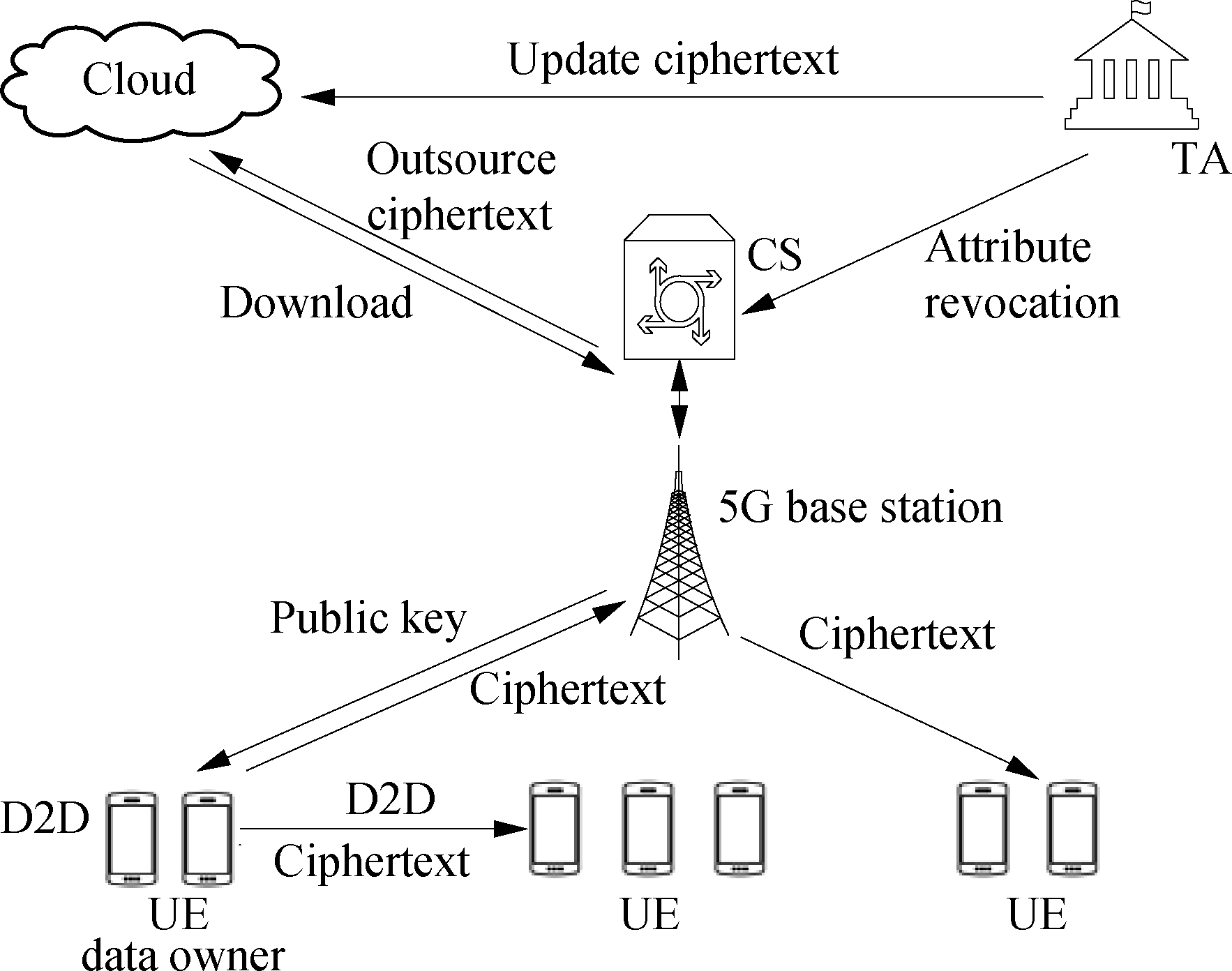
Fig.1 System architecture of the NDA-CP-ABE scheme
Trusted Authority (TA) is a trusted entity and is responsible for generating the security parameter. The TA outputs the secret keys and the corresponding update keys to the UE and performs the user management and attribute revocation process. Core Server (CS) is the core server of the 5G infrastructure and provides high-speed Internet service. The CS controls the normal operation of the base stations, which is responsible for transferring data to the other entities, including the D2D devices. The Cloud is responsible for storing the data uploaded from the UE. It also provides the ciphertext update service for attribute revocation and user management. UE communicate with each other through the D2D channel. The data owner of the UE defines the access policy and directly transmits the ciphertext (CT) to the other UE. The data owner of the UE can also outsource the ciphertext to the Cloud for further use.
2.2 Construction of the NDA-CP-ABE scheme
2.2.1 System initialization
The steps of system initialization are as follows.
1) D2D setup. The CS generates a public/private key pair (pi,si) for each UEi, where pi is the public key and si is the secret key for D2D discovery. Then the CS sends the key pair (pi,si) to UEi through the secure channel.
2) Secure D2D discovery. UE1 generates R=rI1t1 and T1(R), where r denotes UE1’s request for D2D discovery; I1 is UE1’s identity information; t1 is the time stamp; and T1(R) is a signature of R with s1. The SHA256 signature algorithm is used to generate the signature for the UE. Then, UE1 broadcasts the request of RT1(R). After receiving the request from UE1, UE2 checks the received R with the R computed by verifying T1(R). After successful verification, UE2 generates RS=r′I2t2 and T2(RS), where r′ denotes UE2’s response for discovery; t2 is the time stamp; I2 is UE2’s identity information; and T2(RS) is the signature of RS with s2. Then, UE2 returns RST2(RS) to UE1. UE1 checks the received RS with the RS computed by verifying T2(RS). After successful verification, the D2D communication channel is opened. The data owner UE1 constructs the secure D2D channel and shares data with UE2, UE3,…, UEn. In the same way, the discovery procedures among UE2, UE3,…, UEn can be finished.
3) TA setup. The TA initializes the system with the TA setup algorithm: TA Setup (1λ)→(SK,PK,{Vk,Pk},τT), which inputs the security parameter λ and outputs SK=(α,β), PK=(e(g,g)α,gβ). SK and PK are the secret key and public key of the TA, respectively. The TA also outputs {Vk=vk,Pk=[gvkH(γk)]β}, which are the secret version key and public key of each attribute γk, respectively. τT denotes the minimum time difference threshold in the system.
4) UE setup. The UE sends its identity information N to the TA, and then the TA conducts the UE Setup algorithm, UE Setup (N)→(GPKN,GSKN), to compute and return each UE’s global public key GPKN=gN and global secret key GSKN=zN.
5) Time synchronization. Each sender of the entities records the current time τ1 when every piece of information is to be sent and appended τ1 to the information. Upon receiving the information from other entities, the receiver entity should obtain the current time τ2. If |τ1-τ2|<τT, the conversation continues. Otherwise, the receiver entity returns τ1τ2e to the sender entity. e denotes the error code of the current conversation.
2.2.2 Secret key generation
In this subsection, the TA generates the secret keys for each UE. The detailed secret key generation step is as follows.
The TA assigns the valid UE a set of attributes Sj and then generates the UE’s secret key SKj:
SKj=(Kj,Kj,k) =[Kj=g1/zj+uj/α,Kj,k=(gvkH(γk))βuj]
where ∀j∈SU, γk∈Sj, uj is randomly chosen, and SU denotes the set of all the UE. After generating the secret keys, the TA securely sends the secret keys to the corresponding UE. The attribute set Sj consists of many attributes according to the UE’s gender, nationality, academic degree, or much other information of different levels.
2.2.3 Ciphertext generation
In this section, UEi (data owner) defines the data access policy and encrypts the data according to the corresponding attributes. The detailed encryption process is as follows.
UEi first chooses a random value s and then sends gs to the TA, where s is the secret value in the LSSS. After receiving gs, the TA computes gαs and constructs the polynomial function 
(mod q) and the exponential function {W0,W1,…,Wm}={ga0,ga1,…,gam}. After that, the TA constructs E={gαsW0,W1,…,Wm}, and sends E to UEi. UEi then generates the ciphertext: CT=(C,Di,E,Ei)={C=Me(g,g)αs, Di=gri, E={gαsW0,W1,…,Wm}, Ei=gλi(Pk)-ri}, where i∈{1,2,…,l}, the value ri and vector v=(s,y2,…,yn) are randomly chosen, and λi=(Mv)i is a share of secret s. UEi shares CT with the other UE such as UEj, directly through the D2D channel. To backup CT, UEi outsources CT to the Cloud.
2.2.4 Data decryption
After receiving CT, UEj first obtains E={gαsW0,W1,…,Wm} from CT and computes 
and then calculates token TK with secret key SKj and CT as follows:
where I={i:ρ(i)∈IA}; IA denotes the set of attributes that satisfy the access structure; and {ωi}i∈IA are the chosen constants that can reconstruct the secret s on the condition that {λi}i∈IA are valid shares of s. After determining TK, UEj can decrypt the ciphertext with GSKj=zj and C as follows: 
2.2.5 Attribute revocation
When the attribute γk of UEμ is revoked, the TA generates a new attribute version key 
for the attribute γk, and then TA calculates the key update key for the non-revoked UE to update the secret key to the latest version: Uj,k=gujAk. The TA then sends Uj,k to the non-revoked UE. Meanwhile, the TA updates the public key of the revoked attribute γk to the latest version: 
Upon receiving the update key Uj,k, the non-revoked UE runs the secret key update algorithm to update SKj to the latest version: 
The TA then generates 
to update the corresponding CT and constructs the polynomial function 
and the exponential function {W0,W1,…,Wm-1}={ga0,ga1,…,gam-1}. Subsequently, the TA constructs E′={gαsW0,W1,…,Wm-1}, and sends E′ to the Cloud.
After receiving E′, the Cloud randomly chooses a value 
in Zp and then updates 
where E′={gαsW0,W1,…,Wm-1}. For the attributes that are revoked, 
2.2.6 User management
When UEμ in the UE set SU is removed from the system for certain reasons, the TA should remove it directly without updating other legitimate UE’s secret keys.
The TA first constructs the polynomial function 
(mod q) and the exponential function {W0,W1,…,Wm-1}={ga0,ga1,…,gam-1}. Then, the TA constructs E′ to the Cloud. After receiving E′, the Cloud updates the ciphertext CT. The remaining legitimate UE, such as UEj, can download CT from the cloud and then compute F. Subsequently, UEj calculates 
When a new user UEn wants to enter the system, the TA constructs the polynomial function 
(mod q) and the exponential function {W0,W1,…,Wm+1}. Then, the TA constructs E′={gαsW0,W1,…,Wm+1} and sends E′ to the Cloud. After receiving E′, the Cloud updates the ciphertext CT. UEn downloads CT from the cloud, and computes F=gαs. Then, UEn calculates TK=e(g,g)sα/zn and finally obtains M.
3 Formal Security Analysis
3.1 Proof of correctness
Theorem 1 The NDA-CP-ABE scheme is correct; that is, legitimate UE can successfully decrypt CT, and can achieve safe attribute revocation and user management.
Proof If UEj, which holds sufficient attributes, satisfies the access policy Fu, it obtains CT and secret keys SKj to compute 
to obtain F=gαs and then calculates 
where e(Kj,F)=e(g,g)suje(g,g)sα/zj, 
UEj then decrypts the ciphertext to obtain the plaintext 
Therefore, UEj can successfully decrypt the ciphertext corresponding to its attribute set.
3.2 Proof of security
Theorem 2 The NDA-CP-ABE scheme can resist a chosen-ciphertext attack (CCA). If an adversary has an advantage ε that can be neglected in polynomial time for attacking the NDA-CP-ABE scheme with at most qk, qc, and qd numbers of queries in the Secret Key Generation phase, Ciphertext Generation phase, and Data Decryption phase, respectively, with maximum time t; then the challenger can solve the DBDH problem with an advantage of Pr=ε(1-qk/2n)/(qkqeqd), which can be neglected in polynomial time.
Proof Suppose that there is an adversary who has advantage ε for attacking the NDA-CP-ABE scheme.
Setup the challenger generates SK=(α,β), PK=(e(g,g)α,gβ), which are the secret key and public key of the TA, respectively, and {Vk=vk,Pk=[gvkH(γk)]β}, which are the secret version key and public key of each attribute γk, respectively. Then, the adversary selects a set of attributes Sk that satisfy the access structure. The challenger then sends the public keys to the adversary of the attribute set Sk.
Phase 1 is that the adversary selectively refers (j,Sj) in SA to the challenger to obtain the corresponding secret key SKj. The challenger then calculates the secret key as follows: SKj=[Kj=g1/zj+uj/α, Kj,k=(gvkH(γk))βuj].
The adversary refers to two messages m0 and m1 of equal length but cannot decrypt the challenge message properly with the queried keys and any other keys from Sk. The challenger then randomly chooses a bit of b in {0,1}, encrypts it under the access structure, and then sends CT to the adversary.
Phase 2 is similar to Phase 1. The adversary refers (j,Sj) in SA to the challenger to obtain the corresponding secret key SKj. However, the secret key does not satisfy the access policy.
When the adversary ends Phase 2, it provides a guess b′ of b. The probability that the adversary will win the game for all arbitrary attribute sets the adversary chooses is 
and the probability of Sj≠Sk is that P2=1-qk/2n. There are qk, qe, and qd numbers of queries in the secret key generation phase, ciphertext generation phase, and data decryption phase, respectively, with advantage ε. Therefore, the advantage ε′ in solving the DBDH problem is ε′<ε(1-qk/2n)/(qkqeqd). The challenger cannot solve the DBDH problem with advantage ε′. Therefore, the adversary cannot breach the NDA-CP-ABE scheme in the polynomial time with a non-neglected advantage. Therefore, NDA-CP-ABE can resist the CCA.
3.3 Collusion attack resistance
Theorem 3 NDA-CP-ABE is secure with collusion attack resistance; that is, it can prevent the collusion attack among the legitimate UE, the revoked UE, and the external attackers.
Proof For the legitimate UE and the revoked UE, the attribute k∈S1 of UE1 is revoked, and UE2 is the legitimate UE with attribute set S2. The ciphertext is encrypted with W=S1∪S2. The key update key, Uj,k=gujAk, is associated with every UE’s identity. Therefore, UE1 and UE2 cannot update their secret key to the latest version and cannot decrypt the ciphertext.
For the legitimate UE and external attacker,UE3 is the legitimate UE with attribute set S3, and UE4 is the network attacker. The ciphertext is encrypted with W=S3∪S4, where S4 denotes the extra attribute set needed to decrypt the ciphertext for UE3. The secret key SKj is associated with uj, which is randomly chosen. Therefore, UE3 and UE4 cannot decrypt the CT, either collectively or individually.
For the collusion attack between the revoked UE, γ5∈S5 of UE5 and γ6∈S6 of UE6 are revoked. The ciphertext is encrypted with W=S5∪S6. The secret key SKj and update key Uj,k=gujAk are associated with uj, which is randomly chosen. Therefore, UE5 and UE6 cannot share the secret keys related to their attributes to decrypt the ciphertext.
3.4 Attribute revocation security
Theorem 4 The scheme can achieve attribute revocation security.
Proof When the attribute set {γk}⊂S of UEμ is revoked, CT should be updated to the latest version: 
where E′={gαsW0,W1,…,Wm-1}. For the attributes that are revoked, 
UEμ calculates the exponent of 
with difficulty. Additionally, because of the revoked UE’s blindness by the random number 
cannot be canceled out. Therefore, the revoked UE cannot successfully attack the NDA-CP-ABE scheme, and the NDA-CP-ABE scheme can realize attribute revocation security.
3.5 User management security
Theorem 5 The NDA-CP-ABE scheme can realize secure, dynamic, and efficient user management.
Proof When UEμ is directly removed from the system, the ciphertext is updated to the latest version 
UEμ calculates the component E′ with difficulty, which prevents UEμ from computing F, which is necessary to decrypt the ciphertext because F≠gαs. Therefore, UEμ cannot decrypt the updated ciphertext. UEμ strives to obtain the plain text of the ciphertext.
UEj is supposed to be the newly joined UE. The TA first constructs 
and UEj can compute F′=gαs. The decryption token is TK=e(g,g)sα/zj. Then, UEj can obtain the plaintext 
Therefore, the new UE dynamically joins the system.
3.6 Security comparison
In this section, the security performance of NDA-CP-ABE is compared with Xue et al.’s scheme [13] (Scheme 1), Wei et al.’s scheme [15] (Scheme 2), Han et al.’s scheme [16] (Scheme 3), Yan et al.’s scheme [19] (Scheme 4), and Li et al.’s scheme [20] (Scheme 5) in terms of attribute revocation, collusion attack resistance, user management, and whether these schemes support the 5G D2D environment in Tab. 1. Therein, “√” and “×” mean that the scheme can and cannot meet the corresponding security goal, respectively.
According to Tab. 1, the NDA-CP-ABE scheme can successfully realize collusion attack resistance, secure attribute revocation, and secure user management in the 5G D2D environment. However, Scheme 1 cannot realize dynamic user management and is not fit for the 5G D2D scenario; Scheme 2 cannot realize secure attribute revocation and is not fit for the 5G D2D scenario; Scheme 3 can only realize partial user management because the algorithm in Scheme 3 cannot support the new users to dynamically enter the system. In addition, Scheme 3 cannot realize attribute revocation, collusion attack resistance, and fitness for the 5G D2D scenario. Scheme 4 cannot realize attribute revocation, collusion attack resistance and dynamic user management. Scheme 5 cannot realize secure attribute revocation and dynamic user management.
Tab.1 Security Comparison
SchemeAttributerevocationCollusion attackresistanceUsermanagement5G D2DenvironmentScheme 1[13]√√××Scheme 2 [15]×√√×Scheme 3[16]××Partial×Scheme 4[19]×××√Scheme 5 [20]×√×√NDA-CP-ABE√√√√
4 Performance Analysis
The performances of computational overhead and storage overhead are compared in this section by comparing the NDA-CP-ABE scheme with the schemes in Refs.[13,15-16,19-20]. The simulation is conducted on an Ubuntu 16.04 system with a 2.20 GHz processor and 4.00 GB RAM.
4.1 Computational overhead
This section compares the NDA-CP-ABE scheme for computational overhead with the schemes in Refs.[13,15-16,19-20] in terms of encryption and decryption. The computational cost of multiplicative operation cm, exponential operation ce, hash function ch, and the pairing operation cp in the group G is considered. The number of attributes na ranges from 2 to 20, and the number of UE nu in the system is 100.
4.1.1 Encryption overhead
The computational cost for encryption among six schemes is compared in Fig.2. The computational cost of the NDA-CP-ABE scheme((3ce+ch)na+cm) is smaller than that of Scheme 1 ((2ce+cm)na). Although the former has (na-1) more multiplicative calculations, the latter has na more hash calculations, and na more exponential calculations. In addition, the encryption cost of the NDA-CP-ABE scheme is much less than those of Scheme 2 to Scheme 5 which are (6ce+4cm+ch)na+(ce+cm)nu, (5ce+3cm)na+3cm+3ce, (2ce+2cm)na+ce, and (5ce+2cm)na, respectively.
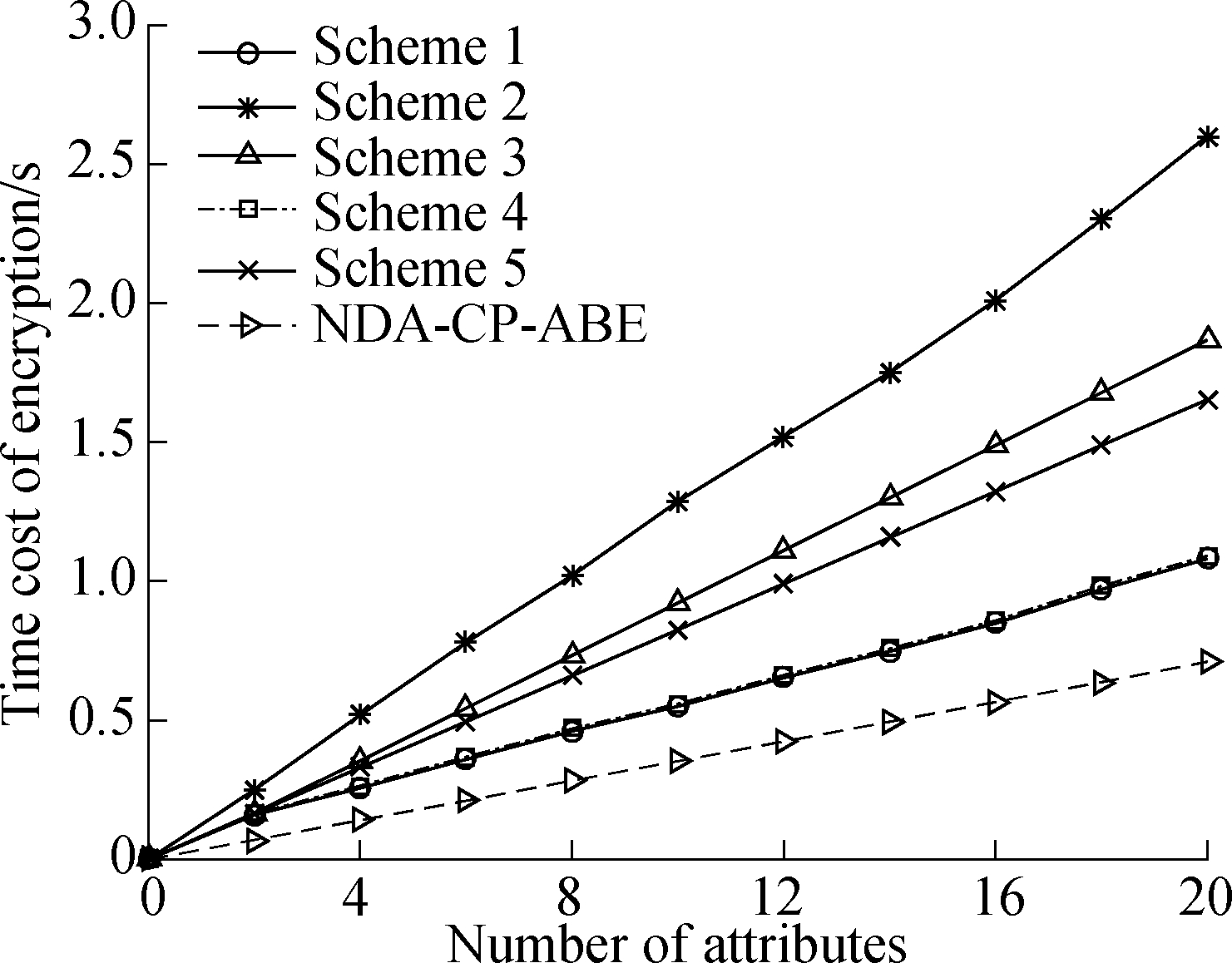
Fig.2 Comparison of encryption time
4.1.2 Decryption overhead
The computational cost for decryption among the six schemes is compared in Fig.3. The decryption cost of the NDA-CP-ABE scheme((2cp+cm+ce)na+cm+2ce) is less than that of Scheme 1 ((3cp+2cm)na+ce). Although the former has (na+1) more exponential calculations, the latter has na more paring calculations and (na-1) more multiplicative calculations. The computational cost of the NDA-CP-ABE scheme is much less than those of Scheme 2 and Scheme 3 which are (4cp+4cm+ce+ch)na and (3cp+2cm+ce)na+2cp+3ce+5cm. The decryption cost of the NDA-CP-ABE scheme is less than that of Scheme 4 ((2cp+3cm)na). Although the former has (na+2) more exponential calculations, the latter has (2na-1) more multiplicative calculations. The decryption cost of NDA-CP-ABE is slightly higher than that of Scheme 5 ((3cp+ce)na) because the latter has na more paring calculations while the former has (na+1) more multiplicative calculations and two more exponential calculations. However, Scheme 5 cannot realize secure attribute revocation and dynamic user management.
Fig.3 Comparison of decryption time
4.2 Storage overhead
In this section, the NDA-CP-ABE scheme for storage overhead of the ciphertext is compared with the schemes in Refs.[13,15-16,19-20]. sm denotes the size of the plaintext M. The storage overhead of the NDA-CP-ABE scheme ((sm+2na+1)|p|) is smaller than those of Scheme 1 to Scheme 5 which are (3na+3+sm)|p|, (5na+4+sm)|p|, (3na+1+sm)|p|, (2na+sm)nj|p|, and (3na+1+sm)|p|, respectively. nj denotes the number of junctions needed in Ref.[19]. Generally speaking, nj>1.
5 Conclusions
1) The secure sharing of data in the 5G D2D environment is realized. The ciphertext policy attribute-based encryption algorithm is adopted to realize safe data sharing. Only the UE with sufficient attributes that satisfy the access policy defined by the data owner can decrypt the ciphertext.
2) Secure attribute revocation in the 5G D2D environment is realized. When the attributes of the UE are revoked, the CP-ABE algorithm only updates other related UE’s attribute keys to control the access rights. The revoked UE can no longer decrypt the ciphertext after the secure attribute revocation.
3) Dynamic and efficient user management in the 5G D2D environment is realized. The polynomial function algorithm is adopted to encrypt the data. When UE loses the permission to the data, the algorithm dynamically removes the UE from the system without updating other UE’s relating attribute keys. When new UE obtains permission to enter the system, the algorithm assigns the UE the access right to the ciphertext without updating the existing UE’s relating attribute keys.
4) The NDA-CP-ABE scheme can withstand a collusion attack among the legitimate UE, the revoked UE, and the external attackers with the secret value related to each piece of UE in the 5G D2D environment.
[1]Tan J, Liang Y, Zhang L, et al. Deep reinforcement learning for joint channel selection and power control in D2D networks[J].IEEE Transactions on Wireless Communications, 2021, 20(2): 1363-1378. DOI: 10.1109/TWC.2020.3032991.
[2]Sahai A, Waters B. Fuzzy identity-based encryption[C]//2005 24th Annual International Conference on Theory and Applications of Cryptographic Techniques. Aarhus, Denmark, 2005: 457-473. DOI: 10.1007/11426639_27.
[3]Bethencourt J, Sahai A, Waters B. Ciphertext-policy attribute-based encryption[C]//2007 IEEE Symposium on Security and Privacy. Oakland, CA, USA, 2007: 321-334. DOI: 10.1109/SP.2007.11
[4]Goyal V, Pandey O, Sahai A, et al. Attribute-based encryption for fine-grained access control of encrypted data[C]//2006 ACM Conference on Computer and Communications Security. Alexandria, VA, USA, 2006: 89-98. DOI: 10.1145/1180405.1180418.
[5]Xue K, Xue Y, Hong J, et al. RAAC: Robust and auditable access control with multiple attribute authorities for public cloud storage[J].IEEE Transactions on Information Forensics and Security, 2017, 12(4): 953-967. DOI: 10.1109/TIFS.2016.2647222.
[6]Li J, Lin X, Zhang Y, et al. KSF-OABE: Outsourced attribute-based encryption with keyword search function for cloud storage[J].IEEE Transactions on Services Computing, 2017, 10(5): 715-725. DOI: 10.1109/TSC.2016.2542813.
[7]Ning J, Cao Z, Dong X, et al. Auditable sigma-time outsourced attribute-based encryption for access control in cloud computing[J].IEEE Transactions on Information Forensics and Security, 2018, 13(1): 94-105. DOI: 10.1109/TIFS.2017.2738601.
[8]Mao X, Lai J, Mei Q, et al. Generic and efficient constructions of attribute-based encryption with verifiable outsourced decryption[J].IEEE Transactions on Dependable and Secure Computing, 2016, 13(5): 533-546. DOI: 10.1109/tdsc.2015.2423669.
[9]Wang N, Fu J, Bhargava B K, et al. Efficient retrieval over documents encrypted by attributes in cloud computing[J].IEEE Transactions on Information Forensics and Security, 2018, 13(10):2653-2667. DOI:10.1109/TIFS.2018.2825952.
[10]Yang K, Jia X. Expressive, efficient, and revocable data access control for multi-authority cloud storage[J].IEEE Transactions on Parallel and Distributed Systems, 2014, 25(7): 1735-1744. DOI:10.1109/TPDS.2013.253.
[11]Hur J, Noh D K. Attribute-based access control with efficient revocation in data outsourcing systems[J].IEEE Transactions on Parallel and Distributed Systems, 2011, 22(7): 1214-1221. DOI: 10.1109/TPDS.2010.203.
[12]Yeh L, Chiang P, Tsai Y, et al. Cloud-based fine-grained health information access control framework for lightweight IoT devices with dynamic auditing and attribute revocation[J].IEEE Transactions on Cloud Computing, 2018, 6(2): 532-544. DOI: 10.1109/TCC.2015.2485199.
[13]Xue Y, Xue K, Gai N, et al. An attribute-based controlled collaborative access control scheme for public cloud storage[J].IEEE Transactions on Information Forensics and Security, 2019, 14(11): 2927-2942. DOI: 10.1109/TIFS.2019.2911166.
[14]Li J, Yao W, Han J, et al. User collusion avoidance CP-ABE with efficient attribute revocation for cloud storage[J].IEEE Systems Journal, 2018, 12(2): 1767-1777. DOI: 10.1109/JSYST.2017.2667679.
[15]Wei L, Liu W, Hu X. Secure and efficient attribute-based access control for multiauthority cloud storage[J].IEEE Systems Journal, 2018, 12(2): 1731-1742. DOI: 10.1109/JSYST.2016.2633559.
[16]Han D, Pan N, Li K. A traceable and revocable ciphertext-policy attribute-based encryption scheme based on privacy protection[J].IEEE Transactions on Dependable and Secure Computing, 2020, 99. DOI: 10.1109/TDSC.2020.2977646.
[17]Cao J, Ma M, Li H, et al. A survey on security aspects for 3GPP 5G networks[J].IEEE Communications Surveys & Tutorials, 2020, 22(1): 170-195. DOI: 10.1109/COMST.2019.2951818.
[18]Zhang A, Chen J, Hu, R Q, et al. SeDS: Secure data sharing strategy for D2D communication in LTE-advanced networks[J].IEEE Transactions on Vehicular Technology, 2016, 65(4): 2659-2672. DOI: 10.1109/TVT.2015.2416002.
[19]Yan Z, Xie H, Zhang P, et al. Flexible data access control in D2D communications[J]. Future Generation Computer Systems, 2018, 82(62): 738-751. DOI: 10.1016/j.future.2017.08.052.
[20]Li Q, Huang L, Mo R, et al. Robust and scalable data access control in D2D communications[J].IEEE Access, 2018, 6: 58858-58867. DOI: 10.1109/ACCESS.2018.2874066.
[21]Krawczyk H. HMQV: A high-performance secure Diffie-Hellman protocol[C]//Advances in Cryptology—CRYPTO 2005. Santa Barbara, CA, USA, 2005: 546-566. DOI: 10.1007/11535218_33.
[22]Wang J M, Lang B. An efficient KP-ABE scheme for content protection in information-centric networking[C]//2016 IEEE Symposium on Computers and Communication (ISCC). Messina, Italy, 2016: 830-837. DOI: 10.1109/iscc.2016.7543839.
[23]Beimel A. Secure schemes for secret sharing and key distribution[D]. Israel: Department of Computer Science, Institution of Technology, 1996.
