Improving power and reducing friction loss are key concerns in the design and research of internal combustion engines. Therefore, research on the friction and lubrication performance of bearings is essential to optimize the design parameters of engines.
A large number of studies have been conducted over the last few decades to assess the influence of various piston design parameters on the performance of combustion engines. For example, the inertial force of the piston and the eccentricity between the crankshaft and cylinder center have been investigated to reduce the horizontal impact force of the piston on the cylinder bore and engine balance[1-3]. The influence of the friction force generated by the piston skirt and ring against the cylinder bore during movement, as well as that of the relative motion of the joints of the slider-crank mechanism (SCM) on the engine power, has also been analyzed[4-6]. The results obtained show that the friction power loss caused by relative motion between the friction pairs is not negligible. Research on methods to improve lubrication between the piston and cylinder[2, 6-7] and simulation of the lubrication models of crankshaft bearings[4, 8] to reduce the friction power loss in the SCM has been performed. The results of these works reveal that friction power losses are significantly reduced by increasing the oil film thickness and become stable on lubricated surfaces.
The lubrication condition of journal bearings often belongs to the mixed-or starved-lubrication regime when the sliding pairs are at the start/end verge or in an overloaded state[9-10]. In this case, the micro asperity contact in the mixed-lubrication regime of the journal bearing would increase the friction and wear at the contact region between the shaft and bearing surfaces[11-12]. Thus, investigating the effect of the surface roughness of the journal bearings on the lubrication performance of a bearing under both hydrodynamic and mixed lubrication conditions is necessary.
Previous research[7, 13] suggested that micro asperity contact with a rough surface exerts a great influence on the lubrication performance of journal bearings. Although some scholars have investigated the effects of the pressure[9-10] and shear stress[7, 14] of the asperity contact on the load-bearing capacity (LBC) and friction force of journal bearings, the effects of the LBC and friction force on the tribological properties of journal bearings in the mixed-lubrication regime have not yet been clarified. Moreover, the aforementioned studies mainly considered the effect of static load and usually ignored the external load acting on the journal bearings[10, 15]. The asperity contact load is known to be directly correlated with the wear profile of the bearing bore and the load carried by surface asperities. During the working cycle of an engine, the dynamic load acting on the crankpin bearing (CB) may rapidly change in terms of direction and intensity under changing speeds[4-5]. These phenomena, to some extent, may aggravate the influence of the micro asperity contact in the mixed-lubrication regime on the tribological properties of the CB and increase the power loss of the engine.
The current paper presents a new numerical simulation method that combines the dynamic SCM and CB lubrication models to evaluate the tribological properties of a CB comprehensively. In contrast to previous studies that only considered LBC and the friction force of the oil film on the tribological properties of the CB, this work completely analyzes the influence of the micro asperity contact and radial clearance on these properties. A program written in MATLAB is then applied to solve the corresponding dynamic and lubrication equations. Various radial clearances and surface roughness values are considered in the mixed-lubrication regime to explain their influence on the tribological properties of CBs.
1 Method
1.1 Dynamic slider-crank-mechanism model
The dynamic force of the SCM model is calculated by assuming that the center of the crankshaft coincides with the cylinder center, as shown in Fig.1.
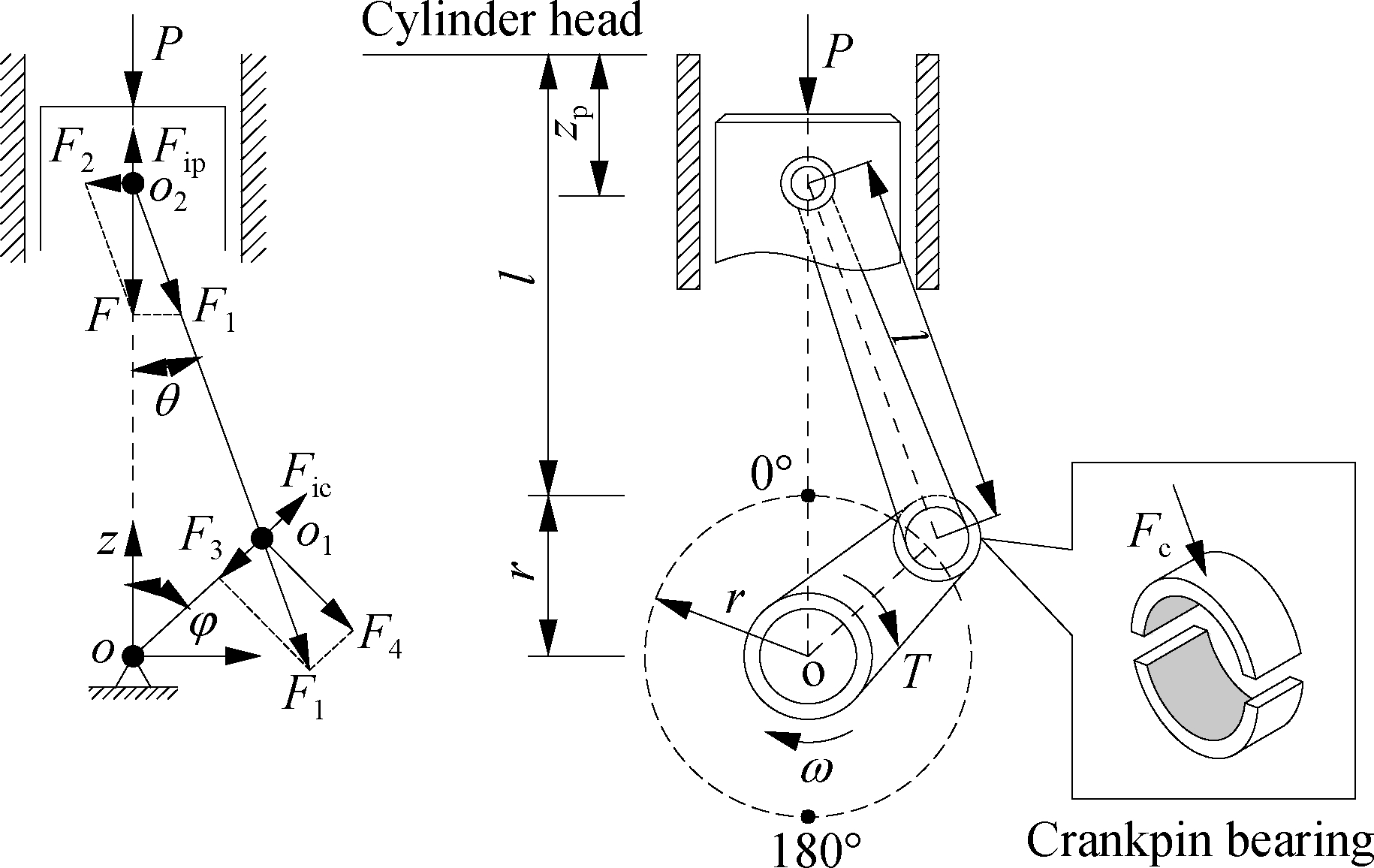
Fig.1 SCM model with lubricated joints
According to the SCM model and its dynamic motion principle, the piston’s acceleration in the z-direction can be determined by[7, 15]
(1)
where λ=r/l; r and ω are the rotational radius and angular velocity of the crankshaft, respectively; and l is the connecting rod length.
Assuming that the mass of the connecting rod is the sum of the masses of the large-rod end (mbr) at o1 and the small-rod end (msr) at o2, the inertial force of the total mass of the piston (mp) and the small-rod end is determined by
(2)
When a combustion gas pressure is exerted on the piston peak (P=pgπR2), the forces acting on the connecting rod, cylinder wall, and crankshaft can be expressed as follows:

(3)
The total mass of the large-rod end of the connecting rod is rotated with an angular velocity of the crankshaft, and the centrifugal inertial force on the rod is written as follows:
Fic=-mbrrω2
(4)
The bearing of the connecting rod provides the crankpin with a rotating motion within the rod. Thus, the total force acting on the CB is
(5)
Changes in force Fc in terms of direction and intensity are then used as the dynamic load to analyze the tribological properties of the CB.
1.2 Crankpin bearing lubrication model
The CB is impacted by the dynamic force Fc and rotated with the same angular velocity ω of the crankshaft. A journal bearing consisting of the shaft imposed by the external dynamic load W0=Fc and rotating inside the bearing with the angular velocity ω is modeled to analyze the tribological properties of the CB; the Cartesian counterpart of this model is also constructed[16], as plotted in Fig.2(a). The surface roughness of the shaft and bearing, which has a great influence on the impact force between the shaft and bearing[11], and the lubrication performance of the journal bearings[10, 15] are further considered in this model, as shown in Fig.2(b).
In Figs.2(a) and (b), rb and rs refer to the bearing and shaft radius (rb>rs), respectively, and the small gap between the bearing and shaft is filled with lubricating oil to generate hydrodynamic pressure. Moreover, e is the eccentricity between the center of the shaft and the bearing; u0=ωrb refers to the relative sliding velocity between the shaft and bearing surfaces; ψ and φ are the attitude angle and angular coordinate, respectively, B is the bearing width; and h and p are the oil film thickness and pressure, respectively. Here h is determined by the relative position between the shaft and bearing and could be expressed as follows[10, 12]:
h=rb-rs+ecosφ=c(1+εcosφ)
(6)
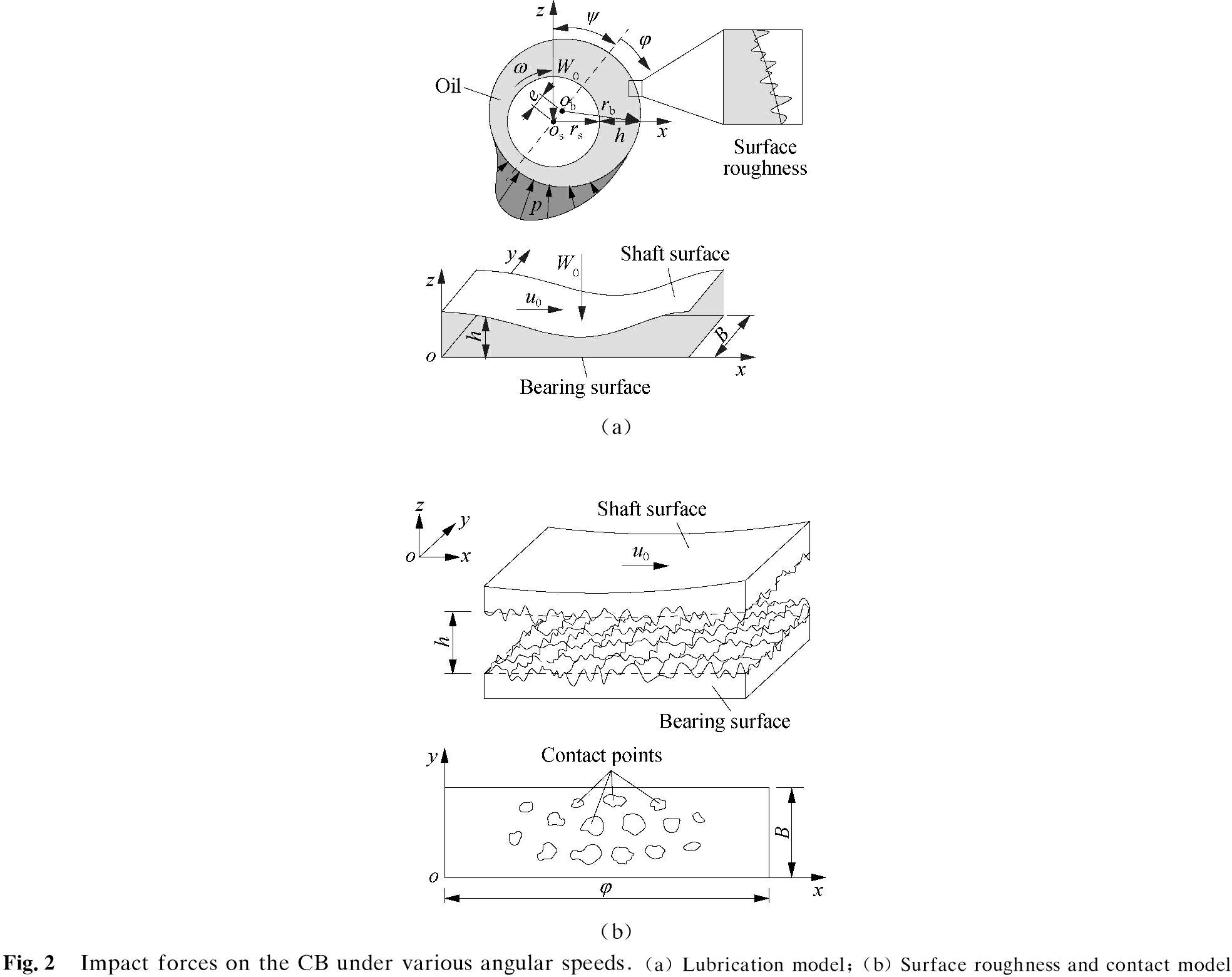
where c=rb-rs and ε=e/c are the radial clearance and eccentricity ratio between shaft and bearing (0<ε<1),respectively.
According to the model in Fig.2(a), the bearing surface is fixed in the x-and y-directions, while the shaft surface only moves in the x-direction under some velocity u0. Thus, the velocity boundary conditions on the CB surfaces can be expressed as
(7)
The lubrication equation of the CB can be conveniently solved by assuming that the influence of the inertia of the lubricant flow is negligible, that the lubricant density and viscosity are constant in the working process, and that the fluid velocity in the z-direction is equal to zero. In practical conditions, however, the CB surfaces are randomly oriented, as shown in Fig.2(b). Thus, the pressure-flow factors of φx and φy reflect the resistance of the surface roughness to the lubricant flow[15], and the shear flow factor φs of the additional flow attributed to these two factors[13] may be employed to determine the expected volumetric flow.
According to the fluid continuity condition, the Reynolds equation of the expected volumetric flow is determined by[15, 17]

(8)
where σ is the variance of the composite surface roughness of the CB and η is the dynamic viscosity of the oil.
The dimensionless form of Eq.(8) is expressed as
![]()
![]()
(9)
where φ=x/rb, Y=y/B, H=h/c, P=p/p0, T=t/t0, u0=ωrb, Λ1=6ηωB2/(p0c2), Λ2=12ηB2/(t0p0c2), β=B/rb, Γ=σ/c, and p0=101 325 Pa is the standard atmospheric pressure.
Eq.(9) can be solved by determining the boundary conditions of the oil film pressure. Assuming that an oil film thickness is distributed on the CB, the inlet/outlet of the lubricant is located at the point at which the maximum film thickness corresponds to φ=0° and 360°. The atmospheric pressure p0 is the ambient pressure around the CB and the inlet/outlet pressure for the computational domain. Thus, the pressure boundary conditions are defined by
(10)
1.3 Mixed hydrodynamic lubrication forces
1.3.1 Load bearing capacity
Under the effect of W0, the LBC generated by the oil film pressure is expressed as[18]
(11)
In addition, in the mixed-lubrication regime of the contact between the shaft and the bearing surfaces, the asperity contact pressure pac greatly influences the LBC when the ratio of the oil film thickness h/σ<4[12]. Assuming that the surface roughness obeys a Gaussian distribution, pac can be calculated according to the asperity contact model of Greenwood and Tripp as follows[9]:
(12)
where E* is the composite elastic modulus; ζ is the asperity radius of curvature; and F5/2(4-h/σ) is the probability of the asperity height of the surface roughness.
Thus, the LBC generated by the pac can be expressed as
(13)
Based on the LBC of the Wof and Wac, the actual LBC of the CB is then determined as follows:
(14)
where Wb is equal to the external dynamic load acting on the CB, as written in Eq.(5).
1.3.2 Friction force and friction coefficient
Under the effect of interfacial shear and asperity contact in the mixed-lubrication regime, the interfacial shear stress τis and asperity contact stress τac are given by [12, 17]
(15)
where τ1 and τ2 are the inter-fluid shear stress and shear stress of the fluid acting on bumpy peaks, respectively; τ0 and μ0 are the shear stress and boundary friction coefficients, respectively.
The total friction force is then defined by
Ff=Fis+Fac=∬τisdxdy+∬τacdxdy
(16)
where Fis and Fac are the friction forces of the oil film and asperity contact, respectively.
After Ff and Wb are determined, the friction coefficient μ of the CB can be calculated by [18]
(17)
The parameters of Wb, Ff, and μ were selected as evaluation indices to analyze the tribological properties of the CB in this study [12, 18]. Two other parameters, namely, Wac and Fac, were also selected to analyze the influence of the asperity contact on the tribological properties of the CB in the mixed-lubrication regime. Thus, increases in LBC and reductions in the frictional force of the CB could be described by objective functions. The computational scheme for the objective functions is conducted in MATLAB, as shown in Fig.3.
2 Results and Discussion
The parameters listed in Tab.1 and the external force Fc=W0 obtained at a crankshaft speed of 2 000 r/min, as indicated in Fig.4,[4, 15] are applied to highlight the effect of the asperity contact in the mixed-lubrication regime on the tribological properties of the CB. The effects of various radial clearances and surface roughness values on the tribological properties of the CB are then investigated.

Fig.3 Computational flowchart
Tab.1 Simulation parameters

ParametersValuesParametersValuesl/mm129.5B/mm20r/mm40R/mm36.5mp/kg0.264rb/mm25mcr/kg0.345p0/Pa101 325msr/kg0.095c/μm10mbr/kg0.250η/(Pa·s)0.02φ/(°)720t0/(MN·m-2)2λ0.309E*/GPa140

Fig.4 Dynamic force of the SCM
2.1 Effect of radial clearance
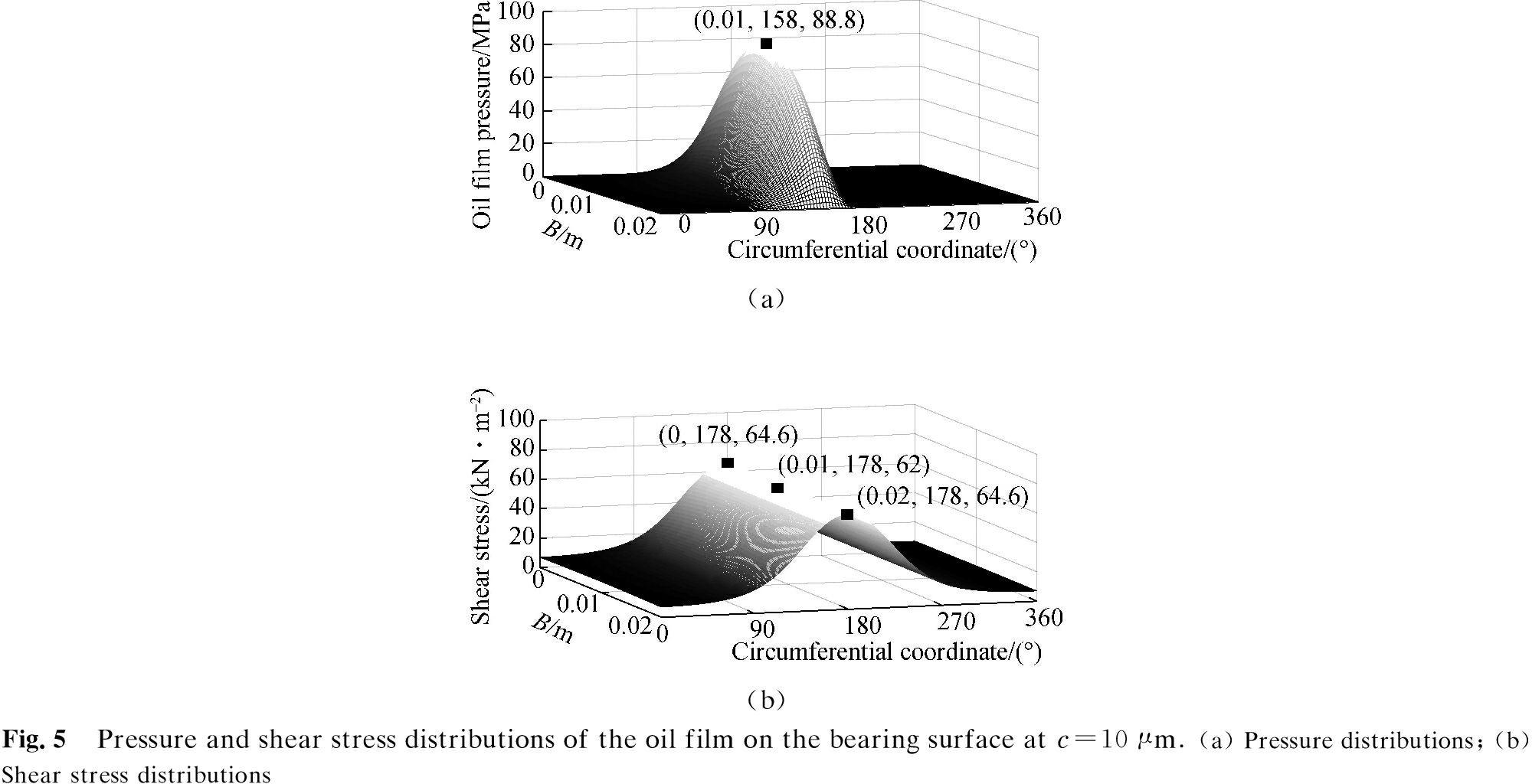
The effects of different radial clearances of (c=5, 10, 15, 20, 25 μm) between the shaft and bearing are simulated, and the distribution results of the oil film pressure and shear stress on the CB surface at c=10 μm are shown in Fig.5. The results indicate that the highest pressures of the oil film are mainly distributed from 90° to 180° of the circumferential coordinates, and the maximum pressure of the oil film (88.8 MPa) occurs at 158° when the bearing width is B/2. The shear stress is uniformly distributed along the bearing width but changes remarkably over the circumferential coordinates evaluated and peaks at 178°.
The oil film pressure and shear stress distributions obtained at a bearing width of B/2 under various radial clearances are illustrated in Fig.6. Fig.6(a) shows that the oil film pressure is greatly increased by increasing c. Conversely, the oil film shear stress increases when c is reduced because the micro asperity contact between the bearing and shaft surfaces in the mixed-lubrication regime increases, which, in turn, increases the friction force. The simulation results of the tribological properties are shown in Fig.7 to clarify the effect of the various radial clearances on the tribological properties of the CB. The results in Figs.7(a) and (b) indicate that the maximum total load Wb increases whereas the total friction force Ff markedly decreases with increasing c, especially at c=25 μm. The tribological properties of the CB are thus improved.

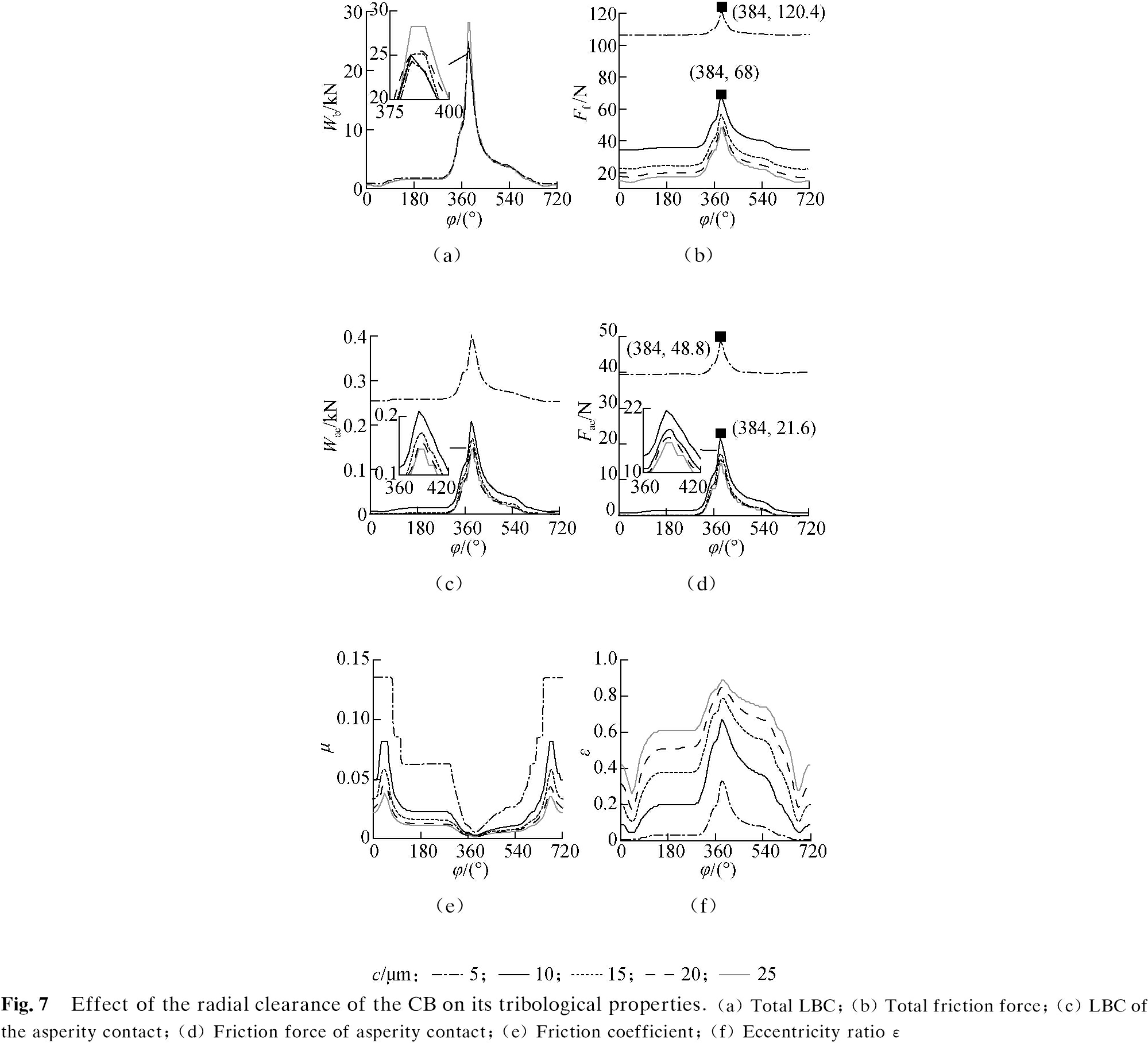
The above results indicate that assessing the effect of the micro asperity contact on the tribological properties of the CB under various radial clearances may be challenging. Thus, the effect of the asperity contact region is highlighted by plotting the results of the LBC and friction force of the asperity contact, as shown in Figs.7(c) and (d). The results indicate that the Wac and Fac of the micro asperity contact increase when c is reduced, especially at c=5 μm. However, Wac is very small in comparison with Wb under the various radial clearances evaluated. Therefore, the LBC of the CB is mainly supported by the oil film, and the radial clearance does not remarkably affect the LBC of the CB. Conversely, as shown in Fig.7(d), the friction force tends to increase with decreasing c and vice versa. In particular, the maximum Fac accounts for 40.5% and 31.8% of the maximum Ff at c=5 μm and c=10 μm, respectively. Therefore, in addition to the friction force Fis of the oil film, the Fac of the asperity contact greatly affects the resistance of the CB.
Under the influence of Fac, the total friction force of Ff increases remarkably under the various radial clearances. As indicated in Fig.7(e), the friction coefficient also increases, particularly at c=5 μm. Moreover, as the radial clearance decreases, the eccentricity ratio ε between the shaft and the bearing change minimally, as shown in Fig.7(f), which improves the stability of the bearing. Although reducing the radial clearance can decrease the eccentricity, an increase in the probability of solid contact will result in a significant increase in friction in the asperity contact region of the CB. In other words, a larger radial clearance can effectively reduce friction. However, an excessively large radial clearance can cause the eccentricity ratio between the shaft and bearing to fluctuate greatly, causing the collision between the shaft and bearing. As the radial clearance gradually increases, the reduction in the friction coefficient becomes very limited. Thus, according to the simulation and analysis results, the optimal radial clearance range providing both anti-friction and anti-impact properties simultaneously is 15 μm≤c≤20 μm.
2.2 Effect of surface roughness
The effect of the surface roughness of the CB (σ=2, 4, 6, 8, and 10 μm) on its tribological properties under the same conditions of a load W0 at 2 000 r/min is also evaluated. The simulation results of the oil film pressure and shear stress distributions at a bearing width of B/2 are shown in Fig.8. The oil film pressure and shear stress increase with decreasing σ and vice versa. Thus, the surface roughness σ can affect the tribological properties of the CB. This finding is further analyzed by plotting the results of the tribological properties, as shown in Fig.9.
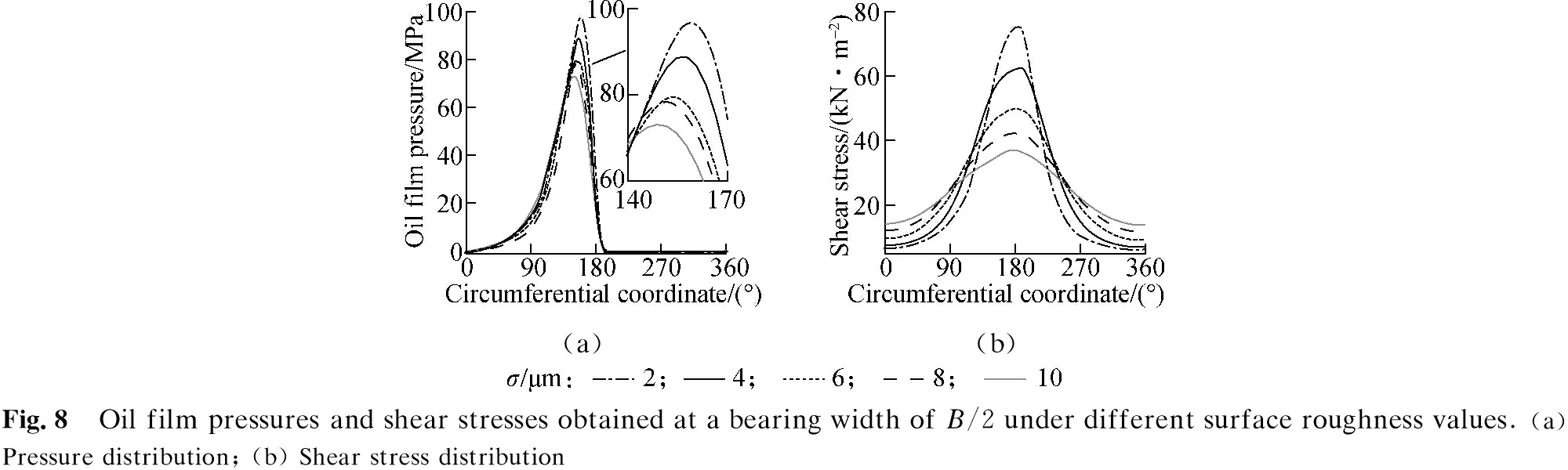
Figs.9(a) and (b) reveal that the maximum Wb is unremarkably affected by the σ while the Ff remarkably increases with increasing σ, especially at σ=8 μm and σ = 10 μm. Figs.9(c) and (d) demonstrate the influence of surface roughness on the Wac and Fac of the asperity contact. The results show that Wac and Fac significantly increase with increasing σ, which could be explained as follows. As the height of the surface roughness increases, the probability of solid contact in the asperity contact region of the CB surfaces also increases, thereby increasing the pressure and stress of the asperity contact. However, Wac is very small in comparison with Wb under the various surface roughness values tested. Thus, the LBC of the CB depends mostly on the oil film pressure. Conversely, the Fac accounts for a remarkable proportion of the total Ff. In particular, the maximum Fac accounts for 68.3% and 77.7% of the maximum Ff at σ=8 μm and σ = 10 μm, respectively. Thus, the resistance of the CB may be concluded to be greatly affected by the friction force of the asperity contact.
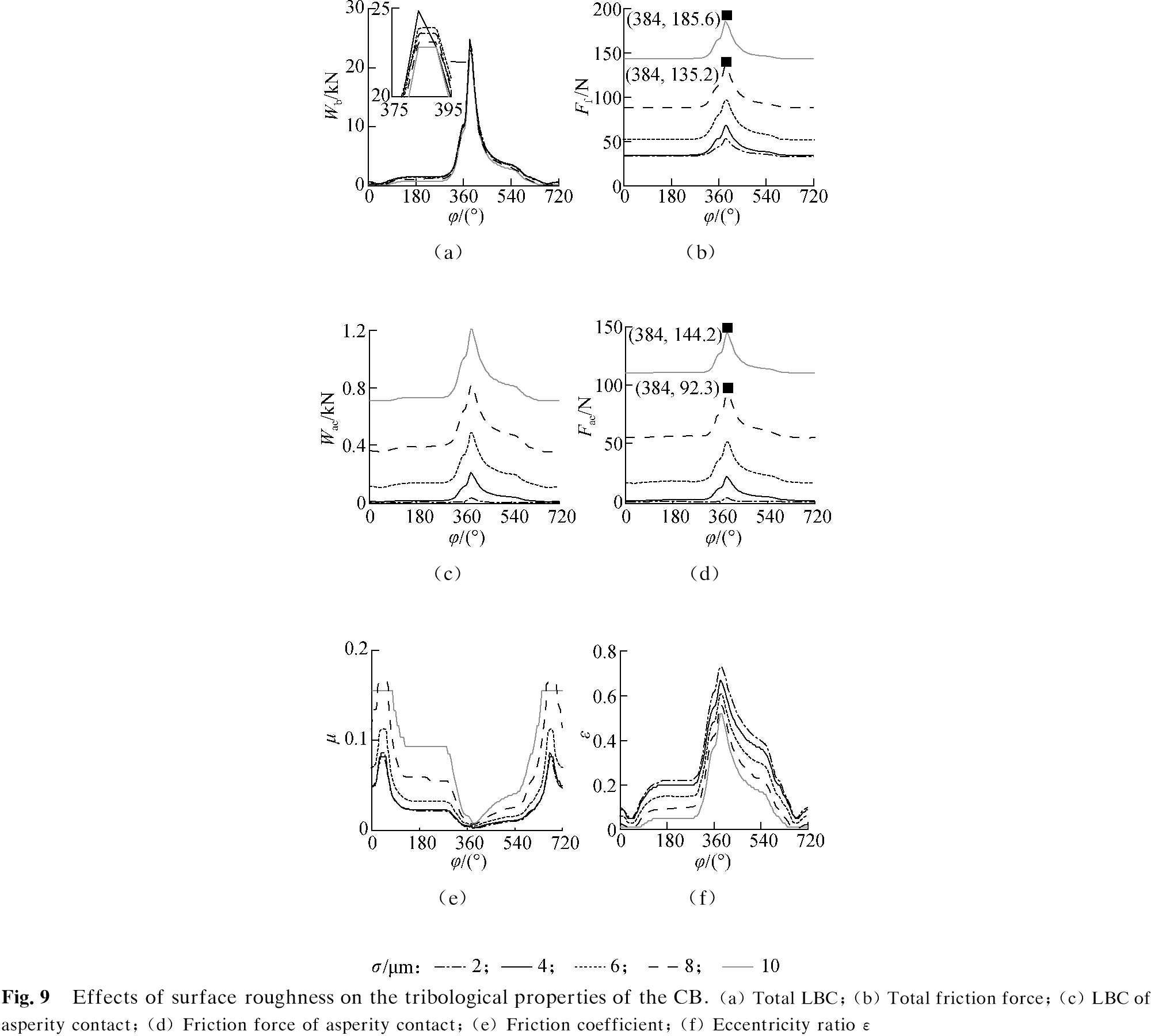
An increase in surface roughness remarkably increases the contact probability between the micro-convex peak and the resistance generated between the solids. Thus, the friction coefficient also increases with Ff, as shown in Fig.9(e). However, the eccentricity ratio is reduced with increasing σ as shown in Fig.9(f). An increase in σ causes the pac in Eq.(12) to increase and the h to decrease. These changes cause a corresponding reduction in the eccentricity ratio ε in Eq.(6), which means a more stable oil film thickness and shaft rotation.
The tribological properties of the CB are affected not only by its micro asperity contact and radial clearance but also by its speed and dimension[17]. Moreover, the temperature of the oil film can affect the tribological properties of the bearing; thus, the effect of the temperature and viscosity of the oil film on the lubrication performance of the CB must be investigated further.
3 Conclusions
1) The influences of the Wac and Fac of the micro asperity contact on the tribological properties of CBs are analyzed[6, 9]. Results show that the Wac has a negligible influence on the tribological properties of the CB, while the Fac greatly affects its resistance. In particular, the maximum Fac accounts for 40.5% of the maximum Ff at c=5 μm and 77.7% of the maximum Ff at σ=10 μm.
2) The Wb significantly increases while the Ff is reduced with increasing radial clearance of the CB. Thus, the tribological properties of the CB are significantly improved. However, an excessively large radial clearance can cause the eccentricity ratio between the shaft and bearing to fluctuate, thereby causing a collision between the shaft and bearing. The results reveal that the optimal radial clearance range providing anti-friction and anti-impact properties simultaneously is 15 μm≤c≤20 μm.
3) Ff is strongly decreased, whereas Wb is unremarkably affected when the surface roughness of the CB is reduced. These effects improve the tribological properties of the CB.
4) The numerical simulation method proposed in this study can not only analyze the tribological properties of the dynamic bearing but also correct the design of bearings and optimize design parameters to enhance the tribological properties of CBs.
[1]Meng X H, Ning L P, Xie Y B, et al. Effects of the connecting-rod-related design parameters on the piston dynamics and the skirt-liner lubrication[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2013, 227(6): 885-898. DOI:10.1177/0954407012464025.
[2]He Z P, Gong W Q,Xie W S, et al. NVH and reliability analyses of the engine with different interaction models between the crankshaft and bearing[J]. Applied Acoustics, 2016, 101: 185-200. DOI:10.1016/j.apacoust.2015.07.014.
[3]Li Y Y, Chen G P, Sun D Y, et al. Dynamic analysis and optimization design of a planar slider-crank mechanism with flexible components and two clearance joints[J]. Mechanism and Machine Theory, 2016, 99: 37-57. DOI:10.1016/j.mechmachtheory.2015.11.018.
[4]Zhao B, Dai X D, Zhang Z N, et al. A new numerical method for piston dynamics and lubrication analysis[J].Tribology International, 2016, 94: 395-408. DOI:10.1016/j.triboint.2015.09.037.
[5]Li Y Y, Chen G P, Sun D Y, et al. Dynamic analysis and optimization design of a planar slider-crank mechanism with flexible components and two clearance joints[J]. Mechanism and Machine Theory, 2016, 99: 37-57. DOI:10.1016/j.mechmachtheory.2015.11.018.
[6]Meng X H, Ning L P, Xie Y B, et al. Effects of the connecting-rod-related design parameters on the piston dynamics and the skirt-liner lubrication[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2013, 227(6): 885-898. DOI:10.1177/0954407012464025.
[7]Jiao R Q, Nguyen V, Van Quynh L, et al. Optimal design of micro-dimples on crankpin bearing surface for improving engine’s lubrication and friction[J].Industrial Lubrication and Tribology, 2021, 73(1): 52-59. DOI:10.1108/ilt-04-2020-0152.
[8]Daniel G B,Cavalca K L. Analysis of the dynamics of a slider-crank mechanism with hydrodynamic lubrication in the connecting rod-slider joint clearance[J]. Mechanism and Machine Theory, 2011, 46(10): 1434-1452. DOI:10.1016/j.mechmachtheory.2011.05.007.
[9]Zhao B, Zhang Z N, Fang C C, et al. Modeling and analysis of planar multibody system with mixed lubricated revolute joint[J]. Tribology International, 2016, 98: 229-241. DOI:10.1016/j.triboint.2016.02.024.
[10]Zhang H,Hua M, Dong G N, et al. A mixed lubrication model for studying tribological behaviors of surface texturing[J]. Tribology International, 2016, 93: 583-592. DOI:10.1016/j.triboint.2015.03.027.
[11]Liu J. A dynamic modelling method of a rotor-roller bearing-housing system with a localized fault including the additional excitation zone[J]. Journal of Sound and Vibration, 2020, 469: 115144. DOI:10.1016/j.jsv.2019.115144.
[12]Zhao B, Zhang Z N, Fang C C, et al. Modeling and analysis of planar multibody system with mixed lubricated revolute joint[J]. Tribology International, 2016, 98: 229-241. DOI:10.1016/j.triboint.2016.02.024.
[13]Gropper D, Wang L, Harvey T J. Hydrodynamic lubrication of textured surfaces: A review of modeling techniques and key findings[J].Tribology International, 2016, 94: 509-529. DOI:10.1016/j.triboint.2015.10.009.
[14]Zhang J J, Zhang J G, Rosenkranz A, et al. Surface textures fabricated by laser surface texturing and diamond cutting—influence of texture depth on friction and wear[J]. Advanced Engineering Materials, 2018, 20(4): 1700995. DOI:10.1002/adem.201700995.
[15]Nguyen V, Wu Z P, Van Quynh L. Optimization of crankpin bearing lubrication under dynamic loading considering effect of micro asperity contact[J].Industrial Lubrication and Tribology, 2020, 72(10): 1173-1179. DOI:10.1108/ilt-02-2020-0072.
[16]Wang P L, Nguyen V, Wu X Y, et al. Research on different structures of dimpled textures on improving the LE-FPL of engine[J].Industrial Lubrication and Tribology, 2021, 73(4): 545-553. DOI:10.1108/ilt-07-2020-0286.
[17]Nguyen V, Zhang J R, Jiao R Q, et al. Research on the effect of crankpin bearing speed and dimension on improving engine power [J]. Journal of Southeast University(English Edition), 2021, 37(2): 119-127. DOI: 10.3969/j.issn.1003-7985.2021.02.001.
[18]Wu Z P, Nguyen V, Zhang Z H, et al. Study on curved surface design of sliding pair based on stepped topography model[J].Industrial Lubrication and Tribology, 2019, 72(1): 86-92. DOI:10.1108/ilt-04-2019-0121.