Chemical looping combustion (CLC) has been developed as a combustion method that can realize inherent separation of carbon dioxide [1-2]. A typical CLC system mainly includes an air rector (AR) and a fuel reactor (FR). Oxygen and heat are continuously transported from the AR to the FR by an oxygen carrier (OC). The coal-direct chemical looping combustion (CDCLC) is a coal-fired CLC approach [3].
The final CDCLC configuration for future practical applications remains under exploration. In our previous studies,a CDCLC system comprising a circulating fluidized bed (CFB) FR, a counter-flow moving bed (CFMB) AR, an inertial separator, and a loop seal was built up. The results proved the feasibility of the configuration design for CDCLC [4]. Moreover, a novel two-stage AR was proposed to improve the carrying capacity of the gas flow in the AR and the power capacity of the CDCLC system. The novel AR was composed of two CFMBs connected in series, which also showed potential advantages in terms of the reaction performance and running cost.
To explore the feasibility of the improved CDCLC system with a two-stage AR, alteration of experimental apparatus would be time-consuming and expensive. With the development in numerical techniques and improved computational capacity, computational fluid dynamics (CFD) modeling has been widely adopted to study the complicated gas-solid flow behaviors [5-7]. Thus far, only a few CFD simulations have been performed on coal-fired CLC, most of which have focused on single reactors [8-9]. In practice, not all the results obtained from single reactor simulations can be directly applied to a CDCLC system, because the coupled effect between the reactors cannot be neglected.
In our previous study, a 3D full-loop numerical model was established for an improved CDCLC system with a high-flux CFB as the FR, two CFMBs connected in series as the two-stage AR, a down-comer, an inertial separator, and a loop seal[4]. To obtain deeper insights into the gas-solid flow dynamics in the system, the solid circulation process and optimization of gas flow paths were studied in detail in this work.
1 Simulation Condition
1.1 Mathematical model
The comprehensive 3D model was built based on our previous study [4]. For each phase, mass and momentum conservation equations were solved. The standard k-ε turbulence model was used to describe the turbulent gas flows. The kinetic theory of granular flow (KTGF) [10] was applied to calculate the conservation of the particle fluctuation energy, where the kinetic energy of the moving particles was expressed using the granular temperature. A detailed description of the models can be seen elsewhere [4].
1.2 Geometry and meshing
Fig.1 shows the 3D model of the improved CDCLC system.
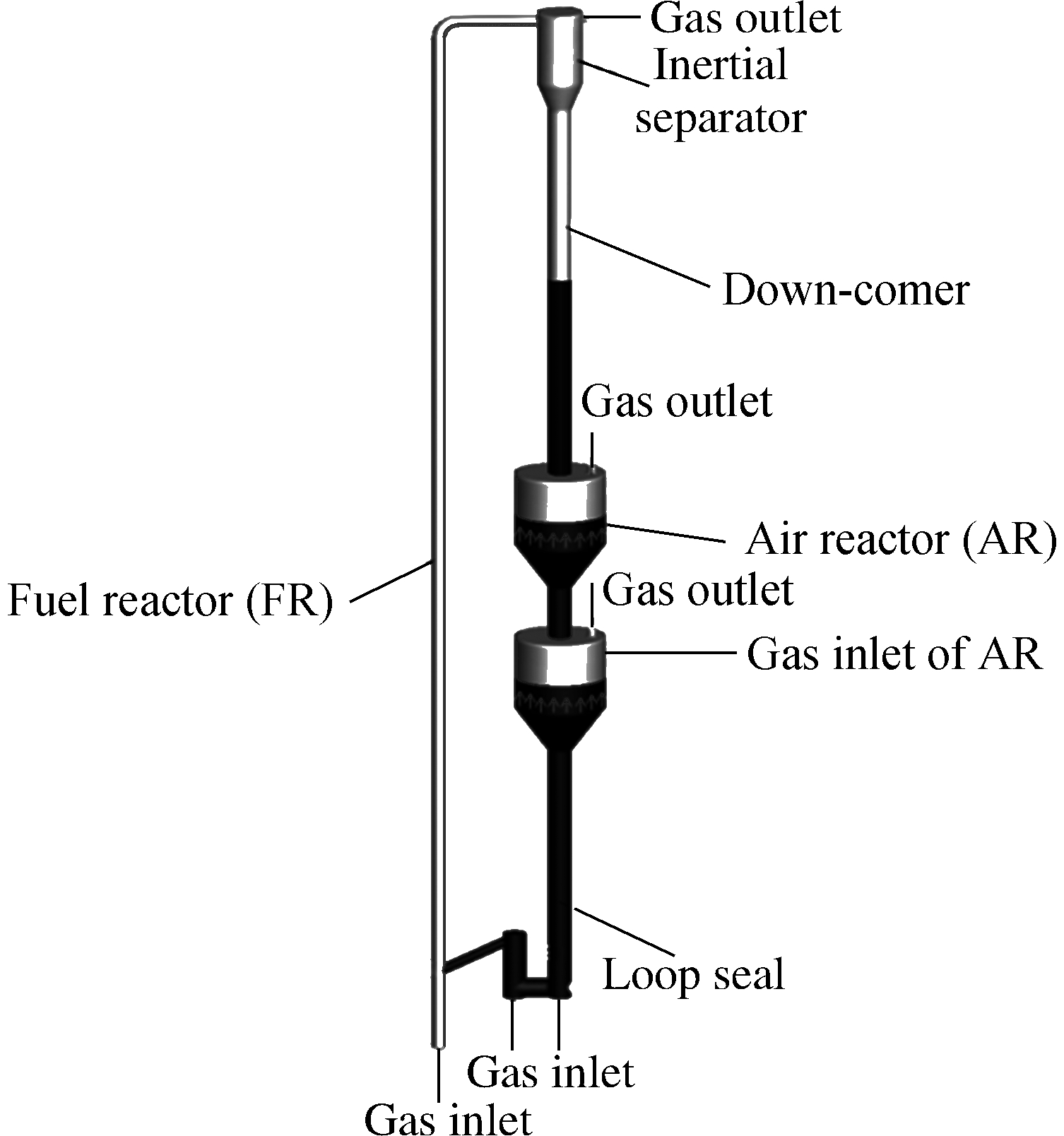
Fig.1 Three-dimensional model of the improved CDCLC system
For the CFB FR, the inner diameter was 60 mm, and the reactor height was 5.8 m. Two identical CFMBs connected in series were adopted as the AR, and the inner diameter and reactor height were 0.418 and 0.400 m, respectively. Considering the computational accuracy and speed, the calculation domain of 638 795 cells was finally selected for this study after the grid independence test.
1.3 Numerical procedure
The pressure-based method was adopted to solve the governing equations [11]. The time step was 0.5 ms, and 20 iterations were set for each time step to ensure convergence of most time steps.
2 Results and Discussion
The particle has a diameter of 0.65 mm and a density of 2 558 kg/m3. Initially, the outlet pressures of the separator, upper CFMB of AR, and lower CFMB of AR were set to 7.4, 10.0, and 17.5 kPa, respectively.
2.1 Solid circulation mechanisms
Particle circulation would affect oxygen and heat transfer in CDCLC systems. With gas introduced to the system, solids initially packed in the system were entrained by gas and moved upwards in the FR. Subsequently, solids from the FR outlet can realize regeneration in the two-stage AR owing to effective separation of the inertial separator. Finally, through the loop seal, the solids returned to the FR. Two monitoring surfaces were set to monitor the solid circulation rates, located at the bottom section of the FR and the top of the down-comer. Fig.2 shows the comparison between the solid circulation rate fluctuations monitored at the two faces. After a computational time of approximately 2 s, particles were detected in the bottom section of the FR, indicating that the solids were gradually transported from the down-comer to the FR. The solid circulation rate increased to a maximum value of approximately 5 kg/s and then gradually decreased because of the dynamic pressure balance. The solid circulation rate fluctuated at approximately 1.2 kg/s steadily when solid circulation was achieved. The solid circulation rates monitored at the down-comer presented similar trends as those monitored at the bottom of the FR. The close solid circulation rate of 1.2 kg/s at the steady state proved the effective separation of solids to the down-comer. However, there was a time delay between the two curves, which was due to the movement of particles from the FR to the down-comer.
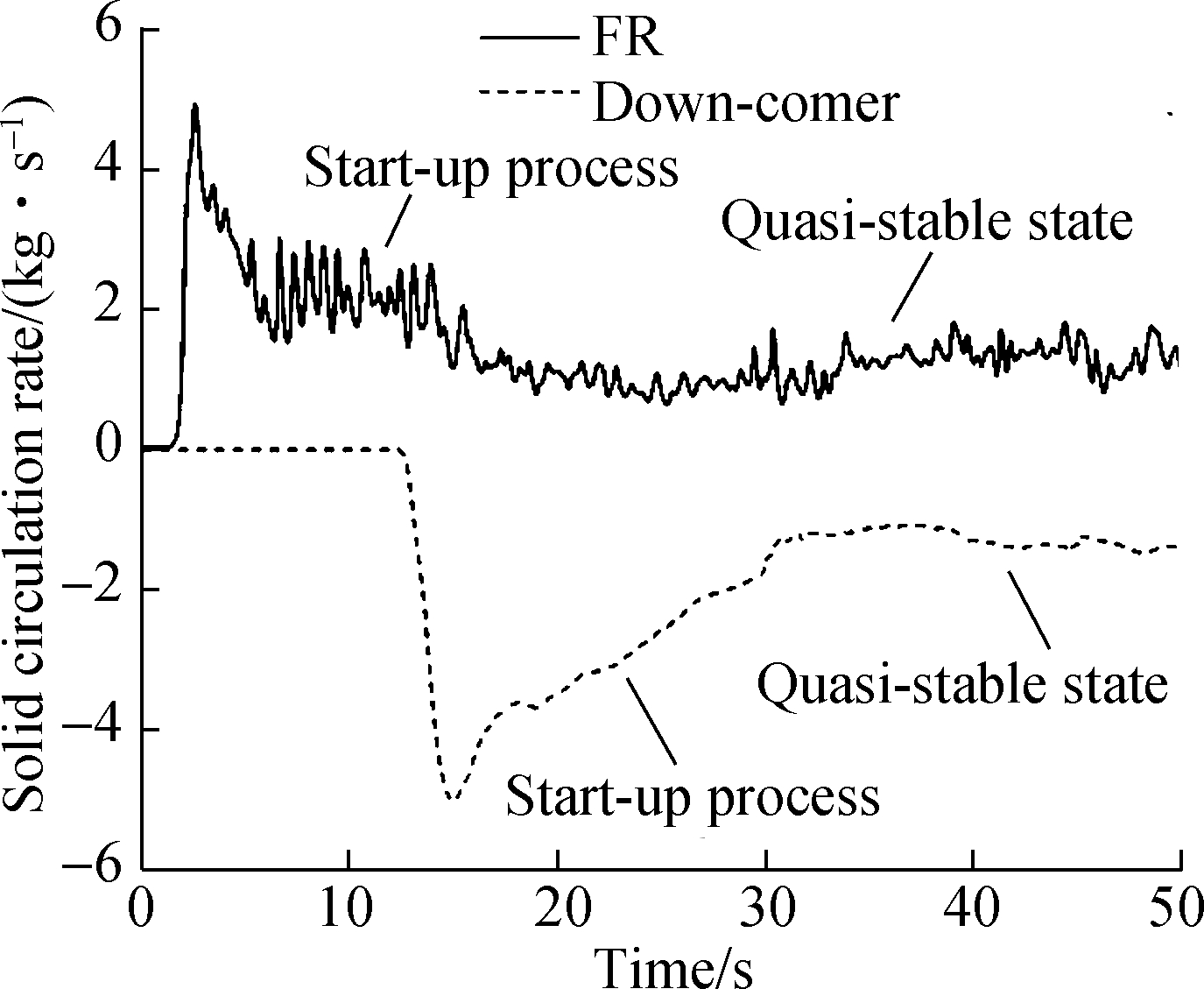
Fig.2 Comparison between solid circulation rate fluctuations monitored at the bottom of FR and the top of down-comer
2.2 Regulation of gas flow paths
Owing to the addition of another CFMB as the AR, the complexity of gas flow paths and the risk of gas leakage between different components were inevitably increased in the improved CDCLC system. Considering the disadvantages, it is essential to restrain gas leakage between the different components in the improved CDCLC system.
The pressure gradient was the fundamental cause of the gas leakage, and hence the leak ratios could be minimized through the pressure regulation.Two parameters Ys,au and Yau,s are used to represent the fraction of the FR gas flowing out from the upper CFMB outlet and the fraction of upper CFMB inlet gas exiting from the separator outlet. Similarly, gas leakage between the two CFMBs could be defined as the fraction of the upper CFMB inlet gas passing into the lower CFMB, and the fraction of lower CFMB inlet gas passing into the upper CFMB, which could be expressed by two parameters Yau,al and Yal,au, respectively.
2.2.1 Effects of pressure difference on gas leakage performance
The separator outlet pressure and upper CFMB AR outlet pressure were set to 7.4 and 17.5 kPa, respectively. The pressure difference ΔP1 between the inertial separator and upper CFMB outlet was changed from 2.1 to 5.1 kPa. Fig.3(a) shows the distributions of the gas leakage ratios (Ys,au, Yau,s). Higher ΔP1 could better restrain the FR gas flowing to the upper CFMB. There was almost no gas leaking from the upper CFMB to the separator when ΔP1 ranged from 2.1 to 3.6 kPa; however, a further increase in ΔP1 could lead to more upper CFMB inlet gas flowing to the separator. As it was difficult to keep the two gas leakage ratios to zero at the same time, and a little FR gas flowing into the upper CFMB was allowed, the optimal pressure difference ΔP1 of 3.6 kPa was finally chosen for the system, which could make sure that no upper CFMB gas flow into the separator, and FR gas leakage fraction Ys,au was less than 1%.
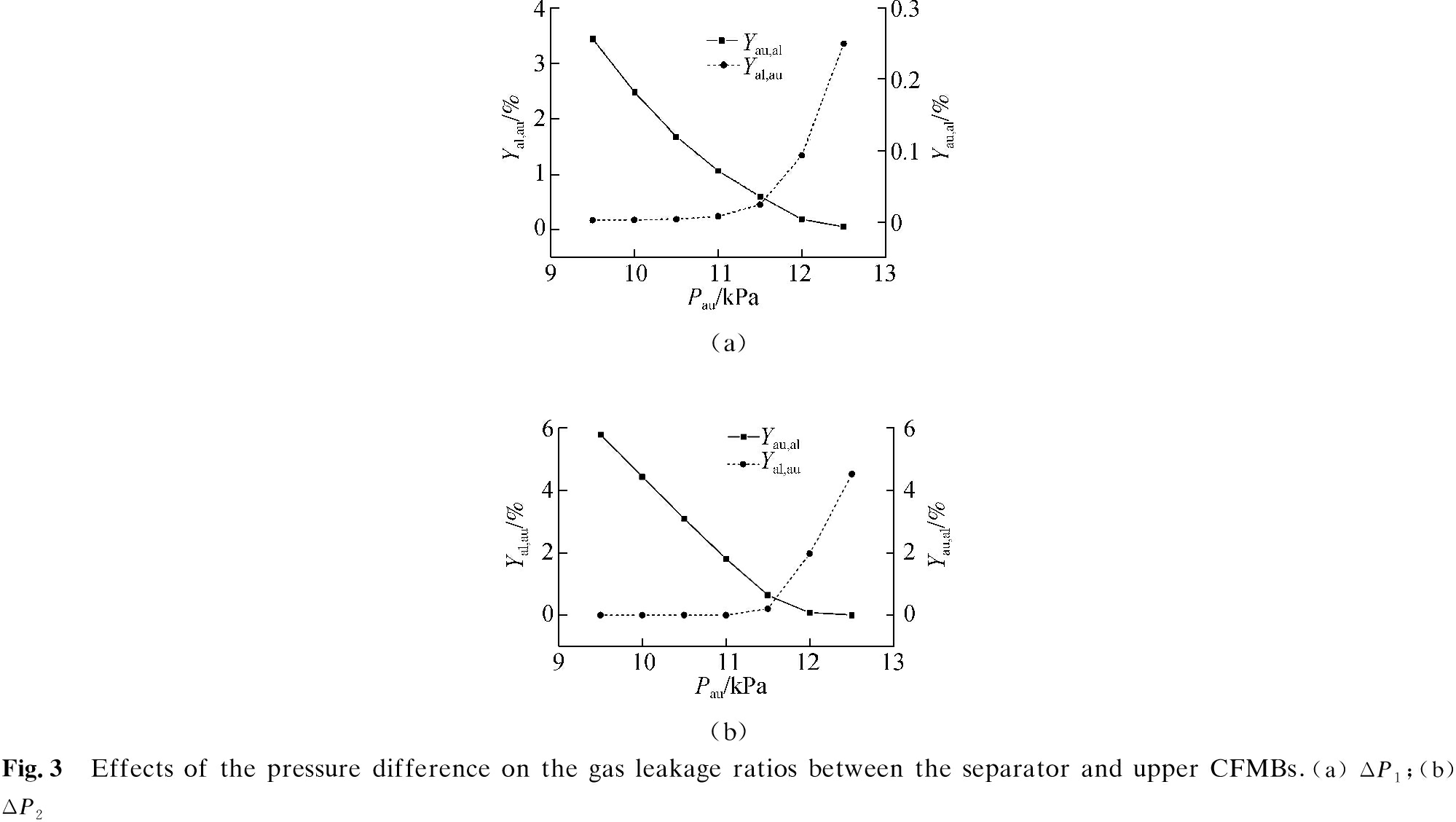
To determine the optimal pressure difference ΔP2 between the upper CFMB outlet and lower CFMB outlet, pressure difference ΔP1 was kept to 3.6 kPa to minimize the gas leakage between the separator and upper CFMB. Fig.3(b) shows the distribution of the gas leakage ratios (Yau,al, Yal,au) with ΔP2 ranging from 1.5 to 4.5 kPa. Yau,al decreased with increasing ΔP2, demonstrating that a higher ΔP2 was helpful in preventing the upper CFMB inlet gas from flowing to the lower CFMB. The gas leakage from the upper CFMB to the lower CFMB disappeared, when ΔP2 increased to 4.0 kPa. Meanwhile, with the increase of ΔP2, Yal,au initially kept at near-zero and then gradually increased. The critical value occurred at ΔP2=3.5 kPa. To minimize the gas leakage between the two CFMBs, the pressure difference ΔP2 of 3.6 kPa at the intersection of two curves was finally selected as the optimal ΔP2 for the system, which could ensure that the gas leakage ratios (Yau,al, Yal,au) were both less than 1%.
2.2.2 Gas distributions at three outlets
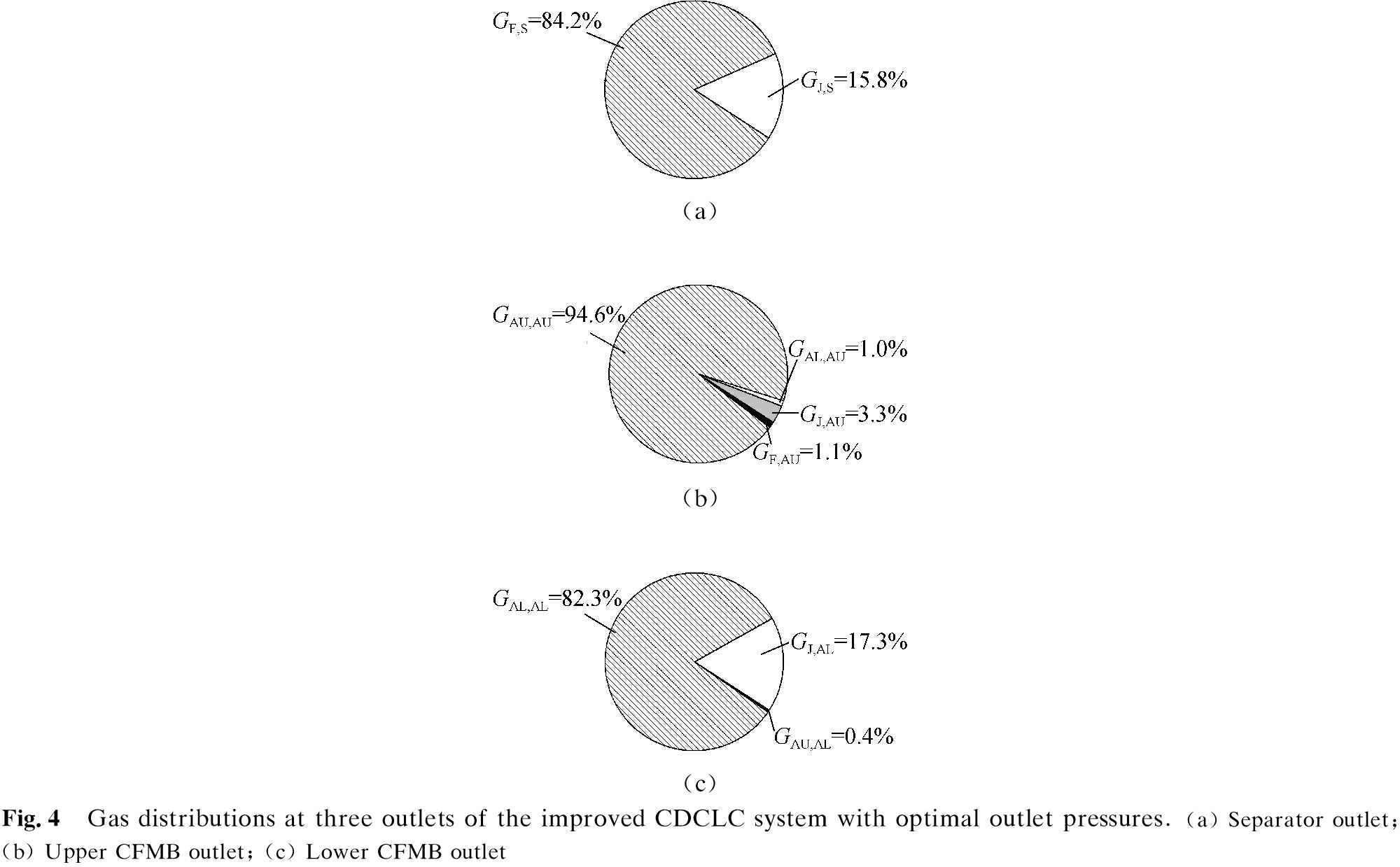
To verify the feasibility of the optimal pressure difference in minimizing the gas leakage, an improved CDCLC system was operated by setting the separator outlet pressure Ps, the upper CFMB outlet pressure and the lower CFMB outlet pressure to 7.4, 11.0 and 14.6 kPa, respectively (ΔP1=3.6 kPa and ΔP2 =3.6 kPa). Fig.4 shows the gas distributions in three outlets of the improved CDCLC system. In the separator outlet, the gases included the FR inlet gas accounting for the major proportion of 84.2% and the loop seal inlet gas taking up 15.8%, indicating that there was no leaking gas from the AR. As for the upper CFMB outlet, the gas from its own inlet occupied the highest percentage of 94.6%, and the total leaking gas just took up a small proportion, and hence, the gas leakage into the upper CFMB had been successfully restrained. In the lower CFMB, 82.3% of the outlet gases were from its own inlet. The gas leaking from the upper CFMB just occupied 0.4%, demonstrating minimization of the gas leakage between two CFMBs. Thus, the optimal AR outlet pressures were able to effectively restrain the gas leakage between different components of the CDCLC system, which was beneficial for achieving high CO2 capture efficiency and stable gas-solids flow states.
3 Conclusions
1) During the start-up process, the solid circulation rate first increased to approximately 5 kg/s and then decreased to approximately 1.2 kg/s, and the trend was related to the dynamic control of the pressure distribution.
2) When the pressure difference between the inertial separator outlet and the upper CFMB outlet (ΔP1) and the pressure difference between the upper CFMB outlet and lower CFMB outlet (ΔP2) were both adjusted to 3.6 kPa, the gas leakage between the inertial separator and two CFMBs were effectively restrained, with the gas leakage ratios being less than 1% under the involved conditions. This can be beneficial for realizing a high CO2 capture efficiency and a stable movement of the solids in the system.
3) With the separator outlet pressure, upper CFMB outlet pressure and lower CFMB outlet pressure set to 7.4, 11.0, and 14.6 kPa, respectively, reasonable gas flow paths were achieved. The gases at the separator outlet included 84.2% FR gas and 15.8% loop seal gas; 94.6% of the gases at the upper CFMB outlet were from its own inlet and 82.3% of the gases at the lower CFMB outlet were from its own inlet.
[1]Wang X D, Shao Y L, Jin B S. Spatiotemporal statistical characteristics of multiphase flow behaviors in fuel reactor for separated-gasification chemical looping combustion of solid fuel[J]. Chemical Engineering Journal, 2021, 412: 128575. DOI: 10.1016/j.cej.2021.128575.
[2]Francisco J V, Carmen R F, I aki A, et al. Assessment of low-cost oxygen carrier in South-western Colombia, and its use in the in-situ gasification chemical looping combustion technology[J]. Fuel, 2018, 218: 417-424. DOI: 10.1016/j.fuel.2017.11.078.
aki A, et al. Assessment of low-cost oxygen carrier in South-western Colombia, and its use in the in-situ gasification chemical looping combustion technology[J]. Fuel, 2018, 218: 417-424. DOI: 10.1016/j.fuel.2017.11.078.
[3]Li S Y, Shen Y S. Numerical study of gas-solid flow behaviors in the air reactor of coal-direct chemical looping combustion with Geldart D particles[J]. Powder Technology, 2020, 361: 74-86. DOI: 10.1016/j.powtec.2019.10.045.
[4]Shao Y L, Zhang Y, Wang X J, et al. Three-dimensional full loop modeling and optimization of an in situ gasification chemical looping combustion system[J]. Energy and Fuels, 2017, 31(12): 13859-13870. DOI: 10.1021/acs.energyfuels.7b02119.
[5]Zhou L, Han C, Bai L, et al. Numerical and experimental study of multiphase transient core-annular flow patterns in a spouted bed[J]. Journal of Energy Resources Technology, 2020, 142(9): 1-13. DOI: 10.1115/1.4047305.
[6]Hamidouche Z, Masi E, Fede P, et al. Unsteady three-dimensional theoretical model and numerical simulation of a 120 kW chemical looping combustion pilot plant. Chemical Engineering Science, 2019, 193: 102-119. DOI: 10.1016/j.ces.2018.08.032.
[7]Banerjee S, Ramesh K A. Computational fluid dynamics simulations of a binary particle bed in a riser-based carbon stripper for chemical looping combustion[J]. Powder Technology. 2018, 325: 361-367. DOI: 10.1016/j.powtec.2017.11.032.
[8]Mahalatkar K, Kuhlman J, Huckaby E D, et al. CFD simulation of a chemical-looping fuel reactor utilizing solid fuel[J]. Chemical Engineering Science, 2011, 66(16): 3617-3627. DOI: 10.1016/j.ces.2011.04.025.
[9]Yin W J, Wang S, Zhang K. Numerical investigation of in situ gasification chemical looping combustion of biomass in a fluidized bed reactor[J].Renewable Energy, 2020, 151: 216-225. DOI: 10.1016/j.renene.2019.11.016.
[10]Ding J M, Gidaspow D. A bubbling fluidization model using kinetic theory of granular flow[J]. AIChE Journal, 1990, 36(4): 523-538. DOI: 10.1002/aic.690360404.
[11]Menon G K, Patnaikuni V S. CFD simulation of fuel reactor for chemical looping combustion of Indian coal[J]. Fuel, 2017, 203: 90-101. DOI: 10.1016/j.fuel.2017.04.084.