Thermal power remains an important power source around the world. NOx emissions emitted from power plants have been troubling human beings for a long time. As a simple, effective, and cheap technology, combustion optimization can cut down NOx emissions through organizing coal combustion in furnaces[1-3].
For in-service boilers, NOx emissions are influenced by operating parameters like oxygen and wind valve openings. The optimization of these parameters based on artificial intelligence can provide satisfactory operation strategies. Many researchers[4-5] have improved the NOx prediction model, providing the basis for low NOx combustion optimization. Optimization algorithms like differential evolution[6], vortex search[7], genetic algorithm[8], and particle swarm optimization[9] have been employed to optimize operating parameters to cut down NOx emissions.
Inspired by the birds flocking, Kennedy et al.[10] proposed particle swarm optimization (PSO) in 1995. PSO is famous for its simplicity and effectiveness. However, it is troubled with the premature and convergence problems. To overcome this disadvantage, researchers have been devoted to improvements in aspects of parameter tunings[11], mutations[12], learning strategies[13], multi-swarms[14], and algorithm hybridizations[15].
Opposition-based learning (OBL) strategy evaluates the original solution and its opposite solution simultaneously[16]. A better solution is retained based on a greedy strategy. OBL has been introduced into PSO to enhance performance[17-18]. However, these OBL based algorithms could not make full use of the obtained information. To utilize the shrunken search space, Wang et al.[19] enhanced the PSO using generalized opposition-based learning (GOBL) characterized by dynamically updated interval boundaries.
To the best of the authors’ knowledge, PSO based on OBL and PSO based on GOBL have not been studied in the low NOx combustion optimization area. This paper studied the adaptability of these two algorithms to the low NOx combustion optimization systematically.
1 Optimization Algorithms
1.1 Particle swarm optimization
In the PSO algorithm, N particles are initialized to form a population in the D-dimensional search space. Each particle has a position vector and a velocity vector, which can be expressed as {xi1, xi2,…, xiD} and {vi1, vi2,…, viD}, respectively. The fitness of each particle can be evaluated by an objective function. In each optimization iteration, each particle records its best position, which is called the historically best position Pi. The best position among all the particles in the population is called the global best position Pg. All particles update their positions and speeds under the guidance of the best position and global best position as
(1)
(2)
where ![]() are the velocity vector and position vector of the i-th particle in the tth generation; ω is the inertia weight, which can balance the capabilities of exploration and exploitation; c1, c2 are acceleration factors; r1 and r2 are random numbers in [0, 1]; and t is the iteration number.
are the velocity vector and position vector of the i-th particle in the tth generation; ω is the inertia weight, which can balance the capabilities of exploration and exploitation; c1, c2 are acceleration factors; r1 and r2 are random numbers in [0, 1]; and t is the iteration number.
1.2 Particle swarm optimization employing an opposition-based learning
To study the adaptability of PSO employing OBL to the low NOx combustion optimization, only the opposition-based learning[20] is introduced to enhance the PSO without other improvements. This is named OBLPSO. In each iteration, each particle generates an opposite particle based on OBL and its current position with a certain probability as
(3)
where aj and bj are the low limit and up limit in the jth dimension and ![]()
1.3 Particle swarm optimization employing a generalized opposition-based learning
GOBL is an improved version of OBL[19], which can utilize the knowledge of the current converged search space. To study the adaptability of PSO employing GOBL to the low NOx combustion optimization, only the GOBL is introduced to enhance PSO with a certain probability, which is named GOBLPSO. The generalized opposition of the jth dimension of xi can be calculated as below.
(4)
where aj(t) and bj(t) are the minimum and maximum values of the jth dimension in the current population, respectively, and ki is a random number in (0,1). If ![]()
2 Combustion Optimization Based on OBLPSO and GOBLPSO
2.1 NOx emission prediction based on extreme learning machine
For a given boiler,the NOx emission is generally influenced by operating parameters like oxygen in the flue gas, over-fire air valve openings, and the rotating speeds of the dynamic separator of the coal pulverizer. These parameters are taken as inputs of the NOx emission prediction model.
Prediction models of NOx emissions and efficiencies were both established based on the extreme learning machine (ELM)[21]. Differential evolution (DE) was employed to optimize input weights and hidden layer thresholds to enhance performances[22]. Moreover, the normalization method and leave-one-out cross validation were also employed.
2.2 Combustion optimization based on OBLPSO and GOBLPSO
NOx emissions at the inlet of selective catalytic reduction equipment are influenced by operating parameters like oxygen, over-fire air valve openings, and secondary air valve openings. The optimization of these parameters can cut down NOx emissions effectively and reduce the operation cost of the selective catalytic reduction equipment. For the studied boiler, the secondary air valve openings are controlled automatically. Four corner openings of each over-fire air layer are different. These over-fire air valve openings and oxygen are optimized by the OBLPSO and GOBLPSO to reduce NOx emissions. Each particle represents a set of operation parameters. The corresponding NOx emission at the inlet of the selective catalytic reduction equipment is taken as the fitness of each particle. When the operating parameters are optimized to reduce NOx emissions, corresponding efficiencies are kept no lower than the original efficiencies.
3 Field Test
The thermal adjustment test on a 660 MW boiler was carried out. The studied boiler is characterized by tangential combustion, π type, single furnace, balanced ventilation, and solid slagging. Each burner has 6 layers of pulverized coal nozzles, 14 layers of secondary air, and 4 layers of over-fire air. The secondary air valve openings are controlled automatically. Openings of the over-fire air in each corner are different from each other. During each case, the coal quality was kept the same and the element analysis was analyzed. There are 18 cases in the thermal adjustment test, including ground conditions, variable oxygen conditions, the variable operation mode of coal pulverizer conditions, variable first air pressure conditions, and variable rotating speeds of the dynamic separator of coal pulverizer conditions.
4 Results and Discussion
4.1 Related parameters
For PSO,OBLPSO, and GOBLPSO, the inertia weight acceleration factors were set as 0.8, 2.5, and 2.0, respectively. The particle number is 30 and the maximum iteration number is 50. The DE algorithm was employed as the comparison algorithm[22-23]. The number of DE parameter vectors is 30. The mutation and the crossover constants are 0.75 and 0.25, respectively. Each algorithm is tested 51 times independently for each case.
4.2 Related results and discussion
Fig. 1 shows the NOx emissions and efficiencies predicted by ELM. Predicted results are very close to the original values. For the training samples and test samples of NOx emissions, the root-mean-square errors are 5.256 5 and 6.608 2 mg/m3, respectively. For the efficiencies of the training samples and test samples, the root-mean-square errors are 1.29×10-4 and 1.34×10-4, respectively. The approximation capability and generalization ability are both satisfactory.

Fig. 2 shows the minimum-optimized NOx emissions based on PSO and DE. It can be seen that the minimum-optimized NOx emissions based on PSO are generally lower than that of DE. This phenomenon is most obvious for Case 6 and Case 13; i.e., PSO is more adaptable for the combustion optimization of the studied boiler than DE.

Fig.2 Minimum-optimized NOx emissions based on PSO and DE
Fig. 3 shows the median-optimized NOx emissions based on PSO, OBLPSO, and GOBLPSO. Generally, the median-optimized NOx emissions based on GOBLPSO are the lowest among the three algorithms. This phenomenon is more obvious for Case 7, Case 8, Case 14, and Case 15. For Case 14, the median NOx emissions optimized by GOBLPSO are up to 15.8 mg/m3 lower than the median NOx emissions optimized by PSO. The GOBL can enhance PSO for the combustion optimization of the studied boiler effectively.

Fig.3 Median-optimized NOx emissions based on PSO, OBLPSO, and GOBLPSO
Fig. 4 shows the minimum-optimized NOx emissions based on PSO, OBLPSO, and GOBLPSO. The advantage of GOBLPSO over the other two algorithms is not too obvious for the minimum-optimized NOx emissions.
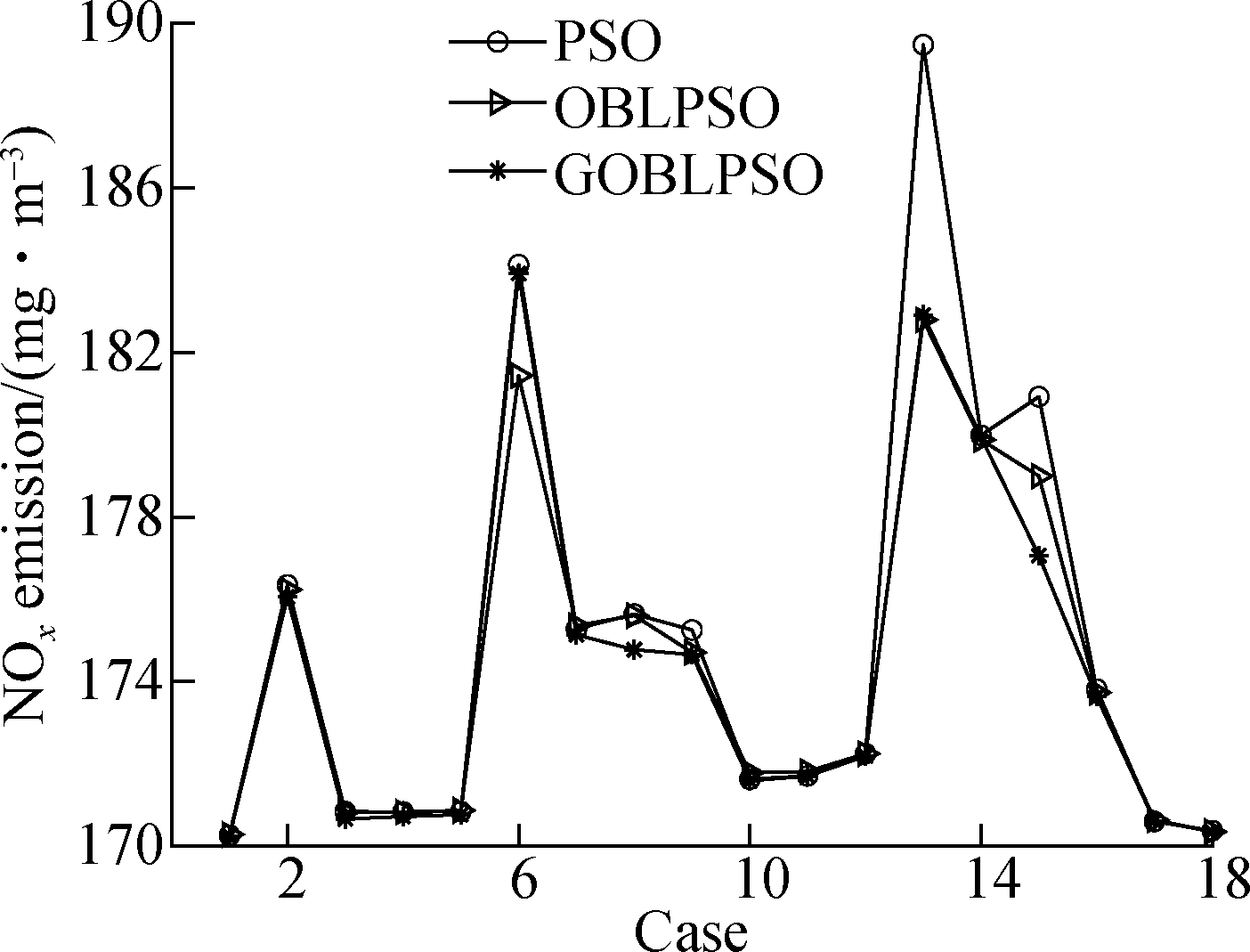
Fig.4 Minimum-optimized NOx emissions based on PSO, OBLPSO, and GOBLPSO
Fig. 5 shows the original efficiencies and minimum-optimized efficiencies based on DE, PSO, OBLPSO, and GOBLPSO. All minimum-optimized efficiencies are not lower than the original efficiencies. When the operating parameters are optimized to reduce NOx emissions, the corresponding efficiencies are kept no lower than the original efficiencies. The optimized results show that this strategy is effective.
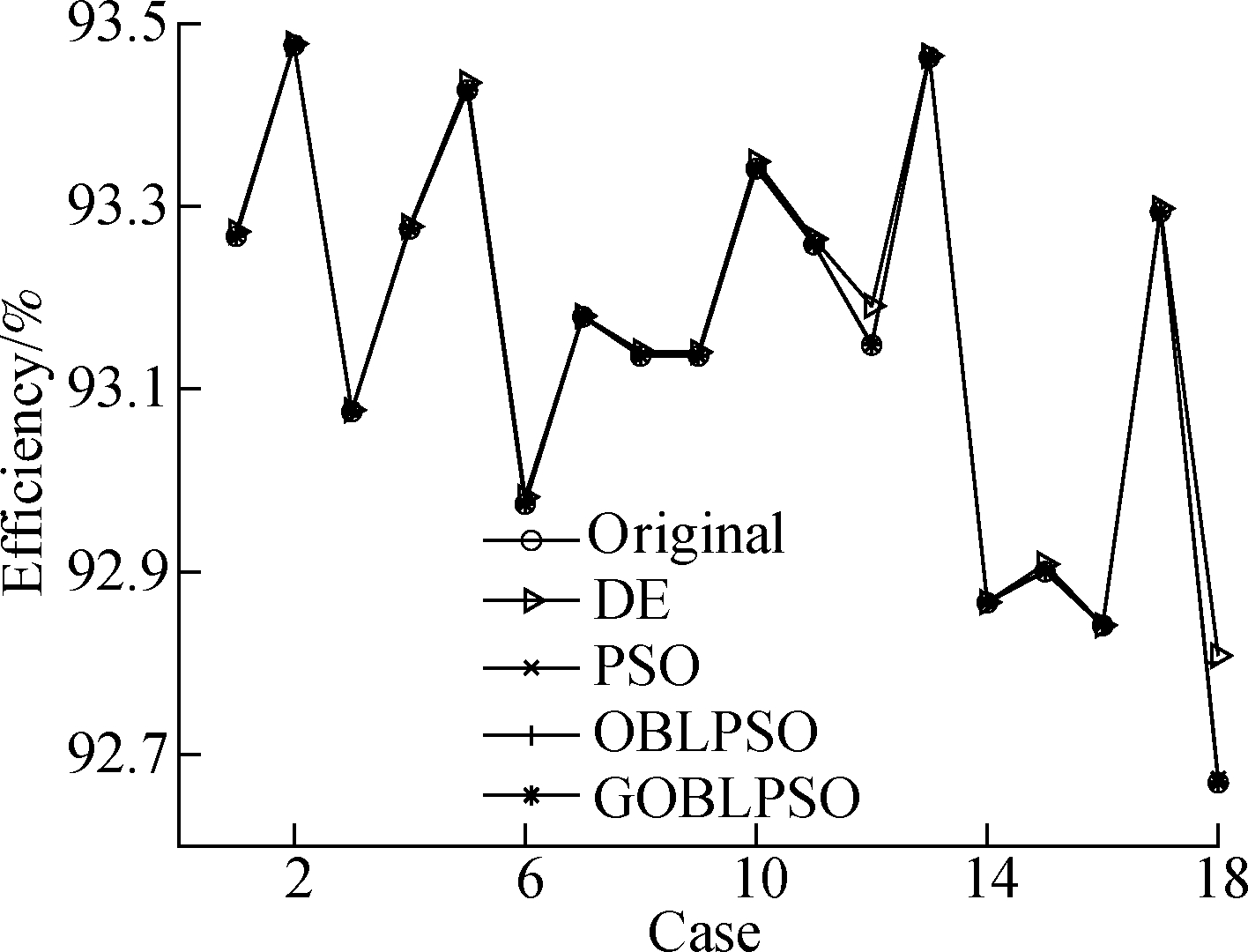
Fig.5 Original efficiencies and minimum-optimized efficiencies
Fig. 6 shows the optimized progress of the median-optimized NOx for Case 8 and Case 14. For both cases, the algorithms can converge in 20 iterations. GOBLPSO can provide the lowest median-optimized NOx emissions among the three algorithms.

5 Conclusions
1)The GOBLPSO outperforms the PSO and OBLPSO in the aspects of median-optimized results. Up to 15.8 mg/m3 NOx emissions are reduced further by the GOBLPSO compared with PSO for the median-optimized NOx emissions in Case 14.
2)Median-optimized processes of some cases based on PSO, OBLPSO, and GOBLPSO show that the processes based on GOBLPSO are satisfactory.
3) GOBL can enhance PSO for the combustion optimization of the studied boiler effectively.
[1]Rahat A A M, Wang C L, Everson R M, et al. Data-driven multi-objective optimisation of coal-fired boiler combustion systems [J].Applied Energy, 2018, 229: 446-458. DOI: 10.1016/j.apenergy.2018.07.101.
[2]Li Q W, Yao G H. Improved coal combustion optimization model based on load balance and coal qualities [J]. Energy, 2017, 132: 204-212. DOI: 10.1016/j.energy.2017.05.068.
[3]Safdarnejad S M, Tuttle J F, Powell K M. Dynamic modeling and optimization of a coal-fired utility boiler to forecast and minimize NOx and CO emissions simultaneously [J]. Computers and Chemical Engineering, 2019, 124: 62-79. DOI: 10.1016/j.compchemeng.2019.02.001.
[4]Tang Z H, Wu X Y, Cao S X. Modeling of the boiler NOx emission with a data driven algorithm [J]. Journal of Chemical Engineering of Japan, 2018, 51(8): 695-703. DOI: 10.1252/jcej.17we335.
[5]Tang Z H, Wu X Y, Cao S X, et al. Modeling of the boiler NOx emission with a data driven algorithm [J]. Journal of Chemical Engineering of Japan, 2018,51(8): 695-703. DOI: 10.1252/jcej.17we335.
[6]Zheng L G, Zhang Y G, Yu S J, et al. Use of differential evolution in low NOx combustion optimization of a coal-fired boiler [C]// 2010 Sixth International Conference on Natural Computation. Yantai, China, 2010: 4395-4399. DOI: 10.1109/ICNC.2010.5583524.
[7]Li X, Niu P F, Liu J P. Combustion optimization of a boiler based on the chaos and Lévy flight vortex search algorithm [J]. Applied Mathematical Modelling, 2018, 58: 3-18. DOI: 10.1016/j.apm.2018.01.043.
[8]Ilamathi P, Selladurai V, Balamurugan K, et al. ANN-GA approach for predictive modeling and optimization of NOx emission in a tangentially fired boiler [J]. Clean Technologies and Environmental Policy, 2013, 15: 125-131. DOI: 10.1007/s10098-012-0490-5.
[9]Zhou H, Zheng L G, Cen K F. Computational intelligence approach for NOx emissions minimization in a coal-fired utility boiler [J]. Energy Conversion and Management, 2010, 51: 580-586. DOI: 10.1016/j.enconman.2009.11.002.
[10]Kennedy J, Eberhart R. Particle swarm optimization [C]// International Conference on Neural Networks. Perth, WA, Australia, 1995: 1942-1948. DOI: 10.1109/ICNN.1995.488968.
[11]Han H G, Lu W, Hou Y, et al. An adaptive-PSO-based self-organizing RBF neural network [J]. IEEE Transactions on Neural Networks and Learning Systems, 2018, 29(1): 104-117. DOI: 10.1109/TNNLS.2016.2616413.
[12]Jiang F, Xia H Y, Tran Q A, et al. A new binary hybrid particle swarm optimization with wavelet mutation [J]. Knowledge-Based Systems, 2017, 130: 90-101. DOI: 10.1016/j.knosys.2017.03.032.
[13]Wang F, Zhang H, Li K S, et al. A hybrid particle swarm optimization algorithm using adaptive learning strategy [J]. Information Sciences, 2018, 436-437: 162-177. DOI: 10.1016/j.ins.2018.01.027.
[14]Xia X W, Gui L, Zhan Z H. A multi-swarm particle swarm optimization algorithm based on dynamical topology and purposeful detecting [J]. Applied Soft Computing, 2018, 67: 126-140. DOI:10.1016/j.asoc.2018.02.042.
[15]Liu Z, Qin Z W, Zhu P, et al. An adaptive switchover hybrid particle swarm optimization algorithm with local search strategy for constrained optimization problems [J]. Engineering Applications of Artificial Intelligence, 2020, 95: 103771. DOI: 10.1016/j.engappai.2020.103771.
[16]Rahnamayan S, Tizhoosh H R, Salama M M A. Opposition-based differential evolution [J]. IEEE Transactions on Evolutionary Computation, 2008, 12(1): 64-79. DOI: 10.1109/TEVC.2007.894200.
[17]Lin H, He X. A novel opposition-based particle swarm optimization for noisy problems [C]// Proceedings of International Conference on Natural Computation. Haikou, China, 2007: 624-629. DOI: 10.1109/ICNC.2007.119.
[18]Wang H, Li H, Liu Y, et al. Opposition-based particle swarm algorithm with cauchy mutation [C]// IEEE Congress on Evolutionary Computation. Singapore, 2007: 4750-4756. DOI: 10.1109/CEC.2007.4425095.
[19]Wang H, Wu Z J, Rahnamayan S, et al. Enhancing particle swarm optimization using generalized opposition-based learning [J]. Information Sciences, 2011, 181: 4699-4714. DOI: 10.1016/j.ins.2011.03.016.
[20]Tizhoosh H R. Opposition-based learning: A new scheme for machine intelligence [C]// Proceedings of International Conference on Computational Intelligence for Modeling Control and Automation. Vienna, Austria, 2005: 695-701. DOI: 10.1109/CIMCA.2005.1631345.
[21]Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: Theory and applications [J]. Neurocomputing, 2006, 70: 489-501. DOI: 10.1016/j.neucom.2005.12.126.
[22]Storn R, Price K. Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces [J]. Journal of Global Optimization, 1997, 11: 341-359. DOI: 10.1023/A:1008202821328.
[23]Bao Z Y, Yu J Z.Intelligent optimization algorithm and its MATLAB example [M]. Beijing: Publishing House of Electronics Industry, 2016:39-42. (in Chinese)