Welding is a commonly used connection method for steel structures. Welding is often affected by the on-site welding environment and welding process, which makes guaranteeing the quality level of the weld difficult[1], resulting in the brittle failure of the beam-column joint weld under rare seismic conditions. Since the 1994 Northridge earthquake in the United States and the 1995 Hanshin earthquake in Japan, researchers have begun to focus on the brittle failure of welds. Accordingly, scholars at home and abroad began to study new types of strengthened and weakened nodes. Wang et al.[2-3] conducted theoretical analyses and experimental research on a sleeve end with sleeve-type joints. Their results showed that the inner and outer sleeve joints follow the sleeve wall. In addition, the increase in thickness will increase the initial stiffness of a node and slow down the rate of stiffness degradation. Liu et al.[4-6] adopted the form of fully bolted nodes, which have good ductility and energy dissipation capacity. Reinforced and weakened nodes can both benefit from the outward movement of plastic hinges, which increases nodes’ ductility and their seismic energy dissipation. New nodes come in many different forms and have been improved and are more innovative compared to traditional nodes. The seismic energy effect on dissipation capacity is also different[7-11].
In this study, based on a new type of friction plastic hinge joint[12], a low-cycle reciprocating loading test was performed on a weakened joint of a novel fabricated beam end. The main factors affecting the mechanical properties of the joint were analyzed and determined. This paper presents the design methods developed by the authors, which work around the plate thickness and weakened joint depth. The new node will allow the modular processing of steel beams and columns, factory processing, and rapid assembly at construction sites, which will not only guarantee the quality of the beams and columns but will also increase construction efficiency.
1 Experimental Investigation
1.1 Composition of joints
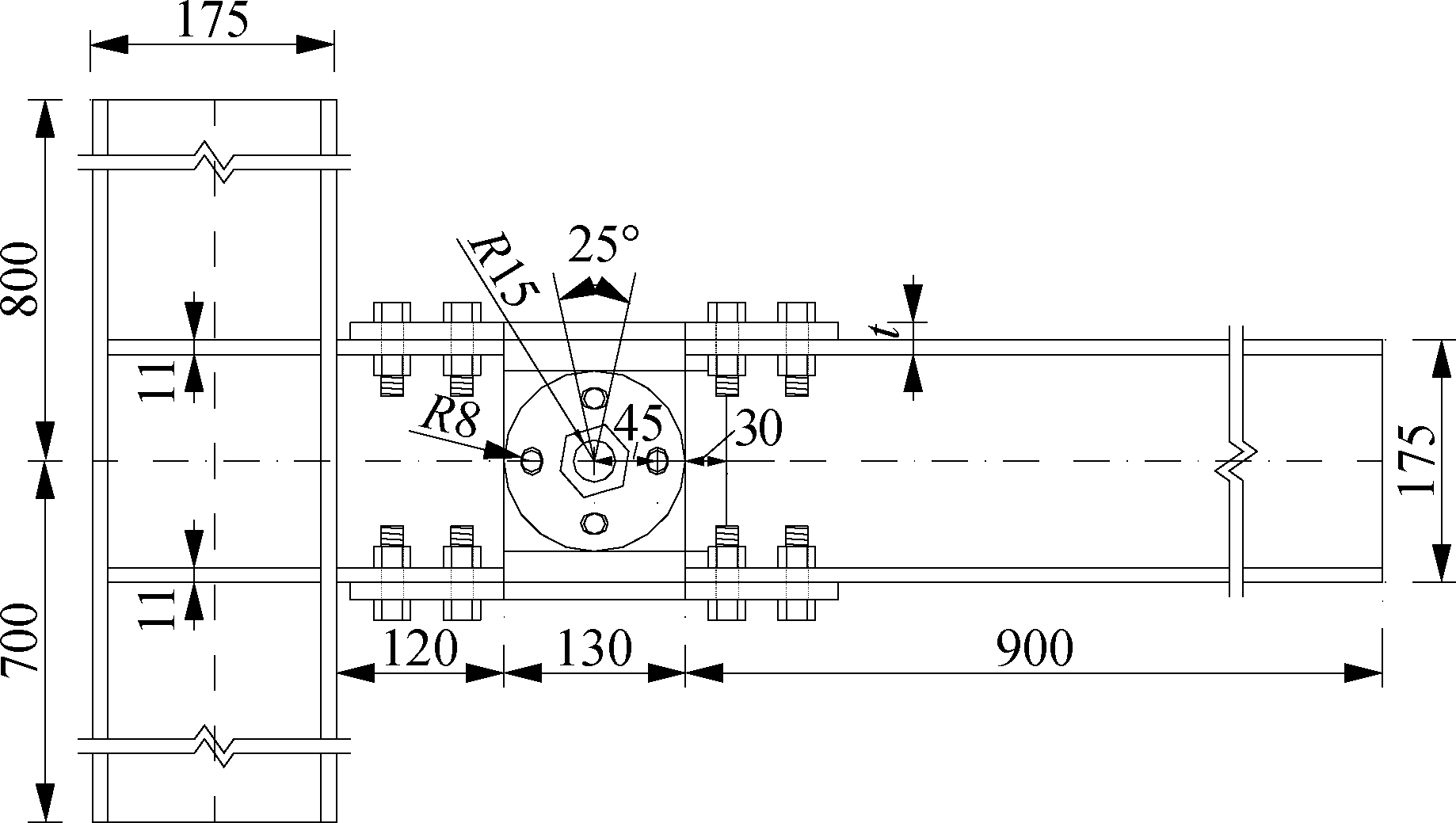
The new weakened node is part of a replaceable spliced plate beam end, which is composed of three parts: the basic unit, the energy consumption unit, and the rotating unit. The structure of the node is shown in Fig.1. The basic unit is composed of H-shaped steel beams and steel columns. The steel beams are divided into short and long beams. The energy dissipation unit refers to the upper and lower dog-bone shaped splicing plates connected to the beam flanges. The splicing plates are arc-shaped weakened plates. The depth was designed to ensure that the first yield section in the test occurs at the deepest weakened position. The rotating unit is composed of single and double connecting plates, which are arranged with rotating bolt holes and limiting bolt holes. Furthermore, the single connecting plate is arranged with circular limiting holes. The double connecting plates are arranged with arc-shaped limiting holes. The single connecting plate is welded to the short beam by double-sided fillet welds, and the double connecting plates are welded to both sides of the web of the long beam through fillet welds. In the initial test process, the test results did not achieve the expected energy consumption effect due to the slippage of the new joints, when the plastic rotation angle reached 0.03 rad. Therefore, in the subsequent improvement test process, the role of the limit bolt was not considered, and whether the beam-column weld will undergo brittle failure when the node yields and consumes energy was observed.

Fig.1 Replaceable splice plate joint
1.2 Specimen design
The specimen design test provides a comparative analysis of the thickness and weakening depth of spliced plates. The parameters of the spliced plates are shown in Tab.1. Single and double connecting plates were connected with M30 high-strength bolts at the center to enable rotation under force. Four 16-mm-diameter holes were open on the single connecting plate around the center bolt, and the double connecting plates had elliptical holes. The size of the elliptical holes were fabricated according to specifications. The specified limit beam-column rotation angle was 0.03 rad[13]. Limit holes were used to limit the relative rotation angles of the beams and columns under earthquake conditions. The energy consumption plate was made of low-quality Q235B steel (steel with a yield strength greater than 235 MPa), and the other parts were made of Q345B steel(steel with a yield strength greater than 345 MPa). Some design parameters of the test piece are shown in Tab.1, and the detailed design of the test piece is shown in Fig.2.
Tab.1 Test part numbers and joint parameters

SpecimensSteel gradeSection size/(mm×mm×mm×mm)Length/mmt/mma/mmColumnQ345BH175×175×8×111500BeamsQ345BH175×175×8×11120,900M168.8S60M308.8S60SJ-1Q235B3501025SJ-2Q235B3501035SJ-3Q235B3501235SJ-4Q235B3501245
(a)
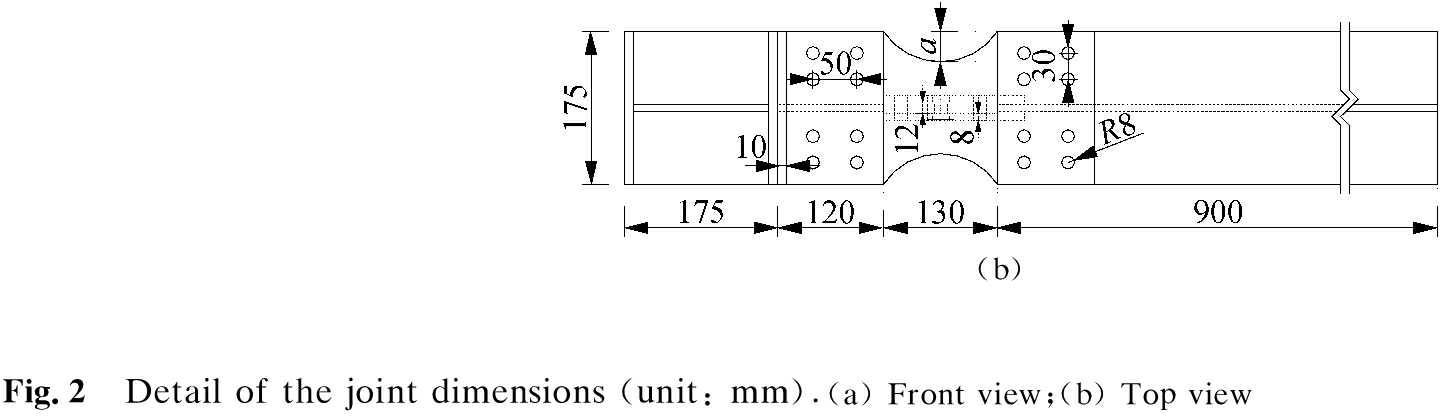
The bolts connecting the energy-dissipating plate and beam flange were grade 8.8 M16 high-strength bolts. The energy-consuming steel plate was made of Q235B steel,whereas the other members, such as the beams and columns, were made of Q345B steel. During the test, no significant deformation was observed in the beams and columns, and the bolt holes did not produce evident extrusion and expansion. Thus, only the energy-dissipating plate and M16 bolts were replaced for each group of tests. The M16 bolts were replaced to ensure that the new set of tests did not cause large slippage prematurely due to the bending and deformation of the bolts.
1.3 Experiment method
The new node test used a pseudo-static loading method. The power unit included a 25 t actuator and a 50 t hydraulic jack. A 25 t actuator was used to provide a loading power for the free end of the beam. A hydraulic jack was placed at the end of the column to provide axial pressure to the end of the column, and a pressure sensor was placed between the end of the column and the hydraulic jack to measure the axial pressure at the end of the column. Before starting the test, a hydraulic jack was used to provide a preload to the column end. The preload was equivalent to approximately 175 kN of axial force at 40% of the full-section yield pressure of the column. The free end of the steel beam was connected to a 25 t actuator through a connecting member. Excessive stress on the beam end was avoided to prevent it from affecting the test results. The connecting member was connected to the actuator in the form of an articulation, which could reduce the change in the loading position of the beam end under a large loading displacement.
1.3.1 Material test
Following GB/T 2975—1998, which determines the locations and test sample preparation of the test pieces for mechanical testing, we tested the flange of the 11 mm steel beam and the web of the 7.5 mm steel beam, and the dog-bone-shaped steel plate samples were tested with 9.5-mm-thick and 11.5-mm-thick splicing plates. For these samples, the energy-consuming plate was selected from the same batch of steel plates, and the beam and column cross-section dimensions were the same. Only the beam flange and web properties varied. The sample size is shown in Fig.3, and the results of the material property tests are shown in Tab.2.
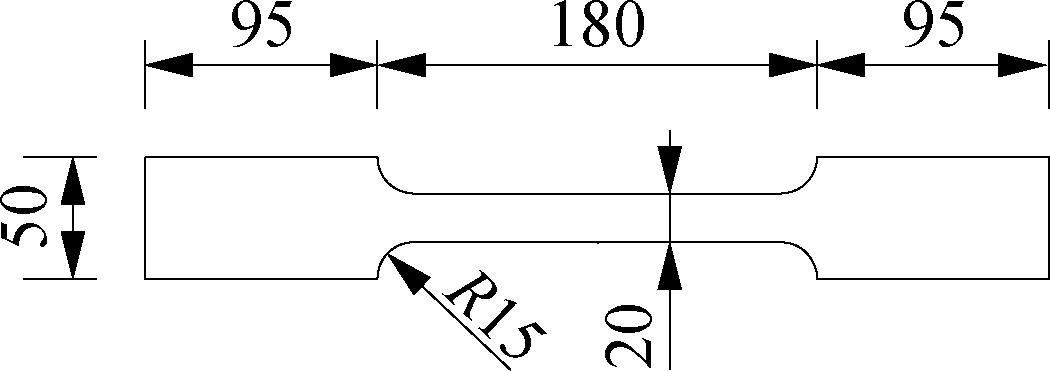
Fig.3 Detailed sample size (unit: mm)
Tab.2 Material properties of plates

Thickness/mmSteel gradeQuantityE/GPafy/MPaεy/%fu/MPaεu/%9.5Q235B3209260.660.16376.608.8411.5Q235B3202285.780.18436.0716.6511.5Q345B3176373.420.33578.7813.697.5Q345B3190378.510.29561.6316.50
1.3.2 Loading device
Loading tests were performed in the Key Laboratory of Earthquake Disaster Reduction in Civil Engineering at Lanzhou University of Technology. The test loading device is shown in Fig.4. A total of four beam-fixing members were used. Two limiting end beams limited the horizontal displacement of the beam to limit the vertical displacement of the column. A hydraulic jack provided an axial force at the horizontal end of the column. A pressure sensor was arranged between the hydraulic jack and column. The pressure sensor was used to measure the axial force at the end of the column in real time. The beam end was provided with horizontal thrust by the actuator to deform the joint. The actual distance between the center position where the steel beam was loaded and the beam-column weld was 930 mm.
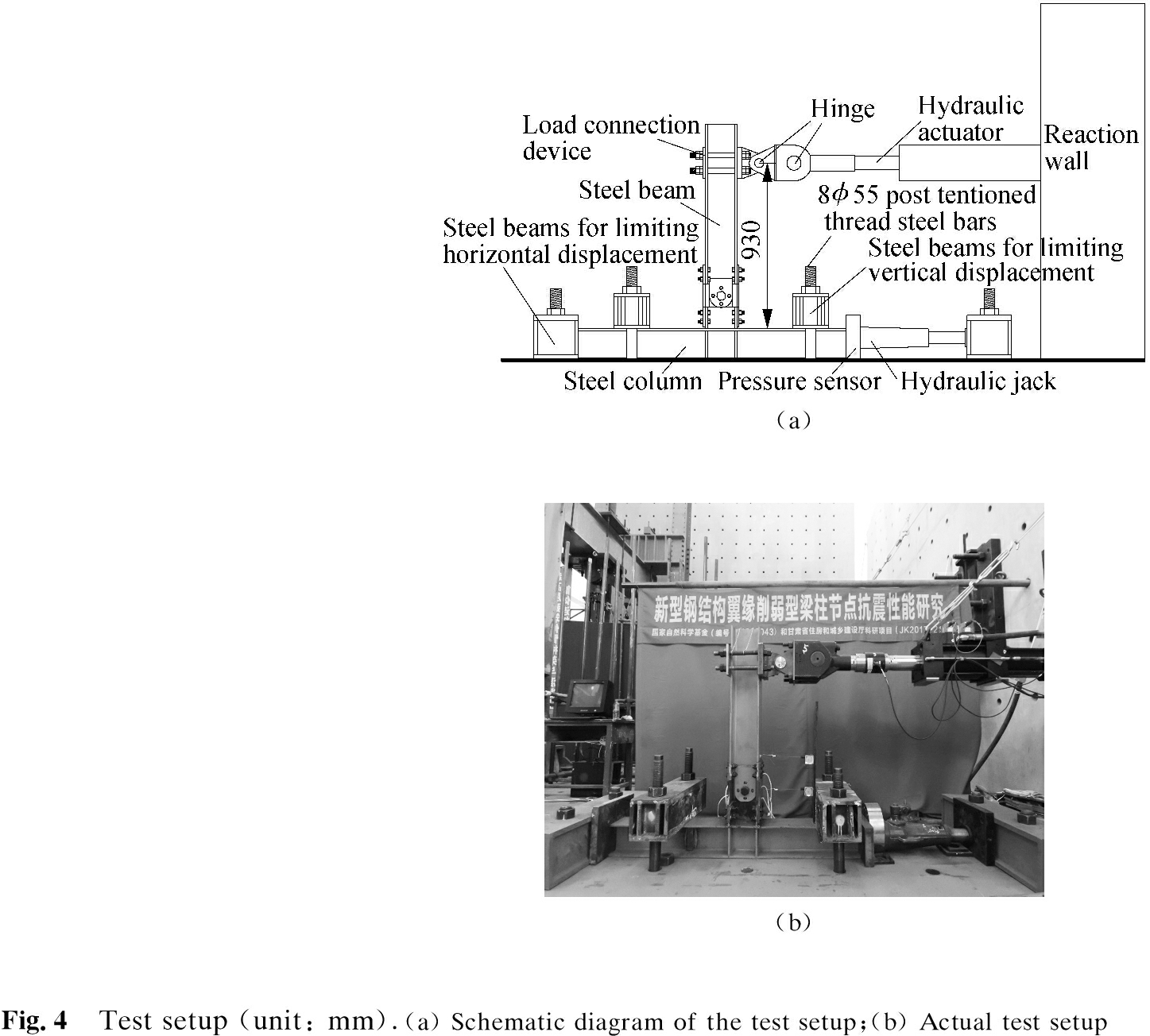
1.3.3 Loading system
The test loading system used a displacement loading method, and the yield displacement was first determined to be approximately 15 mm using the finite element software ABAQUS. The yield displacement refers to the corresponding loading displacement when any element of the splicing plate reaches the yield, and the yield displacement loading test was divided into three stages, i.e., 5, 10, and 15 mm, which were less than the yield displacement. Then, each stage was cycled twice. The load displacements after the yield displacements were 30, 45, 60, 75, 90, and 105 mm, and three displacement cycles were applied. The test was ended when a component failure occurred, e.g., cracking of the weld seam or tearing of bolt holes. The bearing capacity was reduced to less than 85% of the ultimate load or the maximum loading displacement of the actuator was reached. The loading displacement is shown in Fig.5.

Fig.5 Loading system
1.3.4 Measurement program
A pressure sensor (see Fig.4(a)) was arranged at the column end of the test piece to measure the axial pressure at the column end. A wire displacement meter was placed at the splicing location of the beam, at the energy dissipation plate, and at the center of the energy dissipation plate. To determine the changes in the stress and strain at the beam end weld and at the energy dissipation plate with the loading displacement, strain gauges were respectively arranged at the beam end weld and the energy dissipation plate. The arrangements of the measuring points for the strain gauges(S1 to S11) and the wire displacements (D1 and D2) are shown in Fig.6.
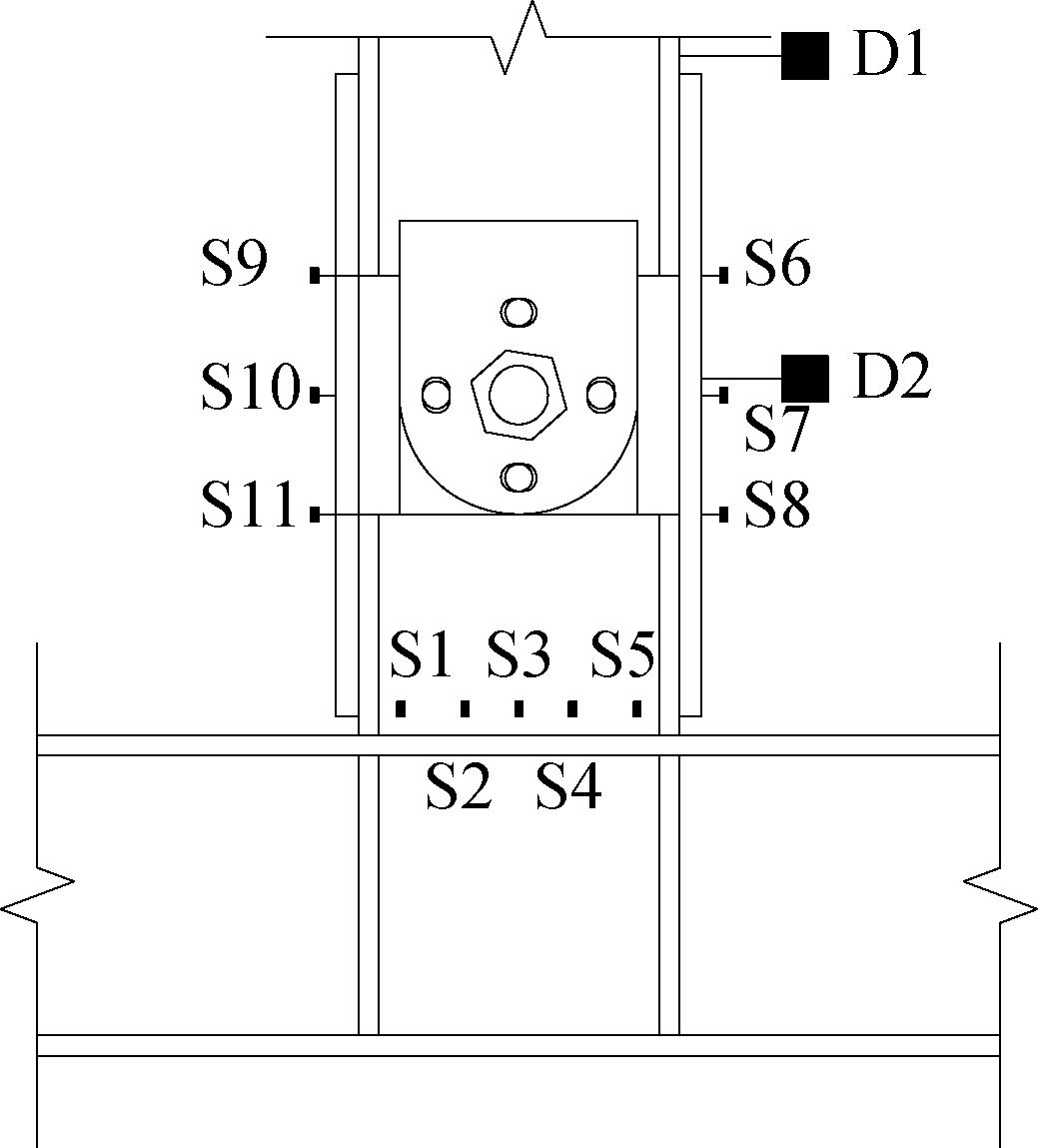
Fig.6 Measuring point layout
2 Results and Discussions
2.1 Destruction phenomenon
The test was performed four times, and the energy-consuming plate was replaced for each test. During the tests, there were gaps between the bolts and bolt holes connecting the energy-consuming plate to the beam, which caused slippage from the beginning of the test. The tests showed that the relative slip between the energy-consuming plate and the flange of the steel beam was 2.5 mm.
For sample SJ-1(t=10 mm, a=25 mm, see Tab.1), there was no evident buckling of the energy dissipation plate before the load displacement reached 75 mm, and a gap caused by the warpage of less than 1 mm appeared on the compression side(refers to the test process; each splice plate specimen under pressure is called the compression side, when under tensile force it is called the tensile side). Moreover, due to warpage, the skeleton curve did not have a significant yield point. When the displacement reached 90 mm in the first cycle, a peak load of 98 kN appeared, and no buckling of the left energy-dissipating plate was evident. The right energy-dissipating plate showed more severe buckling in the subsequent loading cycle, and no buckling was evident on the left side at the end of the test. When the loading displacement was 105 mm, the bearing capacity of the node gradually decreased to 73 kN, and the test was completed. Before the loading displacement of SJ-2 (t=10 mm, a=35 mm, see Tab.1) reached 60 mm, the test piece did not break. The main source of the noise was the displacement of the connecting member at the joint between the beam end and actuator, which caused the sliding up and down along the beam. When the loading displacement reached 60 mm, the energy-dissipating plate on the tension side began to show a stretching phenomenon with a slight sound, and the bending of the energy-dissipating plate on the compression side was not evident. When the loading displacement reached 75 mm in the first cycle, the energy-dissipating plate on the compression side showed a significant bend, the tensile length of the tension side increased, and the bearing capacity increased. No significant decrease in the bearing capacity occurred during the three cycles of loading. With the first cycle load of 90 mm, severe buckling deformation occurred on the tension side, the strain gauge near the center of the energy dissipation plate fell off, and the joint between the energy dissipation plate and beam warped. The bolts also became loose. With the second cycle load of 90 mm, the bearing capacity decreased and was lower than 85% of the peak value. At this time, the test ended.
For sample SJ-3 (t=12 mm, a=35 mm, see Tab.1), due to the small weakening depth and large thickness of the energy-dissipating plate, SJ-3 shows a more obvious slip phenomenon when the loading displacement reached 60 mm, and the buckling of the energy dissipation plate occurred during the first cycle load of 90 mm. At this time, left and right energy-dissipating plates slightly buckled, and the peak load reached 98 kN. A significant buckling phenomenon occurred in the first cycle load of 105 mm. The stress damage reduced the bearing capacity to less than 85% or 80 kN. Before the loading displacement of sample SJ-4(t=12 mm, a=45 mm, see Tab.1) reached 75 mm, the bearing capacity continued to increase as the loading displacement increased. During the first cycle of 75 mm, the left energy-dissipating plate buckled, and the center strain gauge of the left energy-dissipating plate fell off. During the first cycle of 90 mm, the buckling deformation of the energy-dissipating plate on the right also began. The test was ended because the bearing capacity dropped to less than 85% of the peak load. Fig.7 shows the buckling of the left and right energy-dissipating plates at the end of each test.

2.2 Hysteretic curves
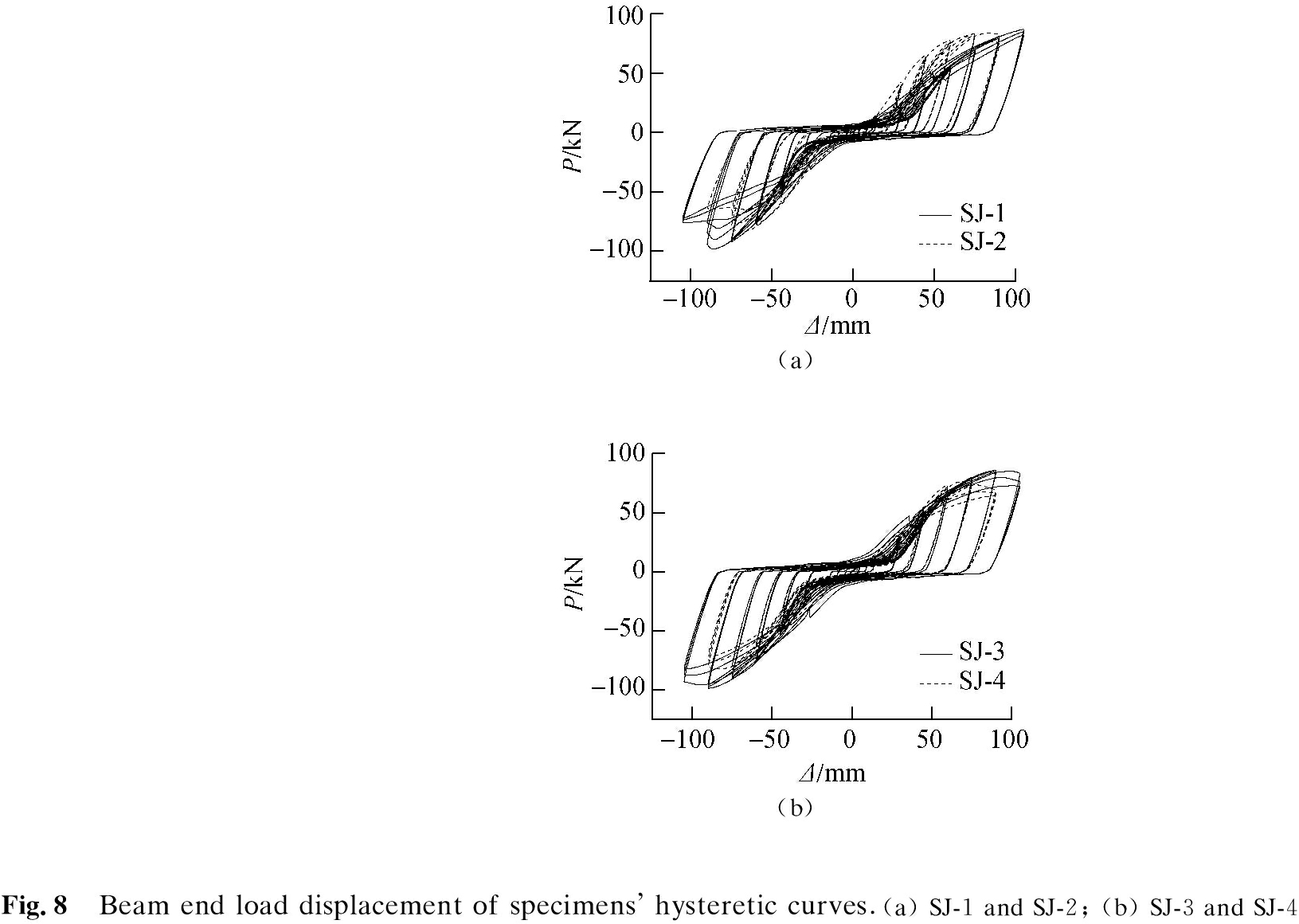
The load displacement (P-Δ) hysteresis curve of each specimen is shown in Fig.8. The hysteresis curves of the four groups of specimens similarly varied, and they all exhibited slip phenomena. The hysteresis curves were generally S-shaped. Samples SJ-1 and SJ-2 were compared. For the same loading displacement, SJ-2 exhibited a higher bearing capacity than SJ-1, mainly because SJ-2 weakened more than SJ-1, and the weakened section was more prone to plastic yielding. However, SJ-2 buckled more easily than SJ-1, causing the bearing capacity to decrease rapidly. Similarly, compared to SJ-3, SJ-4 had a higher bearing capacity under the same loading displacement, and the bearing capacity decreased more rapidly with the increasing loading displacement.
Strain gauges were arranged at the center of each set of splicing plates. SJ-1 and SJ-3 are taken as examples to analyze the strain curves of the splicing plate during loading (see Fig.9) and the strain at the weld (see Fig.10). The results of the strain curve in Fig.9 combined with the material properties in Tab.2 show that the splice plates of SJ-1 and SJ-3 both plastically yielded after the beam end loading displacement reached ± 45 mm, i.e., the strain reached 0.16%. The load-bearing capacity mainly depended on the plasticity development of the tension side splicing plate. At this time, the compression side-splicing plate was prone to buckling deformation after reaching the plastic stage, which would cause the compression side splicing plate to lose its bearing capacity. In Fig.9(a), the splicing plate where S10 is located did not show signs of buckling, and plastic development was not evident.

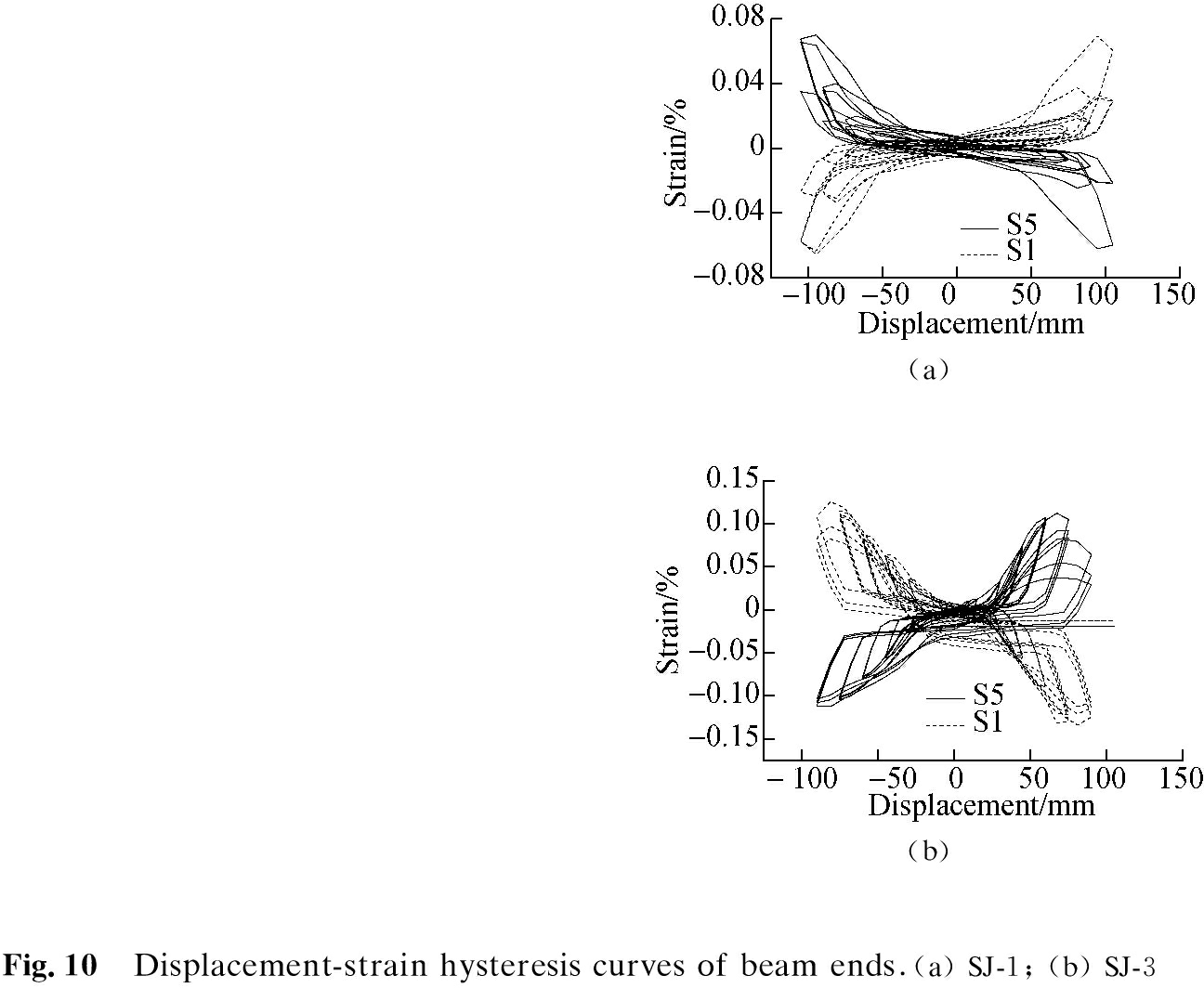
The results of the strain curve in Fig.10 combined with the results in Tab.2 show that the maximum strain at the beam-column weld was less than 0.3%, indicating that the stresses at this location during the loading of SJ-1 and SJ-3 were less than the yield stress. Thus, the beam-column internal force on the weld was less than the bearing capacity. In summary, when the yielding energy consumption of the splicing panel occurred, the cross-section of the beam-column weld was still in the elastic stage, which protected it and allowed the outward movement of the plastic hinge.
2.3 Skeleton curve
The skeleton curves of all the specimens were basically the same. Each curve was divided into an elastic phase, a slip phase, and an elastoplastic phase. At the beginning of loading, due to insufficient machining accuracy, only some bolts were subjected to shearing forces, and other bolts only provided a pre-tensioning force. The splicing plate was prone to elastic deformation. When the splicing plate was subjected to a certain force, sliding relative to the beam flange began. When the slippage reached its limit, all the splicing bolts bore the shear force together, the bearing capacity of the joints rapidly increased, and the splicing plate quickly reached the yield. Due to the influence of slippage factors, the skeleton curve has no evident yield point. The skeleton curves are shown in Fig.11. These curves indicate that after the peak load of all four groups of specimens, the bearing capacity rapidly decreased. The main reason was that when the displacement increased, the plastic strength of the energy-dissipating plate on the tension side decreased, and the bearing side lost its bearing capacity after severe buckling. The maximum bearing capacity was mainly related to the cross-sectional area of the weakened position of the energy-consuming plate. The larger the cross-sectional area was, the greater the peak load became. When the loading displacement was small, the energy-consuming plate did not buckle, and the energy-consuming plates on both sides bore the acting force simultaneously. When the energy-dissipating plate buckled, the bearing capacity of the tension side increased, and the local buckling load capacity of the compressed side decreased, which caused the reaction force of the node to increase slowly or even decrease. Compared with SJ-1 and SJ-2, the greater the weakening depth at the same thickness, the higher the bearing capacity in the early stage of loading. However,at the later loading stage, the SJ-2 bearing capacity decreased faster than that of SJ-1, mainly because the greater the weakening depth is, the more likely the splicing plate will buckle.

Fig.11 Skeleton curves
2.4 Loading capacity
The bearing capacity degradation refers to the index of the same displacement load gradually decreasing with the increase in the number of loading cycles, as described by the following bearing capacity degradation formula:
(1)
where ηj is the degradation factor of the bearing capacity for the j-th stage loading and p1,j and p1,j are the absolute maximum beam end loads for the first and i-th cycles during the j-th stage loading, respectively.
During testing, when the loading displacement was less than or equal to 15 mm, two cycles were applied for each stage. The maximum bearing capacity ratio of the second and first cycles of each stage of loading was selected as the degradation coefficient of the bearing capacity. When the loading was greater than 15 mm, three loading cycles were applied for each stage, and the ratio of the maximum bearing capacity of the second and first cycles of each stage of displacement loading was selected as the bearing capacity degradation coefficient. The bearing capacity degradation coefficient curve is shown in Fig.12. Before the absolute value of the loading displacement reached 75 mm, the fluctuation range of the bearing capacity degradation coefficient was mainly concentrated between 0.9 and 1.0. Fig.12 shows that the bearing capacity degradation is not evident. This was mainly due to the strain hardening of the steel. After the absolute value of the loading displacement reached 75 mm, the bearing capacity severely degraded due to the buckling deformation and large plastic deformation of the splicing plate.

Fig.12 Bearing capacity degradation curves
2.5 Stiffness degradation capacity
Stiffness degradation is an important index of the seismic energy consumption of a node. Stiffness reflects the ability of a node to resist elastoplastic deformation under cyclic loading conditions. Stiffness degradation represents the required load increase needed to reach the same peak load. The stiffness degradation curve in Fig.13 first decreases, then increases, and finally decreases again. The appearance of this type of curve is mainly related to the energy consumption mechanism of the new type of weakened joint at the beam end. The first stage of stiffness degradation was mainly due to the increase in the number of loading cycles. Then, the preload force of the splicing plate bolts decreased, the friction force decreased, and the stiffness decreased accordingly. The second stage corresponded to the rapid elastic deformation of the splicing plate after slipping. The rigidity increased in the third stage. At the third stage, the loading displacement reached ±45 mm. With the increase in the plastic deformation of the tension side splice plate and the buckling deformation of the compression side splice plate, the stiffness began to decrease again.
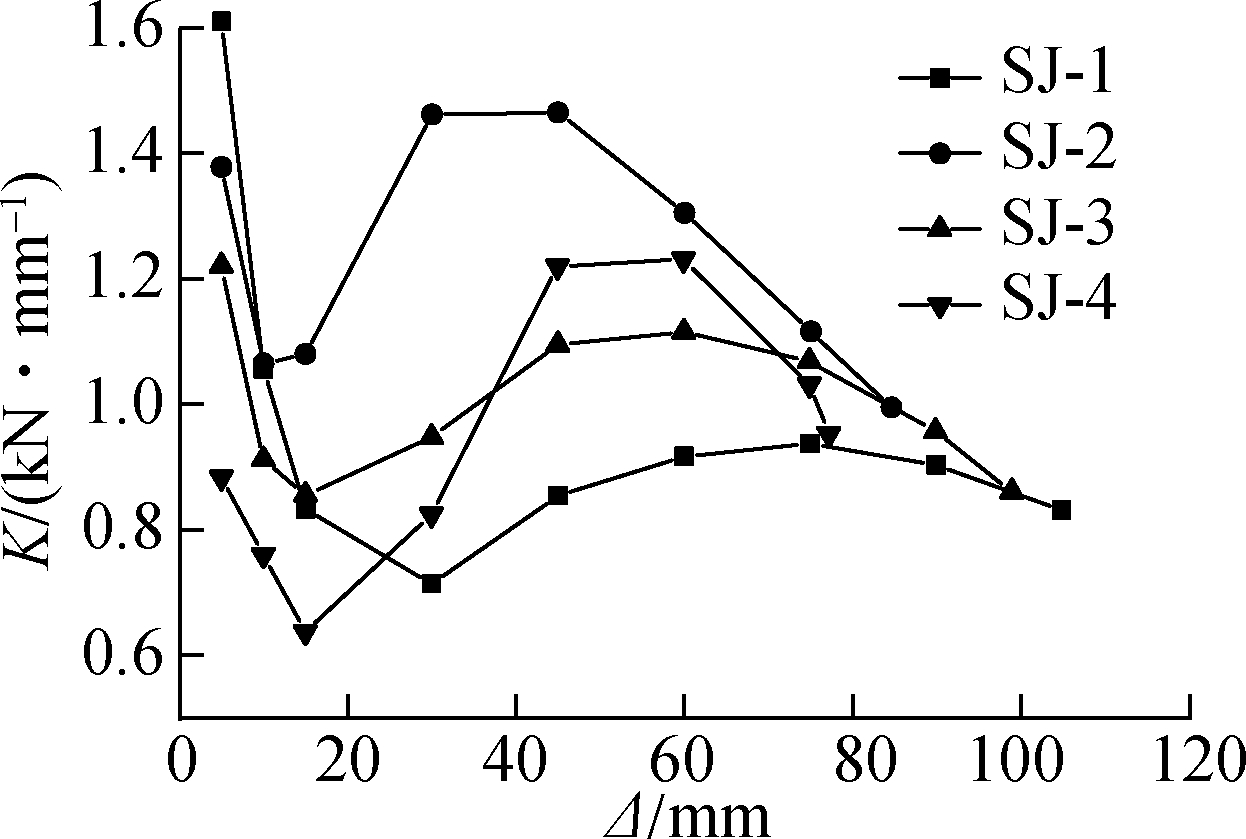
Fig.13 Stiffness degradation curves
2.6 Ductility and energy dissipation
Ductility is an important indicator of earthquake resistance in building structures. Generally, the ductility coefficient should be greater than 3.0 to meet the design requirements. The skeleton curves show that the new fabricated beam end weakened joint had long elastic and slipping phases. When the loading position was greater than 45 mm, the energy-dissipating plate yielded and consumed energy. Plasticity did not easily develop due to the buckling, which eventually led to a small ductility coefficient. In the pseudo-static tests, the actuator was extended in the positive direction (PD) and contracted in the negative direction (ND). Tab.3 shows the peak load Pm, failure load P0.85, yield displacement Δy, and displacement Δu corresponding to the failure load and displacement ductility coefficient μ=Δu/Δy. The absolute value of the yield displacement was 45 mm, which was obtained based on the data collected from strain gauges S7 and S10 on the splicing plate. The ductility coefficient results in Tab.3 show that the weakening of the splicing plate caused the bearing capacity to decrease faster, and the ductility coefficient decreased accordingly. In this test, the effect of the thickness of the splicing plate on the ductility coefficient was not evident.
Tab.3 Ductility coefficients of the quasi-static tests

SpecimensPm/kNPDNDP0.85/kNPDNDΔu/mmPDNDΔy/mmPDNDμPDNDSJ-187.16-98.1682.32-72.56104.67-105.0045-452.332.33SJ-284.17-84.1671.45-64.6290.09-89.9545-452.022.00SJ-385.96-99.0371.93-82.88104.94-105.0045-452.332.33SJ-477.20-82.6563.59-71.8890.04-89.9545-452.022.00
The new node exhibited a significant slip phenomenon, which also resulted in a small energy consumption capacity in the early stage. When the absolute value of the load displacement was less than 45 mm, the main energy consumption mode was friction energy consumption. After the absolute value of the load displacement was 45 mm or more, the energy consumption capacity gradually increased. The total energy consumption capacity is shown in Fig.14. The energy consumption curve shows that SJ-3 had the largest energy consumption capacity.The main reason was that the thickness of the splicing plate was larger than that of SJ-1 and SJ-2, and the weakened joint depth was smaller than that of SJ-4. Thus, SJ-3 could maintain sufficient rigidity and strength. Therefore, increasing the weakening depth could make the splicing plate more prone to buckling, and increasing the thickness of the panel delayed the occurrence of panel buckling. Thus, reducing the weakened joint depth and increasing the thickness would effectively improve the ductility of the joint and the energy consumption.

Fig.14 Accumulated energy dissipation-loading history curves
3 Theoretical Analysis
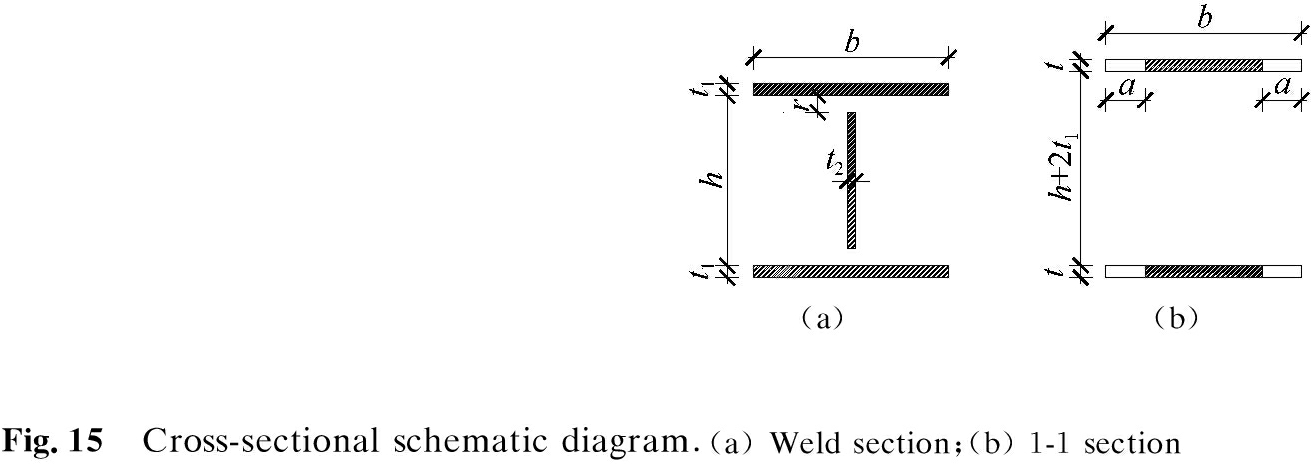
At present, many forms of steel structural beams and columns are rigidly welded. These components use butt welding with full penetration of flanges and webs. A schematic diagram of the weld is shown in Fig.15(a). The flange was not subjected to shear forces, and the shear stress distribution on the web was uniform. The formula for calculating the shear stress is as follows:
(2)
where τf is the shear stress of the weld at the web position; r is the size of the craft hole (holes reserved to prevent the intersection of the two welds); h is the height of the web; t2 is the thickness of the weld at the web; and F is the concentrated force acting on the load point at the beam end.
The weld at the web position was subjected to the combined effects of normal and shear stresses. The Von Mises yield criterion formula is defined as follows:
(3)
Therefore,
(4)
where σf is the normal stress of the weld at the web and σ1 is the yield strength of the weld at the web. Due to the poor plasticity of the weld, which is prone to brittle failure, the tensile and compressive strength design value ![]() of the weld are often used instead, and 1.1 is the strength design value increase factor for calculating the reduced stress.
of the weld are often used instead, and 1.1 is the strength design value increase factor for calculating the reduced stress.
The flexural bearing capacity of the beam-column weld section is calculated as follows:
(5)
Substituting Eq.(4) into Eq.(5) yields
MRω=σ1(b-2t1)t1(h+t1)+
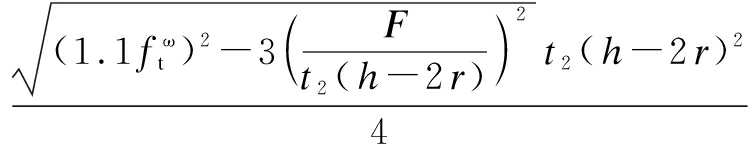
(6)
For section 1-1, it was assumed that the point on the section where the energy dissipation plate weakened the most reached the plastic deformation stage. The bending bearing capacity of the section in the plastic phase can be expressed as follows:
(7)
where t1 and b indicate the flange thickness and width of the beam, respectively, and the calculated thickness and length of the weld at the wing; MRω is the bending capacity of the weld section; MRr is the flexural bearing capacity of section 1-1; a is the weakened joint depth on one side of the splicing plate; t is the thickness of the splicing plate; σ2 is the yield strength of the splicing plate material; and γx1 and γx2 are the plastic development coefficients of the weld and 1-1 sections, respectively.
The weld was prone to brittle failure. Regardless of the plastic development, it was assumed that γx1=1, the energy-dissipating plate was separated from the web in section 1-1, and γx2=1. To weaken the section before the weld section yielded, the following criteria must be met:
γx1MRω=Mω
(8)
γx2MRr<Mr
(9)
where Mω is the bending moment on the weld section and Mr is the bending moment at section 1-1.
When the concentrated force F on the beam reached a certain value, section 1-1 began to yield, but the beam-column joint weld section had not yet begun to yield. Thus, this condition can ensure the safety of the weld and protect the beam-column joint.
4 Conclusions
1) During the test loading process, the beam-column joint welds were not broken, and the plastic deformation mainly occurred at the weakened position of the splice plate, which achieved the design goal of the plastic hinge moving outward and protecting the beam-column joint welds.
2) As the thickness of the splicing plate increases, the energy dissipation capacity of the joint can be increased, and the occurrence of buckling of the splicing plate on the compression side can be delayed. The increased depth of the splicing plate will increase the plastic deformation capacity of the splicing plate, but the ultimate bearing capacity drops.
3) During the loading process, the spliced plate first undergoes obvious plastic deformation. Then, the buckling phenomenon gradually becomes more obvious as the loading displacement increases. The machining error of the test pieces and the loss of the bolt pre-tightening force cause the obvious slippage of the splicing plate. Relative slippage occurs between the splice plate and the beam flange, resulting in a low initial rotational stiffness of the joint, which is not conducive to the control of the displacement angle between floors in a steel frame building.
4) Due to the influence of the splice plate slip, the hysteresis curve has an overall S shape, and the ductility coefficient value of the node is less than 3.0, indicating that the node cannot fully exert the plastic energy dissipation capacity during the earthquake resistance process, and the energy dissipation capacity is weak.
[1]Yu H R, Li W B, Cheng W J, et al. Experimental study on behaviors of steel frame beam-column connections with initial weld cracks[J]. Journal of Southeast University(Natural Science Edition), 2020, 50(3): 409-416. DOI:10.3969/j. issn. 1001-0505.2020.03.001.(in Chinese)
[2]Wang Y, Ma Q Q, Yang S S. Mechanical properties of beam-column connection joints using inner sleeve composite bolts in fabricated steel structure[J]. Journal of Tianjin University: Science and Technology, 2016, 49(S1): 73-79. DOI:10.11784/tdxbz.(in Chinese)
[3]Dong J L, Wang Y, Zhuang P, et al. Experimental study on seismic behaviors of steel frames with Haunch Reinforced Section Connections[J]. China Civil Engineering Journal,2016,49(1):69-79. DOI:10.15951/j.tmgcxb.2016.01.009.(in Chinese)
[4]Liu X C, Xu A X, Zhang A L, et al. Static and seismic experiment for welded joints in modularized prefabricated steel structure[J]. Journal of Constructional Steel Research, 2015, 112: 183-195. DOI: 10.1016/j.jcsr.2015.05.003.
[5]Liu X C, Yang Z W, Wang H X, et al. Seismic performance of H-section beam to HSS column connection in prefabricated structures[J]. Journal of Constructional Steel Research, 2017, 138: 1-16. DOI: 10.1016/j.jcsr.2017.06.029.
[6]Liu X C, Zhan X X, Pu S H, et al. Seismic performance study on slipping bolted truss-to-column connections in modularized prefabricated steel structures[J]. Engineering Structures, 2018, 163:241-254. DOI: 10.1016/j.en gstruct.2018.02.043.
[7]Bu Y D, Wang Y Q, Zhao Y P. Study of stainless steel bolted extended end-plate joints under seismic loading[J]. Thin Walled Structures, 2019, 144: 106255. DOI:10.1016/j.tws.2019.106255.
[8]Shi Q, Yan S L, Kong L L, et al. Seismic behavior of semi-rigid steel joints—Major axis T-stub and minor axis end-plate[J]. Journal of Constructional Steel Research, 2019, 159: 476-492. DOI: 10.1016/j.jcsr.2019.04.036.
[9]Yang S S, Wang Y, Ma Q Q. Experimental study on seismic behavior of prefabricated outer sleeve-overhang plate joint between column and beam[J]. China Civil Engineering Journal, 2017,50(11):76-86. DOI: 10.15951/j.tmgcxb.2017.11.008.(in Chinese)
[10]Zhang A L, Wang Q, Jiang Z Q, et al. Experimental study of earthquake-resilient prefabricated steel beam-column joints with different connection forms[J]. Engineering Structures,2019, 187: 299-313. DOI: 10.1016/j.engstruct.2019.02.071.
[11]Wang Y Q, Qiao X L, Jia L G, et al. Experimental research on seismic behavior of stainless steel beam-column connections with different link modes[J]. Journal of Southeast University(Natural Science Edition), 2018, 48(2):316-322. DOI:10.3969/j. issn. 1001-0505.2018.02.020.(in Chinese)
[12]Li X D, Wang Q T, Ma G T. Mechanical properties of a novel plastic hinge seismic fuse based on frictional energy dissipation to avoid brittle failures in beam-to-column moment-resistant joints[J].Arabian Journal for Science and Engineering, 2020, 45(5): 3695-3706. DOI:10.1007/s13369-019-04214-w.
[13]Hamburge R O, Hooper J D, Sabol T, et al. Recommended seismic design criteria for new steel moment-frame buildings[EB/OL].(2000-01)[2020-09-30]. https://www.researchgate.net/publication/242586370_Recommended_Seismic_Design_Criteria_for_New_Steel_Moment-Frame_Buildings.