With the promotion of digitalization, networking, and intelligent technology, modern war has presented a systematic development trend, which leads to the paradigm of equipment development changes from weapon plat form centric to system of systems (SoS) centric[1]. Hence, the contribution rate of weapons to equipment SoS, as an important basis for equipment development and weapon allocation scheme selection[2], should be evaluated.
At present, considerable research has been done on the SoS contribution rate, which mainly focuses on the following aspects: Firstly, the basic concept of the SoS contribution rate was analyzed one-sidedly, only taking the SoS combat capability into account without considering other attributes of the SoS. Secondly, the evaluation process of the SoS contribution rate[3-4] only included combat opponents and combat capability, without considering other constraints, such as other evaluation conditions and perspectives. Thirdly, as regards the evaluation method of the SoS contribution rate[5-7], the definition and calculation formula of the SoS contribution rate were presented from the perspective of SoS effectiveness[8]. The evaluation model and steps of equipment SoS contribution rate based on a rough set were proposed[9]. The equipment SoS contribution rate evaluation method based on evidence reasoning was also proposed after building multi-perspective and multi-level evaluation indicators[10]. The advantages and disadvantages of four measurement methods of the SoS contribution rate were compared[11].
The above studies on the SoS contribution rate made some achievements, but the following shortcomings were encountered: 1) A simple definition of the SoS contribution rate is given. 2) The unreasonable situation of the SoS contribution rate calculation formula is not considered. 3) The evaluation process is not systematic and comprehensive, specifically under a certain condition or perspective to simply evaluate the contribution rate. 4) The evaluation model and method do not consider the interaction between variables, so the calculated contribution rate value is not accurate enough.
In view of the problems existing in the above-mentioned studies, a method based on the structural equation model (SEM) was proposed to evaluate the equipment SoS contribution rate during wartime.
1 Redefinition of the contribution rate
1.1 SoS contribution rate
To study the concept of the equipment SoS contribution rate, four issues should be clarified: 1) evaluation object, that is, the equipment as the contributor; 2) evaluation background, that is, the SoS as the contributed objects; 3) evaluation conditions, under which conditions the contribution is generated; and 4) evaluation perspective, from which perspective the contribution is evaluated.
Firstly, the evaluation object refers to the equipment to be evaluated, the concept of which has basically reached a consensus.
Secondly, the evaluation background refers to the SoS to be evaluated, which can be divided into two categories: The first category is called the peacetime equipment SoS, that is, a collection of all equipment types and models at a specific application background within a period of peacetime. It is determined by the application background of the SoS, focusing on the equipment strength and development planning, not specific combat missions. The second category is called the wartime equipment SoS, that is, a collection of all equipment types and models for specific combat missions. It is a subset of the peacetime equipment SoS, corresponding to specific combat missions.
Finally, the evaluation perspectives will be different according to the evaluation background. If the evaluation background is the peacetime equipment SoS, then the SoS structure optimization, SoS capacity improvement, technological leap (improvement of the overall technical content of the equipment SoS), and efficiency improvement will generally be taken as evaluation perspectives. Nevertheless, if the wartime equipment SoS is used as the evaluation background, then the SoS optimization, SoS combat capability, SoS combat efficiency, and mission completion effects (mainly including the benefit, time, and cost of completing the mission) are generally taken as the evaluation perspectives.
On the basis of the above analysis, the definition of the equipment SoS contribution rate in peacetime and wartime is given. The peacetime equipment SoS contribution rate refers to the measurement of the contribution of certain equipment to a certain SoS in a non-war situation. The contribution includes optimizing the SoS structure and improving SoS capabilities, technology, and benefits. The wartime equipment SoS contribution rate refers to the measurement of the contribution of certain equipment to a certain SoS in the case of war. The contribution includes optimizing the SoS structure and improving SoS combat capabilities, combat efficiency, SoS compatibility, operation effect, and mission completion effect. The wartime equipment SoS contribution rate is regarded as the main research object.
1.2 New calculation formula of the SoS contribution rate
The original calculation formula of the SoS contribution rate is as follows:
(1)
where GH is the contribution rate of equipment H to SoS; J is the SoS attribute value (e.g., capability and effect); JinH is the SoS attribute value, including equipment H; and JexH is the SoS attribute value, excluding equipment H. Eq. (1) shows the ratio of the increment of the SoS attribute value to the original SoS attribute value, which excludes equipment H.
However, Eq. (1) has the following problems: Firstly, there is a lack of consideration of combat capability requirements. Combat capability requirements should be considered because if the SoS still cannot meet the combat capability requirements after the addition of equipment H, the significance of studying the contribution rate of equipment H to the SoS is not evident. For example, the nominal value of the reconnaissance range for landing combat is 300 km. The reconnaissance range when equipment H is not included in the SoS is 50 km, and the reconnaissance range when included is 250 km. Then, the contribution rate calculated according to Eq. (1) is 400%, which is large, but the SoS is still unable to meet the combat capability requirements. Hence, the contribution rate value in this case cannot reflect the true contribution of equipment H. Secondly, Eq.(1) does not apply to the case where the original SoS has blank attributes. For example, after adding the precision-guided weapon H to the SoS, the equipment SoS, which does not have the precision strike capability, produces the precision strike capability. Accordingly, the result of calculating the contribution rate using Eq. (1) tends to infinity and loses its reference significance.
To solve the above problems, a set of formula pairs for calculating the SoS contribution rate is proposed:
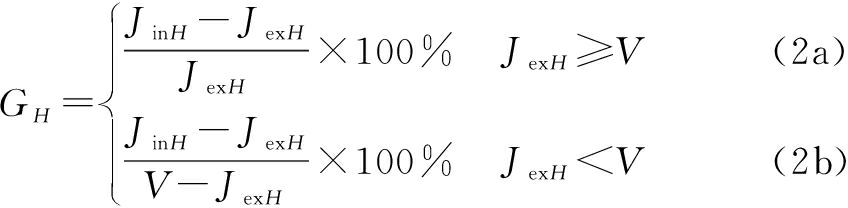
where V is the SoS attribute value when the SoS can only meet the combat capability requirements and V is the SoS attribute nominal value.
If the attribute value of the original SoS is greater than the SoS attribute nominal value, then Eq. (2a) will be applied. The calculated contribution rate value can reflect the degree of improvement of the attribute. This study examined this case just as an example.
If the attribute value of the original SoS is less than the nominal value of the SoS attribute or even blank (the value is 0), Eq. (2b) will be applied. At this time, if the calculated contribution rate value is less than 100%, then the SoS cannot always meet combat capability requirements after adding equipment H. If the contribution rate value is greater than or equal to 100%, then the SoS can meet the combat capability requirements after adding equipment H, and the equation still has practical significance in the case where the original SoS attribute value is blank.
2 Evaluation Process
The contribution rate of the wartime equipment SoS is not a single fixed value. Because different conditions, perspectives, and combat phases lead to different results, a multi-angle, multi-factor, and multi-stage comprehensive evaluation is needed. Fig. 1 shows a three-dimensional coordinate chart of the contribution rate of the wartime equipment SoS.
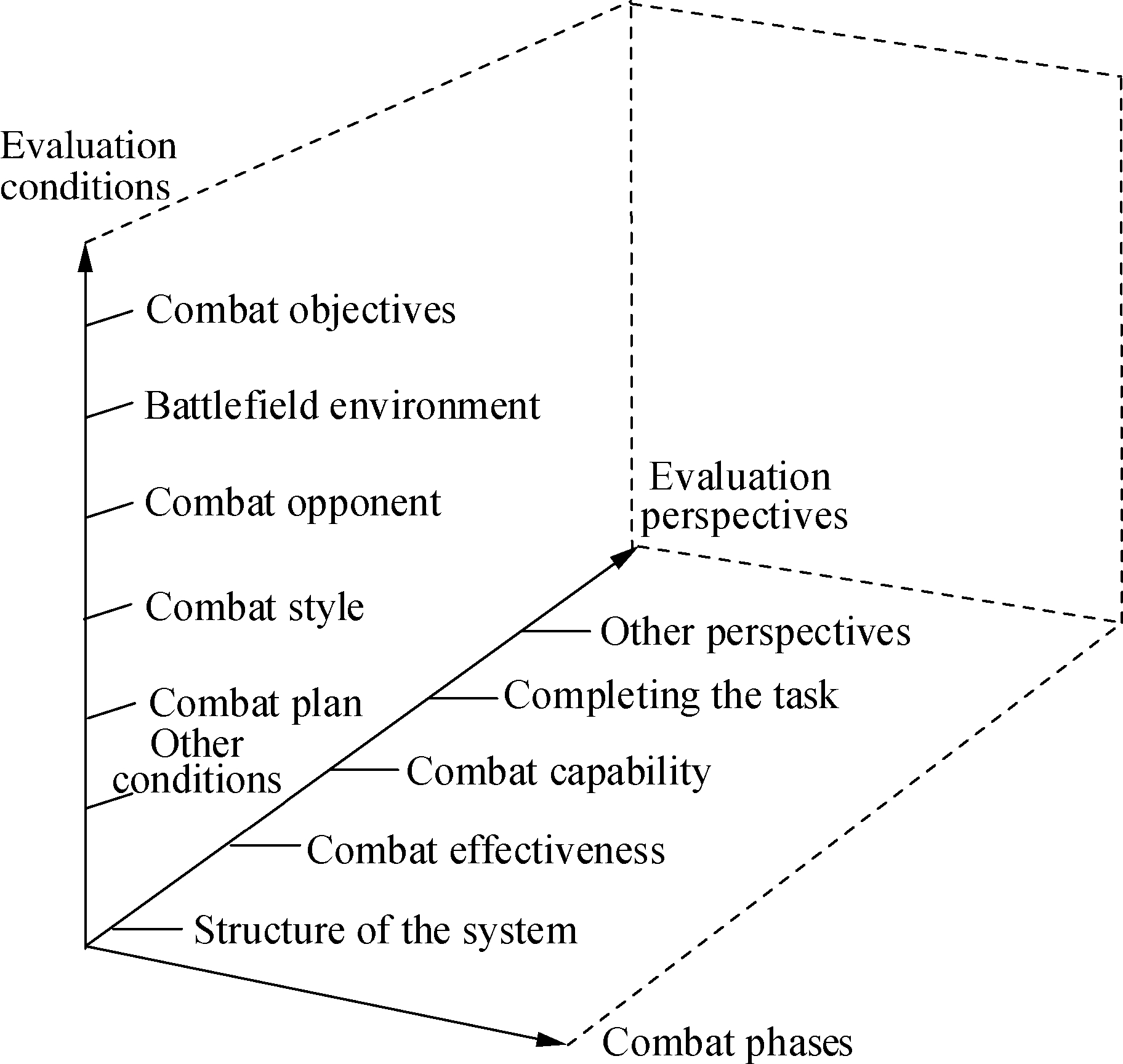
Fig.1 Three-dimensional coordinate diagram of the wartime equipment SoS contribution rate
2.1 Evaluation steps
The evaluation process of the wartime equipment SoS contribution rate is presented as follows:
1) Determine evaluation objects and goals. For example, the object is equipment H, and the goal is to evaluate the equipment H contribution rate to combat the efficiency of the Y equipment SoS.
2) Determine the evaluation background. To ensure that the SoS is a peacetime or wartime equipment SoS, the mission, capability, structural, and functional requirements are analyzed.
3) Determine the evaluation conditions. The evaluation conditions are mainly for the wartime equipment SoS, including the combat objectives, battlefield environment, combat opponents, combat styles, and combat plans.
4) Determine the evaluation perspective. The SoS contribution rate can be evaluated from single or multiple perspectives. The main evaluation perspectives include SoS capability, combat efficiency, SoS structure, and mission completion effect.
5) Build the evaluation indicator framework of the equipment SoS contribution rate. After comprehensively considering the analysis results of the preceding four aspects, the corresponding evaluation indicator framework is established.
6) Modeling and calculation. The data obtained from experiments, training, exercises, and expert research are used to perform calculations after modeling.
7) Present the evaluation results. The calculation results are discussed and analyzed, and then the targeted opinions and suggestions are given to assist in command decision-making.
2.2 Evaluation perspective and corresponding indicator framework
On the basis of completing the first three evaluation steps, it is necessary to determine from which perspective to evaluate the contribution rate. Accordingly, five perspectives are proposed, namely, structure, function (ability, effectiveness), operation, environment, and mission completion, as shown in Fig. 2. Each perspective evaluates the contribution rate through corresponding evaluation indicators. Fig.3 presents the evaluation indicator framework constructed for each evaluation perspective.
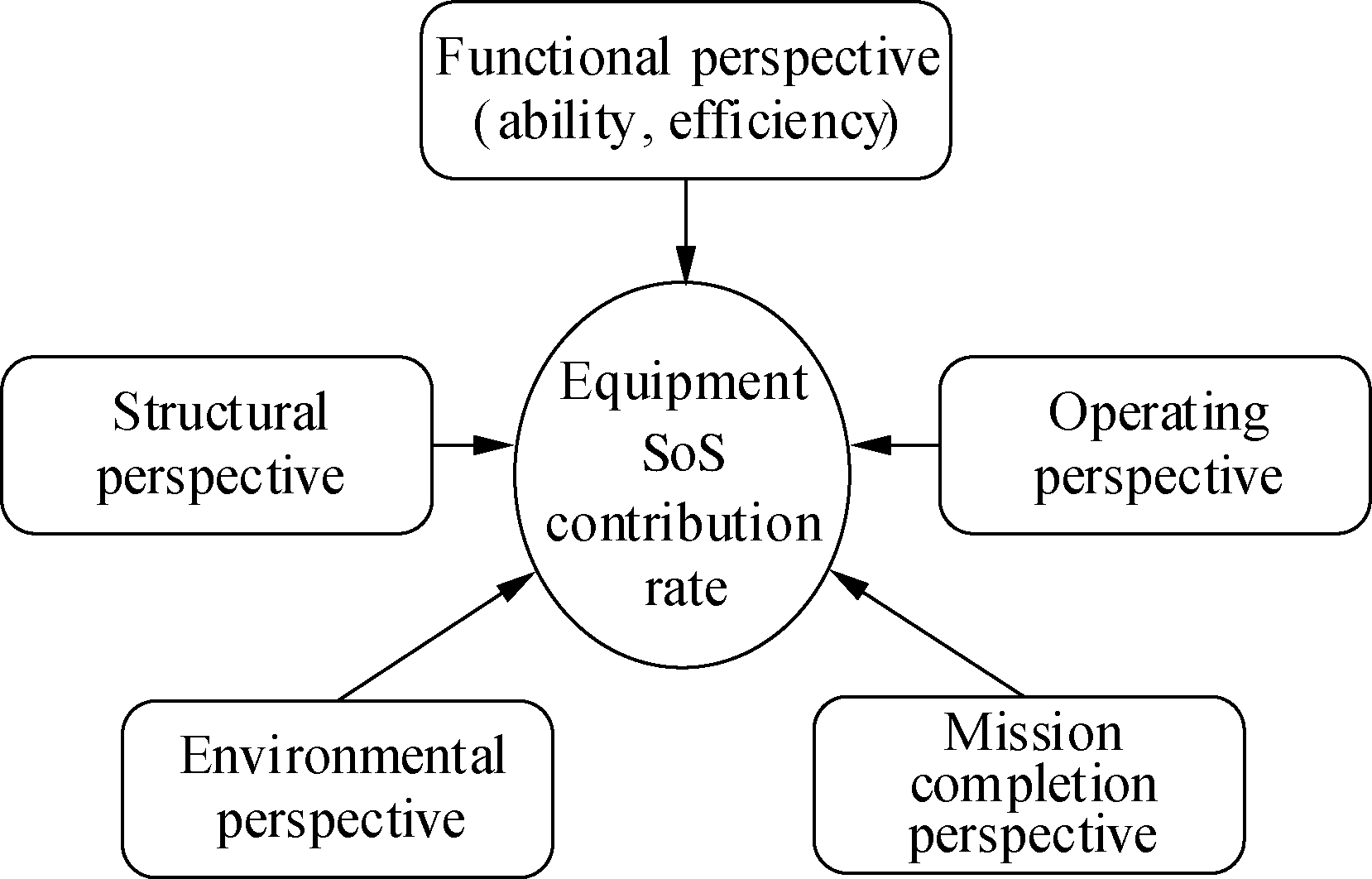
Fig.2 Evaluation perspective of the wartime equipment SoS contribution rate
The structure of the SoS encompasses the relationship and coupling between the equipment in the SoS. The wartime equipment SoS is composed of many kinds of equipment, and their relations and functions mainly include quantitative relations (e.g., proportion of combat, information, and support equipment), space-time relations, information connectivity relations, and combat coordination relations). The evaluation indicator framework of the SoS structure optimization contribution rate is shown in Fig. 3(a).
The structure determines the function, which is determined by the role and relationship of various equipment in the wartime equipment SoS. The function mainly includes combat ability and efficiency. Combat capability (static concept) refers to the ability of the equipment SoS to complete the combat mission. Combat efficiency (dynamic concept) refers to the effectiveness of achieving the combat object under the specific threat, environment, combat style, and combat plan. The evaluation indicator frame-Operation is the performance of the SoS behavior, which is the premise of function realization. After adding new equipment into the SoS, the changed structure will change operating modes, and the optimization of the operating modes will increase the efficiency of function realization. For example, after the early warning radar is incorporated into the equipment SoS for combat on the island, it can be combined with precision-guided weapons to achieve a more efficient and faster attack on the enemy. For another example, after adding the tactical data link into the border counterattack combat equipment SoS, the SoS synergy capability will be greatly improved. The evaluation indicator framework of the SoS operational effect contribution rate is shown in Fig. 3(d).
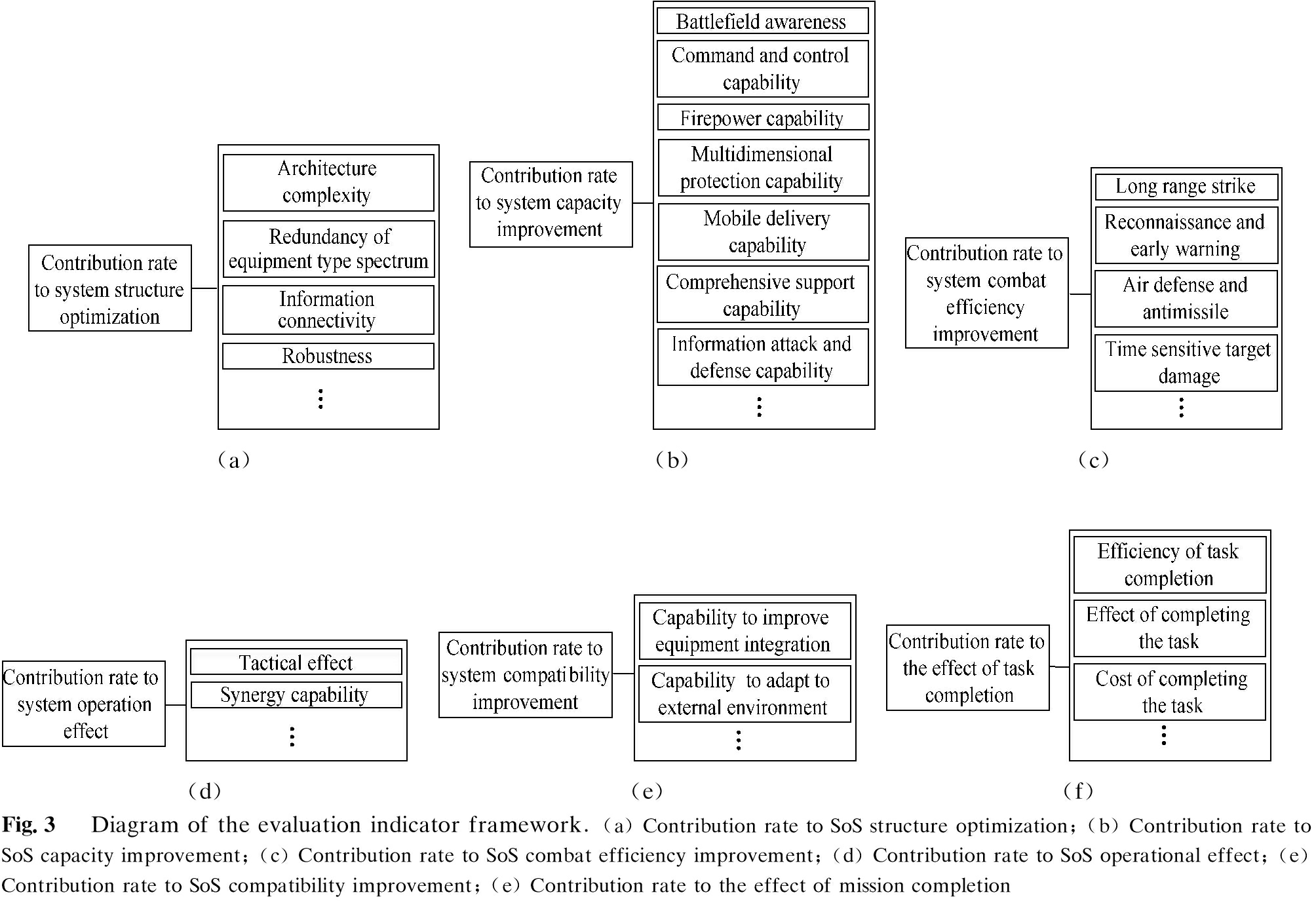
works of the SoS capacity and combat efficiency improvement contribution rate are shown in Figs. 3(b) and (c).
The environment is the sum of external factors, which restrict the operation of the SoS. The environment here is a broad concept, including external environments, such as operational threats, battlefield environments, and operational styles, and equipment-environment-personnel coupling. The evaluation indicator framework of the SoS compatibility improvement contribution rate is shown in Fig. 3(e).
Completing the mission is the ultimate goal of the wartime equipment SoS. The evaluation indicator framework of the contribution rate to the effect of task completion is shown in Fig. 3(f).
3 Evaluation Model
3.1 SEM of the fire interception capability evaluation
The firepower interception capability evaluation indicators and their relationships were obtained through the expert survey method in this section, as shown in Fig. 4. According to the evaluation indicators, the SEM of the firepower interception capability evaluation is established, as shown in Fig. 5, the explicit variable is represented by a square, and the latent variable is represented by an ellipse. X={x1, x2,…,x9} is the p×1-dimensional vector composed of exogenous explicit variables. Y={y1, y2, y3} is the q×1-dimensional vector composed of explicit endogenous variables. Δ={δ1, δ2,…,δ9} is the p×1-dimensional vector composed of error terms of X. ξ={ξ1, ξ2, ξ3} is the m×1-dimensional vector composed of exogenous latent variables. M and n are the numbers of the exogenous and endogenous latent variables, respectively. η is the n×1-dimensional vector composed of an endogenous latent variable, and ηi is the element of the matrix η. ζ is the n×1-dimensional vector composed of interpretation errors, representing the residual term of SEM, and ζi is the element of the matrix ζ. λ represents the relationship between the latent and explicit variables. φ represents the relationship between exogenous latent variables. γ is the parameter indicating the influence of the exogenous latent variables on the endogenous latent variables.
The corresponding relationship between the indicators in Fig. 4 and the variables in Fig. 5 is shown in Tab.1,which shows two categories of SEM variables: one category is the latent and explicit variables mentioned above, and the other category is the exogenous and endogenous variables. Exogenous variables refer to the variables that only affect other variables but are not affected by other variables; they are also called independent variables. Endogenous variables refer to variables represented or affected by other variables; they are also called dependent variables.
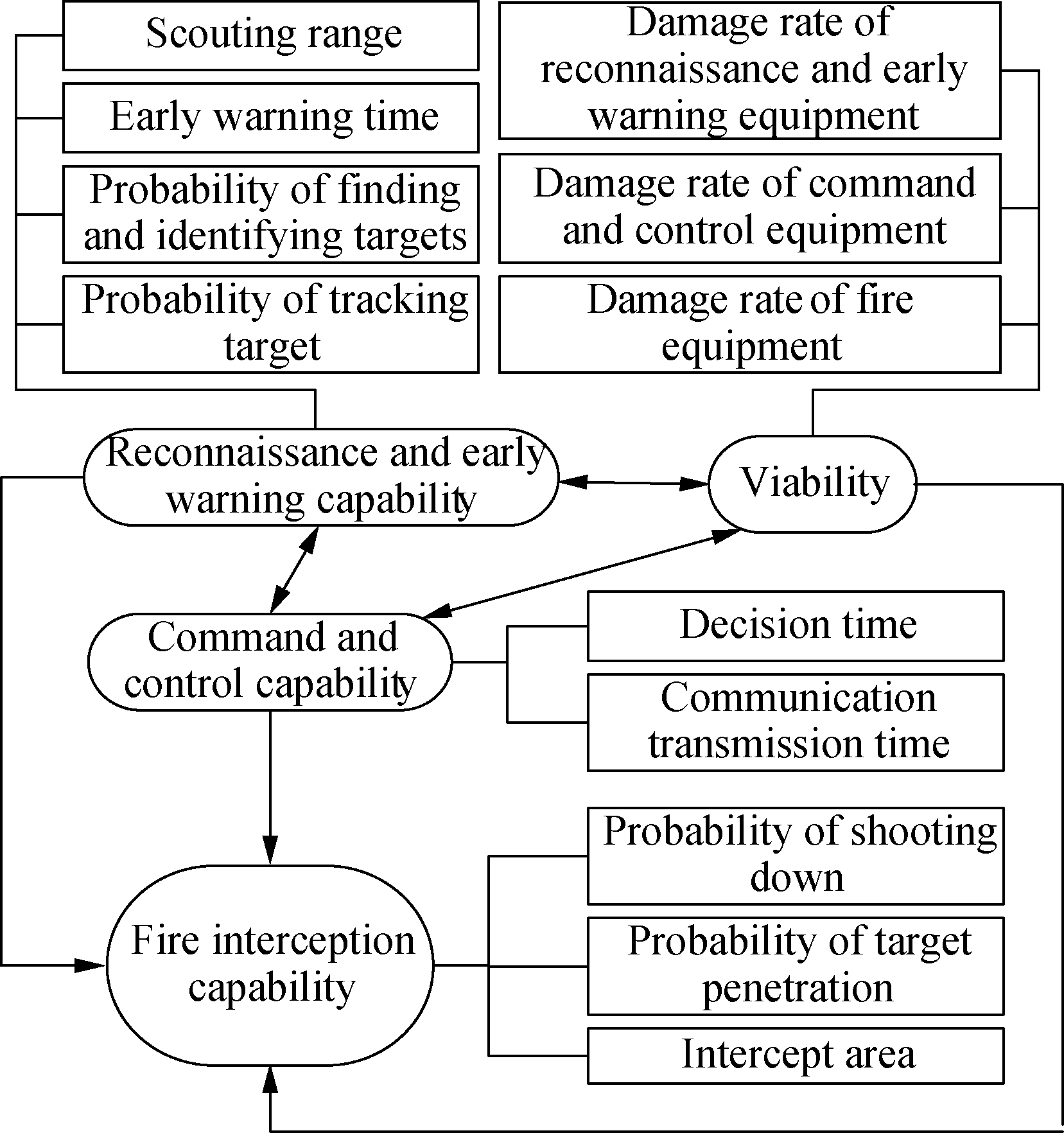
Fig.4 Firepower interception capability evaluation indicators
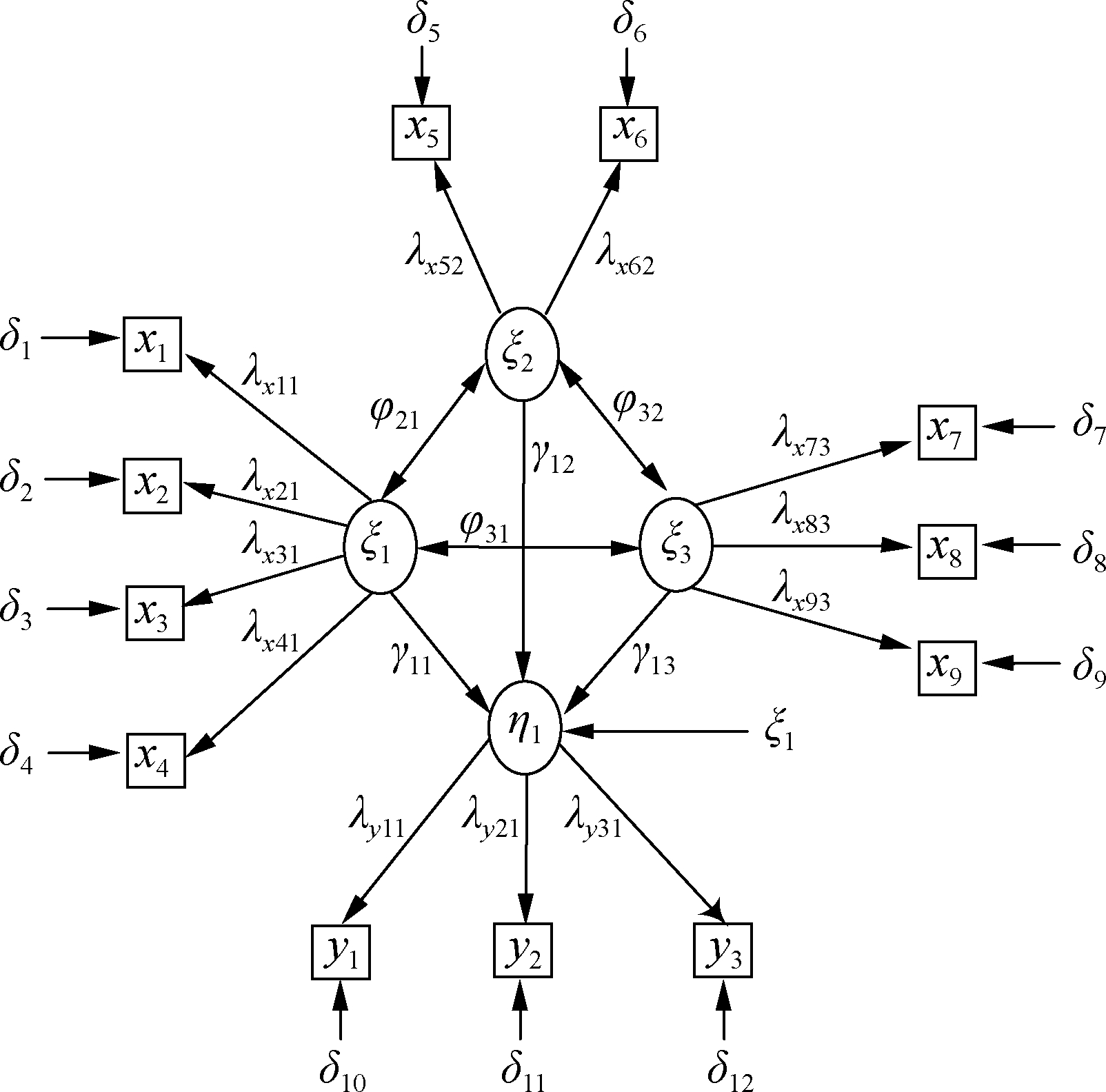
Fig.5 SEM of the firepower interception ability evaluation
Tab.1 Corresponding variables in SEM
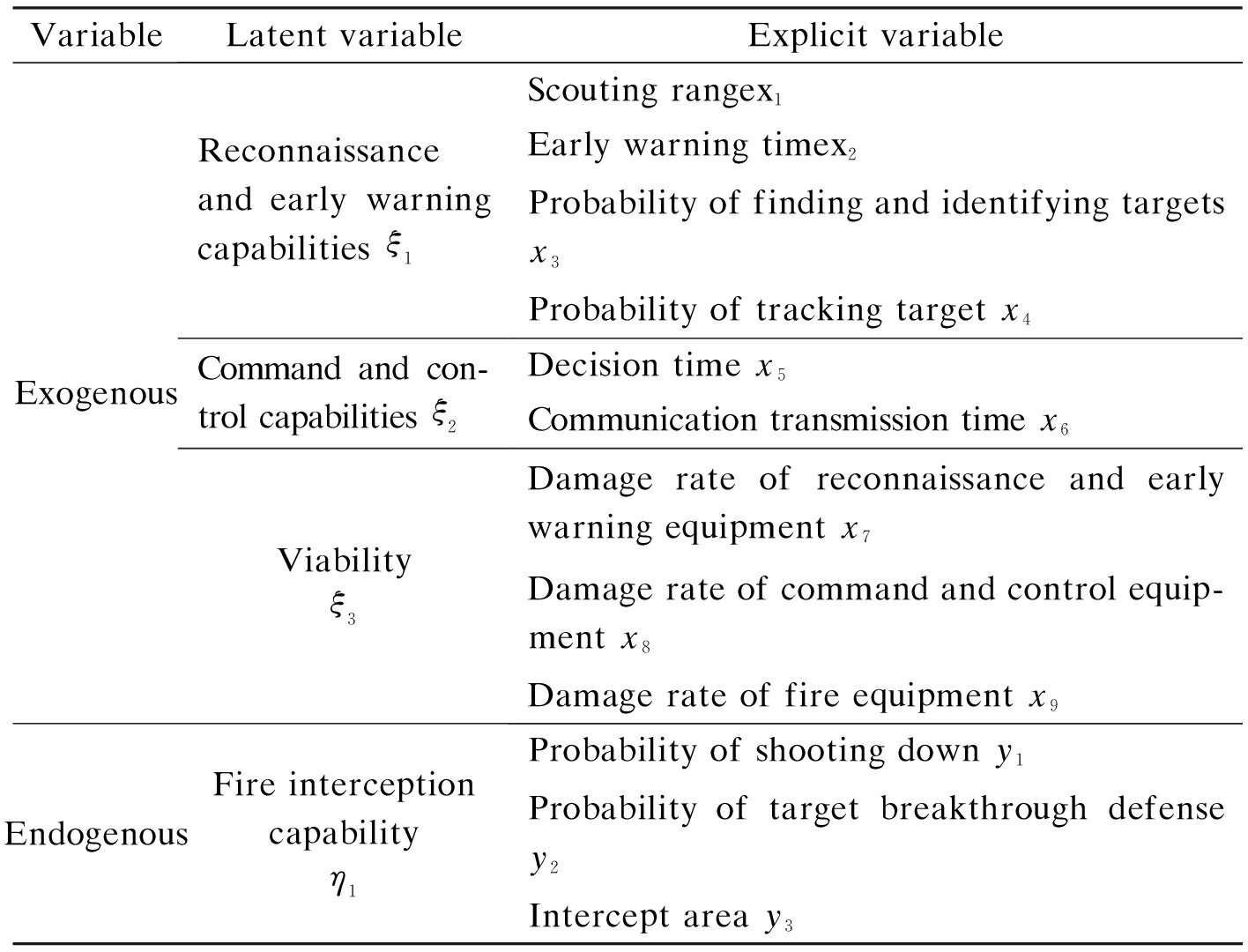
VariableLatent variableExplicit variableExogenousReconnaissance and early warning capabilities ξ1Command and con-trol capabilities ξ2Viabilityξ3Scouting rangex1Early warning timex2Probability of finding and identifying targets x3Probability of tracking target x4Decision time x5Communication transmission time x6Damage rate of reconnaissance and early warning equipment x7Damage rate of command and control equip-ment x8Damage rate of fire equipment x9EndogenousFire interceptioncapabilityη1Probability of shooting down y1Probability of target breakthrough defense y2Intercept area y3
The measurement equation of the model is
X=Λxξ+δ
(3)
Y=Λyη+ε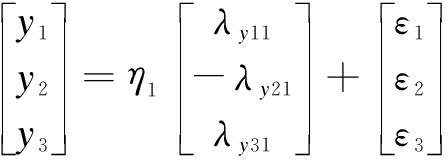
(4)
The structural equation of the model is
η=Bη+Γξ+ζ=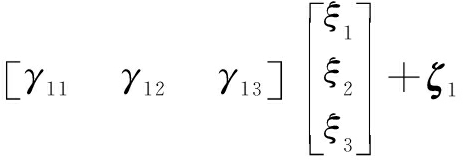
(5)
According to the above measurement equation, the quantitative relationship model between the first-level and second-level indicators can be obtained and used as the capability evaluation model. Λx is the p×m-dimensional relation matrix of X and ξ. Λy is the q×n-dimensional relation matrix of Y and η. B is the n×n-dimensional matrix and represents the relationship between endogenous variables. Γ is the n×m-dimensional matrix and represents the effect of ξ on η. ε is the q×1-dimensional vector composed of the error terms of Y. p is the number of exogenous explicit variables, and q is the number of endogenous explicit variables.
The calculation model of the reconnaissance and early warning capability is
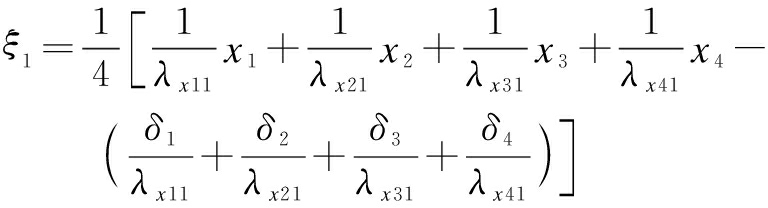
(6)
The calculation model of the command and control capability is
(7)
The calculation model of viability is
(8)
The calculation model of fire interception capability is
(9)
Through the above model, the problem of capacity calculation is converted into the problem of parameter calculation.
3.2 Solvability analysis of the SEM
The solvability analysis of the SEM is to test whether the unknown parameters in the model can be estimated. If the model is not solvable, then the model needs to be modified again until it is solvable. The solvability of the SEM mainly follows the t-rule.
There are p+q explicit variables in SEM, which can produce (p+q)(p+q-1)/2 covariances and p+q variances, so (p+q)(p+q-1)/2 different equations with unknown parameters are obtained. Therefore, as long as the number t of unknown parameters satisfies the following equation:
(10)
then SEM is solvable. There are 9 explicit exogenous variables, 3 explicit endogenous variables, and 31 parameters to be evaluated in the model, according to the t-rule ![]() Thus, the model is solvable.
Thus, the model is solvable.
3.3 Estimation and test of unknown parameters in SEM
Under the condition that the SEM can be solved, the unknown parameters in SEM should be estimated, and the estimation results should be tested. Considering that there are too many schemes, Tab.2 only lists the values of the significant variables in the SEM of some typical schemes. Particularly, the value of various explicit variables mostly involves military secrets, so the data from simulation in Tab.2 are not the true values of the explicit variables.
The SEM of the firepower interception capability and the indicators of the explicit variables are inputted into the LISREL8.51 software. The maximum likelihood estimation method is used for unknown parameter estimation, and the S-test method is used for the unknown parameter test. The S-test method is described as follows: If the absolute value of the S-test value is less than 2, then the parameter is unimportant and redundant in the model. If the absolute value of S is greater than 2, then the parameter is necessary.
Tab.2 Values of explicit variables in the SEM under different schemes
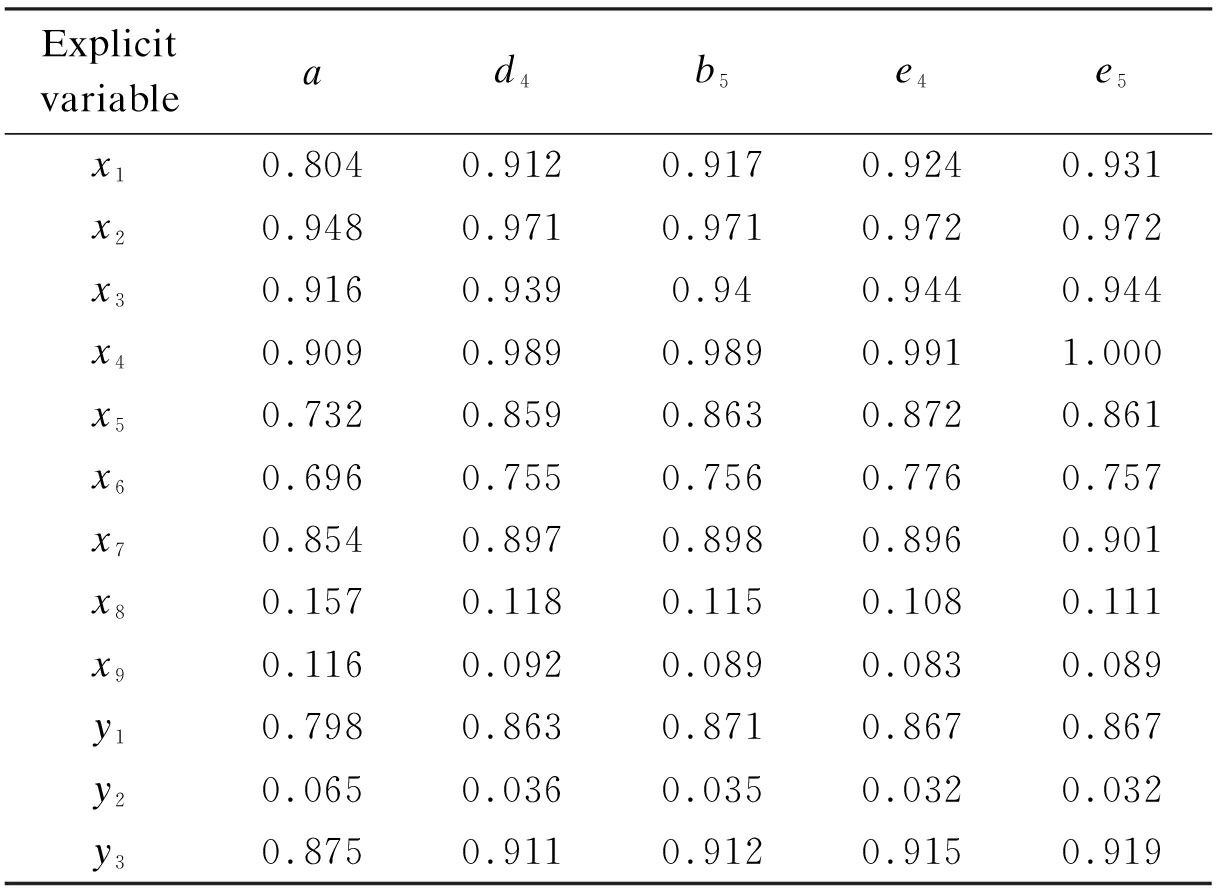
Explicitvariablead4b5e4e5x10.8040.9120.9170.9240.931x20.9480.9710.9710.9720.972x30.9160.9390.940.9440.944x40.9090.9890.9890.9911.000x50.7320.8590.8630.8720.861x60.6960.7550.7560.7760.757x70.8540.8970.8980.8960.901x80.1570.1180.1150.1080.111x90.1160.0920.0890.0830.089y10.7980.8630.8710.8670.867y20.0650.0360.0350.0320.032y30.8750.9110.9120.9150.919
Tab.3 Parameter estimated value and S-test value of SEM

ParameterEstimatedvalueS-testvalueParameterEstimatedvalueS-testvalueλx110.725.53δ50.195.85λx210.764.55δ60.114.77λx310.796.35δ70.184.50λx410.815.02δ80.154.81λx520.868.71δ90.177.16λx620.786.12ε10.165.95λx730.825.39ε20.196.55λx830.756.07ε30.187.12λx930.887.47φ10.744.37λy110.725.94φ20.687.25λy210.657.04φ30.814.61λy310.874.03γ110.877.24δ10.126.77γ120.835.51δ20.157.84γ130.758.27δ30.144.10ζ10.115.36δ40.145.87
Tab.3 shows the parameter estimated value and S-test value in SEM. The S-test value of all parameters is greater than 2, so all 31 parameters are necessary. Moreover, from the estimated values of γ and φ, there are strong coupling relationships between the reconnaissance and early warning capabilities, command and control capabilities, and survivability, which all have a strong influence on the fire interception ability.
3.4 Fitting test
The fitting test indicators of the SEM are mainly used to test the fitting degree between the estimated value and the true value of the parameters. Several typical fitting indicators and their evaluation standards are listed in Tab.4. Tab.4 shows that the values of the fitting indicators are within the acceptable range, so the estimated value of the parameter is close enough to the true value, and the estimated value of the parameters can be used for calculation. The smaller the value of root mean square error of approximation (RMSEA), the better; the closer the value of the other parameters to 1, the better.
Tab.4 Test parameters and standards for fitting

Fitting indexRMSEANFINNFICFIValue 0.0150.9460.9880.982
4 Results and Discussion
The data from Tabs.2 and 3 are incorporated into Eq.(10) to obtain the fire interception capability evaluation value l′i(i=1, 2, …, 21) of each equipment’s SoS scheme. Then, l′i is standardized to obtain the standard evaluation value according to Eq. (12), as shown in Tab.5.
(11)
Tab.5 Evaluation values of the firepower interception capability and SoS contribution rate

SchemenSeGA 081.2BB1896.318.60B21298.020.69B31698.020.69B42098.020.69B52498.020.69CC1893.415.02C21294.716.63C31694.716.63C42094.716.63C52494.716.63DD1896.16.03D21289.39.98D31693.214.78D42097.820.44D52410023.15EE1889.69.48E21292.113.42E31695.617.73E42010023.15E52410023.15 Notes:n is the number of K-type air defense weapon sys-tems; Se is the standard evaluation value of fire interception capability; and G is the system contribution rate.
The equipment SoS of scheme A does not include the K-type air defense weapon equipment. In scheme B, it is a single-layer group configuration. In scheme C, it is a single-layer linear configuration. In scheme D, it is a double-layer group configuration. In scheme E, it is a double-layer linear configuration. The schematic diagram of the configuration is shown in Fig. 6. Essentially, if the configuration is a double-layer configuration with 20 sets of equipment, then each layer of defense lines is composed of 10 sets of equipment.
Under the condition that the combat mission can be completed without the K-type air defense weapon equipment, Eq. (2a) is used to calculate the SoS contribution rate, and the results are shown in Tab.5. Schemes B, C,
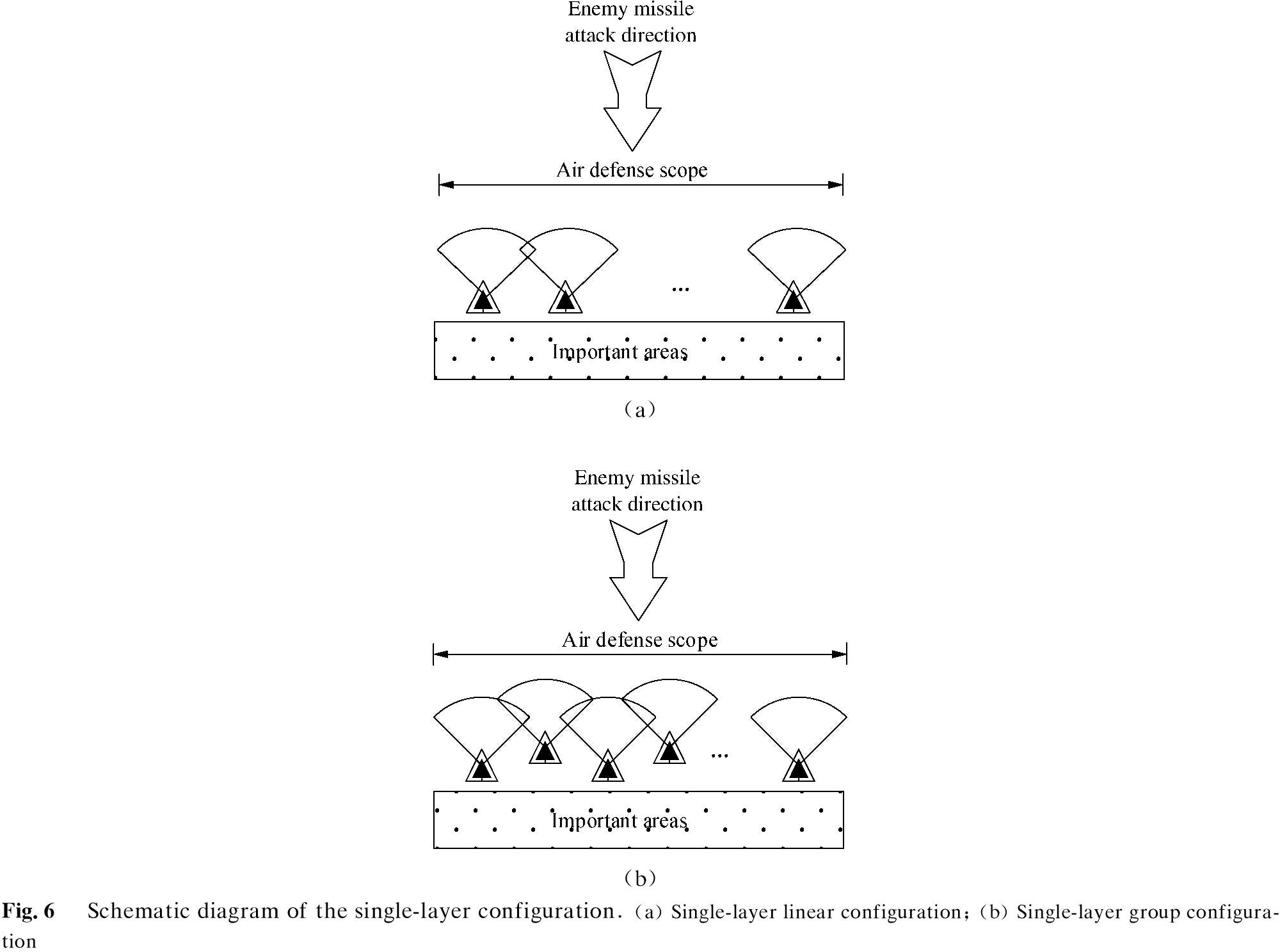
D, and E correspond to the single-layer group configuration, single-layer linear configuration, double-layer defense group configuration, and double-layer linear configuration, respectively.
Comparing schemes B and C, the linear configuration has a wider firepower coverage than the group configuration. Ten sets of K-type air defense weapon equipment can fully cover the airspace of our important areas, whereas the group configuration requires 12 sets. With concentrated firepower, the interception capability of the single-layer group configuration is clearly stronger than the single-layer linear configuration in the case of full airspace coverage, so increasing the number of weapon systems will not increase the contribution rate.
Comparing schemes B and D, as can be seen from B5 and D5, increasing the number of defense lines with the group configuration does not significantly increase the contribution rate in the case of full airspace coverage. This result is determined by the characteristic that the firepower of the group configuration is concentrated; that is, the single-layer defense line of the group configuration does not intercept the target, and the multi-layer defense lines are also not easy to intercept. In schemes D5 to D1, blind areas appear in the airspace as the number of air defense weapon equipment decreases, and the contribution rate significantly drops.
Comparing schemes C and E, particularly schemes C4 and E4, increasing the number of defense lines with the linear configuration significantly improves the contribution rate in the case of a full airspace coverage. This result is determined by the characteristic that the firepower of the linear configuration is more dispersed; that is, multiple layers of defense lines increase the early warning time, thereby intercepting more targets and making up for the lack of the firepower of the linear configuration. In schemes E4 to E1, blind areas appear in the airspace as the number of air defense weapon equipment decreases, and the contribution rate significantly drops.
5 Conclusions
1) The number of defense lines of the air defense weapon equipment has a greater impact on the linear configuration than the group configuration.
2) The two-layer linear configuration should be adopted when the amount of K-type air defense weapon equipment is sufficient, and scheme E4 that costs less should be selected.
3) The single-layer group configuration should be adopted when the number of K-type air defense weapon equipment is insufficient, and scheme B2, in which the contribution value is higher, should be selected.
[1]Wan C, Xiong W, Ye Y, et al. Research on development strategy of weapon equipment in antagonistic environment[C]// The 11th Annual IEEE International Systems Conference. Beijing, China, 2017:221-225.DOI: 10.1109/SYSCON.2017.7934732.
![]() M, Yavuz S, K
M, Yavuz S, K l
l nçN. Weapon selection using the AHP and TOPSIS methods under fuzzy environment[J]. Expert Systems with Applications, 2009, 36(4):8143-8151. DOI: 10.1016/j.eswa.2008. 10.016.
nçN. Weapon selection using the AHP and TOPSIS methods under fuzzy environment[J]. Expert Systems with Applications, 2009, 36(4):8143-8151. DOI: 10.1016/j.eswa.2008. 10.016.
[3]Li D, Hu X. Redundant and fault-tolerant algorithms for real-time measurement and control systems for weapon equipment[J]. ISA Transactions, 2017, 67:398. DOI: 10.1016/j.isatra.2017.01.005.
[4]Wang M. An integrated analysis and modeling framework for weapon equipment system evolution[C]// The 6th International Symposium on Project Management. Wuhan, China, 2018: 598-606. DOI: DOI: 10.1016/j.isatra.2017.01.004.
[5]Chi Y, Li J C, Yang K W, et al. An equipment offering degree evaluation method for weapon system-of-systems combat network based on operation loop[J]. Atlantis Press, 2016, 2(1):477-488. DOI: 10.2991/978-94-6239-180-2_46
[6]Jia Z, Ding L S, Zhou Y F. Ieee. Process design of a capability-based weapon equipment requirements analysis system[C]// The Fifth International Conference on Software Defined Systems. Shanghai, China, 2018: 74-79. DOI:10.2991/978-94-6239-180-2 _68.
[7]Wang M, Zhang H Q, Zhang K. A model and solving algorithm of combination planning for weapon equipment based on epochera analysis method[J]. AIP Conference Proceedings, 2017, 1890(1):1-7. DOI: 10.1063/1.5005319.
[8]Li X, Lü B, Jiang Y. Research on civil-military integration degree of weapon equipment research and production by system dynamics model[C]// The 29th Chinese Control and Decision Conference. Chongqing, China, 2017: 2403-2406. DOI:10.1109/ CCDC.2017.7978917.
[9]Pei D, Qin D G. Evaluation of contribution rate of weapon equipment system of systems capability based on conditional evidential network[C]// The 8th IEEE International Conference on Software Engineering and Service Science. Beijing, China, 2017: 459-463. DOI: 10.1109/ICSESS.2017.8342955.
[10]Li X S, Lü B. Research on weapon equipment civil-military integration development mode based on Fuzzy Petri Net[C]// The 36th Chinese Control Conference. Dalian, China, 2017:10398-10402. DOI: 10.23919/ChiCC.2017.8029011.
[11]Qu Q, He X H, Zhang W C. Analysis of operational effectiveness index of army weapon equipment system[C]// International Conference on Computer Science and Technology. Guangzhou, China, 2017: 100-106. DOI: 10.23919/ChiCC.2017.8598431.