Studying the lubricating properties ofan engine’s crankpin bearings(CBs)to ameliorate the lubrication and friction performance(LFP)of engines is a topic of interest for many researchers.On the basis of the design parameters of an engine, the influence of the CB’s dimensions, such as the radius of the bearing and crankpin(rb and rc), the bearing width(B), the gap between the crankpin and bearing(c= rb-rc), and the CB’s surface roughness(σ)on the LFP, has been researched[1-5].The parameters of rb, rc, B, c, and σ of the CB were also optimized to enhance the CB’s LFP[6-8].Results indicated that the CB’s LFP was significantly ameliorated by the optimization of the CB’s dimensions.The investigations also emphasized that the friction force(Ff)and solid asperity contact force(Wac)generated in the elastic hydrodynamic lubrication(EHL)region of the CB with a minimum oil film thickness(ho)below 10 μm were still high[5, 8-9], particularly at the engine’s combustion stroke.Thus, to reduce the Ff and Wac and improve the LFP of the CB, the ho and the oil film pressure(p)in the EHL region should be increased.However, improving p and ho by using only the parameters of the optimized CB is difficult.
To enhance the p and ho, on the basis of research on microtextures added to the non-slip surface of friction pairs[10-14], an optimal design of the circular textures(CTs)of microtextures with a distribution density of {a×b}={6×6} was applied on the bearing surface to ameliorate the LFP[15].This approach enhanced not only the p and ho but also the CB’s LFP.However, the results of the Ff and Wac of the CB using the CTs{6×6} were still greater than that of the CB using the parameters of rb, rc, B, c, and σ optimized in Ref.[8].Furthermore, the study used only one type of CTs{6×6}.The wedge-shaped textures(WSTs)and the square textures(STs)of the microtextures designed on the journal bearings also significantly affected the tribological properties of journal bearings but have not been a topic of concern so far.Thus, the effectiveness of the microtextures in improving the CB’s LFP has not been fully reflected yet.
On the basis of existing research on microtextures designed for friction pairs and journal bearings, the effect of the distribution density and shape of various microtextures, including CTs, STs, WSTs, circles-ellipses, and circles-triangles, on the lubrication performance was investigated[16-19].The results indicated that the microtextures could significantly affect the vibration and acoustics of contacting pairs[19].However, with a 5-20 μm depth of microtextures designed on the contacting pairs, the Ff and Wac were remarkably reduced, especially with both the CTs and STs[17-18].Therefore, the CTs and STs of microtextures were designed and used on the bearing surface to ameliorate the friction and lubrication effectiveness of journal bearings[20-22].However, the external load(W0)that impacts the shaft, which greatly affected the p and ho in the EHL region of the journal bearings, was ignored or assumed to be constant in the above research.The influence of the microtextures of the WSTs, STs, and combined square-circular textures(CSCTs)on the CB’s LFP under the impact of a change in W0 has not yet been fully researched and evaluated in existing research.
On the basis of the CB’s dimensions optimized in Ref.[8], the CTs of microtextures optimized in Ref.[15], and a hydrodynamic model of the CB, the above issues were elucidated by proposing and researching a design of different microtextures of the WSTs, STs, CTs, and CSCTs on the bearing surface to improve the LFP of engines under different external loads of W0 impacting on the crankpin at an engine speed of 2 000 r/min.The p, Ff, Wac, and the friction coefficient(μ)of the CB are selected as the objective functions to evaluate the CB’s LFP.This study aims to assess the influence of various microtextures on enhancing the lubrication effectiveness and reducing the frictional power loss of engines.
1 Modeling of CB Lubrication and Microtextures
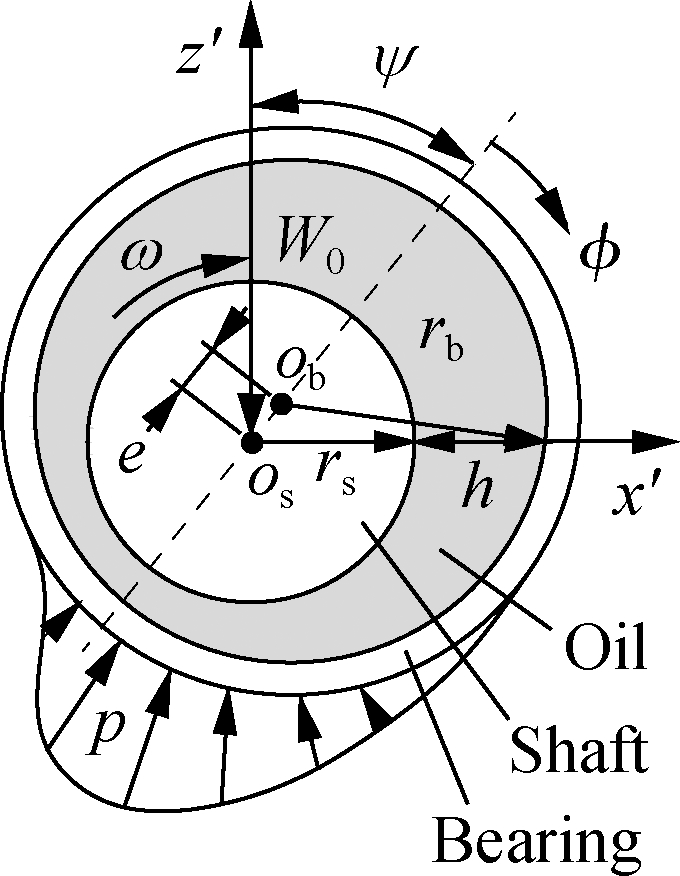
A CB hydrodynamic lubrication model supported by the W0 is established in Fig.1(a)to assess the effect of various microtextures on ameliorating the CB’s LFP.To simplify the design process of the different microtextures on the bearing surface, the bearing surface modeled in the Cartesian counterpart[22] is applied to design the WSTs, STs, CTs, and CSCTs for improving the ho and p.The depth of all the textures is assumed to be the same, and the distance between each texture designed on the bearing surface is equidistant in the x-and y-directions, as shown in Fig.1(b).
(a)

(b)
Fig.1 Model of the CB’s lubrication and different textures.(a)Lubrication model;(b)Different microtextures distributed on the bearing surface
In Fig.1, ω, φ, and ψ are the angular velocity, angular coordinate, and attitude angle of the crankpin in the bearing, respectively; e is the eccentricity between the shaft and bearing centers; R is the radius of the CTs; Ab is the area of the bearing surface; u is the moving velocity of the crankpin in the bearing; Lx and Ly are the bearing length and width, respectively; lx and ly are the dimensions of the texture surfaces; ls is the length and width of WSTs or STs; and ht is the maximum depth of WSTs, STs, and CTs, respectively.
Given rc<rb and a small gap c that always exists in the CB, an eccentricity ratio e of the CB is given by ε=e/c, and ho is determined by ho=c(1+εcosφ).
According to the model of different microtextures designed on the bearing surface in Fig.1(b), the actual oil film thickness created by c and ht is written as
h=ht+ho=ht+c(1+εcosφ)
(1)
The mathematical equations of WSTs, STs, CTs, and CSCTs are presented below to determine the shape and the ht of different microtextures.
1.1 Wedge-shaped textures
On the basis of the design of WSTs in Fig.1(b), the relationships lx and ly between the WSTs and Ab in the x-and y-directions are calculated by

(2)
where a and b are the number of microtextures distributed in the x-and y-directions, respectively.
The shape equations of WSTs are given by
(3)
The depth equation of WSTs is written as
(4)
where xi and yj are the coordinates of WSTs in the x-and y-directions, i=1,2,3,…,a and j=1,2,3,…,b.
1.2 Square textures
With the design of STs in the same Fig.1(b), the relationships lx and ly between STs and Ab are calculated by Eq.(2), and the shape equations of STs are determined by Eq.(3).Herein, h=ho+ht, and ht is a constant.
Circular textures: On the basis of the structure of CTs in Fig.1(b), the relationships lx and ly between CTs and Ab are calculated by
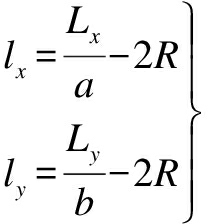
(5)
Thus, the equations of the shape and the h of CTs are
(6)
where xi=(i-0.5)(lx+2R)and yj=(j-0.5)(ly+2R)are the CT center coordinates in the x-and y-directions, respectively, and ht=Rc(1-cosα)is the depth of CTs.
1.3 Combined square-circular textures
On the basis of the CSCTs designed in Fig.1(d), the relationships lx and ly between CSCTs and Ab in the x-and y-directions are written as

(7)
According to the shape and depth equations of STs and CTs calculated in Eqs.(3)and(6), the shape and depth equations of CSCTs could be rewritten as follows:
i=2a,j=2b-1
(8)
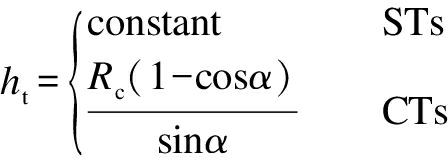
(9)
All the shape and depth equations of WSTs, STs, CTs, and CSCTs are then calculated and simulated by combining Eqs.(3),(6), and(8).
2 Application of Reynolds Equations
Reynolds equations were applied to compute the h and p of the friction pairs or journal bearings[5,23].In this study, the lubrication equations of the CB are computed under an acting W0 on the crankpin, the CB’s σ, and the depth and structure of WSTs, STs, CTs, and CSCTs on the bearing surface.To perform the calculation, some assumptions of the model need to be given as follows: 1)The bearing surface is fixed, and the crankpin surface moves only on the bearing surface with a velocity of u=rb×ω in the x-direction; 2)The oil film’s velocity in the centripetal motion and the inertia of the oil flow are very small; 3)The characteristics of the dynamic viscosity(η)and density of the oil film are unaltered during the CB’s operation.
Therefore, a general form of the Reynolds equations and a dimensionless form are given based on the CB’s hydrodynamic lubrication model as follows[8,15]:
(10)
(11)
where αs and(αx,αy)are the factors of the pressure and shear flows; X=x/Lx; Y=y/Ly; γ=Lx/Ly; H=h/c; P=p/p0; Λ=6ηωLy2/(p0c2); Γ=12ηωLy2/(t0p0c2); T=t/t0; Δ=σ/c; and p0=101 325 Pa is the atmospheric pressure.
To calculate the p and h in Eq.(10), their boundary conditions need to be defined as follows: 1)h always exists and distributes over the bearing surface, 2)the maximum value of h at φ=0° in Fig.1(a)is defined as the inlet oil film at m and outlet oil film at n in Fig.1(c), 3)the inlet and outlet pressures and the boundary pressures of the CB at m, n, g, and q in Fig.1(c)are defined by the same p0, and 4)the pc in the CB’s cavitation region is computed by pc=ps with p≤ps and pc=p with p>ps(ps is the saturation pressure).Thus, the boundary pressures of the bearing surface are calculated by p(φ=0°)=p(φ=360°)=p and p(x=0)=p(x=B)=0, and both the h and p can then be determined.
3 Evaluation Indexes of LFP
Under the acting W0 on the crankpin, the load-bearing capacity of CB defined by W=Wof+Wac must balance with W0 to ensure the normal operation of CB.Consequently, p needs to be increased to enhance the load-bearing capacity Wof of the oil film.Concurrently, the pac generated in the EHL region needs to be decreased to reduce the Ff and Wac of CB[5,8].Ff and W are strongly affected by both p and h[3].Therefore, the different microtextures of WSTs, STs, CTs, and CSCTs are used to enhance the p and h, thereby improving the CB’s LFP.In assessing the influence of the different microtextures on ameliorating the LFP, the indexes of the increase of p and the reduction of Ff, Wac, and μ that are selected as objective functions are then determined as follows:
1)Pressure distribution of the oil film.The oil film’s pressure distribution is determined in Eq.(10).
2)CB’s friction force.The friction force Ff generated in CB is determined by two friction forces that are generated due to the oil film motion and the solid contact of two CB surfaces in the EHL region.Thus, Ff is described as follows[7]:
Ff=∬Ab(τac+τ)dxdy
(12)
where τac and τ are the asperity contact stress and interfacial shear stress of the CB surfaces, respectively.
3)EHL’s asperity contact force.In the EHL region, the Wac is generated when h<10 μm[5].On the basis of the equation of the asperity contact pressure ![]() pac is then used to calculate Wac as follows:
pac is then used to calculate Wac as follows:
(13)
4)CB’s friction coefficient.On the basis of the value of Ff determined by Eq.(12)and W0, the μ of CB is then determined as follows[5,9]:
(14)
4 Simulation and Discussion
4.1 Computation of various microtextures
To compute the various microtextures of WSTs, STs, CTs, and CSCTs and to assess their effectiveness in ameliorating the CB’s LFP compared with the existing results of the CB parameters optimized in Ref.[8]and CTs{6×6} optimized in Ref.[15], the optimized CB parameters and optimized CTs{6×6} listed in Tab.1 are used as input parameters to simulate the results under the W0 acting on the crankpin at a speed of 2 000 r/min(see Fig.2).
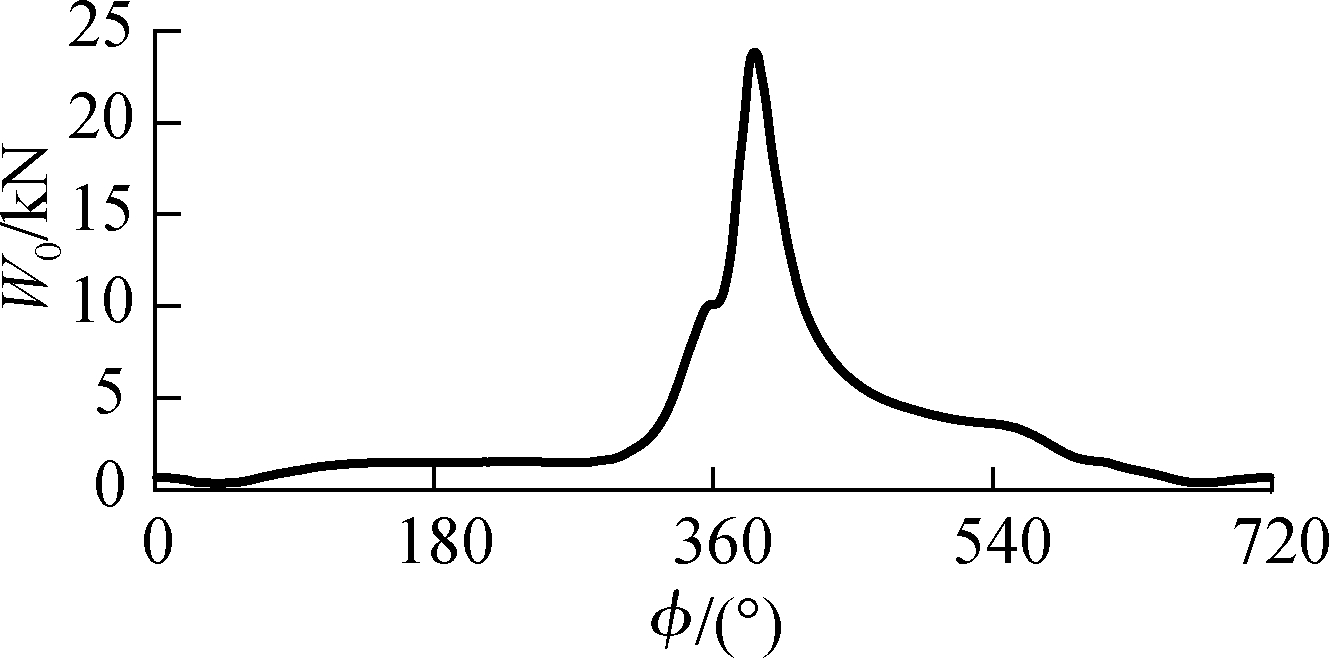
Fig.2 Data of W0 acting on the crankpin of CB
The research results of CTs in Ref.[24]showed that the distribution density of CTs{12×6} improves the tribological properties better than that of CTs{6×6}.Therefore, to compute and compare the effectiveness of the WSTs, STs, CTs, and CSCTs for ameliorating the CB’s LFP, the parameters of all the microtextures listed in Tab.1 are distributed on the Ab of the CB as follows: 1)The matrix {a×b} of all microtextures distributed on the Ab in the x-and y-directions is chosen by a=12 and b=6; 2)The CB’s length and width are defined by Lx=2πrb=126.1 mm and Ly=B=18.06 mm; 3)The radius of CTs and the length and width of WSTs or STs are defined by R=ls/2=0.85 mm; 4)The depth of all the microtextures is defined by ht=5.5 μm.
Tab.1 Optimal parameters of CTs and CB
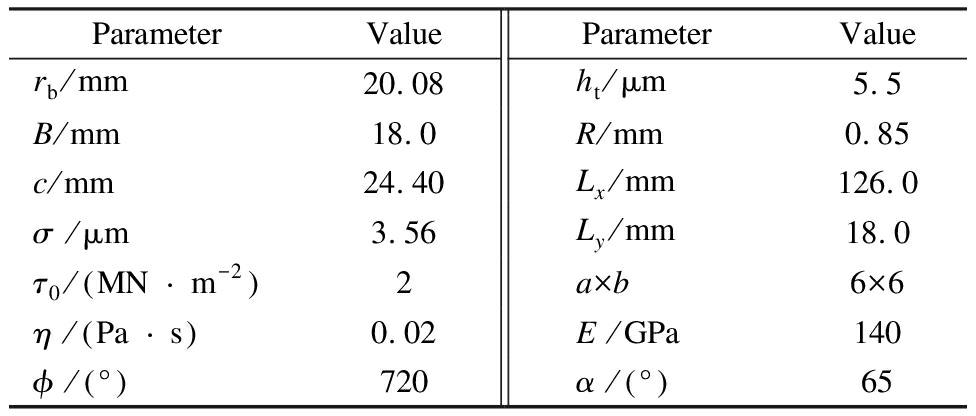
ParameterValueParameterValuerb/mm20.08ht /μm5.5B/mm18.0R/mm0.85c/mm24.40Lx /mm126.0σ /μm3.56Ly /mm18.0τ0 / MN m-2 2a×b6×6η / Pa s 0.02E /GPa140ϕ / ° 720α / ° 65
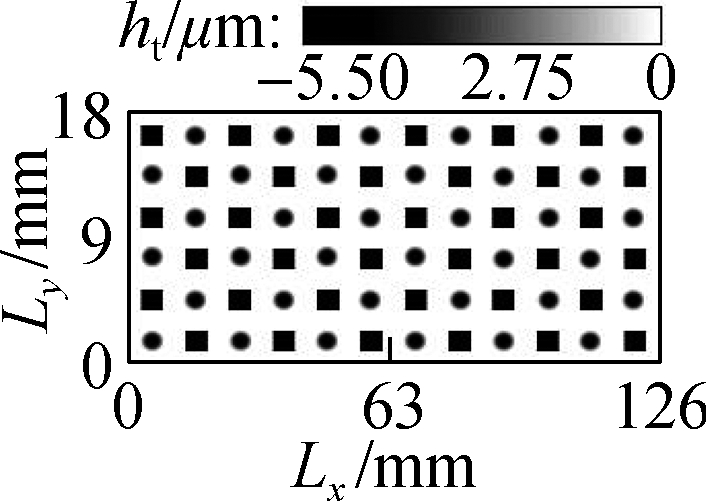
In accordance with the defined input parameters, the mathematical equations of the CB, and the determined microtextures, an algorithm program written in MATLAB is applied to calculate the objective functions under the same simulation condition.From the simulation results, the distribution densities of WSTs, STs, CTs, and CSCTs on the Ab are indicated in Fig.3.The results in Fig.3 are then applied to compute and analyze the h and p and CB’s LFP.
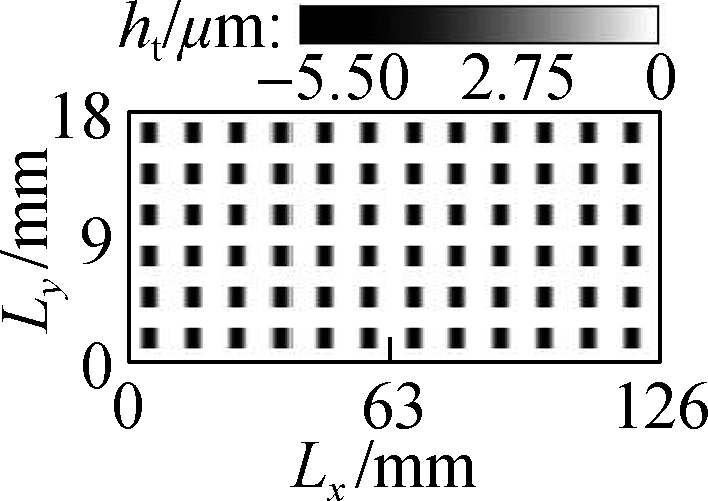
(a)
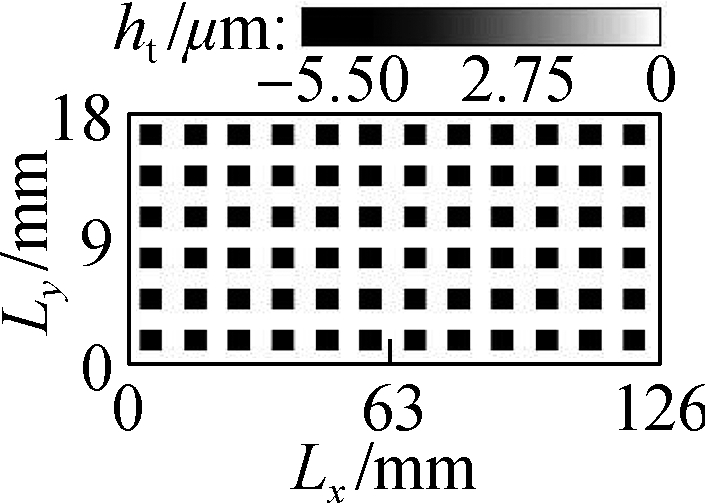
(b)
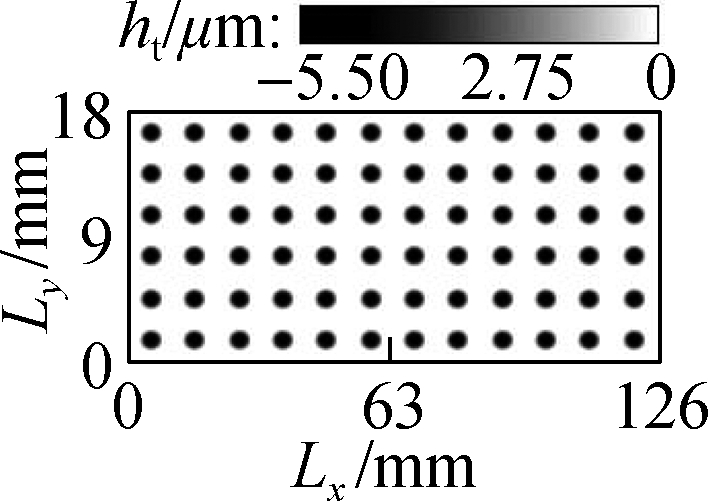
(c)
(d)
Fig.3 Distribution results of different microtextures on the bearing surface.(a)WSTs;(b)STs;(c)CTs; and(d)CSCTs
4.2 Discussions
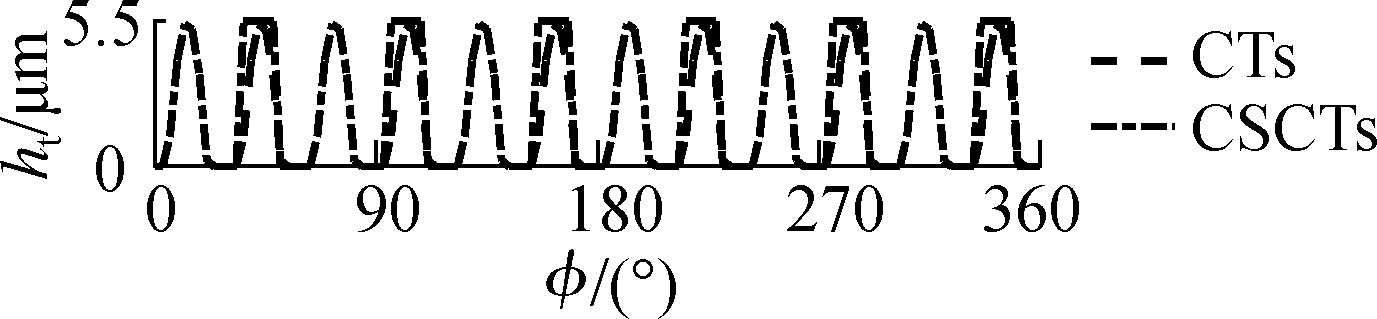
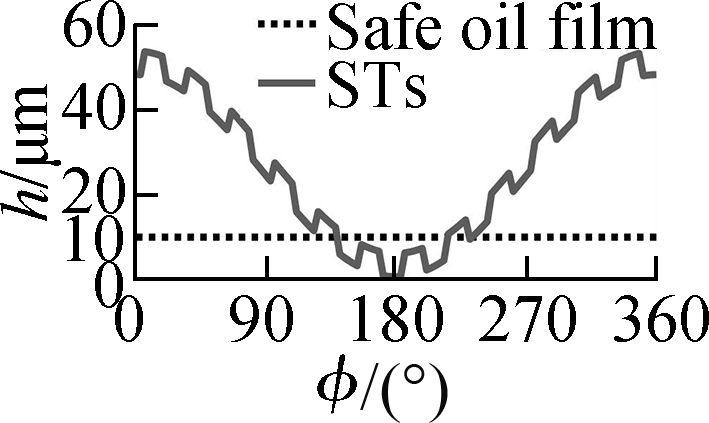
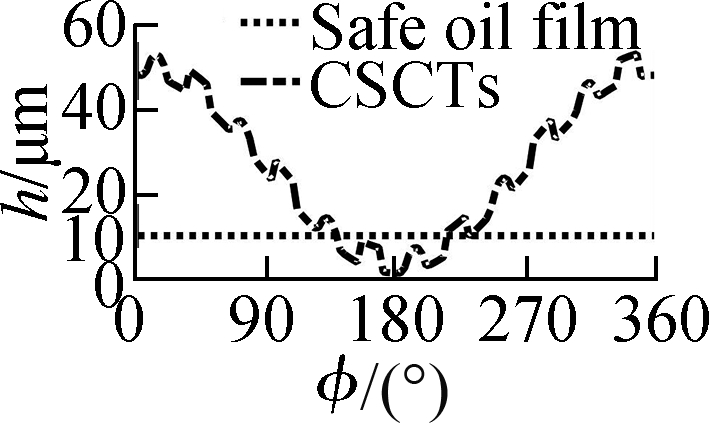
The ht=5.5 μm of WSTs, STs, CTs, and CSCTs is computed and indicated in Fig.4.The h added by the ht is then plotted in Fig.5.Fig.5 shows that the h is smaller than the safe oil film thickness in Ref.[5]at a range from 198° to 212° of the circumferential coordinate.This result could be due to the maximum W0 acting on the crankpin at the combustion cycle of the engine.Therefore, the e of the CB is increased and the h is decreased.In the EHL region with h ≤ 10 μm, both the Ff and Wac could be strongly increased.Therefore, both the p and h in this region should be enhanced to ameliorate the CB’s LFP.
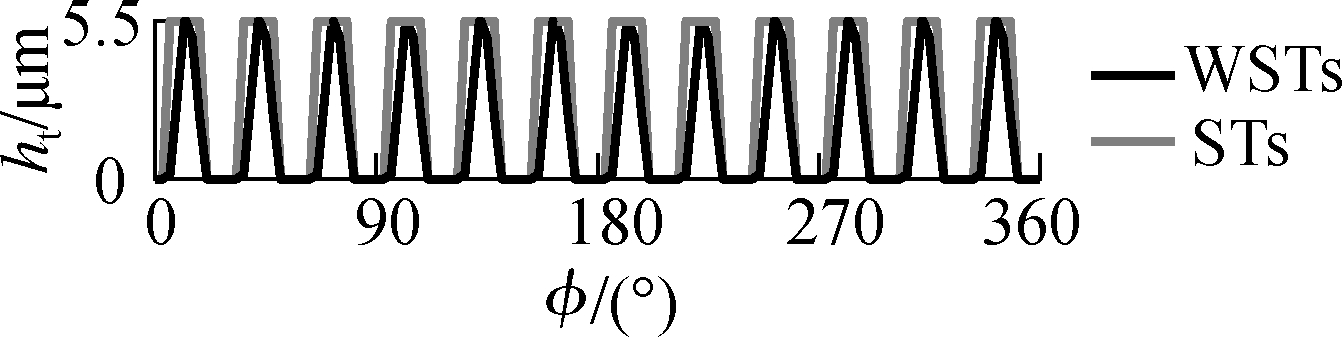
(a)
(b)
Fig.4 Oil film thickness ht of different microtextures.
(a)WSTs and STs;(b)CTs and CSCTs

(a)
(b)

(c)
(d)
Fig.5 Oil film thickness h added by ht.(a)WSTs;(b)STs;(c)CTs;(d)CSCTs
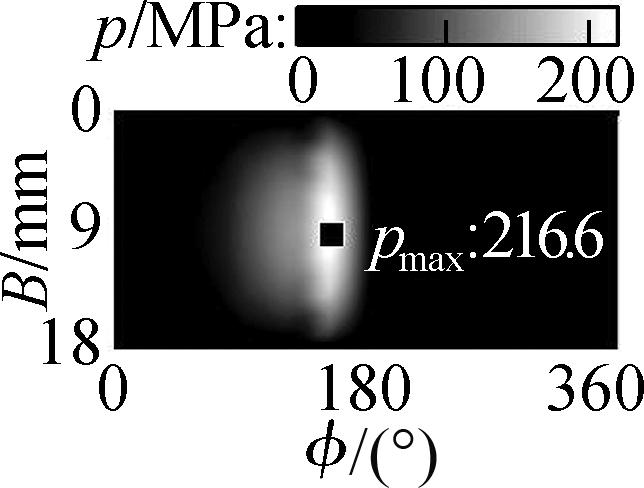
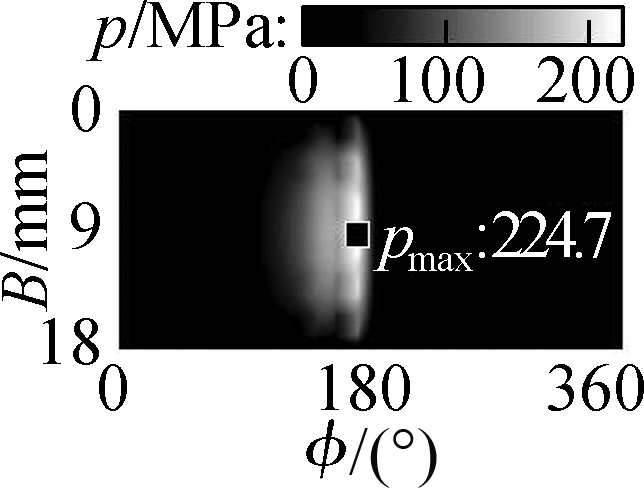
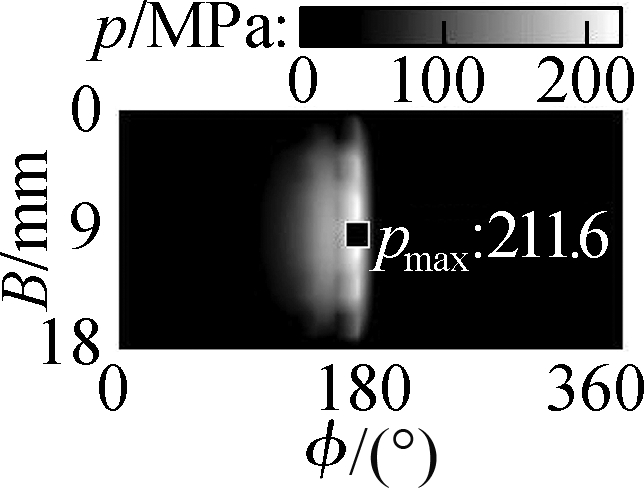
With the ht=5.5 μm of all the microtextures added on the bearing surface, the result of the h in Fig.5 is also enhanced.Thus, the p is also increased in comparison to the condition without microtextures, especially in the EHL region, as shown in Fig.6.Fig.6 shows that the maximum values of the p with the use of WSTs, STs, CTs, and CSCTs are 216.6, 224.7, 211.6, and 207.5 MPa, respectively.All their maximum p are substantially increased compared with that of 189.4 MPa without microtextures in Refs.[7-8].In addition, the comparison results of the maximum p with the use of different microtextures show that STs have the highest maximum p.This result is similar to the result of STs designed in journal bearings[13, 18].This finding means that both the Ff and Wac in the EHL region could be substantially ameliorated by STs.To clarify this argument, all the Ff, Wac, and μ are calculated and given in Figs.7(a),(b), and(c), respectively, on the basis of the simulation results of h and p in Figs.4 and 5.
(a)
(b)
(c)
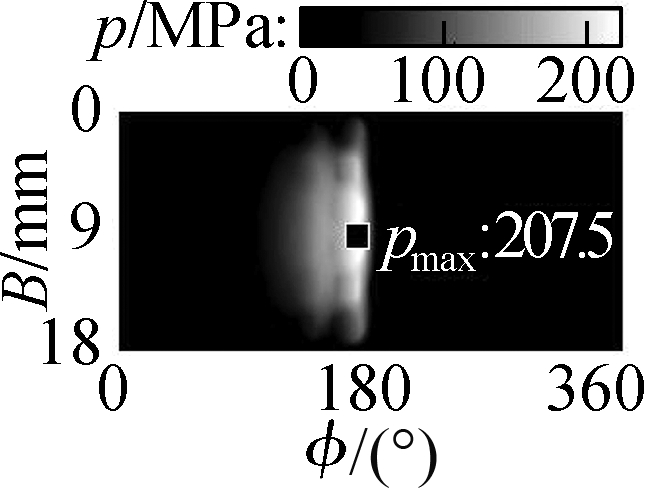
(d)
Fig.6 p on the bearing surface with different microtextures.(a)WSTs;(b)STs;(c)CTs;(d)CSCTs
The simulation results show that both the Ff and Wac obtain the maximum values in the EHL region; these results are similar to those in Ref.[22].In addition, all the Ff, Wac, and μ added by the different microtextures are smaller than those without microtextures.These results were also demonstrated in Refs.[16,21-22].Under the influence of the various structures of microtextures, all the values of Ff, Wac, and μ with the use of STs are substantially decreased compared with those of other structures of WSTs, CTs, and CSCTs.The average values of Ff, Wac, and μ denoted by ![]() respectively, are listed and compared in Tab.2.The results indicate that the
respectively, are listed and compared in Tab.2.The results indicate that the ![]() with WSTs are lower than those with CTs and CSCTs, while the
with WSTs are lower than those with CTs and CSCTs, while the ![]() with STs are the lowest.Particularly, the
with STs are the lowest.Particularly, the ![]() are greatly ameliorated by 28.5%, 14.5%, and 33.2% and by 34.4%, 26.3%, and 43.6% compared with the CB dimensions optimized in Ref.[8]and CTs{6×6} optimized in Ref.[15], respectively.The better result of STs could be due to the stable ht of STs, as shown in Fig.3(b).Thus, ht could affect the increase of the p.In contrast, the maximum ht of CTs and CSCTs is obtained only at R and ls/2, as shown in Figs.3(c)and(d).Furthermore, on the basis of the dimension of STs with R=ls/2=0.85 mm, the circle area(SCTs=πR2)is smaller than the square area of STs
are greatly ameliorated by 28.5%, 14.5%, and 33.2% and by 34.4%, 26.3%, and 43.6% compared with the CB dimensions optimized in Ref.[8]and CTs{6×6} optimized in Ref.[15], respectively.The better result of STs could be due to the stable ht of STs, as shown in Fig.3(b).Thus, ht could affect the increase of the p.In contrast, the maximum ht of CTs and CSCTs is obtained only at R and ls/2, as shown in Figs.3(c)and(d).Furthermore, on the basis of the dimension of STs with R=ls/2=0.85 mm, the circle area(SCTs=πR2)is smaller than the square area of STs ![]() Therefore, the contact region between the bearing surface and the crankpin surface with the use of CTs is greater than that with STs.This condition could also be a cause for the decrease in the Ff and Wac of CB, especially in the EHL region.Thus, the value of μ with the use of STs is also the lowest.
Therefore, the contact region between the bearing surface and the crankpin surface with the use of CTs is greater than that with STs.This condition could also be a cause for the decrease in the Ff and Wac of CB, especially in the EHL region.Thus, the value of μ with the use of STs is also the lowest.
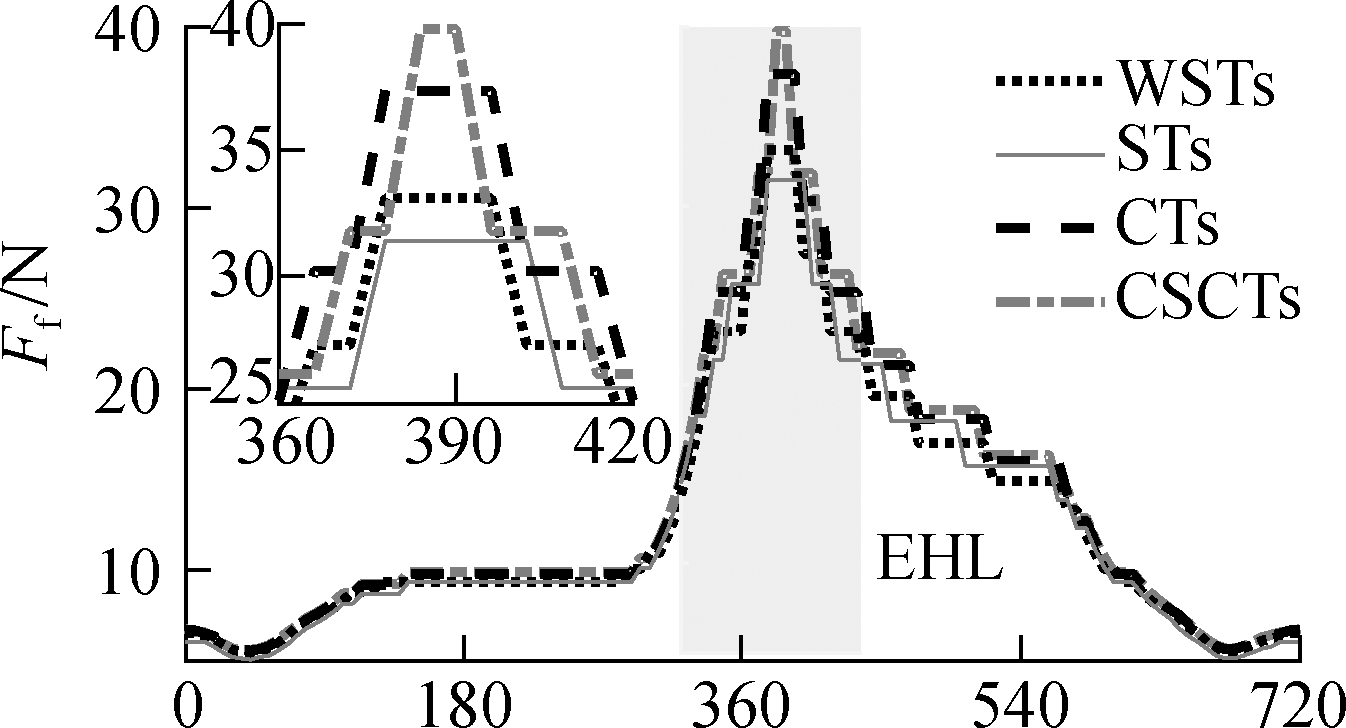
(a)
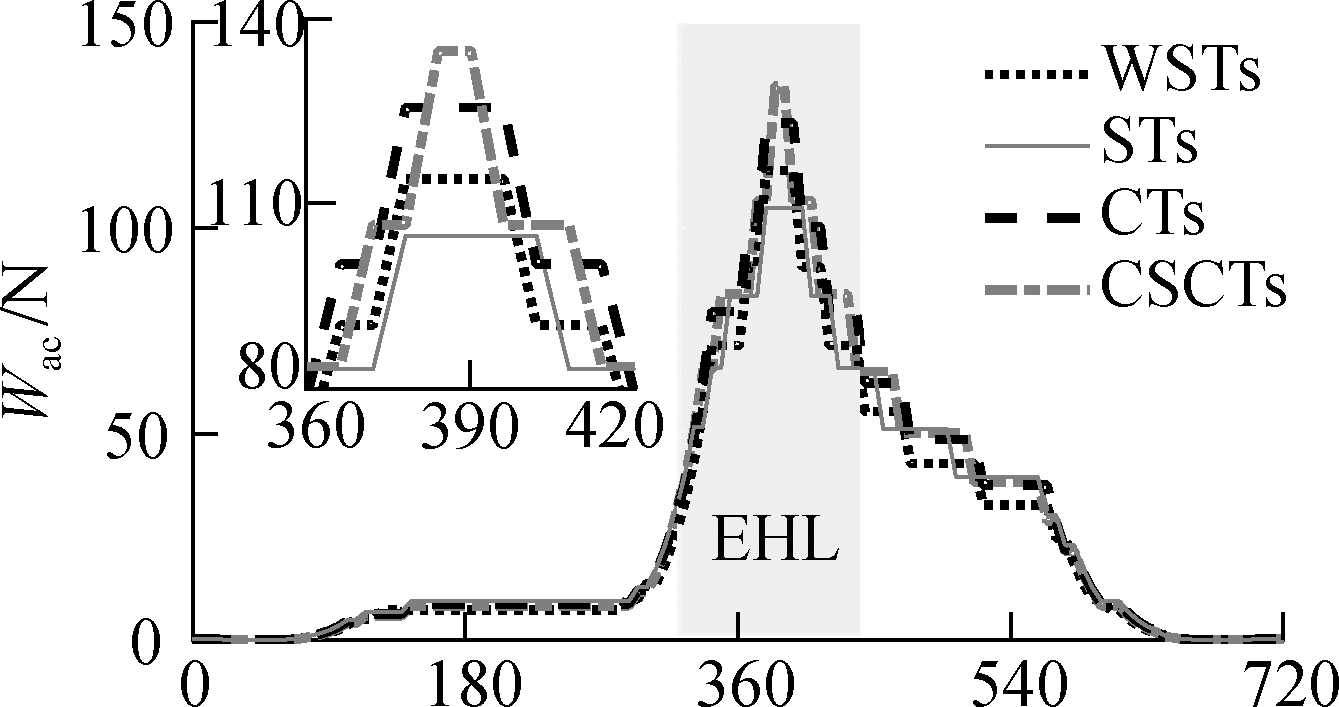
(b)
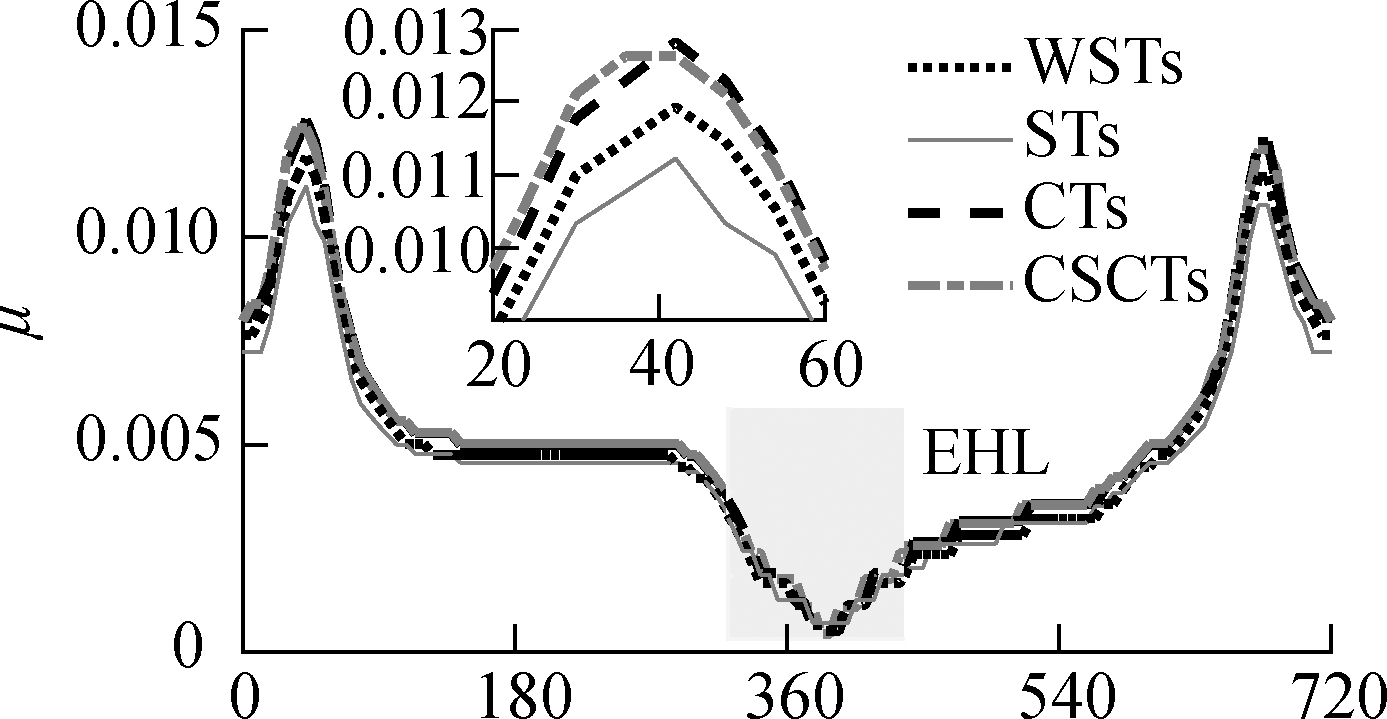
(c)
Fig.7 CB’s LFP with various microtextures.(a)Friction force;(b)Asperity contact force;(c)Friction coefficient
Tab.2 Average values of Ff, Wac, and μ

CB surface with textures F/N W/N μ/10-3Optimized CTs 6×6 15 22.9138.3913.51Optimized CB dimensions 8 21.0233.1111.44Dimpled textures 12×6 WSTs15.2029.727.81STs15.0228.297.64CTs16.1930.248.42CSCTs16.1930.688.53
The simulation results of CTs{12×6} are also compared with the results of CTs{6×6}[15] and the optimized CB dimensions[8], as provided in Tab.2.The calculation results indicate that all the ![]() are lower than those of the optimized CTs and CB because the simulation model uses the optimized parameters of both CTs and CB, while Ref.[8]optimized only the CB dimensions, and Ref.[15]used only the optimal parameters of CTs{6×6}.Moreover, the distribution density of STs with a=12 in the x-direction is more than twice that of CTs with a=6.Thus, the contact region between two surfaces of CB can be substantially decreased, resulting in Ff and Wac in the EHL region being lower than in the case where CTs are used with a=6.However, further increasing the density of a reduces the distance lx of microtextures.Thus, the cavitated region of the oil film pressure is increased, and the increase of the p is limited[3, 10].Therefore, the design of STs{12×6} on the bearing surface should be selected to ameliorate the CB’s LFP.
are lower than those of the optimized CTs and CB because the simulation model uses the optimized parameters of both CTs and CB, while Ref.[8]optimized only the CB dimensions, and Ref.[15]used only the optimal parameters of CTs{6×6}.Moreover, the distribution density of STs with a=12 in the x-direction is more than twice that of CTs with a=6.Thus, the contact region between two surfaces of CB can be substantially decreased, resulting in Ff and Wac in the EHL region being lower than in the case where CTs are used with a=6.However, further increasing the density of a reduces the distance lx of microtextures.Thus, the cavitated region of the oil film pressure is increased, and the increase of the p is limited[3, 10].Therefore, the design of STs{12×6} on the bearing surface should be selected to ameliorate the CB’s LFP.
5 Conclusions
1)The shape of STs is better than that of WSTs, CTs, and CSCTs in ameliorating the LFP under different simulation conditions.![]() with STs are significantly reduced by 7.2%, 7.8%, and 10.4%, respectively, compared with those of CSCTs.
with STs are significantly reduced by 7.2%, 7.8%, and 10.4%, respectively, compared with those of CSCTs.
2)The LFP of the CB using STs was remarkably ameliorated compared with that of the optimized dimensions of CTs and CB.![]() were greatly ameliorated by 28.5%, 14.5%, and 33.2% and by 34.4%, 26.3%, and 43.6% in comparison with the CB dimensions optimized in Ref.[8]and CTs{6×6} optimized in Ref.[15], respectively.
were greatly ameliorated by 28.5%, 14.5%, and 33.2% and by 34.4%, 26.3%, and 43.6% in comparison with the CB dimensions optimized in Ref.[8]and CTs{6×6} optimized in Ref.[15], respectively.
3)The contact of the crankpin and bearing surfaces always generates a friction force, which not only increases the frictional power loss but also decreases the CB durability of engines.Therefore, the CB surfaces designed by the STs could contribute to reducing the frictional power loss and increasing the durability of engines.
4)On the basis of the effectiveness of the STs in improving the CB’s LFP, these findings could also be applied to other journal bearings to enhance their lubrication performance and reduce their friction.
[1] Liu K,Xie Y B, Gui C L.A comprehensive study of the friction and dynamic motion of the piston assembly[J].Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 1998, 212(3): 221-226.DOI:10.1243/1350650981542038.
[2] Guzzomi A L, Hesterman D C, Stone B J.Variable inertia effects of an engine including piston friction and a crank or gudgeon pin offset[J].Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2008, 222(3): 397-414.DOI:10.1243/09544070jauto590.
[3] Wang X L, Zhang J Y, Dong H.Analysis of bearing lubrication under dynamic loading consideringmicropolar and cavitating effects[J].Tribology International, 2011, 44(9): 1071-1075.DOI:10.1016/j.triboint.2011.05.002.
[4] Meng X H, Ning L P, Xie Y B, et al.Effects of the connecting-rod-related design parameters on the piston dynamics and the skirt-liner lubrication[J].Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2013, 227(6): 885-898.DOI:10.1177/0954407012464025.
[5] Zhao B, Dai X D, Zhang Z N, et al.A new numerical method for piston dynamics and lubrication analysis[J].Tribology International, 2016, 94: 395-408.DOI:10.1016/j.triboint.2015.09.037.
[6] Fesanghary M, Khonsari M M.Topological and shape optimization of thrust bearings for enhanced load-carrying capacity[J].Tribology International, 2012, 53: 12-21.DOI:10.1016/j.triboint.2012.03.018.
[7] Nguyen V L, Zhang J R, Jiao R Q, et al.Effects of crankpin bearing speed and dimension on engine power[J].Journal of Southeast University(English Edition), 2021, 37(2): 119-127.DOI: 10.3969/j.issn.1003-7985.2021.02.001.
[8] Nguyen V, Wu Z P, Le V.Optimization of crankpin bearing lubrication under dynamic loading considering effect of micro asperity contact[J].Industrial Lubrication and Tribology, 2020, 72(10): 1173-1179.DOI:10.1108/ilt-02-2020-0072.
[9] Zhang H,Hua M, Dong G N, et al.A mixed lubrication model for studying tribological behaviors of surface texturing[J].Tribology International, 2016, 93: 583-592.DOI:10.1016/j.triboint.2015.03.027.
[10] Kovalchenko A, Ajayi O, Erdemir A, et al.The effect of laser surface texturing on transitions in lubrication regimes during unidirectional sliding contact[J].Tribology International, 2005, 38(3): 219-225.DOI:10.1016/j.triboint.2004.08.004.
[11] Tomanik E, Profito F J, Zachariadis D C.Modelling the hydrodynamic support of cylinder bore and piston rings with laser textured surfaces[J].Tribology International, 2013, 59: 90-96.DOI:10.1016/j.triboint.2012.01.016.
[12] Etsion I.Modeling of surface texturing in hydrodynamic lubrication[J].Friction, 2013, 1(3): 195-209.DOI:10.1007/s40544-013-0018-y.
[13] Gropper D, Wang L, Harvey T J.Hydrodynamic lubrication of textured surfaces: A review of modeling techniques and key findings[J].Tribology International, 2016, 94: 509-529.DOI:10.1016/j.triboint.2015.10.009.
[14] Zhang H,Hua M, Dong G Z, et al.Optimization of texture shape based on genetic algorithm under unidirectional sliding[J].Tribology International, 2017, 115: 222-232.DOI:10.1016/j.triboint.2017.05.017.
[15] Jiao R Q, Nguyen V L, Le V, et al.Optimal design of micro-dimples on crankpin bearing surface for improving engine’s lubrication and friction[J].Industrial Lubrication and Tribology, 2021, 73(1): 52-59.DOI:10.1108/ilt-04-2020-0152.
[16] Pei S Y, Ma S L,Xu H, et al.A multiscale method of modeling surface texture in hydrodynamic regime[J].Tribology International, 2011, 44(12): 1810-1818.DOI:10.1016/j.triboint.2011.07.005.
[17] Rosenkranz A, Costa H L, Profito F, et al.Influence of surface texturing on hydrodynamic friction in plane converging bearings—an experimental and numerical approach[J].Tribology International, 2019, 134: 190-204.DOI:10.1016/j.triboint.2019.01.042.
[18] Grützmacher P G, Profito F J, Rosenkranz A.Multi-scale surface texturing in tribology—current knowledge and future perspectives[J].Lubricants, 2019, 7(11): 95.DOI:10.3390/lubricants7110095.
[19] Liu J,Xu Y J, Pan G.A combined acoustic and dynamic model of a defective ball bearing[J].Journal of Sound and Vibration, 2021, 501: 116029.DOI:10.1016/j.jsv.2021.116029.
[20] Hu T, Xie L X, Liu J R.Effects of rotor surface texture on rotary vane actuator end sealing performance[J].Tribology International, 2019, 140: 105868.DOI:10.1016/j.triboint.2019.105868.
[21] Marian M,Grützmacher P, Rosenkranz A, et al.Designing surface textures for EHL point-contacts—transient 3D simulations, meta-modeling and experimental validation[J].Tribology International, 2019, 137: 152-163.DOI:10.1016/j.triboint.2019.03.052.
[22] Martan J, Moskal D, Smeták L, et al.Performance and accuracy of the shifted laser surface texturing method[J].Micromachines, 2020, 11(5): 520.DOI:10.3390/mi11050520.
[23] Zhang H,Hua M, Dong G N, et al.Boundary slip surface design for high speed water lubricated journal bearings[J].Tribology International, 2014, 79: 32-41.DOI:10.1016/j.triboint.2014.05.022.
[24] Hua W L, Nguyen V, Le V.Analysis of dimensions of surface textures on lubrication and friction of an engine[J].SAE International Journal of Engines, 2021, 15: 03-15-01-0001.DOI:10.4271/03-15-01-0001.