With the increasing complexity of modern equipment, maintenance technology, and costs, corrective maintenance concepts cannot satisfy the requirements of equipment maintenance reliability and economy; as such, the maintenance strategy of economic optimization has been continuously studied.With in-depth studies on preventive maintenance and the urgent need for a multicomponent maintenance economy, numerous multipart opportunity maintenance models have been developed[1-2].In a multicomponent system, stochastic, structural, and economic dependence usually exist between components[3], and opportunity maintenance is a common strategy that involves applying economic dependence to reduce maintenance costs[4].Xu et al.[5] quantified the economic relevance between different instruments and verified the effectiveness of opportunistic maintenance.Van Horenbeek et al.[6] considered the dependencies between components and established a dynamic predictive maintenance strategy for multicomponent systems.Salari et al.[7] created an opportunistic maintenance model for a two-component system with economic relevance and different failure modes.Hu et al.[8] used the Wiener process to establish an opportunistic maintenance model for a series of systems composed of two economically relevant degraded components.In addition to the correlation between components, opportunistic maintenance can be conducted on the basis of the relationship between external conditions and systems.Besnard et al.[9] combined failure opportunities with the measured wind farm data and developed an opportunity repair model to minimize maintenance costs.Zhang et al.[10] used a Markov chain model to describe the wind speed time series and proposed an opportunistic maintenance strategy by considering random weather conditions and spare part inventory.Yang et al.[11] established an opportunity maintenance strategy for a randomly waiting production system.Zheng et al.[12] considered the three types of failures of components and put forward an opportunistic maintenance strategy related to the influence of wind speed.Considering the opportunity of maintenance, Zhang et al.[13] created a two-level maintenance threshold strategy and applied simulation to verify the economic advantages of this strategy.
In most studies, only a single repair condition is set to determine the repair method of components.Although benefits can be guaranteed to a certain extent, comprehensive opportunity maintenance control conditions are consistent with actual operating conditions.Therefore, multipart opportunistic maintenance under cost-effectiveness and imperfect maintenance is proposed.In this study, cost-benefit analysis based on the failure rate is proposed by considering the recovery degree of the failure rate of various maintenance methods.Specific maintenance methods are determined by comparing the cost-benefit ratios of different maintenance methods.A preventive maintenance decision-making model for imperfect maintenance of wind turbines is also established.Finally, it is compared with a model that does not consider the cost-effectiveness ratio and opportunity maintenance to verify the economics and effectiveness of the proposed model.
1 Maintenance Model
1.1 Maintenance model assumptions and maintenance strategy
Opportunity maintenance is one of the most commonly used methods in multicomponent systems.The principle of opportunity maintenance is shown in Fig.1.For a system composed of multiple components, each component has an opportunity maintenance reliability threshold Ro and preventive maintenance reliability threshold Rp.When one of the components runs to tp, its reliability reaches Rp, and preventive maintenance is performed on that component while providing an opportunity for other components to be repaired.
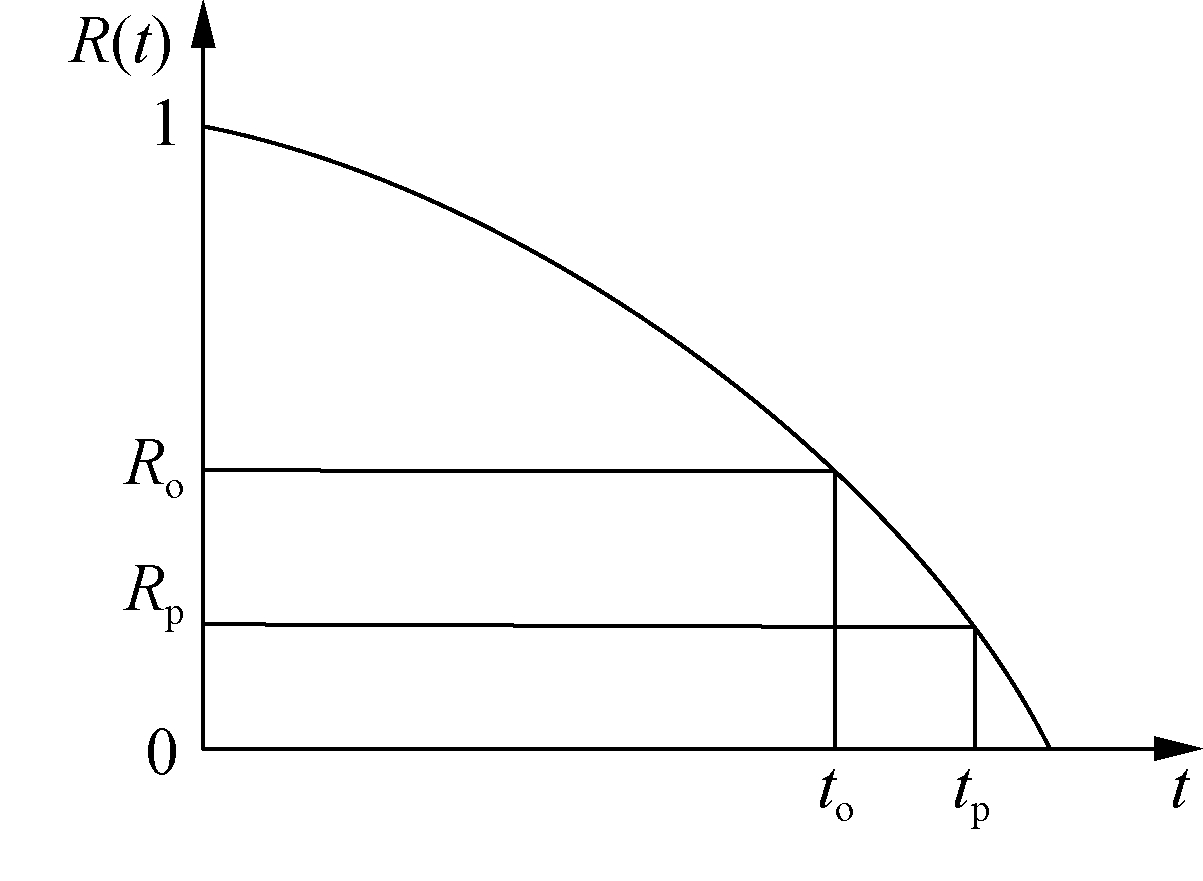
Fig.1 Schematic of opportunity maintenance
For other components, the repair methods are as follows:
1)When the reliability of a given component is R>Ro, no maintenance is performed on the component.
2)When the reliability of the component is Rp<R≤Ro, the component is in the opportunity maintenance interval.It is undergoing preventive maintenance, so it can be repaired.
Preventive maintenance and opportunistic maintenance involve two maintenance methods: imperfect maintenance and replacement.In this study, the maintenance method is selected and determined through cost-effectiveness analysis to obtain a more economical maintenance method.
The following model assumptions are made:
1)The fault distribution of components in a system is independent of one another and obeys the Weibull distribution.
2)The unexpected failure of the system is completed with minimum maintenance, which does not change the failure rate of the system.
3)The system starts in a completely new state.
4)The system has sufficient maintenance resources during maintenance.
1.2 Evolution of failure rate
If the failure of the system follows the two-parameterWeibull distribution with the shape parameter of β and the scale parameter of γ, the expression of the failure rate is
(1)
The failure rate decreases after the imperfect preventive maintenance of the component.However, as the number of repairs increases, the recovery rate of the failure rate lessens, and the failure rate increases.The relationship between the failure rate function of the equipment before and after imperfect maintenance can be defined as[14]
λi,m(t)=bi-1λi-1,m(t+ηi-1Ti-1,m)
(2)
where i=1, 2, …, n is the amount of preventive maintenance; Ti-1,m is the working time of the(i-1)-th maintenance cycle of m; ηi-1 is the age reduction factor, and 0<ηi-1 < 1; bi-1>1 is the hazard rate increase factor; λi,m(t)is the failure rate distribution function of m before the i-th preventive maintenance.
The failure rate function in the i-th preventive maintenance cycle Ti of m can be written as
![]()
2≤i≤n, t∈[0,Ti)
(3)
1.3 Determination of a nonequal maintenance cycle
Each component exists independently and does not affect other components, and the reliability of components changes with the failure rate after each imperfect repair or replacement.The relationship between the failure rate and reliability is
(4)
Considering the constraint of the preventive maintenance reliability threshold Rp, the failure risk of each preventive maintenance cycle is the same, so the reliability equation is as follows:
(5)
Eq.(5)can be transformed into the following equation:
![]() λ1(t)dt=
λ1(t)dt=![]() λ2(t)dt=…=
λ2(t)dt=…=![]() λi(t)dt=-lnRp
λi(t)dt=-lnRp
(6)
where ![]() λi(t)dt is the cumulative failure risk during the i-th maintenance interval.
λi(t)dt is the cumulative failure risk during the i-th maintenance interval.
According to Eqs.(1)and(6), T1 can be calculated.Combining Eqs.(1),(3)and(6), the i-th nonequal maintenance cycle can be obtained as

2≤i≤n
(7)
Opportunistic maintenance can improve the current repair time of components and affect the subsequent repair cycles.Therefore, ![]() should meet the following conditions:
should meet the following conditions:
(8)
where ![]() -th maintenance cycle when opportunistic maintenance is considered for
-th maintenance cycle when opportunistic maintenance is considered for ![]() is the new failure rate function, which can be determined by Eq.(3)and the previous i-1 actual maintenance cycle.
is the new failure rate function, which can be determined by Eq.(3)and the previous i-1 actual maintenance cycle.
When opportunistic maintenance occurs, it affects the failure rate and service interval of the component in the next cycle.Therefore, in the calculation of the unequal maintenance period, the maintenance time of other components and the reliability of the current component should be considered comprehensively.Then, if the first i-1 maintenance interval of m is known, ![]() can be obtained from Eqs.(3)and(8)as
can be obtained from Eqs.(3)and(8)as

2≤i≤n
(9)
where Tk,m is the actual operating cycle of m, 1≤k≤i-1.
1.4 Maintenance costs of multi-component systems
In the maintenance of multi-component systems, the following maintenance costs are mainly considered: minimal maintenance cost(Cv,m), imperfect maintenance cost(Cp,m), opportunistic maintenance cost(Co,m), preventive replacement costs(Cf,m), opportunity replacement cost(Cr,m), and downtime loss(Cd).
1.4.1 Dynamic minimum total maintenance cost
When m has an unexpected failure in the i-th cycle, minimum maintenance is conducted, and no opportunity for maintenance is available.The maintenance cost in an imperfect maintenance cycle can be expressed as
Cv,i,m=CmFi,m
(10)
where Cm is the single maintenance cost; Fi,m=![]() λi(t)dt is the minimum number of repairs in the i-th cycle of m.
λi(t)dt is the minimum number of repairs in the i-th cycle of m.
1.4.2 Imperfect preventive maintenance cost
If m undergoes incomplete preventive maintenance in the i-th cycle, its total cost includes the cost of single imperfect maintenance and the downtime loss:
Cp,i,m=Ch,m+tp,mCd
(11)
where Ch,m is the single imperfect maintenance cost of m; tp,m is the single imperfect maintenance time of m; Cd is the cost of loss per unit time.
1.4.3 Imperfect opportunity maintenance cost
When part m receives the opportunity to repair, its total costs include the costs of imperfect opportunity maintenance and penalty.The penalty cost for opportunity maintenance to repair m at the i-th maintenance is
(12)
where Cs,m is the penalty fee per unit time.Therefore, the imperfect opportunity maintenance cost of m in the i-th maintenance interval is
Co,i,m=Cg,m+Cc,i,m
(13)
where Cg,m is the single imperfect opportunity maintenance cost of m.
1.4.4 Preventive replacement cost
When m is replaced in the i-th cycle, its cost includes the replacement cost of the component and the downtime loss:
Cf,i,m=Ce,m+CdTf
(14)
where Ce,m is the replacement cost of m; Tf is the time required for replacement.
1.4.5 Opportunity replacement cost
When m has an opportunity for maintenance in the i-th cycle and meets the replacement conditions, m can be replaced with an opportunity.The cost includes the replacement cost of m and the penalty fee for early replacement:
Cr,i,m=Cf+Ce,m
(15)
where Cf is a fixed penalty fee.
The preventive maintenance of multi-component systems is an ongoing periodic process, and the components during each cycle have different maintenance methods.The following factors are introduced to facilitate calculation:
where ψi,m indicates whether m has maintenance activity during the i-th shutdown.
If part m needs maintenance, the reliability of the component can be determined in the opportunistic maintenance interval or the preventive maintenance interval according to the following equation:
The maintenance method of m during the i-th shutdown is
The maintenance method of m during the i-th shutdown is
Combined with the above various maintenance methods, the maintenance cost of m during the i-th shutdown maintenance of the system can be described as
(16)
The total cost of N components in the system at the i-th shutdown for maintenance is
(17)
In the interval[0,T], the system has performed M maintenance, the total maintenance cost is
(18)
1.5 Choice of the maintenance method
The failure rate of the component can be restored after imperfect maintenance but cannot return to 0:
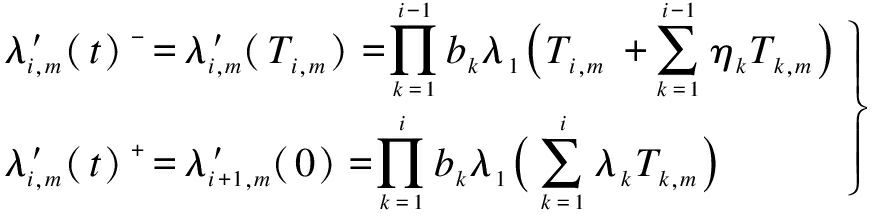
(19)
The difference in the failure rate before and after imperfect maintenance is used to express the repair effect, which is expressed as follows:
(20)
After replacement, the failure rate of the parts can decrease to 0:

(21)
After being replaced, the part is restored as new, and the difference in the failure rate before and after the replacement is equivalent to the failure rate before maintenance:
(22)
If the part fails unexpectedly during maintenance intervals, the failure rate of the parts cannot be changed after the minimum maintenance.
When the system shuts down for the i-th time at time t, if m is in the preventive maintenance interval, the recovery level of the failure rate is used as the maintenance effect.The cost-effectiveness ratio of the imperfect preventive maintenance can be obtained as
(23)
After replacement, the failure rate of the component becomes 0, and the cost-effectiveness ratio of preventive replacement can be obtained as
(24)
According to Eqs.(23)and(24), the method of preventive maintenance for the i-th component m can be determined, so qi,m is assigned as follows:
When the system shuts down for the i-th time at time t, if m is in the opportunity maintenance interval, the recovery level of the failure rate as the maintenance effect is taken, and the cost-effectiveness ratio of the imperfect opportunity maintenance is
(25)
After replacement, the failure rate of the component becomes 0, and the cost-effectiveness of the opportunity replacement is
(26)
According to Eqs.(25)and(26), the i-th opportunity maintenance mode of m can be determined, so Oi,m is assigned as
2 Numerical Examples
In this section, an example is used to verify the effectiveness of the wind power system maintenance method proposed in this paper.In this example, four key components in each wind turbine are studied: the rotor, the main bearing, the gearbox, and the generator.The failure rate is independent of one another and obeys the two parameters of the Weibull distribution.These parameters and the reliability of each component are shown in Tab.1.The age reduction factor is ηi=i/(3i+7),and the hazard increasing factor is bi=(12i+1)/(11i+1)[15].
Tab.1 Weibull distribution parameters and reliability parameters
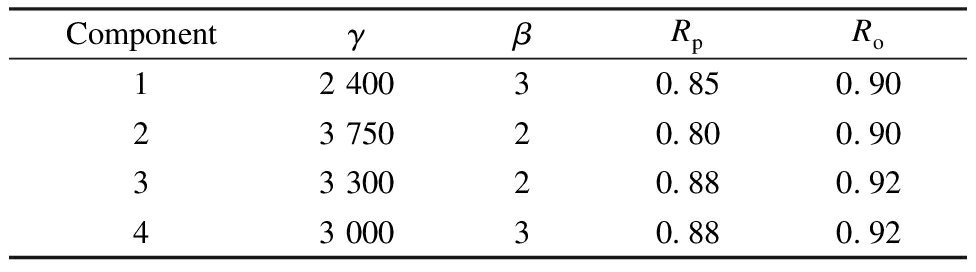
ComponentγβRpRo12 40030.850.9023 75020.800.9033 30020.880.9243 00030.880.92
In a previous study[16], the maintenance parameters of each component are specified(see Tab.2).
Tab.2 Maintenance parameters
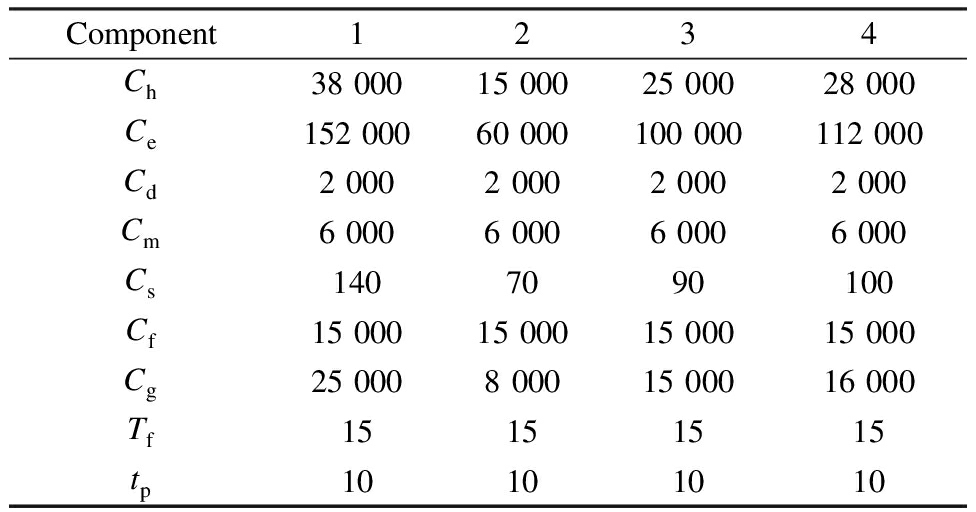
Component1234Ch38 00015 00025 00028 000Ce152 00060 000100 000112 000Cd2 0002 0002 0002 000Cm6 0006 0006 0006 000Cs1407090100Cf15 00015 00015 00015 000Cg25 0008 00015 00016 000Tf15151515tp10101010
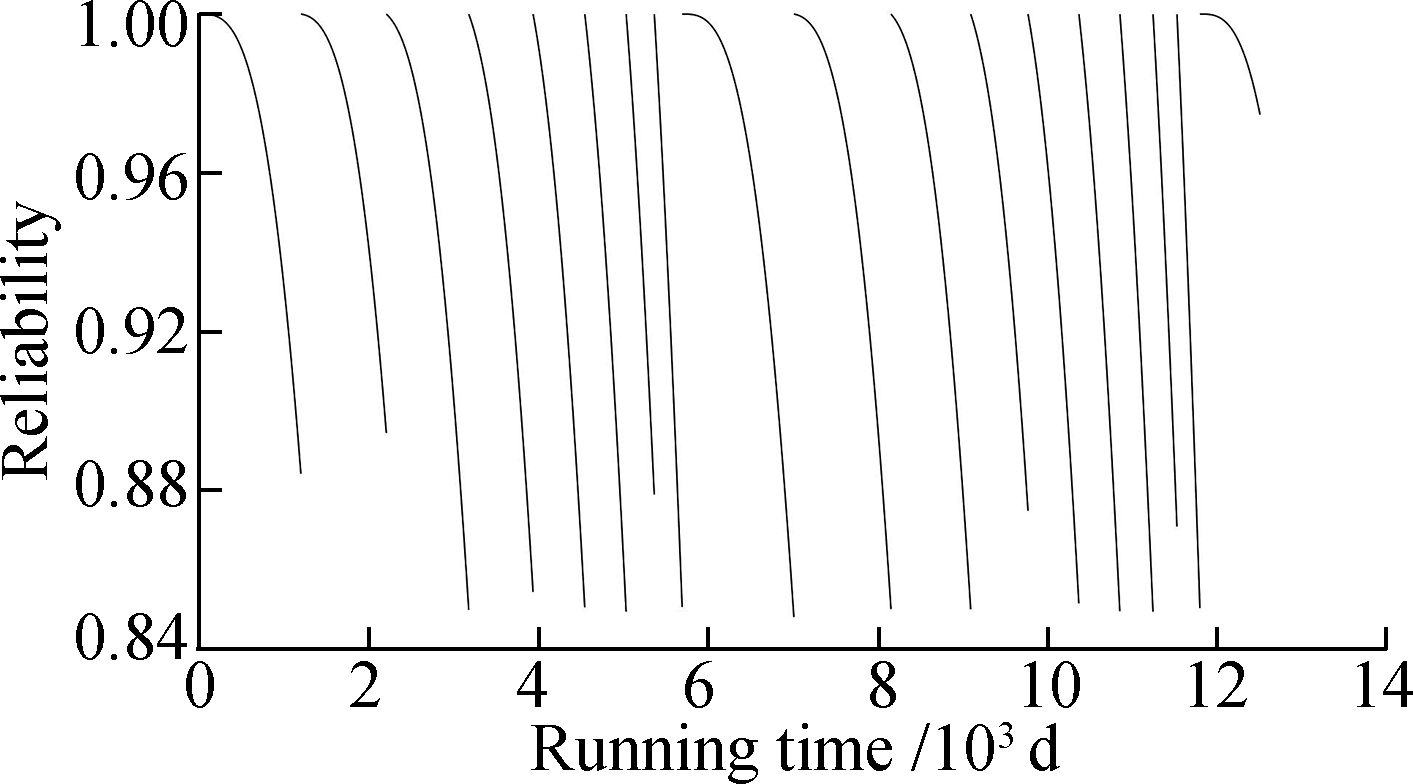
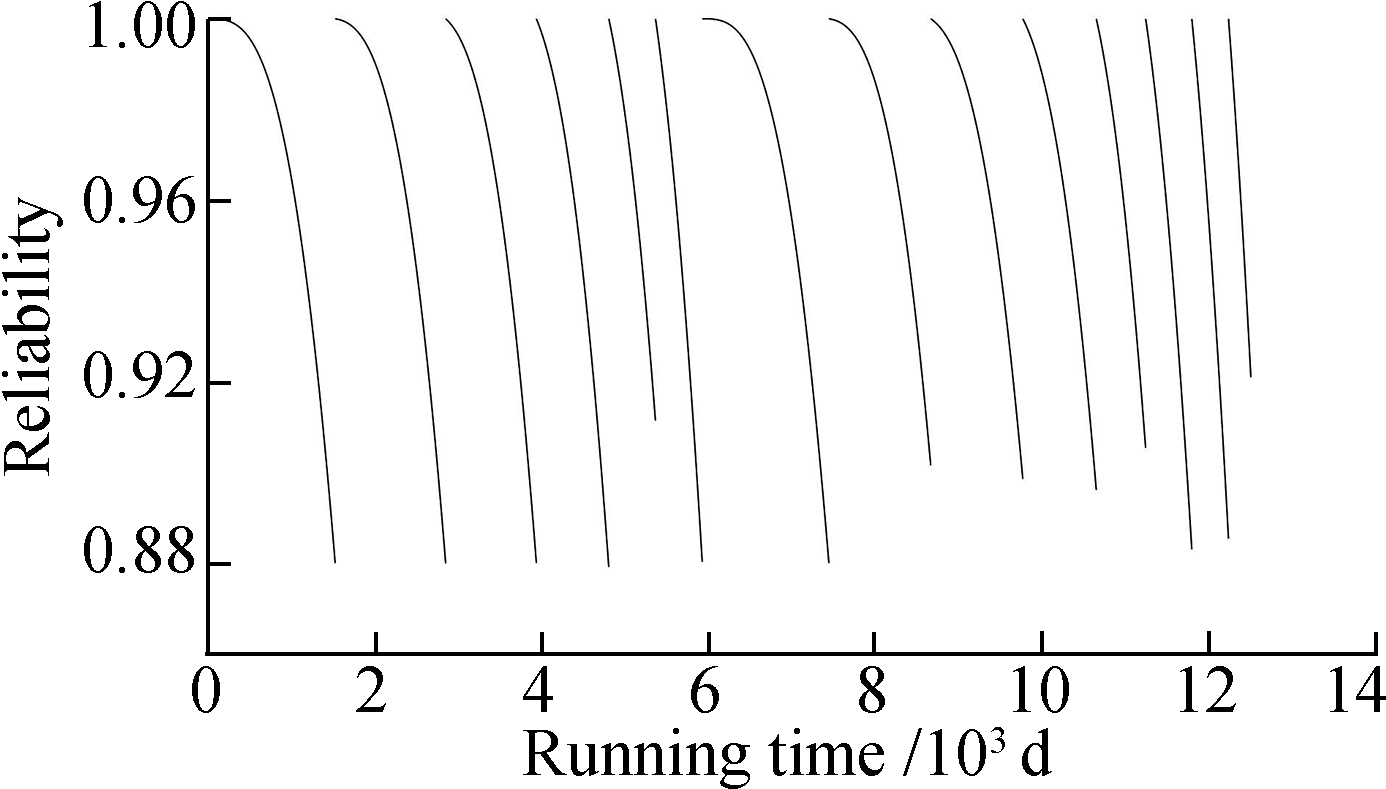
A reliability change curve for each component during the operation time of[0, 12 500]d is obtained on the basis of the data in Tab.1, Tab.2, and the proposed model(see Fig.2).Several representative strategies are selected from the specific maintenance plan for analyzing the samples.
(a)

(b)

(c)
(d)
Fig.2 Reliability curves.(a)Component 1;(b)Component 2;(c)Component 3;(d)Component 4
At 1 195 d, Component 3 initially reaches the preventive maintenance time.At this time, the reliability of Component 1 is 0.883 9, which is in the opportunity maintenance interval, and it can be opportunistic maintenance.The cost-effectiveness ratio of the imperfect opportunity maintenance is better than that of opportunity replacement.The reliabilities of Components 2 and 4 are 0.903 5 and 0.938 8, respectively, which are greater than their opportunity maintenance reliability threshold.As such, no maintenance is performed.
When the system runs to 9 764 d, Component 4 reaches the preventive maintenance reliability threshold.At this time, the reliability of Components 1, 2, and 3 are within the opportunity maintenance interval, and maintenance can be performed simultaneously.The cost-effectiveness ratio of the imperfect opportunistic maintenance for Components 1 and 3 is less than that of replacement; in this way, the imperfect opportunity maintenance is chosen.The replacement cost-effectiveness ratio of Component 2 is less than that of imperfect opportunity maintenance; thus, Part 2 is replaced.
By the time the system runs to 12 500 d, Part 1 has carried out nine imperfect preventive maintenances, six imperfect opportunity maintenances, and two preventive replacements.Part 2 has undergone eight opportunistic imperfect maintenances and two opportunity replacements.Part 3 has undergone eight imperfect preventive maintenances, five imperfect opportunity maintenances, and two preventive replacements.Part 4 has been under seven imperfect preventive maintenances, five imperfect opportunity maintenances, and one preventive replacement.
The maintenance strategy, combined with Fig.2 and the specific maintenance plan described above, can reasonably determine the maintenance method according to the actual reliability of components.When the preventive maintenance of a component is performed, in most instances, one or more components can be maintained, the fixed repair costs can be shared equally, and downtime and costs can be saved.The reliability of the components has a certain periodicity.After several imperfect maintenances, the degree of system deterioration accumulates to a certain extent, and the failure rate of each part increases.Consequently, the maintenance interval shortens when it reaches a certain level.The cost-effectiveness ratio of incomplete repair is higher than the cost-effectiveness ratio of replacement.Therefore, replacement is used to restore the parts as new and ensure the stable operation of the whole system, which is consistent with the actual operation.
3 Model Comparison Study
The economy and effectiveness of the multipart opportunity maintenance strategy based on cost-effectiveness are verified by comparing it with the single-part preventive maintenance model without cost-effectiveness and opportunity maintenance.The optimization results of the single-component preventive maintenance strategy can be derived on the basis of the same maintenance parameters.
The comparison between the two models is shown in Tab.3.Strategy 1 means single-component preventive maintenance(replacement); Strategy 2 means preventive maintenance opportunities considering cost-effectiveness; Mpm, Mom, Mpr, and Mor are the amounts of preventive maintenance, opportunistic maintenance, preventive replacement, and opportunistic replacement, respectively.The total number of preventive maintenances decreases from 34 to 24, and the number of replacements decreases from 10 to 7 in the proposed model compared with that of the single-component preventive maintenance model, although the model adds 24 opportunistic maintenances.After calculation, the maintenance cost is reduced from 3.073 2 million yuan to 2.699 6 million yuan.The cost of opportunistic maintenance is much lower than the replacement cost, and the total maintenance cost is reduced by 373 600 yuan; that is, saving 12.16% of the maintenance costs, which shows that the preventive opportunistic maintenance model based on the cost-effectiveness ratio is more economical.
Tab.3 Maintenance strategy and cost comparison

ComponentStrategy 1Strategy 2MpmMprMpmMomMprMorGearbox939620Bearing720802Generator1038520Rotor827510
4 Conclusions
1)Cost-effectiveness analysis involving multiple maintenance methods based on the failure rate is applied to the multicomponent opportunity maintenance strategy, which effectively overcomes the lack of only considering reliability in the previous opportunity maintenance strategy.It also conforms to the actual maintenance situation.
2)The comprehensive consideration of the economic relevance between multiple components, the effect of opportunistic maintenance on the reliability of each component, the recovery degree of different maintenance methods, and the cost-effectiveness based on the failure rate are used as the control conditions of the maintenance method.The economical and reasonable maintenance method is selected to ensure that wind turbines can run with high reliability while saving on maintenance costs.
3)The cost-effectiveness maintenance model based on reliability changes is more economical and feasible.The results show that this strategy can describe the economic relevance between multiple components, improve the maintenance coordination of the system, and save maintenance costs by applying this method to wind turbines for verification.
[1] Ding F F, Tian Z G.Opportunistic maintenance for wind farms considering multi-level imperfect maintenance thresholds[J].Renewable Energy, 2012, 45(1): 175-182.DOI: 10.1016/j.renene.2012.02.030.
[2] Abdollahzadeh H, Atashgar K, Abbasi M.Multi-objective opportunistic maintenance optimization of a wind farm considering limited number of maintenance groups[J].Renewable Energy, 2016, 88: 247-261.DOI: 10.1016/j.renene.2015.11.022.
[3] Nzukam C, Voisin A, Levrat E, et al.Opportunistic maintenance scheduling with stochastic opportunities duration in a predictive maintenance strategy[J].IFAC-Papers OnLine, 2018, 51(11): 453-458.DOI: 10.1016/j.ifacol.2018.08.348.
[4] Liu G, Chen S, Jin H, et al.Optimum opportunistic maintenance schedule incorporating delay time theory with imperfect maintenance[J].Reliability Engineering & System Safety, 2021, 213: 107668.DOI: 10.1016/j.ress.2021.107668.
[5] Xu B, Han X S,Sun H B, et al.A new opportunistic maintenance optimization model for power generating unit[J].Proceedings of the Chinese Society of Electrical Engineering, 2018, 38(1):120-129.DOI:10.13334/j.0258-8013.pcsee.162236.(In Chinese)
[6] Van Horenbeek A, Pintelon L.A dynamic predictive maintenance policy for complex multi-component systems[J].Reliability Engineering & System Safety, 2013, 120(1): 39-50.DOI: 10.1016/j.ress.2013.02.029.
[7] Salari N, Makis V.Optimal preventive and opportunistic maintenance policy for a two-unit system[J].International Journal of Advanced Manufacturing Technology, 2016, 89: 665-673.DOI: 10.1007/s00170-016-9127-x.
[8] Hu J, Shen J, Shen L.Opportunistic maintenance for two-component series systems subject to dependent degradation and shock[J].Reliability Engineering & System Safety, 2020, 201: 106995.DOI: 10.1016/j.ress.2020.106995.
[9] Besnard F, Patrikssont M, Strombergt A B, et al.An optimization framework for opportunistic maintenance of offshore wind power system[C]//IEEE 2009 Power tech Conference. Bucharest,Romania, 2009: 1-7.DOI: 10.1109/PTC.2009.5281868.
[10] Zhang C, Gao W, Yang T, et al.Opportunistic maintenance strategy for wind turbines considering weather conditions and spare parts inventory management[J].Renewable Energy, 2019, 133: 703-711.DOI: 10.1016/j.renene.2018.10.076.
[11] Yang L, Zhao Y, Peng R, et al.Opportunistic maintenance of production systems subject to random wait time and multiple control limits[J].Journal of Manufacturing Systems, 2018, 47: 12-34.DOI: 10.1016/j.jmsy.2018.02.003.
[12] Zheng R, Zhou Y, Zhang Y.Optimal preventive maintenance for wind turbines considering the effects of wind speed[J].Wind Energy, 2020, 23(11): 1987-2003.DOI: 10.1002/we.2541.
[13] Zhang C, Gao W, Guo S, et al.Opportunistic maintenance for wind turbines considering imperfect, reliability-based maintenance[J].Renewable Energy, 2017, 103: 606-612.DOI: 10.1016/j.renene.2016.10.072.
[14] Zhou X J, Lu Z Q, Xi L F, et al.Opportunistic preventive maintenance optimization for multi-unit series systems with combing multi-preventive maintenance techniques[J].Journal of Shanghai Jiaotong University(Science), 2010, 15(5): 513-518.DOI: 10.1007/s12204-010-1042-y.
[15] Zhou X J, Xi L F, Lee J.Reliability-centered predictive maintenance scheduling for a continuously monitored system subject to degradation[J].Reliability Engineering & System Safety, 2007, 92(4): 530-534.DOI: 10.1016/j.ress.2006.01.006.
[16] Tian Z G, Jin T D, Wu B, et al.Condition based maintenance optimization for wind power generation systems under continuous monitoring[J].Renewable Energy, 2011, 36(5): 1502-1509.DOI: 10.1016/j.renene.2010.10.028.