Difficulties with mastering rational numbers center on decimals and fractions[1].Hence, strategies between decimal and fraction processing are crucial for rational number learning, making them a focus of numerical cognition research.Several studies have used neural imaging, which substantially contributed to the development of neurophysiological models associating neural substrates with magnitude processing.One of these neurofunctional theories, Dehaene’s triple-code model[2], suggests that magnitude processing can be decomposed into verbally and visually encoded mechanisms as well as analog magnitude numerosity.Although most studies based on the model have focused on the whole processing of integers or decimals and fractions separately, there have been few studies focusing on the similarities and differences between decimal and fraction processing.Furthermore, although additive effects of notation perception and semantic distance suggest that distinct stages of identification and semantic access function successively[3] during magnitude processing, few studies have attempted to isolate identifiable stages from the confounded magnitude processing.
Theories explaining evolutionary numerosity have centered on alignments between a sense of an inherent entity and an acquired symbolic fraction[4-6].During the identification stage, a bipartite-structured fraction inherently implies a discretized entity, while a unidimensional decimal suggests a continuous entity.The alignments suggest ontological distinctions that deeply affect the strategy with which an individual identifies them[4-5].On the other hand, the distance effect is an important indicator during the semantic access stage[7].Numeral pairs further apart are quicker and easier to compare(e.g., 1 to 9 vs.7 to 8).Based on distance effects, greater reliance is placed on an exact strategy for decimals, while an approximate strategy is emphasized for fractions[8].However, these interferences have only been verified in behavioral studies.Therefore, reevaluating the early entity systems to explore neural spatiotemporal dissociation of symbolic fraction identification strategies and semantic access strategies is important.
According to previous event-related potential(ERP)studies, high-level identification related to strategy selection is usually reflected in the P2 component, whereas the activation of semantic access affected by the distance effect is mainly reflected in P2 and N2 components[7,9-13].Other studies have shown that strategic processing starts within 250 ms poststimulus and that approximation elicits a greater P2 component[14-15].On the other hand, N2 has been observed in response to the exact calculation strategy, which involves more semantic information stored in the memory[11,13].
An “isolation” paradigm has been designed to separate substages from magnitude processing, which might also prompt participants to use holistic representation[16-18].The present study aims to dissociate the number type-dependent identification strategies associated with entity preference and the semantic strategies associated with distance effect.It is hypothesized that topography signatures and ERP waveforms of P2 and N2 related to the significant number type effect and its interactions with the entity or distance effects may be detected.
1 Methods
1.1 Participants
Fifty-eight right-handed college students(28 males, Mage=21.57, Sage=1.34)without known dyscalculia were recruited.All subjects received financial compensation for their participation and were asked to sign an informed consent form.The experiment was approved by the Ethics Committee of the Affiliated Zhongda Hospital, Southeast University, China.
1.2 Stimulus and procedure
All the participants performed a comparison task consisting of two types of symbolic fractions(i.e., decimal and fraction)and two types of entity(i.e., continuous and discretized).Three hundred and twenty comparison pairs were designed.For each trial, the participants were first presented with an entity in bar or pie diagram form and were required to remember the entity magnitude.A fraction or a decimal is then presented on the screen until the participant responded by stating which magnitude was larger.The following highly controlled experimental settings were used: 1)complex decimals and infrequently used fractions both consist of two digits.2)In the fraction task block, no common components were shown between the symbolic fraction and non-symbolic fraction pairs.3)The pairs under decimals and fractions are more or less the same in terms of potentially relevant properties, such as the numerical distances.Different task orders were counterbalanced across the participants.The instructions emphasized both speed and accuracy.Two types of distances between the magnitude of the entity and the fraction were used: the average “close” distance was 0.11 and the average “far” distance was 0.45.E-prime 2.0 procedure(Psychology Software Tools, Pittsburgh, PA)was used to control the whole experiment.The sequence of events in a single trial is shown in Fig.1.
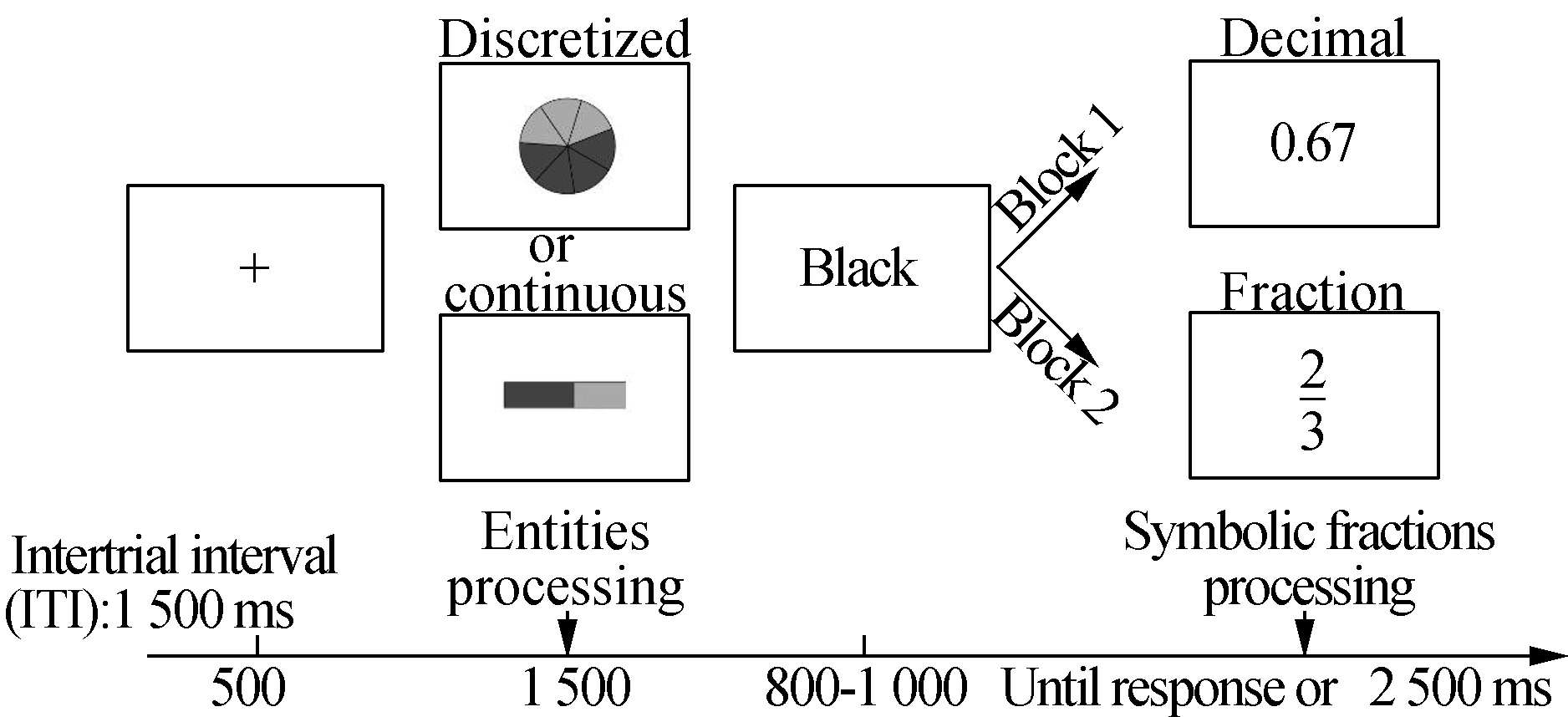
Fig.1 Experimental time sequence in a single trial
1.3 Data analysis
Continuous electroencephalogram(EEG)data were recorded on a 64-channel Neuroscan Inc.(Herndon, Virginia, USA)using the international 10 to 20 system with an average reference on the bilateral mastoids.The sampling rate was 1 000 Hz with a passband filter of 0.1 to 40 Hz.All inter-electrode impedances were below 5 kΩ.Electr-ooculographic signals were simultaneously recorded.Preprocessing of EEG data included rejecting paroxysmal time windows, reducing ocular artifacts, and low-pass filtering below 30 Hz(24 dB/oct)using Scan 4.5 software.During the processing of entity and symbolic fractions, EEG recordings were segmented into 1200-ms epochs with a baseline of 200 ms.Epochs of entity processing and symbolic fraction processing were time-locked to the onset of the entity and symbolic fraction, respectively.Artifact rejection was set at a threshold of ±80 μV.Only epochs with correct responses were retained for calculating the grand average ERP waveforms and topographical distributions of the two processing stages.
After visual inspection of the ERP data and consideration of previous ERP studies[10,19-20], 15 electrodes in five regions(frontal, central, parietal, parieto-occipital, and occipital)were selected with triple laterality(left, middle, and right).Continuous EEG data were segmented into two kinds of epochs.Epochs of-200 to 1 000 ms relative to the onset of the entity and to the onset of the symbolic fraction were associated with entity processing and symbolic fraction processing, respectively.The P2(210 to 270 ms)and N2(270 to 350 ms)components were analyzed for entity processing, while the P2(170 to 250 ms)and N2(250 to 350 ms)components were analyzed for symbolic fraction processing.A significance level of 0.05 was used to apply Greenhouse-Geisser correction for nonsphericity and Bonferroni correction for multiple comparisons.
2 Results
2.1 Behavioral results
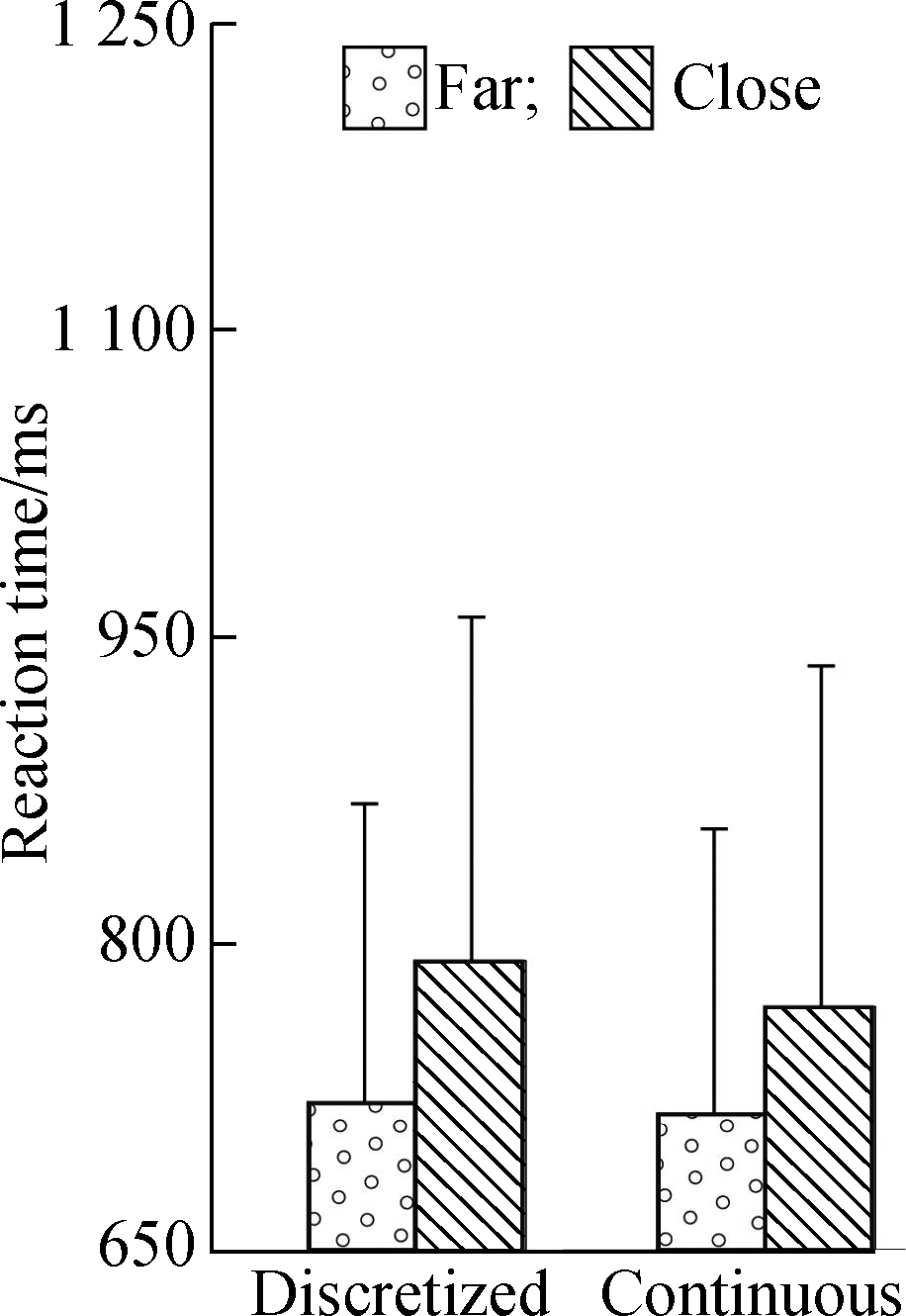
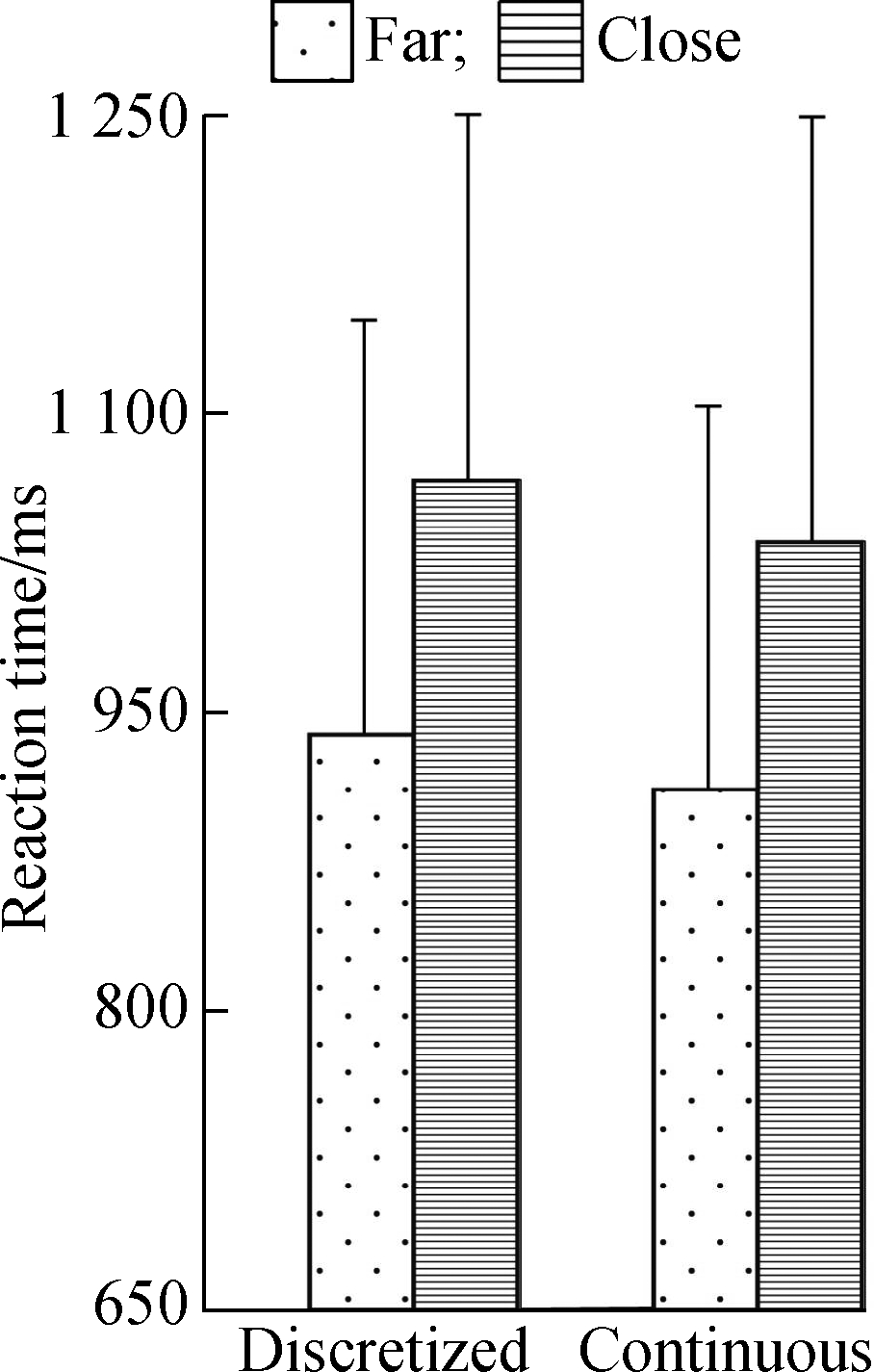
Fig.2 shows the mean reaction time(RT)and accuracy rate(ACC)for decimals and fractions.Repeated-measures ANOVA was used to analyze the number type(i.e., fraction and decimal), distance(i.e., far and close), and entity(i.e., discretized and continuous).
(a)
(b)
(c)
(d)
Fig.2 Behavioral results in decimals and fractions as a function of distance and entity.(a)Mean reaction time in decimals;(b)Mean reaction time in fractions;(c)Accuracy rate in decimals;(d)Accuracy rate in fractions
For RT, the main number type effect was significant(F(1,57)=46.45, p<0.001, 
at 93 ms for decimals, faster than the RT for fractions.The main effect of distance was significant(F(1,57)=438.39, p<0.001, 
at 238 ms for the far distance, faster than the RT for the close distance.Entity effect was also significant(F(1,57)=20.78, p<0.001, 
21 ms for continuous entities, faster than the RT for discretized entities.Number type-distance interaction was significant for decimals(F(1,57)=23.74, p<0.001, 
as the RT for far distance was 206 ms faster than the RT for close distance(p<0.001).However, the distance effect was more pronounced for fractions at 271 ms for the far distance(p<0.001).The entity-distance interaction was marginally significant(F(1,57)=3.96, 
For continuous entities, RT was 226 ms faster for the far distance than for the close distance(p<0.001).A more dramatic distance effect was observed for discretized entities at 249 ms for the far distance, which was faster than the RT for close distance(p<0.001).
For ACC, the main effect of number type was significant(F(1,57)=47.02, p<0.001, with 3.35% higher accuracy for decimals.The main distance effect was also significant(F(1,57)=598.09, p<0.001, 
with 15.08% higher accuracy for the far distance.Number type-distance interaction was also significant 
.Follow-up simple effect analyses showed that for decimals, the far distance has 12% higher accuracy than the close distance(p<0.001).Similarly, the distance effect was also more pronounced for fractions with 18.1% higher accuracy for the far distance(p<0.001).Additionally, number type, entity, and distance interactions of ACC were marginally significant(F(1,57)=3.55, p=0.065, 
For the far distance, continuous entities showed 0.2% higher accuracy than discretized entities in decimals.Discretized entities showed 0.7% higher accuracy in fractions but did not reach the significant level(ps>0.05).
Results showed longer RTs on fractions than on decimals, yielding a 93 ms difference on the number type effect.Moreover, 3.35% more errors were made on fractions than on decimals, ruling out any potential speed and accuracy trade-offs in the experimental paradigm.
2.2 ERP results
Repeated-measures ANOVA was used to analyze the number type, entity, and laterality(i.e., left, midline, and right)for entity processing and number type, distance, and laterality for symbolic fraction processing.Mean amplitudes of P2 and N2 were evaluated.ERP waveforms are illustrated in Figs.3 and 4.
2.2.1 Entity processing
For the P2, mainly the posterior P2(P2p)component, entity and laterality interactions were only significant at the parietal and parieto-occipital regions(Fs(2,114)>5.52, ps<0.01, 
This shows that the entity effect was more pronounced at bilateral sites with larger P2p for discretized entities(ps<0.05)than for continuous entities.
For the anterior N2(N2f)component, number type-entity interactions were significant at the frontal and parietal regions(Fs(1,57)>4.27, ps<0.05, 
with entity effect only for decimals showing larger N2f for continuous entities(p<0.05).The entity-laterality interactions(Fs(2,114)>8.25, ps<0.001, 
were also significant with entity effect at C3 and P3(ps<0.05).For the posterior N2(N2p)component, there was a significant entity effect of opposite polarity in the parieto-occipital region only for fractions, with larger N2p for discretized entities(p<0.05), which was indicated by the number type-entity interaction(F(1,57)=4.25, p<0.05, 
Number type, entity, and laterality interactions were profound(Fs(2,114)>7.25, ps<0.01, 
because of the marginally significant entity effect for fractions with larger N2p evoked by discretized entities at P4, PO4, and O2(ps ≤ 0.066).
(a)
(b)
(c)
(d)
(e)
(b)
(g)
(h)
(i)
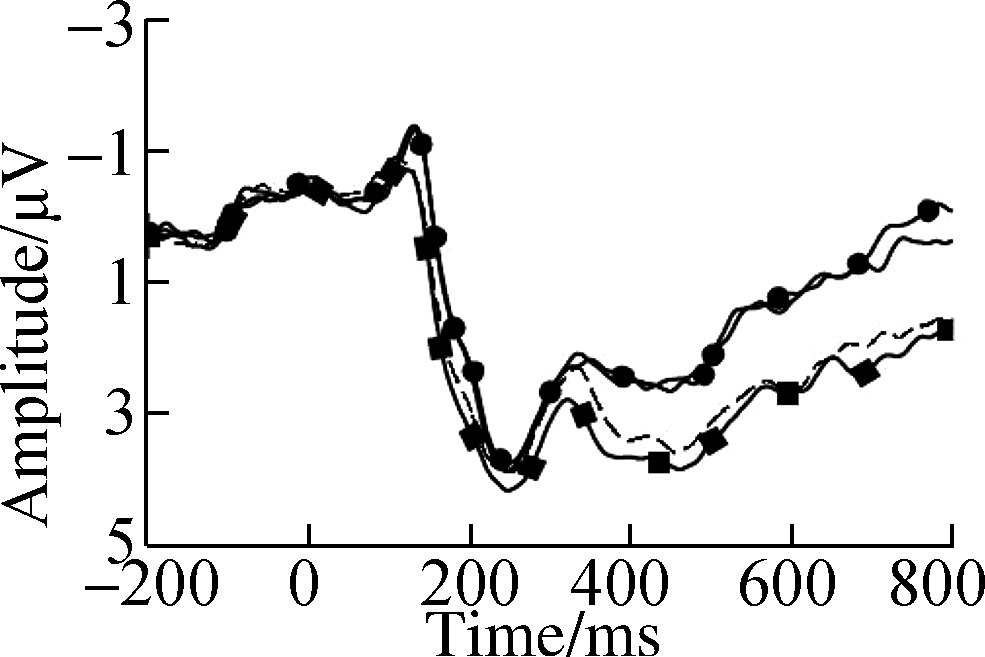
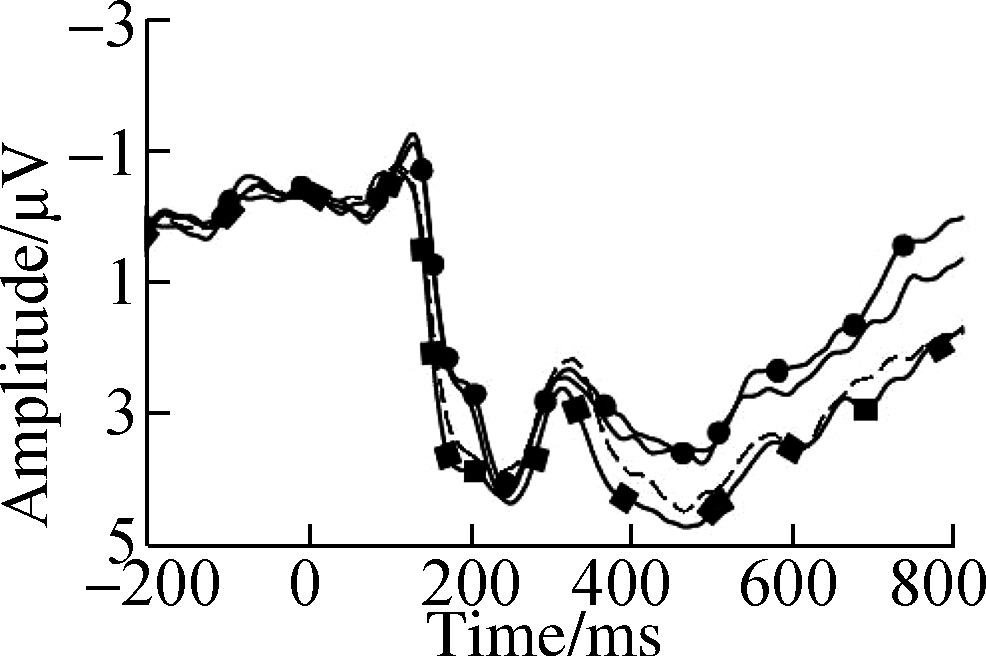
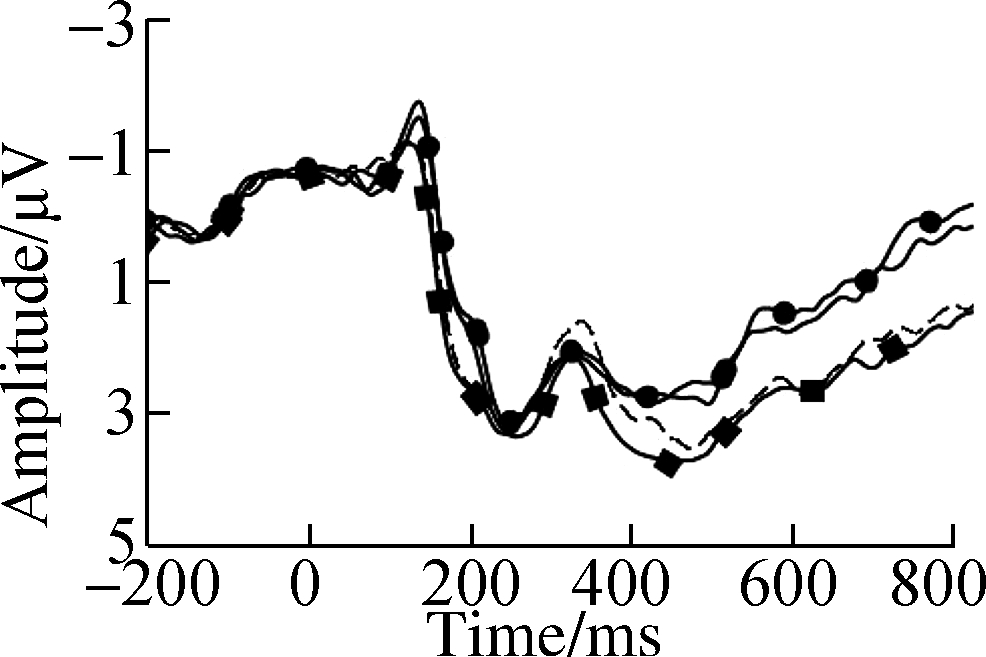
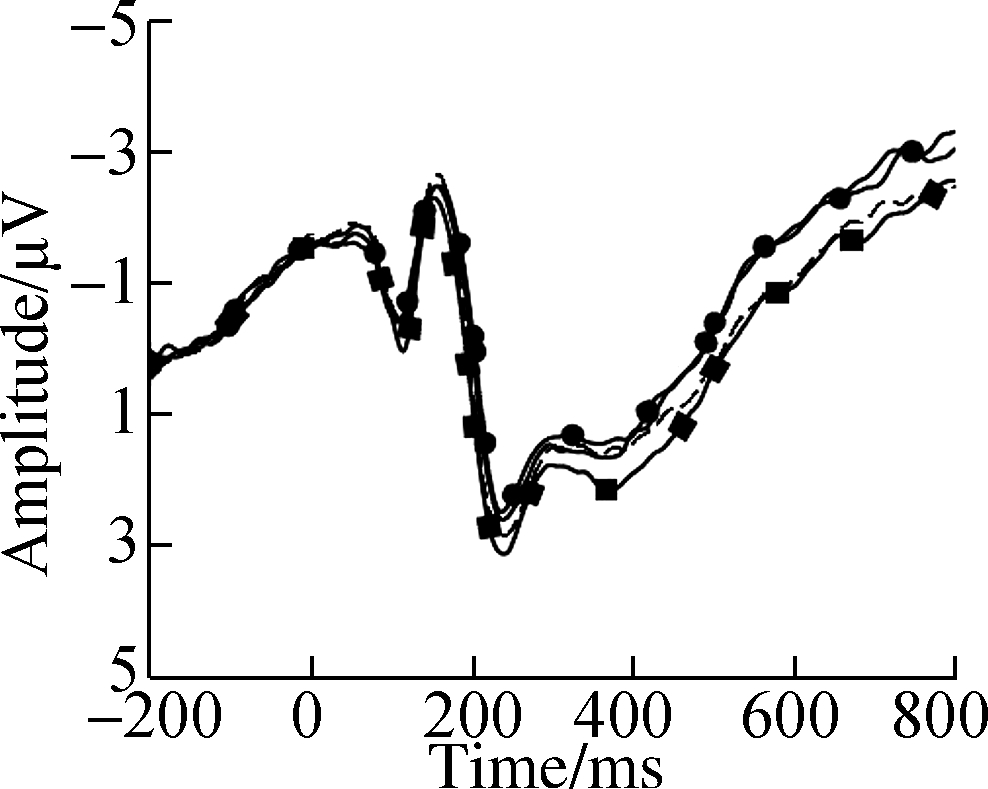
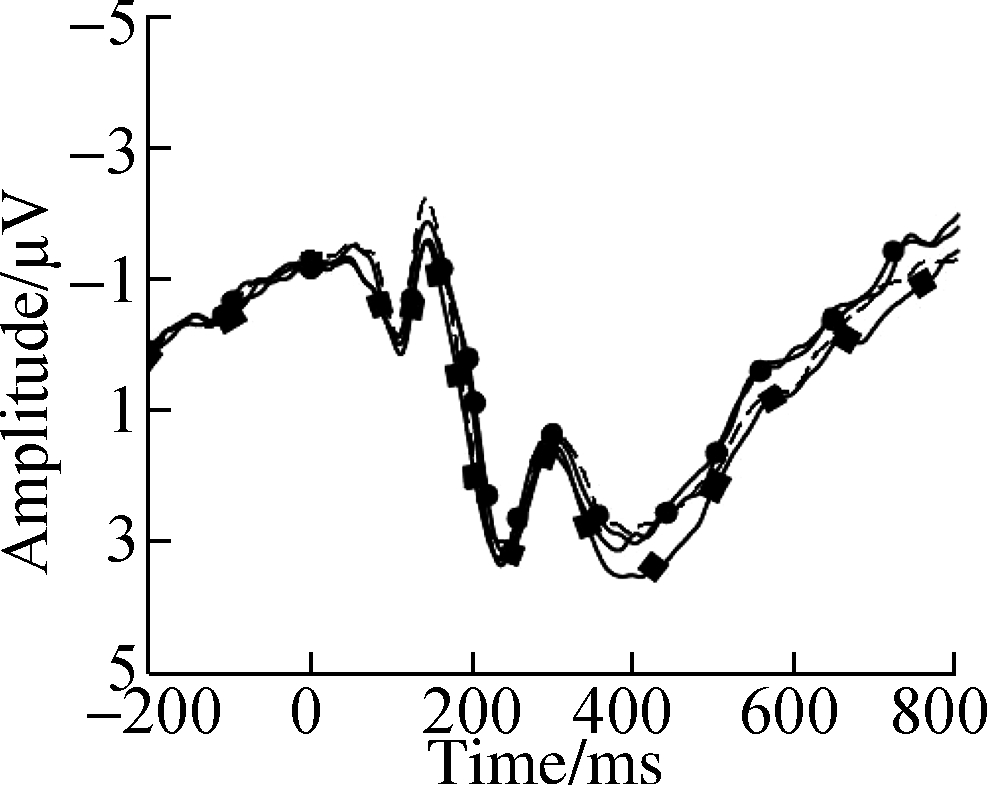
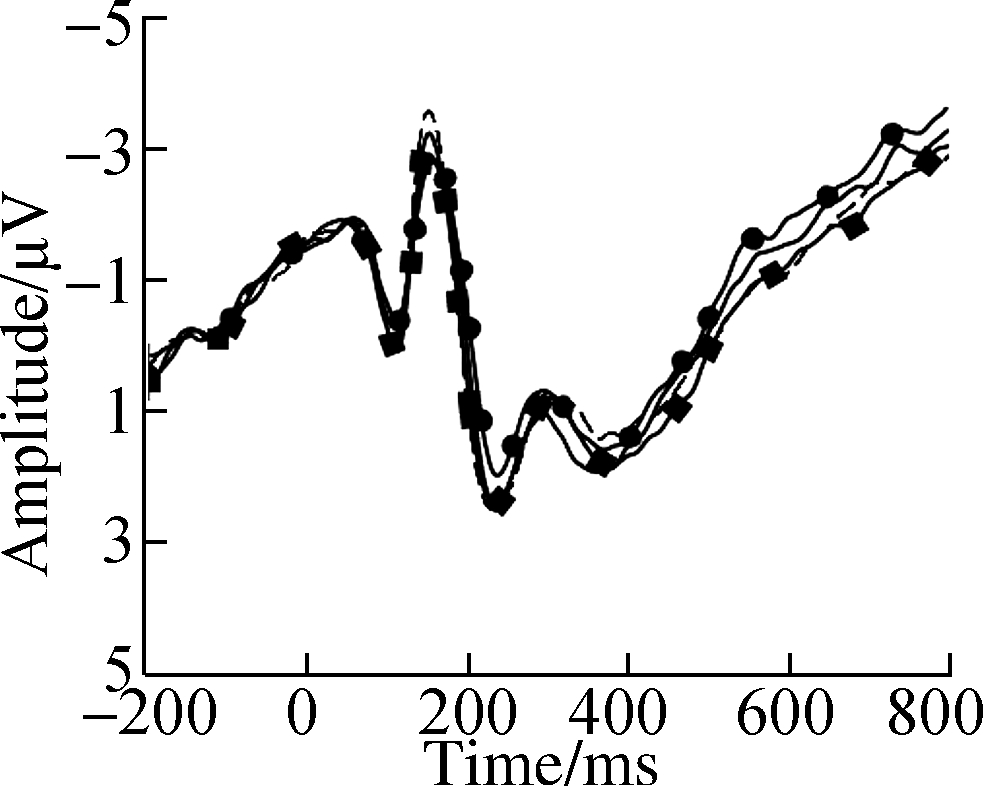
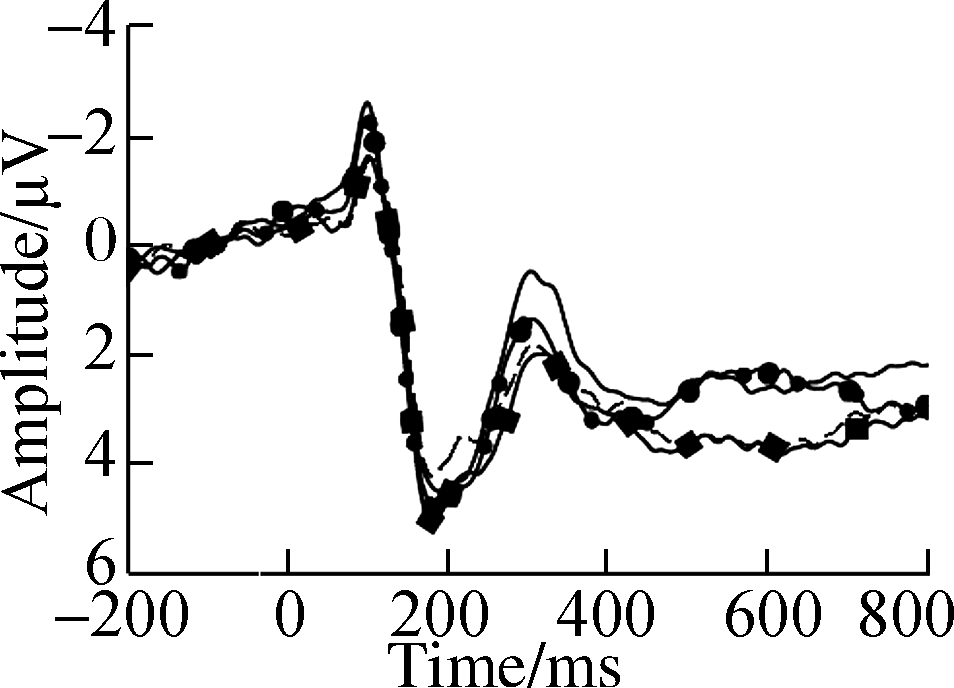
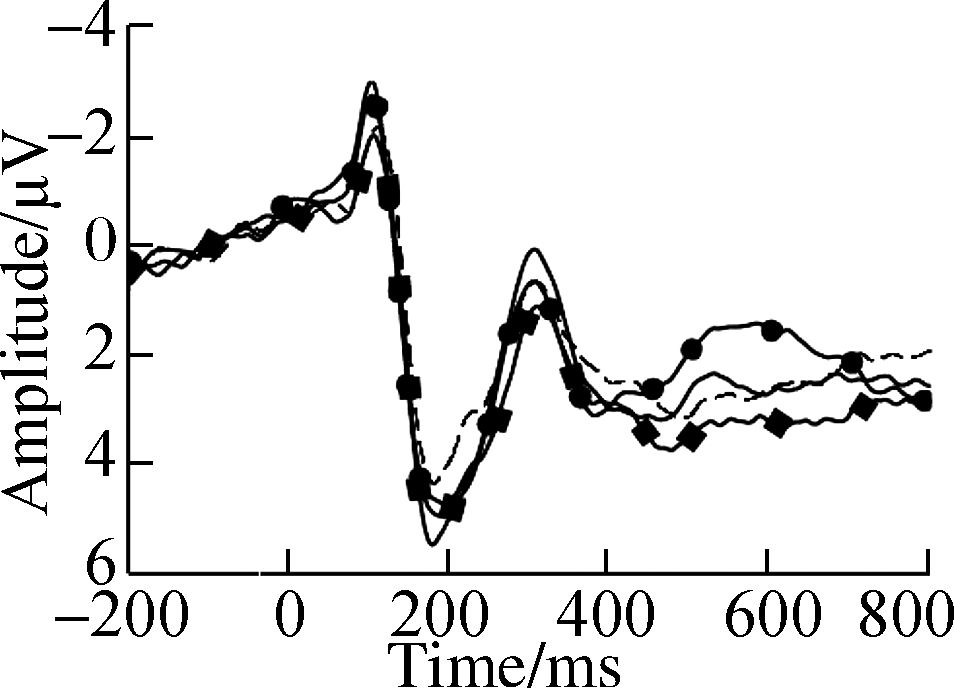
Fig.3 Grand average ERP waveforms over typical electrodes for decimals and fractions during entity processing.(a)C3 electrode;(b)Cz electrode;(c)C4 electrode;(d)P3 electrode;(e)Pz electrode;(f)P4 electrode;(g)PO3 electrode;(h)POz electrode;(i)PO4 electrode
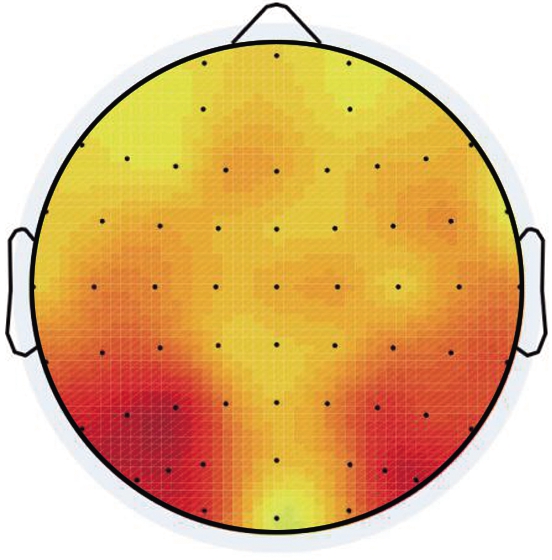
Topographic maps of entity effect are shown in Fig.5, where the ERP of continuous entitiesis are subtracted from that of discretized ones.The entity effect appears to be associated with number types at the time window of P2, indicating a bilateral advantage at parietal to occipital sites under decimals compared with fractions.Moreover, the entity effect interacted with number types at the time window of N2, revealing a right-lateralized parietal to occipital negativity for fractions but a left-lateralized anterior-centered positivity for decimals.
(a)
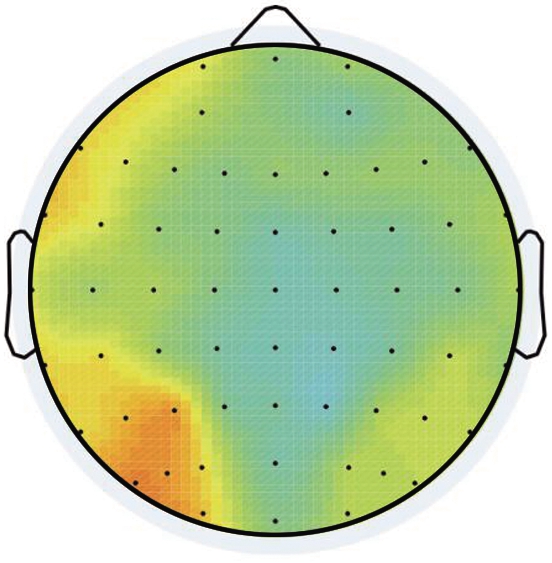
(b)
(c)
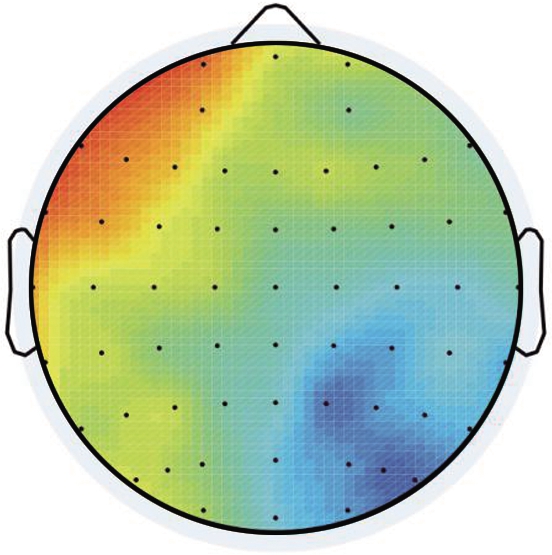
(d)
Fig.5 Topographical maps of entity effect.(a)Decimals during 210 to 270 ms poststimulus;(b)Fractions during 210 to 270 ms poststimulus;(c)Decimals during 270 to 350 ms poststimulus;(d)Fractions during 270 to 350 ms poststimulus
2.2.2 Symbolic fraction processing
For the P2 component, the distance effect was significant at the frontal lobe(F(1,57)=4.48, p<0.05, 
with a larger amplitude for the far distance than for the close distance.There were significant number type, distance, and laterality interactions at the frontal and central regions(Fs(1,57)>4.27, ps<0.05, 
with distance effect for fractions with larger P2 at Fz, F4, Cz, and C4(ps<0.01).
For the N2 component, the main number type effect was significant with decimals having larger N2 amplitudes than fractions, widely distributed at centro-occipital regions(Fs(1,57)=8.84, ps<0.01, 
For the N2f component, the number type effect for F3, C3, and Cz(ps<0.01)was more pronounced for number type when there was a laterality interaction of N2f(Fs(2,114)>13.45, ps<0.001, 
The number type and distance interaction(Fs(1,57)>6.07, ps<0.05, 
was also significant for decimals at the fronto-central lobes, with a larger N2f component for the far distance than for the close distance(ps<0.05).For the N2p component, an opposite-polarity distance effect was observed for fractions(ps<0.05)with a larger N2p component for the close distance, widely distributed at the centro-occipital regions as indicated by the number type and distance interaction(Fs(1,57)>6.00, ps<0.05, Additionally, three-way interactions(Fs(2,114)>4.35, ps<0.05, were significant.Distance effect with larger N2 for the far distance with decimals was over F3, C3, and Cz(ps<0.05).There was also an opposite-polarity distance effect with larger N2 for the close distance with fractions over Cz and C4(ps<0.01).
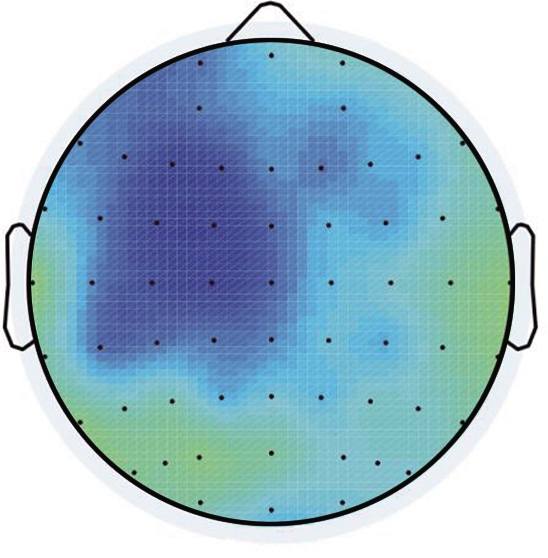
Fig.6 shows topographic maps of the distance effect, where the ERP of the close distance is subtracted from that of the far distance.The distance effect, characterized by a right-lateralized focal positivity, was widely distributed over the frontal to parietal electrodes for fractions at the time window of P2.On the other hand, the distance effect was obvious over the left-lateralized frontal to centro-parietal sites for decimals at the time window of N2.An opposite-polarity distance effect for fractions was widely distributed at the posterior and right-lateralized anterior regions.
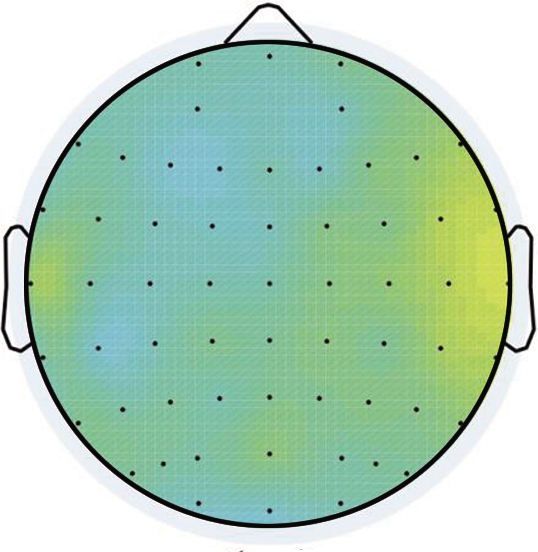
(a)
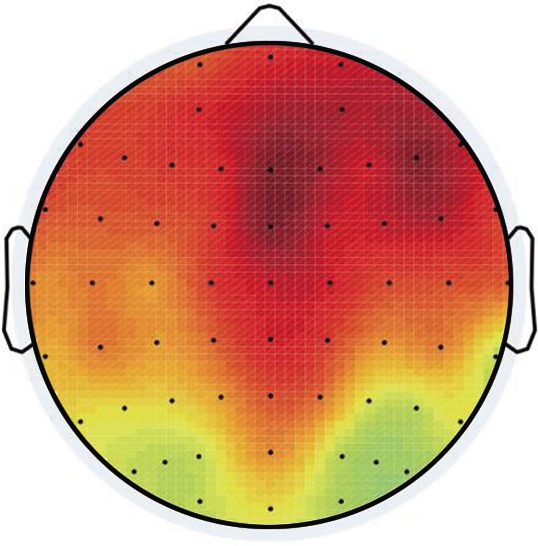
(b)
(c)
(d)
Fig.6 Topographical maps of distance effect.(a)Decimals during 170 to 250 ms poststimulus(b)Fractions during 170 to 250 ms poststimulus;(c)Decimals during 250 to 350 ms poststimulus(d)Fractions during 250 to 350 ms poststimulus
3 Discussion
The behavioral data showed clear number type effects on both RT(i.e., slower performance on fractions)and ACC(i.e., poorer performance on fractions), which were not influenced by any speed and accuracy trade-offs.These findings are in line with previous research on decimal and fraction comparisons[8,21-22].Moreover, distance effects were significant, which is consistent under each condition, and dramatically affected RT and ACC, which demonstrated that fraction pairs adopted the holistic strategy as expected[16].Thus, with the rather large entity effect, distance effects, and a complex comparison task, significant differences in ERP measures can trigger such differences in behavioral data even in mathematically skilled adults who use verbally exact strategies to compare decimals and visually approximate strategies to compare fractions.The identification and semantic access stages were dissociated to investigate the differences in processing strategies between number types using entity and distance effects.
3.1 Entity processing
The entity effect was detected in the P2 component, which connects sensory processing to high-level discrimination.Consistent with number identification, entity identification was indexed by P2p, involving the vision-related bilateral parietal-occipital junctions located at the bilateral fusiform as observed via functional magnetic resonance imaging[3].Greater bilateral P2p may be elicited with discretized entities because of visual perception requirements[10].The behavioral data suggested that the surface format of an entity also influences the later numerosity process[9].The topography of P2 showed that decimals elicited more activation at bilateral posterior sites than fractions.The P2 results replicated the results by Zhang et al.[18], who observed stronger engagement of attentional resources in decimals than in fractions[9-10].
Consistent with the above-mentioned hypothesis, the neurophysiological evidence in N2 with interactions between number type and entity confirmed the alignments between the entity and symbolic fraction[4-6].Significantly larger N2f results were detected for continuous entities under decimals, while an opposite-polarity entity effect was observed with larger N2p for discretized entities under fractions, as shown in Fig.4.A previous study attributed the left lateral N2f for decimal-continuous alignment to retrieval and memorization retention for later calculation, with greater preceding attentional effort and working memory load[17].Another study suggested that higher proficiency and familiarity underlying a unidimensional decimal-continuous preference can increase activation of the phonological network and improve magnitude retrieval processing automatically[13].On the other hand, Beek et al.associated the right lateral N2p for the fraction-discretized alignment with visuospatial resources and perceptual processing[23].The extra difficulty within bidimensional fraction-discretized alignment affected initial magnitude accessing and reduced retrieval efficiency, which extended to semantic comparison.The behavioral data showed a large distance effect of RT for fractions and discretized entities, probably because of greater reliance on complex problem-solving when accessing magnitude.Moreover, behavioral tendencies showed higher accuracy for continuous entities in decimals and discretized entities in fractions.Therefore, the results suggest that distinctive strategies are applied during entity processing with phonological retrieval for decimal-continuous alignment and visuospatial processing for fraction-discretized alignment.
(a)
(b)
(c)
(d)
(e)
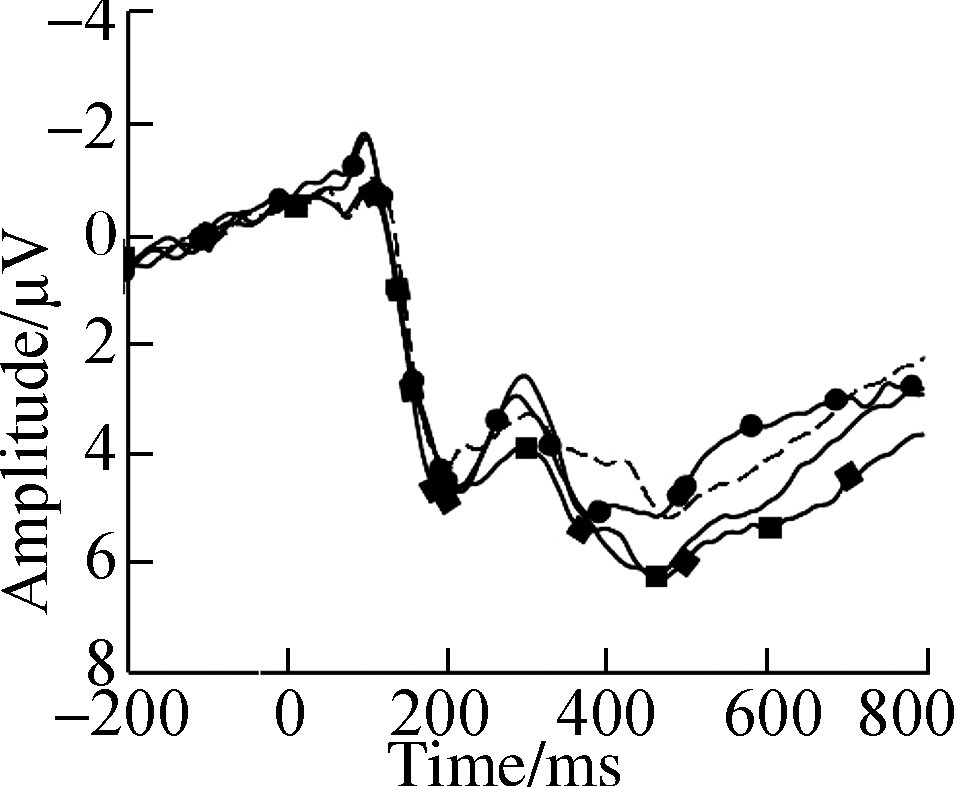
(f)
(g)
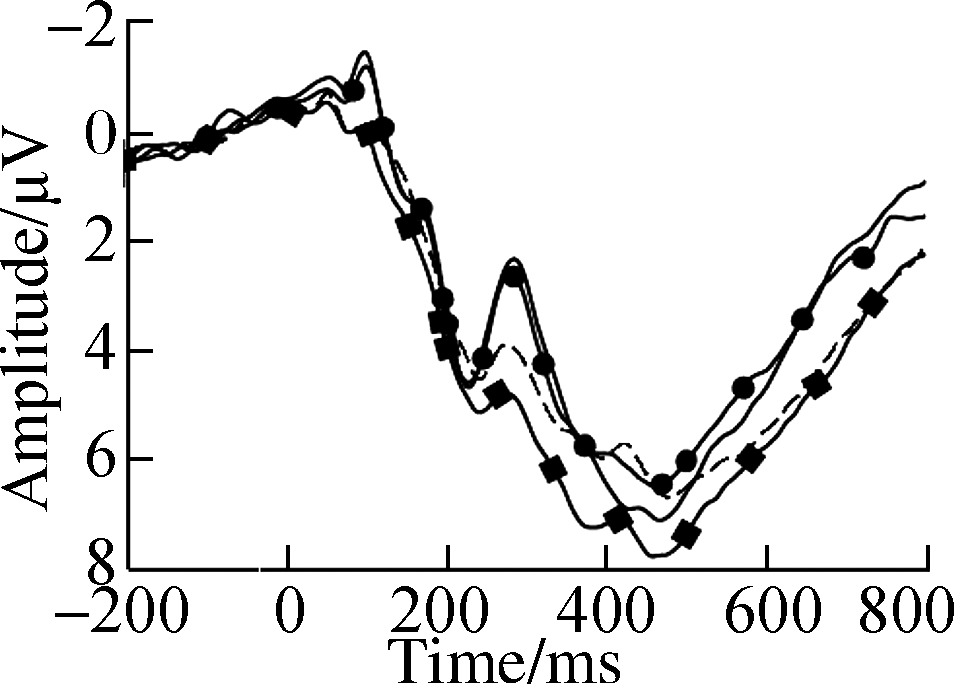
(h)
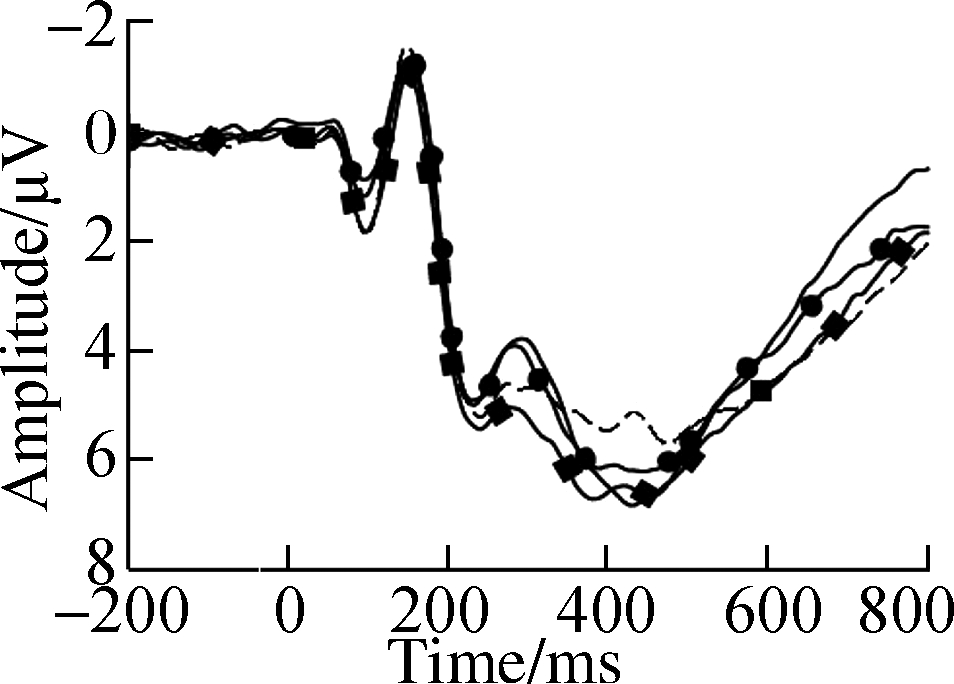
(i)
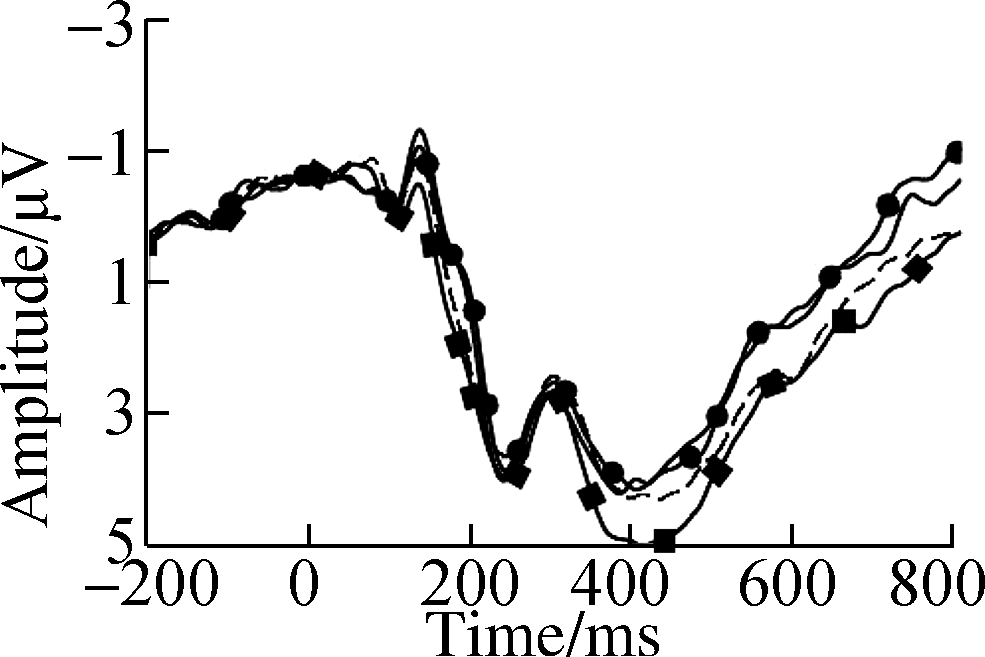
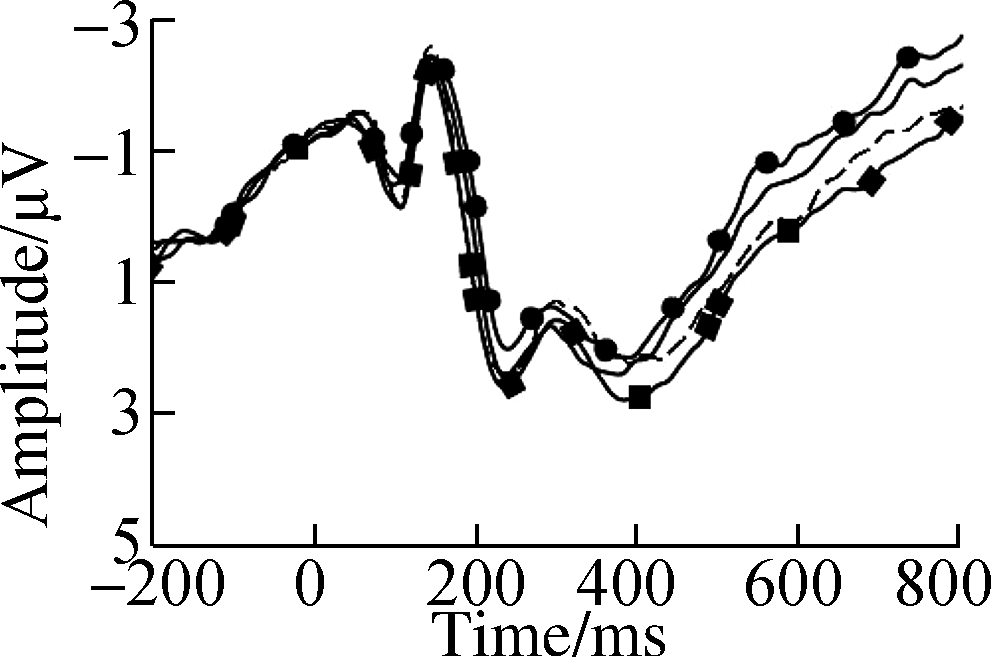
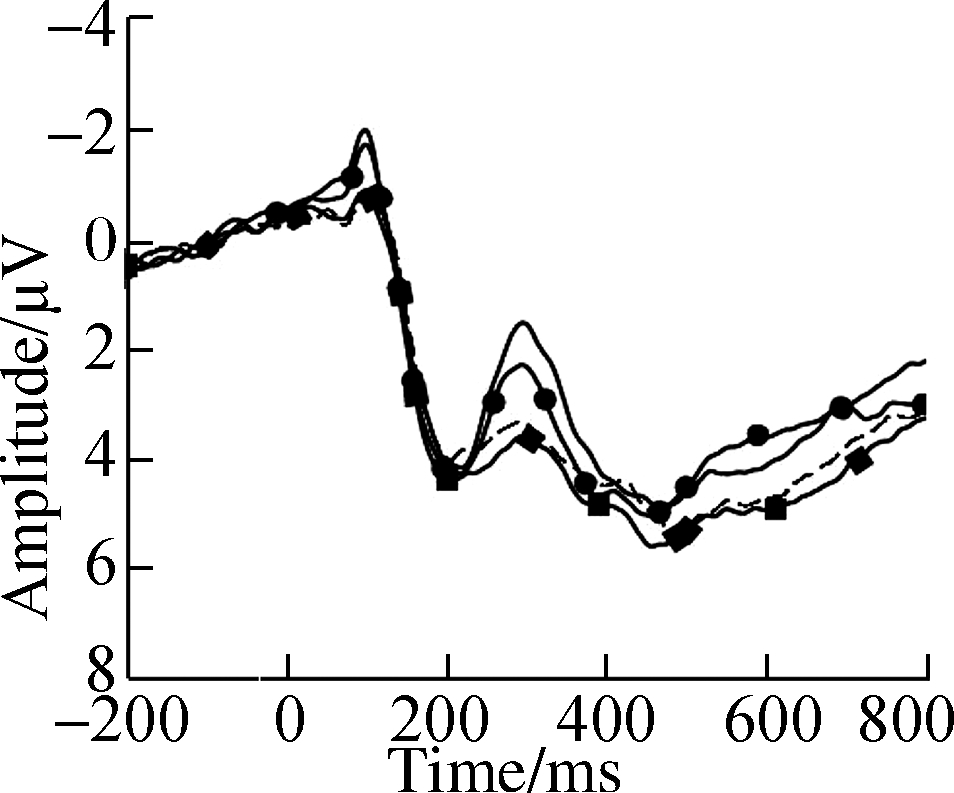
Fig.4 Grand average ERP waveforms over typical electrodes for decimals and fractions during symbolic fraction processing.(a)F3 electrode;(b)Fz electrode;(c)F4 electrode;(d)C3 electrode;(e)Cz electrode;(f)C4 electrode;(g)P3 electrode;(h)Pz electrode;(i)P4 electrode
These ontological dissociations have significant pedagogical implications.In China, for example, distinct teaching sequences and strategies are used to explain decimals and fractions.Usually, a continuous entity within the measurement system(e.g., length, money)is used to explain decimals in lower grades, whereas collection models and entity models with equation sublines are applied for fractions in higher grades[24].Hence, although these two number types are based on the same semantic system, students learn to recognize them via different strategies.One relevant behavioral study investigated verbal vs.visuospatial working memory resources(WMs)used by adults when processing decimals vs.fractions.They found that those who performed poorly relied only on verbal WM while those who performed better relied on both verbal and visuospatial WM[25].Considering the abovementioned findings, unbalanced development between verbal and visuospatial strategies in decimal and fraction processing might exist in rational number learning.However, such alignments should be treated with caution.Nevertheless, other studies have shown that the confined number type and entity interactions did not exert top-down control of number types or showed overlapping effects in terms of advantages in decimal and fraction processing[21,26].Future neuropsychological studies should integrate these concepts to support the above exploratory inferences.
3.2 Symbolic fraction processing
Results showed larger N2 amplitudes in decimal processing than in fraction processing, suggesting that number type differences occurred during conceptual identification and procedural semantic integration.Consequently, the left-lateralized N2f and N2p showed a high level of precision within the exact processing mechanism[27-28].Subtraction operations activated a frontoparietal network, indicating procedural-based operations[28].The number type effects indicated in the behavioral data also confirmed previous studies[5,8] that have shown better processing of decimals than of fractions.The number type effect has shown that decimals are typically solved by exact strategies, requiring greater cognitive control, rote fact extraction, arithmetic procedure retrieval, and phonological processing[11,13].However, fractions could not be processed by direct memory retrieval.
As expected, significant interactions of number type and distance were observed in P2 and N2 components, indicating number type-dependent semantic access.Results showed that the distance effect of fractions was first observed at the time window of P2.This replicated the results of Temple and Posner[29], showing larger P2 for the far distance under nonsymbolic conditions.This is possibly due to an advantage in fraction to entity conversion[1], where participants translate fractions back to entities then compare nonsymbolic pairs.The right-lateralized anterior P2 was also active in shortcut calculation(rounding)and source analysis located the dipole within the right posterior cingulate cortex[11].P2 lateralization suggests that participants were more likely to apply an approximate strategy for fractions.A previous study observed similar P2 activation in different decimal and fraction processing affected by complex task contexts that might have also triggered larger P2 for fraction, although decimal processing was not affected by the variation of task demands[30].On the other hand, automatic evaluation of numerical distance for decimals corresponded to larger left-lateralized N2f at the time window of N2[10,12-13,23].However, for fractions, N2p of opposite polarity with larger amplitude for close distance was significant.This suggests that the approximate strategies based on vision-related processing(e.g., recoding a fraction into a more familiar form like making 3/7 close to 1/2 or transforming it into an equivalent entity)can activate the classic “numeral” parietal area, particularly when the distance of comparison pairs is close[11,23].However, Chen et al.[30-31] found larger N2f in complex context for a fraction.In their comparison pairs that usually had the numerator “1”, participants selected the smaller denominator believing that the larger the denominator, the smaller the value will be.This rule switching may have triggered the N2f, which indexes a componential representation beyond the scope of the holistic premise.In some comparison tasks for fractions, fixation times of eye tracking were higher for numerators than for denominators.Participants might use an approximation strategy by assuming denominators were equal[16].Decimal format prompted frequent eye regressions between nonsymbolic images and symbolic numbers, which revealed that decimal processing involves a more precise comparison strategy[32].In accordance with ERP interactions, the behavior data in the current study also revealed a dramatic distance effect for fractions, indicating that fraction semantic processing is relatively inaccurate.For decimals, the exact strategy relies on phonological networks of the left frontoparietal circuit for rote fact retrieval and subtraction, while for fractions, a more error-prone and time-consuming approximate strategy relies on visuospatial networks of the biparietal and right-lateralized fronto-central lobes for magnitude manipulation.
Interestingly, the activated centro-occipital network was related to larger number type effects for decimals and larger distance effects for fractions.This supports the suggestion that the posterior brain area centered on the “numeral” parietal is not specific to a number type, perception, or computation.Rather, shared brain regions may correspond to abstract models in the triple-code model, which is associated with phonological retrieval to complete arithmetic procedures, or to broader focus on a visual stimulus[17,33].
3.3 General discussion
It is important to note that in terms of decimal and fraction comparisons, the findings in the current study are consistent with past studies[18,30-31].Zhang’s first attempt to explore the distance effect dissociation between decimals and fractions did not yield significant distance and number type interactions, but the distinct topographical maps of distance effect were quite similar to the ones in the present study(see Fig 6)[18].Their results were not self-consistent, probably because the distance effect in their study was not strong enough to evoke distinct semantic processing.It seems that previous studies reach an agreement on the difficulty hypothesis; i.e., participants have more difficulty with fractions compared with decimals, which explained the number type—specific processing.However, these past studies cannot answer the question based on the difficulty hypothesis: When did the discrepancy exactly occur? What strategies were adopted with respect to decimal and fraction processing during confounded magnitude comparison? Converging evidence from a set of ERP components in the current study revealed online temporal differences in strategic processing that stem from separated conceptual and procedural processing of number type coupled with entity and distance effects.The hypothesis stating that different strategies depend on number formats evoked by different ontological types of entities and different types of distance is raised.This is compatible with but goes beyond previous literature.
Overall, the ERPs results from the present experiment are consistent with the behavioral data and provide the following important information: 1)ERP and topography differences between decimals and fractions were found to appear as early as 210 ms after the entity onset, indicating strategic identification.On the other hand, distinct semantic access strategies took place as early as 170 ms after the presentation of the symbolic fraction.2)ERPs were associated with larger left lateral N2f for continuous entities under decimals, but the opposite polarity of entity effect was observed with larger right lateral N2p for discretized entities under fractions.The result supported the hypothesis that decimal-continuous and fraction-discretized alignments deeply affected the identification strategies, which activated the phonological and visuospatial networks, respectively.3)For symbolic fraction processing, centro-occipital N2p and left-lateralized N2f components for decimals were larger than those for fractions, suggesting that number type differences occurred during conceptual identification and procedural semantic integration.4)Moreover, the left-lateralized fronto-central distance effect of N2 indicated that participants applied exact strategies with rote arithmetic retrieval in a verbal format for decimals.In contrast, the number type by distance interactions of right-lateralized fronto-central P2 and biparietal N2 showed that participants used approximate strategies with complex magnitude processing in visuospatial format for fractions.
The present findings are relevant to mathematics education since some students still use incorrect strategies to solve comparison problems[16].An empirical reference was provided in the current study for detecting brain activity in terms of notation-specific strategy when mathematically skilled adults are taking into account its magnitudes holistically.Notably, stereotypic strategy for decimal and fraction processing indicates that sound development and essential connection between decimals and fractions have not been well established.To address this, different forms of visual aids that consider entity-symbolic fraction alignments and provide concrete and contextual experience will have a great impact on arousing students’ verbal and visuospatial resources to understand conceptual knowledge of rational numbers.Rational number comparison and number line estimation might make a great contribution to students’ proficiency in procedural knowledge of rational numbers.Making use of these strategies in the conceptual and procedural understanding of decimals and fractions may help students use their experience of entities in the real world to bootstrap their knowledge of rational numbers.
4 Conclusions
1)Decimal and fraction strategies are dissociated by systematically varying both entity and distance effects.The entity and distance effects specific to number type observed here extend the empirical knowledge of the triple-code model.
2)For identification strategies, the alignment of decimal and continuous entities is based on the phonological network, while the alignment of fraction and discretized entities relies on visuospatial resources.
3)For semantic strategies, an exact strategy with rote arithmetic retrieval in verbal format is used for decimals, while the approximate strategy with complex magnitude processing in a visuospatial format is used for fractions.
Acknowledgements
The authors would like to thank Zhou Xinlin of the State Key Laboratory of Cognitive Neuroscience and Learning, IDG/McGovern Institute for Brain Research, Beijing Normal University, for his truly helpful assistance and support.
[1] Ni Y, Zhou Y D.Teaching and learning fraction and rational numbers: The origins and implications of whole number bias[J].Educational Psychologist, 2005, 40(1): 27-52.DOI: 10.1207/s15326985ep4001_3.
[2] Dehaene S, Cohen L.Towards an anatomical and functional model of number processing[J].Mathematical Cognition, 1995, 7(1): 83-120.
[3] Pinel P, Dehaene S, Riviere D, et al.Modulation of parietal activation by semantic distance in a number comparison task[J].Neuroimage, 2001, 14(5): 1013-26.DOI: 10.1006/nimg.2001.0913.
[4] Rapp M, Bassok M, DeWolf M, et al.Modeling discrete and continuous entities with fractions and decimals[J].Journal of Experimental Psychology: Applied, 2015, 21(1): 47-56.DOI: 10.1037/xap0000036.
[5] Lee H S, DeWolf M, Bassok M, et al.Conceptual and procedural distinctions between fractions and decimals: A cross-national comparison[J].Cognition, 2016, 147: 57-69.DOI: 10.1016/j.cognition.2015.11.005.
[6] Sokolowski H M, Fias W, Mousa A, et al.Common and distinct brain regions in both parietal and frontal cortex support symbolic and nonsymbolic number processing in humans: A functional neuroimaging meta-analysis[J].Neuroimage, 2017, 146: 376-394.DOI: 10.1016/j.neuroimage.2016.10.028.
[7] Szucs D, Csepe V.The effect of numerical distance and stimulus probability on ERP components elicited by numerical incongruencies in mental addition[J].Cognitive Brain Research, 2005, 22(2): 289-300.DOI: 10.1016/j.cogbrainres.2004.04.010.
[8] DeWolf M, Grounds M A, Bassok M, et al.Magnitude comparison with different types of rational numbers[J].Journal of Experimental Psychology: Human Perception and Performance, 2014, 40(1): 71-82.DOI: 10.1037/a0032916.
[9] Cao B, Li F, Li H.Notation-dependent processing of numerical magnitude: Electrophysiological evidence from Chinese numerals[J].Biological Psychology, 2010, 83(1): 47-55.DOI: 10.1016/j.biopsycho.2009.10.003.
[10] Jiang T, Qiao S, Li J, et al.Effects of symbol type and numerical distance on the human event-related potential[J].Neuropsychologia, 2010, 48(1): 201-210.DOI: 10.1016/j.neuropsychologia.2009.09.005.
[11] Luo W, Liu D, He W, et al.Dissociated brain potentials for two calculation strategies[J].Neuroreport,2009,20(4):360-364.DOI:10.1097/WNR.0b013e328323d737.
[12] Zhou X L, Chen C S, Dong Q, et al.Numerical distance effect in the N240 component in a number-matching task[J].Neuroreport, 2006, 17(10): 991-994.DOI: 10.1097/01.wnr.0000221840.12632.9f.
[13] Zhou X L, Chen C S, Dong Q, et al.Event-related potentials of single-digit addition, subtraction, and multiplication[J].Neuropsychologia, 2006, 44(12): 2500-2507.DOI: 10.1016/j.neuro psychologia.2006.04.003.
[14] El Yagoubi R, Lemaire P, Besson M.Different brain mechanisms mediate two strategies in arithmetic: Evidence from event-related brain potentials[J].Neuropsychologia, 2003, 41(7): 855-862.DOI: 10.1016/s0028-3932(02)00180-x.
[15] Stanescu-Cosson R, Pinel P, Van de Moortele P, et al.Understanding dissociations in dyscalculia: A brain imaging study of the impact of number size on the cerebral networks for exact and approximate calculation[J].Brain, 2000, 123: 2240-2255.DOI: 10.1093/brain/123.11.2240.
[16] Obersteiner A, Tumpek C.Measuring fraction comparison strategies with eye-tracking[J].ZDM Mathematics Education, 2015, 48(3): 255-266.DOI: 10.1007/s11858-015-0742-z.
[17] Szucs D, Csepe V.Access to numerical information is dependent on the modality of stimulus presentation in mental addition: A combined ERP and behavioral study[J].Cognitive Brain Research, 2004, 19(1): 10-27.DOI: 10.1016/j.cogbrainres.2003.11.002.
[18] Zhang L, Wang Q, Lin C, et al.An ERP study of the processing of common and decimal fractions: How different they are[J].PLoS One, 2013, 8(7): e69487.DOI: 10.1371/journal.pone.0069487.
[19] Salillas E, Carreiras M.Core number representations are shaped by language[J].Cortex, 2014, 52: 1-11.DOI: 10.1016/j.cortex.2013.12.009.
[20] Arsalidou M, Taylor M J.Is 2+2=4? Meta-analyses of brain areas needed for numbers and calculations[J].Neuroimage, 2011, 54(3): 2382-2393.DOI: 10.1016/j.neuroimage.2010.10.009.
[21] DeWolf M, Chiang J N, Bassok M, et al.Neural representations of magnitude for natural and rational numbers[J].Neuroimage, 2016, 141: 304-312.DOI: 10.1016/j.neuroimage.2016.07.052.
[22] DeWolf M, Bassok M, Holyoak K J.Conceptual structure and the procedural affordances of rational numbers: Relational reasoning with fractions and decimals[J].Journal of Experimental Psychology: General, 2015, 144(1): 127-150.DOI: 10.1037/xge0000034.
[23] Van Beek L, Ghesquier P, De Smedt B, et al.The arithmetic problem size effect in children: An event-related potential study[J].Frontiers in Human Neuroscience, 2014, 8: 756.DOI: 10.3389/fnhum.2014.00756.
[24] Qiu K, Wang Y.Conceptual distinctions and preferential alignment across rational number representations[J].European Journal of Psychology of Education, 2020,36:865-881.DOI: 10.1007/s10212-020-00502-4.
[25] Hurst M, Cordes S.Working memory strategies during rational number magnitude processing[J].Journal of Educational Psychology, 2017, 109(5): 694-708.DOI: 10.1037/edu0000169.
[26] Luck S J.Multiple mechanisms of visual-spatial attention: Recent evidence from human electrophysiology[J].Behavioural Brain Research, 1995, 71: 113-123.DOI: 10.1016/0166-4328(95)00041-0.
[27] Benavides-Varela S, Basso Moro S, Brigadoi S, et al.N2pc reflects two modes for coding the number of visual targets[J].Psychophysiology, 2018, 55(11): e13219.DOI: 10.1111/psyp.13219.
[28] De Smedt B, Holloway I D, Ansari D.Effects of problem size and arithmetic operation on brain activation during calculation in children with varying levels of arithmetical fluency[J].Neuroimage, 2011, 57(3): 771-781.DOI: 10.1016/j.neuroimage.2010.12.037.
[29] Temple E, Posner M I.Brain mechanisms of quantity are similar in 5-year-old children and adults[J].Proceedings of the National Academy of Sciences of the United States of America, 1998, 95: 7836-7841.DOI: 10.1073/pnas.95.13.7836.
[30] Chen M, Wang Q, Zhang L.An ERP study on the processing of common and decimal fractions affected by contexts[J].Psychological Research, 2013, 6(3): 29-38.DOI: CNKI:SUN:OXLY.0.2013-03-006.(in Chinese)
[31] Zhang L, Xin Z, Li F, et al.An ERP study on the processing of common fractions[J].Experimental Brain Research, 2012, 217(1): 25-34.DOI: 10.1007/s00221-011-2969-4.
[32] Plummer P, DeWolf M, Bassok M, et al.Reasoning strategies with rational numbers revealed by eye tracking[J].Attention, Perception, & Psychophysics, 2017, 79(5): 1426-1437.DOI: 10.3758/s13414-017-1312-y.
[33] Schmithorst V J, Brown R D.Empirical validation of the triple-code model of numerical processing for complex math operations using functional MRI and group independent component analysis of the mental addition and subtraction of fractions[J].Neuroimage, 2004, 22(3): 1414-1420.DOI: 10.1016/j.neuroimage.2004.03.021.