Cast steel nodes are a kind of prefabricated integral casting node.They have flexible and various forms and a good mechanical performance and hence are an ideal form for complex structural nodes[1].However, the number of cast steel’s void defects is far more than that of hot-rolled steel because of different production processes[2].The existence of defects destroys the material’s continuity, leading to a decline in the structure’s mechanical properties.
Metal is a ductile material, whose failure is often related to the nucleation, growth, and coalescence of voids caused by a load until macroscopic cracks are formed[3].Therefore, it is necessary to examine the changes of microvoids and their effects on the macro-mechanics of materials to truly reflect the damage evolution process.However, the traditional industrial flaw detection method has low accuracy, making it difficult to determine the distribution and size of micro-defects inside the casting.Moreover, the original bilinear model does not consider internal material damages, causing insufficient assessment of the structural safety and reliability.
In fracture mechanics, current constitutive material models can be divided into two types: Macroscopic models, such as the Lemaitre model, do not consider the micromechanisms of ductile damage[3-4].Gurson[5] coupled the evolution of voids with the equivalent plastic strain of a material based on volume cell models and deduced a relatively complete microscopic damage model.Subsequently, Tvergaard[6] and Needleman et al.[7] modified the model and formed the Gurson-Tvergaard-Needleman(GTN)damage model, which is widely used in the research of metal properties.This model uses the yield function to describe the yield behavior of materials and the void volume fraction to define the failure of materials, which can accurately describe the failure results of metal materials compared with the bilinear model[8].
Since the proposal of the GTN damage model, many scholars have applied it to simulate the damage evolution process of metals.Xu et al.[9] simulated the tensile behavior of corroded reinforcing bars in concrete under a carbonized environment.Liu et al.[10] simulated the effect of MnS inclusions on the initiation and propagation of cracks in as-cast 304 stainless steel at high temperatures.Steglich et al.[11] studied the interaction between the plastic anisotropy and void growth of aluminum alloy 2198.The above instances fully indicate that the GTN damage model promotes the development of micro-damage mechanics and establishes a good connection between experimental verifications and the finite element method(FEM), and its application has become increasingly widespread [12].
In this study, the bearing capacity of cast steel nodes was calculated based on the bilinear model and GTN damage model.The relationship between the model parameters and the failure results of cast steel nodes under different loads was also examined.
1 GTN Damage Model and Its Parameters
1.1 GTN damage model
The yield function of the GTN damage model can be expressed as follows:
(1)
where σeq is the effective von Mises stress; σy is the initial yield stress of the matrix material; σm is the hydrostatic stress; q1, q2, and ![]() are the correction parameters.
are the correction parameters.
The damage variable f* is a function of the total void volume fraction f, which is expressed as
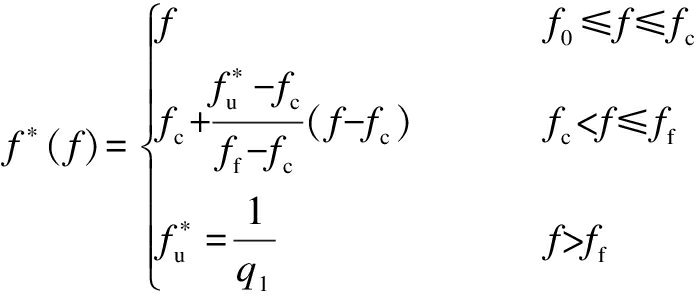
(2)
where f0 is the initial void volume fraction; fc is the critical void volume fraction; ff is the void volume fraction at the fracture; ![]() is the ultimate value of the damage parameter.
is the ultimate value of the damage parameter.
The yield surface of the GTN damage model connects the yield with the damage of the material, so the yield surface will gradually shrink with the increase in f*, reflecting the continuous deterioration of materials due to damage evolution, as shown in Fig.1.When f* = 0, Eq.(1)degenerates into a von Mises yield function.
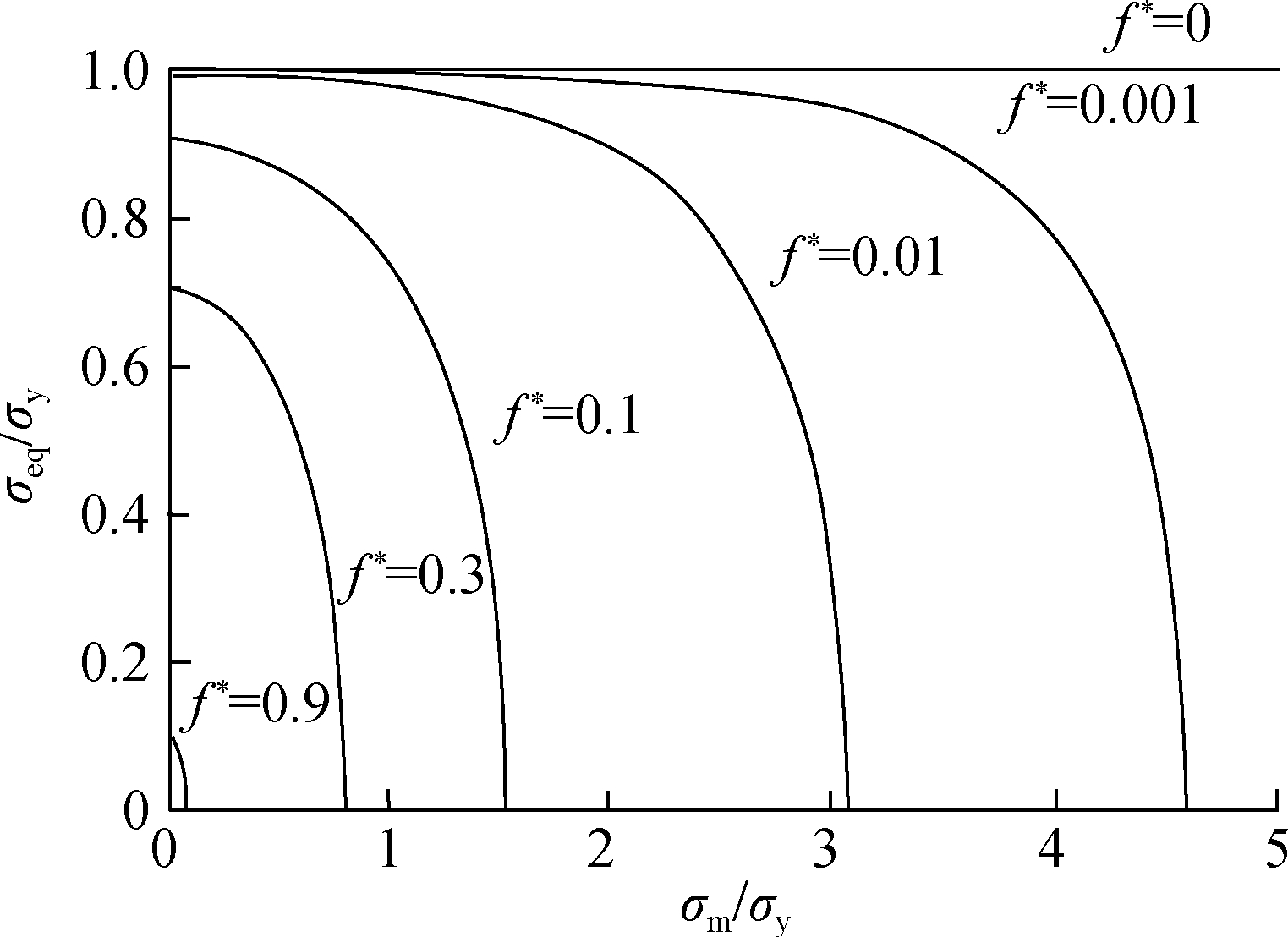
Fig.1 Yield surface of the GTN damage model
The total void volume fraction f in the GTN damage model includes the initial void volume fraction f0, growing void volume fraction fgr, and nucleated void volume fraction fnu:
f=f0+fgr+fnu
(3a)
The increment expression is
df=dfgr+dfnu
(3b)
Due to the incompressibility of the matrix material, the growth of the initial voids depends on the plastic strain[13]:
dfgr=(1-f)dεp∶I
(4)
where εp is the plastic strain and I is the second-order unit tensor.
Generally, nucleation will only occur when the stress exceeds the critical value, and the number of nucleation increases with the strain’s increase[14]:
(5)
where ![]() is the equivalent plastic strain; fN is the volume fraction of void nucleating particles; εN is the mean nucleation strain; SN is the corresponding standard deviation.
is the equivalent plastic strain; fN is the volume fraction of void nucleating particles; εN is the mean nucleation strain; SN is the corresponding standard deviation.
Eqs.(1)to(5)constitute the GTN damage model, which can simulate the entire process of void nucleation, growth, coalescence, and fracture.In this model, Eqs.(3)to(5)describe the nucleation and growth of voids, and Eqs.(1)to(2)determine the influence of voids’ coalescence and fracture on the bearing capacity.
1.2 Parameters in the GTN damage model
The GTN damage model has nine parameters, which can be divided into three groups.The first group is the correction parameters, including q1, q2, and q3; the second is the void volume fractions, including f0, fc, and ff; and the third is the nucleation parameters, including fN, εN, and SN.To construct the GTN damage model, it is necessary to calibrate the optimal combination of parameters.At present, the common methods to calibrate the parameter values in the GTN damage model are metallographic analysis, cell element method, and finite element reverse method[12].However, even with the proposal of the GTN damage model, it was not easy to obtain all the parameters through experiments because of their numerous material parameters.Therefore, researchers studied on the model parameters’ calibration of different materials and achieved some results[4,10,15-20], which provide a reliable basis for applying the model.
Yan et al.[21-23] calibrated the model parameters of G20Mn5N cast steel using the finite element reverse method combining the three-dimensional X-ray microtomography technique and numerical simulation.The results in Tab.1 show that the numerical simulation results are in good agreement with the experimental results.
Tab.1 Optimal combination of the GTN damage model for G20Mn5N cast steel

q1q2q3f0/10-3fcff/10-2fNεNSN1.51.02.252.70.034.50.010.250.05
2 Evaluation of Cast Steel Node’s Bearing Capacity
2.1 Material properties
The cast steel node selected in this study has four intersecting tubes, located in a large-span steel structure.The overall schematic diagram of the node and the number of each tube are shown in Fig.2.The material of the cast steel node is G20Mn5N cast steel, and its chemical composition and basic mechanical properties are shown in Tabs.2 and 3.
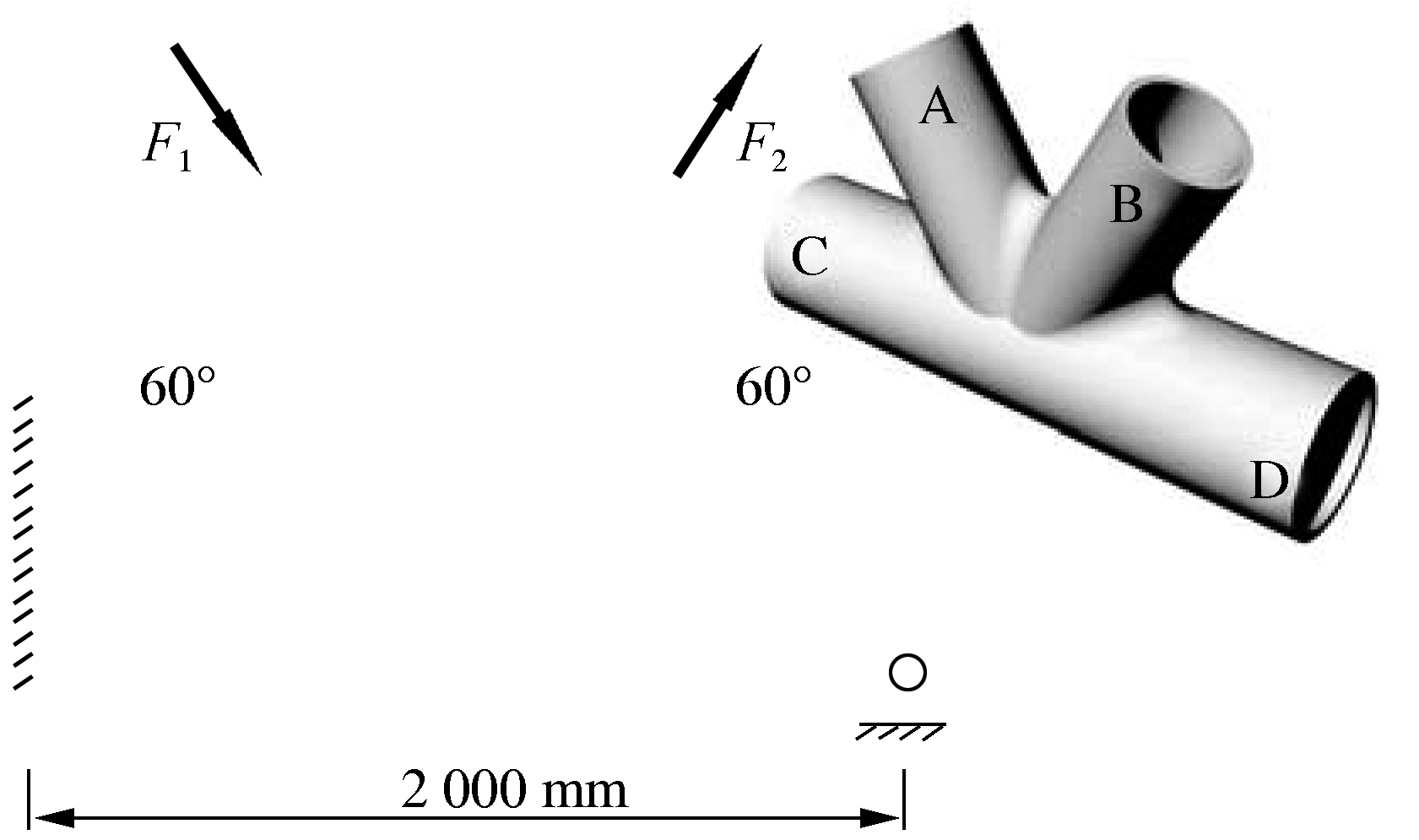
Fig.2 Overall schematic diagram of the cast steel node
Tab.2 Chemical composition of the G20Mn5N cast steel %
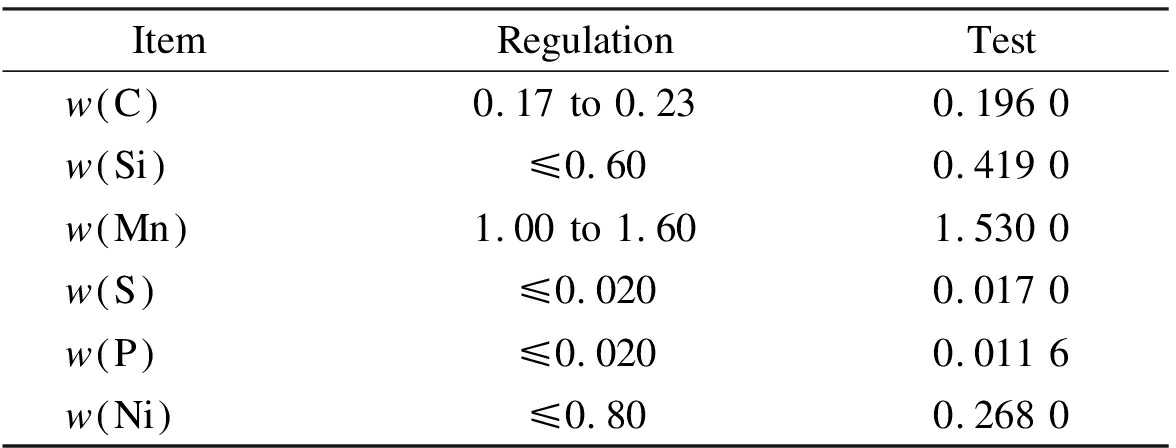
ItemRegulationTestw C 0.17 to 0.230.196 0w Si ≤0.600.419 0w Mn 1.00 to 1.601.530 0w S ≤0.0200.017 0w P ≤0.0200.011 6w Ni ≤0.800.268 0
Tab.3 Mechanical properties of the G20Mn5N cast steel

ItemElastic modulus/GPaYield strength/MPaUltimate strength/MPaElongation/%Regulation206300480 to 620≥20Test23032048331.9
2.2 Establishment of the cast steel node model
The FEM software ABAQUS was used to model and calculate the cast steel node with C3D10m solid elements.A fixed constraint is imposed on the main tube port C.A displacement constraint in the X and Y directions is imposed on the main tube port D.According to the requirements of JGJ/T 395—2017[24], the main part of the cast steel node should be in an elastic stage under complex stress.Meanwhile, the local stress concentration area is allowed to transit to the plastic stage.Therefore, a 1 161 284N compressive load is applied to branch tube port A, and a 2 237 085N tensile load is applied to branch tube port B.
There are stress concentration areas at the branch tube ports A and B, so mesh encryption is performed in these areas.Tab.4 and Fig.3 show different mesh densities cases.Fig.4 shows the stress and displacement calculation results of branch tube port B by different cases.The model’s von Mises stress and resultant displacement results stabilize when the branch tube port’s mesh density reaches 9 mm, so this mesh density is selected for calculation.
Tab.4 Different mesh density cases mm2

CaseMesh encryption areaMesh transition areaMesh sparsity area1151515212131539121547101555915

Fig.3 Mesh density model of the cast steel node
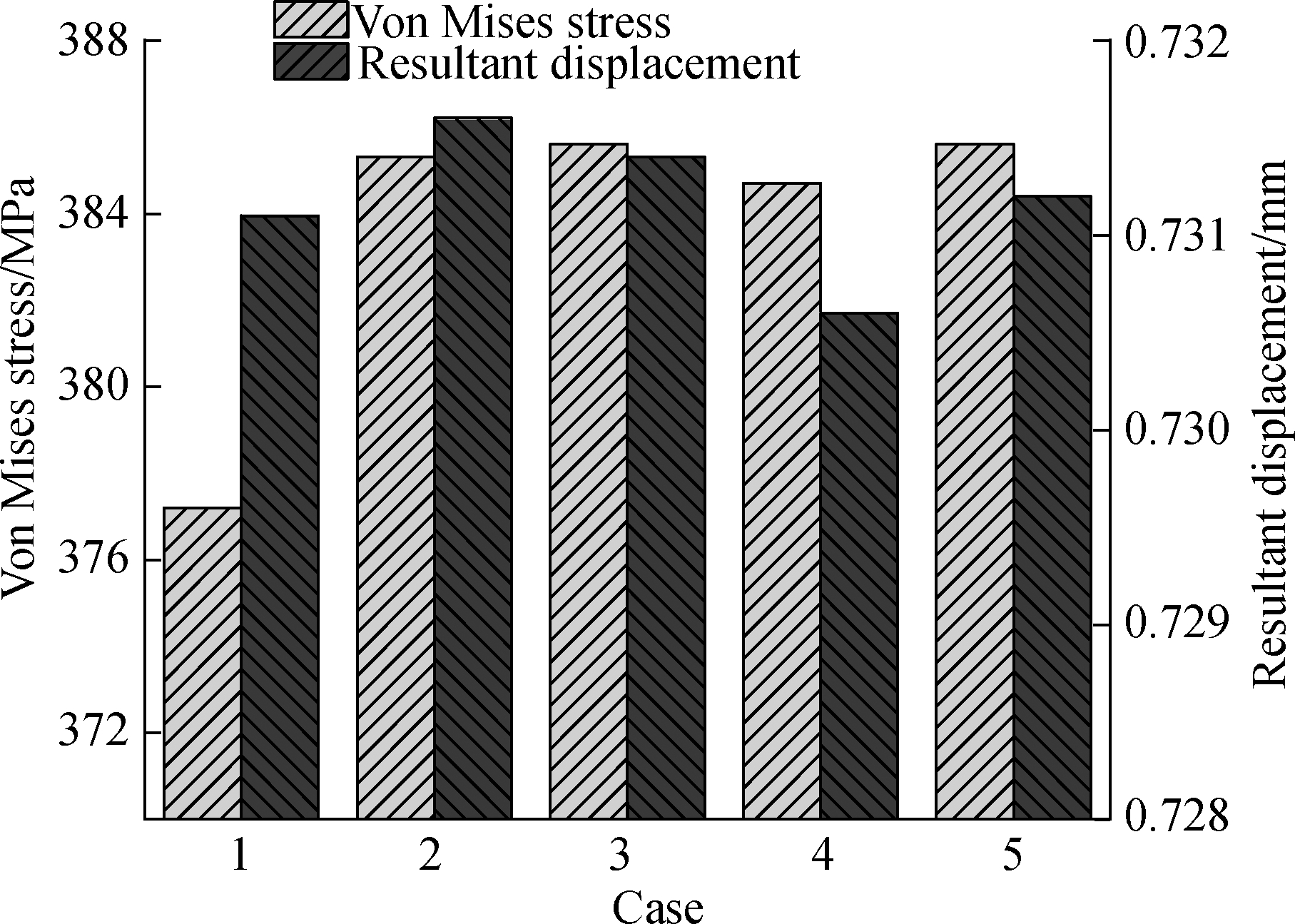
Fig.4 Von Mises stress and resultant displacement results by different mesh densities
2.3 Service limit state
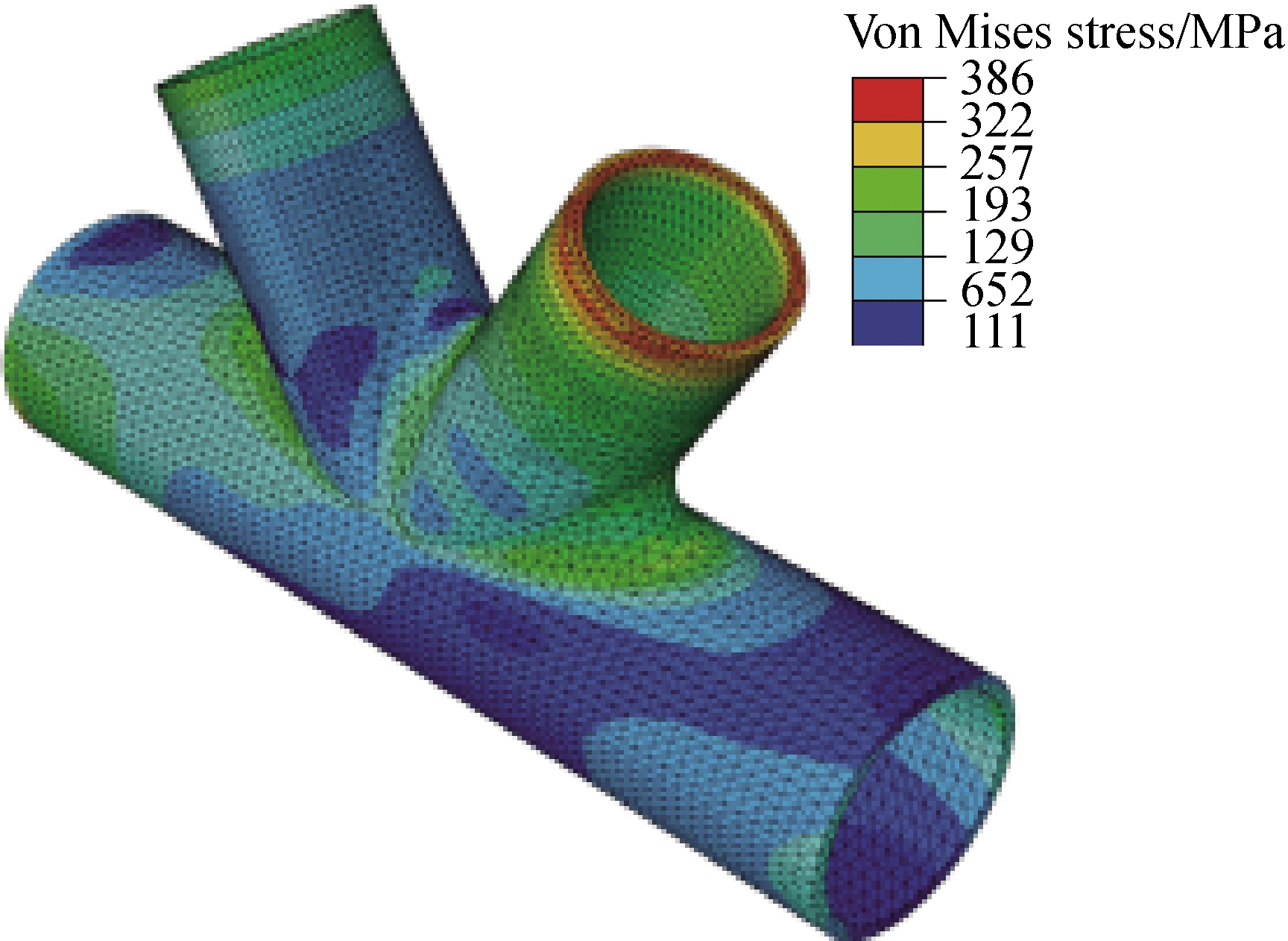
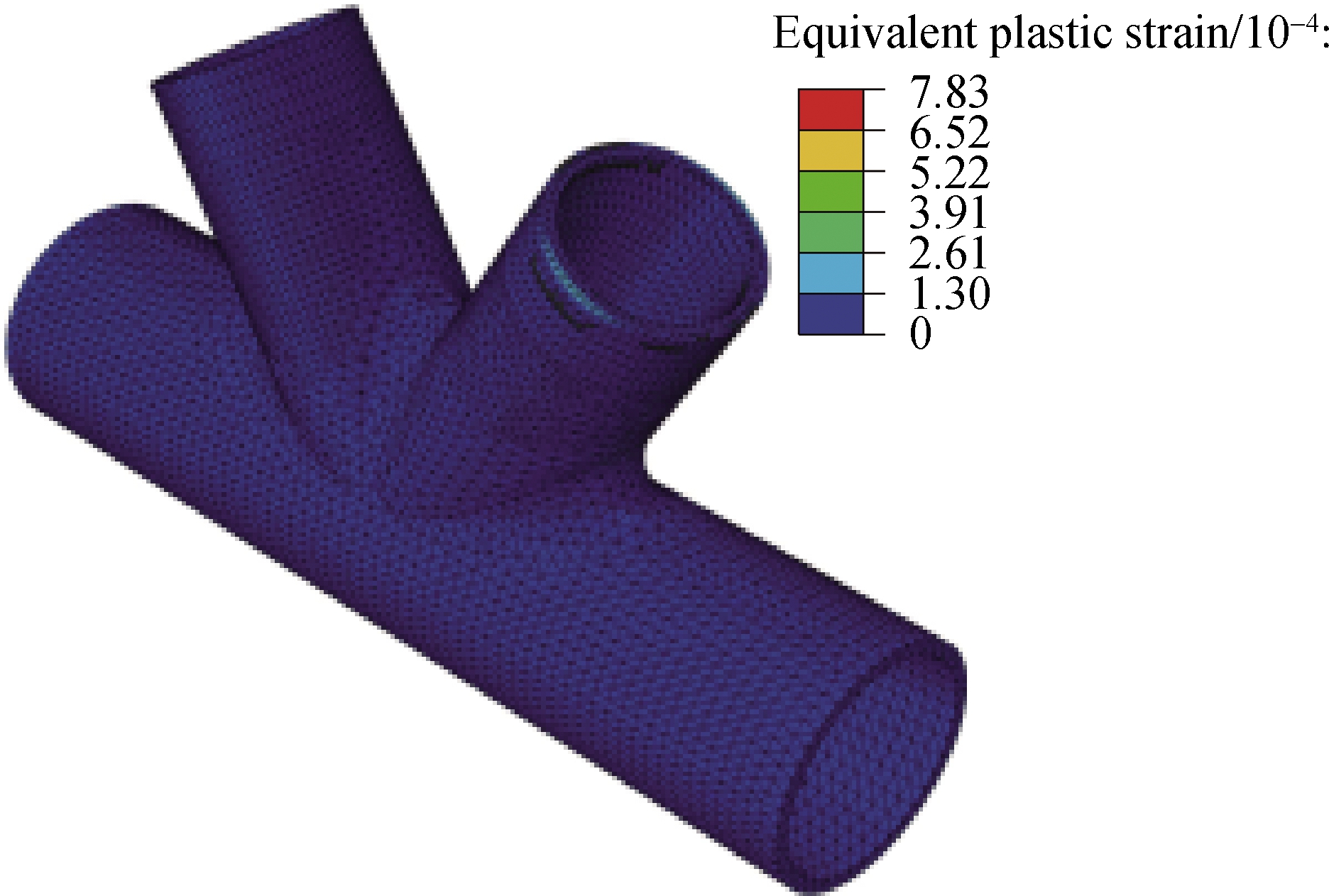
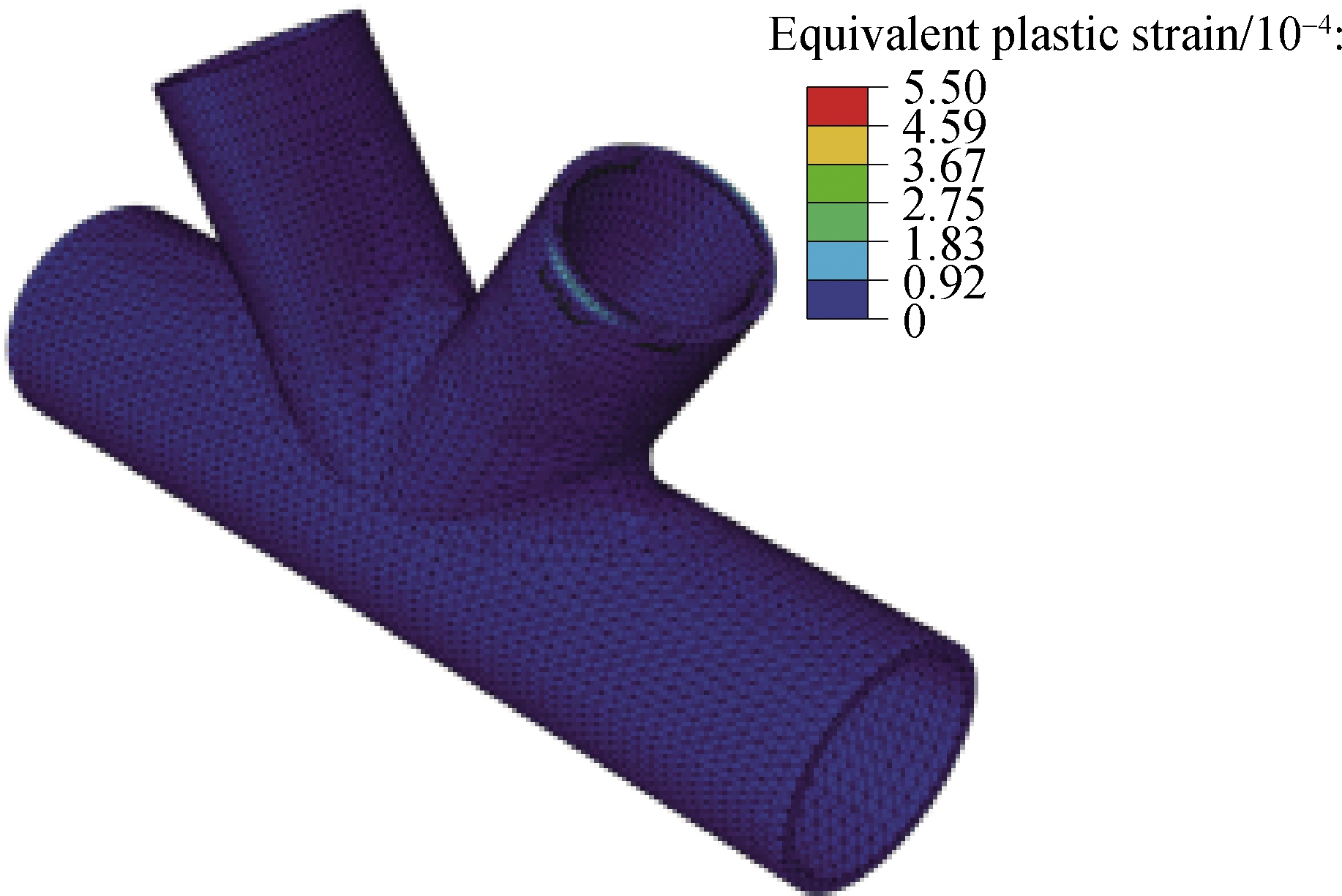
Figs.5 and 6 show the Von Mises stress and the equivalent plastic strain contour of the cast steel node calculated by the bilinear model and GTN damage model under the design load.Branch tube port B yields based on the two constitutive models, but the yielding area is small and most areas are still in the elastic stage.
The maximum Von Mises stress values of cast steel nodes calculated based on the two constitutive models are 364 and 386 MPa.The difference between the two values is minute, and the value based on the GTN damage model is slightly large.Whether the damage is considered or not has little effect on the service limit state of cast steel nodes.The reason is that the main areas of cast steel nodes do not transit to a yielding stage under the design load, and the damage in the nodes has not yet evolved.
(a)
(b)
Fig.5 FEM results based on the GTN damage model.(a)Von Mises stress contour;(b)Equivalent plastic strain contour

(a)
(b)
Fig.6 FEM results based on the bilinear model.(a)Von Mises stress contour;(b)Equivalent plastic strain contour
2.4 Ultimate limit state
The ultimate limit state of the cast steel node mainly refers to the maximum axial force when the node is damaged due to excessive local deformation under a load[25].According to JGJ/T 395—2017[24], the extreme point of the load-displacement curve calculated by the FEM should be taken as the ultimate limit capacity.
Fig.7 shows the load-displacement curves of the branch tube ports A and B calculated by the two constitutive models.Whether the bilinear model or GTN damage model is adopted, branch tube port A yields before branch tube port B, but the relative displacement in the ultimate limit state for branch tube port B is greater than that of branch tube port A.

Fig.7 Load multiple-relative displacement curve of branch tube ports A and B
The load-displacement curves obtained by the two constitutive models have good consistency in the elastic, yielding, and coinciding in the strengthening stage, but there are differences in the degradation stage.The load-displacement curve calculated by the GTN damage model fails earlier, and the strength decreases faster.The ultimate bearing capacity based on the bilinear model and GTN damage model is 1.95 and 1.93 times of the load, respectively, which meets the requirements of JGJ/T 395—2017 that the ultimate limit capacity should be 1.5 times greater than the design load.
Based on this analysis, the damage evolution behavior of materials has a specific impact on the ultimate limit state of the cast steel node.After considering the material performance degradation caused by damage, the failure process of components after reaching the ultimate limit capacity is rapid.Although the stress level of cast steel nodes in the service limit state is in the elastic stage, it is likely to transit the plastic stage under ultimate loads, such as seismic action.The GTN damage model can effectively predict the failure results of cast steel nodes in the ultimate limit state.
3 Model Parameters in the GTN Damage Model
3.1 Effect of model parameters on the load-displacement curves
After evaluating the bearing capacity of the cast steel node, the effects of the model parameters(fc, ff, fN, and εN)on the load-displacement curves of the cast steel node were studied.
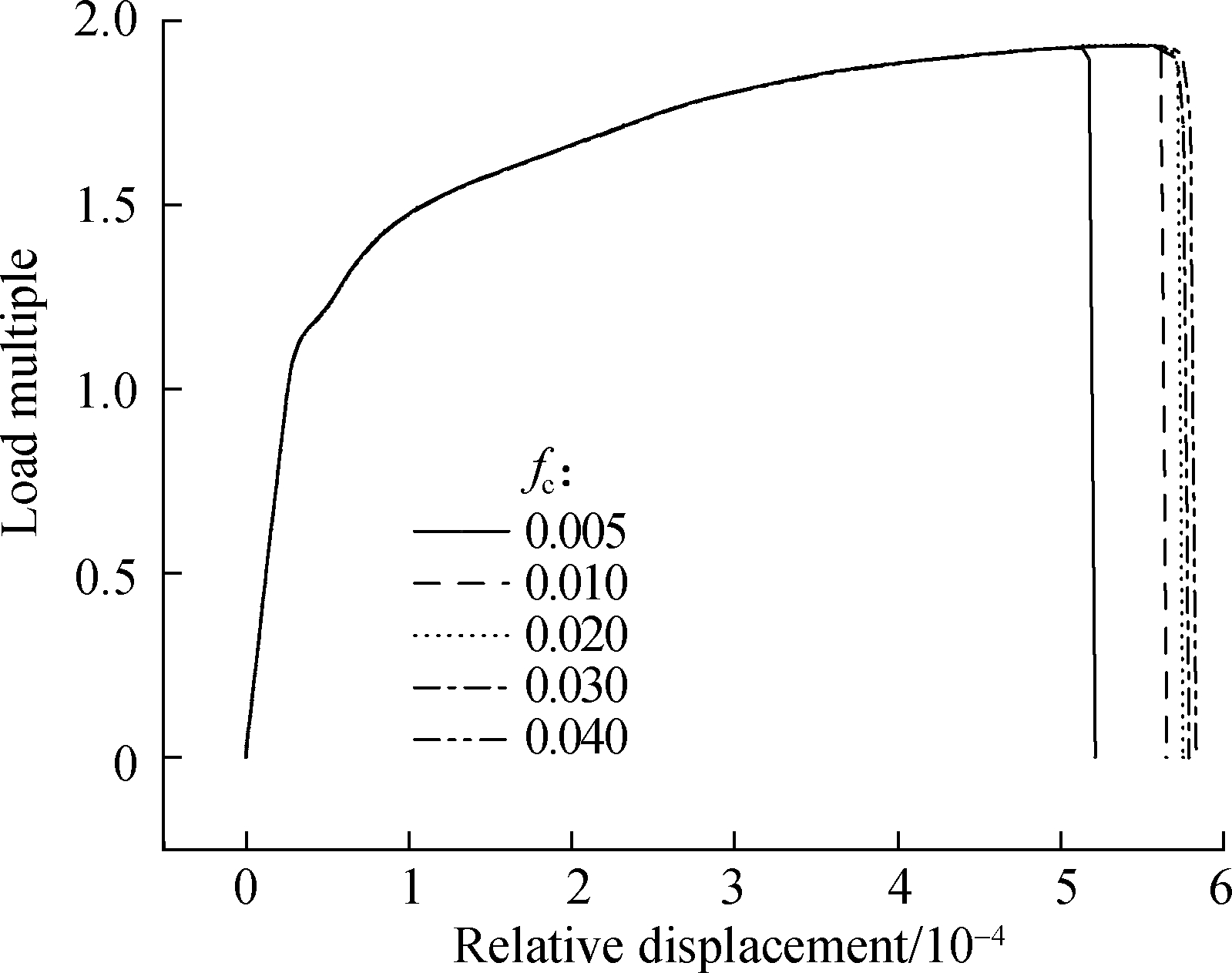
Fig.8 shows that fc does not affect the curve’s trend, but for the same void nucleation and growth rate, the larger fc is, the longer the time needed for the void to coalesce.Therefore, the critical failure point will be delayed.
(a)
(b)
(c)
(d)
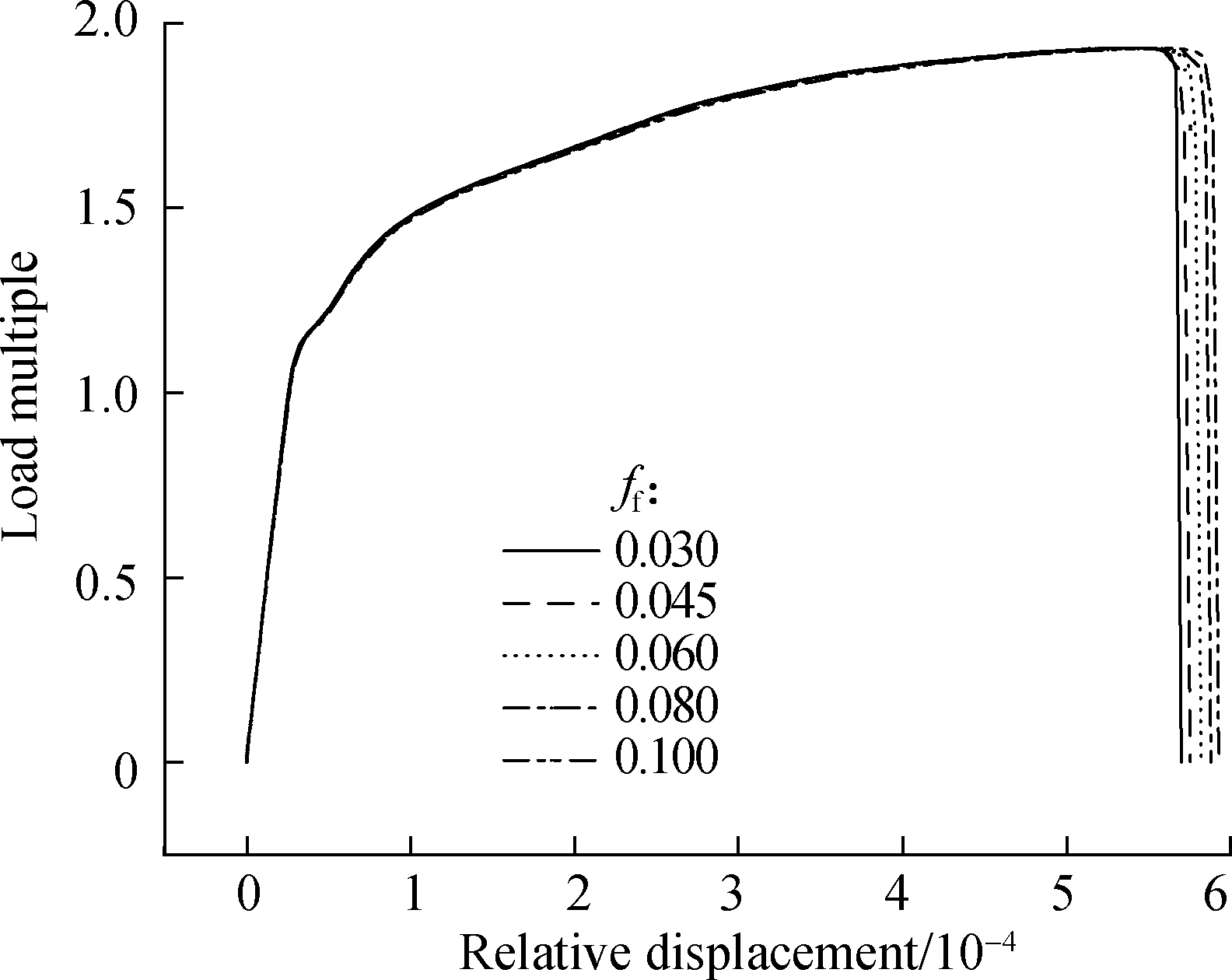
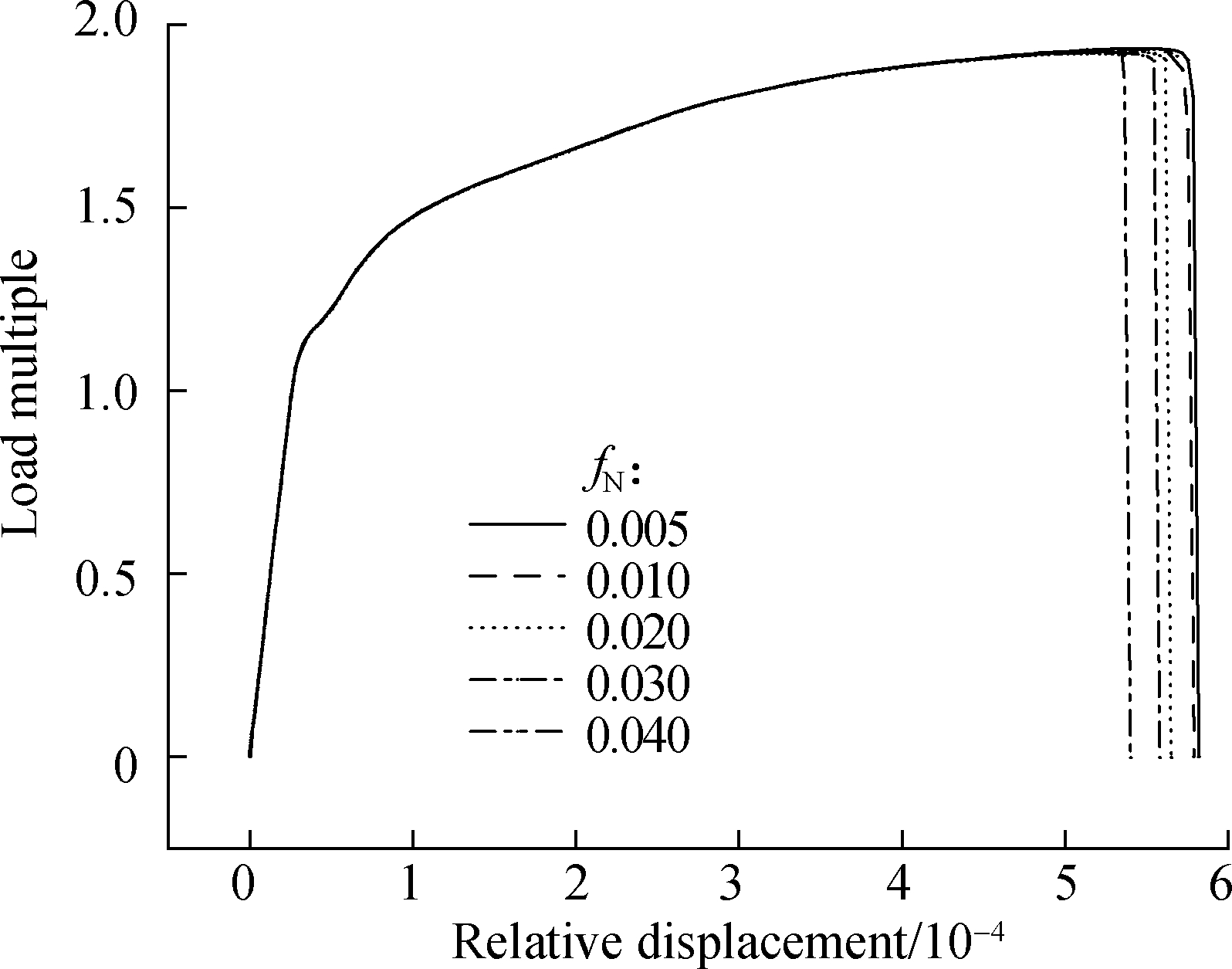
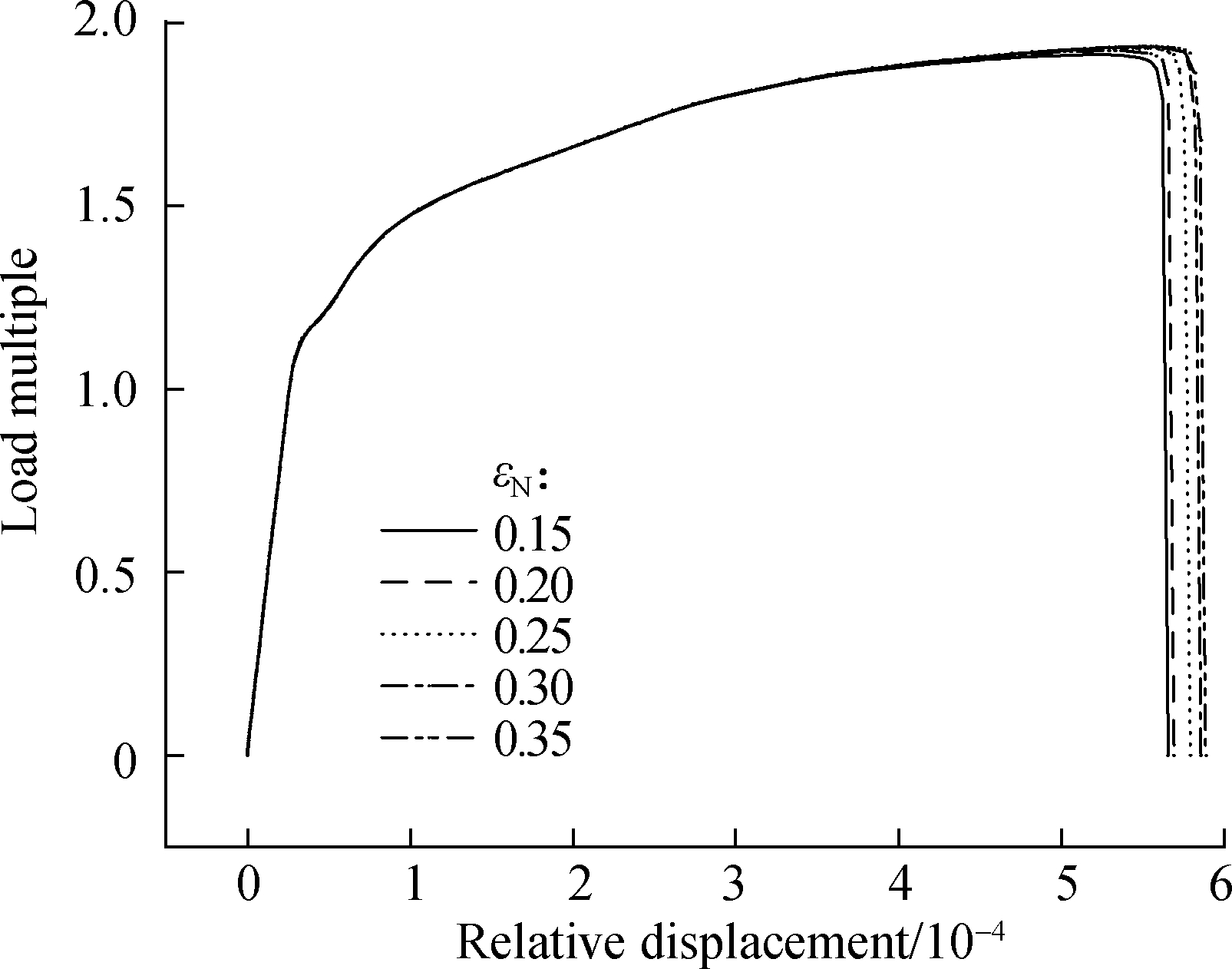
Fig.8 Effects of nucleation parameters on the load multiple-relative displacement curves.(a)fc;(b)ff;(c)fN;(d)εN
The influence of ff on the curve is similar to fc.When the test conditions and other model parameters are identical, the larger ff is, the longer the voids needed nucleate and grow to ff, and the critical failure point will move backward.
By increasing fN, the larger the void volume fraction is due to the micro-defects in the material, the faster the critical failure point will be reached, leading to a short fracture displacement.
dfnu is an approximately normal distribution concerning an equivalent plastic strain, so the strain at the maximum point of the void nucleation velocity is εN.The larger the εN is, the smaller the void nucleation velocity is, and the higher the bearing capacity of cast steel nodes is.
3.2 Evolution of the void volume fraction under a load
In this section, we examine the evolution of the void volume fraction(f, fgr, and fnu)and plastic strain index(PEMAG and PEEQ)by the GTN damage model.The uniaxial tensile load and cyclic load applied to the cast steel node are shown in Figs.9 and 10.The evolution of the void volume fraction and plastic strain index at branch tube port B are shown in Figs.11 and 12.
Fig.11 shows the evolution of the variables under auniaxial tensile load.When the materials transit to the yielding stage under the load, fgr and fnu rapidly increase after the PEEQ(equivalent plastic strain)accumulates to a certain extent, and fnu increases faster.f and the PEMAG(plastic strain magnitude)have similar variations, indicating that the GTN damage model effectively couples the damage parameters and the plastic strain of the matrix material.It also explains why the bilinear and GTN damage models’ load-displacement curves differ after the yielding stage.
Fig.12 shows the evolution of these variables under a cyclic load.f rises in steps during the load process, and the growth rate becomes increasingly faster.Eq.(4)shows that fgr is related to PEMAG.PEMAG is positive during tension and negative during compression.Therefore, fgr changes positively and negatively with the cyclic load, and its horizontal stage corresponds to the unloading stage.Eq.(5)shows that fnu is related to the PEEQ.The PEEQ increases during the loading stage and remains unchanged during the unloading stage, so fnu rises in steps during the loading process.
Fig.9 Uniaxial tensile load
Fig.10 Cycle load
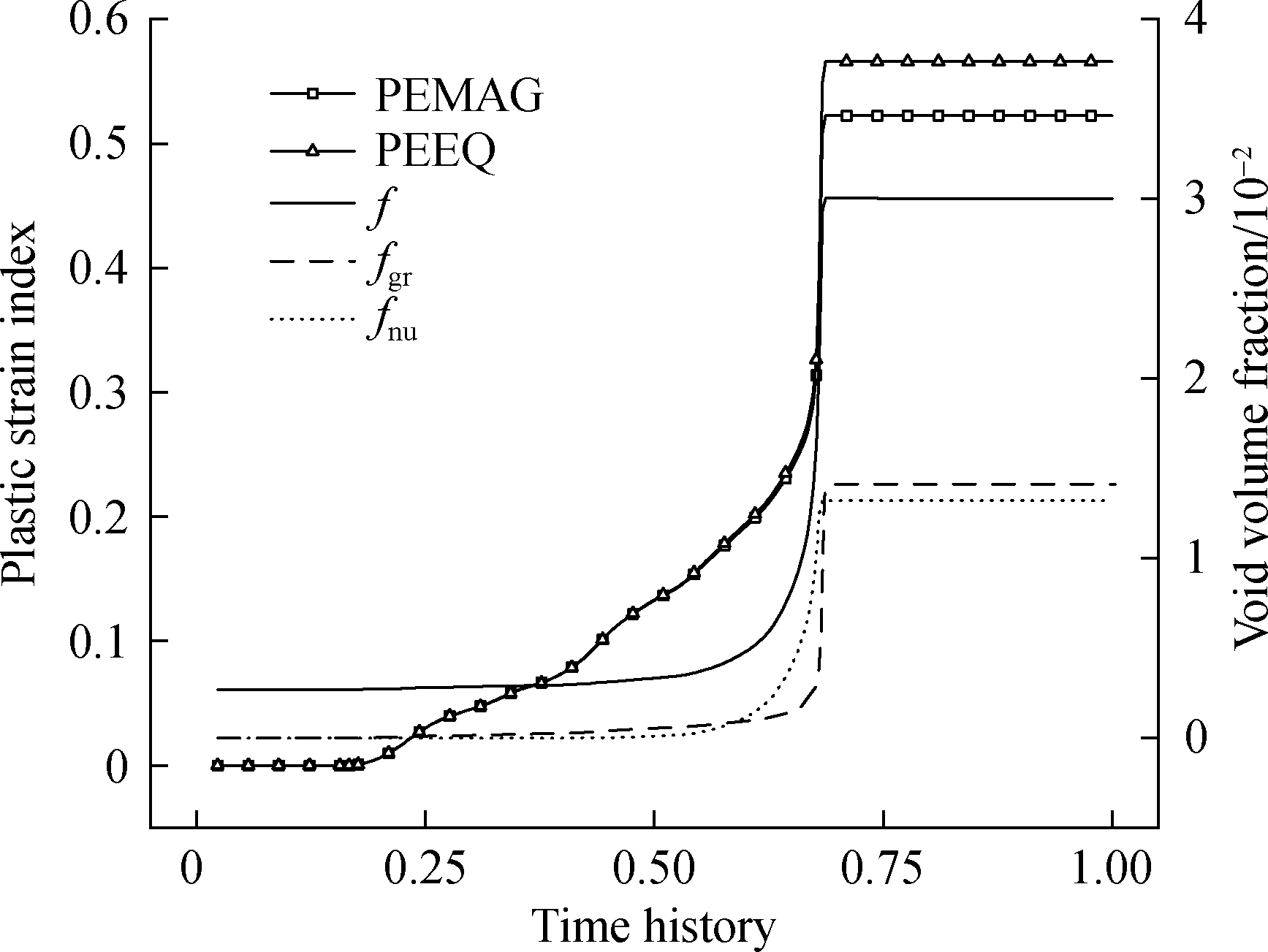
Fig.11 Evolution of the void volume fraction and plastic strain index with a uniaxial tensile load
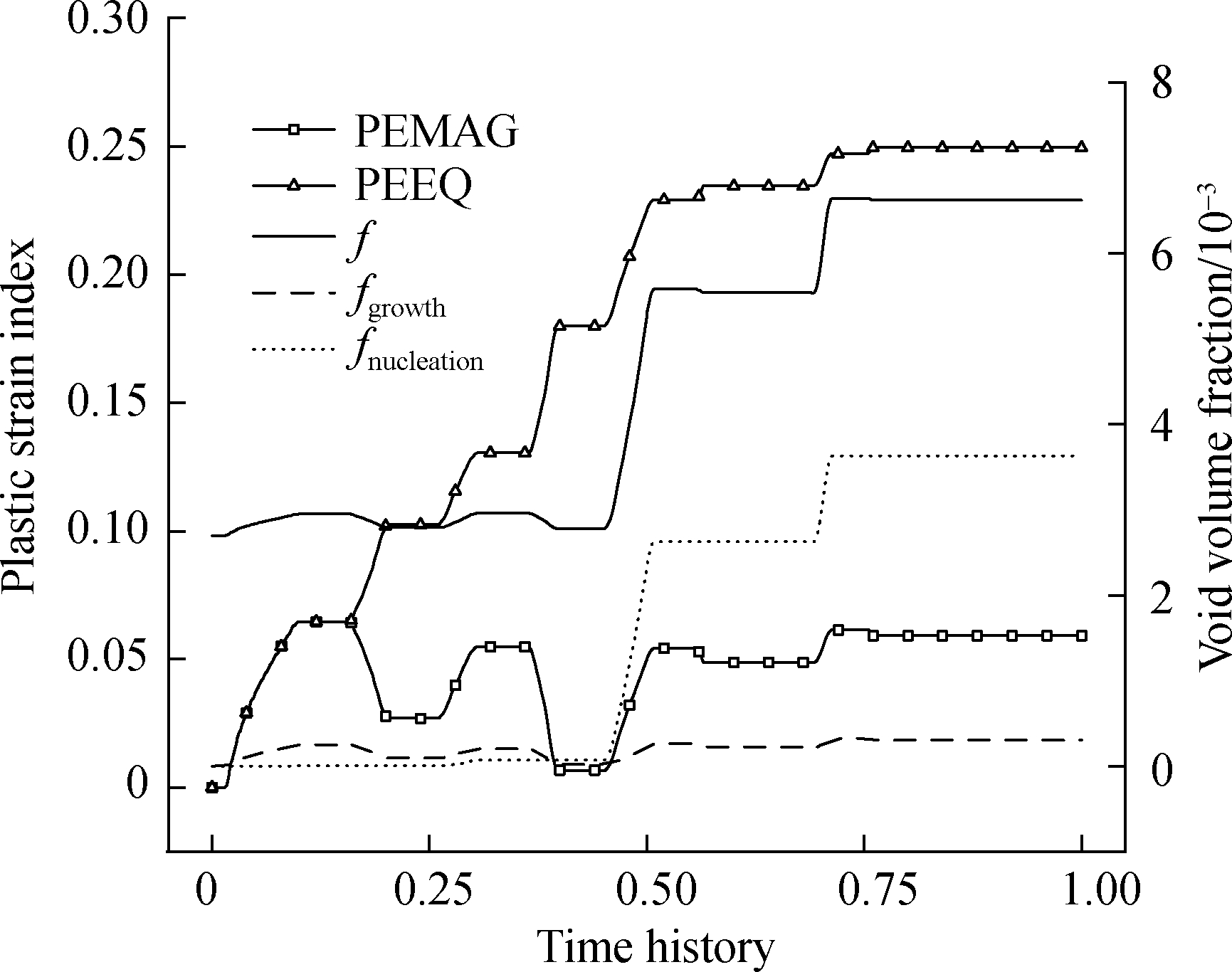
Fig.12 Evolution of the void volume fraction and plastic strain index with a cycle load
4 Conclusions
1)Based on the bilinear model and GTN damage model, the bearing capacity of the cast steel node was evaluated.The results show that there is a specific influence on the ultimate limit state.The cast steel node has an earlier failure time and faster failure speed considering the GTN damage model.
2)The influence of each model parameter on the failure critical point of the cast steel node was compared and analyzed.The results show that as fN increases, the critical failure point moves forward; as fc, ff, and εN increase, the critical failure point moves backward.
3)The evolution of the void volume fraction and plastic strain index is similar under the uniaxial tensile load.However, under the cyclic load, fgr and fnu are respectively affected by the PEMAG and PEEQ, which show different evolution laws.
[1] Yin Y, Li S, Han Q H, et al.Material parameters in void growth model for G20Mn5QT cast steel at low temperatures[J].Construction and Building Materials, 2020, 243:1-15.DOI: 10.1016/j.conbuildmat.2020.118123.
[2] Blair M, Monroe R, Beckermann C, et al.Predicting the occurrence and effects of defects in castings[J].The Journal of The Minerals, 2005, 57(5):29-34.DOI: 10.1007/s11837-005-0092-3.
[3] Zhao C F, Li Z X.Influence of geometrical features of meso-defects on damage evolution of metal structure[J].Applied Mechanics and Materials, 2015, 723:21-25.DOI: 10.4028/www.scientific.net/AMM.723.21.
[4] Springmann M, Kuna M.Identification of material parameters of the Gurson-Tvergaard-Needleman model by combined experimental and numerical techniques[J].Computational Materials Science, 2005, 32(3/4):544-552.DOI: 10.1016/j.commatsci.2004.09.010.
[5] Gurson A L.Porous rigid-plastic materials containing rigid inclusions-yield function, plastic potential, and void nucleation[J].Physical Metallurgy of Fracture, 1978(5): 357-364.DOI: 10.1016/B978-0-08-022138-0.50058-7.
[6] Tvergaard V.Influence of voids on shear band instabilities under plane-strain conditions[J].International Journal of Fracture, 1981, 17(4): 389-407.DOI: 10.1007/BF00036191.
[7] Needleman A, Tvergaard V.An analysis of ductile rupture in notched bars[J].Journal of the Mechanics and Physics of Solids, 1984, 32(6): 461-490.DOI: 10.1016/0022-5096(84)90031-0.
[8] Roux E, Bernacki M, Bouchard P O.A level-set and anisotropic adaptive remeshing strategy for the modeling of void growth under large plastic strain[J].Computational Materials Science, 2013, 68:32-46.DOI: 10.1016/j.commatsci.2012.10.004.
[9] Xu Y D, Qian C X.Application of Gurson-Tvergaard-Needleman constitutive model to the tensile behavior of reinforcing bars with corrosion pits[J].Plos One, 2017, 8(1): 1-7.DOI: 10.1371/journal.pone.0054368.
[10] Liu X G, Wang C, Deng Q F, et al.High-temperature fracture behavior of MnS inclusions based on GTN model[J].Journal of Iron and Steel Research International, 2019, 26:941-952.DOI: 10.1007/s42243-018-0202-4.
[11] Steglich D, Wafai H, Besson J.Interaction between anisotropic plastic deformation and damage evolution in Al 2198 sheet metal[J].Engineering Fracture Mechanics, 2010, 77(17):3501-3518.DOI: 10.1016/j.engfracmech.2010.08.021.
[12] Li G, Cui S S.A review on theory and application of plastic meso-damage mechanics[J].Theoretical and Applied Fracture Mechanics, 2020, 109: 1-12.DOI: 10.1016/j.tafmec.2020.102686.
[13] Zhang Z L, Thaulow C, Ødegård J.A complete Gurson model approach for ductile fracture[J].Engineering Fracture Mechanics, 2000, 67(2):155-168.DOI: 10.1016/S0013-7944(00)00055-2.
[14] Chu C C, Needleman A.Void Nucleation effects in biaxially stretched sheets[J].Journal of Engineering Materials and Technology, 1980, 102(3): 249-256.DOI: 10.1115/1.3224807.
[15] Acharyya S, Dhar S.A complete GTN model for prediction of ductile failure of pipe[J].Journal of Materials Science, 2008, 43(6):1897-1909.DOI: 10.1007/s10853-007-2369-0.
[16] Zhou J, Gao X, Sobotka J C, et al.On the extension of the Gurson-type porous plasticity models for prediction of ductile fracture under shear-dominated conditions[J].International Journal of Solids and Structures, 2014, 51(18):3273-3291.DOI: 10.1016/j.ijsolstr.2014.05.028.
[17] Kami A, Dariani B M, Vanini A S, et al.Numerical determination of the forming limit curves of anisotropic sheet metals using GTN damage model[J].Journal of Materials Processing Technology, 2014, 216:472-483.DOI: 10.1016/j.jmatprotec.2014.10.017.
[18] Zhao P J, Chen Z H, Dong C F.Experimental and numerical analysis of micromechanical damage for DP600 steel in fine-blanking process[J].Journal of Materials Processing Tech, 2016, 236:16-25.DOI: 10.1016/j.jmatprotec.2016.05.002.
[19] Jiang W, Li Y Z, Su J.Modified GTN model for a broad range of stress states and application to ductile fracture[J].European Journal of Mechanics A/solids, 2016, 57:132-148.DOI: 10.1016/j.euromechsol.2015.12.009.
[20] Gholipour H, Biglari F R, Nikbin K.Experimental and numerical investigation of ductile fracture using GTN damage model on in-situ tensile tests[J].International Journal of Mechanical Sciences, 2019, 164:1-15.DOI: 10.1016/j.ijmecsci.2019.105170.
[21] Yan H D, Jin H, Yao R G.Prediction of the damage and fracture of cast steel containing pores[J].International Journal of Damage Mechanics, 2020, 29(1):1-18.DOI: 10.1177/1056789519872000.
[22] Yan H D, Tang Q, Jin H.Damage evolution analysis on cast steel joints with porosity defects[J].Journal of Southeast University(Natural Science Edition), 2019, 49(5):904-910.DOI:10.3969/j.issn.1001-0505.2019.05.013.(in Chinese)
[23] Yan H D, Jin H.Damage evolution analysis of cast steel GS-20Mn5V based on modified GTN model[J].Journal of Southeast University(English Edition), 2018, 34(3):364-370.
[24] Ministry of Housing and Urban-rural Development of the People’s Republic of China.Technical specification for cast steel structure: JGJ/T 395—2017[S].Beijing: China Construction Industry Press, 2017.(in Chinese)
[25] Luo L S, Wen H G, Duan X N.Research on bearing capacity of circular steel tubular KX-joint[J].Steel Structure, 2018, 33(2):56-59,109.(in Chinese)