The staggered floor structure, as a new type of structural system, has the advantages of lowering the building floor height and economizing traffic area by reducing the connecting slope length of adjacent areas.These offer some room for the construction of parking garages and other architectural features.The mechanical properties of staggered floor structures are different from those of traditional structures.In the Code for the Seismic Design of Buildings(GB 50011—2010)[1], structures with larger staggered floors are classified as irregular planar structures, and the storied layout of floor slabs with great plane stiffness has a great effect on the force of such structures.
In 1906, the American scholar Turner first used the beamless floor in Minneapolis, Minnesota, USA [2].Since then, domestic and international scholars have carried out detailed research on the slab-column structure, thereby achieving fruitful results in the slab-column joint anti-punching shear [3-4] and the slab-column structure calculation model[5-6].Domestic scholars have also conducted studies on different forms of staggered floor structures, such as staggered floor shear wall structure [7], staggered floor masonry structure[8], and staggered floor frame structure and joint[9-10], and proposed suggestions for the seismic design of related structures.Furthermore, the variation law of the shear force in the staggered floor structure area with different heights under the action of frequent and rare earthquakes was studied through the elastic and elastoplastic time-history analysis.Many scholars have argued that the adverse effects of splits on the structure are reflected in the following two aspects: 1)The floor is divided into several pieces, and each part is misplaced, thus weakening the performance of the floor coordination of the whole structure; 2)Due to the floor splits, short vertical members are formed in some parts, which concentrates the force and is not conducive to earthquake resistance.
Based on theoretical analysis and data research, Zhou[11] derived the calculation method of the horizontal shear and punching bearing capacity of the short-column joints under vertical load for the staggered floor slab-column structure.Wang[12] used the ANSYS finite element software to carry out time-history analysis on the staggered floor slab column and ordinary slab-column structures; proposed three different seismic measures of lifting structure, including bottom connection, top connection and shear wall; and compared their seismic effects.
In view of certain problems, such as the existing research on staggered floor structures being more focused on the frame structure and shear wall structure and the lack of experimental data support, the current paper discusses the failure modes and seismic performances of the joints by testing two reinforced concrete slab-column-boundary beam joints under low cyclic loading.
1 Experiment Design
The prototype structure of the test specimen was a staggered floor slab-column structure with a column grid size of 6 000 m×4 000 mm and a story height of 2.8 m.The truncated body was extracted from the anti-bending and symmetrical lines of the intermediate lattice plate of the prototype structure, as well as the anti-bending point of the column.The final specimen size of 1∶2 reduced-scale was adopted and determined according to the size of the laboratory loading device.According to the Code for the Seismic Design of Buildings(GB 50011—2010), the seismic design grade of structure is Grade Ⅱ.In the design of SSCJ, the slab reinforcement is magnified 1.4 times to strengthen the flexural strength of the slab in order to obtain the failure mode of the short column.According to the latest study, the main factors affecting the seismic performance of staggered slab-column structure include the following: slab thickness, staggered height, axial-compression ratio, shear-compression ratio, the side beam, and hooping in the column.In the present study, two of the mentioned factors were studied.The two test specimens were labeled SCJ1 and SCJ2, respectively, considering the influence of slab thickness and column sections.The geometrical size and reinforcement of the specimens are shown in Fig.1 and Tab.1, respectively.

(a)
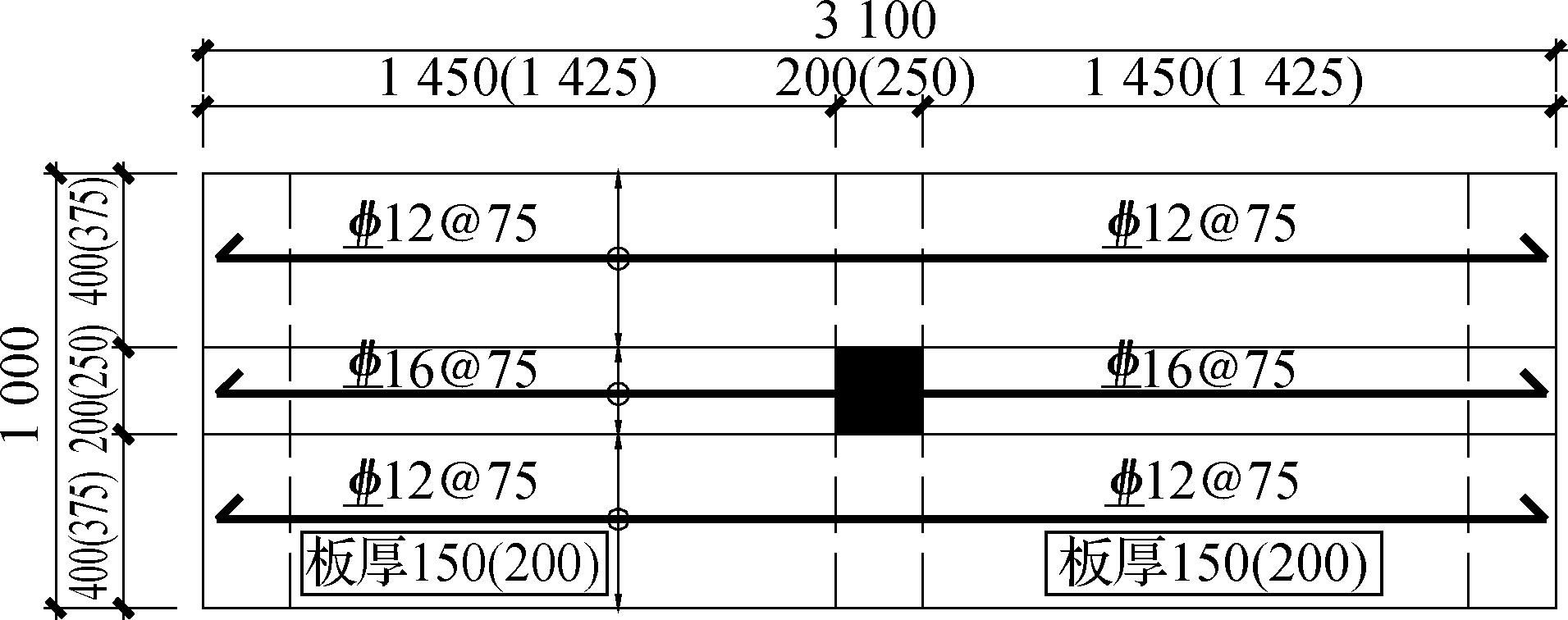
(b)
Fig.1 Design parameters of joints(unit:mm).(a)Profile of the specimen;(b)Plan of the specimens
Tab.1 Reinforcement information of joints

No.Column cross-section/ mm×mm Thickness of plate/mmStirrup/mmColumn longitudinalbar/mmBoundary beamlongitudinal bar/mmLoading beamlongitudinal bar/mmLoading beamstirrup/mmBoundary beamstirrup/mmSCJ1200×200150Φ6@1004Φ202Φ16 2Φ162Φ12 2Φ12Φ8@200Φ8@100SCJ2250×250200Φ6@1004Φ202Φ16 2Φ162Φ12 2Φ12Φ8@200Φ8@100
2 Test Loading and Contents
2.1 Loading device
A low cyclic loading test was carried out on the specimens, in which the joint testing machine was used as the loading device.Moreover, the upper and lower column ends of the specimens were fixed hinges, and the plate ends were free.The loading device is shown in Fig.2.As can be seen, two sets of four hydraulic jacks were configured on both sides of the loading beams of the node to realize repeated synchronous loading.Hydraulic jacks have a range of 20 T and a stroke of 200 mm.Constant axial pressure was applied on top of the column through a large-range hydraulic jack.Steel block pads were pre-set at the upper and lower ends and on both sides of the column.Meanwhile, four steel blocks with welded steel bars were used on both sides of the column ends to clamp the column head and emulate the hinge support at the column ends, thus limiting its horizontal displacement.
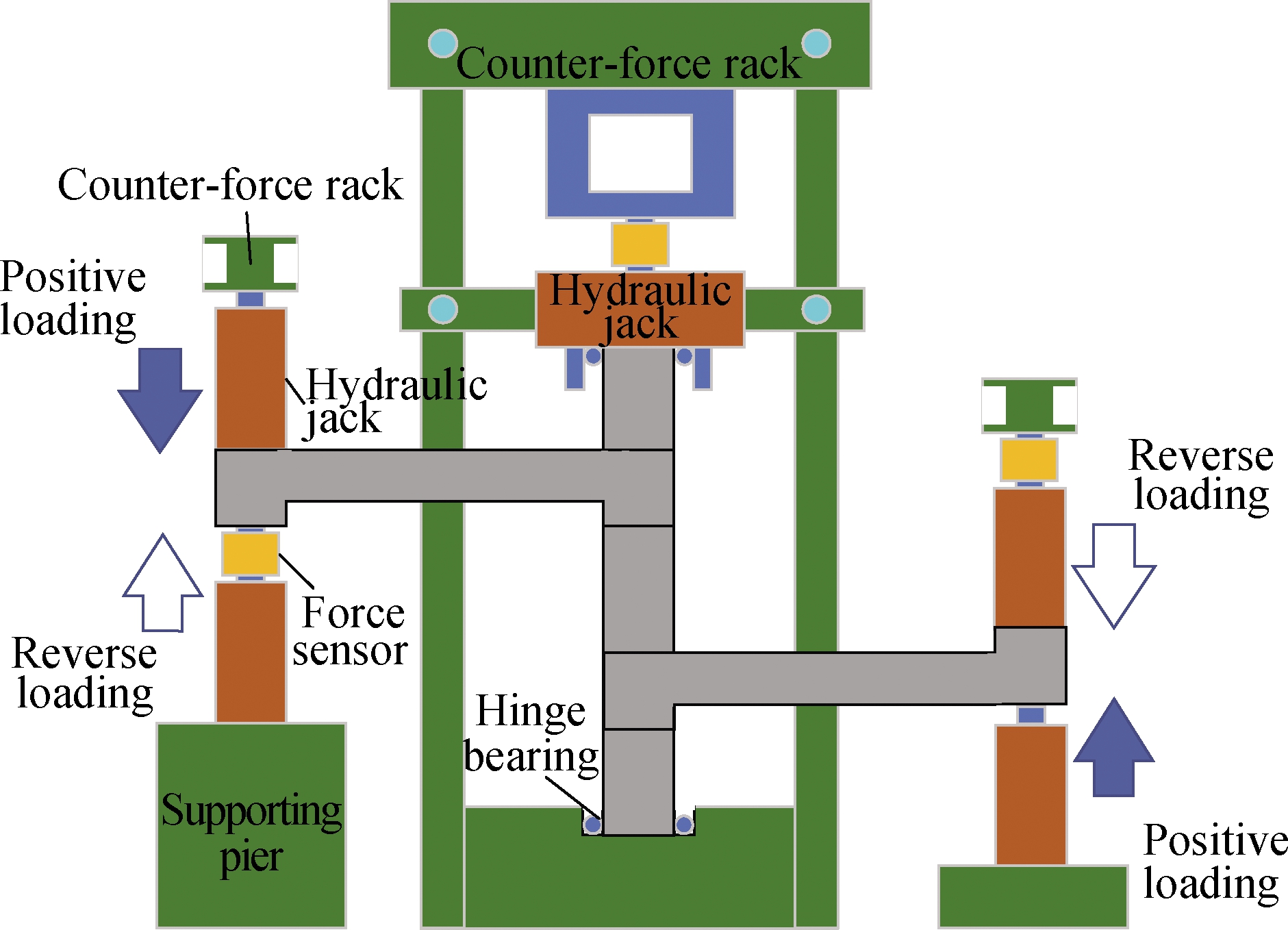
Fig.2 Loading device
2.2 Loading system
In the test preparation stage, the vertical load, i.e., the axial force 0.2fcbh, was applied and kept constant during the test.The displacement load was applied symmetrically in the forward and reverse directions during the tests, and the displacement of each stage was 1.2 times that of the previous stage.The initial displacements of SCJ1 and SCJ2 were 3 and 6 mm, respectively.When cracks appeared in the specimen, the number of loading cycles was adjusted from one to three times.When the load dropped to 85% of the peak load, the specimen was considered damaged.The displacement loading system is shown in Fig.3.
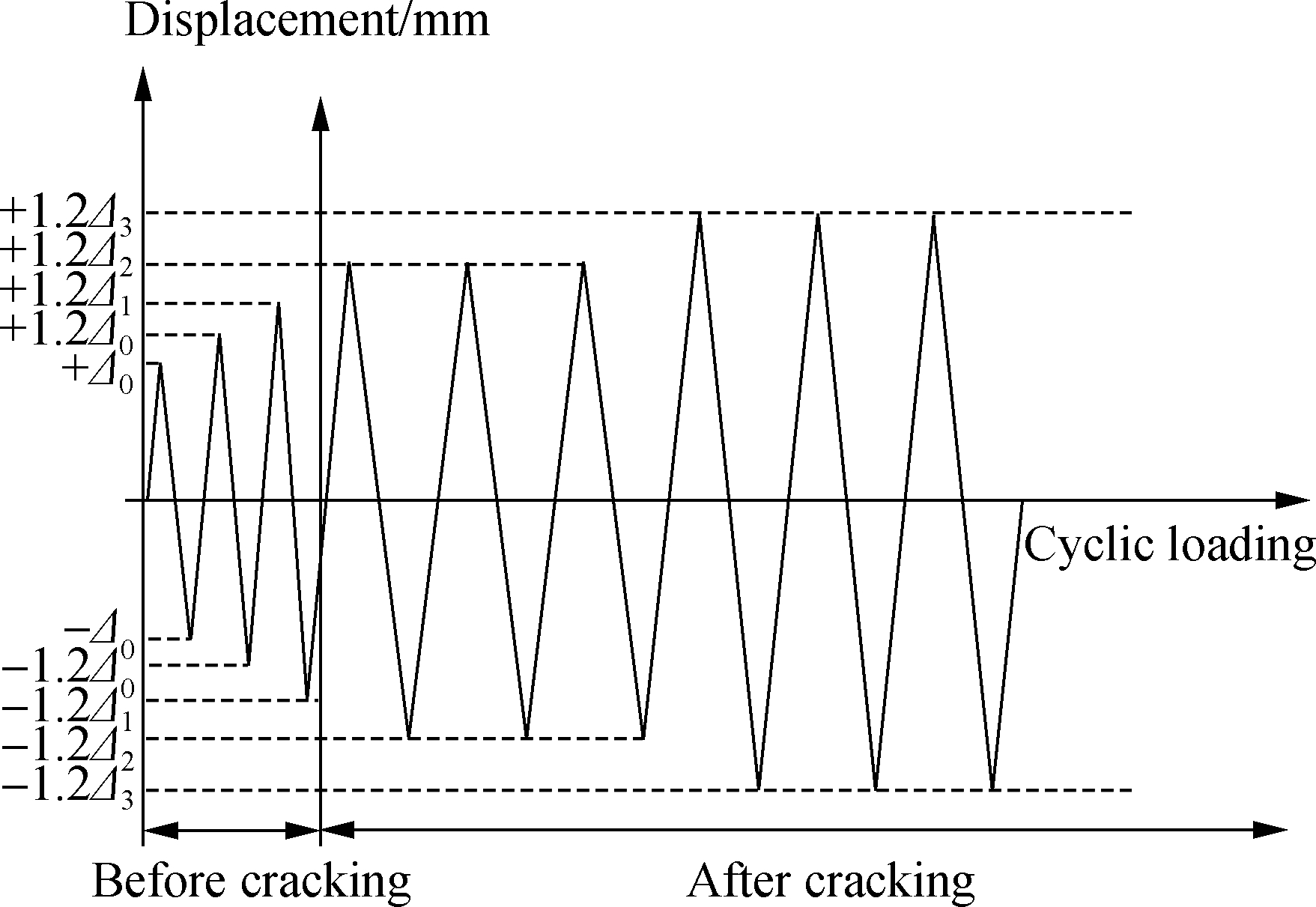
Fig.3 Loading process
As shown in Fig.2, the loading direction is specified as follows: when the high plate is subjected to a downward force, and the low plate is subjected to the anti-symmetric upward force of the same magnitude, it is called forward loading and the corresponding displacement is positive.Otherwise, it is called negative loading, and the corresponding displacement is negative.
3 Material Properties
3.1 Mechanical properties of reinforcement
The specimens used were HRB400 indented bar except for HPB235 plain round bar for column stirrups.The steel bar was divided into four numbers according to strength and diameter.Three groups of tensile tests were conducted for each numbered steel bar on a 300 kN testing machine in the mechanics laboratory according to the requirements of the Tensile Test Method for Metal Materials in Laboratory(GB/T 228—2002).The material mechanical properties of the steel bar obtained from actual measurements are listed in Tab.2.
Tab.2 Mechanical properties of the steel reinforcement

Bardiameter/mmStrength gradeYield strength/MPaUltimate tensilestrength/MPaSpecificelongation/%Elasticmodulus/GPaPoisson ratio6HPB23531136116.72100.28HRB40058166211.02000.216HRB40050061414.12000.220HRB40046866421.52000.2
3.2 Mechanical properties of concrete
The specimen concrete was pumped concrete with a strength grade of C30.The three cubic concrete standard test blocks with a side length of 150 mm were made simultaneously on-site and then cured for 28 d under the same environmental conditions as the specimens.The concrete material property test was completed on the 2 000 kN compression-testing machine in the structure laboratory according to the requirements of the Standard for Test Methods of Mechanical Properties of Ordinary Concrete(GB/T 228—2010).The obtained measured material mechanical properties of concrete are listed in Tab.3.The experimental values of the cube compressive strength fcu and the axial tensile strength ft in the table are calculated and determined according to the formula described in the provisions of the Code for Design of Concrete Structures.
Tab.3 Mechanical properties of concrete MPa

StrengthgradeCube compressivestrength fcuAxial tensilestrength ftElasticmodulus EcC3030.01.5724 937.13
4 Test Results and Analysis
4.1 Crack propagation and failure behaviors
For the SCJ2 specimen, cracks appeared near the core area of the upper boundary beam when the displacement reached 6.80 mm.Transverse cracks along the width of the slab appeared first at the edge of the low slab column under negative loading.As the loading continued, oblique cracks appeared in the upper, middle, and lower columns.Meanwhile, “eight shape” and “inverted eight shape” oblique cracks due to torsion appeared in the upper and lower plate boundary beams, gradually developing to the core area as the loading continued.Radioactive torsion cracks also appeared on the top surface of the boundary beam.With the increase of the load, the cracks continued to widen and extend, eventually causing the concrete on the surface of the boundary beam to flake.In turn, this crushed the concrete at the root of the upper column, and the baroclinic rod in the middle column was fractured.
For the SCJ1 specimen, the occurrence of cracks was basically consistent with that observed in the SCJ2 specimen.When the negative loading displacement reached 7.07 mm, several parallel bending cracks along the width of the plate appeared in the plate.As the loading continued, three 45°-60° oblique cracks appeared at the root of the upper column, and one 45° oblique crack appeared at the root of the lower column, while the oblique crack in the middle column was not obvious.Again, “eight-shaped” and “inverted eight-shaped” oblique cracks appeared in the boundary beam of the top and bottom floors.With the increase of loading displacement, oblique cracks extended to the core area, which was mainly caused by the torsion of the boundary beam in the core area.
4.2 Hysteric curves
Fig.4 shows the respective load-displacement hysteretic curves of the SCJ1 and SCJ2 specimens; here, the load in the hysteretic curve is the average load of the upper and lower slabs.As shown in the figure, the specimen material was in the elastic stage at the initial loading stage, and the load-displacement hysteresis curve appeared to be approximately a straight line.After the reinforcement yield, the slope of the loading curve decreased slightly with the increase of the load, and the reduction increased at an accelerated rate.Under the same displacement loading, the slope of the last cycle was less than that of the previous one, indicating that the stiffness of the specimen was degraded.When the steel bar was unloaded after yielding, the curve became steep and the displacement changed slowly.With the decrease of the load, the curve tended to be flat and the deformation recovery was gradually accelerated, suggesting that the hysteresis phenomenon of recovery deformation occurred.The slope of the unloading curve decreased with the increase of repeated loading times, and the stiffness of the components degraded continuously.After complete unloading, the specimen showed residual deformation and accumulated continuously.
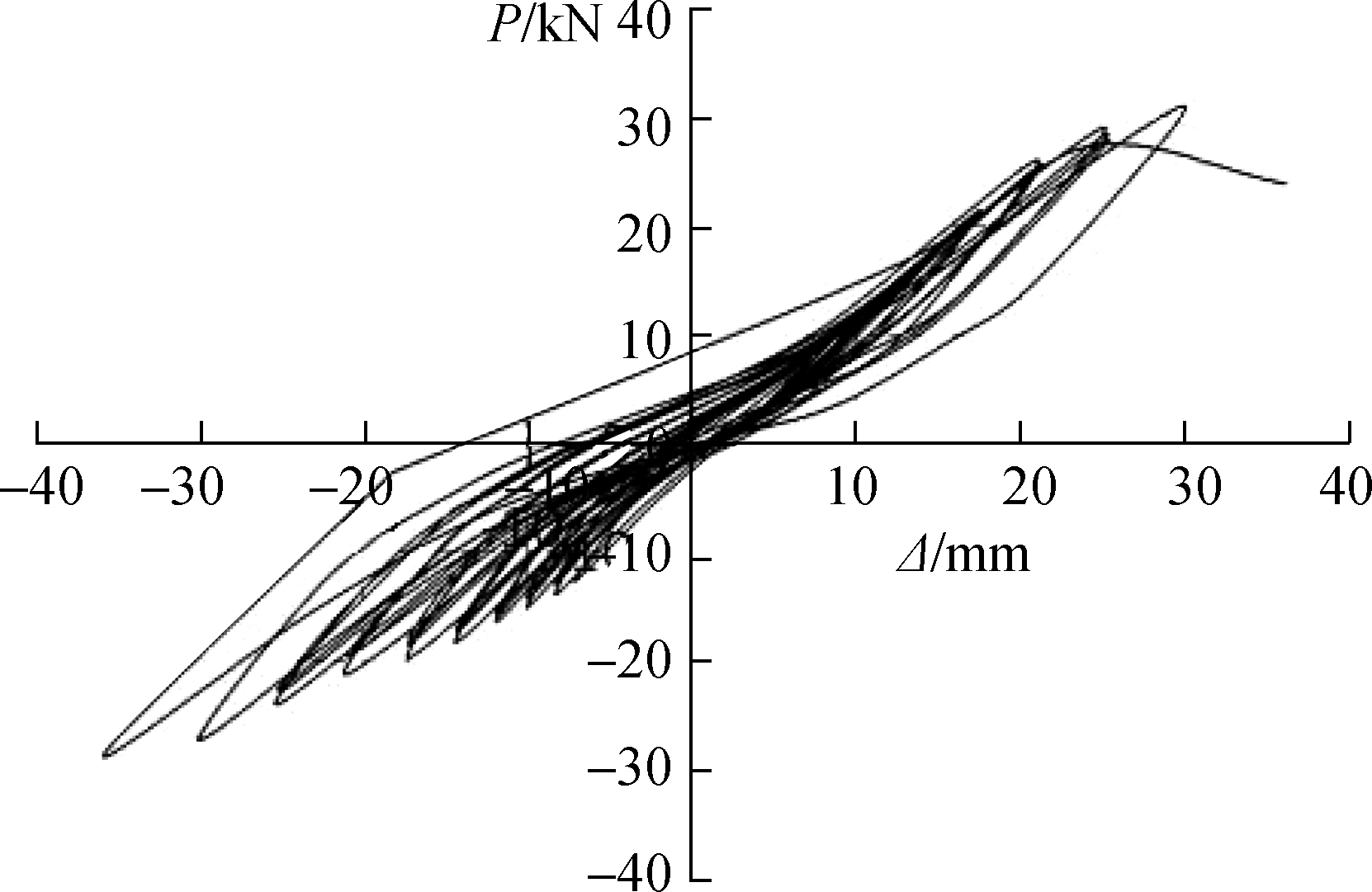
(a)
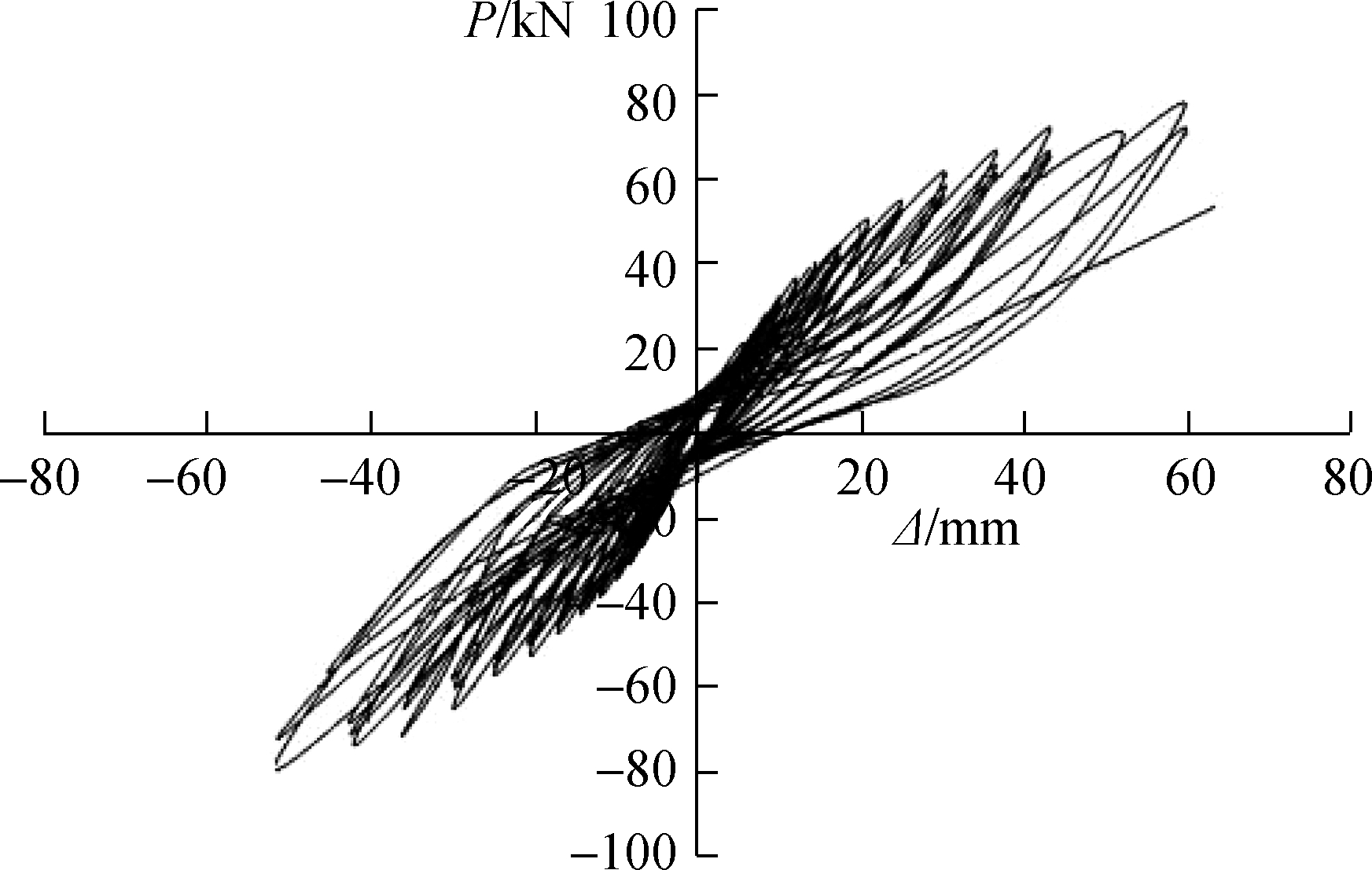
(b)
Fig.4 Load-displacement hysteric curves.(a)SCJ1;(b)SCJ2
As can be seen from the hysteretic curves of SCJ1 and SCJ2, the narrow and long hysteretic curves reveal an obvious pinching phenomenon, and the curves are in the inverse “S” shape, indicating that the SSCJ have weak energy dissipation capacity, poor ductility, and poor seismic performance.It should be emphasized that, due to the abnormal calibration of the force sensor, numerous cracks have appeared in the specimen SCJ1 during the forward preloading.Thus, the damaged component can only be reloaded with low-cycle repeated loading.At the same time, the residual deformation of the hysteretic loop curve shows obvious asymmetry, that is, the residual deformation is smaller under forward unloading and larger under negative unloading.
4.3 Skeleton curves and key points
The load-displacement skeleton curves of the SCJ1 and SCJ2 specimens are shown in Fig.5.Due to the damage in preloading, the skeleton curve presents the characteristics of asymmetry.What needs to be defined at this point is the fact that the crack load is determined based on a thorough consideration of the crack observation and the obvious changes in the skeleton curve.Here, the peak load is the maximum load, while the ultimate load is the load that drops to 85% of the peak load.The yield load value is obtained by the simplified method to determine the yield point of slate-column joints, as shown in Fig.6[13].The load and deformation results of the cracking point, yield point, peak point, and limit point are shown in Tab.4.

(a)

(b)
Fig.5 Load-displacement skeleton curves.(a)SCJ1;(b)SCJ2
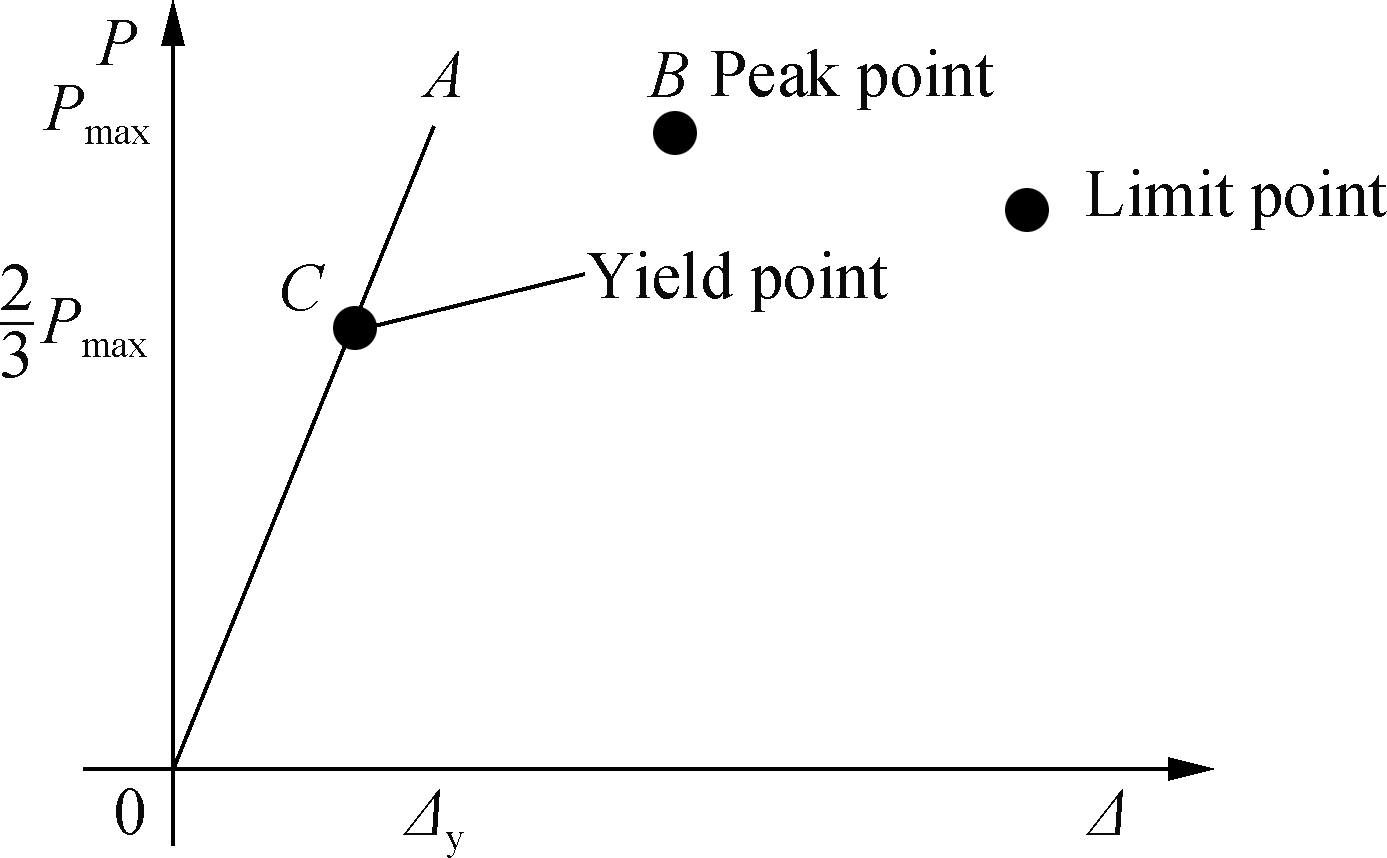
Fig.6 The diagram of the yield load determination method
Tab.4 Data sheets of key points of load-displacement skeleton curves
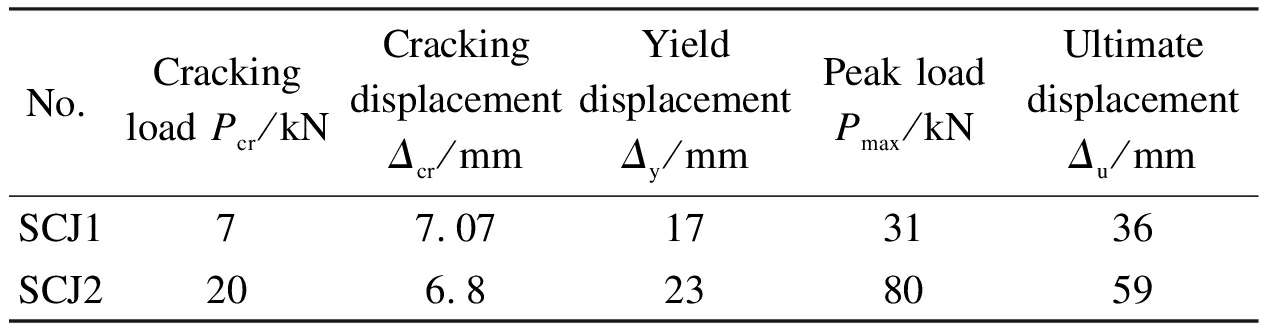
No.Crackingload Pcr/kNCracking displacementΔcr/mmYield displacementΔy /mmPeak loadPmax/kNUltimatedisplacementΔu/mmSCJ177.07173136SCJ2206.8238059
5 Conclusions
1)Brittle shear failure occurs in two SSCJ under cyclic loading.As the load increases, diagonal cracks appear in the staggered floor short column.
2)The stress process of joints under cyclic loading can be divided into uncracked stage, crack development stage, and failure stage.The stirrup in the short column plays a vital role in the horizontal shear resistance of the SSCJ.Thus, the design of stirrup reinforcement should be focused on during the design phase.
3)The number of cracks in the core area of the joints is not that high compared to the column, boundary beam, and strengthened plate.Furthermore, the reinforcement in the core area of the joints has serious bond slip based on the analysis of the hysteresis curve of the joints.This means that the anchoring treatment should be strengthened.
[1] Ministry of Housing and Urban-Rural Development of the People’s Republic of China.Code for seismic design of building: GB 50011—2010[S].Beijing:China Architecture & Building Press, 2010.
[2] Gasparini D A.Contributions of C.A.P.Turner to development of reinforced concrete flat slabs 1905—1909[J].Journal of Structural Engineering, 2002, 128(10): 1243-1252.DOI:10.1061/(asce)0733-9445(2002)128: 10(1243).
[3] Walker P R, Regan P E.Corner column-slab connections in concrete flat plates[J].Journal of Structural Engineering, 1987, 113(4): 704-720.DOI:10.1061/(asce)0733-9445(1987)113: 4(704).
[4] Lu X L, Ma Y C, Yang Z.Analysis of connections of slab to edge column under shear and unbalanced moment[J].Journal of Tongji University, 1998, 26(8): 357-360.(in Chinese)
[5] Han S W, Park Y M, Kee S H.Stiffness reduction factor for flat slab structures under lateral loads[J].Journal of Structural Engineering, 2009, 135(6): 743-750.DOI:10.1061/(asce)st.1943-541x.0000001.
[6] Wu Q, Cheng W R.Study of calculating width of equivalent beam for slab-column structure subjected to horizontal forces[J].Industrial Construction, 2004, 34(3): 77-79.DOI: 10.3321/j.issn:1000-8993.2004.03.024.(in Chinese)
[7] Xu Z G, Huang X K, Gao J, et al.A seismic performance analysis on a shear-wall high-rise structure with staggered floors in high earthquake intensity regions[J].Building Structure, 2012, 42(4): 69-74.DOI:10.19701/j.jzjg.2012.04.011.(in Chinese)
[8] Mao R P.Split-level building damaged in Wenchuan earthquake analysis[J].Engineering Mechanics, 2010, 27(S1): 118-121.(in Chinese)
[9] Long J T, Chen Y, Wang H, et al.Seismic performance analysis of staggered floors in frame structures[J].Structural Engineers, 2018, 34(5): 58-65.DOI:10.15935/j.cnki.jggcs.2018.05.009.(in Chinese)
[10] Wang Z J, Han F X.Shearing force analysis of split-level region for a split-level structure with uniform mass distribution under earthquake[J].Journal of Vibration and Shock, 2011, 30(7): 91-95.DOI:10.13465/j.cnki.jvs.2011.07.049.(in Chinese)
[11] Zhou J.Research on staggered flat plate structure connections[D].Nanjing: Southeast University, 2006.(in Chinese)
[12] Wang J.Research on aseismic behavior of staggered flat plate structure[D].Nanjing: Southeast University, 2008.(in Chinese)
[13] Park R.State of the art report ductility evaluation from laboratory and analytical testing[C]//Proceedings of Ninth World Conference on Earthquake Engineering. Tokyo, Japan, 1988: 605-616.