Research on wind effects on large cooling towers began in the 1970s worldwide[1-5], and the topic of science still receives much attention today[6-11].Our previous research[12-13] proved using quantifiable data that free-stream turbulence significantly influences wind effects on cooling towers.Although the differences in wind loads observed by Cheng et al.[12-13] among different turbulence intensity cases are supposed to result from the discrepancy of the turbulence intensity, we should not disregard that uncertainties in physical experiments can also cause discrepancies.Thus, some effective techniques should be employed to compare the significance of the turbulence intensity with that of the uncertainty in physical experiments.If free-stream turbulence is proven to have a significant influence, then the practice of disregarding the turbulence intensity effects in research and design should be improved.
Most wind engineering design and research are based on the empirical knowledge obtained by generalizing large quantities of experimental data because physical experiments are usually costly and time-consuming.For wind loads on large cooling towers, empirical formulae are obtained for the mean wind pressure distribution[14], fluctuating wind pressure distribution[15-17], spectra of fluctuating pressures[18], and cross-spectra of fluctuating pressures[19].Some of these empirical formulae[18-19] are obtained by fitting large quantities of experimental data obtained under multiple turbulence intensities, which should be strengthened by considering the turbulence intensity effects for conservativeness.Other empirical formulae are based on full-scale measurements[15-16] or physical model tests with the atmospheric boundary layer(ABL)simulation[17], whose engineering backgrounds are usually cooling towers with heights no greater than 165 m.They are defined by the Chinese standard DL/T 5339—2006[20] as small-sized cooling towers, which are usually located in wind environments with high turbulence intensities.However, cooling towers with heights greater than 165 m are usually subjected to ABL winds with much lower turbulence intensities.In this regard, those formulae based on small-sized cooling towers should also be adjusted to accommodate large cooling tower cases.
In view of this narrative,in this study, first, the one-way analysis of variance(ANOVA)technique is employed to analyze the significance of the turbulence intensity with our previous full-scale physical experiments[12].Second, based on the calculated significance of the turbulence intensity, an empirical formula updating method that considers the turbulence intensity effects is proposed and presented using a case study.Finally, the effectiveness of the empirical formula updating method is demonstrated by comparing the updated empirical results with the full-scale measurement data.
1 ANOVA for the Significance of Turbulence Intensity
1.1 Basic theories
Some factors might influence the experimental results, and the grades of the factors are called levels.When one factor with more than two levels should be considered for an experiment, one-way ANOVA is a useful practice to analyze the significance of that factor.Supposing that there are r levels for factor A and n repetitions of the experiment are conducted for each level, Tab.1 can be obtained.
Tab.1 Experimental results for one-way ANOVA

LevelRepetition of the experiment12 j nSumof rowsAverageof rows1X11X12 X1j X1nT1 X12X21X22 X2j X2nT2 X2︙︙︙︙︙︙︙iXi1Xi2 Xij XinTi Xi︙︙︙︙︙︙︙rXr1Xr2 Xrj XrnTr Xr
In Tab.1, Xij is the j-th experimental result at the i-th level; ![]() If the factor does not significantly affect the experimental results, then all Xij should come from the same normal population N(μ,σ2).Thus, we can formulate a hypothesis H0: μ1=μ2=…=μr=μ.If the hypothesis is true, then only the uncertainty in the experiment causes the difference between Xij.If the hypothesis is false, then the uncertainty in the experiment and factor cause the difference between Xij.ANOVA aims to separate the difference caused by the uncertainty from that caused by the factor and examine hypothesis H0 by comparing the two differences.The basic theories of one-way ANOVA are as follows:
If the factor does not significantly affect the experimental results, then all Xij should come from the same normal population N(μ,σ2).Thus, we can formulate a hypothesis H0: μ1=μ2=…=μr=μ.If the hypothesis is true, then only the uncertainty in the experiment causes the difference between Xij.If the hypothesis is false, then the uncertainty in the experiment and factor cause the difference between Xij.ANOVA aims to separate the difference caused by the uncertainty from that caused by the factor and examine hypothesis H0 by comparing the two differences.The basic theories of one-way ANOVA are as follows:
(1)
Suppose that ![]() then, ST=SA+SE.Because the degrees of freedoms for SE and SA are n-r and r-1, respectively,
then, ST=SA+SE.Because the degrees of freedoms for SE and SA are n-r and r-1, respectively, ![]() SE~χ2(n-r),
SE~χ2(n-r), ![]() and SE and SA are independent of each other.Thus, an F-test can be utilized to examine the significance of factor A:
and SE and SA are independent of each other.Thus, an F-test can be utilized to examine the significance of factor A:
(2)
If F>Fα(Fα is the critical value corresponding to test level α), then H0 should be rejected.If F<Fα, then H0 should be accepted.
1.2 ANOVA results
The overviews of the full-scale measurements for wind effects on the prototype Pengcheng cooling tower are previously reported by Cheng et al.[12], which are not repeated here.Using the fluctuating wind pressure coefficients measured at 20° and 80° on the prototype at different turbulence intensities, two ANOVA tables are established(see Tabs.2 and 3).Using data listed in Tab.2, we calculated that SA=0.089, SE=0.003, and F=133.5.Supposing that α=0.05, Fα=19.4 is found in the critical value table for the F-test.Accordingly, F>Fα is obtained, which indicates that differences between the data measured at 20° on the prototype are mainly caused by the turbulence intensity effects.Similar results can be obtained by processing the data measured at 80° on the prototype(see Tab.3).In sum, the ANOVA results suggest that the turbulence intensity has a significant influence on the fluctuating wind pressure distribution.
Tab.2 Fluctuating wind pressure coefficients measured at 20° on the prototype

Turbulenceintensity/%Repetition of experiment1234Sum ofrowAverageof row1.540.0180.0260.020.0210.0850.0214.230.0310.0420.040.0450.1580.04010.810.2200.1900.1870.2510.8480.212
Tab.3 Fluctuating wind pressure coefficients measured at 80° on the prototype
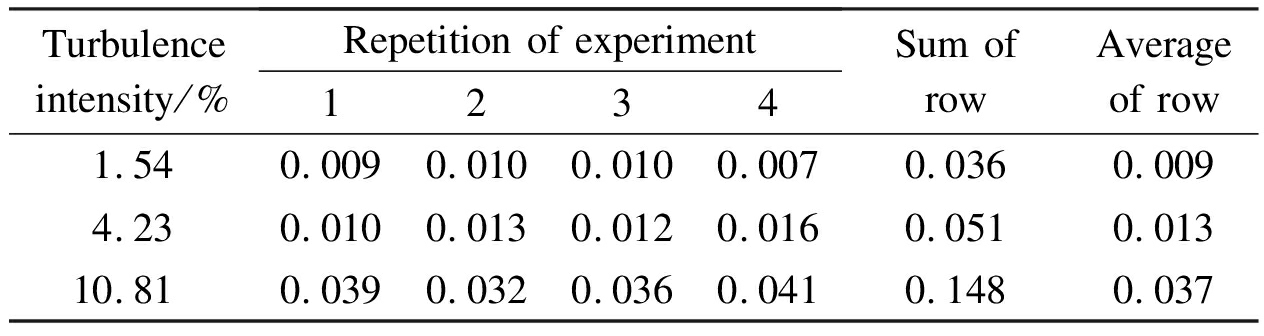
Turbulenceintensity/%Repetition of experiment1234Sum ofrowAverageof row1.540.0090.0100.0100.0070.0360.0094.230.0100.0130.0120.0160.0510.01310.810.0390.0320.0360.0410.1480.037
Moreover, according to Ref.[14], the following equation can be utilized to describe the spectra of fluctuating pressures on large cooling towers:
(3)
where n is the frequency and a, b, and c are the parameters possibly depending on the turbulence intensity.The spectra of the fluctuating pressures measured at 20° on the prototype at different turbulence intensities are fitted based on Eq.(3), and the identified parameters a, b, and c in Eq.(3)are listed in Tabs.4 to 6, respectively.Using the data listed in Tab.4, we calculated that SA=0.278, SE=0.003 06, and F=409.In addition, Fα=19.4 is found in the critical value table with α=0.05.Thus, F>Fα is obtained, which indicates that differences between parameter a in Eq.(3)calculated for different time intervals are mainly caused by the turbulence intensity effects.A similar situation also holds true when ANOVA is undertaken for the data listed in Tabs.5 and 6.In this regard, it is proven that turbulence intensity also has a significant influence on the spectra of fluctuating pressures on large cooling towers.
Tab.4 Identified parameter a for the spectra of fluctuating pressure coefficients measured at 20° on the prototype
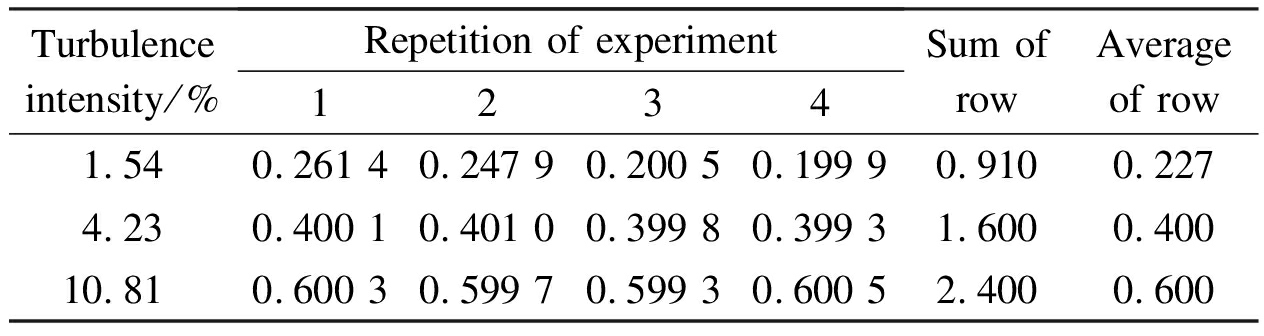
Turbulenceintensity/%Repetition of experiment1234Sum ofrowAverageof row1.540.261 40.247 90.200 50.199 90.9100.2274.230.400 10.401 00.399 80.399 31.6000.40010.810.600 30.599 70.599 30.600 52.4000.600
Tab.5 Identified parameter b for the spectra of fluctuating pressure coefficients measured at 20° on the prototype
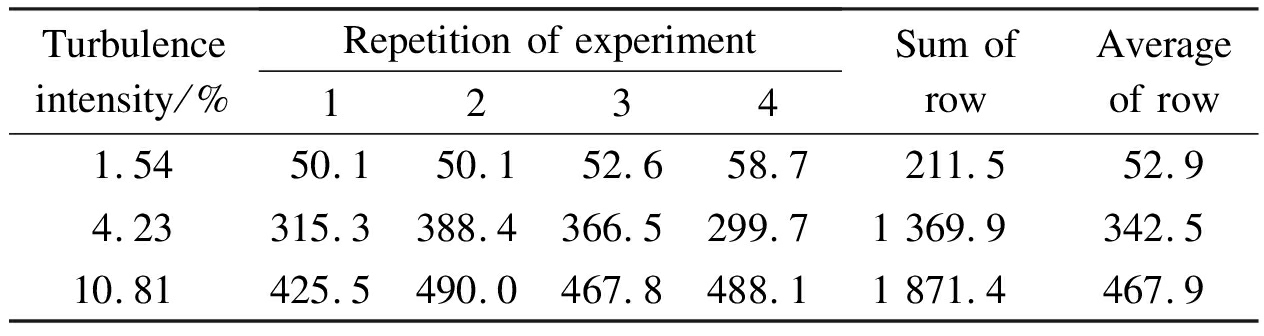
Turbulenceintensity/%Repetition of experiment1234Sum ofrowAverageof row1.5450.150.152.658.7211.552.94.23315.3388.4366.5299.71 369.9342.510.81425.5490.0467.8488.11 871.4467.9
Tab.6 Identified parameter c for the spectra of fluctuating pressure coefficients measured at 20° on the prototype

Turbulenceintensity/%Repetition of experiment1234Sum ofrowAverageof row1.545.0635.0645.9155.08021.1225.2814.237.6946.4578.95811.67034.7798.69510.8115.83118.24418.80618.47971.36017.840
2 Empirical Results for Wind Pressures on Cooling Towers
Because the free-stream turbulence is proven to be a significant influence on wind effects on cooling towers in the previous section, the empirical results for wind pressures on cooling towers based on the practice of disregarding the turbulence intensity effects should be improved.In this portion of the study, empirical results for wind effects on cooling towers(i.e., mean and fluctuating wind pressure coefficients, spectra of fluctuating pressures, and coherences between fluctuating pressures)are presented, which will be updated for turbulence intensity effects in the next section.
2.1 Mean and fluctuating wind pressure coefficients
According to Ref.[14], the empirical formulae of the proposed mean and fluctuating wind pressure distributions should agree with the obtained full-scale measurement results.A number of investigators have measured the mean and fluctuating wind pressure coefficients on several prototype cooling towers, which are reproduced from Ref.[14], as shown in Fig.1.In Fig.1(a), most mean wind pressure distributions agree well, suggesting that the effects of turbulence intensity on the mean wind pressure coefficients are negligible.Only the values obtained on the Maoming tower appreciably differ from the other sets of values due to the absence of ribs on the external surface of that tower.In Fig.1(b), the agreement between the two fluctuating wind pressure distributions is generally good.The limited discrepancy between the two curves in Fig.1(b)should be the turbulence intensity effects.The results of the empirical formulae for the mean and fluctuating wind pressure distributions are reported by DL/T 5339—2006[20] and Liu[21], respectively.They are also shown in Fig.1, where the empirical formulae of the proposed mean and fluctuating wind pressure distributions agree well with the full-scale measurement results.

(a)
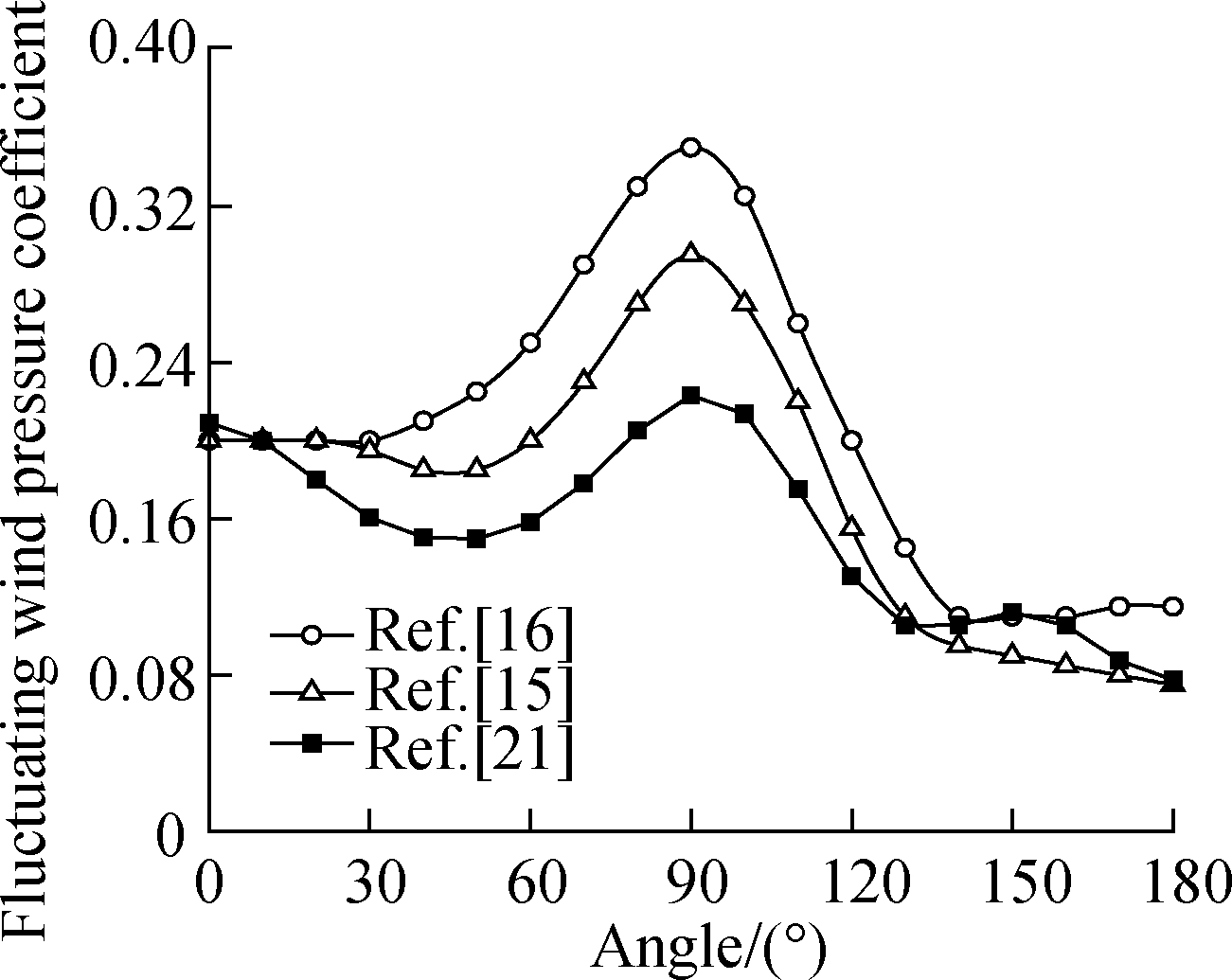
(b)
Fig.1 Full-scale measurement results obtained on a number of cooling towers.(a)Mean wind pressure distributions;(b)Fluctuating wind pressure distributions
2.2 Spectra of fluctuating pressures
According to Ref.[18], the following expressions can describe the spectra of fluctuating pressures on large cooling towers:
(4)
(5)
(6)
(7)
where n is the frequency; the parameters a1(θ), b0(θ), and βp(θ)are given in the figures; α is the power law exponent; D is the diameter of the throat; and ![]() is the integral scale of turbulence.
is the integral scale of turbulence.
2.3 Coherences between fluctuating pressures
According to Ref.[19], when θ≤100°, θ′≤100°, the following expressions can describe the circumferential coherence between fluctuating pressures on large cooling towers:
(8)
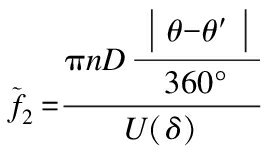
(9)
where θ is the included angle between point 1 and the stagnation point; θ′ is the included angle between point 2 and the stagnation point; β3=25; U(δ)is the mean wind speed at the gradient height δ; and C2(θ,θ′)is given in figures.According to Simiu and Scanlan[14], the coherences between pressures on the windward region(θ≤100°), on the one hand, and pressures on the leeward region(θ′>100°), on the other, are negligible.
3 Updating Methods for Empirical Results
According to Cheng et al.[13], free-stream turbulence significantly influences the dynamic characteristics of wind effects on cooling towers.Because the fluctuating wind pressure coefficients around the full half-circle monotonically linearly increase with the increase in turbulence intensity[13], the following equation is employed to update the empirical fluctuating wind pressure distributions measured on small-sized cooling towers with high turbulence intensities(see Fig.1(b)):
(10)
where σp(z1,θ)is the updated fluctuating wind pressure coefficient measured at height z1 circumferential position θ; σp(z2,θ)is the original fluctuating wind pressure coefficient measured at height z2; and Iu(z1)and Iu(z2)are the empirical turbulence intensities for height z1 and z2, respectively.Because z1>z2, Iu(z1)<Iu(z2); Δσp(z3,θ)is the discrepancy between the fluctuating wind pressure coefficient measured at circumferential position θ on height z3 of the cooling tower model in the laminar flow in the wind tunnel and fluctuating wind pressure coefficient measured at the same position on the cooling tower model in the turbulent flow simulated in the wind tunnel; ΔIu is the turbulence intensity measured at height z3 in the turbulent flow simulated in the wind tunnel.
Furthermore,Cheng et al.[13] found that the spectra of fluctuating pressures measured at different positions around the half-circle change irregularly with the increase in turbulence intensity.Because the empirical formulae for the spectra of fluctuating pressures(Eqs.(4)to(7))are obtained by fitting large quantities of experimental data measured in the turbulent flow and laminar flow, Eq.(11)is employed to update the results calculated using the empirical formulae for conservativeness.This condition is based on the fact that the turbulence intensity of the realistic ABL wind approximately varies from zero to the values simulated in conventional ABL wind tunnels[13]:
Spupd(z,θ,n)=Spemp(z,θ,n)+|Spexp1(z,θ,n)-
Spexp2(z,θ,n)|
(11)
where Spupd(z,θ,n)and Spemp(z,θ,n)are the updated and original spectrum of the pressure fluctuation at frequency n for height z circumferential position θ, respectively, and Spexp1(z,θ,n)and Spexp2(z,θ,n)are the spectrum of the pressure fluctuation measured at the same position on the cooling tower model in the wind tunnel with and without the ABL simulation, respectively.Cheng et al.[13] found that a similar situation holds true for coherences between fluctuating pressures(they change irregularly with the increase in turbulence intensity).Accordingly, an equation similar to Eq.(11)is employed to update the results calculated using Eqs.(8)and(9):
Rfupd(θ,θ′,n)=Rfemp(θ,θ′,n)+|Rfexp1(θ,θ′,n)-
Rfexp2(θ,θ′,n)|
(12)
where Rfupd(θ,θ′,n)is the updated circumferential coherence between fluctuating pressures measured at the circumferential position θ and circumferential position θ′; Rfemp(θ,θ′,n)is the corresponding original circumferential coherence; and Rfexp1(θ,θ′,n)and Rfexp2(θ,θ′,n)are the circumferential coherences measured on the cooling tower model in the wind tunnel with and without the ABL simulation, respectively.
4 Overview of Wind Tunnel Tests
As mentioned in Section 3, wind tunnel tests with and without the ABL simulation are both required for updating the empirical results of wind loads on cooling towers for turbulence intensity effects.Thus, they are undertaken in the TJ-3 wind tunnel of Tongji University in Shanghai, China.
The wind tunnel is a closed-circuit rectangular cross-section wind tunnel, wherein the size of the test section is 15 m in width, 2 m in height, and 14 m in length.The test wind speed can be continuously controlled within the 1.0-17.6 m/s range.The non-uniformity of the wind speed of the flow field in the test zone is less than 1%, the turbulence intensity is less than 0.5%, and the average flow deviation angle is less than 0.5°.Using spires and ground roughness blocks(see Fig.2(a)), the ABL turbulent flow field of the countryside open terrain is simulated for the test.Without these passive devices, the laminar flow field is obtained.Based on the scenario of Pengcheng large cooling towers[12], the test model and surroundings are modeled on a geometric scale of 1∶200 using synthetic glass(see Fig.2(b)).The wind tunnel blocking rate is approximately 3% for the test, and the wind tunnel test wind speed is 12 m/s.

(a)

(b)
Fig.2 Model test scenario in the TJ-3 wind tunnel.(a)ABL terrain simulation;(b)1∶200 rigid models
36 × 12 taps are arranged on 12 vertical sections and 36 horizontal circular directions for the pressure measuring tower model.DSM3000 electronic pressure scanners from Scanivalve Corp.are used to obtain the wind pressures on the tower surfaces in the laminar flow and ABL turbulent flow.The signal data are acquired at a sample rate of 312.5 Hz, and the sample length is 6 000 data at one tap in each run.By sticking paper belts along the vertical direction and adjusting the incoming flow velocity, the actual static characteristics of the prototype cooling tower at high Reynolds number(Re)are successfully simulated in the reduced-scale model with lower Re.The turntable rotates from 0° to 360° at 22.5° intervals, but only the case with the same wind direction as that observed in the engineering site of Pengcheng electric power station on Nov.29, 2011 is considered[12].Therefore, the empirical results updated using the model test data can fairly compare with the wind effects measured on the prototype.
5 Updated Empirical Results and Full-Scale Measurement Data
Based on the methods described in Section 3, the results presented in Section 2 are updated using the wind tunnel test data.Then, the updated empirical results are compared with the full-scale measurement data obtained on the prototype Pengcheng cooling tower(the field test wind speed is 12.06 m/s at the height of the measurement section)[12].As stated in Section 2.1, the effects of turbulence intensity on the mean wind pressure coefficients are negligible, so only the dynamic empirical results are updated.
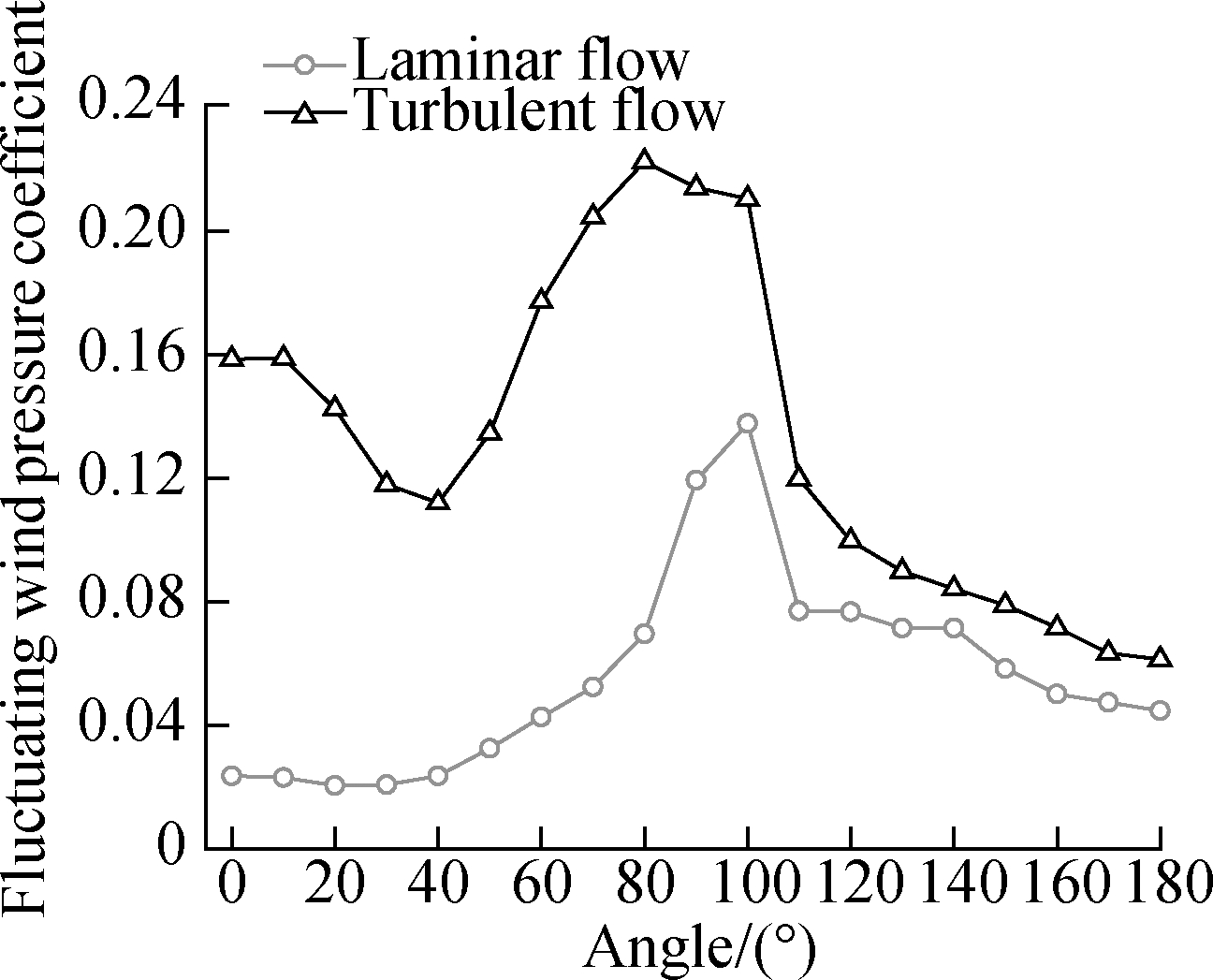
The fluctuating wind pressure distributions measured on the scaled model in the wind tunnel are shown in Fig.3(a).As can be seen, the model test results obtained in the turbulent flow are much greater than those obtained in the laminar flow.Using the discrepancy of the model test data measured in the two flow fields, the two empirical results reported by Ruscheweyh[15] and Sageau[16] are updated following Eq.(10), given that the two empirical results are both obtained at the approximately 90 m height and the full-scale measurement results are obtained at a 130 m height(see Fig.3(b)).The comparison results of the original and updated empirical results with the full-scale data presented in Fig.3(b)clearly indicate that the agreements are better for the updated empirical results than for the original empirical results.Moreover, the updated empirical results are notably different from the full-scale measurement results at certain locations in Fig.3(b), e.g., at 60° and 100°.Although the field measurement data are generally treated as the targets of physical modeling, they might be inaccurate in certain cases, e.g., 1)when the static reference pressure established for the full-scale measurement can hardly play the same role as the static pressure in the wind tunnel and 2)when the full-scale velocity field lacks stationarity and homogeneity.Based on our experiences, the full-scale data presented in Fig.3(b)roughly reflect the trend of fluid physics, but they might not be perfect at certain local points due to the limitations of the field measurement technique.We suppose that the empirical results presented in Fig.3(b)are correct with regard to the fluctuating wind pressure coefficients calculated at 60° and 100°.
(a)

(b)
Fig.3 Fluctuating wind pressure distributions.(a)Model test results;(b)Empirical results and in-situ data
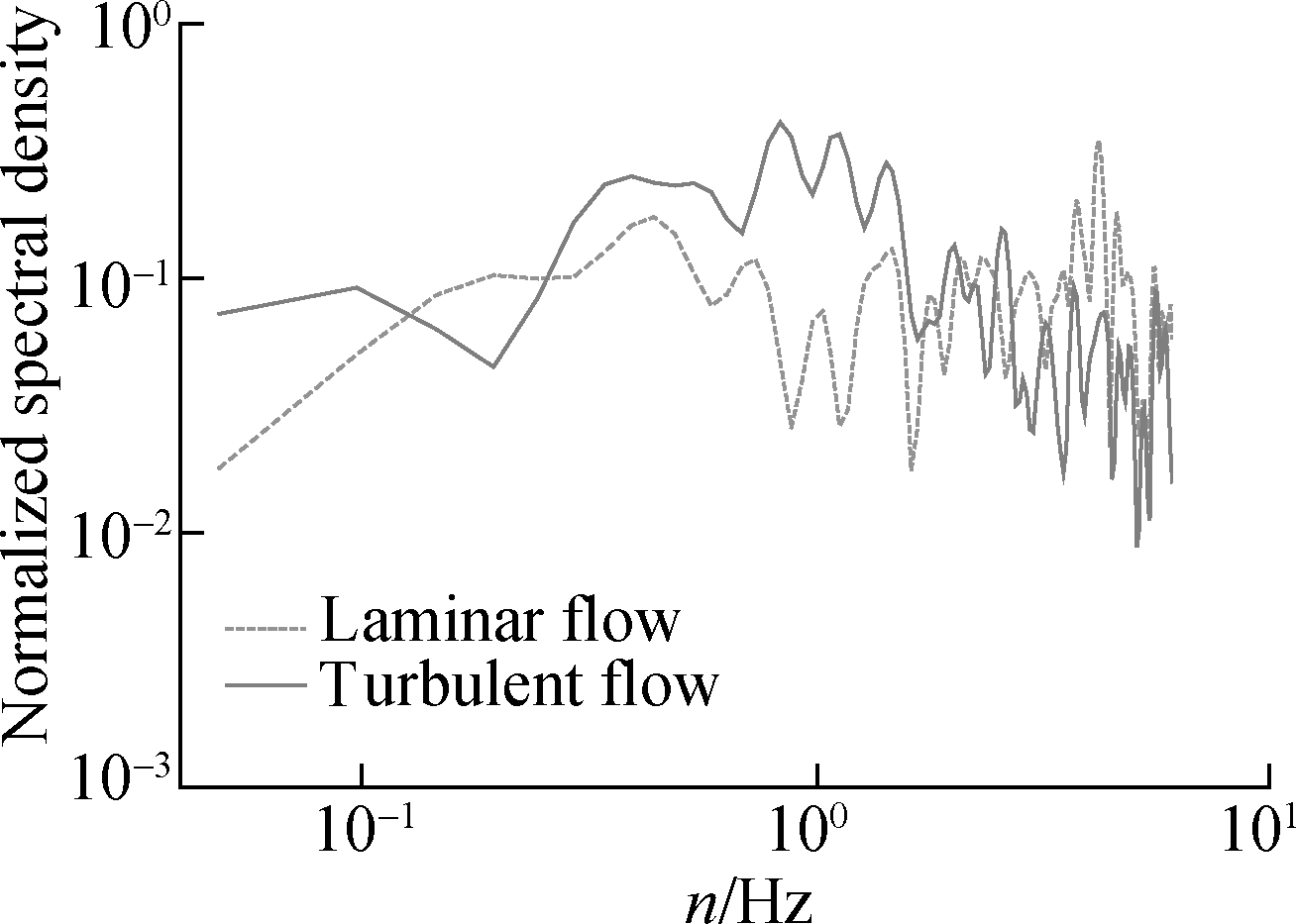
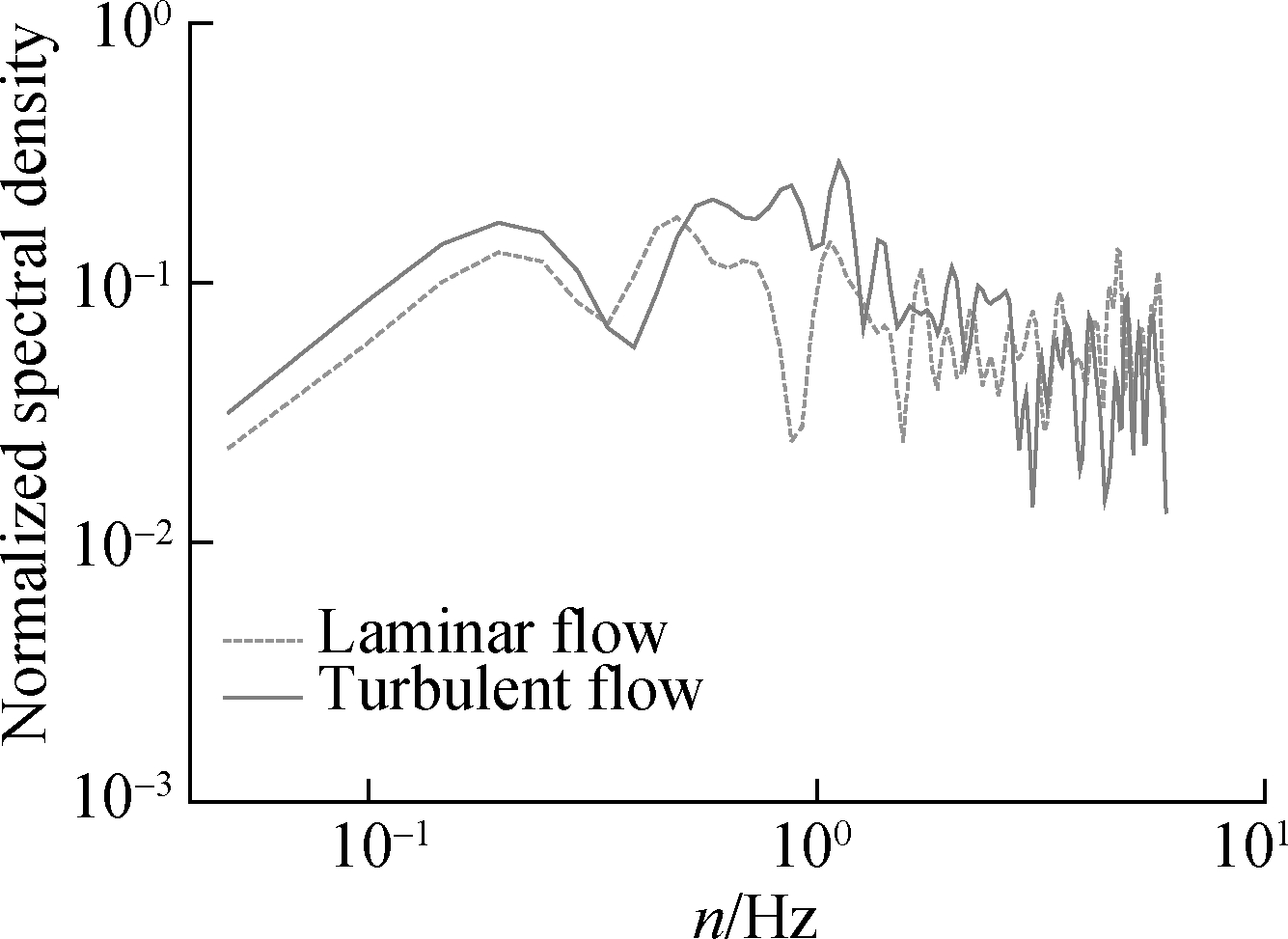
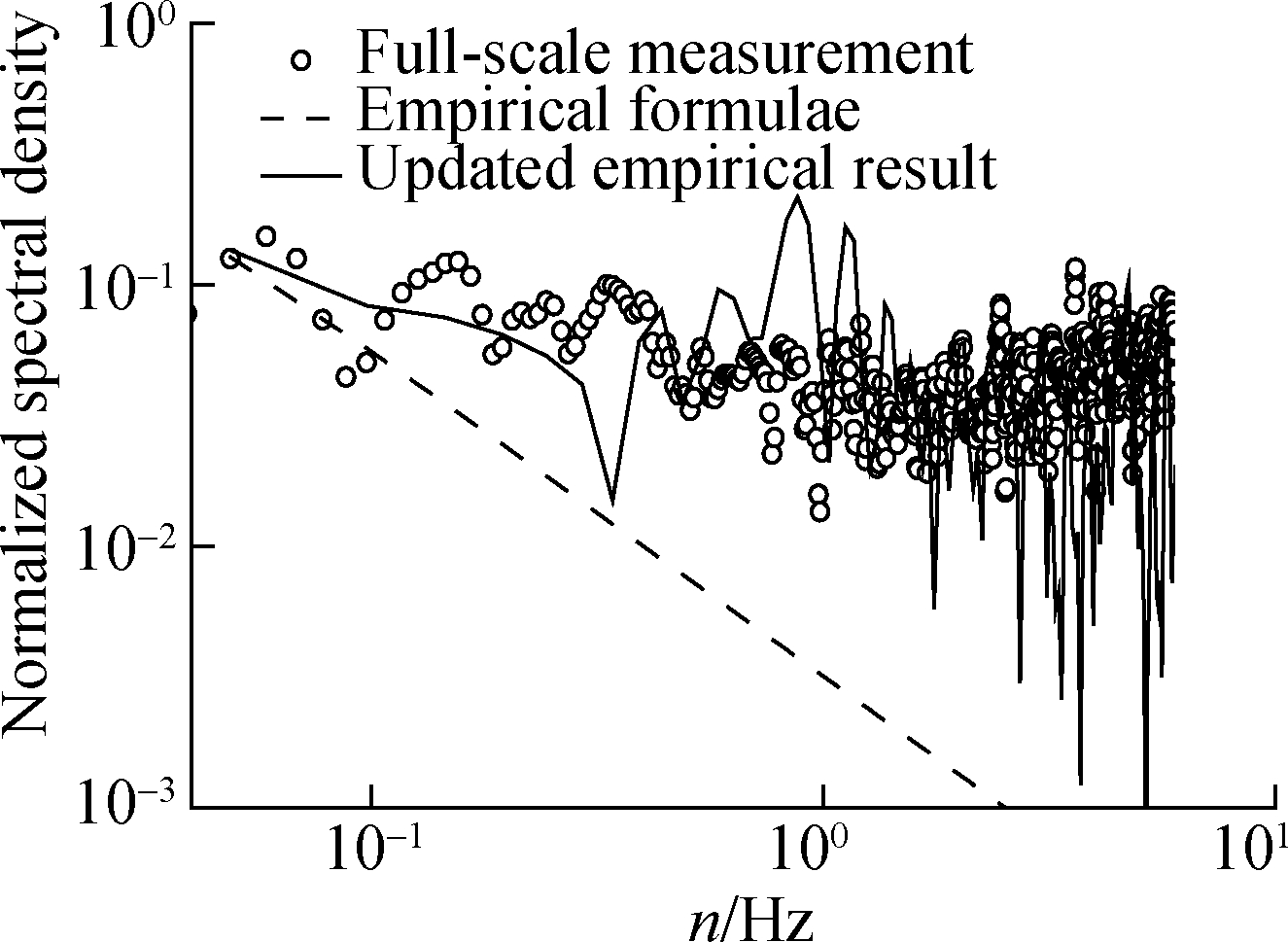
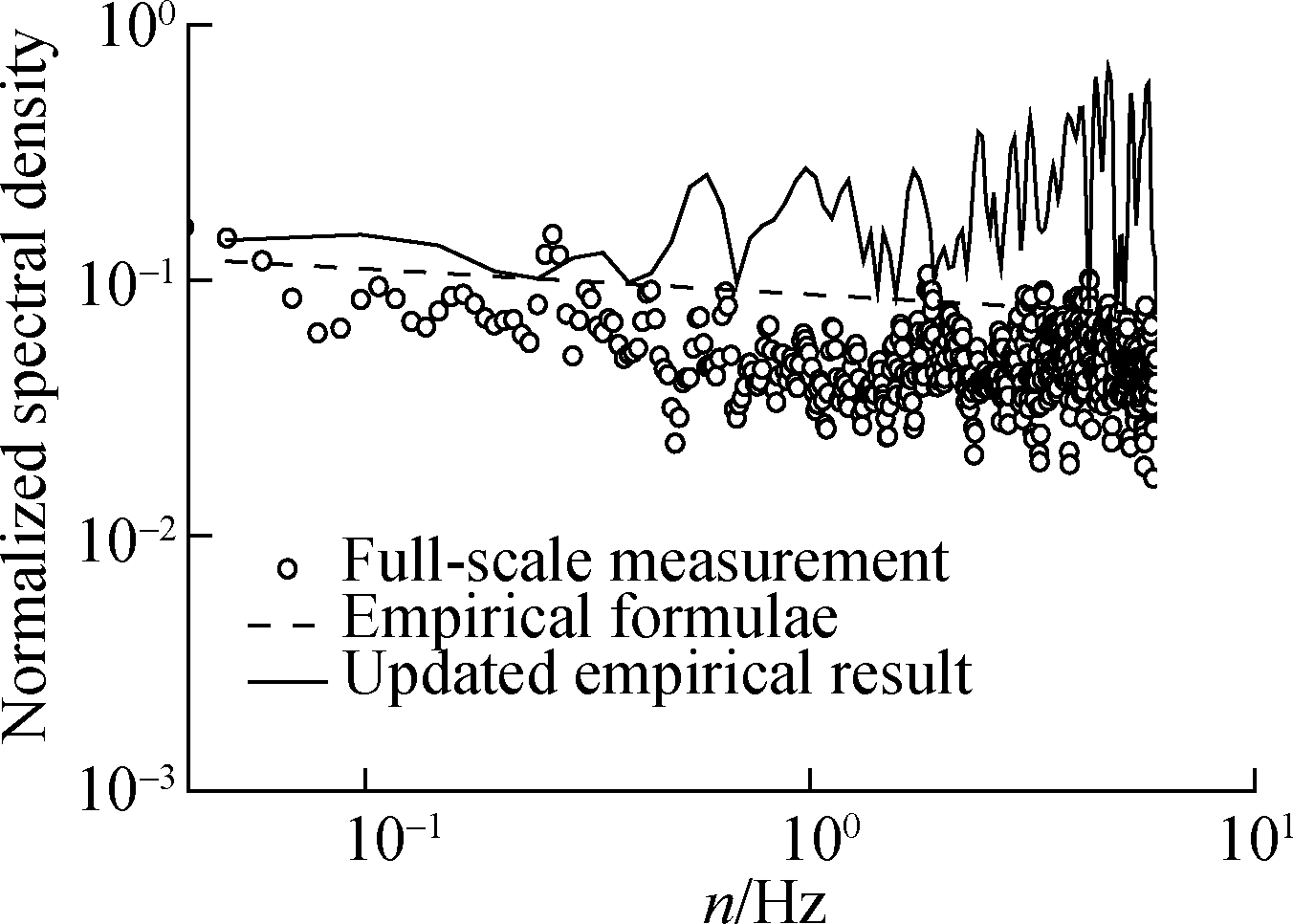
Figs.4(a),(c), and(e)show the power spectral densities of fluctuating wind pressures measured at three positions(the subtitles in Fig.4 refer to the included angles between the measurement points and stagnation point)on the scaled model in the wind tunnel.Comparing the result measured in the laminar flow and that measured in the turbulent flow, one can hardly determine which one of them is greater than the other.For conservativeness, the absolute values of the discrepancies between the data measured in the two flow fields are employed for updating the empirical formulae(Eqs.(4)to(7)).The empirical power-spectral densities of the fluctuating wind pressures are updated according to Eq.(11)and compared with the full-scale data, as shown in Figs.4(b),(d), and(f).As shown in Figs.4(b)and(d), the updated empirical results are accurate for use, and it might be unsafe to directly utilize the original empirical formulae(Eqs.(4)to(7)).In particular, the updating practice is better for results calculated at the windward side(see Figs.4(b)and(d))than for results calculated at the leeward side(see Fig.4(f)).This condition is probably because the fluid physics is quite different at different locations.Therefore, the unified updating practice to all locations might lead to a certain inaccuracy.The corresponding revision of the unified updating practice is being undertaken by the authors now.However, due to the limited article length, this topic will be reported in another article.
(a)

(b)
(c)
(d)

(e)
(f)
Fig.4 Power-spectral densities.(a)Model test results at 30°;(b)Empirical results and in-situ data at 30°;(c)Model test results at 50°;(d)Empirical results and in-situ data at 50°;(e)Model test results at 130°;(f)Empirical results and in-situ data at 130°
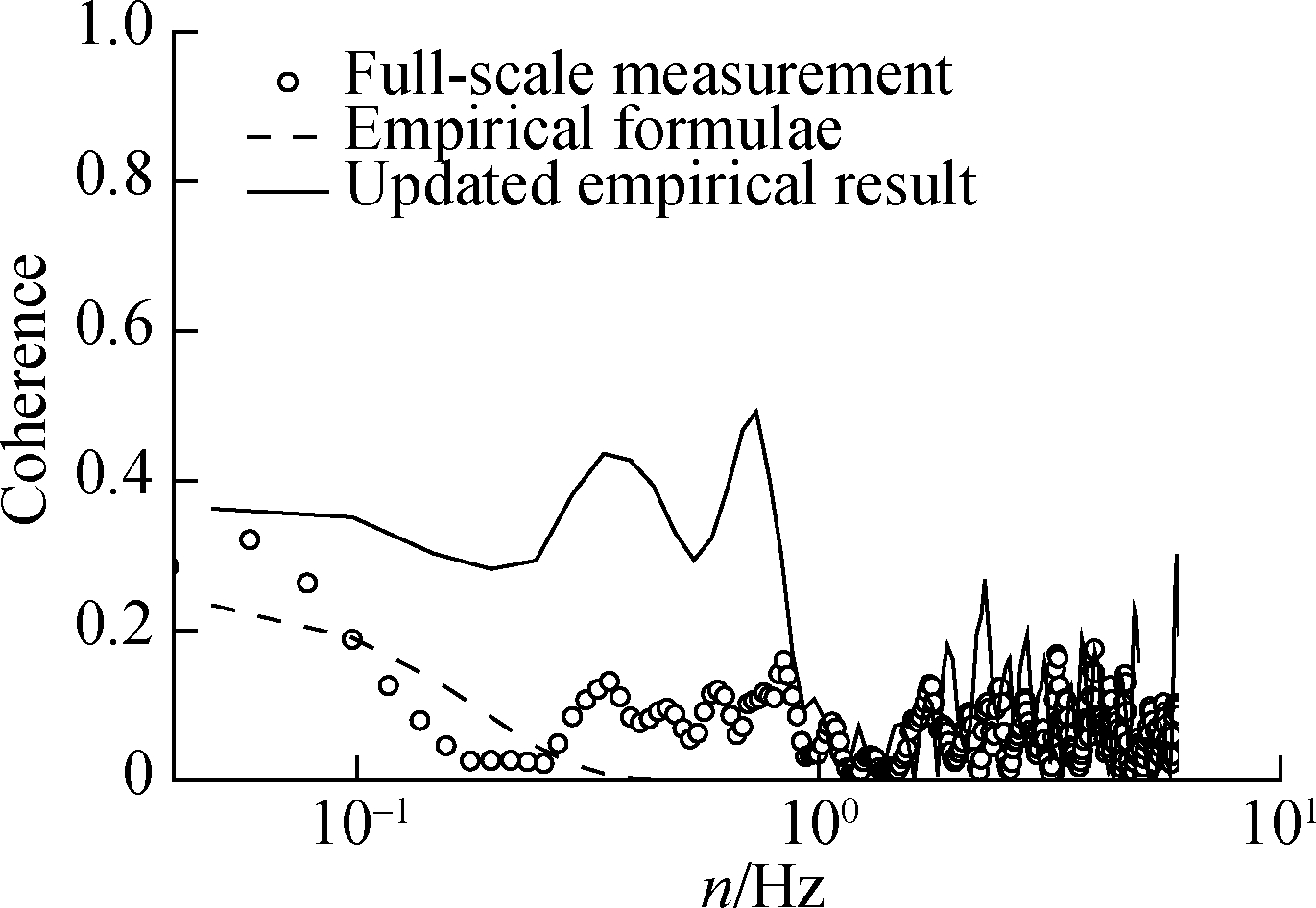
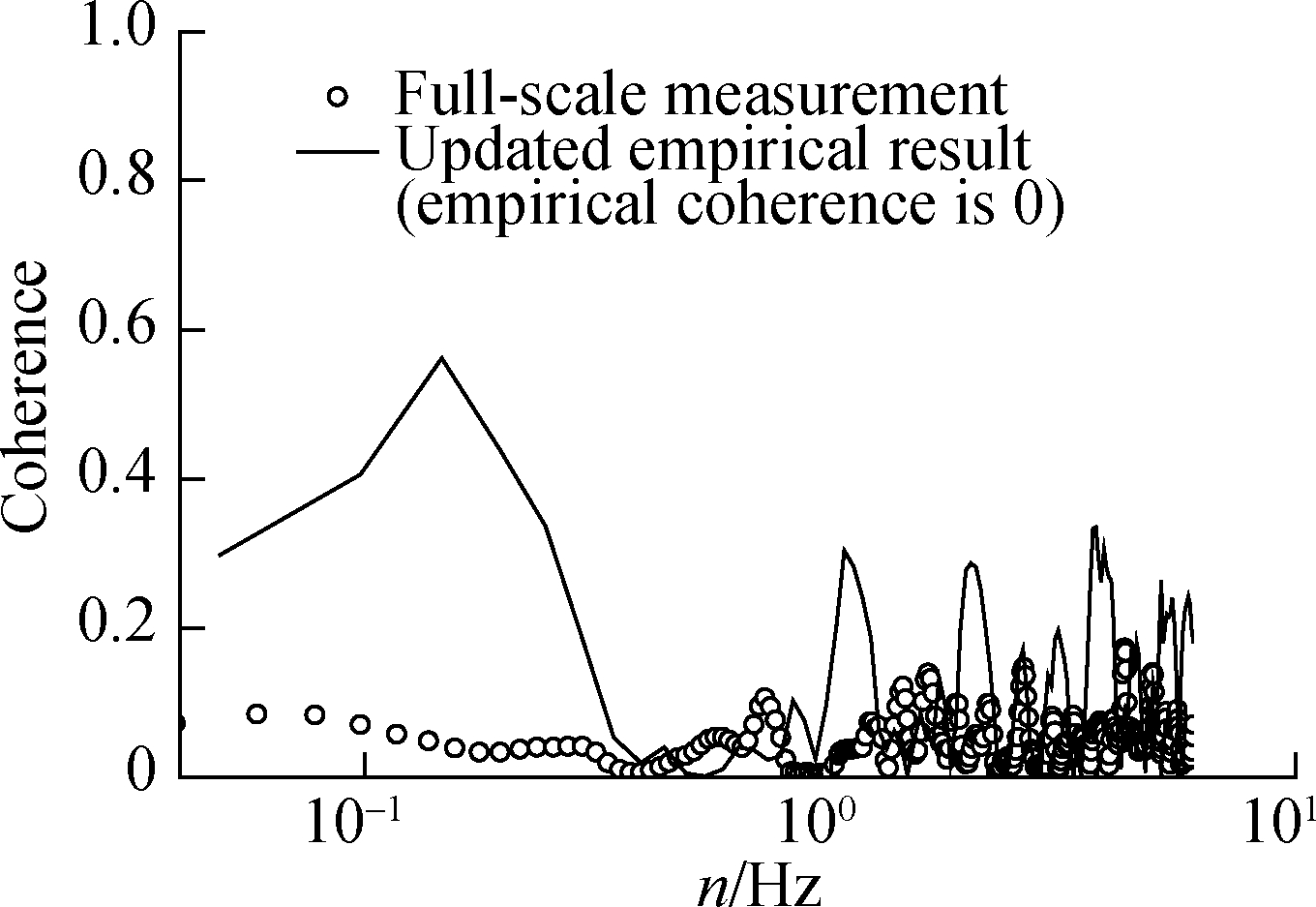
Figs.5(a),(c), and(e)describe the effects of turbulence intensity on the coherences between the wind pressure coefficient samples obtained at 20° and other positions on the scaled model in the wind tunnel.Because it is difficult to tell whether the free-stream turbulence can strengthen or reduce the coherences, Eq.(12)also relies on the absolute values of the discrepancies between data measured in the two flow fields to update the empirical results.The updated empirical coherences are also compared with the full-scale data in Figs.5(b),(d), and(f), which suggests that the updated empirical results are slightly conservative for use.
6 Conclusions
1)The one-way ANOVA technique is employed to analyze the influence of the turbulence intensity on our previous full-scale measurement data.The results clearly indicate that the variations of wind effects measured on the prototype Pengcheng cooling tower are basically the effects of turbulence intensity rather than the effects of the inherent uncertainties in our physical experiments.

(a)

(b)

(c)
(d)

(e)
(f)
Fig.5 Coherence functions between the wind pressure coefficient samples obtained at 20° and other positions.(a)Model test results for 20°-50° coherence;(b)Empirical results and in-situ data for 20°-50° coherence;(c)Model test results for 20°-90° coherence;(d)Empirical results and in-situ data for 20°-90° coherence;(e)Model test results for 20°-120° coherence;(f)Empirical results and in-situ data for 20°-120° coherence
2)The comparison of the empirical results of wind loads on cooling towers with the corresponding full-scale measurement data shows that the empirical fluctuating wind pressure distributions are too conservative for use.Although the frequency-domain empirical formulae may lead to unsafe structural designs, the practice of generalizing empirical results of wind loads on cooling towers from physical experimental data, which disregards the turbulence intensity effects, is improved.
3)Updating methods for the empirical results of wind loads on cooling towers for turbulence intensity effects are formulated.The comparisons of the updated empirical results and full-scale measurement data suggest that economic efficiency and conservativeness will be balanced if the updated empirical results are employed for the wind engineering design.
[1] Niemann H J, Pröpper H.Some properties of fluctuating wind pressures on a full-scale cooling tower[J].Journal of Wind Engineering and Industrial Aerodynamics, 1975, 1: 349-359.DOI:10.1016/0167-6105(75)90029-X.
[2] Sollenberger N J, Scanlan R H, Billington D P.Wind loading and response of cooling towers[J].Journal of the Structural Division, 1980, 106(3): 601-621.DOI:10.1061/jsdeag.0005383.
[3] Niemann H J, Ruhwedel J.Full-scale and model tests on wind-induced, static and dynamic stresses in cooling tower shells[J].Engineering Structures, 1980, 2(2): 81-89.DOI:10.1016/0141-0296(80)90034-6.
[4] Armitt J.Wind loading on cooling towers[J].Journal of the Structural Division, 1980, 106(3): 623-641.DOI:10.1061/jsdeag.0005384.
[5] Pirner M.Wind pressure fluctuations on a cooling tower[J].Journal of Wind Engineering and Industrial Aerodynamics, 1982, 10(3): 343-360.DOI:10.1016/0167-6105(82)90006-X.
[6] Ke S T, Liang J, Zhao L, et al.Influence of ventilation rate on the aerodynamic interference between two extra-large indirect dry cooling towers by CFD[J].Wind and Structures, 2015, 20(3): 449-468.DOI:10.12989/was.2015.20.3.449.
[7] Ke S T, Du L Y, Ge Y J, et al.A study on the average wind load characteristics and wind-induced responses of a super-large straight-cone steel cooling tower[J].Wind and Structures, 2017, 25(5): 433-457.
[8] Ke S T, Du L Y, Ge Y J, et al.Multi-dimensional wind vibration coefficients under suction for ultra-large cooling towers considering ventilation rates of louvers[J].Structural Engineering and Mechanics, 2018, 66(2): 273-283.
[9] Ke S T, Xu L, Ge Y J.Study of random characteristics of fluctuating wind loads on ultra-large cooling towers in full construction process[J].Wind and Structures, 2018, 26(4): 191-204.
[10] Ke S T, Du L Y, Ge Y J, et al.A study on the action mechanism of internal pressures in straight-cone steel cooling tower under two-way coupling between wind and rain[J].Wind and Structures, 2018, 27(1): 11-27.
[11] Ke S T, Zhu P, Ge Y J.Effects of different wind deflectors on wind loads for extra-large cooling towers[J].Wind and Structures, 2019, 28(5): 299-313.
[12] Cheng X X, Dong J, Peng Y, et al.Effects of free-stream turbulence on wind loads on a full-scale large cooling tower[J].Advances in Structural Engineering, 2018, 21(10): 1437-1453.DOI:10.1177/1369433217747404.
[13] Cheng X X, Chen X, Ge Y J, et al.A new atmospheric boundary layer wind tunnel simulation methodology for wind effects on large cooling towers considering wind environment variations[J].Advances in Structural Engineering, 2019, 22(5): 1194-1210.DOI:10.1177/1369433218809899.
[14] Simiu E, Scanlan R H.Wind effects on structures[M].New York: John Wiley & Sons, 1996.
[15] Ruscheweyh H.Wind loadings on hyperbolic natural draught cooling towers[J].Journal of Wind Engineering and Industrial Aerodynamics, 1975, 1: 335-340.DOI:10.1016/0167-6105(75)90027-6.
[16] Sageau J F.Caracterisation des champs de pression moyens et fluctuants a la surface des grands aerorefrigerants[R].Chatou, France: Electricite de France, Direction des Etudes et Recherches, 1979.
[17] Davenport A G, Isyumov N.The dynamic and static action of wind on hyperbolic cooling towers, Research Report No.BLWTI-66[R].London, Ontario, Canada: University of Western Ontario, 1966.
[18] Pröpper H, Welsch J.Wind pressures on cooling tower shells[M]//Wind Engineering.Amsterdam: Elsevier, 1980: 465-478.DOI:10.1016/b978-1-4832-8367-8.50048-6.
[19] Hashish M G, Abu-Sitta S H.Response of hyperbolic cooling towers to turbulent wind[J].Journal of the Structural Division, 1974, 100(5): 1037-1051.DOI:10.1061/jsdeag.0003775.
[20] China Electric Power Planning & Engineering Institute.Code for hydraulic design of fossil fuel power plants: DL/T 5339—2006[S].Beijing: China Planning Press, 2018.(in Chinese)
[21] Liu X P.On-spot measurement of stochastic wind pressure and its evaluation of multiple effects[D].Shanghai: Tongji University, 2013.(in Chinese)