With advantages of a high firing speed, large firing area, long firing range, excellent mobility, and heavy firepower density weaved in a short time, the multiple launch rocket system(MLRS)has found its place in modern warfare.Theoretical and experimental results of the launch dynamics show that reducing the initial perturbation of the rocket can significantly improve the firing accuracy of the MLRS.The establishment of an accurate launch dynamics model and an appropriate dynamics method is needed for analyzing the launch dynamics process of the MLRS.
The launch dynamics of the MLRS is a new subject that studies the force, motion law, and control process of the MLRS during launch and then studies the theory, technology, and test methods of force, motion, and control.Based on the transfer matrix method of a linear multibody system, Rui et al.[1] established the launch dynamics model of the MLRS, solved the difficult problem of calculating the vibration characteristics of a rigid elastic coupled multibody system of the MLRS, and studied the influence of random factors such as gusts on the launch process of the MLRS.Some researchers explored the MLRS’ vibration control system[2-3], optical lever test technology[4], and the non-full tube firing scheme[5].
An efficient multibody dynamics method is important for multibody systems like the MLRS.In 1989, Rui et al.[6] developed the transfer matrix method for multibody systems(MSTMM), which avoided the need for global dynamic equations.Instead, the involved matrices have a low order, and the setup of the overall transfer equation is highly programmable.The Riccati transfer matrix method for multibody systems(RMSTMM)was developed by introducing the Riccati transformation in the MSTMM, i.e., dividing state vectors into two parts, to improve the numerical stability of the MSTMM[7-8].
A sensitivity analysis is needed to analyze the influence of structural parameters.Commonly used sensitivity analysis methods include the finite difference method(FDM), adjoint variable method(AVM), and the direct differentiation method(DDM).The DDM has many characteristics, such as arguably the most conceptually straightforward sensitivity analysis method, high numerical stability, insensitivity to the parameter perturbation, and easy application for different structural problems[9].RMSTMM is a highly programmable algorithm.The disadvantage of the complicated deduction of sensitivity analysis equations can be avoided by combining the DDM and the RMSTMM.
The genetic algorithm(GA)is a common algorithm for the dynamic optimization of multibody systems.GA is first produced by Professor Holland in 1973[10].Many kinds of hybrid genetic algorithms have been researched by many.GA has been used for the dynamic optimization of the milling robot[11], knee rehabilitation[12], 6-DOF vibration isolation[13], and human-machine coupling[14].
This paper establishes the launch dynamics model of the MLRS and carries out the launch dynamics simulation calculation using the RMSTMM initially.A novel sensitivity analysis method for the launch dynamics of the MLRS is developed, which is based on the RMSTMM and DDM.By the proposed method, the sensitivity of some structural parameters of the MLRS is calculated, and factors influencing the launch dynamic response of the MLRS are analyzed.The multiobjective dynamics optimization of the MLRS is carried out by combining the sensitivity analysis results and GA.Dynamic responses of the pitching part of the MLRS are considerably reduced.
1 Launch Dynamics Modeling and Simulation Calculation of MLRS Based on RMSTMM
1.1 Launch dynamics model of MLRS
According to the natural properties of various components of the MLRS, a nonlinear dynamic model for a typical MLRS is shown in Fig.1(a), which consists of body elements, hinge elements, and boundary points.Body elements and hinge elements are numbered uniformly.Fig.1(b)presents the topology of the MLRS model, describing the relationship among the state vectors of elements and the transfer directions.
(a)
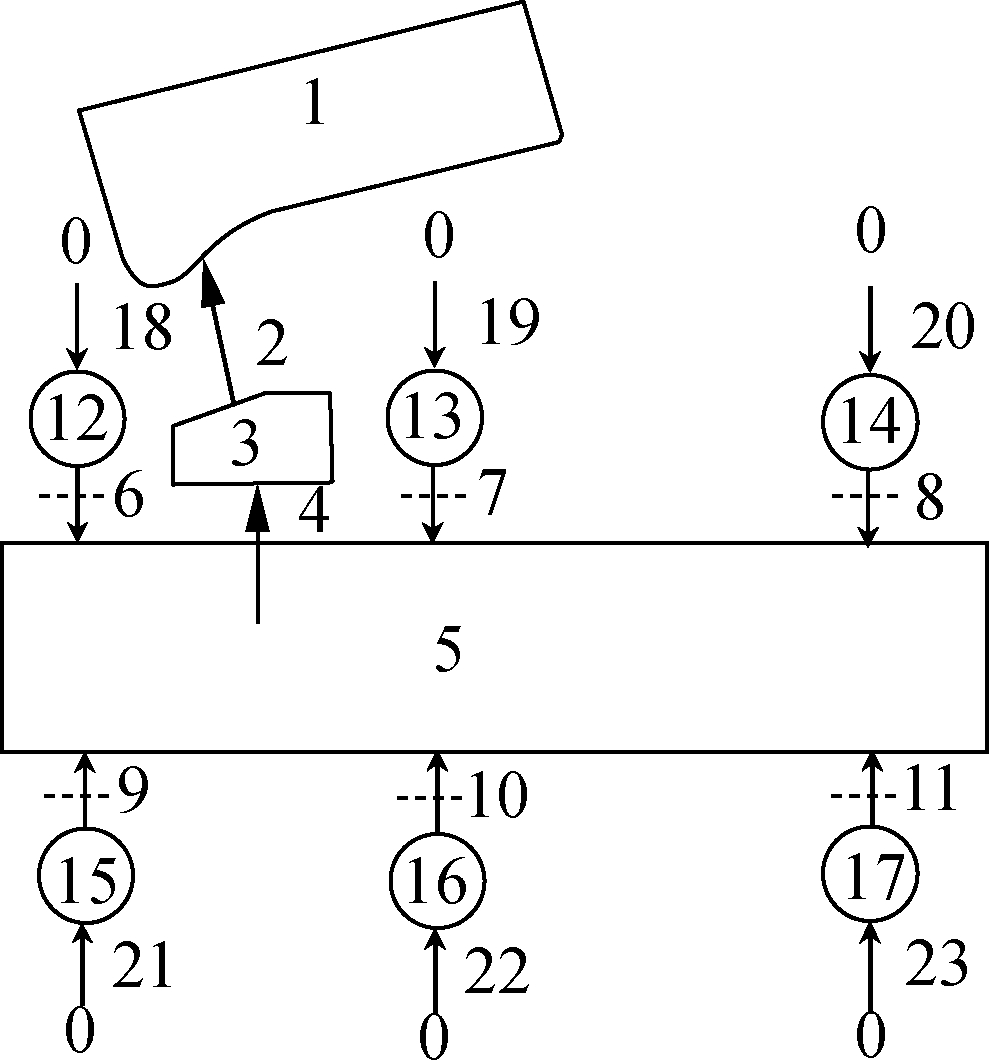
(b)
0—ground; 1—pitching part; 2—elastic pin hinge connecting the revolving part and pitching part; 3—revolving part; 4—elastic pin hinge connecting the pitch part and chassis; 5—chassis; 6-11—parallel springs and dampers connecting the chassis and the wheels; 12-17—wheels; 18-23—parallel springs and dampers connecting the wheels and the ground
Fig.1 The MLRS model.(a)Nonlinear dynamics model;(b)Topology
1.2 Launch dynamics analysis of MLRS based on RMSTMM
The state vector of each connection end, e.g., point P, is divided into two complementary parts.One part includes the acceleration and angular acceleration.The other part includes internal forces and torques, namely
(1)
The state vector of the connecting point P can be transformed by the Riccati transformation
za,P=SPzb,P+eP
(2)
where SP is the Riccati transfer matrix of point P, which is a 6×6 matrix, and eP is the column matrix corresponding to the nonhomogeneous term.
Transfer equations of the element j are
zj,O=Ujzj,I+fj
(3)
where Uj,fjare the transfer matrices of element j, which can be obtained by the transfer matrix library.
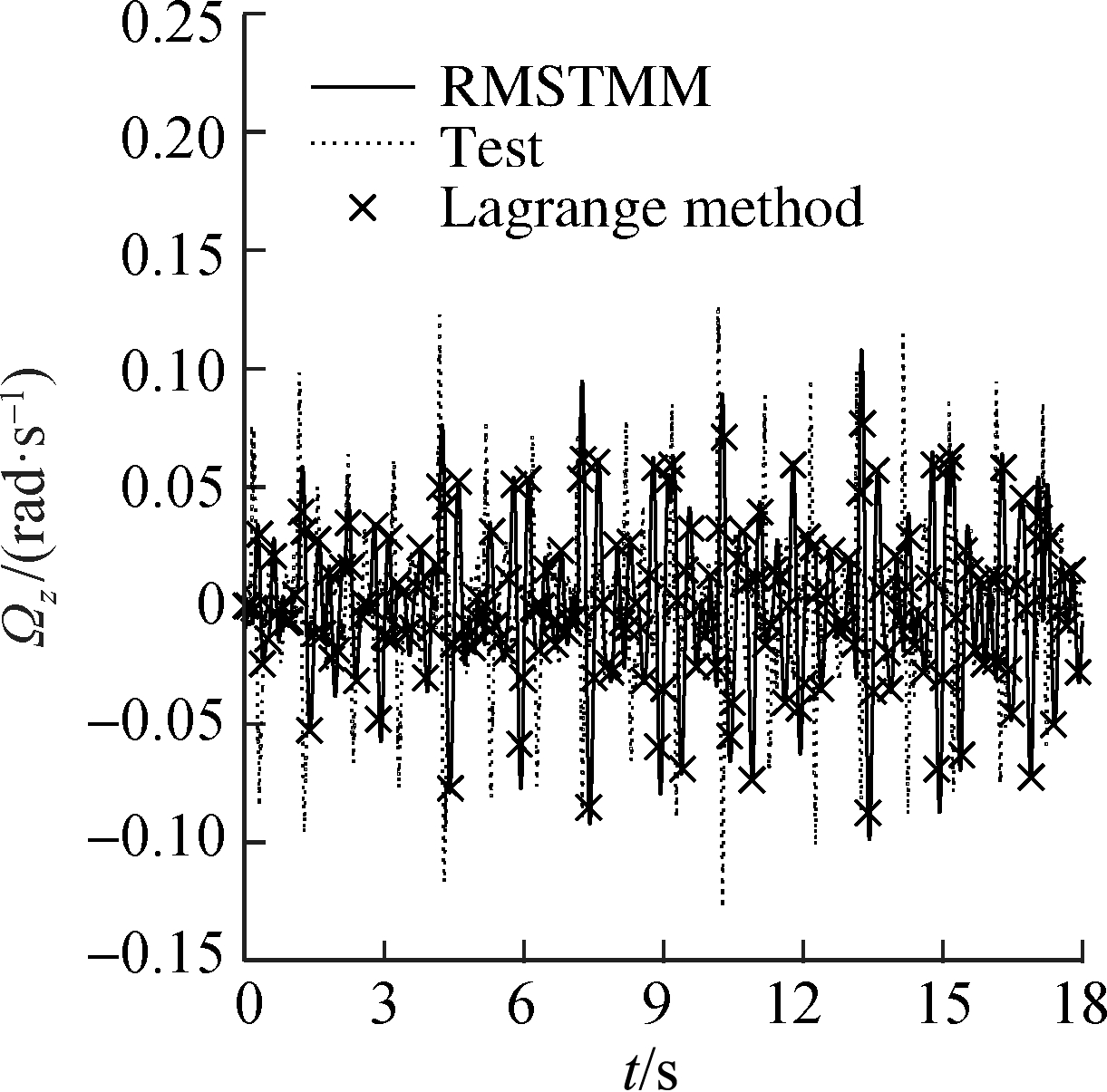
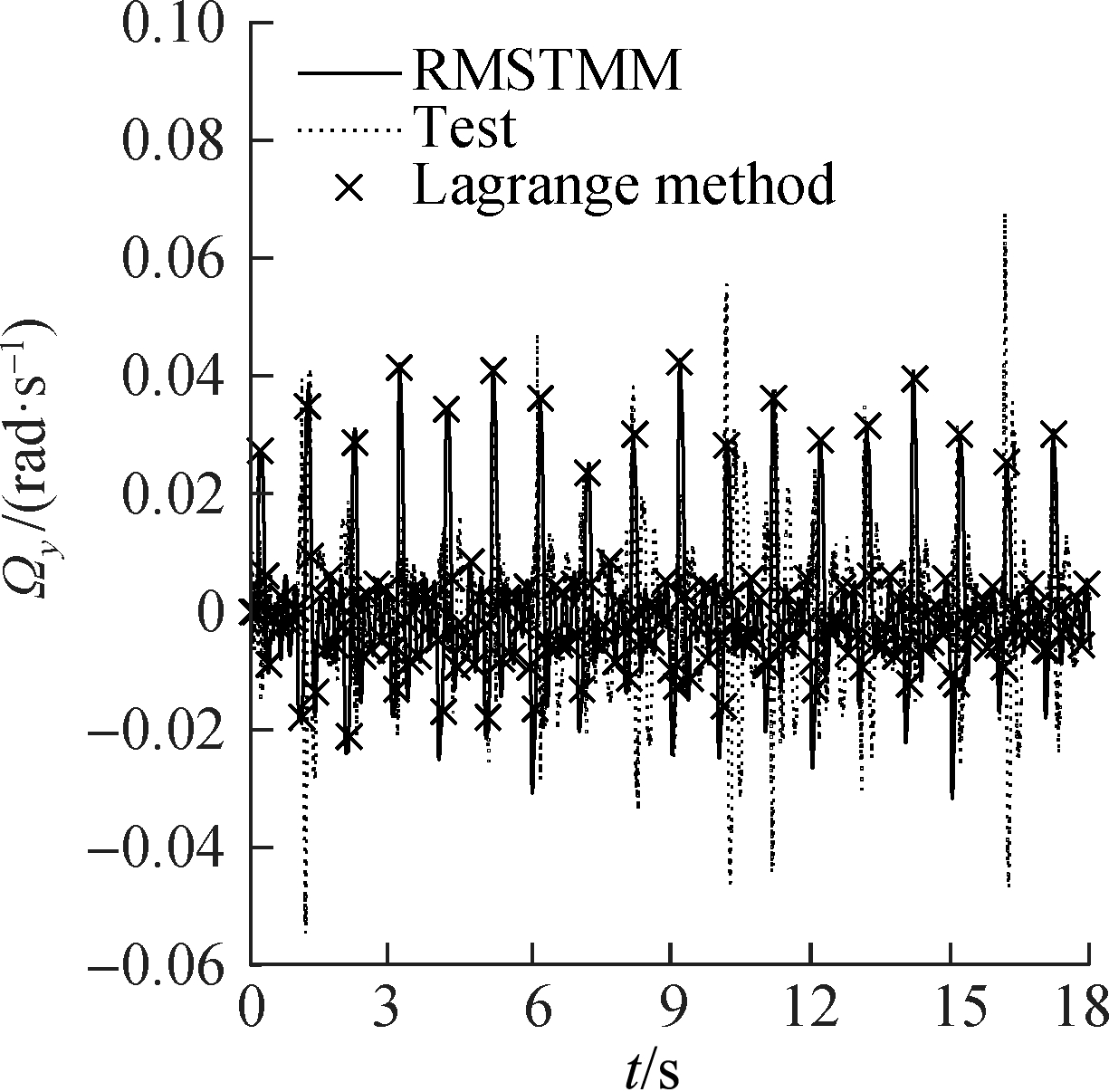
The inertial measurement unit(IMU)was used to test the attitude angular velocity of the pitch part.Fig.2 shows the comparison between the simulation results and test results of the MLRS.The simulation results of the proposed method agreed with the Lagrange method and test results, proving that the launch dynamics model can accurately reflect the launch dynamics of the MLRS.
(a)
(b)
Fig.2 Comparison between simulation results and test results of the MLRS.(a)Pitching direction;(b)Revolving direction
2 Sensitivity Analysis of MLRS Based on the DDM
2.1 Sensitivity analysis model of the launch dynamics of the MLRS
The stiffnesses of each part of the MLRS are chosen as the design variables, denoted as w, and the objective functions are the mean value and variance of the angular velocity of the pitching part when the rockets exit the muzzle, namely
(4)
where 
are the mean of the angular velocity; 
are the variances of the angular velocity of the pitching part in the revolving direction and pitching direction when the rockets exit the muzzle.The sensitivity of the objective function can be obtained by the differentiation of Eq.(4)with respect to w, namely
(5)
According to Eq.(5), the key to calculating the sensitivity of the objective function is to calculate the sensitivity of the dynamic response of the MLRS.
2.2 Sensitivity analysis method for the MLRS
In RMSTMM, the differentiation of ωy,ωz with respect to the design variable w can be obtained by the differentiation of the state vector z as follows:
where 
of each connection point can be obtained by recursive along the transfer direction.Sensitivities of the state vector of each connection point, namely 
can then be obtained by the differentiation of the Riccati transfer equation, namely
This proposed sensitivity analysis method has several advantages, such as high programming, no need for global dynamic equations, no requirement of the differentiation of global dynamic equations.Fig.3 shows that the time consumption of the proposed method was much lower than that of the DMM based on the Lagrange method.As the body number increased, the computation time gap between the two methods became increasingly large.This indicated that the proposed method has the advantage of a lower computational time cost.
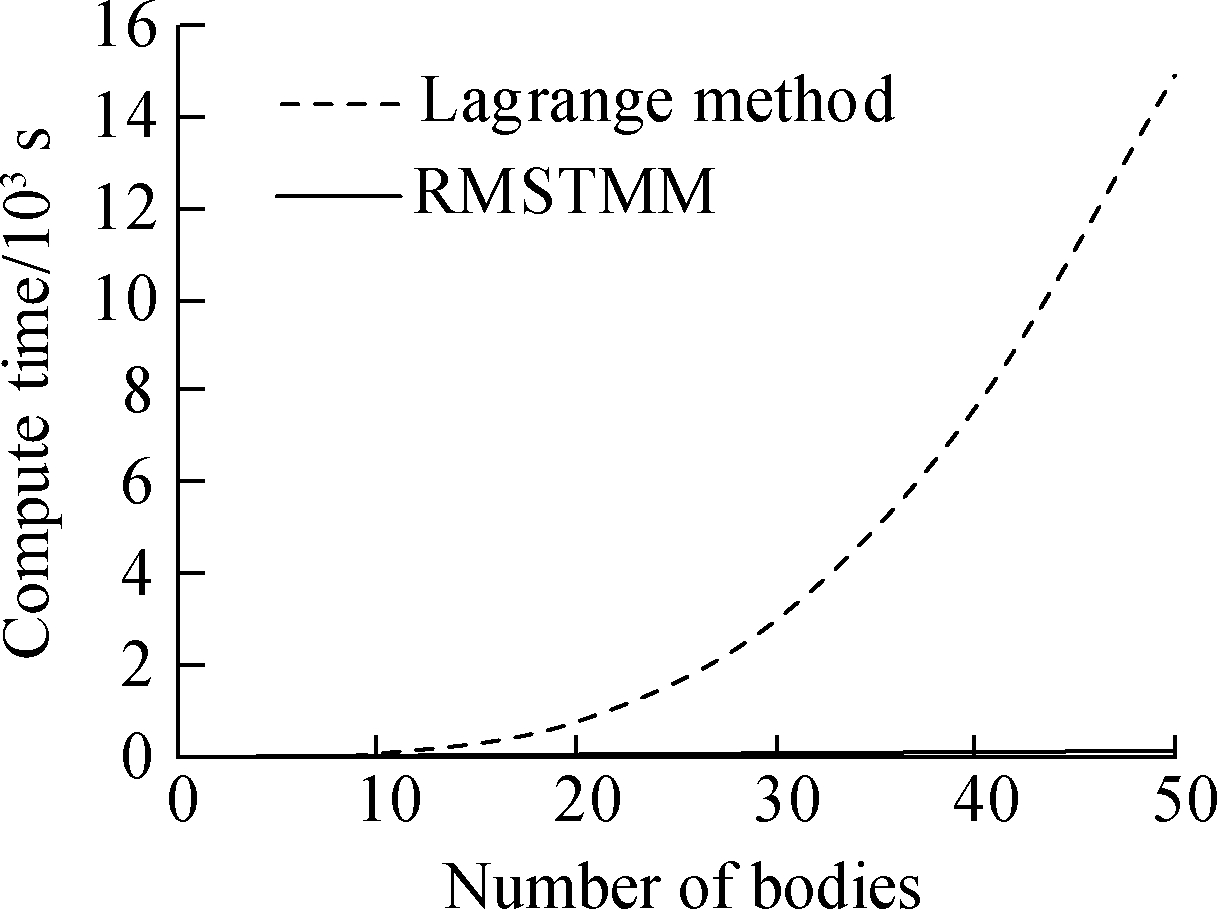
Fig.3 The comparison between simulation results and test results of the MLRS
2.3 Sensitivity analysis results of the MLRS
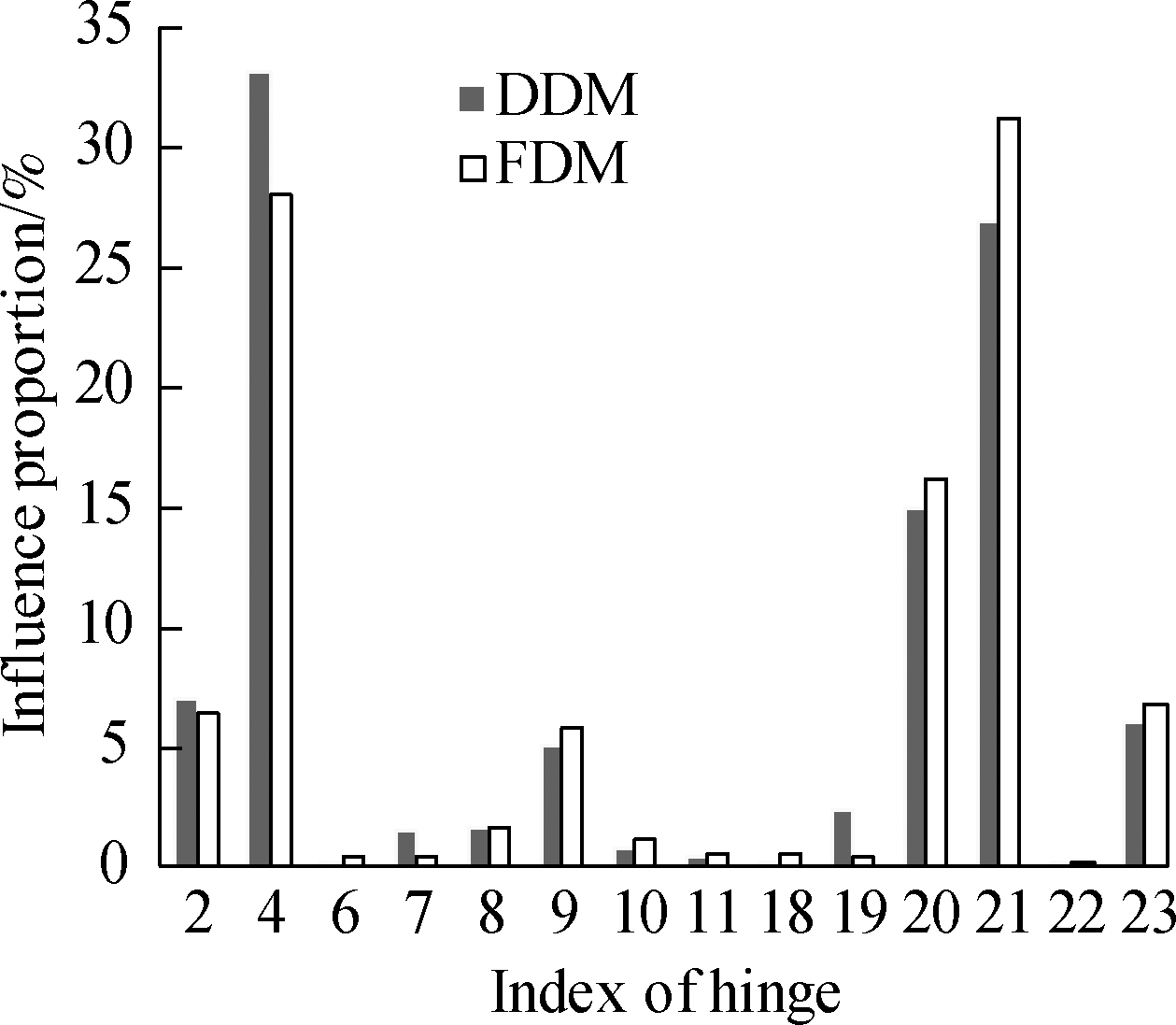
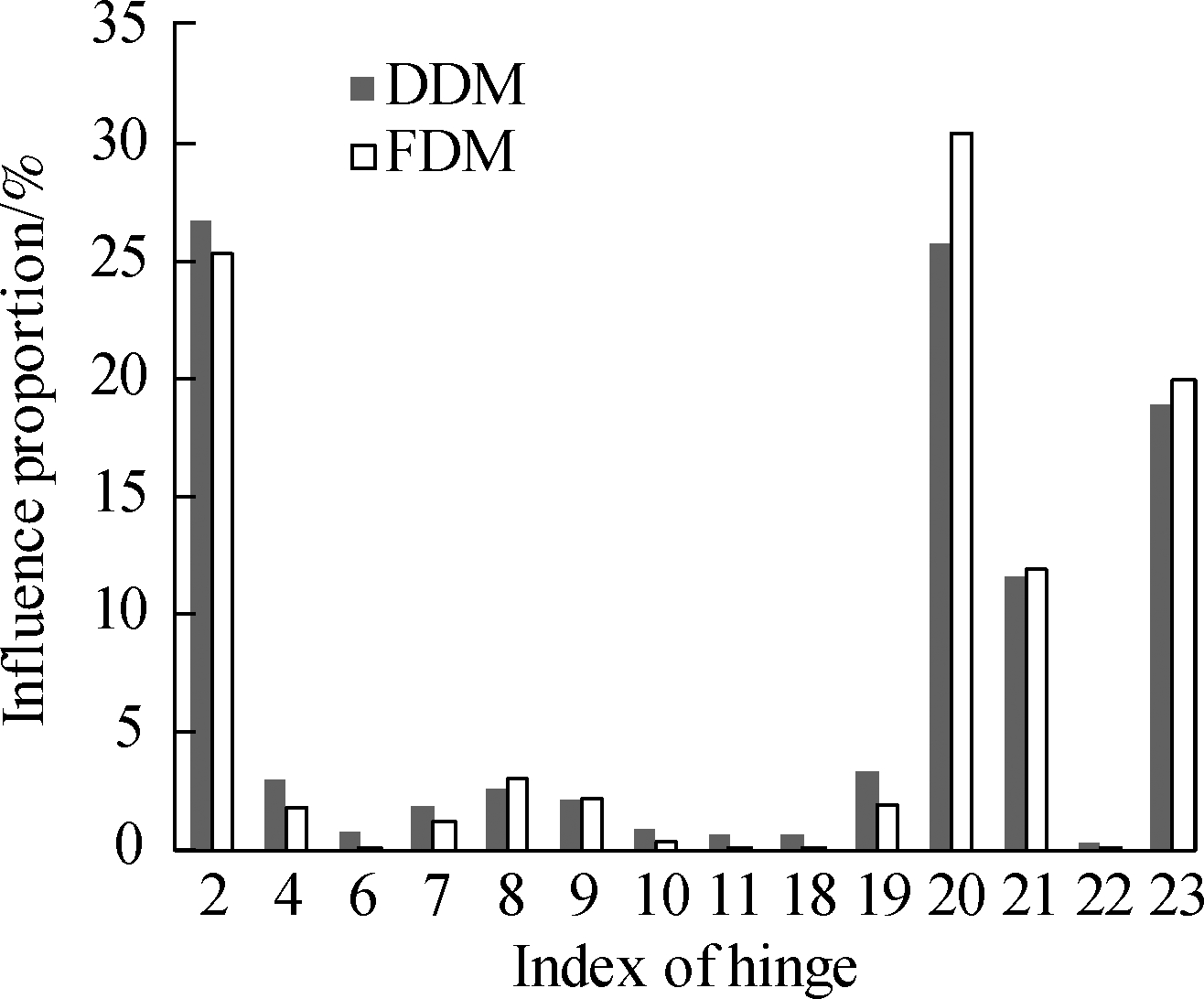
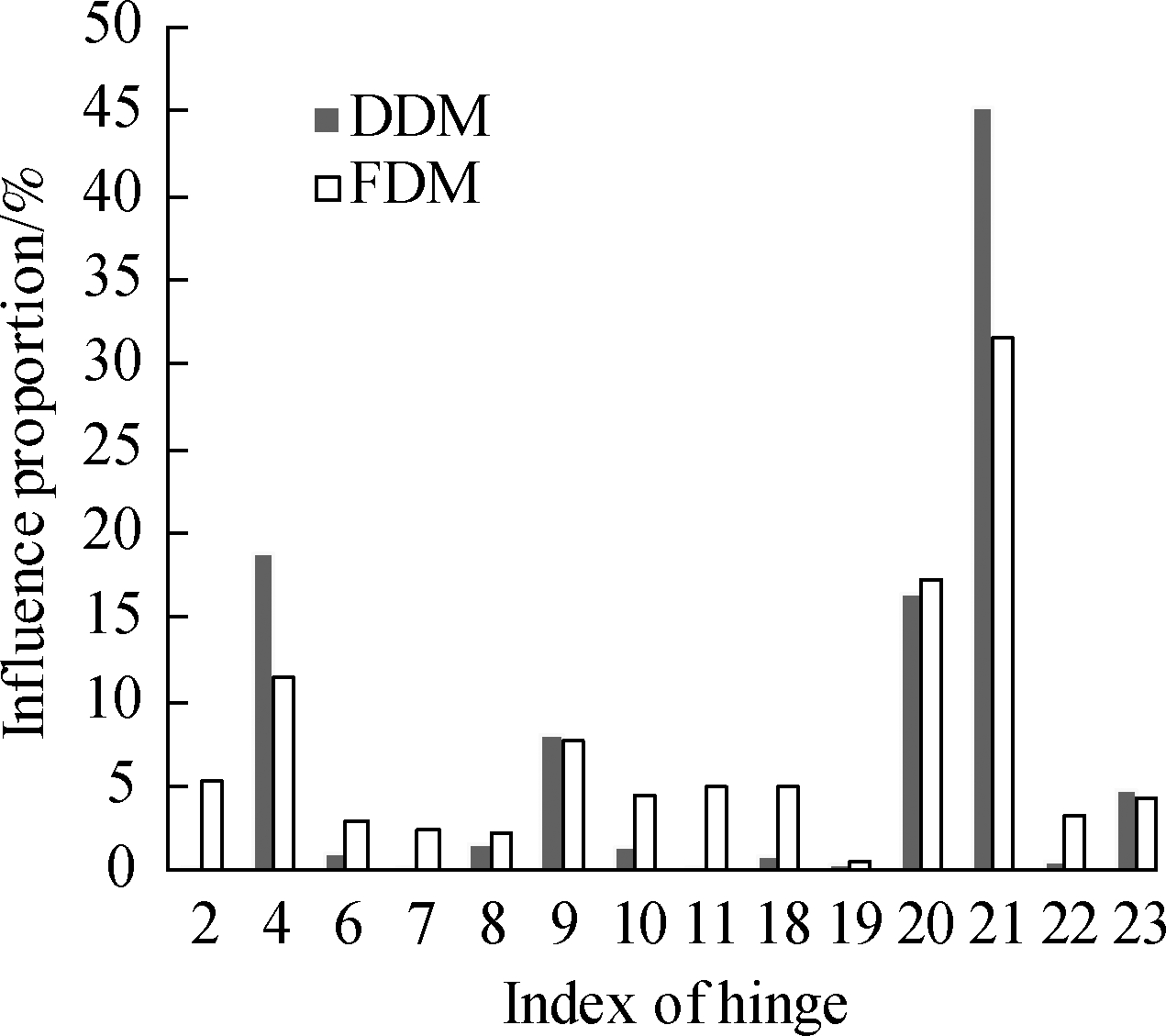
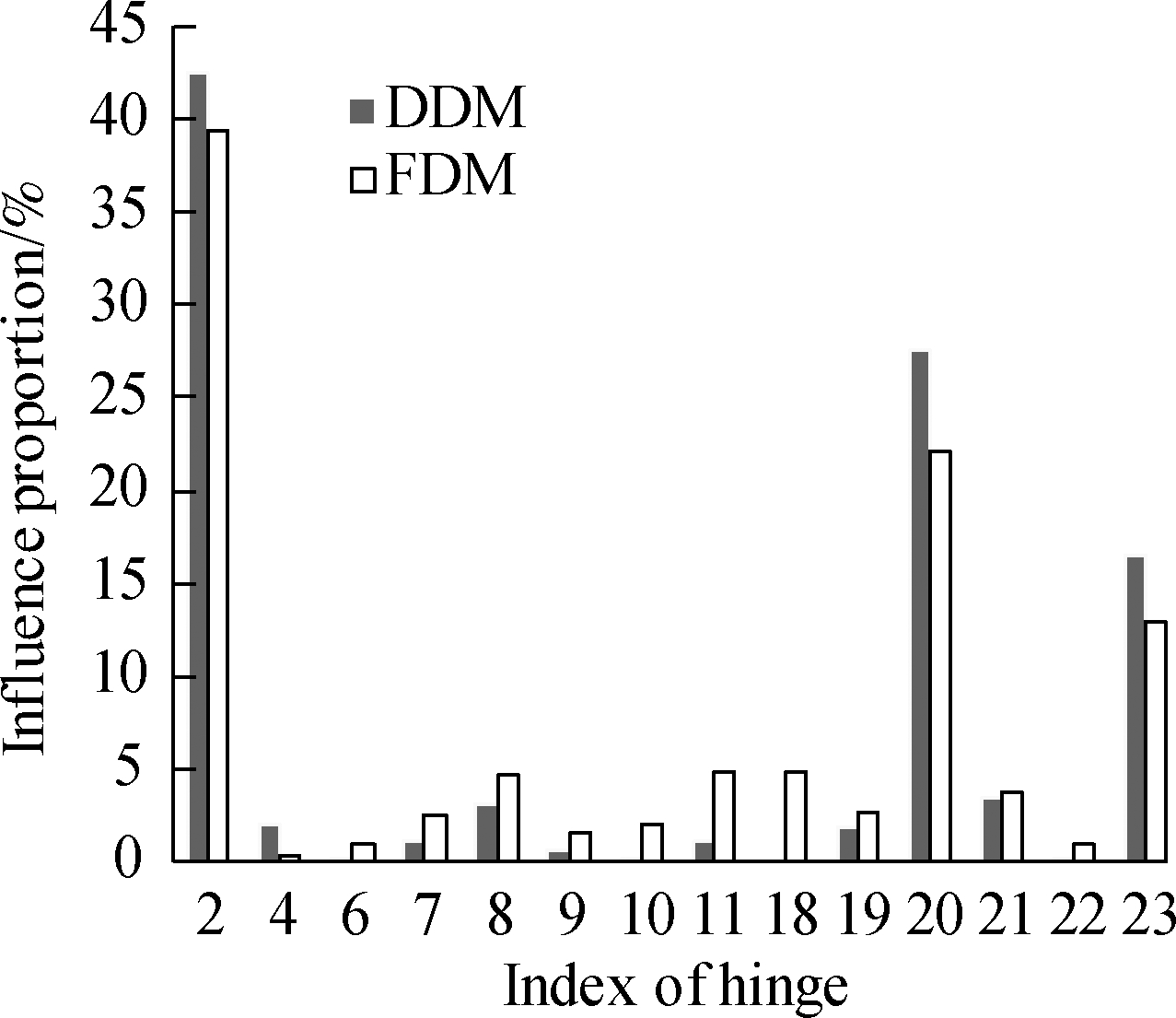
The influence proportion of the mean of the angular velocity computed by the two methods(DDM and FDM)can be seen in Fig.4, and the influence proportion of the variance can be seen in Fig.5.The FDM computes the influence proportion by giving each design parameter 0.1% disturbance.
(a)
(b)
Fig.4 Influence on the mean value of the angular velocity.(a)Revolving direction;(b)Pitching direction
(a)
(b)
Fig.5 Influence on the variance of the angular velocity.
(a)Revolving direction;(b)Pitching direction
According to the calculation results in Figs.4 and 5, the main factors that affect the launch dynamic response are hinge 2(connecting the pitching part and the revolving part), hinge 4(connecting the revolving part and the chassis), hinge 20, hinge 21, and hinge 23(connecting the wheels and the ground).
3 Dynamics Optimization of the MLRS
Based on the sensitivity analysis result, Kr2,Kr4,K20,K21,K23 are chosen as the design parameters in the optimization of the MLRS.The objective functions are the variances of the angular velocity, namely 
The optimization of the MLRS is a multiobjective optimization problem.
A common solution to the multiobjective optimization problem is to transform the multiobjective problem into a single-objective problem by a specific function and to solve the multiobjective optimization problem by the single-objective function optimization method.By the geometric mean method, the optimization function is transformed as 
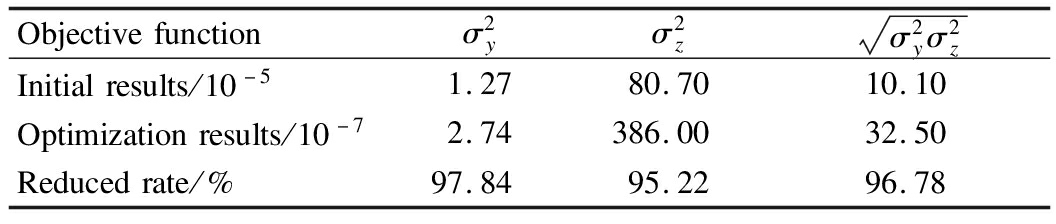
Tabs.1 and 2 show the optimization results obtained by the GA.
Tab.1 Optimization results of design parameters MN·m/rad
DesignparametersKr2Kr4K20K21K23Optimizationresults9.647.252.683.260.168
It can be seen from Tab.2 that the variance of the angular velocity when the rocket exits the muzzle in both directions has been reduced significantly, with reduced rates of 97.84% and 95.22%.By optimizing these five parameters, the dynamics response of the pitching part of the MLRS is reduced significantly.
Tab.2 Optimization results of the objective function
Objectivefunctionσ2yσ2zσ2yσ2zInitialresults/10-51.2780.7010.10Optimizationresults/10-72.74386.0032.50Reducedrate/%97.8495.2296.78
4 Conclusions
1)Based on the RMSTMM, the launch dynamics model of the MLRS was established, and the launch dynamics simulation was carried out and validated by test results.
2)A DDM has been applied to the formulation for the sensitivity analysis of multibody systems, and a novel sensitivity analysis method for the launch dynamics of the MLRS was proposed.The proposed method has several advantages, such as low computation time cost, high programming, no need for global dynamic equations, and no requirement for the differentiation of global dynamic equations.Based on the proposed method, the main factors influencing the launch dynamic response of the MLRS are analyzed.
3)A multiobjective optimization method for the MLRS is developed.The optimization method yielded reduced rates of 97.84% and 95.22% for the variance of the angular velocity in different directions.The dynamics response of the pitching part of the MLRS is found to be significantly reduced.
[1] Rui X,Lu Y,Wang G.Simulation and test methods of launch dynamics of multiple launch rocket system[M].Beijing:National Defense Industry Press,2003:10-15.(in Chinese)
[2] Gu L,Rui X,Wang G,et al.A novel launch dynamics measurement system for multiple launch rocket system and comparative analysis with numerical simulations[J].Defence Technology,2021,17(2):671-681.DOI:10.1016/j.dt.2020.11.007.
[3] Gu L,Rui X,Wang G,et al.A novel vibration control system applying annularly arranged thrusters for multiple launch rocket system in launching process[J].Shock and Vibration,2020:1-14.DOI:10.1155/2020/7040827.
[4] Zhou Q,Rui X,Tao Y,et al.Deduction method of the overall transfer equation of linear controlled multibody systems[J].Multibody System Dynamics,2016,38(3):263-295.DOI:10.1007/s11044-015-9487-2.
[5] Miao Y,Wang G,Rui X,et al.Study on test dynamics method of non-full loading firing for multiple launch rocket system[J].Mechanical Systems and Signal Processing,2019,122:463-479.DOI:10.1016/j.ymssp.2018.12.043.
[6] Rui X,Wang G,Lu Y,et al.Transfer matrix method for linear multibody system[J].Multibody System Dynamics,2008,19(3):179-207.DOI:10.1007/s11044-007-9092-0.
[7] Chen G,Rui X,Yang F,et al.Study on the natural vibration characteristics of flexible missile with thrust by using Riccati transfer matrix method[J].Journal of Applied Mechanics,2016,83(3):31006.DOI:10.1115/1.4032049.
[8] Gu J,Rui X,Zhang J,et al.Riccati transfer matrix method for linear tree multibody systems[J].Journal of Applied Mechanics,2017,84(1):11008.DOI:10.1115/1.4034866.
[9] Dopico D,Zhu Y,Sandu A,et al.Direct and adjoint sensitivity analysis of ordinary differential equation multibody formulations[J].Journal of Computational and Nonlinear Dynamics,2015,1(10):11012.DOI:10.1115/1.4026492.
[10] Holland J H.Genetic algorithms and the optimal allocation of trials[J].SIAM Journal on Computing,1973,2(2):88-105.DOI:10.1137/0202009.
[11] Huynh H N,Assadi H,Dambly V,et al.Direct method for updating flexible multibody systems applied to a milling robot[J].Robotics and Computer-Integrated Manufacturing,2021,68:102049.DOI:10.1016/j.rcim.2020.102049.
[12] Ardestani M M,Moazen M,Jin Z.Gait modification and optimization using neural network-genetic algorithm approach:Application to knee rehabilitation[J].Expert Systems with Applications,2014,41(16):7466-7477.DOI:10.1016/j.eswa.2014.06.034.
[13] Jiang M,Rui X,Zhu W,et al.Optimal design of 6-DOF vibration isolation platform based on transfer matrix method for multibody systems[J].Acta Mechanica Sinica,2020,37(1):127-137.DOI:10.1007/s10409-020-01004-8.
[14] Ren B,Liu J,Chen J.Simulating human-machine coupled model for gait trajectory optimization of the lower limb exoskeleton system based on genetic algorithm[J].International Journal of Advanced Robotic Systems,2020,17(1):255.DOI:10.1177/1729881419893493.