As a noncontact deformation measurement method, digital image correlation(DIC)[1] has been widely used in scientific research and engineering fields.The computational efficiency of DIC is particularly important for the online and long-term monitoring of industrial and medical measurements.With the high-efficiency inverse compositional Gauss-Newton(IC-GN)algorithm and CPU-and GPU-based parallel methods, real-time two-dimensional(2D)DIC[2] and three-dimensional(3D)DIC[3] have been realized.
In real-time measurement applications[4-5], measured deformation fields need to be transmitted in real time for control and monitoring.However, various cables used in traditional wire transmission make wirings in complex measurement sites extremely inconvenient, and the maintenance requires considerable manpower and financial resources.With the rapid development of wireless communication technology, wireless technology is gradually being applied in scientific research, industrial production, and other fields, thus enabling the wireless real-time transmission of measured results.The application of wireless technology can make real-time transmission in complex measurement scenes more flexible and convenient than ever.
Wireless local area networks(WLANs)and 4G are the two most widely used wireless transmission technologies.In various measurement scenarios, the establishment of a WLAN is challenging, especially at complex measurement sites.Compared with WLAN technology, wireless transmission technology based on 4G is not limited by distance and requires no installation of access point equipment to establish a network before measurement.Accordingly, 4G technology is more convenient, suitable, and recommended for the wireless transmission of real-time measured results.
However, the bandwidth of 4G networks is lower than that of WLANs.Owing to the influence of network configuration and terminal equipment, the peak rate of 4G networks for the uplink can reach approximately 20 Mbit/s.Considering the limitation of the bandwidth, the size of transmitted data is a significant factor that affects transmission stability.Recently, the computational speed of real-time DIC based on a heterogeneous parallel computing model can reach up to 1.6 × 106 points/s [6].The data type of the calculated displacement field is a double-precision floating point, which occupies 8 bytes per point.Accordingly, there are approximately 200 Mbit/s of U and V displacement field data in DIC for wireless transmission.Considering the transmission stability and future improvement of the computational efficiency of DIC, compression encoding for the wireless transmission of the displacement field is in great demand and deserves further research.
Many studies have been conducted on the data compression of floating points.Isenburg et al.[7] described a lossless method for compressing floating-point coordinates in mesh data using predictive coding.Lü et al.[8] proposed a fast and lossy compression algorithm for point-cloud models based on data-type conversion.In their study, a minimum spanning tree and arithmetic coding were used to encode the point-cloud data of the floating point.Zhang’s research group used principles of digital fringe projection to encode 3D range data within the three-color channels(RGB)of a regular 2D image [9-12].The 2D image can be further compressed using traditional image compression techniques(e.g., PNG and JPEG).This approach achieved high compression ratios and high-quality 3D reconstructions.Based on this approach, researchers have studied methods based on phase encoding[13], space-filling curves[14], and multiwavelength depth encoding[15] for 3D range geometry compression.However, to the best of our knowledge, there is no study on the data compression of displacement fields.
Regardless of lossy and lossless methods, researchers expect to achieve the highest possible accuracy.However, the measurement accuracy of DIC displacement can only reach 0.01 pixels at present, which already meets most of the requirements of the displacement measurement.Even if the compression approach can maintain accurate decimal places of the displacement field, redundant precision is meaningless and leads to a high computational complexity and low compression ratio.Considering the practical attainable accuracy of the displacement measurement and future improvement of precision, 0.001 pixels is defined as the compression target.
JPEG[16] and JPEG 2000 [17-19], which are based on a discrete cosine transform(DCT)[20-22]and discrete wavelet transform(DWT)[23-26], respectively, are two classical image compression standards used to achieve good compression ratios.Moreover, High-Efficiency Video Coding(HEVC)[27]and Versatile Video Coding(VVC)[28]are two state-of-the-art video compression standards.HEVC and VVC can be implemented on image coding and achieve excellent compression efficiency at the cost of high computational complexity.Considering the current calculation speed of DIC and transmission bandwidth, it is not necessary to pursue extremely high compression ratios.Compression ratios supporting real-time transmission are acceptable.By comparison, the compression speed needs to be considered.Based on the above considerations, JPEG and JPEG 2000 are well studied, and two improved data compression encoding methods based on the DCT and DWT are proposed.
Some researchers have combined image compression techniques using the DCT and DWT with DIC[29].The key difference between our works is the objects to be compressed.Yang et al.[29] compressed digital images before DIC calculation, whereas our objective is the displacement fields calculated by DIC.Data elements in the displacement field are double-precision floating point types; they are not integers, such as elements in an image.In traditional image compression, low-frequency components are seen more importantly than high-frequency components.Corresponding quantization introduces loss of information.On the contrary, a high compression accuracy(0.001 pixels)of the displacement field is required, and as such, the compression operation in Yang’s work and the quantization modules in JPEG and JPEG 2000 are not gratifying.Particularly, in Yang’s work, only a fixed percentage of coefficients that have the greatest values are saved after the DCT and DWT, which introduces a huge loss of information.Considering these significant properties, improved non-integer and integer quantization are studied.Without confusion, non-integer and integer quantization are named for the data type of data after quantization.
1 Data Compression Based on the DCT
1.1 Preprocessing and the DCT
Displacement fields are preprocessed in three steps: valid region extraction, matrix expansion, and level shifting[19].Displacement fields after preprocessing are usually grouped into 8 × 8 blocks and inputted to the DCT individually.
1.2 Non-integer quantization
In JPEG, each block is quantized with a specified 64-element quantization table owing to the visual characteristics of the human eye.However, in contrast to general images, the displacement field is not sensed by the eyes but for subsequent operations, and the compression target is to achieve an accuracy of 0.001 pixels for each element.According to this, the quantization step in JPEG 2000 [18] is modified to make each element uniformly quantized, which can be given by
(1)
where Δb is the quantization step; εb is the parameter satisfying 0 ≤εb< 25; μb is the parameter satisfying 0≤μb<211.The improved non-integer quantitative formula, which is specifically designed for floating-point data in the displacement field, is given by
(2)
where Aij is the coefficient before quantization; ![]() is the coefficient after quantization; round()is the function that rounds off coefficients to the nearest decimal or integer.Eq.(2)rounds off
is the coefficient after quantization; round()is the function that rounds off coefficients to the nearest decimal or integer.Eq.(2)rounds off ![]() to three decimal places to compress the quantized data.Subsequently, the data type of
to three decimal places to compress the quantized data.Subsequently, the data type of ![]() is changed from a double-precision to a single-precision floating point.
is changed from a double-precision to a single-precision floating point.
The inverse non-integer quantitative formula is given by
(3)
where ![]() is the reconstructed coefficients after dequantization.
is the reconstructed coefficients after dequantization.
2 Data Compression Based on the DWT
2.1 Preprocessing and the DWT
The preprocessing of DWT-based displacement field compression is similar to that of the DCT-based method.Notably, the DWT processes the displacement field as a whole without grouping it into blocks.The purpose of matrix expansion is to facilitate the partitioning of code blocks in subsequent bit-plane coding.
Considering the displacement fields of the floating point and the target of lossy compression, Daubechies 9/7 floating-point filter bank with superior lossy compression performance was selected as the DWT filter rather than the Le Gall 5/3 filter bank.Compared with the convolution-based filtering mode, the lifting-based mode provides a remarkable memory reduction and computational complexity of the DWT.As such, the lifting-based mode was applied.
2.2 Integer quantization
Similar to the quantization step in DCT-based compression, Δb as specified by Eq.(1)was applied to each subband.Subsequently, to facilitate bit-plane coding, the coefficients after the DWT were transformed into integers and quantized by an integer quantization formula for floating points, which is given by
(4)
where floor()is the function that rounds off coefficients toward the negative infinity.Subsequently, the data type of ![]() was changed to a single-precision floating point.
was changed to a single-precision floating point.
The operation of integer dequantization was conducted using
(5)
where γ is a reconstruction parameter satisfying 0≤γ<1 chosen by the decoder.
3 Experiments and Results
To verify the effectiveness of the improved compression methods based on the DCT and DWT, a displacement field(177×194)in axial compression was inputted into the proposed algorithms as an example.Parameters in Eq.(1)were empirically fixed at μb = 28 and εb=1 in both methods [19,30].All algorithms proposed in this work were implemented using MATLAB 2018b and tested on a middle-end desktop computer.
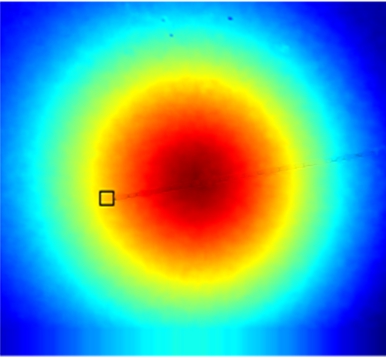
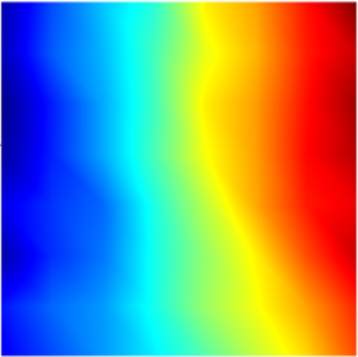
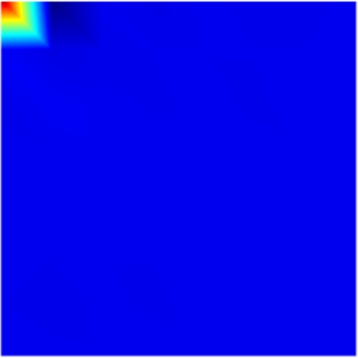
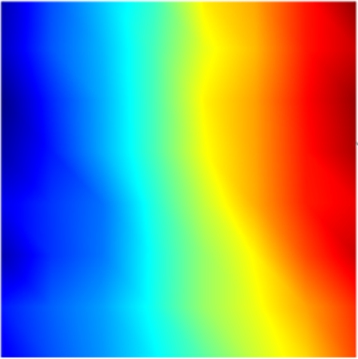
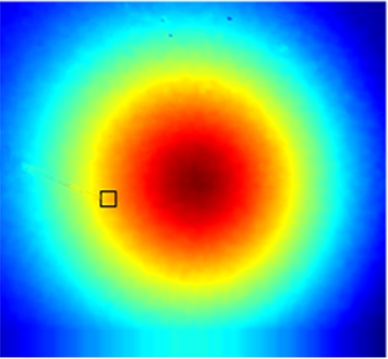
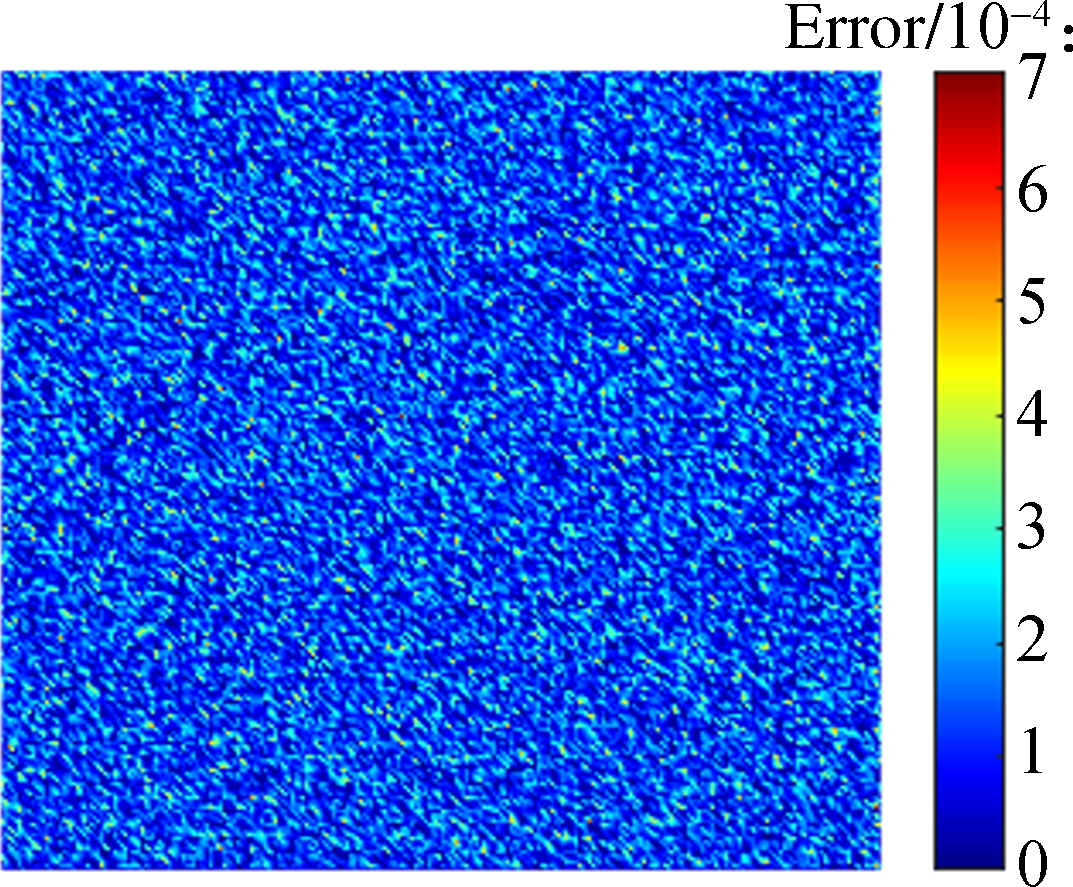
The experimental results based on the DCT are shown in Fig.1.In the sender of the DCT-based method, the displacement field after preprocessing was divided into 8×8 blocks, and each block was inputted to the DCT and quantizer for individual encoding.Subsequently, in the receiver, the encoded bitstream was decoded and dequantized, and the inverse discrete cosine was transformed to reconstruct the recovered displacement field.Fig.1 illustrates the entire process.To avoid confusion, the right color bar is only related to the error map in Fig.1(i).As shown in Fig.1(i), the maximum error between the original and recovered displacement fields is 0.0007 pixels, which achieves the set compression accuracy(0.001 pixels).The corresponding compression ratio is 14.83%.Accordingly, the computational time of the sender and receiver is 0.157 s(relevant computational speed is approximately 2.2 × 105 points/s)and 0.142 s(2.4 × 105 points/s), respectively.
(a)
(b)
(c)

(d)

(e)

(f)
(g)
(h)
(i)
Fig.1 DCT-based experimental results of the displacement field in axial compression.(a)Displacement field after preprocessing;(b)8 × 8 block in(a);(c)DCT of(b);(d)Block after quantization from(c)for encoding;(e)Block decoded from bitstream;(f)Block after dequantization from(e);(g)IDCT of(f);(h)Recovered displacement field reconstructed from blocks;(i)Error map between the original and recovered displacement fields
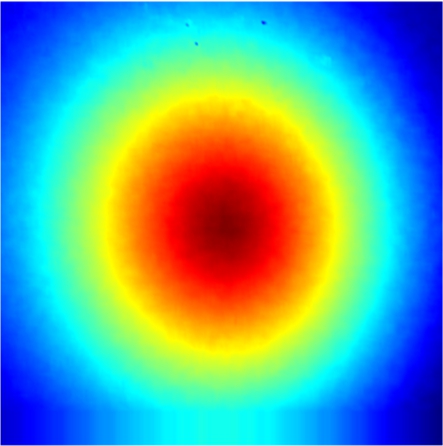
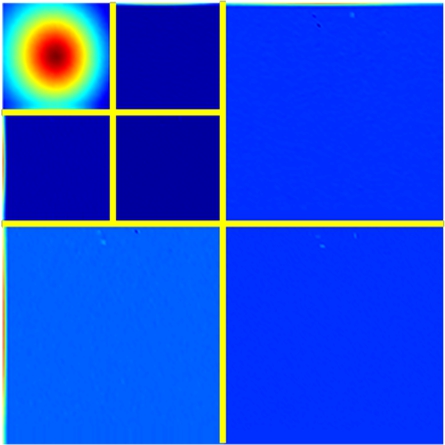
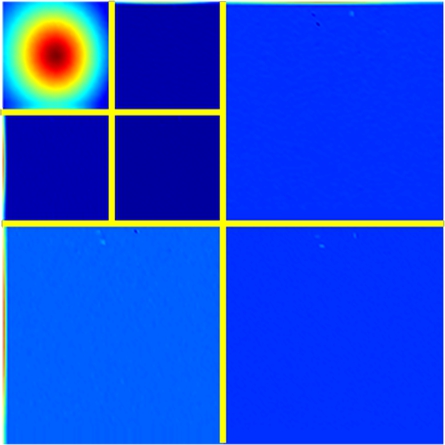
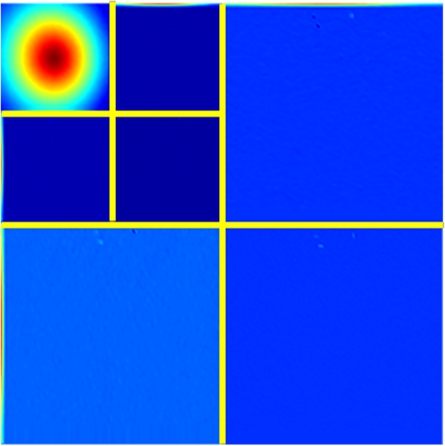
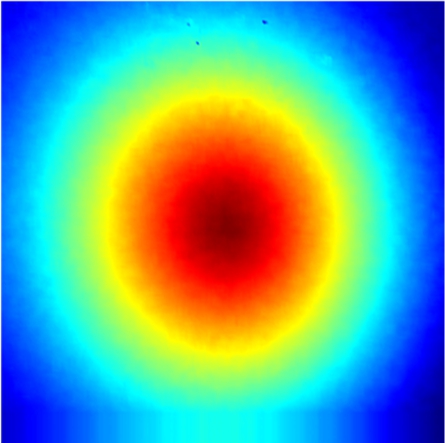
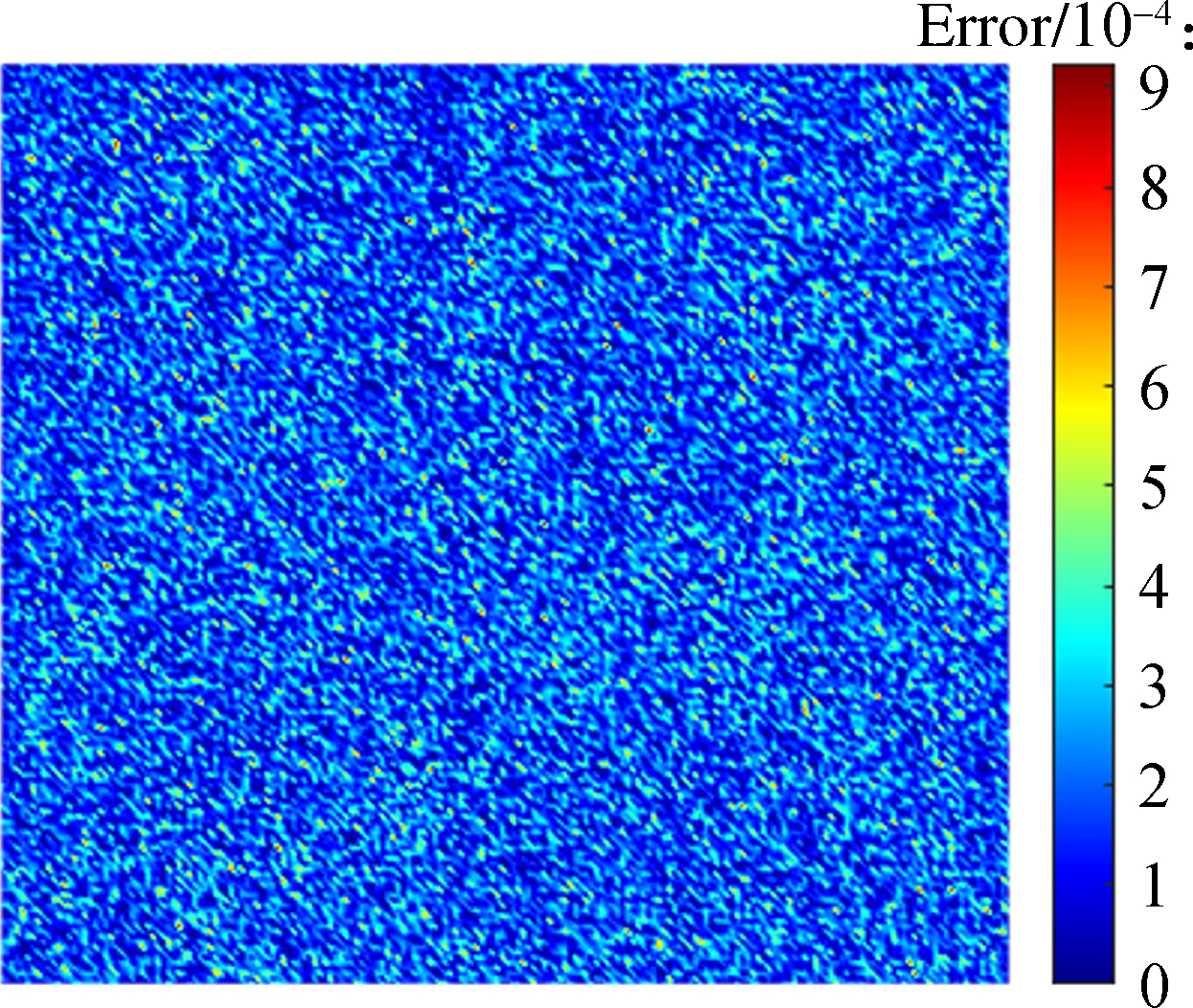
In DWT-based compression,γ=0.5 in the dequantizer was chosen to result in midpoint reconstruction.The value can always obtain satisfactory results empirically.The DWT-based experimental results are shown in Fig.2.In the sender, the displacement field was preprocessed, discrete wavelet transformed, quantized, and encoded to the bitstream.Subsequently, the decoded bitstream after dequantization was inputted to the IDWT to recover the displacement field in the receiver.The right color bar is only related to Fig.2(g).The maximum error in Fig.2(g)is 9×10-4 pixels, and the corresponding compression ratio is 32.81%.The computational times of the sender and receiver are 7.950 s(4 300 points/s)and 20.389 s(1 700 points/s), respectively.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Fig.2 DWT-based experimental results of the displacement field in axial compression.(a)Displacement field after preprocessing;(b)Two-level DWT of(a);(c)Displacement field after quantization from(b)for encoding;(d)Displacement field decoded from bitstream;(e)Displacement field after dequantization from(d);(f)IDWT of(e);(g)Error map between the original and recovered displacement fields
To further assess the compression ratio and computational efficiency of the two improved compression methods, the displacement fields of four typical experiments(uniform stretching, three-point bending, four-point bending, and axial compression)were inputted into the proposed algorithms.The speckle patterns of the four experiments are shown in Fig.3.The patterns in Figs.3(a)and(c)are water transfer printing speckles, whereas those in Figs.3(b)and(d)are artificial speckles.Five groups of displacement fields under different loads were selected in each experiment, and the corresponding sizes of the displacement field were 256 × 32(uniform stretching), 59 × 358(three-point bending), 109 × 261(four-point bending), and 177 × 194(axial compression).All fields were calculated using the IC-GN algorithm.The corresponding procedures and parameters are identical to the verification above except for εb.εb is a more effective parameter affecting the quantization step than μb.Accordingly, μb was fixed at 28, and εb was selected(ranging from 0 to 25)for a fixed step of 1.

(a)

(b)

(c)

(d)
Fig.3 Speckle patterns of four typical experiments.(a)Uniform stretching;(b)Three-point bending;(c)Four-point bending;(d)Axial compression
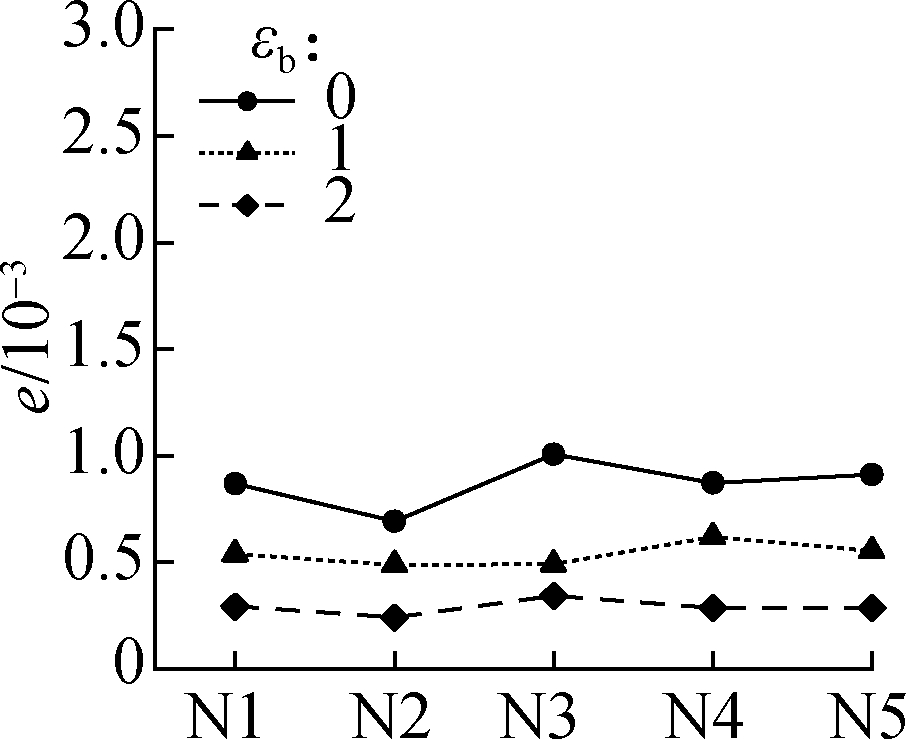
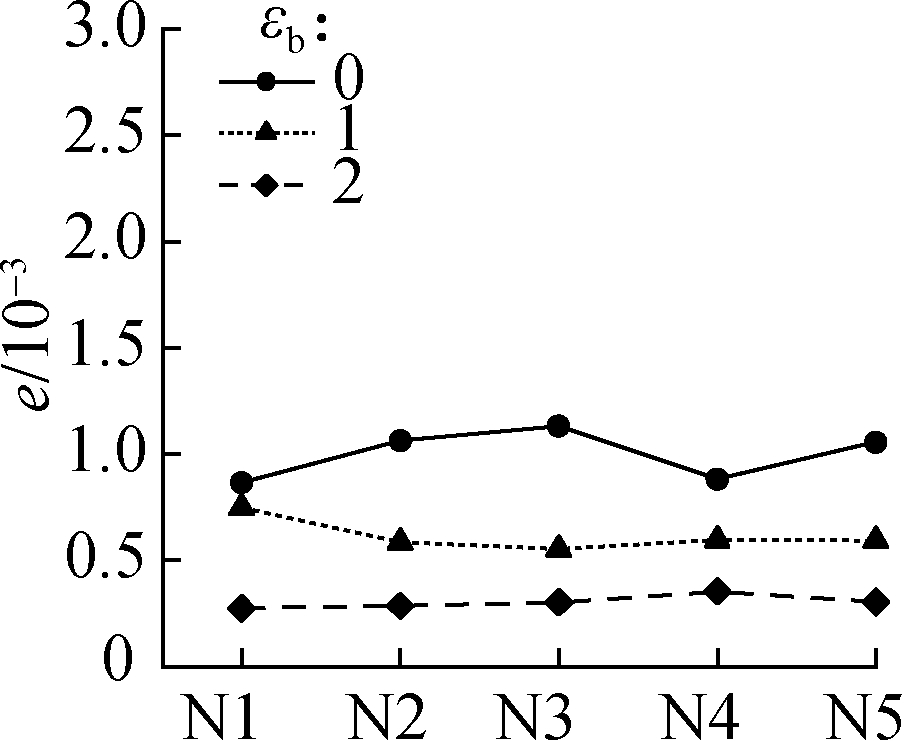
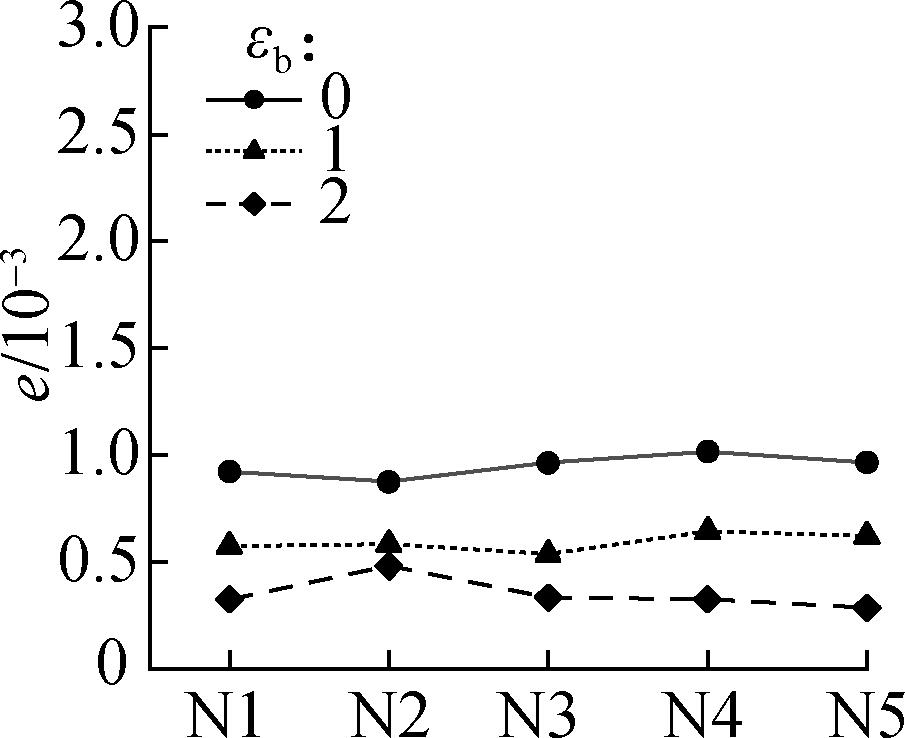
Five repeated experiments named N1 to N5 were carried out.Figs.4 and 5 show the maximum error e between the original and recovered displacement fields when μb=28 and εb=0, 1, 2(the three values of εb are the most representative)based on the DCT and DWT, respectively.According to Eq.(1), εb is inversely proportional to the quantization step size.The figures show that a large value of εb can achieve a high compression accuracy, and a compression accuracy that is too high inevitably results in a low compression ratio.The selection of an appropriate value of εb is required.When εb=1, only the maximum error of the fifth group of the displacement field in axial compression exceeds the set of 0.001 pixels.The error(0.001 1 pixels)is acceptable, and the parameter εb=1 is recommended for the two improved compression methods.
(a)
(b)
(c)

(d)
Fig.4 DCT-based maximum error between the original and recovered displacement fields in four typical experiments.(a)Uniform stretching;(b)Three-point bending;(c)Four-point bending;(d)Axial compression
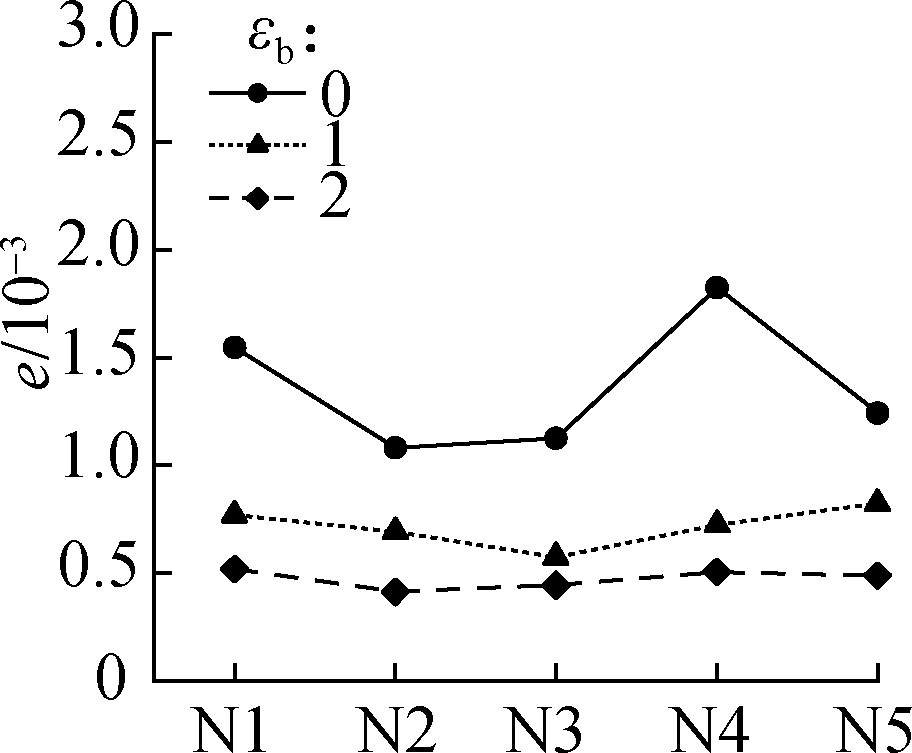
(a)
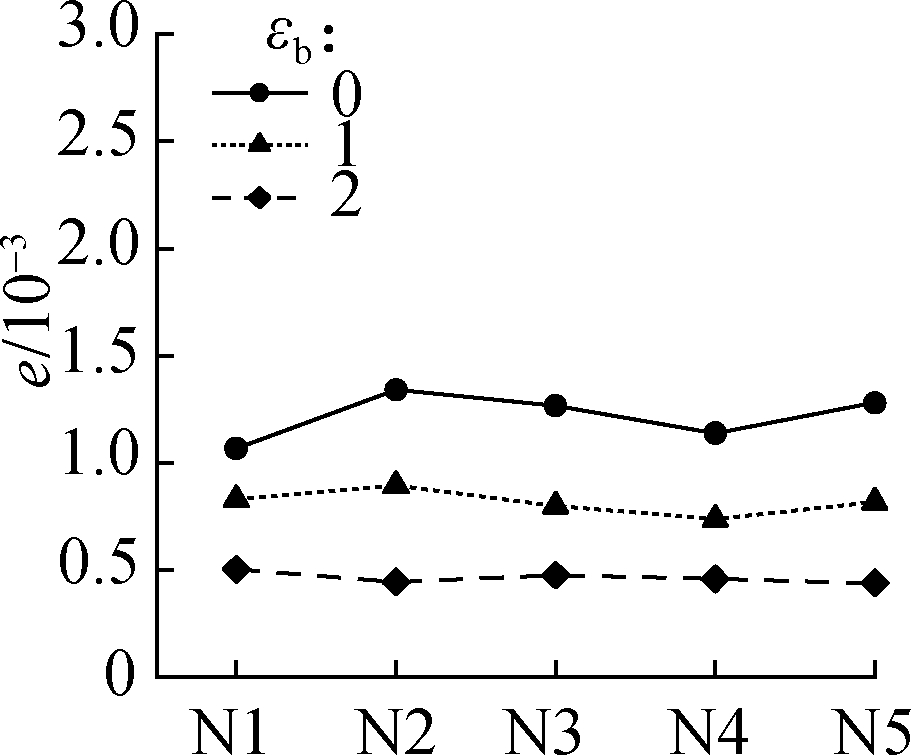
(b)
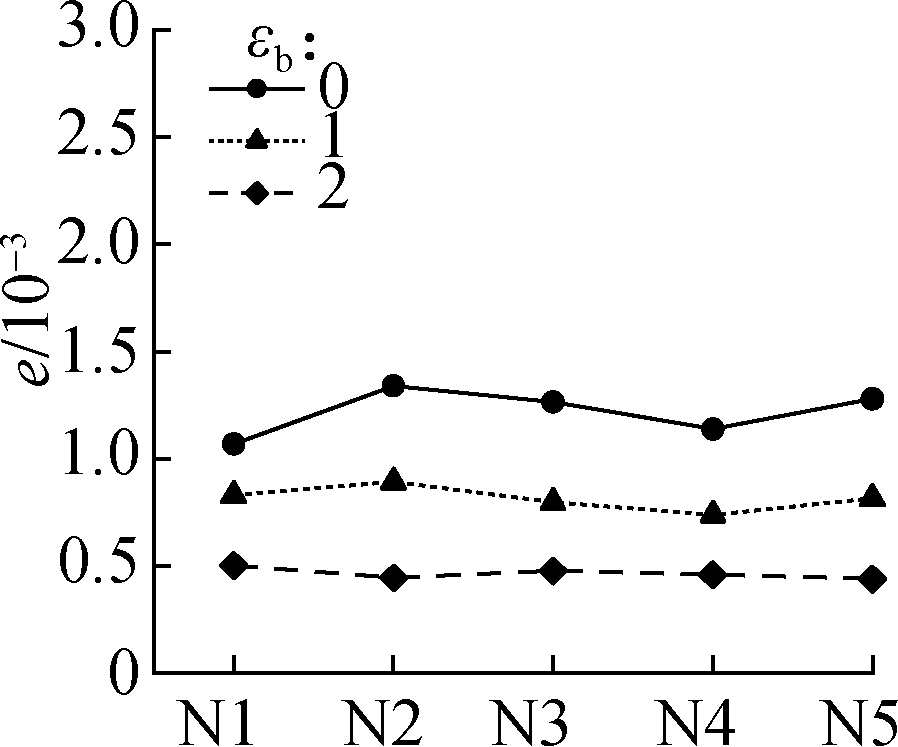
(c)
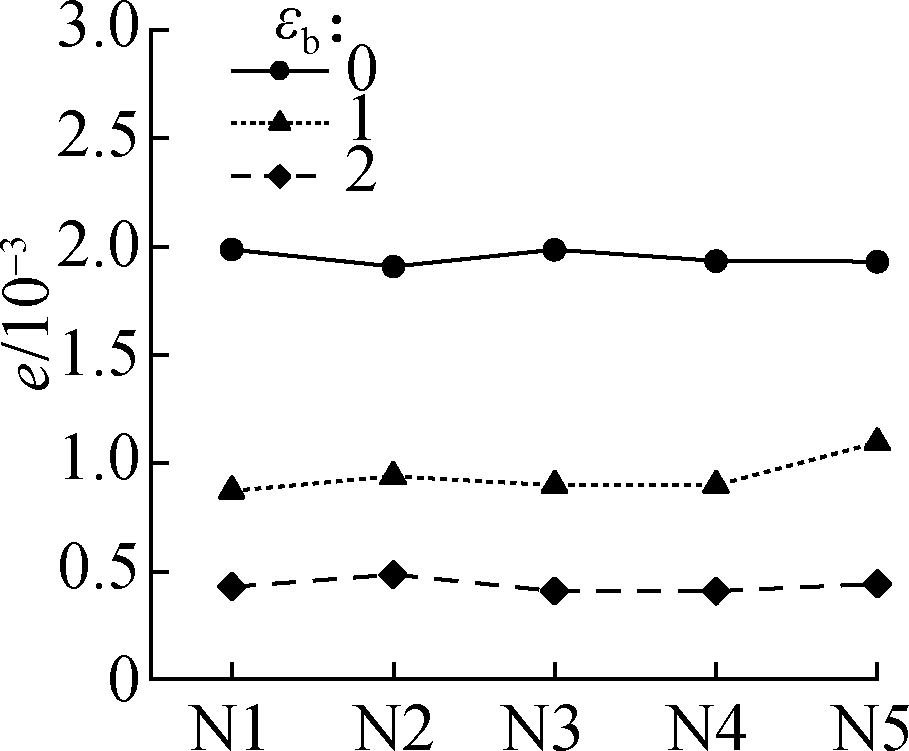
(d)
Fig.5 DWT-based maximum error between original and recovered displacement fields in four typical experiments.(a)Uniform stretching;(b)Three-point bending;(c)Four-point bending;(d)Axial compression
When εb is set to 1, the compression ratios based on the DCT and DWT of all 20 groups of displacement fields are shown in Fig.6.The compression ratio of the DCT-based fields in Figs.6(a),(b), and(c)is less than 10%, and the ratio in Fig.6(d)is between 10% and 15%.All ratios of the DWT-based fields are over 15%, and several of those in Fig.6(a)are greater than 40%.The compression ratio of the DCT-based method is much higher than that of the DWT-based fields.
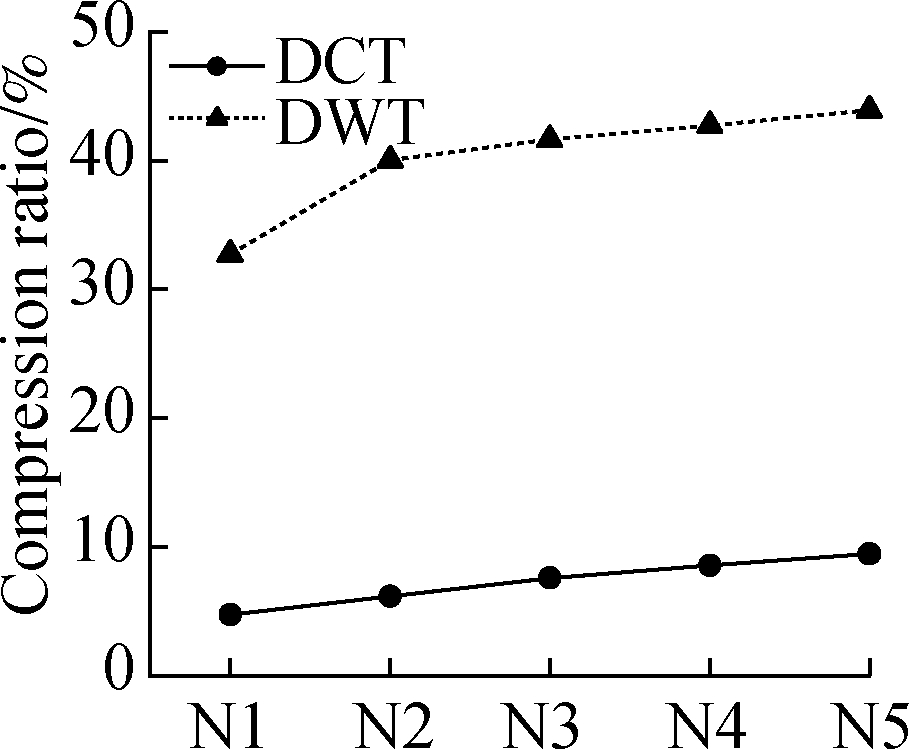
(a)
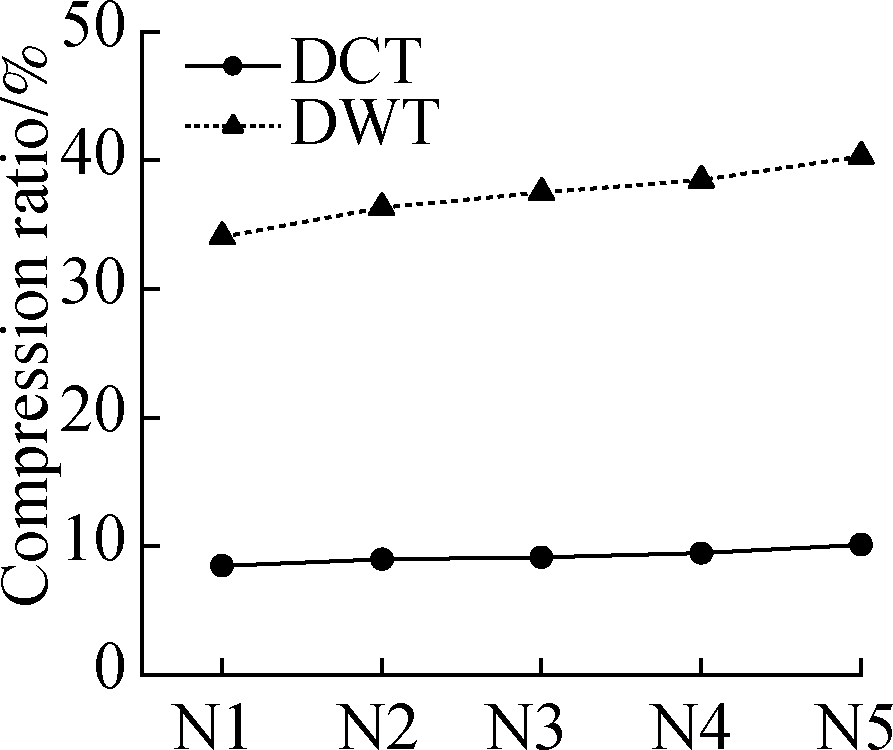
(b)
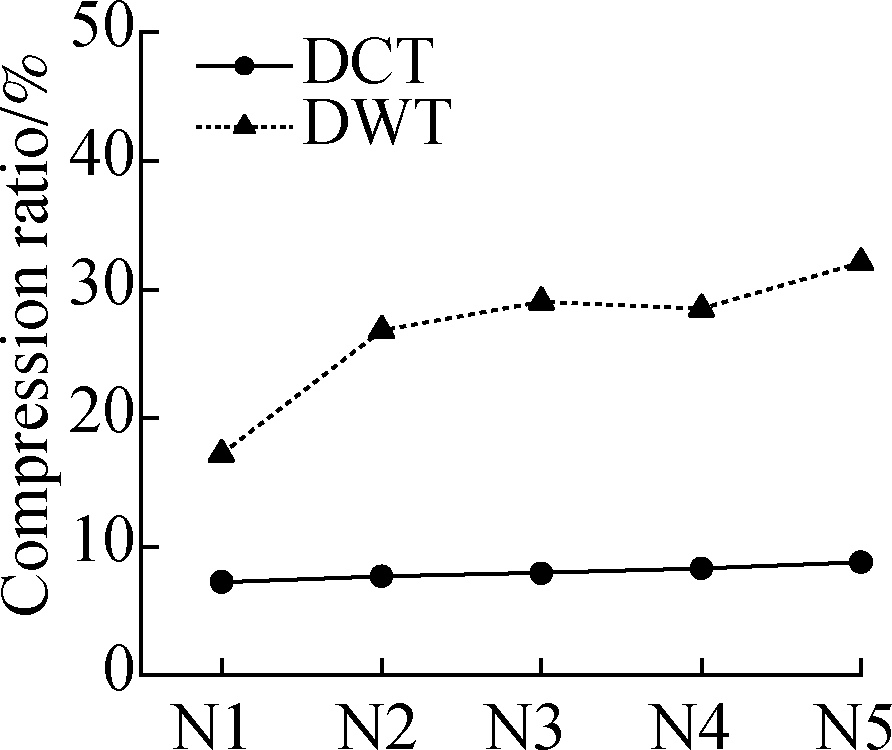
(c)
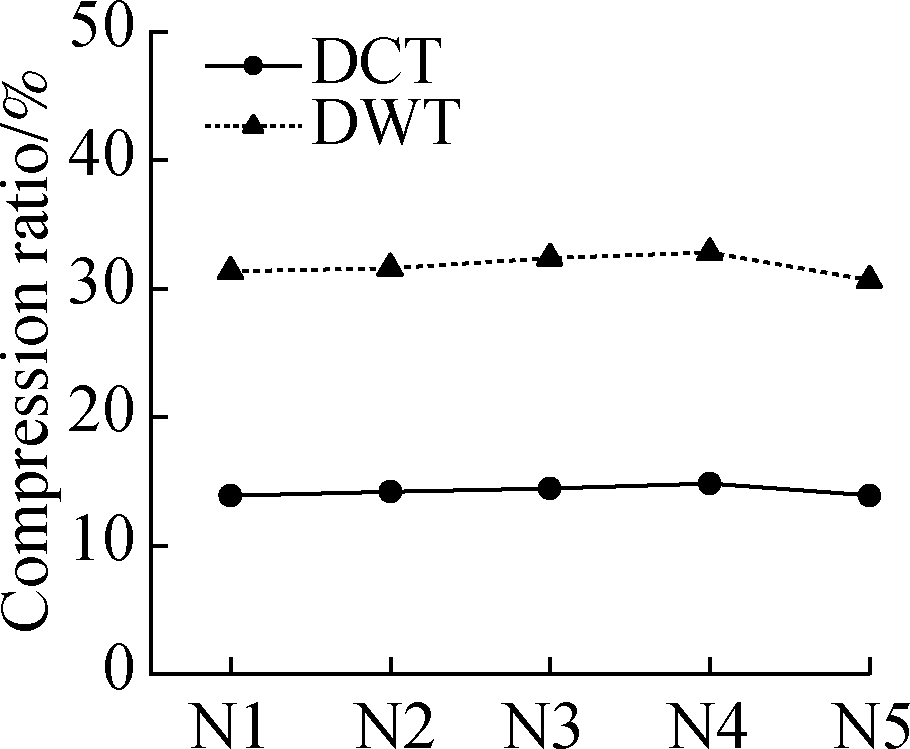
(d)
Fig.6 Compression ratio based on the DCT and DWT in four typical experiments.(a)Uniform stretching;(b)Three-point bending;(c)Four-point bending;(d)Axial compression
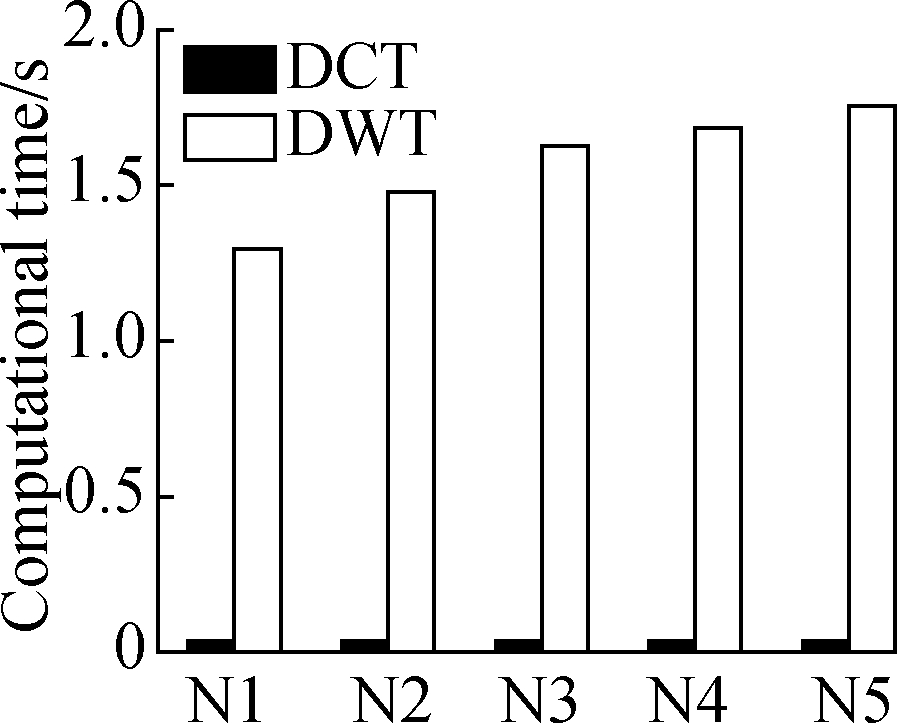
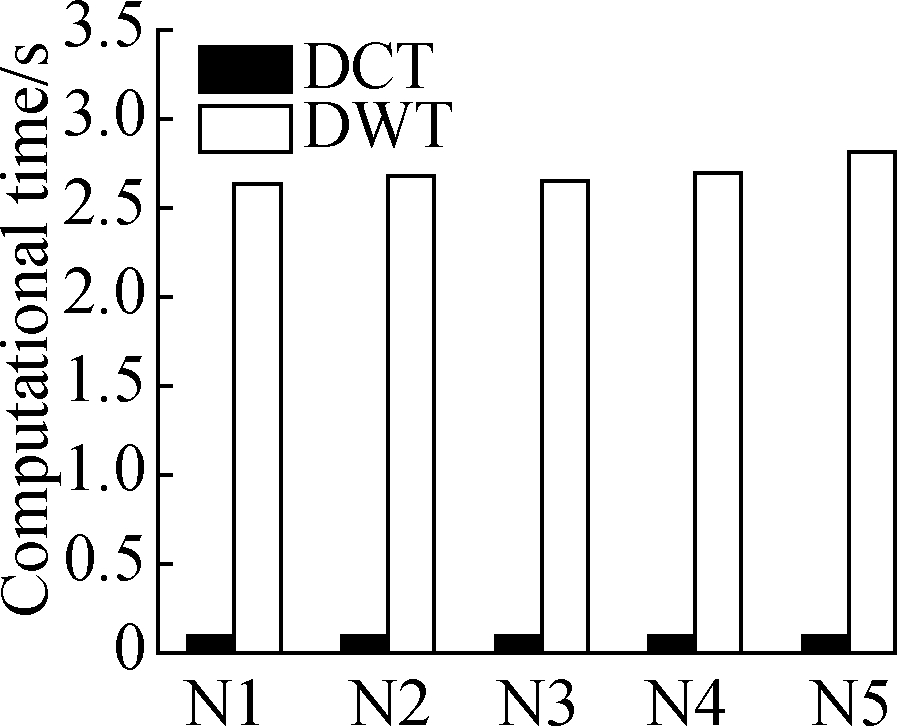
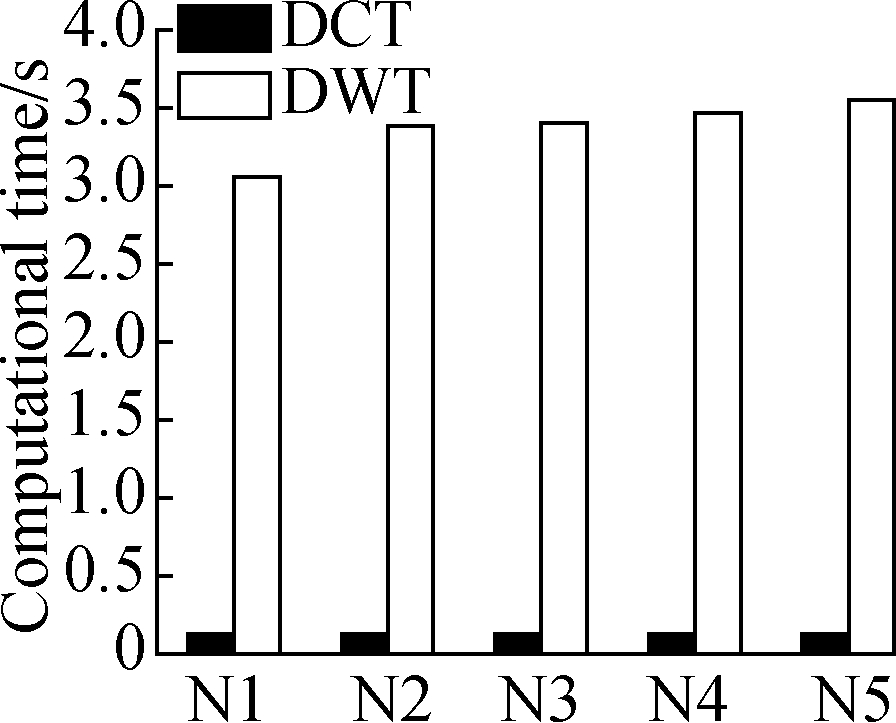
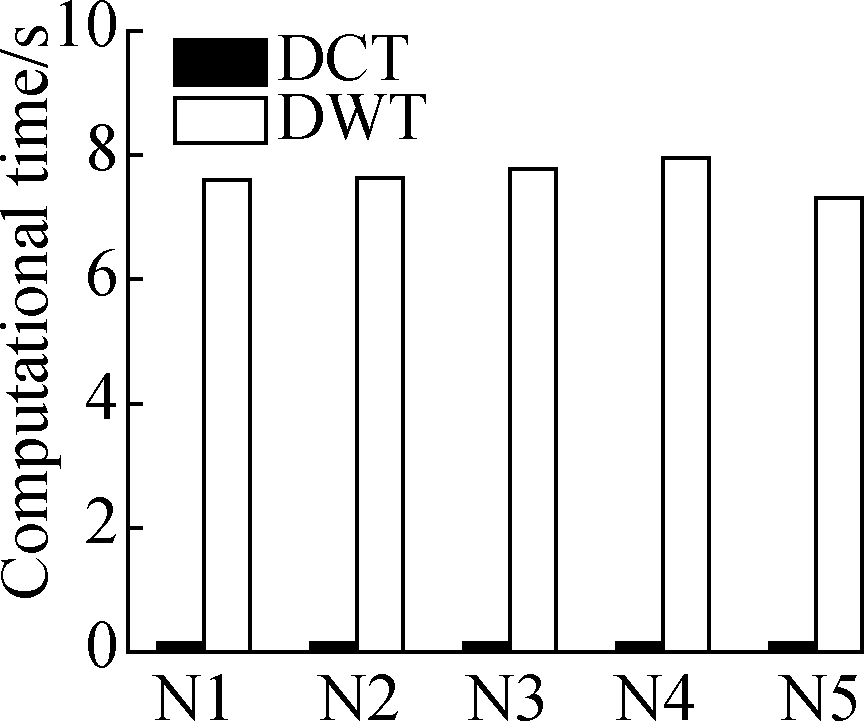
The corresponding computational times of the two proposed algorithms are shown in Figs.7 and 8.In the DCT-based method, the computational time of the sender ranges from 0.037 to 0.157 s.Accordingly, the time of the receiver is 0.032 to 0.143 s.The relevant DCT-based computational speed of the sender and receiver can reach approximately 2.5×105 points/s.However, the DWT-based computational time of the sender ranges from 1.297 to 7.950 s(4 500 to 9 000 points/s), and the time of the receiver is 1.908 to 20.389 s(1 500 to 4 000 points/s), which is greater than 30 times that of the DCT-based method.Compared with the DWT-based method, the DCT-based method shows a much faster computation speed and a remarkable compression performance.
(a)
(b)
(c)
(d)
Fig.7 Computational time of the sender based on the DCT and DWT in four typical experiments.(a)Uniform stretching;(b)Three-point bending;(c)Four-point bending;(d)Axial compression
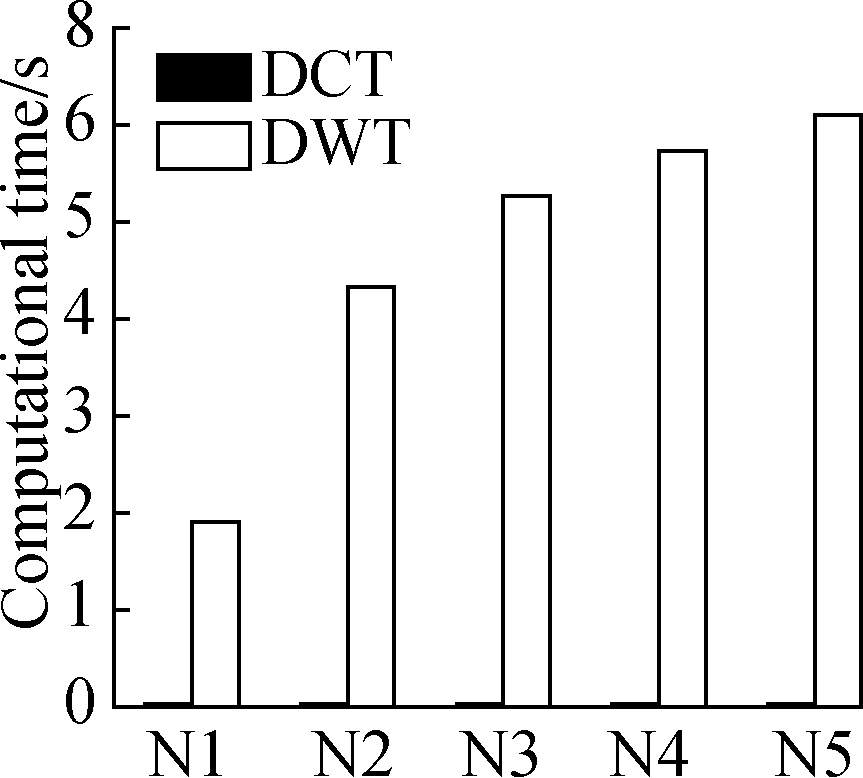
(a)
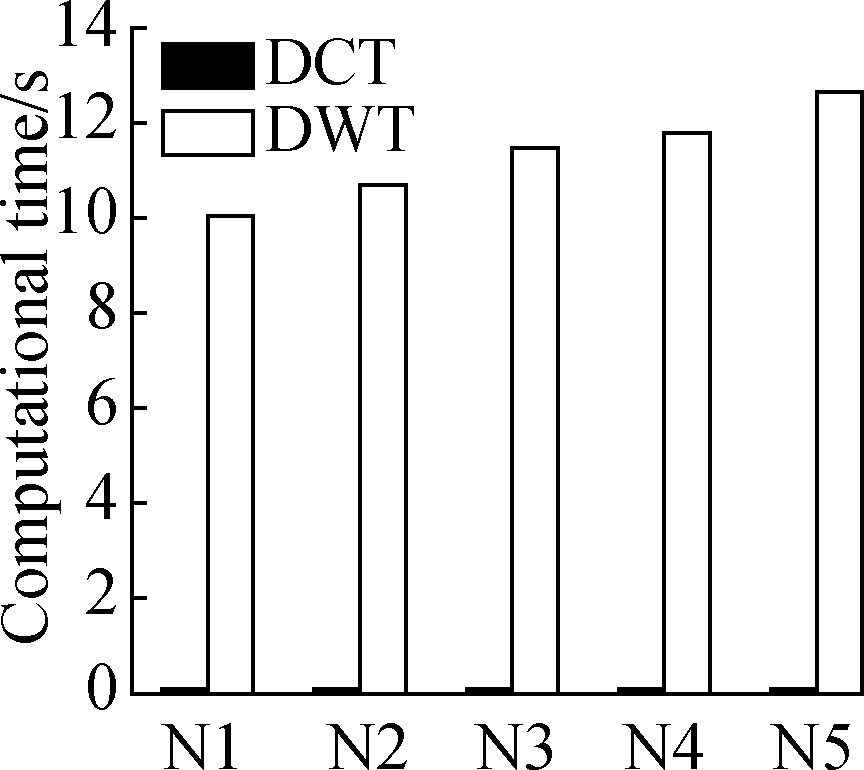
(b)
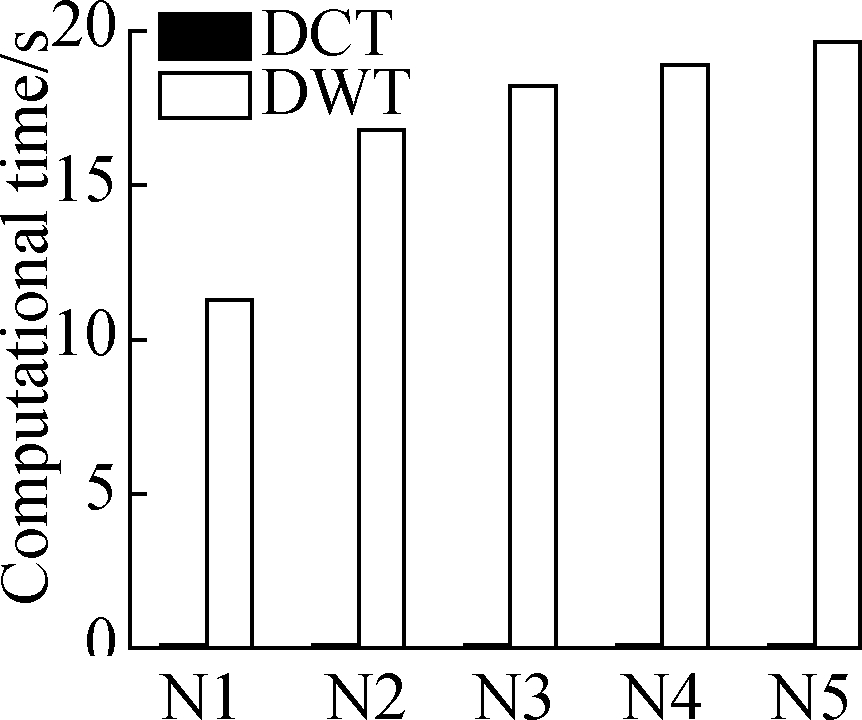
(c)

(d)
Fig.8 Computational time of the receiver based on the DCT and DWT in four typical experiments.(a)Uniform stretching;(b)Three-point bending;(c)Four-point bending;(d)Axial compression
4 Conclusions
1)In this work, with a compression accuracy of 0.001 pixels, two improved compression methods based on the DCT and DWT are proposed to realize the compression encoding of displacement fields for wireless transmission.To verify the effectiveness of the proposed methods, the displacement fields in typical experiments were used to demonstrate the selection of parameter εb, compression ratio, and computational time.The results show that the DCT-based data compression is more effective for the wireless transmission of real-time measured displacement fields.Nonetheless, the DWT-based compression has its own advantages.Functions such as regions of interest, truncation, and progressive transmission of the bit stream can be realized in this framework.This framework is more flexible than the DCT-based method, and more useful functions can be added in the future.
2)The parallel computation can be further conducted in the process of compression encoding for real-time transmission.Significantly, parallel computation has been implemented in numerous practices of data, image, and video compression methods and achieves a considerable improvement in compression effectiveness.Moreover, hardware implementation in compression and wireless transmission should be developed to establish a complete system for remote real-time wireless acquisition of displacement fields.
3)With regard to the improvement of computational speed in real-time DIC in the future, the compression ratio needs to be further reduced for the satisfaction of the transmission stability and bandwidth limit.State-of-the-art codecs, including HEVC and VVC, may be studied to achieve high compression ratios.However, the corresponding computational complexity will increase, which needs more effort on parallel computation and hardware implementation for real-time transmission.
[1] Pan B, Qian K M, Xie H M, et al.Two-dimensional digital image correlation for in-plane displacement and strain measurement: A review[J].Measurement Science and Technology, 2009, 20(6): 1-17.DOI: 10.1088/0957-0233/20/6/062001.
[2] Wan T Y, Qian K M, Seah H S, et al.A flexible heterogeneous real-time digital image correlation system[J].Optics and Lasers in Engineering, 2018, 110: 7-17.DOI: 10.1016/j.optlaseng.2018.05.010.
[3] Shao X X, Dai X J, Chen Z N, et al.Real-time 3D digital image correlation method and its application in human pulse monitoring[J].Applied Optics, 2016, 55(4): 696-704.DOI: 10.1364/ao.55.000696.
[4] Xue Y, Cheng T, Xu X H, et al.High-accuracy and real-time 3D positioning, tracking system for medical imaging applications based on 3D digital image correlation[J].Optics and Lasers in Engineering, 2017, 88: 82-90.DOI: 10.1016/j.optlaseng.2016.07.002.
[5] Wu R, Kong C, Li K, et al.Real-time digital image correlation for dynamic strain measurement[J].Experimental Mechanics, 2016, 56(5): 833-843.DOI: 10.1007/s11340-016-0133-6.
[6] Huang J W, Zhang L Q, Jiang Z Y, et al.Heterogeneous parallel computing accelerated iterative subpixel digital image correlation[J].Science China—Technological Sciences, 2018, 61(1): 74-85.DOI: 10.1007/s11431-017-9168-0.
[7] Isenburg M, Lindstrom P, Snoeyink J.Lossless compression of predicted floating-point geometry[J].Computer-Aided Design, 2005, 37(8): 869-877.DOI: 10.1016/j.cad.2004.09.015.
[8] Lü S, Da F P, Huang Y.A fast and lossy compression algorithm for point-cloud models based on data type conversion[J].Journal of Graphics, 2016, 37(2): 199-205.DOI: 10.11996/JG.j.2095-302X.2016020199.(in Chinese)
[9] Hou Z L, Su X Y, Zhang Q C.Virtual structured-light coding for three-dimensional shape data compression[J].Optics and Lasers in Engineering, 2012, 50(6): 844-849.DOI: 10.1016/j.optlaseng.2012.01.012.
[10] Karpinsky N, Zhang S.Composite phase-shifting algorithm for three-dimensional shape compression[J].Optical Engineering, 2010, 49(6): 1-6.DOI: 10.1117/1.3456632.
[11] Zhang S.Three-dimensional range data compression using computer graphics rendering pipeline[J].Applied Optics, 2012, 51(18): 4058-4064.DOI: 10.1364/ao.51.004058.
[12] Gu X F, Zhang S, Huang P S, et al.Holoimages[C]//Proceedings of the 2006 ACM Symposium on Solid and Physical Modeling.Cardiff, UK, 2006: 129-138.DOI: 10.1145/1128888.1128906.
[13] Bell T, Vlahov B, Allebach J P, et al.Three-dimensional range geometry compression via phase encoding[J].Applied Optics, 2017, 56(33): 9285-9292.DOI: 10.1364/AO.56.009285.
[14] Chen X, Zhang S.Three dimensional range geometry and texture data compression with space-filling curves[J].Optics Express, 2017, 25(21): 26103-26117.DOI: 10.1364/OE.25.026103.
[15] Bell T, Zhang S.Multiwavelength depth encoding method for 3D range geometry compression[J].Applied Optics, 2015, 54(36): 10684-10691.DOI: 10.1364/AO.54.010684.
[16] Wallace G K.The JPEG still picture compression standard[J].Communications of the ACM, 1991, 34(4): 30-44.DOI: 10.1145/103085.103089.
[17] Christopoulos C, Skodras A, Ebrahimi T.The JPEG 2000 still image coding system: An overview[J].IEEE Transactions on Consumer Electronics, 2000, 46(4): 1103-1127.DOI: 10.1109/30.920468.
[18] Taubman D S, Marcellin M W.JPEG 2000: Image compression fundamentals, standards and practice[M].Amsterdam, the Netherlands: Kluwer Academic Publishers, 2001: 87-142.DOI: 10.1007/978-1-4615-0799-4.
[19] Rabbani M, Joshi R.An overview of the JPEG 2000 still image compression standard[J].Signal Processing: Image Communication, 2002, 17(1): 3-48.DOI: 10.1016/s0923-5965(01)00024-8.
[20] Ahmed N, Natarajan T, Rao K R.Discrete cosine transform[J].IEEE Transactions on Computers, 1974, 23(1): 90-93.DOI: 10.1109/T-C.1974.223784.
[21] Chen W H, Smith C H, Fralick S C.A fast computational algorithm for the discrete cosine transform[J].IEEE Transactions on Communications, 1977, 25(9): 1004-1009.DOI: 10.1109/TCOM.1977.1093941.
[22] Lam E Y, Goodman J W.A mathematical analysis of the DCT coefficient distributions for images[J].IEEE Transactions on Image Processing, 2000, 9(10): 1661-1666.DOI: 10.1109/83.869177.
[23] Daubechies I, Sweldens W.Factoring wavelet transforms into lifting steps[J].Journal of Fourier Analysis and Applications, 1998, 4(3): 247-269.DOI: 10.1007/bf02476026.
[24] Rioul O, Vetterli M.Wavelets and signal processing[J].IEEE Signal Processing Magazine, 1991, 8(4): 14-38.DOI: 10.1109/79.91217.
[25] Shensa M J.The discrete wavelet transform: Wedding the a trous and Mallat algorithms[J].IEEE Transactions on Signal Processing, 1992, 40(10): 2464-2482.DOI: 10.1109/78.157290.
[26] Sweldens W.The lifting scheme: A custom-design construction of biorthogonal wavelets[J].Applied and Computational Harmonic Analysis, 1996, 3(2): 186-200.DOI: 10.1006/acha.1996.0015.
[27] Sullivan G J, Ohm J-R, Han W-J, et al.Overview of the high efficiency video coding(HEVC)standard[J].IEEE Transactions on Circuits and Systems for Video Technology, 2012, 22(12): 1649-1668.DOI: 10.1109/TCSVT.2012.2221191.
[28] Xu X Z, Liu S.Recent advances in video coding beyond the HEVC standard[J].APSIPA Transactions on Signal and Information Processing, 2019, 8: 1-10.DOI: 10.1017/atsip.2019.11.
[29] Yang J, Bhattacharya K.Combining image compression with digital image correlation[J].Experimental Mechanics, 2019, 59(5): 629-642.DOI: 10.1007/s11340-018-00459-y.
[30] Skodras A, Christopoulos C, Ebrahimi T.The JPEG 2000 still image compression standard[J].IEEE Signal Processing Magazine, 2001, 18(5): 36-58.DOI: 10.1109/79.952804.