China is a country with the largest population living in a plateau region in the world.Due to the unique natural conditions and historical development, the highway system plays an important role in transportation in plateau regions.In the past decade, China’s western plateau region has experienced a rapid economic development and urbanization process, and the highway transport capacity has also been improved significantly.
The plateau region in China is characterized by high altitudes and large areas.The famous Qinghai-Tibet Plateau occupies 24% of the country’s total land area with an average altitude of more than 4 000 m.The oxygen content at high altitudes is different from that in plain areas.Recent studies show that the air’s oxygen content decreases by 30.18 g/m3 with every 1 km increase in altitude.In a plateau area with an elevation of more than 4 000 m, the oxygen partial pressure is only approximately 60% of that on a plain area[1].The special geographical conditions and historical development make highway networks very complicated, which forms a unique driver-vehicle-road-environment relationship, with evident time-varying, space-variant, and temporal coupling characteristics in plateau areas[2].Highway design is usually based on the selected design speed to determine appropriate alignments and ensure vehicle safety in China.However, even with a fixed design speed, driving is a dynamic process that is affected by driver characteristics, road geometry, vehicle performance, and roadway environment.The operating speed can reflect the significant influence of these characteristics on the actual driving.Accordingly, a design speed method has been adopted for highway design in China, extended by the operating speed methods for highway safety evaluation[3-4].Meanwhile, several countries have formed a complete highway design system based on the operating speed method.
With reference to observations and investigations and mathematical and statistical regression analyses of actual vehicle speeds on typical highways, an operating speed prediction model has been established suitable for the roadway characteristics in China, which has been included in the specification[4].The prediction model relies on initial research results[5], which are conducted based on the original measured data of the Tongchuan-Huangling Highway in Shaanxi, Yuxi-Yuanjiang Highway in Yunnan, Taiyuan-Jiuguan Highway, Jincheng-Yangcheng Highway, and Jincheng-Jiaozuo Highway in Shanxi.However, these roads are located at low altitudes, and the average altitude of China’s plateau regions is above 4 000 m.
A low-pressure and low-oxygen environment has a negative impact on driving performance and vehicle mechanical performance[6].The acceleration time and acceleration distance of a vehicle become longer, while the maximum vehicle speed and maximum gradeability decrease.For drivers, as the oxygen content decreases, various cognitive abilities, including vision, hearing, memory, thinking, and attention, will decrease to varying degrees[7].The influence of a plateau environment on the operating speed and whether the operating speed prediction model used in the specification applies to the plateau region is a topic that is unstudied but worthy of investigation.
1 Literature Review
Since 1950, more research efforts have been gradually addressed on the prediction model of the operating speed by establishing the correlation between the operating speed and road geometric parameters.Since then, many operating speed prediction models considering various factors have been established on this basis[8].
In China,the operating speed prediction model is obtained based on the existing research abroad[9-10], along with many experimental data and regression analyses of the operating speed of different models on various sections.Focusing on relevant research results, the speed model of low-grade highways is optimized and improved in the Specifications for Highway Safety Audit published in 2015[4].
In the current operating speed calculation method, a highway is generally divided into a straight road section, longitudinal road section, curved segment, and combined road section with a curved road slope depending on the method of unit partitioning.To overcome the centrifugal force in the curved segment, the vehicle will reduce the speed with the increase in curvature.Moreover, the smaller the radius, the larger the vehicle speed change.
When the speed is reduced to a certain value, which satisfies drivers’ comfort, the vehicle will keep moving at a constant speed.Then, the vehicle will accelerate at the end of the curve.The speed is sometimes even higher than the curve segment’s entrance speed with a straight back section.When the back section is a small radius curve that constitutes the ogee section, the vehicles will continue to slow down.Meanwhile, the sight distance on the plan curve has a particular influence on the vehicle speed.Consequently, the drivers become more nervous and reduce the operating speed when faced with a limited sight distance.
Moreover, related research shows that the operating speed on the curved segment is also influenced by the deflection angle, length of the front straight segment, pavement condition, and other factors(e.g., shoulder width).The operating speed model used in the specification takes the entrance speed, curve radius, and curve radius after the curve segment as influencing factors[11].
However,there are few studies on operating speed prediction models for roadways in plateau areas, where the driving and vehicle performance is greatly affected by the low-pressure and low-oxygen environment.
2 Methodology
2.1 Principal stepwise regression method
The principal stepwise regression method is often used to provide an initial screening of candidate variables when a large group of variables exists.The partial correlation coefficient is used to determine the order in which variables are selected into the equation.The stepwise regression method is simple, and the resulting regression equation has few variables and retains the most significant important variables.In practice, this method has also been proven to be effective and has high prediction accuracy.In addition, considering that economic variables may have multicollinearity, stepwise regression can correct multicollinearity to a certain extent.Therefore, the stepwise regression method was applied in this study.
2.2 Standard coefficient
Standardized regression coefficients are coefficients that will be obtained if you standardized each independent and dependent variable.Here standardizing is defined as subtracting the mean and dividing it by the standard deviation of a variable.A regression analysis of these standardized variables will yield standardized coefficients.When there are vastly different units involved for the variables, this method makes comparisons between the variables.The formula for the standardized regression coefficient is
(1)
where sy and sxj are the standard deviations for the dependent variable and the corresponding j-th independent variable.
2.3 R-squared increment
The R-square will be changed if the status of the variable is changed.If the variable is currently in the model, then the R-squared value will decrease if the variable is removed.If the variable is currently out of the model, then the overall R-squared value will increase if the variable is added.Large values here indicate critical independent variables.
3 Data Preparation
3.1 Study sites
In Tibet, due to the complex terrain and geological conditions in the plateau region, a small number of intercity expressways and low-grade two-lane highways form a road transportation network.
By 2020, the mileage of two-lane highways accounted for 98% of the total mileage of highways opened to traffic.The main highways in Tibet are National Highway 318, National Highway 109, and National Highway 219.Among them, National Highway 109 and National Highway 318 intersect as “one vertical and one horizontal road” in Lhasa.By 2019, Tibet has five high-grade highways, three of which are under construction.Among the five highways, the Lalin Expressway and airport expressway have been completed.
Because of good representation, National Highway 318 and Lalin Expressway were selected as test roads in this study.We believe that studying the operating speeds in National Highway 318 and the Lalin Expressway will play an important role in highway construction and traffic safety in plateau regions.
3.1.1 National Highway 318
National Highway 318 starts from Shanghai in the east and ends at Xigaze in Tibet in the west, covering a total distance of 5 476 km.National Highway 318 promotes the flow of resources from the east to the west.It supports the development of various industries in counties and cities along the route and is of considerable significance to the economic development of Tibet.The section selected for this experiment is a two-way two-lane road near Lhasa, with a design speed of 60 km/h and a width of 10 m.
3.1.2 Lalin Expressway
The Lalin Expressway connects Lhasa, the capital of Tibet, and Linzhi, a prefecture-level city.It is an intercity two-way four-lane highway with a total length of 410 km, a design speed of 100 km/h, and a width of 24.5 m.Lalin Expressway has not been officially included in the highway network, and a large number of trucks are currently prohibited.
Based on the Technical Standard of Highway Engineering, the vehicles involved are divided into five types: small passenger cars, large passenger cars, articulated trucks, heavy trucks, and articulated trains[11].Combined with the main objectives of this study, the above-mentioned vehicle types were mainly divided into cars and other large vehicles.In addition, because large vehicles were restricted in the Lalin Expressway, only small passenger cars were observed.
3.2 Data collection
In this research, Bushnell’s handheld radar velocimeter(model: 10-1911CN)was used to observe the operating speed.A slope ruler was used to measure the slope of the longitudinal slope, and a stopwatch was used to measure headway.The characteristic point section observation method was adopted to measure the vehicle’s operating speed at the start, middle, and end points of the curve with the handheld radar velocimeter.The vehicle type, color, and license plate number of the vehicle were simultaneously recorded to facilitate the comparison method of the license plate number in the later period and ensure continuity.
When the vehicle was far away, the observer used a handheld speedometer to measure the speed from a hidden position and behind to prevent the driver from taking deceleration measures or other operations after noticing the experimenter’s measurement of the speed.
3.3 Data process
Based on the sample size requirement, 250 vehicle speed data were measured in each experimental section.Considering the impact of traffic flow on the vehicle speed, every five data were grouped into one group in chronological order.
Some improper driving behaviors(e.g., driver’s driving habits and phone calls)caused some vehicles to speed up.In this case, the vehicle whose observed speed exceeded the designed speed by 20% would be considered an abnormal situation and eliminated.
In addition, the drawing of box plots does not impose any restrictive requirements on the data and judge abnormal values based on quartiles and interquartile ranges, so abnormal values will not have a significant impact on the judgment standard.This experiment also used box plots to eliminate outliers twice.When an abnormal value occurs at one of the feature points, the data in the data group covering the feature point also need to be eliminated.As shown in Tab.1, the data was processed according to the above principles.
Tab.1 Data after eliminating outliers
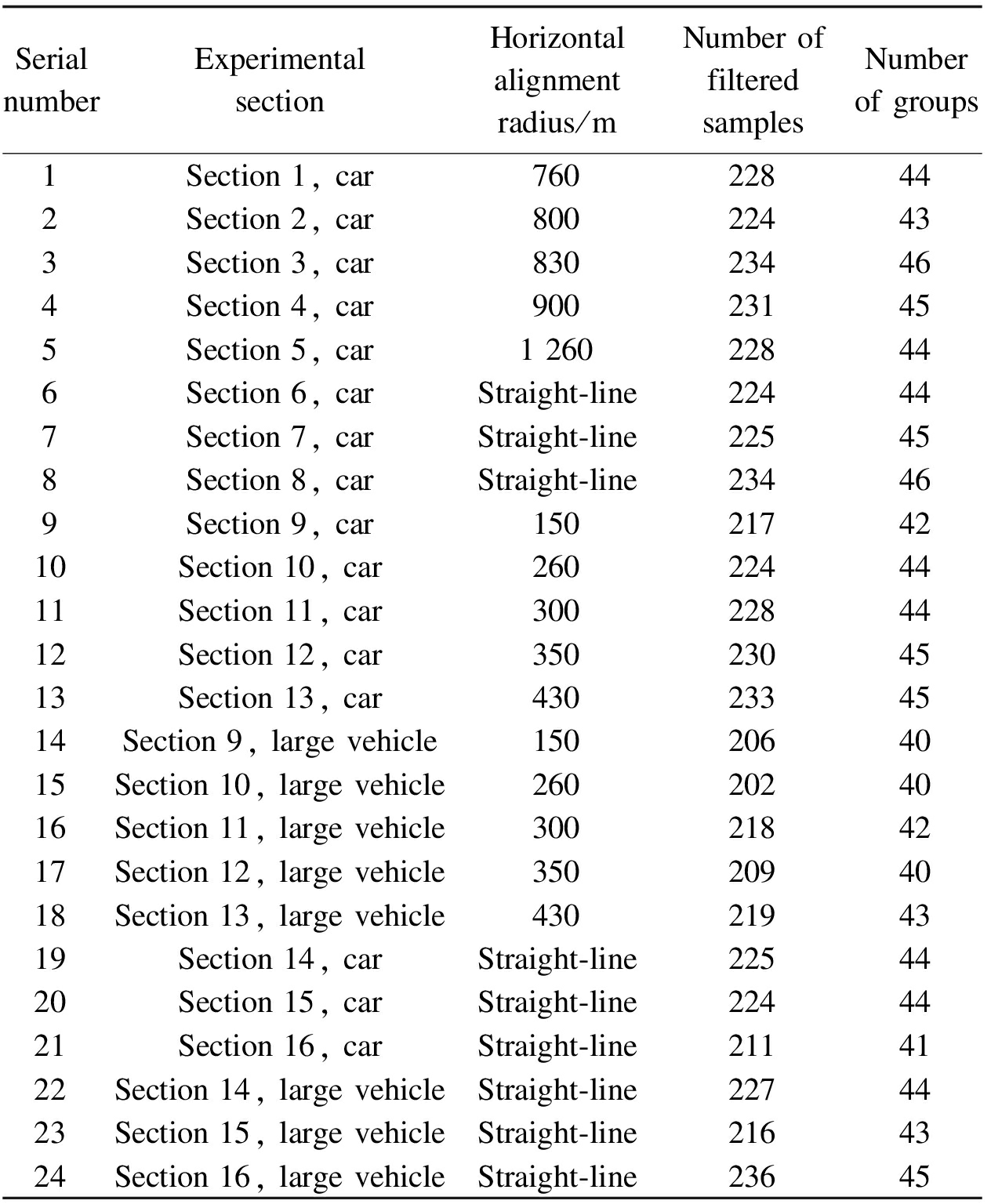
SerialnumberExperimentalsectionHorizontalalignmentradius/mNumberoffilteredsamplesNumberofgroups1Section1,car760228442Section2,car800224433Section3,car830234464Section4,car900231455Section5,car1260228446Section6,carStraight-line224447Section7,carStraight-line225458Section8,carStraight-line234469Section9,car1502174210Section10,car2602244411Section11,car3002284412Section12,car3502304513Section13,car4302334514Section9,largevehicle1502064015Section10,largevehicle2602024016Section11,largevehicle3002184217Section12,largevehicle3502094018Section13,largevehicle4302194319Section14,carStraight-line2254420Section15,carStraight-line2244421Section16,carStraight-line2114122Section14,largevehicleStraight-line2274423Section15,largevehicleStraight-line2164324Section16,largevehicleStraight-line23645
Because the normal distribution of data is required for t-test and correlation tests, it is necessary to perform a normality test on the original data.The single sample size of the experiment is 200 to 250, which is less than 2 000, so the Kolmogorov-Smirnov test was adopted to measure the normality of the speed in the sample.
Tab.2 shows the descriptive statistics of the driving speed of large vehicles at the end of the National Highway 318 road curve.This set of data was applied as an example for normality testing.After eliminating outliers for the normality test result table, the result complies with the normal distribution, with a significance higher than 0.05.In the distribution histogram and standard Q-Q plot, the releasing point is close to a straight line, which means that the speed data obey the normal distribution.Other data in the paper also obeyed the normal distribution based on the results of the normality tests.
Tab.2 Descriptive statistics example
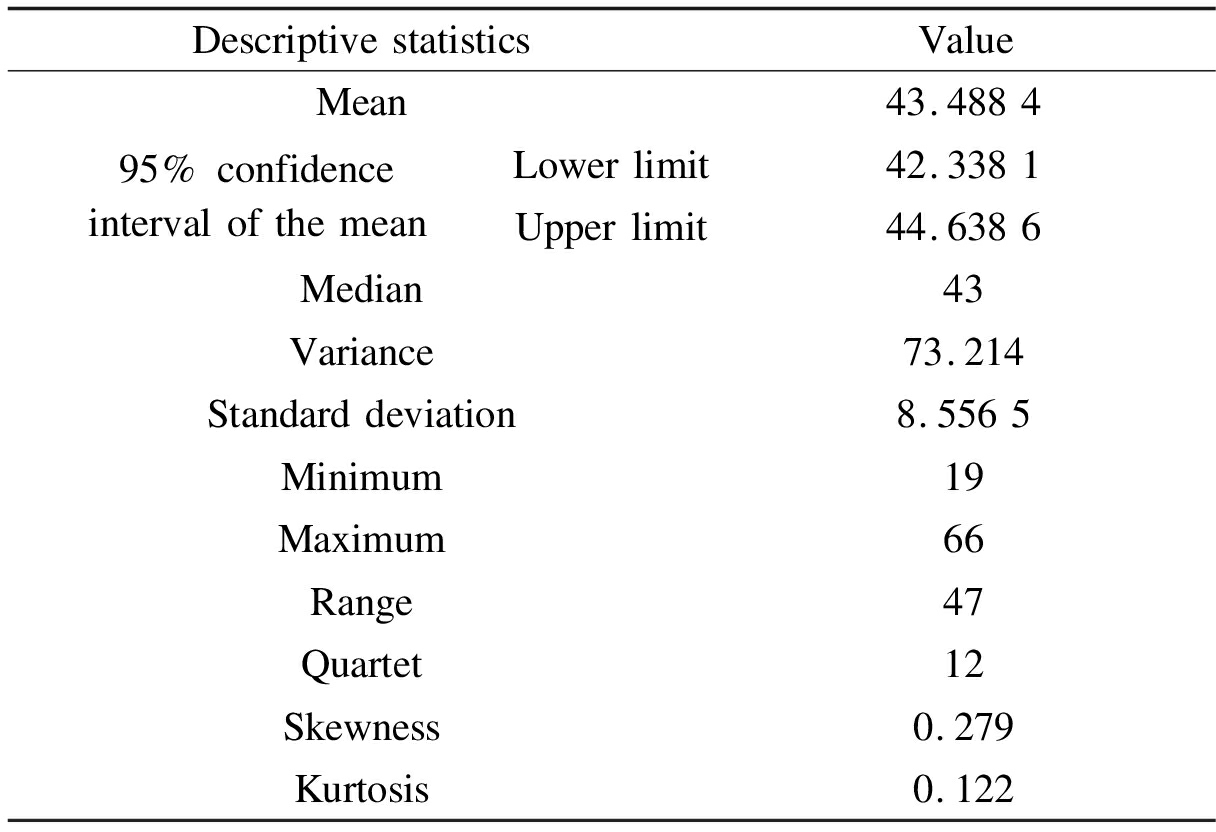
DescriptivestatisticsValueMean43.488495%confidenceintervalofthemeanLowerlimit42.3381Upperlimit44.6386Median43Variance73.214Standarddeviation8.5565Minimum19Maximum66Range47Quartet12Skewness0.279Kurtosis0.122
4 Analysis and Results
First, the speed reduction before the flat curve was analyzed based on previous models.Then, the stepwise regression method was adopted to select the factors that significantly influence the operating speed.Finally, the operating speed operation models were proposed on the Lalin Expressway and National Highway 318 with the selection of the most satisfactory equation.
4.1 Speed reduction before the flat curve
When calculating the operating speed prediction value of the horizontal curve section, the connection between the horizontal curve section itself and the front and rear sections is often ignored, and the influence range of the horizontal curve section on the operating speed is limited to the horizontal curve section.When a straight-line section is connected to a flat curve with a small radius, the driver will often take slight deceleration measures in advance on the straight section.Therefore, the flat curve also has a certain impact on the operating speed of the road section at the front end of the curve.
To study the speed reduction value of the starting point of the horizontal curve, a sample test was made for the vehicle speed at the starting point of the horizontal curve on National Highway 318 and the Lalin Expressway and the vehicle speed on the straight line before the curve.
For the Lalin Expressway, the car did not decelerate in a statistically significant manner before entering the flat curve section.However, for National Highway 318, large and small cars have a clear early deceleration behavior before entering the flat curve section with a small radius.
The results show that for cars, the probability P-value of the speed difference between the starting point of the horizontal curve of the test section(a horizontal curve section with a radius of 150 m)and the operating speed of the straight-line section ahead is less than 0.10, and there is a significant difference within the 90% confidence interval.For large vehicles, the probability P-value of the speed difference between the starting point of the horizontal curve of the test sections(flat curve section with radii of 150 and 260 m, respectively)and the operating speed of the straight-line section ahead is less than 0.10, which has a significant difference within the 90% confidence interval.
Accordingly, the model obtained through the regression analysis of the speed reduction value of the starting point of the flat curve section is shown in Tab.3.
Tab.3 Speed reduction value at the starting point

VehicletypeSpeedreductionmodelR2CarΔv=0.203v0-10.826lnR20.788LargevehicleΔv=0.140v0-10.897lnR20.827
Note: v0 is the operating speed of the vehicle 100 m in front of the starting point of the horizontal curve.
4.2 Corresponding factors
According to the analysis of the speed influencing factors on the plan curve, the operating speed at the middle of the curve is related to the radius, curve length, and operating speed of the start and end.Moreover, the operating speed at the end of the curve is related to the alignment condition after the curve segment.The basic form of the speed prediction model of a curved segment used in the previous research can be summarized as follows:
(2)
(3)
where vin,vm,vout denote the operating speed of the entrance, middle, and end of the curve, respectively; R1 and R2 are the radius of the curve and the curve behind; L and ω are the straight-line length and angle of the plane curve, respectively.
4.3 Operating speed model on the Lalin Expressway
The main stepwise regression analysis was performed on the operating speed at the midpoint of the curve and the end of the curve.The operating speed of the midpoint of the curve significantly correlated with vin and ![]() with P-values less than 0.05.Meanwhile, the end of the curve’s operating speed significantly correlated with vin,
with P-values less than 0.05.Meanwhile, the end of the curve’s operating speed significantly correlated with vin, ![]() with P-values less than 0.05.
with P-values less than 0.05.
Based on the results of the regression, the operating speed regression equations at the midpoint and end point of the plane curve can be obtained:
(4)
(5)
The regression model is suitable for sections with a radius less than 1 260 m due to the limitation of the sample.
4.4 Operating speed model on National Highway 318
Similarly, a prediction model for the operating speed of National Highway 318 was established.While calculating the speed prediction of the curved segment, the cohesion of sections, before or after the curved segment, is often overlooked.The influence on the operating speed is always limited to the range of the curved segment.However, when the radius of the plan curve in front is small, drivers tend to slow down slightly on the tangent section in advance.Therefore, the plan curve also has a positive influence on the section’s operating speed before the curve.In this study, the curved segment models were divided into two cases: 1)followed by a tangent section and 2)followed by a curve section.Due to the limited design data, considering the accuracy of parameter acquisition, only the radius of the curve was used as an influencing factor, and the basic regression model proposed is presented in Tab.4.
Tab.4 Basic form of the operating speed of the curved segment

MiddleofthecurveEndofthecurvevm=mvin+nlnR1+ovout=mvm+nlnR1+pvm=mvin+nR1+ovout=mvm+nR1+pvm=mvin+nR1+oR21+pvout=mvm+n1R1+o1R21+pvm=mvin+nR1+ovout=mvm+nR1+p
Note: m, n, o, and p denote the coefficients, respectively.
5 Prediction
The residual is the difference between the observed value and fitted value from the regression equation, which cannot be explained by the regression equation.Therefore, the residual error can be regarded as the observation error if the model is correct.
During the regression analysis, some assumptions were made on the error, and these errors were independent of each other with the zero mean value and fixed variance.To obtain the confidence interval and conduct hypothesis testing, the error was also assumed to be normally distributed.
A normal test was performed on the error between the experimental data and the fitted value to judge the validity of the regression model.S-W normality tests were used for each speed regression model, and the Sig-value of each model was greater than 0.05, which means that the difference between the observed value and the fitting value of the regression model followed the normal distribution.The results showed that the residual value conforms to the assumption.
The average relative errors are 4.57% and 6.39% at the midpoint and end point of the curve, respectively.With the standard prediction model, the average relative errors of the midpoint and end point of the curve are 5.67% and 9.01%, respectively.Hence, the prediction accuracy of the model in this paper is higher than that of the standard model.In addition, the existing models do not perform well in predicting the running speed at the end of the curve, and the predicted speed is mostly higher than the actual speed, which also confirms the influence of the plateau environment on the vehicle and driver performance[12].Moreover, the changes in vehicle dynamics to the driving speed are mainly reflected in the acceleration phase after the midpoint of the planning curve.
6 Discussions and Future Directions
By calculating the relative error between the calculated value and the measured value of the operating speed, the prediction model proposed in this paper showed better performance than the prediction model in the specification.In a plateau environment, the impact of the vehicle dynamic performance changes on the operating speed on flat-curve sections is mainly reflected in the acceleration phase after the midpoint of the flat curve.This paper summarizes relevant research results and analyzes the impact of environmental conditions on the operating speed in plateau regions.Considering the characteristics of roads in Tibet, the representative National Highway 318 and Lalin Expressway were selected as test sites.
By collecting the measured field data, the outliers in the sample were removed according to the interquartile distance method, and then the normality of the remaining data samples was tested.
Based on the filtered data, the drivers’ active deceleration behavior in front of the horizontal curve was studied.Sampling tests were performed to compare the speed at the beginning of the horizontal curve of the National Highway 318 and Lalin Expressway and the previous straight line.It is inferred that the vehicles have clear early deceleration behavior before entering a flat curve section with a small radius.Moreover, a plateau speed reduction model was obtained(see Tab.3).
Considering the nonlinear regression and stepwise regression methods, the operating speed model of typical highways in plateau regions was established, as shown in Tab.5.
Tab.5 Summary of the operating speed models

ExpresswayVehicletypePositionOperatingspeedmodelLalinExpressway,designspeed100km/h,two-wayfour-lanestructure,roadwidth24.5mCarMidpointvm=8.844+0.935vin-2.961R21Endvout=36.505+0.815vm-12.090R21-6.503R22NationalHighway318,designspeed60km/h,two-waytwo-lane,roadwidth10mCarMidpointvm=0.794vin-2561.547R1+19.608CarEnd(connectingstraightline)vout=0.711vm+632.765R1+22.605CarEnd(connectingcurve)vout=0.508vm+632.765R1+10.826lnR2+22.605LargevehicleMidpointvm=0.845vin-521.994R1+6.918LargevehicleEnd(connectingstraightline)vout=0.977vm-814.915R1+8.717LargevehicleEnd(connectingcurve)vout=0.837vm-814.915R1+10.897lnR2-10.00
The research results of this study have filled the knowledge gap in this field to a certain extent.We have outlined the following possible future directions:
1)Because of the limitation of the experimental conditions, we can only build a speed prediction model of specific feature points.Hence, it is suggested to refine the operating speed model with GPS continuous velocity measurement in future to predict the characteristics of the speed change throughout the entire length of the horizontal curve.
2)The combination of horizontal and vertical curves is an essential consideration in roadway design.However, the sections fitting the condition in this combination are rare in Tibet.We can focus on this aspect in the future.
3)Due to the limitation of experimental conditions, the alignment parameters of the selected experimental part are not diversified enough.Therefore, it is essential to expand the sample data to improve the effectiveness of the model.Moreover, more experiments should be conducted at higher elevations to determine the accuracy of the proposed model.
7 Conclusions
1)Based on Bushnell’s handheld radar speedometer 10-1911CN, the speed characteristics at the starting, mid, and end points of a plane curve were observed on Lalin Highway and China National Highway 318.
2)The stepwise regression method was proposed to determine the significant parameters and examine the prediction models of the operating speed of cars and large vehicles for the two highways.
3)Reserved test group data were utilized to prove the validity and practicality of the proposed models.Compared with traditional methods, the established models can produce more accurate prediction results and deeply examine the nonlinear relationships between parameters and the predicted operating speed.
[1] Zhou G M, Liu R L, Xu X, et al.Effects of plateau environment on power performance of vehicles and measures to improve power performance in plateau[J].Equipment Environmental Engineering, 2014, 11(3): 45-51, 75.DOI: 10.7643/issn.1672-9242.2014.03.010.(in Chinese)
[2] Hu L W, Xue G, Li L Y, et al.Analysis of coupling of highway traffic risks in geological and meteorological environment of plateau regions[J].China Journal of Highway and Transport, 2018, 31(1): 110-119.DOI:10.19721/j.cnki.1001-7372.2018.01.013.(in Chinese)
[3] Zhu Z D.Research on operating speed of two-lane highways based on environment[D].Beijing: Beijing University of Technology, 2011.(in Chinese)
[4] Ministry of Transport of People’s Republic of China.Specifications for highway safety audit: JTG B05—2015[S].Beijing: People’s Communications Publishing House, 2016.(in Chinese)
[5] Zhang Z L.Research of two-lane highway alignment design method based on the operating speed[D].Chongqing: Chongqing Jiaotong University, 2010.(in Chinese)
[6] Xu J L, Lei T, Jia X L, et al.Maximal gradient of highway in high-altitude area based on typical truck’s climbing performance[J].Journal of Tongji University(Natural Science), 2017, 45(6): 854-860.DOI: 10.11908/j.issn.0253-374x.2017.06.010.(in Chinese)
[7] Yu L X.Combustion and emission characteristics of heavy diesel engines at different altitudes[D].Beijing: Beijing Institute of Technology, 2014.(in Chinese)
[8] Raichle M E.Food for thought: Altitude versus normal brain function[M].New York: Springer US, 1999.
[9] Shallam R D K, Ahmed M A.Operating speed models on horizontal curves for two-lane highways[J].Transportation Research Procedia, 2016, 17: 445-451.DOI:10.1016/j.trpro.2016.11.086.
[10] Al-Masaeid H R, Hamed M, Aboul-Ela M, et al.Consistency of horizontal alignment for different vehicle classes[J].Transportation Research Record, 1995, 1500: 178-183.
[11] Ministry of Transport of People’s Republic of China.Technical standard of highway engineering: JTG/B01—2014[S].Beijing: People’s Communications Publishing House,2014.(in Chinese)
[12] Duan Z H, Xu J L, Ru H, et al.Classification of driving fatigue in high-altitude areas[J].Sustainability, 2019, 11(3): 817.DOI:10.3390/su11030817.