As a critical component of intelligent transportationsystems, traffic flow prediction plays a vital role in providing traffic state predictions and implementing control measures for traffic management departments.At present, there are mainly two categories of traffic flow prediction methods: model-based and data-driven methods.
Dynamic traffic simulation models can be the typical example of the former, such as DynaMIT-R and Visum-online.However, the model algorithm and software application in this method are very complex, and real-time simulations require substantial computing resources.The latter method is mainly based on historical data and uses statistical analysis and machine learning to make predictions.It has the advantages of a simple algorithm, efficient online operation, and accurate prediction for small-scale road networks.Therefore, this method has also become a research focus in recent years.
Traffic flow prediction methods driven by data can be divided into three categories: 1)linear prediction method based on time series theory and Kalman filter theory, such as the autoregressive integrated moving average(ARIMA)forecasting model[1], and Kalman filter forecasting model [2]; 2)nonlinear prediction method based on chaos theory, such as chaos of traffic system[3] and multi-step prediction algorithm of traffic flow based on chaos theory[4]; 3)intelligent prediction method based on machine learning, such as support vector regression(SVR)model[5], random forest(RF)model[6], and long short-term memory(LSTM)neural network speed prediction model[7-8].Intelligent prediction methods have gradually become the mainstream method of short-term traffic flow forecasting because of their advantages of accurate forecasting, fast calculation, and good feasibility.However, the current related research mainly focuses on the optimization of model parameters and the exploration of application scenarios.It still lacks the processing of collected data to reflect the traffic situation comprehensively.
In response to the above problems, this paper proposes a short-term traffic flow prediction model combining phase space reconstruction(PSR)and extreme gradient boosting(XGBoost)algorithms, which mainly include four parts: data preprocessing, PSR, complex network analysis, and XGBoost model training and prediction.The advantages of the model in terms of prediction accuracy and calculation speed are verified through examples.
1 Improved Data Preprocessing Method
Data preprocessing is the premise of data analysis, especially the filling of missing and abnormal data.However, traditional data filling methods lack the pertinence of the research object, especially the analysis of the state of a transportation system.On this basis, this paper proposes a data filling method based on a hierarchical clustering algorithm and traffic flow state.The data in this paper are the measured speed data of an expressway in Guangzhou from August 1st to September 25th, 2016.The time span is eight weeks, the time interval of data collection is 10 min, and the total number of data sets is 8 064.
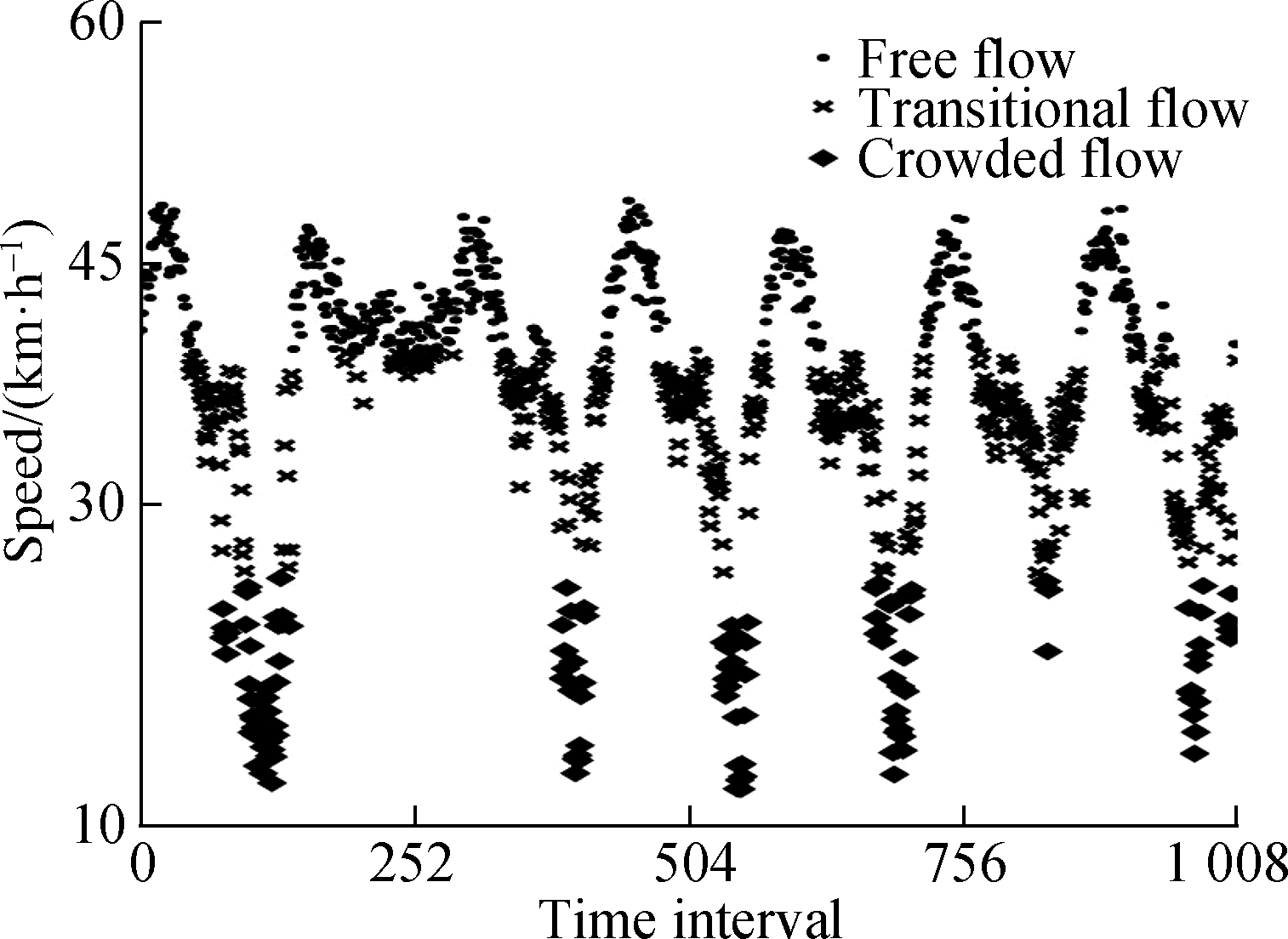
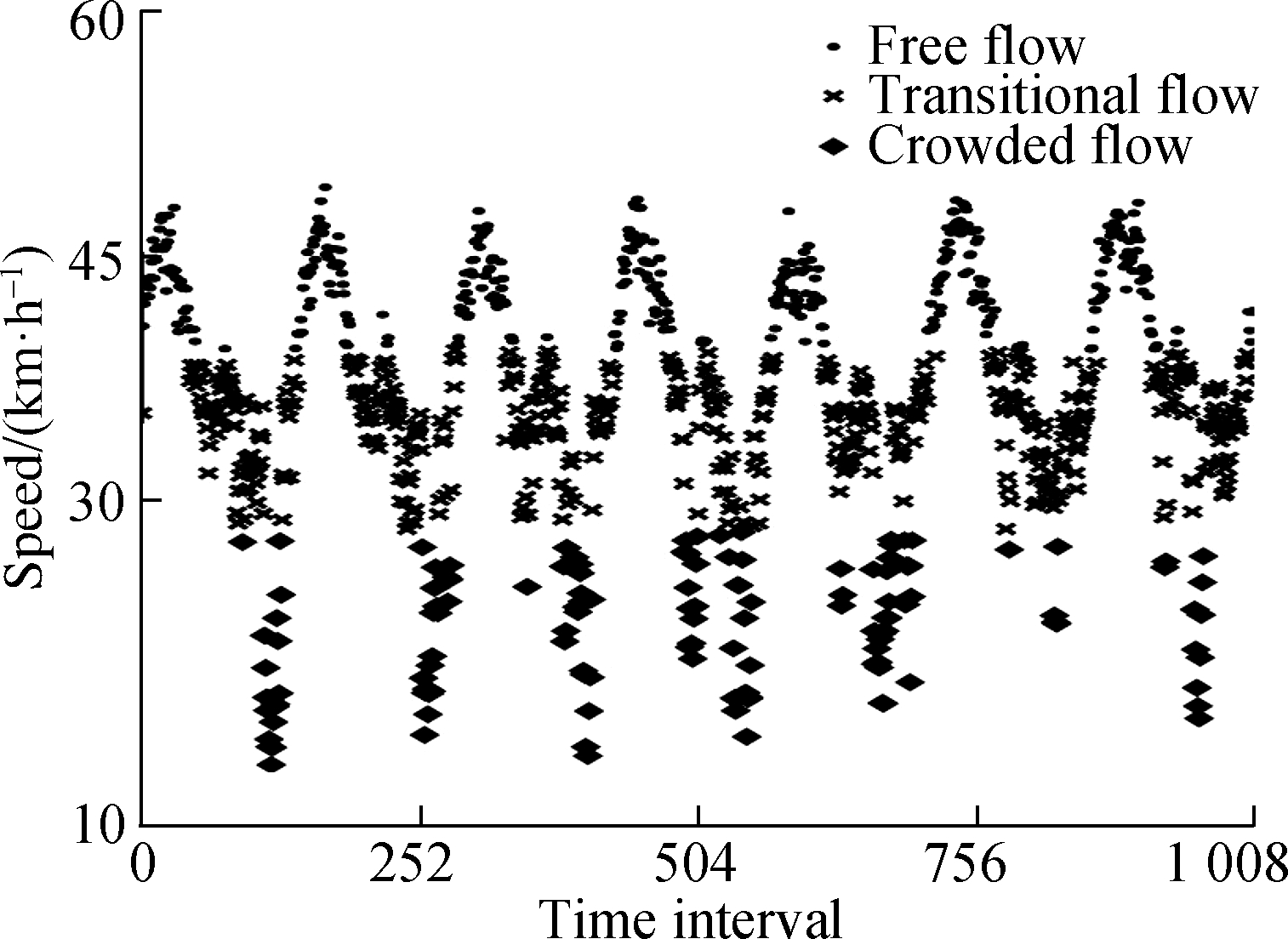
The main processes of the hierarchical clustering algorithm used to fill in missing and abnormal values are as follows: 1)Clustering speed data are processed by the hierarchical clustering algorithm.Fig.1 shows the data clustering results of the first and second weeks in the time series data.The hierarchical clustering algorithm can clearly divide the speed value into three categories.2)According to the clustering results, the traffic conditions of different categories are identified.According to the basic graph theory, the clustering results can be identified as free flow, transition flow, and congested flow.3)The traffic state where the missing or abnormal value is located is determined.4)Fill it with the average value of data in the same state.
(a)
(b)
Fig.1 Hierarchical clustering results.(a)First week;(b)Second week
2 Data Reconstruction
From the perspective of the meso-traffic flow model, the various dimensional states of the transportation system evolve over time to obtain a sequence of multidimensional state parameters to form a phase space.However, in the actual data acquisition process, only a certain dimensional component of the system can be acquired through the detector.Suppose v={vi|i=1,2,…n} is the speed sequence of the traffic system, where vi represents the average speed of vehicles in a certain period of time and n is the length of the time sequence.The one-dimensional component can be reconstructed into a multidimensional data matrix by
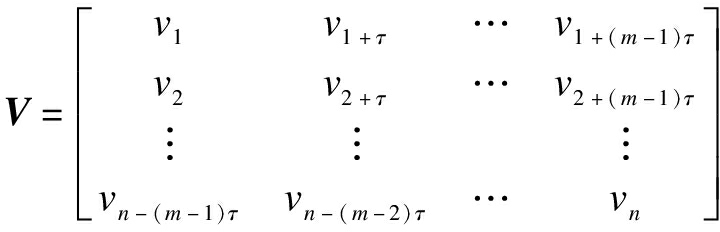
(1)
where V is the data matrix after reconstruction; τ is the delay time; m is the embedding dimension.
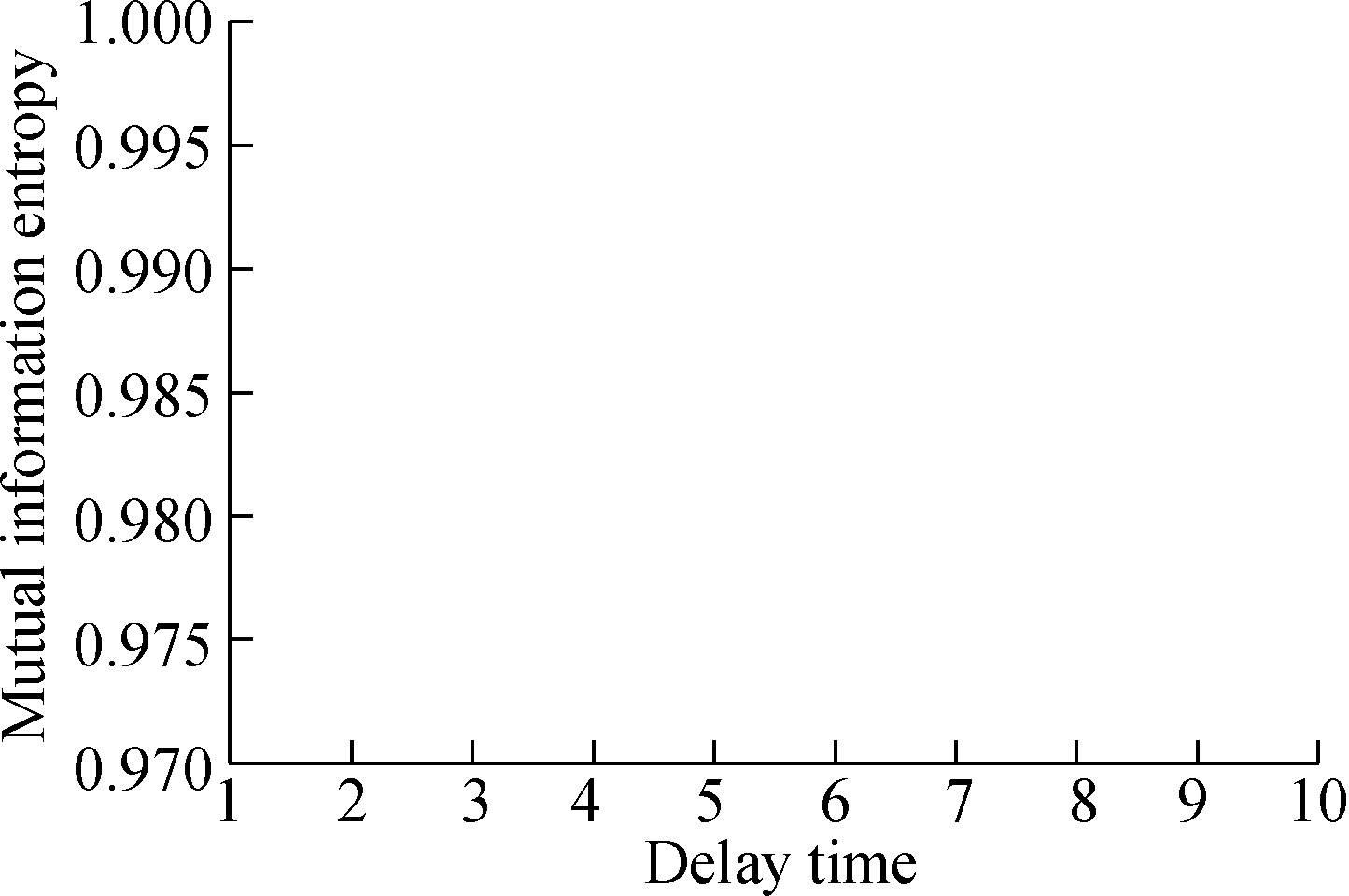
The selection of parameters is the key to PSR.For the delay time τ, the mutual information method is used[9-10].For two sequences, mutual information entropy is positively correlated with the degree of correlation between two sequences.Therefore, by calculating the mutual information entropy of the initial sequence and the sequence delay by τ, the correlation between the sequences can be determined.Fig.2(a)shows the variation of mutual information entropy with delay time, where the best delay time is 2.
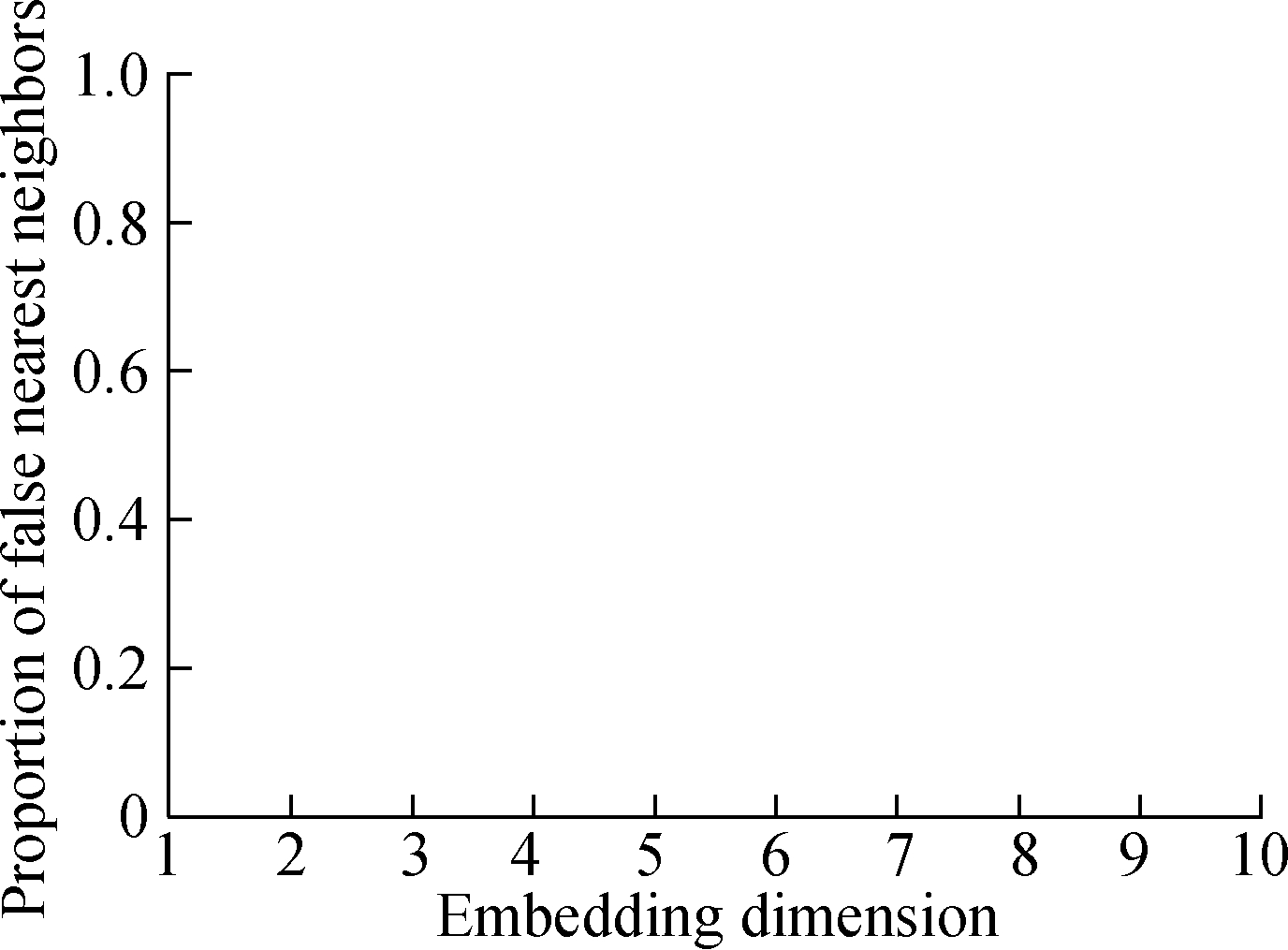
For the embedding dimension m, the false k-nearest neighbor method is used[9-10].The calculation idea of the false k-nearest neighbor method is to gradually eliminate false neighbors by increasing the dimensionality of the phase space until the proportion of false nearest neighbors remains unchanged.Fig.2(b)shows that as the embedding dimension increases, the proportion of the false k-nearest neighbors rapidly decreases and then stabilizes.The acceptable value of the embedding dimension is 6.
(a)
(b)
Fig.2 Phase space reconstruction parameter selection.(a)Delay time;(b)Embedded dimension
3 Complex Network Analysis
The data matrix after PSR reflects the evolution of multidimensional states.When constructing a time series complex network, the vector in the matrix is used as the network node, and the connection between nodes is determined by the node distance and critical threshold.If the node distance is smaller than the threshold, then there is a connection between the nodes.
The choice of the critical threshold is very important to the construction of the network.In this study, the threshold through the network density is examined.In a chaotic system network, there are many clusters of different sizes.As nodes in a cluster are adjacent to one another, the degree will rapidly increase as the threshold within the cluster radius changes.When the threshold is close to the average radius of all clusters, the edge increase will reach the maximum rate, and exceeding the threshold will result in redundant connections between nodes.Therefore, the critical threshold can select the point where the network density grows the fastest.Fig.3 shows that when the threshold is 25, the network density grows the fastest, so it is used as the network connection threshold.
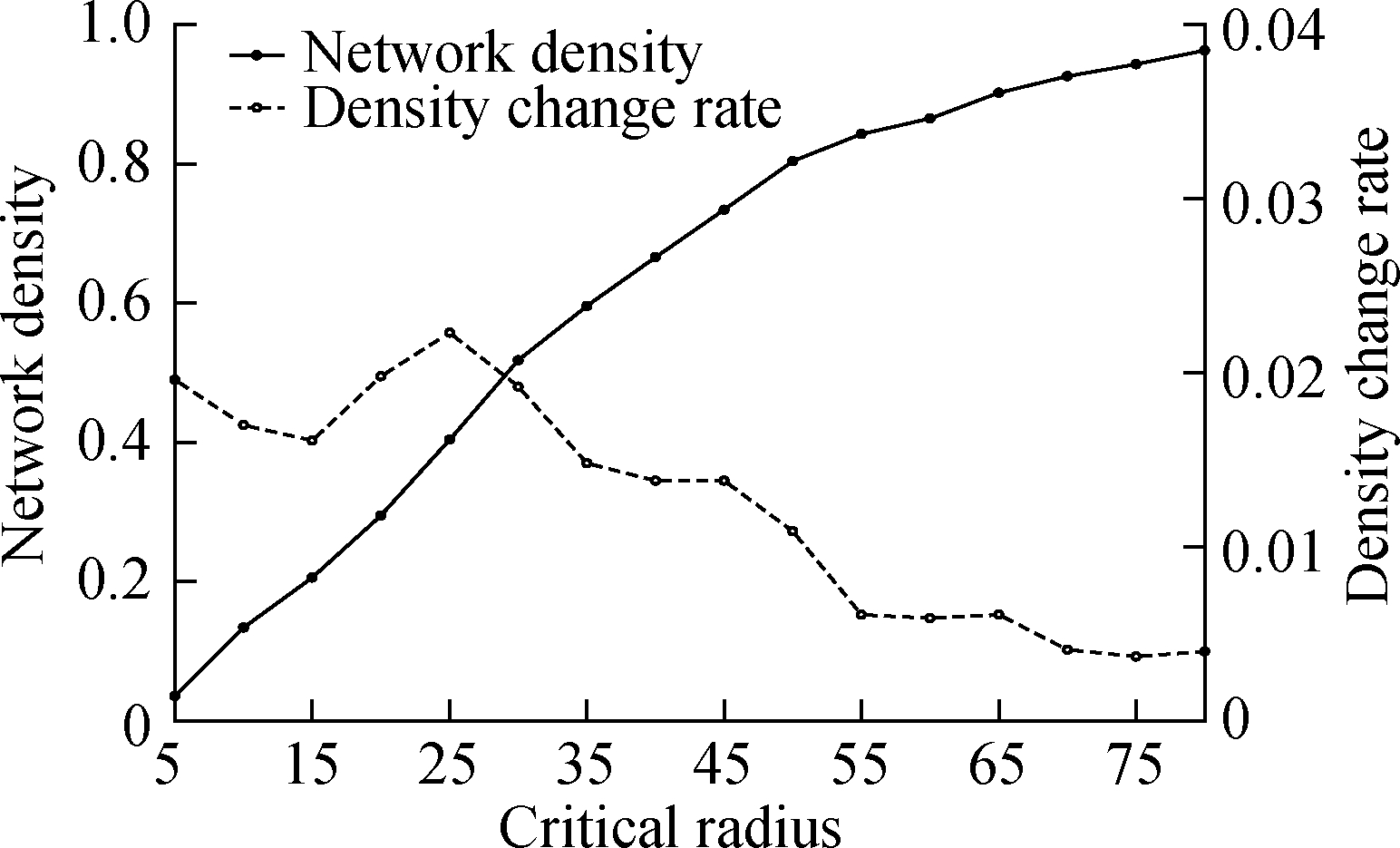
Fig.3 Selection of the complex network connection threshold
Fig.4 plots a complex network of the time series of daily period data.From the perspective of the topological structure, the network is mainly composed of clusters of different sizes, without isolated nodes or clusters.From the perspective of quantitative indicators, the Pajek software is used to calculate the degree of nodes in the network.The distribution of node degrees is shown in Fig.5.Its distribution in double logarithmic coordinates can be fitted with a straight line with a negative slope.The finding shows that the network presents a scale-free characteristic.According to existing research conclusions[11], the network has scale-free characteristics, and the reconstructed time series data has strong robustness and noise resistance and is suitable for prediction.
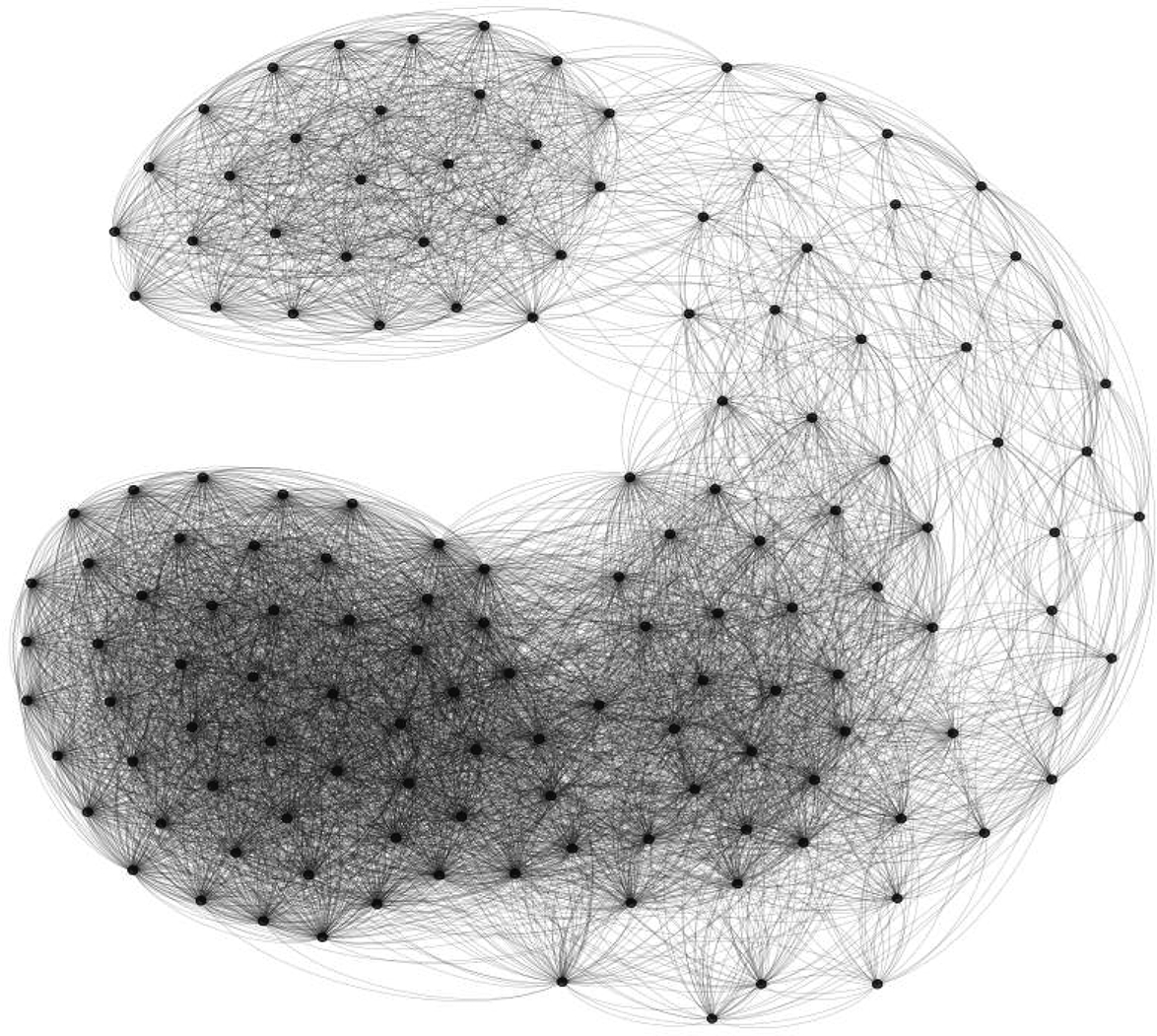
Fig.4 Complex network topology diagram
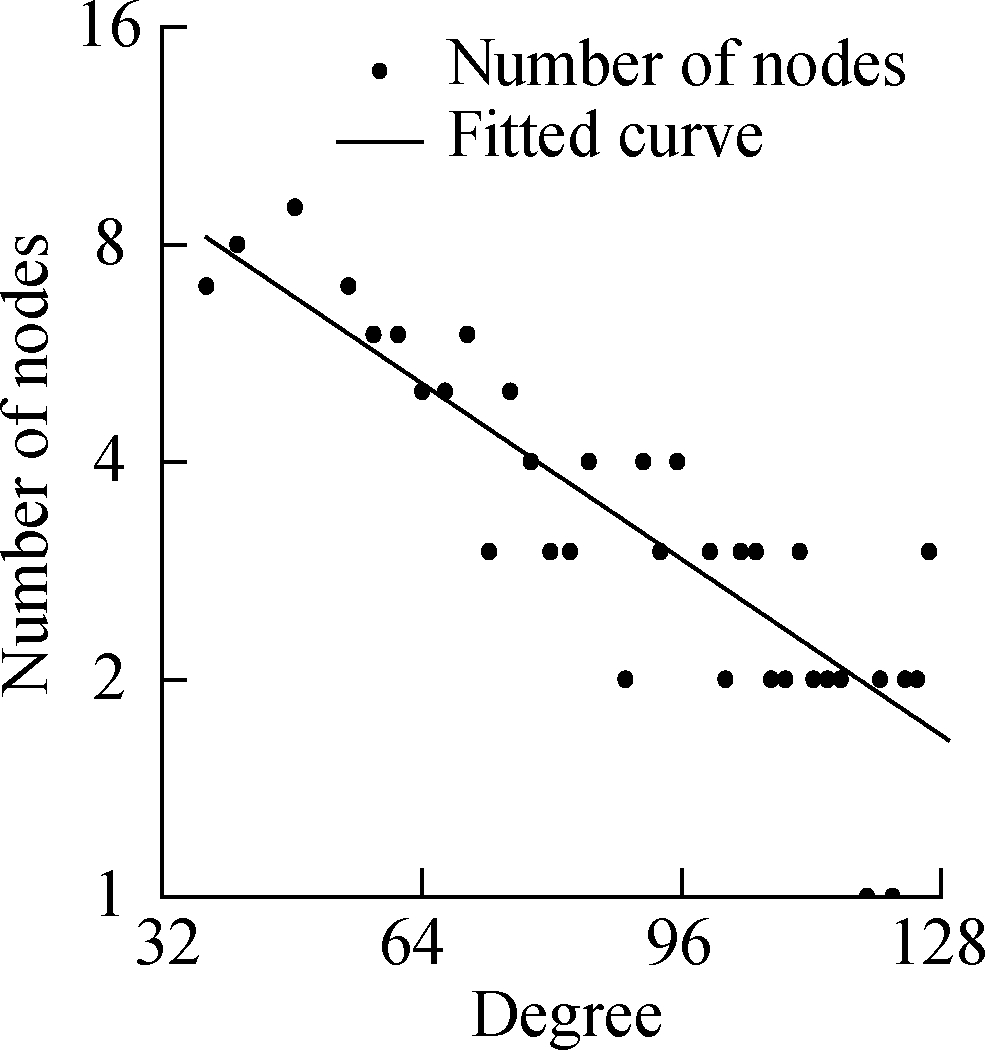
Fig.5 Degree distribution of network nodes
4 Traffic Flow Prediction
4.1 XGBoost
XGBoost is improved on the basis of the gradient boosting decision tree(GBDT)algorithm[12].The construction of each tree in XGBoost is completed by fitting the negative gradient of the loss function of the previous model.To make up for the shortcomings of GBDT in terms of prediction accuracy and overfitting, XGBoost introduces regularization in the objective function to quantify the complexity of the tree model.The complexity of the tree model mainly depends on the number and weight of leaf nodes—the lower the complexity of the tree model, the stronger the generalization ability of the model.Intuitively speaking, when the model expects to minimize the objective function, the model is inclined to choose a simple tree model with a strong generalization ability for prediction.The objective function of the XGBoost model can be calculated by
![]()
![]()
(2)
where L is the objective function; l(·)is the loss function of predicted value and expected value; yj is the j-th expected value; ![]() is the j-th predicted value;fk is the k-th tree model; Ω(·)is the complexity of the tree model(i.e., regular term); γ is the complexity cost; T is the number of leaf nodes; λ is the penalty coefficient; ω is the weight of the leaf node.
is the j-th predicted value;fk is the k-th tree model; Ω(·)is the complexity of the tree model(i.e., regular term); γ is the complexity cost; T is the number of leaf nodes; λ is the penalty coefficient; ω is the weight of the leaf node.
In addition, an approximate method of the greedy algorithm is used to control the splitting of the tree in the XGBoost model.The approximation algorithm avoids the greedy algorithm to enumerate data, but it is highly suitable for building a tree model with multidimensional data characteristics.This fact also theoretically explains the role of PSR in enhancing the dimension of data in this model.
4.2 Experimental analysis
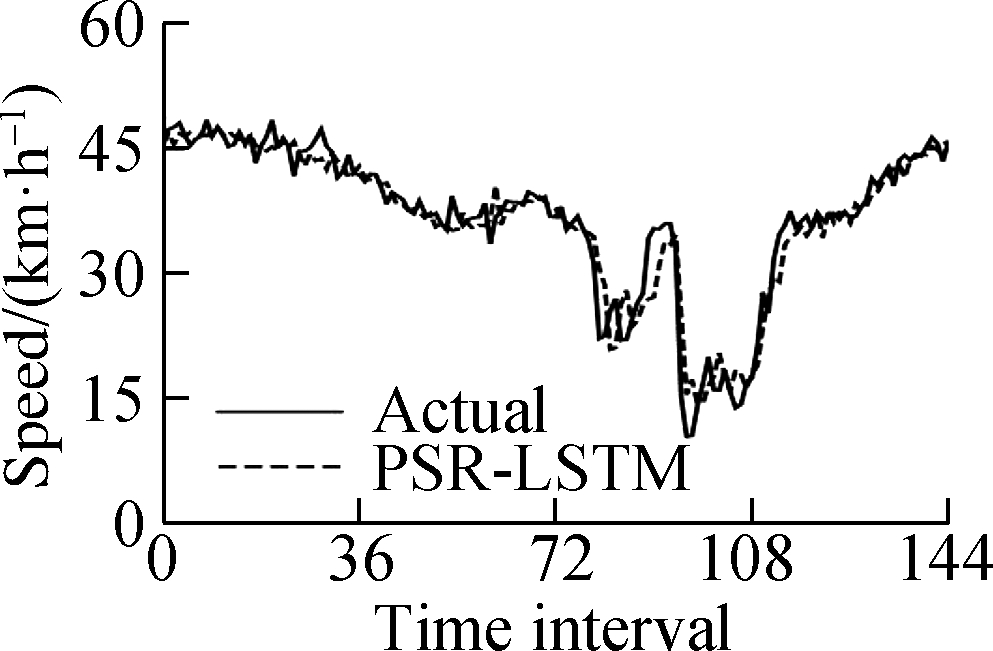
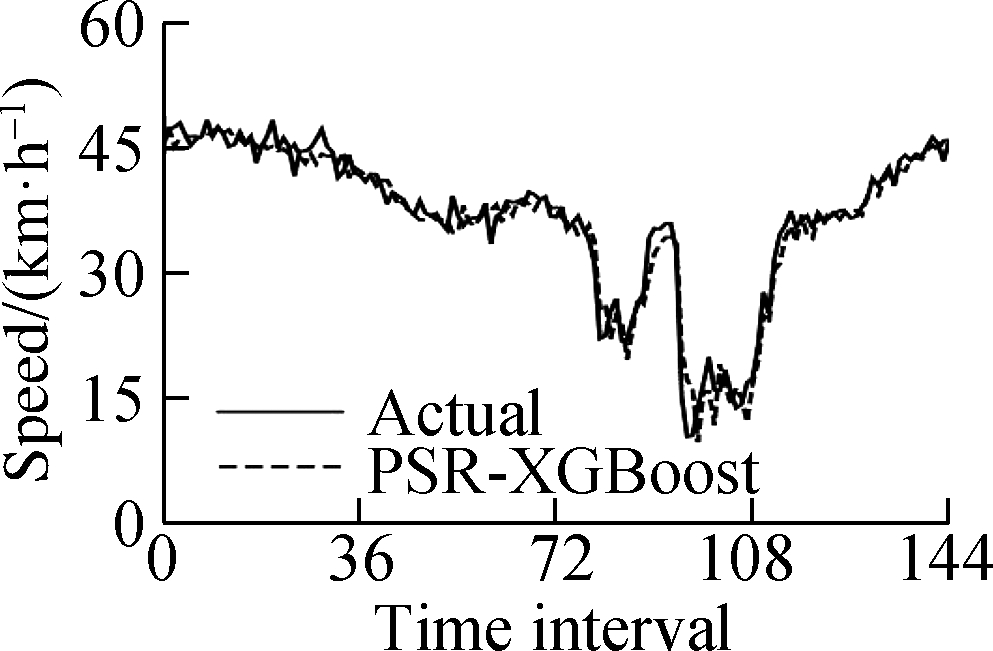
This experiment uses a computer with an Intel Core i7 processor and 8 GB memory.To verify the feasibility of the PSR-XGBoost method proposed in this paper, five control models were designed, namely, ARIMA, XGBoost, PSR-RF, PSR-SVR, and PSR-LSTM.The parameters of the model are determined by grid search and step-by-step experiments.Fig.6 shows the fit of the predicted and actual values of the model.The results show that the prediction value of the PSR-XGBoost model fits better than that of other control prediction models.
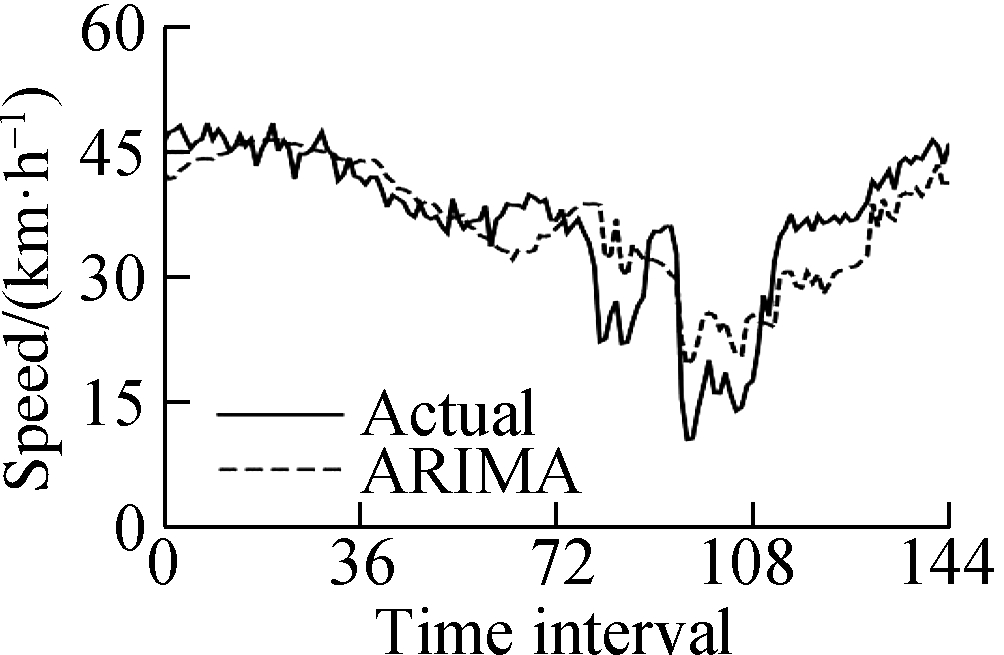
(a)
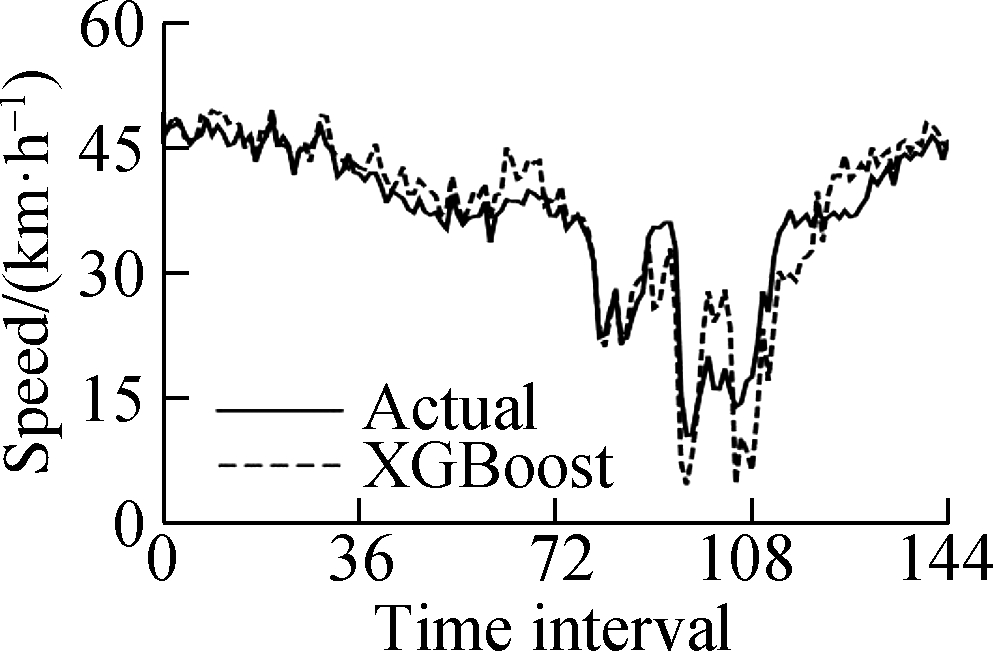
(b)
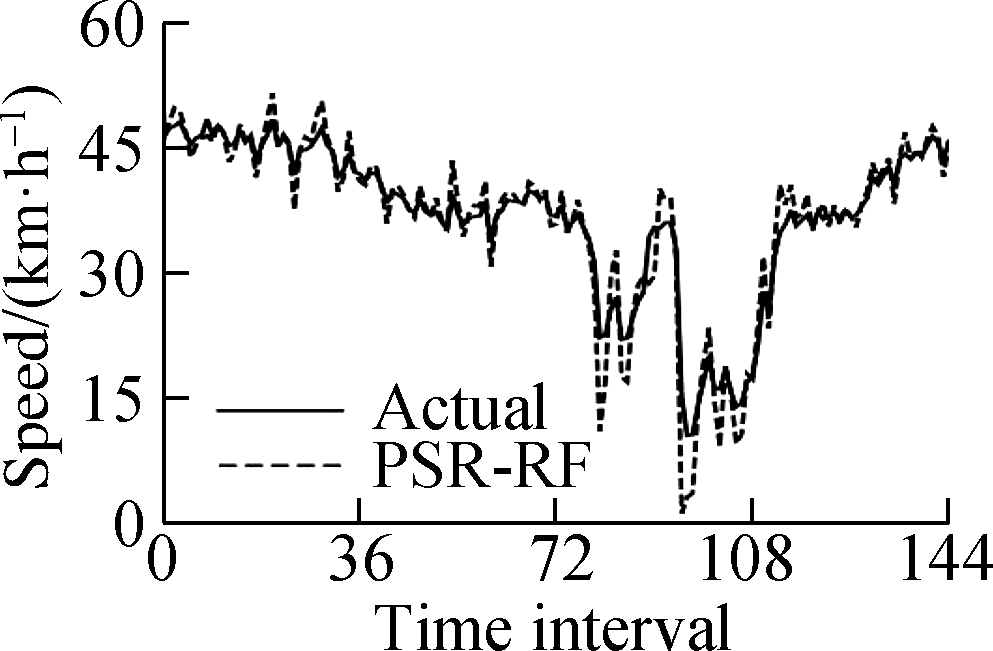
(c)
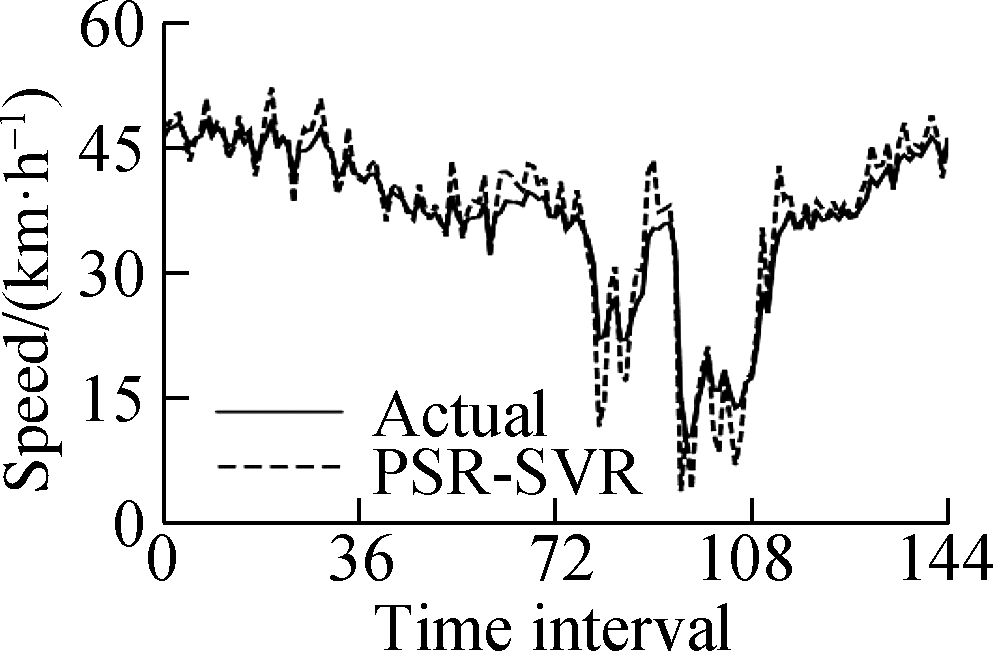
(d)
(e)
(f)
Fig.6 Model prediction results.(a)Autoregressive integrated moving average(ARIMA);(b)Extreme gradient boosting(XGBoost);(c)PSR-RF;(d)PSR-SVR;(e)PSR-LSTM;(f)PSR-XGBoost
To quantitatively describe the prediction effect of the model, the following evaluation indicators are introduced: mean square error(MSE), average absolute error(MAE), and average absolute percentage error(MAPE).Tab.1 shows the evaluation index table of the six model prediction results.
Tab.1 Model prediction performance index table

CategoriesModelMSEMAEMAPE/%Time/sExperimentalmodelPSR-XGBoost5.3991.6326.27817.35Controlmodel XGBoost16.9243.00012.00510.21ARIMA24.0044.02014.3779.58PSR-SVR13.4892.3039.17321.15PSR-RF10.4121.8817.67032.70PSR-LSTM6.4361.7286.39945.83
The experimental results show that the prediction accuracy indicators MSE, MAE, and MAPE of the PSR-XGBoost model are 5.339%, 1.632%, and 6.278%, respectively, and the calculation time is 17.35 s.Compared with the XGBoost model, the PSR-XGBoost model enriches the structure of the tree model by increasing the data dimension and greatly improves the prediction effect of the model.Compared with the mathematical statistics model, the calculation time of the PSR-XGBoost model is longer, but the three accuracy indicators, MSE, MAE, and MAPE, increased by 77.5%, 59.4%, and 56.3%, respectively.Compared with the PSR-SVR, PSR-RF, and PSR-LSTM models, the prediction accuracy of the PSR-XGBoost model improved to a certain extent; the MSE increased by 59.9%, 48.1%, and 16.1%; the MAE increased by 29.1%, 13.2%, and 5.6%; and the MAPE increased by 31.6%, 18.1%, and 1.9%, respectively.Although the prediction accuracy of the PSR-XGBoost and PSR-LSTM models are not much different, the time required for the prediction is significantly reduced.
5 Conclusions
1)The improved data preprocessing method is specific to traffic data.This method can effectively identify the road traffic state through the hierarchical clustering algorithm and fill in missing and abnormal data based on the traffic state.
2)PSR can map one-dimensional data to a multidimensional matrix, effectively solving the problem of low basic data dimensions, optimizing the model input, enriching the model structure, and improving the prediction accuracy.In addition, complex network methods can analyze and verify the characteristics of reconstructed data.
3)Considering the prediction accuracy and computing efficiency, the PSR-XGBoost model has advantages over mathematical-statistical models and other machine learning algorithms and can be used as an effective method for short-term traffic flow prediction.
[1] Han C, Song S, Wang C H.A real-time short-term traffic flow adaptive forecasting method based on ARIMA model[J].Journal of System Simulation, 2004, 16(7): 1530-1532,1535.DOI: 10.3969/j.issn.1004-731X.2004.07.042.(in Chinese)
[2] Yang G F,Xu R, Qin M, et al.Short-term traffic volume forecasting based on ARMA and Kalman filter[J].Journal of Zhengzhou University(Engineering Science), 2017, 38(2): 36-40.DOI: 10.13705/j.issn.1671-6833.2017.02.009.(in Chinese)
[3] Tian Z D.Chaotic characteristic analysis of network traffic time series at different time scales[J].Chaos Solitons & Fractals, 2020, 130: 109412.DOI: 10.1016/j.chaos.2019.109412.
[4] Jia X C, Chen X M, Gong J L, et al.Multi-step short-term traffic flow prediction based on chaotic theory[J].Journal of Transport Information and Safety, 2013, 31(6): 27-32.DOI: 10.3963/j.issn.1674-4861.2013.06.006.(in Chinese)
[5] Wu Q.Research and application of short-term traffic flow forcasting based on support vector machine regression[D].Xi’an: Chang’an University, 2016.(in Chinese)
[6] Zhang L Z,Alharbe N R, Luo G C, et al.A hybrid forecasting framework based on support vector regression with a modified genetic algorithm and a random forest for traffic flow prediction[J].Tsinghua Science and Technology, 2018, 23(4): 479-492.DOI: 10.26599/TST.2018.9010045.
[7] Ma X L, Tao Z M, Wang Y H, et al.Long short-term memory neural network for traffic speed prediction using remote microwave sensor data[J].Transportation Research Part C: Emerging Technologies, 2015, 54: 187-197.DOI: 10.1016/j.trc.2015.03.014.
[8] Zhao J D,Gao Y, Yang Z Z, et al.Truck traffic speed prediction under nonrecurrent congestion: Based on optimized deep learning algorithms and GPS data[J].IEEE Access, 2019, 7: 9116-9127.DOI: 10.1109/ACCESS.2018.2890414.
[9] Li Y Y.Research on the short-term traffic flow forecasting method of based on phase space reconstruction and SVR[D].Beijing: Beijing Jiaotong University, 2018.(in Chinese)
[10] Matilla García M, Morales I, Rodríguez J M, et al.Selection of embedding dimension and delay time in phase space reconstruction via symbolic dynamics[J].Entropy, 2021, 23(2): 221-221.DOI: 10.3390/e23020221.
[11] Gao Z K, Jin N D.Complex network from time series based on phase space reconstruction[J].Chaos, 2009,19(3): 033137.DOI: 10.1063/1.3227736.
[12] Chen T Q,Guestrin C.XGBoost: A scalable tree boosting system[C]//The 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.San Francisco, CA, USA, 2016: 785-794.DOI: 10.1145/2939672.2939785.