Personalized recommendation systems have become ubiquitous in the information industry, and they have been applied to classic online services.Traditional recommendation systems have been widely studied under the assumption of a stationary environment, where user preferences are assumed to be static[1-2].However, such models fail to explore users’ interests when few reliable user-item interactions are provided, such as that in a cold-start scenario.They also fail to model the dynamics of user preferences, thus leading to poor performance.Therefore, the research into interactive recommendation systems(IRSs)has flourished in recent years.IRSs consider recommendations as sequential interactions between systems and users.The main idea in modeling IRSs is to capture the dynamic nature of user preferences and achieve optimal recommendations in a time period T[3].IRS research has two directions: contextual bandit and reinforcement learning(RL).Although contextual bandit algorithms have been used in different recommendation scenes, such as collaborative filtering[4-5] and e-commerce recommendation[6], they are usually invalid in nonlinear models and demonstrate too much pessimism toward recommendations.RL is a suitable learning framework for interactive recommendation tasks as it does not suffer from such issues.In the study of applying RL to IRSs, the themes include large action spaces, off-policy training[7-8], and online model framework[9].
The interactive recommendation problem in the current study is set in a cold-start scenario, which provides nothing about items or users other than insufficient observations of user-item ratings.A deep RL framework[10], which can be regarded as a generalized neural Q-network, is adopted to tackle the above problem.As for the representation of items, an embedding lookup table X∈RN×de is adopted, with each item e being represented as a vector xe∈Rde.The embedding lookup table is trained end to end in the framework.However, because such an embedding layer is optimized by user-item interactions in interactive recommendations and lacks an explicit encoding of crucial collaborative signals, an item similarity graph is proposed, and an embedding propagation layer constructed by graph neural networks(GNNs)is devised in this work to refine items’ embeddings by aggregating the embeddings of similar items.
Given the graph structure from the data in recommendation systems, designing a proper graph and utilizing GNNs in recommendation systems are appealing.
User-item bipartite graphs are constructed in traditional recommendation methods for improved performance in rating prediction tasks[11], while sequence graphs are transformed in sequential recommendation methods to capture sequential knowledge[12].Knowledge graphs[13] are utilized for additional information.By introducing an item similarity bipartite graph in the recommendation framework, we make interactive recommendations effective because of the deep exploitation in structural item similarity information inferred from user-item interactions.A user-item bipartite graph is suggested in the RL framework for interactive recommendations[14].
In sum, a new graph called an item similarity graph is built in this study to alleviate the computational burden while showing comparative structural information as a user-item bipartite graph.Then, a graph-enhanced neural interactive collaborative filtering(GE-ICF)framework, which devises an embedding propagation layer into an RL framework, is proposed for interactive recommendation tasks.Empirical studies on a real-world benchmark dataset are conducted, and the results show that the proposed GE-ICF framework outperforms baseline methods.
1 GE-ICF Framework’s Method
1.1 Preliminaries
A typical recommendation system has a set of m users U={1, 2, …, m} and n items I={1, 2, …, n} with an observed feedback matrix Y∈Rm×n, where yij represents the feedback from user i to item j.Here feedback can be explicit(e.g., rating, like/dislike choice)or be implicitly inferred from watching time, clicks, reviews, etc.For cold-start users in this study, an interactive recommendation process is conducted in a time period T between the recommender agent and a certain user.At each time step t in the interaction time period {0, 1, 2, …, T}, the recommendation agent calculates item it to be recommended by policy π:st→I and suggests it to certain user u, where st represents the user state at time step t.Then, the user gives feedback yu,it on the recommended item to the recommender agent, and this feedback guides the agent in updating the user’s state and making next-round recommendations.The goal of designing an interactive recommendation system is to design a policy π that maximizes Gπ(T)as
(1)
where Gπ(T)is the expected cumulative feedback in a time period T.Although exploiting the user state at the current time step facilitates the derivation of accurate recommendations and maximization of immediate user feedback yu,it, the exploration of items for recommendation is necessary for completing user profiles and maximizing cumulative user feedback G(T), which is regarded as the delayed reward for a recommendation.RL is a sequential decision learning framework that is aimed at maximizing the sum of delayed rewards from an overall aspect[10].Therefore, RL is applied in our system to balance exploitation and exploration during interactive recommendations.
The essential underlying model of RL is a Markov decision process(MDP).An MDP occurs between agents and the environment.In this study, the agent is the proposed recommendation system, and the environment is equivalent to the users of the system, as well as all the movies recorded in the system.The MDP is defined with five factors(S,A,P,D,γ).These factors are introduced and instantiated in the IRS for cold-start users.Fig.1 illustrates the interactive recommendation in the MDP formulation.
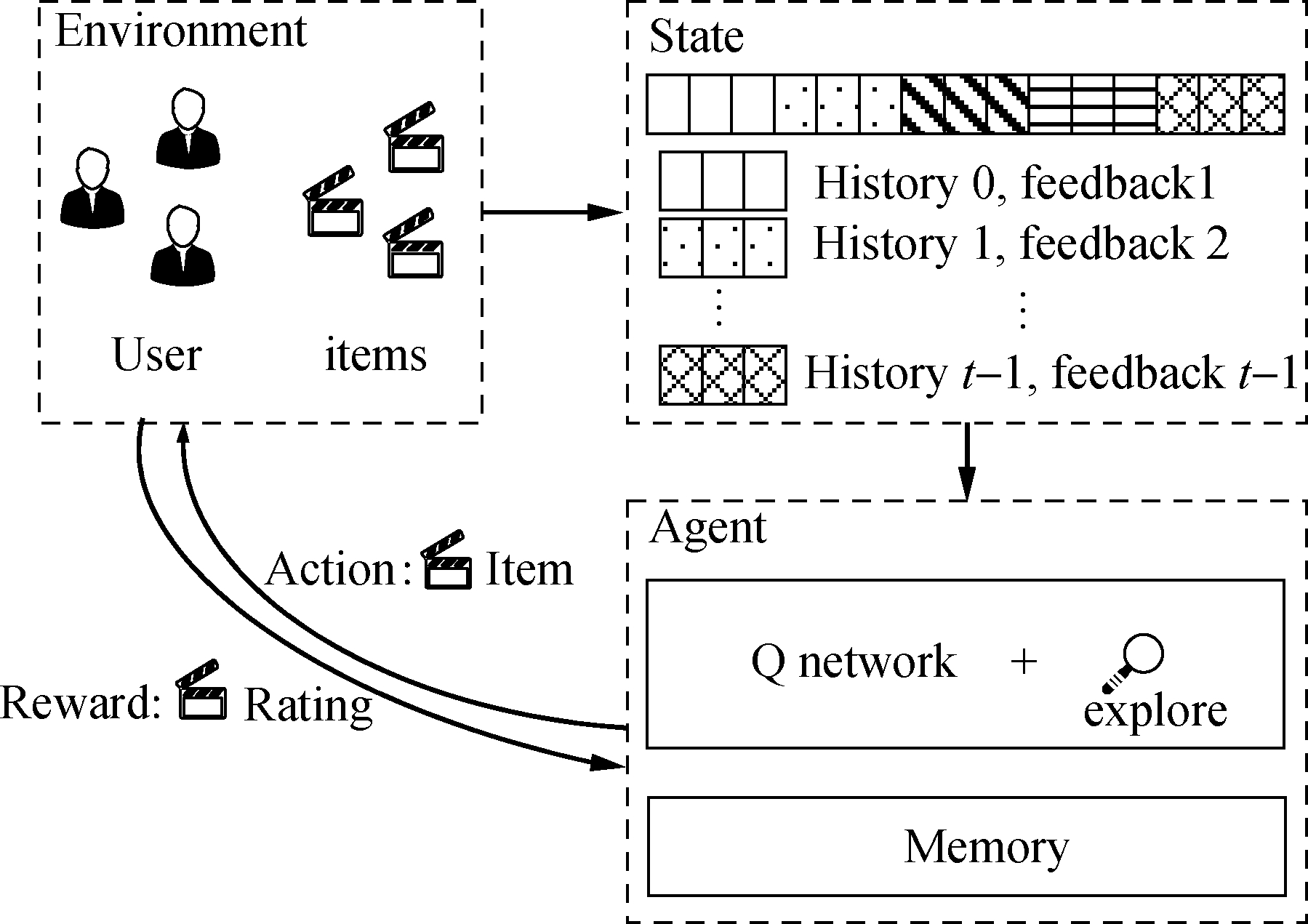
Fig.1 Interactive recommendation process in MDP formulation
State space S contains a set of states st.In this study, a state at time t: st={i0,yu,i0,…,it-1,yu,it-1} denotes the browsing history and corresponding feedback of a user u before time t.To reflect the change of user interests with time, the items in st are sorted in chronological order.
Action space A is equivalent to item set I in a recommendation.An action at time t: at∈A denotes the item recommended to a user by the recommender system according to current user state st.
Reward D is a set the recommender system receives depending on user feedback.
Feedback yu,it on the recommended item it is returned by user u, and it may be explicit or implicit depending on certain systems.The recommendation system receives immediate reward rst,at according to the feedback.Rewards may not be the same as feedback; that is, reward shaping technology may be used to improve algorithm performance.
Transition probability p(st+1|st,at)defines the probability of state transition from st to st+1 after an item is recommended as an action.An MDP is assumed to have a Markov property; that is, it satisfies p(st+1|st,at,…,s1,a1)=p(st+1|st,at).p(st+1|st,at)= 1 is set at any time step, which means that the state at the next time step t+1 is determined once state st and action at are fixed.In this work, the state at t+1 is updated by appending action at and corresponding feedback yu,it to state st; that is, it is accumulative.
Discount factor γ∈[0,1]defines the discount factor measuring the importance of future reward in the present state value.Specifically, γ=0 means that the recommender agent only considers the immediate reward while γ=1 means that all future rewards are thought to be as important as the immediate reward.
Solving the RL task is to find an optimal policy πθ:S A that maximizes the expected cumulative rewards from a global view.The expected cumulative rewards can be presented by a value function
A that maximizes the expected cumulative rewards from a global view.The expected cumulative rewards can be presented by a value function ![]()
![]() Note that Eπθ is the expectation under policy πθ, t is the current time step, and rt+k presents the immediate reward at a future time step t+k.A variant of neural network Q(s,a;θ)(i.e., Q-network)[15] is adopted to estimate the policy πθ.A Q-network adopts the experience replay mechanism and a periodically updated target network to ensure the coverage of the model.A finite-size memory called a replay buffer is applied, and transition samples represented by(st,at,rt,st+1)are stored there for sampling and model training.
Note that Eπθ is the expectation under policy πθ, t is the current time step, and rt+k presents the immediate reward at a future time step t+k.A variant of neural network Q(s,a;θ)(i.e., Q-network)[15] is adopted to estimate the policy πθ.A Q-network adopts the experience replay mechanism and a periodically updated target network to ensure the coverage of the model.A finite-size memory called a replay buffer is applied, and transition samples represented by(st,at,rt,st+1)are stored there for sampling and model training.
In the recommendation procedure,the state space and action space are represented by item vectors.In practice, building item vectors by one-hot encoding is not efficient enough because of the one-hot encoding’s extremely high dimension and sparsity, especially in problems with a large action space.Instead, we train dense, low-item vectors end to end in the RL framework.GNNs are integrated into the embedding process because of their superiority in representation learning.
1.2 Item similarity bipartite graph construction
Although a user-item interaction bipartite graph is widely used in collaborative filtering, it suffers from huge data size and a high calculational burden.Therefore, we propose to build an item similarity bipartite graph with the assumption that a user’s interest does not change frequently.On the basis of this assumption, we count the frequency of two items simultaneously existing in one user’s history.Assume that two items exist in n users’ histories; they are thought to be similar if n≥g, where g denotes an item similarity coefficient.An edge exists between two similar item nodes in the item similarity graph.We set all edges to have equal weights initially and learn the contribution of each neighbor to central nodes with an attention network.A toy sample of a user-item interaction bipartite graph and an item similarity bipartite graph is illustrated in Fig.2.

Fig.2 Illustration of a user-item interaction bipartite graph and an item similarity bipartite graph.(a)User-item interaction bipartite graph;(b)Item similarity bipartite graph
Through the design of the item similarity graph, structural information among items is modeled with the graph size sharply decreasing because user nodes are no longer built in it.
1.3 Model architecture
We now present details of the proposed GE-ICF framework, the architecture of which is illustrated in Fig.3.The framework is structured with four components: 1)an embedding layer that initializes all item embeddings in the system; 2)an embedding propagation layer that refines the item embeddings by injecting structural item similarity relations; 3)a stacking self-attention block that takes item embeddings and a user’s corresponding feedback as input to generate a user profile; 4)a policy layer that predicts the most preferable item for the user.The framework is trained end to end with Q-learning[15].
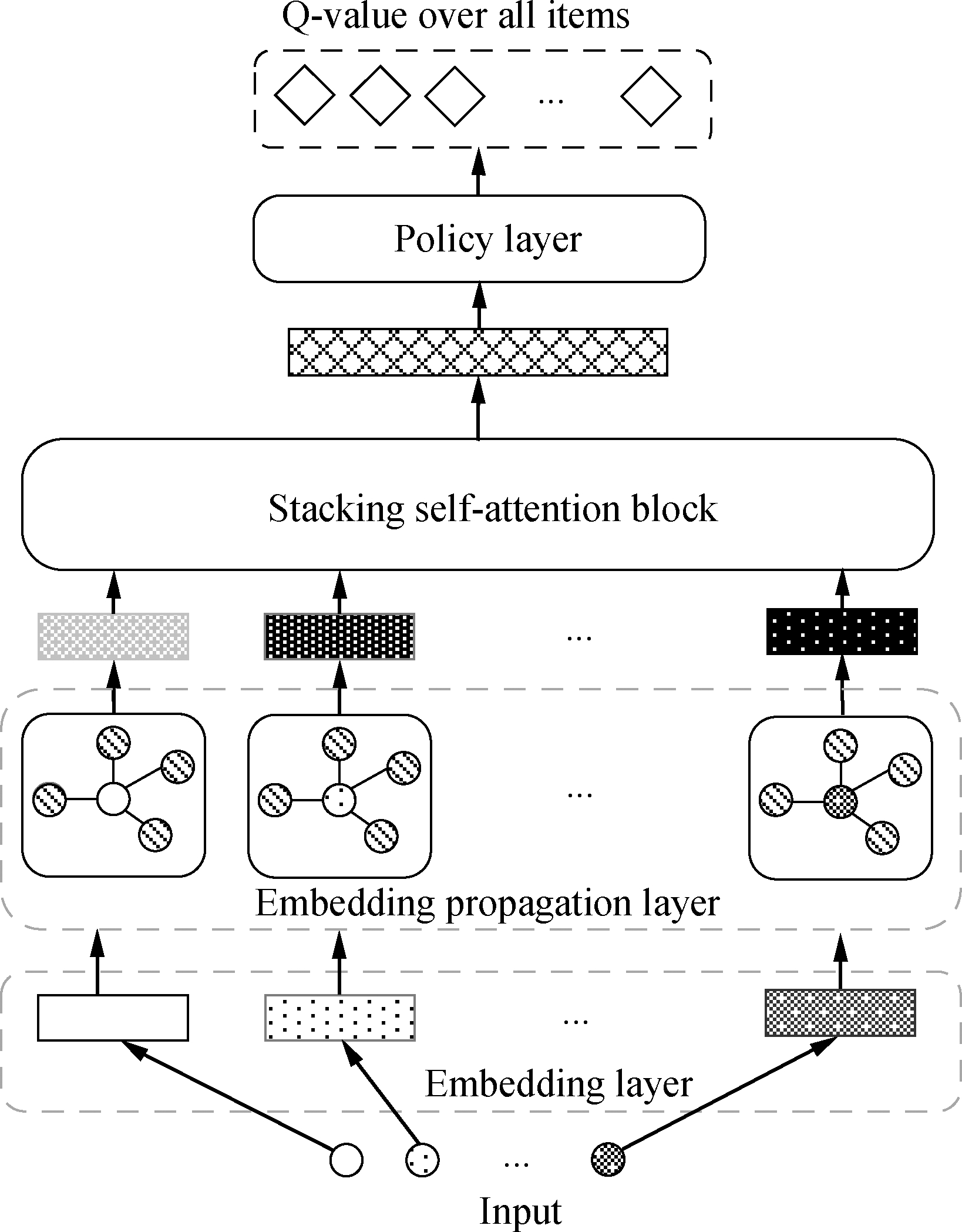
Fig.3 Architecture of the GE-ICF framework
1.3.1 Embedding layer
Given a user state st={i0,yu,i0,…,it-1,yu,it-1}, we first represent items it with embedding vectors.We build an embedding lookup table X∈RN×de for the initialization of all N items’ embeddings in the system, with de denoting the embedding size.The embedding lookup table is initialized randomly and optimized in an end-to-end style.In contrast to traditional collaborative filtering methods, which take these ID embeddings as items’ final embeddings, they are refined by propagating the information of similar items on an item similarity graph in the GE-ICF framework, thus leading to effective item representations.
1.3.2 Embedding propagation layer
We develop an embedding propagation layer from the idea of GAT.This layer aims to aggregate similar items’ features to refine the central nodes’ embedding vectors.It takes the embedding lookup table X∈RN×de and item similarity bipartite graph as input and outputs a graph-aware embedding lookup table X′∈RN×d′e, thus transforming an item i’s embedding vector from xi∈Rde to x′i∈Rd′e.
A shared weight matrix W∈Rde×d′e is necessary in the first step for transforming inputted embedding vectors into high-order features.This step allows the framework to obtain sufficient expressive power.Then, an attention mechanism attention: Rd′e×Rd′e→R is adopted to measure different importance levels of neighbor nodes for central nodes in the form of attention coefficients:
eij=attention(Wxi,Wxj)
(2)
where eij is an attention coefficient calculated to measure the contribution of a neighbor node j∈Ni for the central node icentral and Ni denotes all the one-hop neighbors of node icentral in the graph as well as the node icentral itself.A softmax function is then applied to all attention coefficients ei* as

(3)
where αij is a normalized attention coefficient that makes all the importance levels of nodes in Ni comparable.
We adopt a single-layer feed forward neural network for the attention mechanism, in which the normalized attention coefficient can be expanded as
αij=softmaxj(eij)=

(4)
where aT∈R2×d′e is a parameter vector for linear transformation;‖ is the concatenation operation; LeakyReLU(·)is a function for nonlinearity modeling.
As the central node icentral is already contained in the node set Ni, the message propagation process and the message aggregation process can be regarded to be conducted simultaneously by a linear combination of the features corresponding to related nodes and the nonlinearity transformation on the combined embedding vector:
(5)
where x′i is a graph-aware embedding vector of item icentral.
We employ multihead attention to stabilize the learning process of self-attention.The final item vectors can be represented by the concatenation or average of K independent attention outputs.We find that concatenation is more sensible to capture graph-aware item representations in this work:
(6)
where k is the serial number of each attention head.
1.3.3 Stacking self-attention block
A user profile is then generated by stacking self-attention blocks with user history and the corresponding feedback, and user history is represented with refined item embeddings.
The numbers of items with different user feedback items in a user’s history show extreme imbalance; that is, positive feedback items are much fewer than negative feedback items with the assumption that unexposed items are negative samples for users.As we use a dataset within an explicit rating in this work, the items in user history are classified with ratings yu,it in user state, and different rated items are processed independently by stacked self-attentive neural networks[10].
1.3.4 Policy layer
With the generated user profile, we apply a two-layerperceptron(MLP)to extract useful information and model corresponding action-value function Qθ(st,·)for all items under the current state:
Qθ(st,·![]()
(7)
where ut is the user profile vector at timestamp t; W(1),W(2) are the weight matrixes of each perceptron layer; b(1),b(2) are the biases of each perceptron layer; ReLU(·)is a function for nonlinearity modeling.
The policy πθ(st)is to recommend item i with maximal Q-value for user u at time t:
πθ(st)=argmaxiQθ(st,i)
(8)
1.4 Model training
We utilize Q-learning[15] to train the whole GE-ICF framework(see Fig.3).The adopted datasets are divided into training set Γtrain and test set Γtest by users.Before the interaction, an item similarity graph is constructed with training users’ interactive data Γtrain and item similarity coefficient g and is applied to the framework.In the t-th trial, a user state st={i0,yu,i0,…,it-1,yu,it-1} is observed, and the item with the largest value calculated by the approximated value function Qθ(st,·)is chosen as corresponding recommendation it.The ζ-greedy policy is used for exploration during training to enrich the learning samples.Then, the recommender agent receives the user’s feedback yu,it on it and maps it into reward rst,it.At the same time, the user state is updated into st+1={i0,yu,i0,…,it,yu,it}.Therefore, a new transition sample(st,it,rst,it,st+1)is generated and stored in the memory buffer for batch learning.
We train the weights in the framework in each episode by minimizing the mean squared error:
error(θ)=E(st,it,ru,it,st+1)~M[(yt-Qθ(st,it))2]
(9)
where
(10)
is the target value from the optimized Bellman equation, and the target network[15] is applied to improve system robustness.γ is a discount factor, and Qθ-(st+1,it+1)is the Q-value calculated by the target network.Efficient learning is adopted[10] in this study, with γ set to be dynamic for improved model training.M is a transition sample set stored in the memory buffer.
2 Experiments
We conduct extensive experiments to answer the following questions:
1)Does the application of GNNs refine the item embeddings and improve the recommendation efficiency?
2)Does the designed item similarity graph achieve comparable results to user-item bipartite graphs while sharply decreasing training time?
3)How does the depth of GNNs influence the final recommendation efficiency?
The experimental settings are reviewed first in the following subsection.Thereafter, the questions are discussed in the Results and Analysis section.
2.1 Experimental setting
2.1.1 Datasets
Experiments on recommendation systems should be conducted online to determine their interactive performance.However, online experiments are not always possible as they require a platform and could possibly sacrifice user experience.Therefore, a stable benchmark dataset, MovieLens 100K, is adopted for the experiment in this work.The statistics of the dataset are summarized in Tab.1.
Tab.1 Summary statistics of datasets

DatasetMovieLens 100KUsers943Items1 682Interactions100 000Interactions per user106.04Interactions per item59.45
To make the experiments reasonable, we assume that each item in a user’s history in the dataset is the user’s instinctive action and is not biased by recommendations.In addition, the ratings from users for items not in their records are assumed to be 0 following existing studies.
2.1.2 Comparison methods
To verify the efficiency of our proposed GE-ICF framework, we select five baselines among different types of recommendations for comparison.
1)Random:A policy uniformly samples items to recommend to users.It is a baseline to output the worst performance, in which no algorithms are used for recommendations.
2)Popular: An algorithm that orders items with the number of ratings and recommends items accordingly.Before the popularity of personalized recommendations, Popular was a most widely adopted policy because of its surprisingly excellent performance on recommendations.
3)Thompson sampling(TS)[5]: An interactive collaborative filtering algorithm achieved with the combination of probabilistic matrix factorization(PMF)and Thompson sampling.Thompson sampling can be replaced with other exploration techniques, such as GLM-UCB.We choose PMF with Thompson sampling as a representation of such techniques to compare it with our algorithm with the goal of balancing exploitation and exploration in recommendations.
4)NICF[10]: A state-of-the-art algorithm that applies RL to interactive collaborative filtering.We refer to its idea on the construction of the DQN-based framework and compare our work with it to verify whether the devised GNNs make sense.
5)GCQN[14]: A DQN-based recommendation that applies a user-item bipartite graph to detect the collaborative signal and uses GRU layers to generate the user profile.
6)GE-ICF:The proposed approach to the interactive recommendation with the item similarity bipartite graph devised.
7)GE-ICF-β: The same architecture as the GE-ICF, except that a user-item bipartite graph is devised in the framework.
We compare GE-ICF and GE-ICF-β to investigate whether the proposed item similarity graph achieves comparable performance in abstracting collaborative signals with the user-item bipartite graph while sharply reducing the burden on calculation.
We adopt cumulative precision during T interactions pT to evaluate the accuracy of recommendations:
(11)
where bt is a parameter indicating whether the recommendation is satisfiable or not and nusers is the number of users.bt=1 if yu,it≥4, and 0 otherwise.As we set the reward rst,it under the same rule, the cumulative precision is equivalent to the cumulative reward in T interactions.
The dataset is divided into three disjoint sets by users: 85% of the users and their interactions are set as a training set, 5% of the users and their interactions comprise the validation set, and the remaining 10% of the users are set as the test set.In our approach, the batch size of learning is set to be 128, and the learning rate is fixed to 0.001.The memory buffer to replay training samples is set as large as 1×106 for sufficient learning, and the exploration factor ζ decays from 1 to 0 during training.The optimizer is chosen to be the Adam optimizer.The item similarity coefficient g is set to be 10.The experiments are conducted on the same machine with a 4-core 8-thread CPU(i5-8300h, 2.30 GHz), Nvidia GeForce GTX 1050 Ti GPU, and 64 GB RAM.We run each model separately five times under five different seeds and average the outputs for the final results.
2.2 Results and analysis
2.2.1 Influence of GNNs
The results of pT over different models on the dataset MovieLens 100K are reported in Tab.2, where T =10, 20, 40.
Tab.2 pT of different models on MovieLens 100K

MethodT=10T=20T=40Random0.292 80.629 61.308 0Popular3.282 06.124 010.660 0TS2.170 53.564 25.465 3GCQN2.869 54.766 36.724 2NICF4.656 88.162 113.762 1GE-ICF4.671 68.290 513.934 7
We compare our proposed framework with five baselines and find that when T=10, 20, and 40, the proposed framework remarkably outperforms the other baselines in terms of recommendation accuracy.This result verifies that the embedding propagation layer we proposed indeed improves the model’s capability of detecting collaborative signals and improves the recommendation accuracy in a cold-start scenario.
2.2.2 Efficiency of the proposed item similarity graph
The algorithms GE-ICF and GE-ICF-β are further compared on pT and seconds per training step(SPT)with T=40 in Tab.3.Although the precision of GE-ICF-β is slightly higher than that of GE-ICF when T is small, the training time of GE-ICF-β is more than one and a half times as long as that of GE-ICF.This result means that the item similarity bipartite graph achieves comparable results to user-item bipartite graphs while the training efficiency is improved remarkably.
Tab.3 Performance comparison between GE-ICF and GE-ICF-β on MovieLens 100K

MethodT=10T=20T=40SPTGE-ICF4.671 68.290 513.934 760.61GE-ICF-β4.717 98.317 913.903 195.73
2.2.3 Influence of GNN depth
To investigate the influence of the GNN layers in the proposed framework, we vary the depths of the GNN layers in the range of {1, 2, 3}.Tab.4 summarizes the experimental results, and the results of the framework without GNN layers are presented for reference.
Tab.4 pT of the GE-ICF framework with different GNN depths on dataset MovieLens 100K
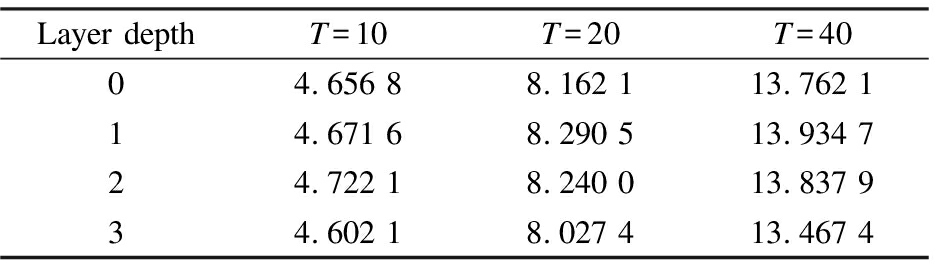
Layer depthT=10T=20T=4004.656 88.162 113.762 114.671 68.290 513.934 724.722 18.240 013.837 934.602 18.027 413.467 4
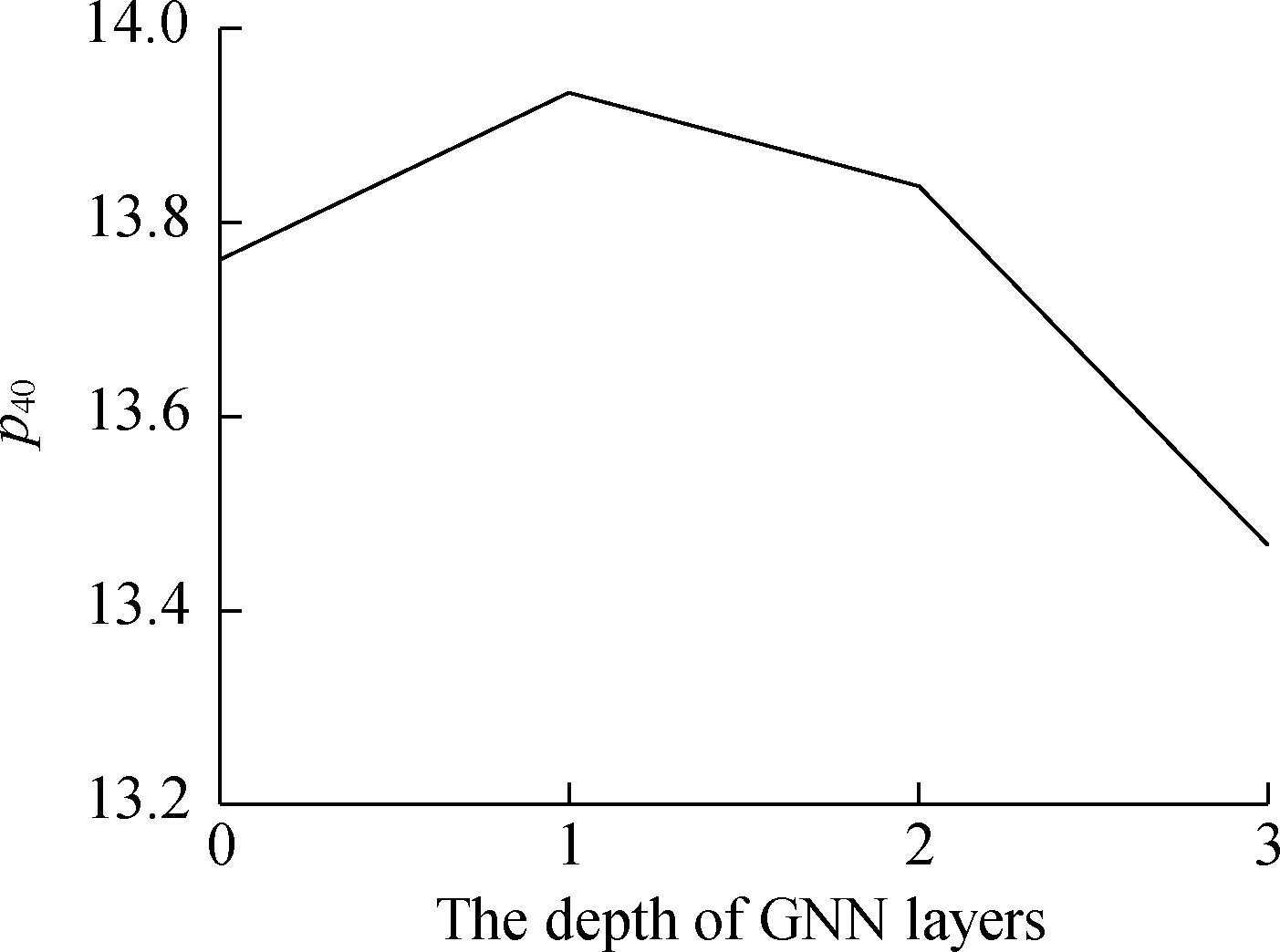
The results in Fig.4 indicate that although the application of GNN layers improves the recommendation precis-ion during time period T, the recommendation performance worsens as the depth of the GNN layers increases.p10 achieves the best performance when the GNN layer depth is equal to 1, and the GE-ICF framework with two GNN layers works the best in the time period T=20, 40.When the layer depth is up to 3, the recommendation efficiency decreases more sharply, even becoming worse than that of the framework without GNN layers.The reason might be that applying an excessively deep architecture would introduce noise to representation learning.Moreover, the multistacking of GNN layers might bring about an over smoothness issue.

(a)

(b)
(c)
Fig.4 pT comparison among GE-ICF framework with different layer depths.(a)p10;(b)p20;(c)p40
3 Conclusions
1)A GE-ICF framework is proposed in this work to enhance neural interactive filtering performance by recommending GNNs to capture collaborative signals.Extensive experiments are conducted on a benchmark dataset in this work.The results indicate that the recommended GNNs indeed make sense for the training of item embeddings and that the proposed GE-ICF framework outperforms others in interactive recommendation tasks.
2)The proposed item similarity graph is of great significance because it contains as much collaborative information as user-item bipartite graphs while sharply decreasing graph size and shortening training time.
3)Our future work involves several possible directions.Firstly, we would like to investigate how to extend the model by incorporating rich user information(e.g., age, gender, nationality, occupation)and context information(e.g., location, dwell time, device)in a heuristic way.Secondly, we are interested in the effective utilization of RL in IRSs under the guidance of the diversity of recommendations, which is the key indicator of model exploration degree.
[1] Wu Y, DuBois C, Zheng A X, et al.Collaborative denoising auto-encoders for top-n recommender systems[C]//Proceedings of the Ninth ACM International Conference on Web Search and Data Mining.Los Angeles, CA, USA, 2016: 153-162.DOI: 10.1145/2835776.2835837.
[2] Chen X, Xu H, Zhang Y, et al.Sequential recommendation with user memory networks[C]//Proceedings of the Eleventh ACM International Conference on Web Search and Data Mining.Los Angeles, CA, USA, 2018: 108-116.DOI:10.1145/3159652.3159668.
[3] Zhao X, Xia L, Tang J, et al.Deep reinforcement learning for search, recommendation, and online advertising:A survey[J].ACM SIGWEB newsletter, 2019: 1-15.DOI: 10.1145/3320496.3320500.
[4] Wang H, Wu Q, Wang H.Factorization bandits for interactive recommendation[C]//Thirty-first AAAI Conference on Artificial Intelligence.San Francisco, CA, USA, 2017: 2695-2702.DOI: 10.5555/3298483.3298627.
[5] Zhao X, Zhang W, Wang J.Interactive collaborative filtering[C]//Proceedings of the 22nd ACM International Conference on Information & Knowledge Management.Los Angeles, CA, USA, 2013: 1411-1420.DOI: 10.1145/2505515.2505690.
[6] Wu Q, Wang H, Hong L, et al.Returning is believing: Optimizing long-term user engagement in recommender systems[C]//Proceedings of the 2017 ACM on Conference on Information and Knowledge Management.Singapore, 2017: 1927-1936.DOI: 10.1145/3132847.3133025.
[7] Zou L, Xia L, Du P, et al.Pseudo Dyna-Q: A reinforcement learning framework for interactive recommendation[C]//Proceedings of the 13th International Conference on Web Search and Data Mining.Houston, TA, USA, 2020: 816-824.DOI: 10.1145/3336191.3371801.
[8] Chen H, Dai X,Cai H, et al.Large-scale interactive recommendation with tree-structured policy gradient[C]//Proceedings of the AAAI Conference on Artificial Intelligence.Honolulu, Hawaii, USA, 2019, 33(1): 3312-3320.DOI: 10.1609/aaai.v33i01.33013312.
[9] Zheng G, Zhang F, Zheng Z, et al.DRN: A deep reinforcement learning framework for news recommendation[C]//Proceedings of the 2018 World Wide Web Conference.Lyon, France, 2018: 167-176.DOI: 10.1145/3178876.3185994.
[10] Zou L, Xia L, Gu Y, et al.Neural interactive collaborative filtering[C]//Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval.Xi’an, China, 2020: 749-758.DOI:10.1145/3397271.3401181.
[11] Wang X, He X, Wang M, et al.Neural graph collaborative filtering[C]//Proceedings of the 42nd International ACM SIGIR Conference on Research and Development in Information Retrieval.Paris, France, 2019: 165-174.DOI: 10.1145/3331184.3331267.
[12] Ma C, Ma L, Zhang Y, et al.Memory augmented graph neural networks for sequential recommendation[C]//Proceedings of the AAAI Conference on Artificial Intelligence, New York, USA, 2020, 34(4): 5045-5052.DOI: 10.1609/aaai.v34i04.5945.
[13] Wang H, Zhao M,Xie X, et al.Knowledge graph convolutional networks for recommender systems[C]//The World Wide Web Conference.Los Angeles, CA, USA, 2019: 3307-3313.DOI: 10.1145/3308558.3313417.
[14] Lei Y, Pei H, Yan H, et al.Reinforcement learning based recommendation with graph convolutional q-network[C]//Proceedings of the 43rd International ACM SIGIR Conference on Research and Development in Information Retrieval.Xi’an, China, 2020: 1757-1760.DOI: 10.1145/3397271.3401237.
[15] Mnih V, Kavukcuoglu K, Silver D, et al.Human-level control through deep reinforcement learning[J].Nature, 2015, 518(7540): 529-533.DOI:10.1038/nature14236.