Minimally invasive surgery has been substantially improved through percutaneous punctures in the past decades, and flexible needle puncture has been widely used for biopsy, brachytherapy, seed implantation, and anesthesia[1].However, performing the percutaneous puncture operation for some refined procedures is still difficult due to the lack of sufficient accuracy on motion control of puncture.The accuracy requirement for general operations is approximately at the millimeter level, while the accuracy requirement for the needle is quite crucial considering eye or infant surgery[2].
Many research achievements have been realized by flexible needle movement modeling in the past years[3].Park et al.[4-5] proposed a probability density equation to calculate the reachable probability density of the needle tip for the random performance of bevel-tip flexible needles during puncture.Furthermore, the random movement is planned in accordance with the probability that the needle tip would reach the predetermined state.Alterovitz et al.[6] considered the uncertain factors caused by individual differences between patients as well as the difficulty in predicting the interaction between the needle and the tissue and described these uncertain factors with a random probability distribution.Zhao et al.[7] established a needle-tissue interaction model that considers the nonlinear and anisotropic characteristics of soft tissues.However, the accuracy of these methods is insufficiently high due to the assumption of linear models for complex nonlinear human tissues.
Many algorithms have also been proposed to plan a suitable puncture path for flexible needles.Huo et al.[8] designed a puncture path plan based on the target particle swarm algorithm and regarded the flexible needle path planning problem as a multi-objective optimization problem.Arora et al.[9] used the Markov decision process to carry out robust path planning and guidance in a complex organization as well as the needle interaction environment.Gao et al.[10] planned the puncture path of flexible needles by using a geometric approximation method and established a forward and inverse kinematics model of flexible needles through D-H parameters and accessibility conditions to pierce the target point accurately.
1 Symbols and Definitions
1.1 Needle tip coordinate system
A bevel-tip flexible needle is constructed to analyze model parameters.The needle comprises an insertion speed υ, a rotation speed ω, and a rotation angle α.When the flexible needle is inserted into human tissue, the soft tissue will exert a reaction force on the oblique surface of the needle tip, which deflects the flexible needle and facilitates its movement along a certain arc.The bending curvature of the flexible needle is approximately constant during the puncture movement; that is, the flexible needle moves along an arc of a fixed radius r.
As shown in Fig.1, the D-H parameter method[10] is used to establish the forward motion model of the puncture needle, and the coordinate(r,L1, L2)is used to obtain the pose transformation of the needle tip relative to the global coordinate system.
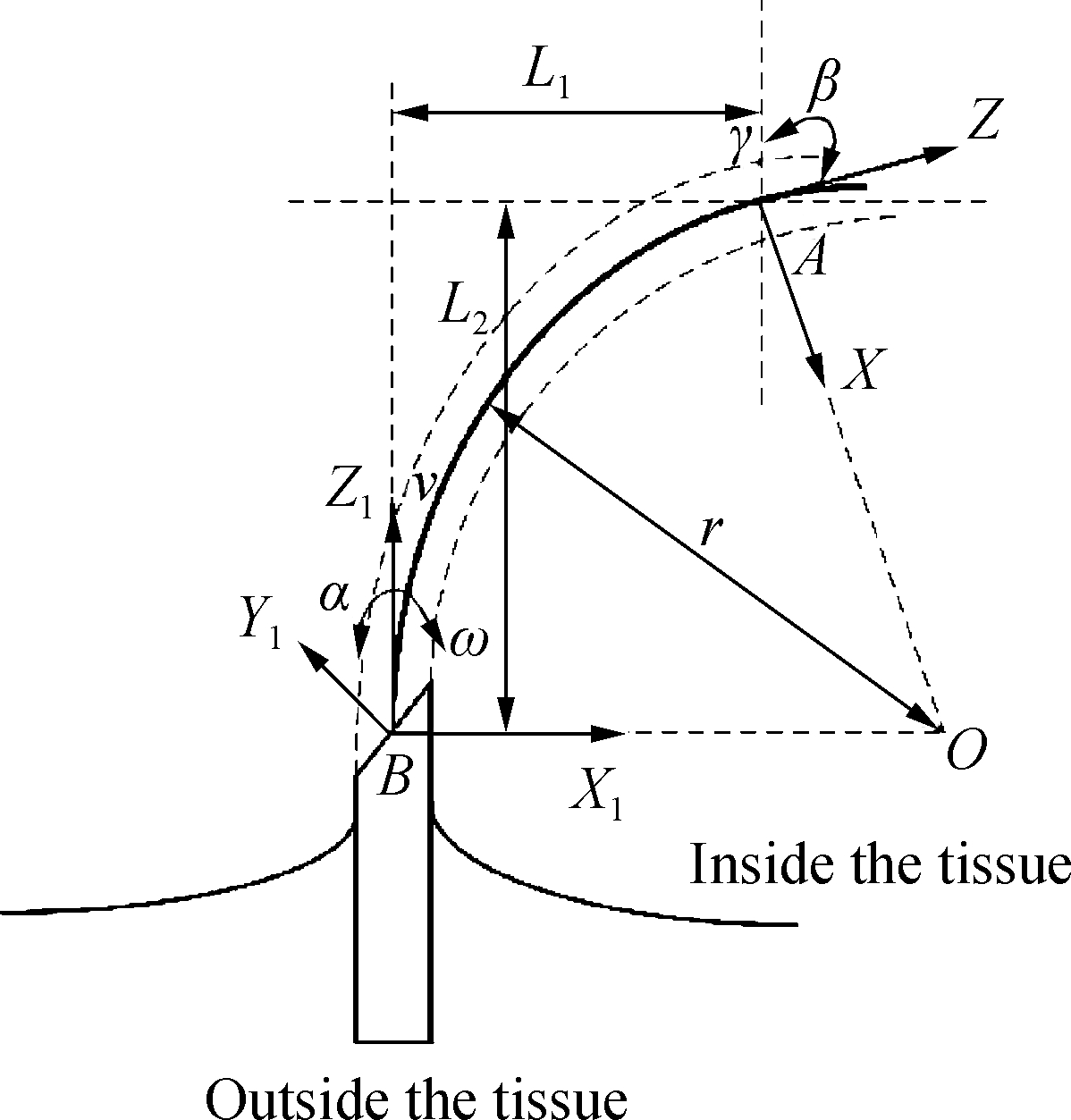
Fig.1 Establishment of puncture needle model in the turning process
1.2 Orthogonal set of flexible needle movement
Assume that the function f(t)considers the time of flexible needle movement, and the vector ζ contains angular velocity ω and linear velocity υ in the fixed reference frame f(t).The special orthogonal vector set SO(3)represents the space rotation matrix R3×3, and the Euclidean motion group SE(3)represents the three-dimensional motion of a rigid body[5].SO(3)can then be expressed as Euler angles α, β, and γ by the following:
R=RZ(γ)RX(α)RY(β)
(1)
(2)
2 Flexible Needle Error Analysis Model
2.1 Random error term
Suppose the input observation points in the experiment are S={S1,S2,…,Sm} and Si∈D⊆Rn, and the corresponding output response points are Z={Z1,Z2,…,Zm} and Zi⊆Rq.
The puncturing process of the needle into the soft tissue can be regarded as quasi-static, which is discretized to establish a model of the interaction between the needle and the soft tissue.Owing to the uncertainty of the needle insertion system, a simple way to capture random phenomena is to add a noise term such that the designed model can search for a reachable workspace with probability.The relational expression of the nonlinear function Y(Si)under Gaussian random noise is as follows:
ω(t)=ω0(t)+λn(t)
(3)
dN(t)=N(t+Δt)-N(t)=n(t)dt
(4)
where λ is the noise parameter; n(t)is Gaussian white noise.
2.2 Fokker-Planck equation model
Let ei(i=1,2,…,6)denote the standard basis for R6, and Ei is the antisymmetric matrix of ei, which is denoted as ![]() [5].The random vector X=[x1 x2 … x6]can be expressed as:
[5].The random vector X=[x1 x2 … x6]can be expressed as:
(5)
Assume that a flexible needle is inserted at a constant speed υ(t)with a rotation at an angular velocity ω(t)and finally reaches the desired posture(position and direction).With k as the curvature of the needle trajectory, an incomplete stochastic differential model with noise(3)can be established
ζdt=[kυ0 0 ω0(t)0 0 υ0]Tdt+[0 0 λ 0 0 0]TdN=
h(t)dt+HdN(t)
(6)
The Fokker-Planck equation is the development of the stochastic differential equation, which describes the probability density distribution function of the flexible needle position and its orientation with time t[5-6]
![]() =
=
![]() =
=
(7)
where ![]() represents the Lie derivative; D1(g,t),D2(g,t)respectively denote the growth rate of the mean and standard deviation of the probability distribution function.
represents the Lie derivative; D1(g,t),D2(g,t)respectively denote the growth rate of the mean and standard deviation of the probability distribution function.
(8)
When g(0)=e, ![]() the formula m(t)=exp(At)=exp(
the formula m(t)=exp(At)=exp(![]() A(τ)dτ)represents the arc trajectory of the flexible needle, where τ is the remaining time to realize the goal.
A(τ)dτ)represents the arc trajectory of the flexible needle, where τ is the remaining time to realize the goal.
The new function F(g,t)can be described as shown below to obtain an approximate functional form of f(g,t)in Eq.(8):
ρ(g,t)=F(m-1(t)g,t)
(9)
Suppose that the initial state of flexible needle movement can be expressed as ρ(g0|g,0)=ζ(g-g0), and D1(g,t)and D2(g,t)are respectively the growth rate of the mean and standard deviation of the probability distribution function, i.e., the drift and diffusion terms of the Fokker-Planck equation[5].
The following formulas can be obtained considering the Brownian motion of molecular collision to calculate the growth rate of the mean and standard deviation:
MΔu+γuΔt=![]() f′(t′)dt′
f′(t′)dt′
(10)
(11)
(12)
where M and T are the Brownian coefficients; u is the growth rate of the mean; γ represents the particle radius; k is medium viscosity.
The following equation can be derived from Eq.(12):
(13)
Assuming the presence of some diffusion in the model, the Fokker-Planck equation can be approximated as a Gaussian distribution function:
(14)
As in Eq.(14), the mathematical model of the flexible needle can be obtained by the Fokker-Planck equation.This model is recorded as the probabilistic path model, and its mean ![]() can be respectively denoted as follows:
can be respectively denoted as follows:
(15)
(16)
The probability density function ρ(g,t)lasts for a short period of time t.Meanwhile, the Fourier transform, which lasts for a long period of time, is used to convert the convolution in the time domain to the product in the frequency domain.
ρ(g,t1+t2)=ρ(g,t1)*ρ(g,t2)
(17)
2.3 Disjunctive Kriging model
Kriging is used to predict spatial modeling and the regression algorithm of random processes based on the covariance function, and its model considers the global certainty and local uncertainty in the experimental process[11].This model is also widely used in prediction, sensitivity analysis, and optimization conditions.However, the ordinary Kriging method is mainly used for linear models and ignores the uncontrollable factors, such as the nonlinearity and anisotropy of flexible needle movements in the soft tissue in puncture environments.Thus, this method produces inevitable errors in needle movement.The innovative point aims to extend the weight coefficient in ordinary Kriging into a nonlinear function and is used for nonlinear estimation on the random motion field of flexible needles.Therefore, this model mainly discusses the establishment of a prediction model based on the disjunctive Kriging method.
The deterministic response Zi∈R of ordinary Kriging[12] for any Si∈D⊆Rn can be expressed as a sum of Fi(t)and Ni(t).Fi(t)describes the motion of flexible needle tips involving position and velocity.Ni(t)is the deviation of Gaussian white noise, which can be defined as:
Zi(t)=Fi(t)+Ni(t) i=0,1,…,q
(18)
Suppose that the known observation point is {Zi=Z(Si)}.Thus, the unknown observation point ![]() is a function of each known observation point Zi, which can be optimized as nonlinear programming.
is a function of each known observation point Zi, which can be optimized as nonlinear programming.
(19)
where fi is a predetermined nonlinear function; ![]() is the disjunctive Kriging estimator.
is the disjunctive Kriging estimator.
![]() assumed to be the orthogonal projection of the real value Z in the vector space formed by fi[Z(Si)]to solve the function in Eq.(19).
assumed to be the orthogonal projection of the real value Z in the vector space formed by fi[Z(Si)]to solve the function in Eq.(19).
(20)
The sample set in this model is assumed to obey the joint normal distribution.Among them, Z(Si)corresponds to the standard normal distribution Y(Si), and the normal deformation function is ψ; therefore, Z(Si)=ψ[Y(Si)], and the equation can be obtained from Eqs.(19)and(20):
(21)
If the function is satisfied, then
(22)
Using the orthogonality of Hermite polynomials, ψ(y)can be expressed as
(23)
(24)
where ηk(y)is a Hermitian polynomial; Ck is a coefficient; k is an integer.
As in Eqs.(20)and(21), the equation can be obtained by using the k-order Hermitian polynomial to convert the above equation:
(25)
where fik is the coefficient of determination; ηk is the k-order Hermitian polynomial; i and k are both integers.
The following equations are obtained in accordance with the conditions of unbiasedness and minimum variance estimated by disjunctive Kriging:
(26)
where Z(S0)represents the true value at the observation point S0; E is the mathematical expectation; VAR is the variance.The following can be deduced from the above formula:
(27)
where ψ0j is the correlation coefficient between Y(S0)and Y(Sj).
Therefore, the relationship between the undetermined parameter fik and ![]() can be satisfied:
can be satisfied:
(28)
where ![]() is the correlation coefficient of Y(Si)and Y(Sj); bk is the k-order Hermitian expansion coefficient, which can be expressed as:
is the correlation coefficient of Y(Si)and Y(Sj); bk is the k-order Hermitian expansion coefficient, which can be expressed as:
(29)
The disjunctive Kriging variance can be obtained as shown below to solve the error assessment after Hermite polynomial expansion in Eq.(29):
(30)
Finally, the parameters obtained by the disjunctive Kriging algorithm(DKA)are evaluated, and the flexible needle puncture path model predicted by the probabilistic path algorithm(PPA)is simultaneously optimized.The errors due to uncertainty and nonlinearity are also reduced.
3 Model Simulation and Experiments
A simulation experiment was conducted to verify the feasibility of the flexible needle prediction model algorithm based on the DKA and validate the nonlinear planning of the optimal puncture path.The puncture path by ρ(g0|g,0), ![]() is initialized and given an input point P0 and target point Pt.Meanwhile, the flexible needle failed to acquire the optimal path, and the mean
is initialized and given an input point P0 and target point Pt.Meanwhile, the flexible needle failed to acquire the optimal path, and the mean ![]() of the PPA planning by the Fokker-Planck equation are obtained.Gaussian random noise is then added, and the variance
of the PPA planning by the Fokker-Planck equation are obtained.Gaussian random noise is then added, and the variance ![]() of the simulation test in the nonlinear environment by the disjunction Kriging is found.Finally, the model obtained the simulation test parameters of the PPA+DKA to update the optimal path.
of the simulation test in the nonlinear environment by the disjunction Kriging is found.Finally, the model obtained the simulation test parameters of the PPA+DKA to update the optimal path.
Many path planning algorithms are available for flexible needle puncture[13].The proposed model can improve the adaptability of puncture areas and avoidance of obstacles considering the nonlinearity and uncertainty of flexible needle puncture environments.Moreover, the model introduces Gaussian noise into the Fokker-Planck equation, optimizes the probability density function, obtains the mean value and covariance, and plans the puncture path with the PPA.The same starting and target points are provided for this simulation experiment in the current study, and the weight coefficient in the ordinary Kriging is extended into a nonlinear function.The nonlinear variance, mean square error, mean, and weighted mean of the disjunction Kriging optimization model are calculated on the basis of Hermitian expansion.The puncture path planned by the PPA based on the Fokker-Planck equation can then be optimized, thereby determining whether the path is optimal.Finally, the results based on the Fokker-Planck equation and DKA are used to predict the flexible needle path.
3.1 Probabilistic path planning based on the PPA
Flexible needle trajectory is assumed to be close to a perfect arc with determinate insertion position and direction to simulate the probabilistic path planning of the flexible needle in an ideal(no obstacle)situation.The unideal situations, including those involving obstacles or the insertion position and direction errors in the system, are also considered.
Errors will occur in the actual operation of the flexible needle due to the uncertainty of the needle position system.Fig.2 shows the path error caused by the insertion position and direction of the flexible needle, and Fig.2(a)demonstrates the prediction of the successful arrival path generated by the PPA for various starting positions near the optimal position.Fig.2(b)shows various starting directions.Fig.2(c)reveals probabilistic path simulation prediction from the starting to the target point under the uncertain situation with random obstacles, and the needle trajectory close to arcs avoids the obstacles.

(a)

(b)

(c)
Fig.2 Path error caused by the insertion position and direction of flexible needle.(a)Probabilistic path generated by position error;(b)Probabilistic path generated by direction error;(c)Probability path under a given obstacle
3.2 Error simulation test based on the DKA
The current study evaluates and predicts factors, such as global certainty, local uncertainty, nonlinearity, and anisotropy, according to the covariance function and continuously optimizes puncture path based on the random probability path planning process to obtain the result of modeling random data using disjunctive Kriging.Assuming that the input is random white noise, the parameter values of the flexible needle puncture process are obtained through multiple simulation verifications.
The variance VAR, mean square error MSE, mean EI, and weighted mean WEI calculated by the DKA with random noise input of the flexible needle are used to evaluate the error simulation effect of flexible needle puncture, as shown in Fig.3.Among the 25 sets of test values, some inherent variability abnormal values caused by irregular muscle tissues are eliminated.VAR is the variance of model evaluation, and the range of all test values after removing outlier values is between 0.4 and 0.8 mm2, which is used to estimate the error of the simulation results of flexible needle puncture.The clinical requirements of flexible needle puncture surgery indicate that the error should not exceed 4 mm2 and the abnormal value is also 1.16 mm2<4 mm2; thus, the simulation results meet the clinical requirements.MSE calculates the average error of the model by evaluating the MSE of multiple points.The measurement range after removing the outlier value is between 0.30 and 0.05 mm2, which is a small error value obtained after several optimizations.EI, which is the expected improvement value of the prediction model, is used to optimize the model continuously, and the range of measurement results after removing outlier values is between 0.02 and 0.08 mm.WEI is based on EI and forecasts the weighted expected value according to the level of different influencing factors, thereby reducing errors.
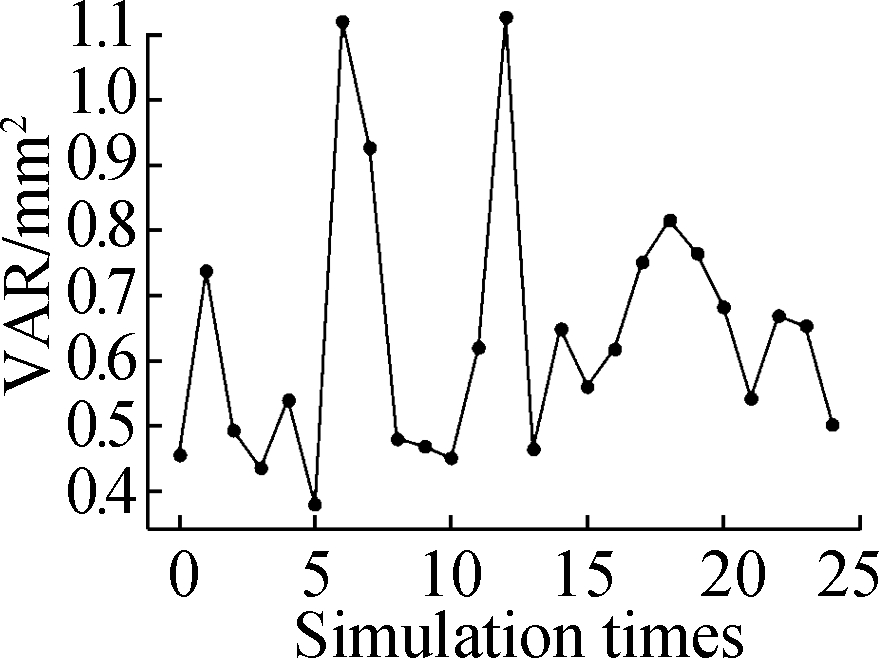
(a)
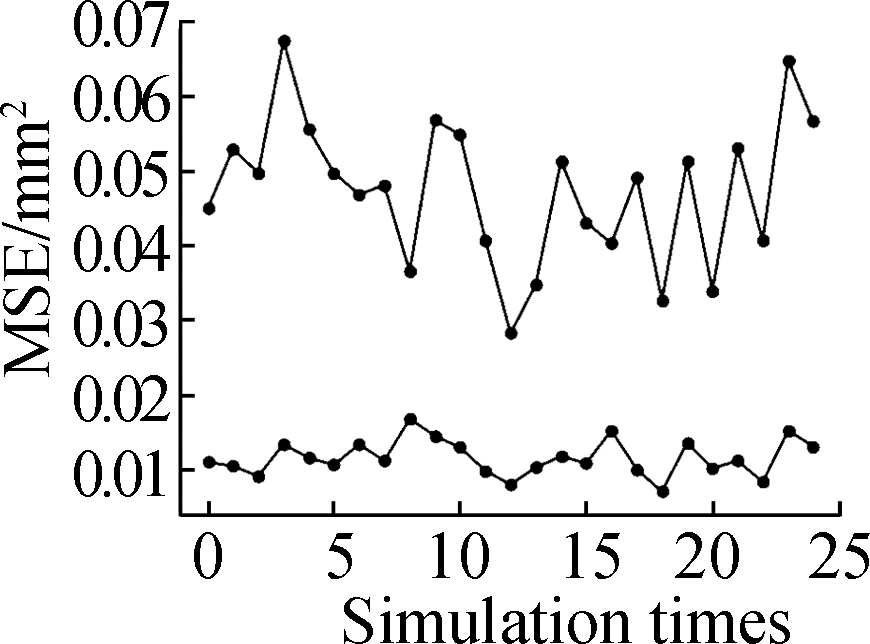
(b)

(c)
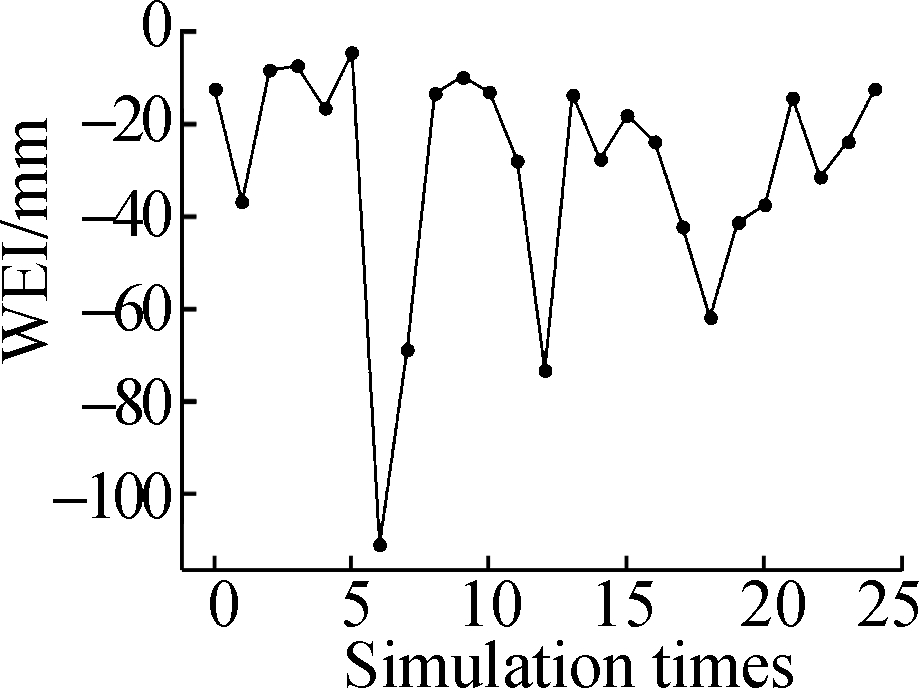
(d)
Fig.3 Estimated puncture parameter values of the flexible needle under the DKA.(a)Variance;(b)Mean square error;(c)Mean;(d)Weighted mean
Fig.4 shows that the simulation tests of the interpolation process have a good fitting effect based on the puncture experiment of the optimal planning path and the error comparison between test and training values under the DKA.The system error of the flexible needle puncture model is much less than 2 mm, which meets the clinical requirements of interventional surgery.This model also increases the probability of reaching the target and reduces errors in an uncertain nonlinear environment, which verifies the effectiveness of the proposed model.
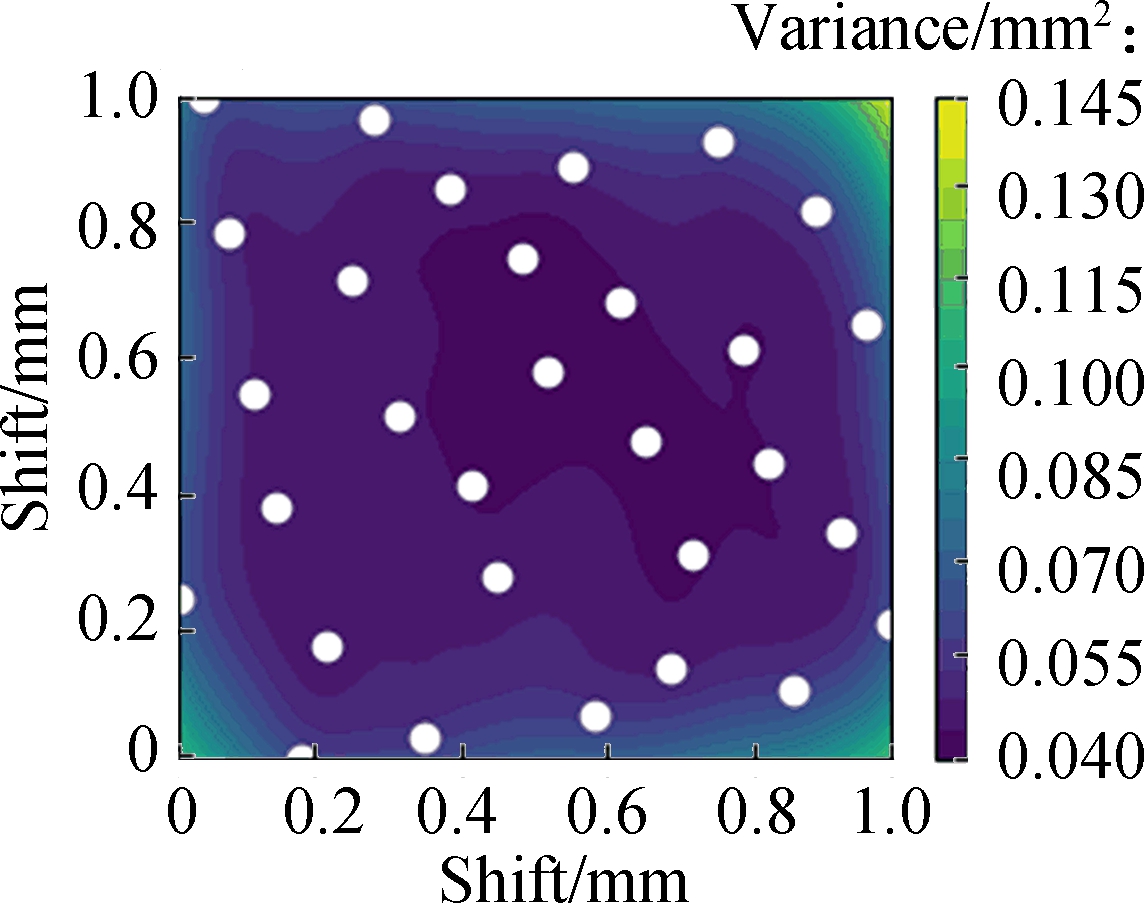
Fig.4 Error distribution map between the test and training values under the DKA
The prediction model, which is based on the DKA as well as the insertion position, insertion direction, and irregularity of inserted tissues and obstacles, reduces the errors in the process of flexible needle puncture.Some previous studies are available in[14-15].The current study used the path planning diagram in the two-dimensional environment to demonstrate the path of the flexible needle puncture soft tissue.The simulation path diagrams under the PPA are shown in Fig.5.Meanwhile, Figs.5(a)to 5(d)present a continuous optimization process plan by the PPA under definite starting and target points and similar obstacle environments.The red line represents the puncture path.The result indicates that the optimization process performed by disjunctive Kriging via continuous interpolation obtains optimized training values based on the test results of the above-mentioned parameters, such as variance and mean, thus allowing the gradual planning of the optimal path based on the PPA.This process also improves the targeting rate of flexible puncture needles.
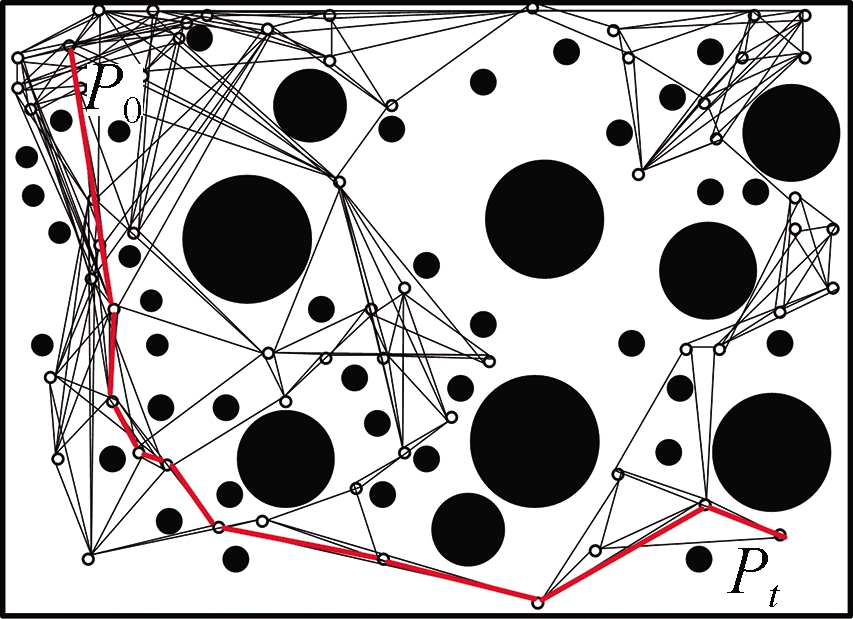
(a)
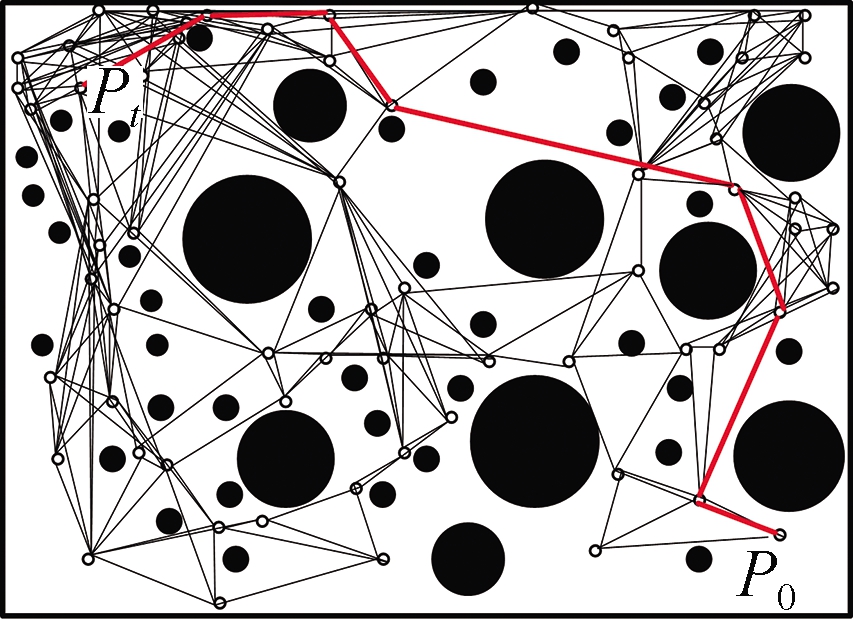
(b)

(c)

(d)
Fig.5 PPA planning diagram.(a)Optimization process 1;(b)Optimization process 2;(c)Optimization process 3;(d)Optimization process 4
3.3 Comparison of the PPA and PPA+DKA
The parameter values that must be optimized for puncture simulation are obtained from the formula derived in module three.Meanwhile, the parameters in the program are optimized through the PPA+DKA and data processing, such as box plots, to obtain the parameter values for the soft tissue puncture optimization of the flexible needle continuously.
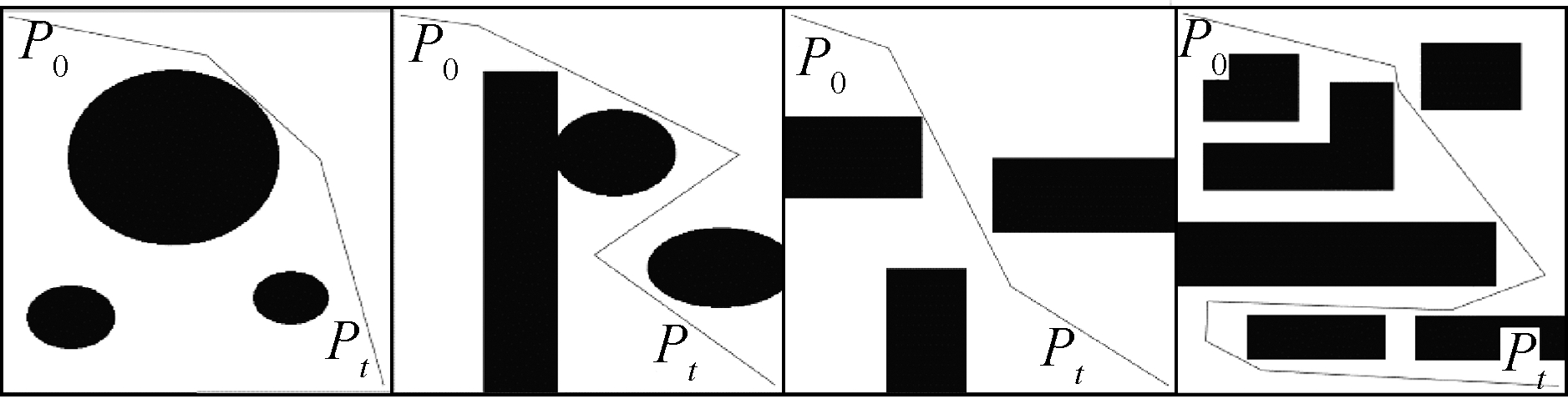
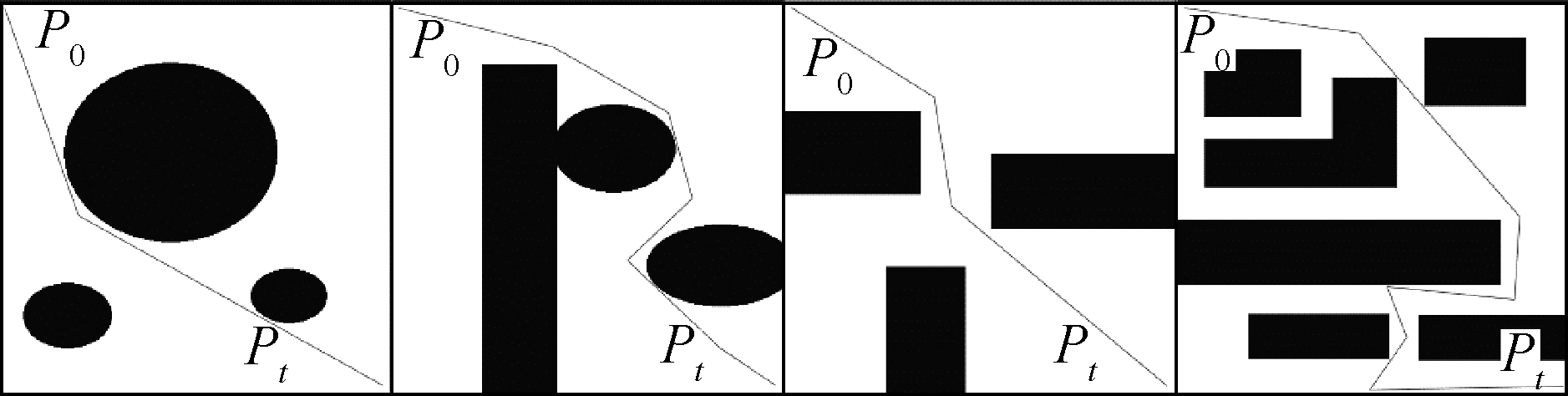
Four different organization maps with obstacles in a nonlinear and uneven environment under the same starting and target point are designed to further verify the proposed model.A comparison simulation with the PPA and PPA + DKA models based on the path model is also performed, as shown in Fig.6.
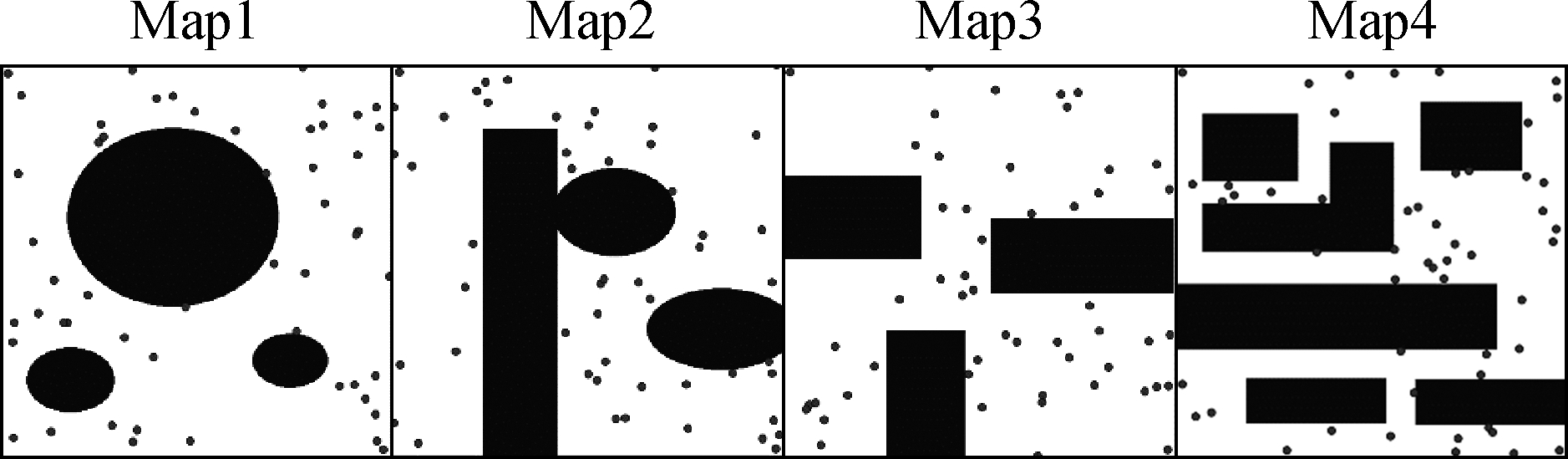
(a)
(b)
(c)
Fig.6 Path contrast diagrams of the PPA and PPA+DKA.(a)Four different organization maps with obstacles in a nonlinear and uneven environment;(b)Path planning of flexible needles under the PPA;(c)Path planning of flexible needles under the PPA+DKA
As shown in Fig.6 and Tab.1, path planning by the PPA+DKA is more flexible than that of the PPA under the same uncertain simulated map environment.The path planning time is slightly increased under the PPA+DKA, but the optimal path length is reduced, and the uncertainty and nonlinearity of the environment are fully considered.The puncture path length of flexible needles in a random environment should be considered for nonlinear soft tissue with different obstacles.A total of 32 experiments on 4 different maps were performed, and each group performed 8 tests.The simulation results are still consistent with the above conclusions.The simulation path planning time and puncture path length value based on the random selection of eight sets of the test are shown in Fig.7.
Tab.1 Simulation data contrast of the PPA and PPA+DKA

Maplabel Path planning time/msOptimal path length/mmPPAPPA+DKAPPAPPA+DKA11.391.366.215.8322.993.136.746.5333.203.226.156.1846.416.339.258.24
Fig.7 indicates that the path training time of most groups of the PPA is longer than that of the PPA+DKA.Meanwhile, the time difference of the selected training groups between the PPA and PPA+DKA after the data filtering process is negligible.The path length of the PPA+DKA is significantly better than that of the PPA.Considering the damage to the human body by flexible needles and the complex environment of nonlinear soft tissues, the PPA+DKA is effective because it can reduce the puncture error and the length of the puncture path and finally reach the target point despite its slightly long calculation time.

(a)

(b)
Fig.7 Contrast simulation value of the PPA and PPA+DKA.(a)Training test time;(b)Training test path length
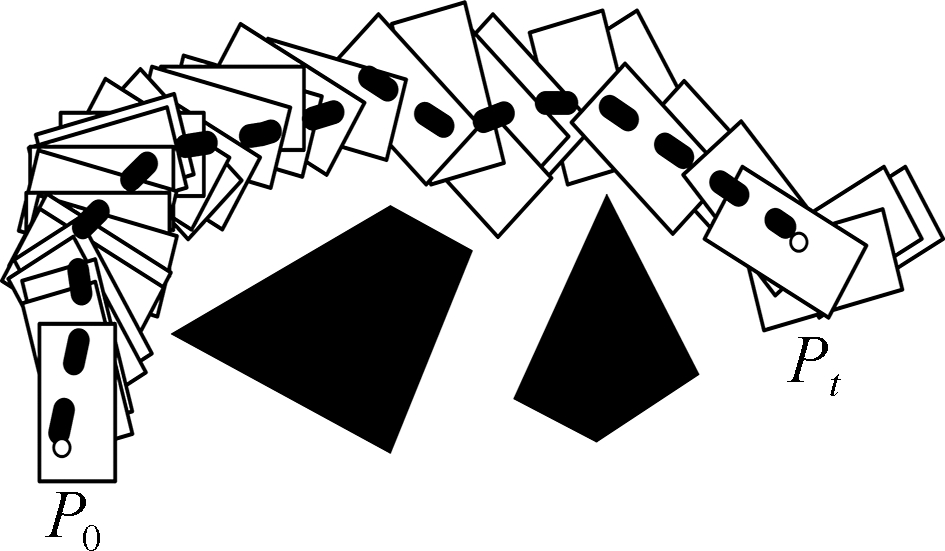
The simulation test path diagram is imitated as a flexible needle tip puncture process shown in Fig.8, which is recorded as the path planning diagram of the PPA and PPA+DKA.The detailed needle tip path planning diagram in Fig.8 shows that the path length of Fig.8(b)is significantly smaller than that of Fig.8(a).The simulation test times of Figs.8(a)and 8(b)are 6.14 and 6.08 ms, respectively, which again verifies the simulation test results in Figs.6 and 7.The above comparative simulation experiment shows that flexible needles can accurately reach target points with the shortest path under the proposed model.

(a)
(b)
Fig.8 Flexible needle path of the PPA and PPA + DKA.(a)Path of the flexible needle puncture tip under the PPA;(b)Path of the flexible needle puncture tip under the PPA+ DKA
4 Conclusions
1)The flexible needle path prediction model effectively improves the target accuracy in needle surgery.The prediction model can reduce uncertainty errors in body membrane tissues.Thus, the proposed model is crucial for biopsy, brachytherapy, and other medical procedures that require accurate needle implantation.
2)This model combines the Fokker-Planck equation to plan the probabilistic path of flexible needles, analyzes the nonlinearity and uncertainty through disjunctive Kriging interpolation, continuously optimizes the model according to test parameter values, and obtains the predicted path error of flexible needles.The results prove that this model improves the target rate and obtains the optimal path in an uncertain environment during the insertion.
3)The proposed algorithm model can also effectively optimize puncture paths under uncertain conditions.Compared with other algorithms, the proposed model uses the Fokker-Planck equation combined with disjunctive Kriging to predict external conditions, thus avoiding the assumption errors caused by the ideal state of linearity and uniformity in soft tissue puncture.This model can effectively handle the generality, uncertainty, and complexity of the puncture environment; it is also consistent with the application of flexible puncture needles in realistic operations.
[1] Zheng M H, Ma J J, Wu C.Twenty year progression and future directions of minimally invasive surgery[J].Chinese Journal of Practical Surgery, 2020, 40: 23-26.DOI: 10.19538/j.cjps.issn1005-2208.2020.01.03.(in Chinese)
[2] Yue L, Kong F T , Liu B,et al.Development of new cable-driven minimally invasive surgical robot[J].International Journal of Automation and Control, 2019, 13: 324-346.DOI: 10.1504/IJAAC.2019.098583.
[3] Ni Z Q, Wang T M, Liu D.Survey on medical robotics[J].Journal of Mechanical Engineering, 2015, 51: 45-52.DOI:10.3901/JME.2015.13.045.(in Chinese)
[4] Park W, Wang Y,Chirikjian S.Path planning for flexible needles using second order error propagation[J].Springer Tracts in Advanced Robotics, 2010, 57: 583-598.DOI: 10.1007/978-3-642-00312-7_36.
[5] Park W, Wang Y,Chirikjian S.The path-of-probability algorithm for steering and feedback control of flexible needles[J].International Journal of Robotics Research, 2010, 29: 813-830.DOI: 10.1177/0278364909357228.
[6] Alterovitz R, Lim A, Goldberg K, et al.Steering flexible needles under Markov motion uncertainty[C]//2005 IEEE/RSJ International Conference on Intelligent Robots and Systems.Las Vegas, CA, US, 2005:120-125.DOI: 10.1109/IROS.2005.1544969.
[7] Zhao Y J, Zhang Y D,Shao J P.Kinematic modeling and experimental study of flexible needle[J].Robot, 2010, 32: 666-673.DOI: 10.3724/SP.J.1218.2010.00666.(in Chinese)
[8] Huo B Y, Zhao X G, Han J D, et al.Puncture path planning for bevel-tip flexible needle based on multi-objective particle swarm optimization algorithm[J].Robotics, 2015, 37:385-394.DOI: 10.13973/j.cnki.robot.2015.0385.(in Chinese)
[9] Arora S, Scherer S.Randomized algorithm for informative path planning with budget constraints[C]//2017 IEEE International Conference on Robotics and Automation.Singapore, 2017:4997-5004.DOI: 10.1109/ICRA.2017.7989582.
[10] Gao D D, Li Q, Lei Y, et al.Geometric approximation approach based research on kinematics of bevel-tip flexible needles[J].Journal of Zhejiang University(Engineering Science), 2017, 51: 706-713.DOI: 10.3785/j.issn.1008-973X.2017.04.010.(in Chinese)
[11] Papachristos C, Khattak S, Alexis K.Uncertainty-aware receding horizon exploration and mapping using aerial robots[C]//2017 IEEE International Conference on Robotics and Automation.Singapore, 2017:4568-4575.DOI: 10.1109/ICRA.2017.7989531.
[12] Ma X L, Zhou K R.Application of disjunctive Kriging technology in reservoir description[J].Journal of China University of Petroleum(Edition of Natural Science).1992, 16: 116-122.(in Chinese)
[13] Dang T,Mascarich F, Khattak S.Graph-based path planning for autonomous robotic exploration in subterranean environments[C]//2019 IEEE/RSJ International Conference on Intelligent Robots and Systems.Macao,China,2019:3105-3112.DOI: 10.1109/IROS40897.2019.8968151.
[14] Webster J, Robert J , Kim J S, et al.Nonholonomic modeling of needle steering.[J].International Journal of Robotics Research, 2006, 25: 509-525.DOI: 10.1177/0278364906065388.
[15] Bircher A, Alexis K,Burri M.Structural inspection path planning via iterative viewpoint resampling with application to aerial robotics[C]//2015 IEEE International Conference on Robotics and Automation.Seattle, WA, US, 2015:6423-6430.DOI: 10.1109/ICRA.2015.7140101.