Welding assembly is a widely used joining method due to its high productive characteristics and is applied in aerospace, aircraft, automobile, and marine engineering industries[1-2].During this process, the existing deformation, residual stress, and temperature distribution have a great impact on the whole product and the assembly performance.Understanding the mechanism of welding deformation and the interrelation among welding distortion, temperature, and residual stress is of paramount importance in the actual manufacturing process.
For welding assembly, researchers focused on the prediction, numerical simulation, and calculation of relative welding problems.To compute the accumulated distortion during welding assembly, Murakawa et al.[3] proposed a prediction method that involves inherent strain theory and interface element formulation and considers the shrinkage caused by heat input and gap size.Considering the effect of jig constraint on welding deformation, Ma et al.[4-5] simulated the transient temperature and welding deformation with the 3D thermal elastic-plastic finite element(FE)method and analyzed the welding residual stress.Bhatti et al.[6] examined the influence of thermo-mechanical material characteristics of different steels on welding residual stress and angular distortion for T-fillet joints.Other researchers also employed the thermal elastic-plastic FE method to predict the residual stress distribution and distortion by considering the effect of different plate thicknesses and welding sequences[7-8].Cheon et al.[9] conducted the numerical thermal-metallurgical-mechanical analysis of the gas metal arc welding process to predict the stress distribution and concentration near the welding line and under nonlinear deflection.Mondal et al.[10] researched the effect of welding sequences on residual stress and angular deformation for arc welding fillet joints with FE simulation.Lee et al.[11] proposed a computationally efficient method to predict welding distortion using scalar input variables and FE-measured distortion rate for large welded structures.Ahmad et al.[12] proposed the thermo-mechanical FE simulation for three-pass TIG welding to analyze the thermal distribution, residual stress, and interpass temperature and investigate the effect of welding speed on residual stress and thermal distribution.Arunkumar et al.[13] presented the transient thermal analysis through ANSYS parametric design language and FE simulation with a 3D conical heat source model to predict the temperature distribution and residual stress.The abovementioned studies mostly employed methods combined with FE, such as the inherent strain theory, equivalent force method, and thermo-elasto-plastic FE method, to predict and simulate welding distortion or residual stress.However, only a few researchers examined the interrelation among welding distortion, temperature, and residual stress and predicted these parameters after welding assembly from qualitative and quantitative perspectives.
In this work, the effect of welding direction, clamping, fixture release time, fixed constraints, and welding sequences on welding properties was analyzed with FE simulation.The mapping relationship between welding deformation, temperature, and residual stress was also explored.Various machine learning algorithms were utilized to predict the variation trend of welding characteristics and establish their mapping relationship.
1 FE-Based Simulation Analysis of Parallel T-joint Welding Assembly Characteristics under Various Conditions
The parallel T-shaped assembly unit was selected as the research object from the whole antenna structure, and its FE model is shown in Fig.1.This unit consists of three web plates and one base plate with thicknesses of 2 and 6 mm, respectively.Other sizes were also marked.Moreover, the black and red arrows denote the welding direction.For the analysis of the welding characteristics of thin-wall parts, the selected key points(points 1 to 30 on the web plate, points 31 to 96 on the base plate)were evenly distributed on the web plate and base plate, and the distance between these points on the base plate and the bottom of web plate was 8 mm.For accurate welding simulation results, the mesh of the connection zone for the web plate and base plate was dense, and the other meshes were relatively sparse.
A 6082 aluminum alloy material was adopted for thin-walled parts.After the welding characteristics of thin-walled parts were analyzed through FE simulation with arc welding, the constraint conditions of the parallel T-shaped thin-walled parts are marked in Fig.1; that is, the fixed constraints are the four corners of the base plate, and the clamping constraint zone of web plates 2 and 3 are the same as the clamping zone for the first web plate.The adopted welding heat source of high energy density was used as the double ellipsoid heat source model to control and reduce welding deformation, as shown in Fig.2.The relative welding parameters for the parallel T-joint thin-walled parts are shown in Tab.1, and the fillet weld dimensions for the FE model are marked in Fig.3.
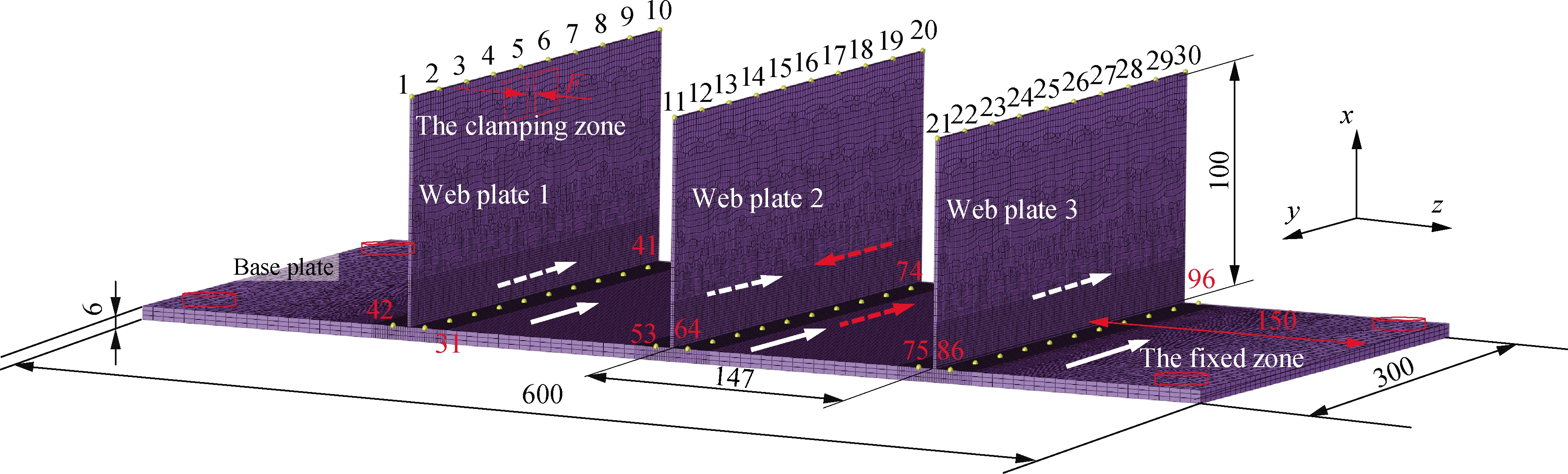
Fig.1 FE model of the parallel T-shaped structure of thin-walled parts(unit:mm)
Tab.1 Relative welding parameters

Welding parameterHeat source parameterWeld sizeWelding speed/(mm·s-1)Welding voltage/VWelding current/AWelding efficiencyFront length/mmRear length/mmWidth/mmDepth/mmThroat thickness ht/mmHorizontal leg length hl/mmVertical leglength vl/mmConcavity c12201800.81.562.52.522.828 432.828 430.2
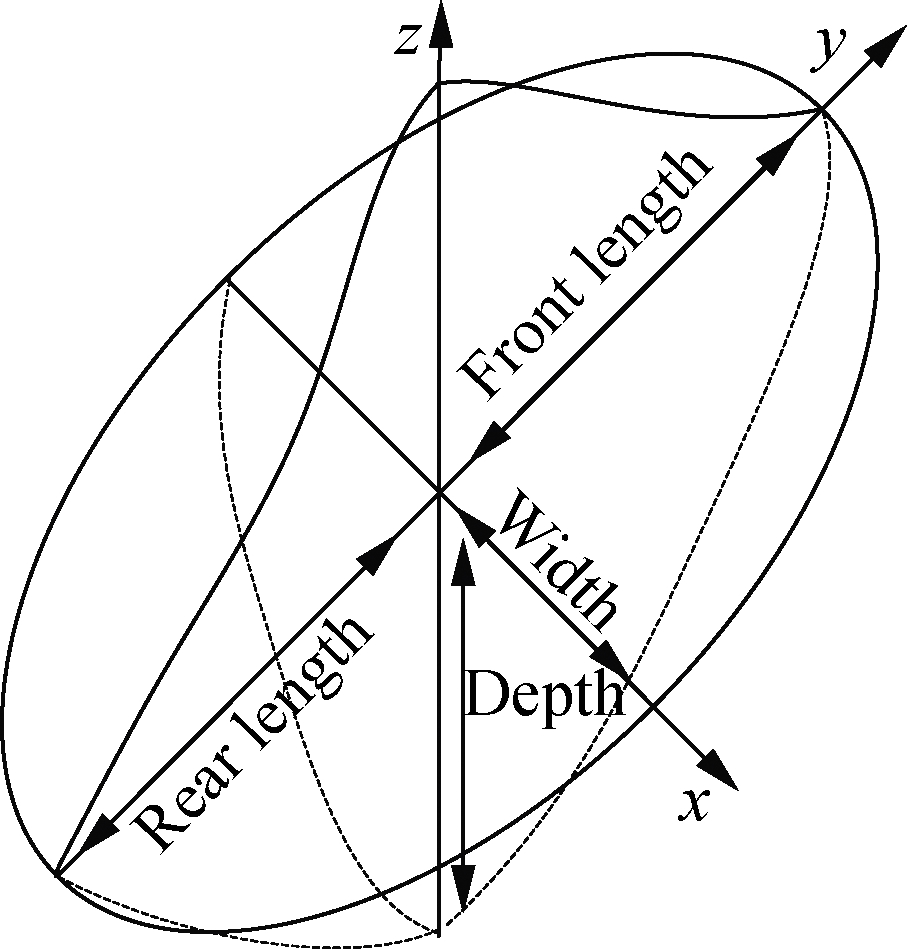
Fig.2 Double ellipsoid heat source model[6,14]

Fig.3 FE model and dimension diagram of fillet weld
In order to better analyze the welding assembly characteristics of thin-walled part structure under various conditions, when the FE simulation analysis is carried out, the clamping force for fixtures is 200 N and its spring stiffness is 1 MN/m, and the relative parameters of welding process are shown in Tab.1.
The differences of four conditions are as follows:
1)The first condition is that three web plates are simultaneously welded, and its welding direction is the black arrow direction which is along the Y-axil negative direction in Fig.1.The total analysis time for the welding process is 360 s, the release time of fixtures is the 240th s, the release time of the fixed constraints is the 360th s.
2)The second condition is that three web plates are simultaneously welded, the welding direction of web plates 1 and 3 is the black arrow direction which is along the Y-axil negative direction, and the welding direction of web plate 2 is the red arrow direction in Fig.1, which is respectively along the Y-axil positive direction and negative direction.The total analysis time for the welding process, the release time of fixtures and the release time of the fixed constraints are the same as the first condition.
3)The third condition is that three web plates together with a base plate are welded.Moreover, the welding time of web plate 1 starts from zero, the welding time of web plate 2 starts from the 75th s, and the welding time of web plate 3 starts from the 150th s, and their welding direction is the black arrow direction which is along the Y-axil negative direction in Fig.1.The total analysis time for the welding process is 600 s, the release time of fixtures is at the 480th s, and the release time of the fixed constraints is at the 600th s.
4)The fourth condition is that three web plates together with base plate are welded, and the beginning time of the welding assembly for web plates 1, 2 and 3 together with base plate are the same as the third condition, and the welding direction of web plates 1 and 3 is the black arrow direction, and the welding direction of web plate 2 is red arrow direction in Fig.1.The total analysis time for welding process, the release time of fixtures and the release time of the fixed constraints are the same as the third condition.
1.1 Effect of welding direction and clamping constraint of fixtures on welding assembly characteristics
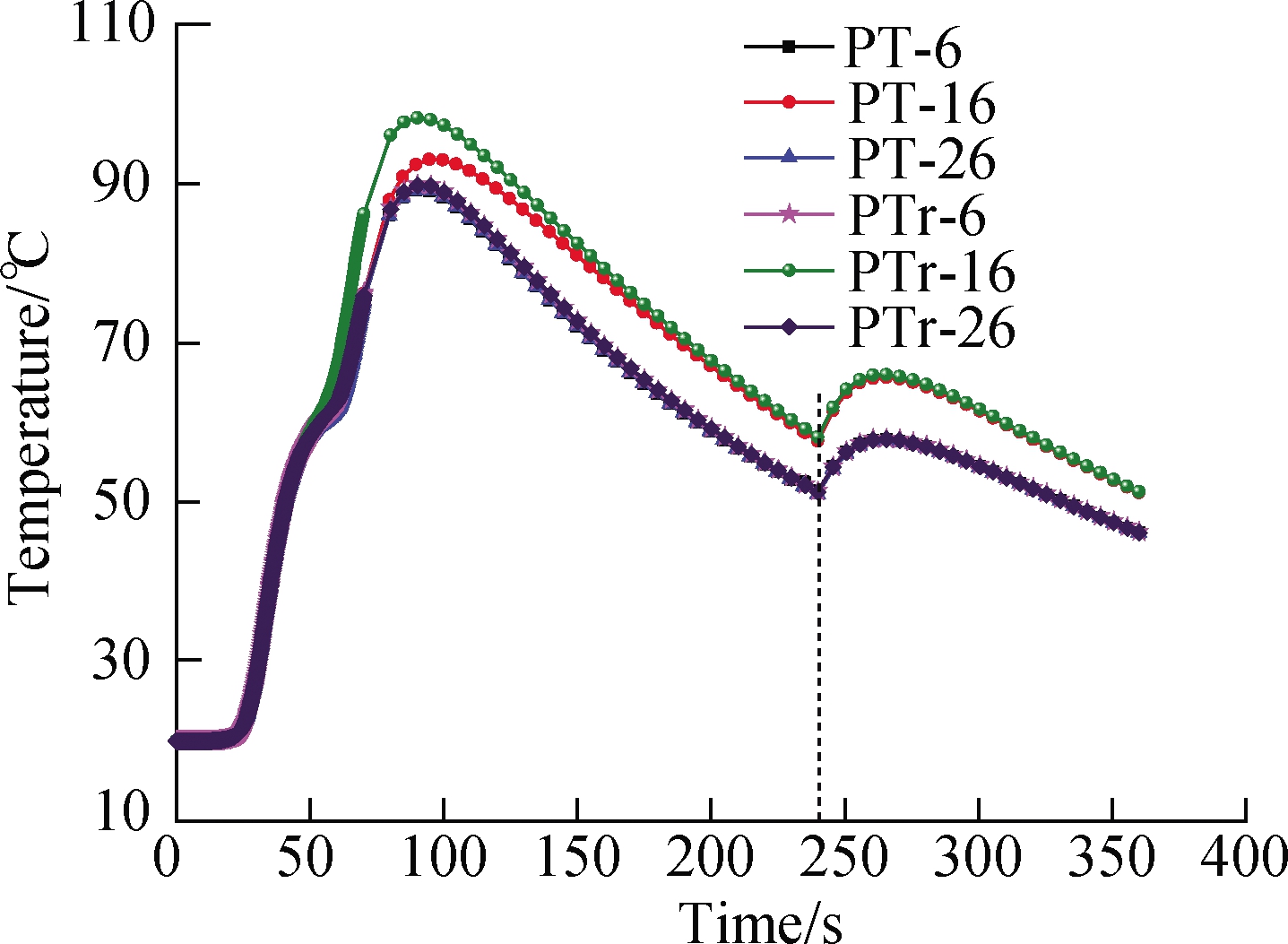
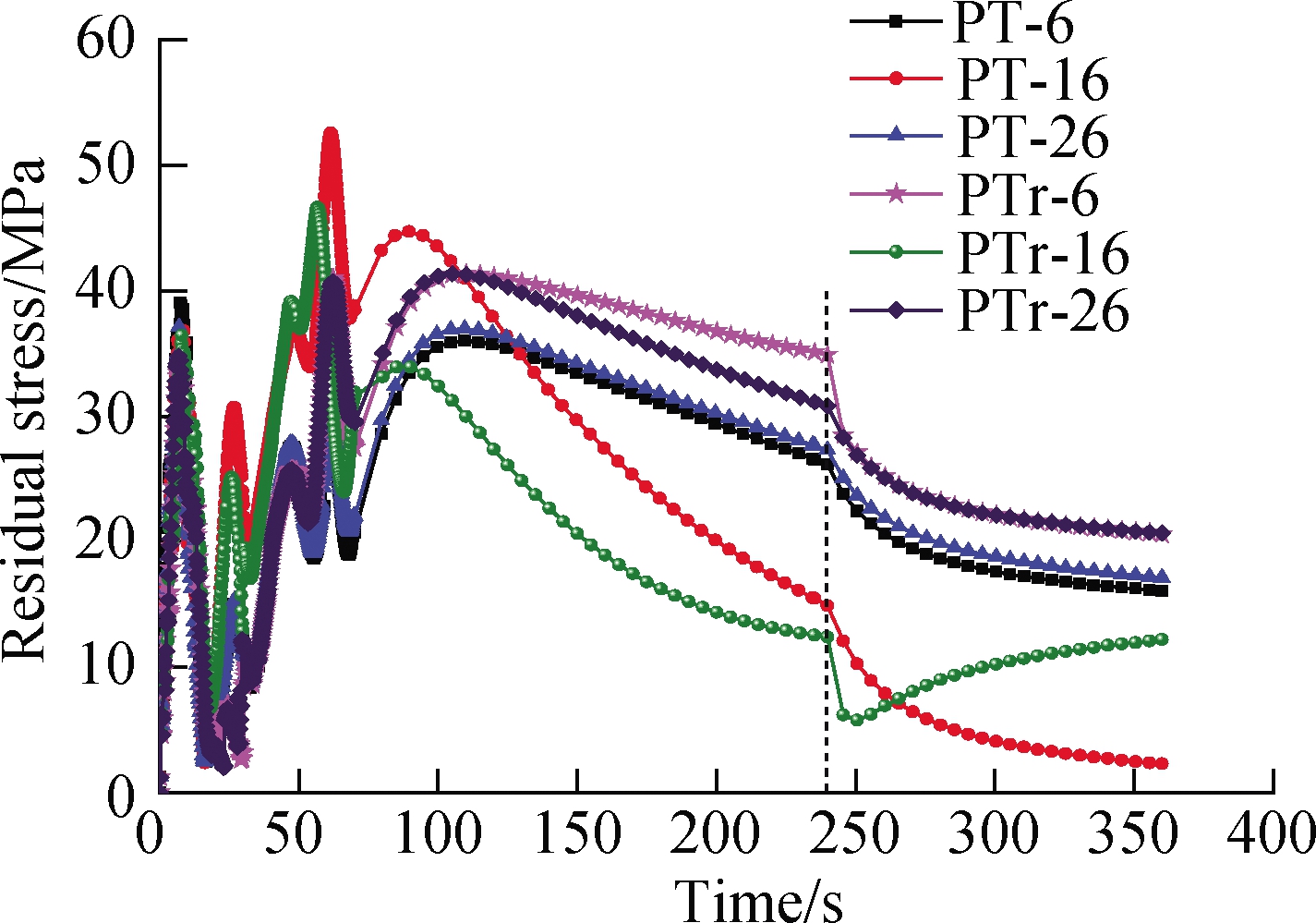
As shown in the T-shaped thin-walled parts in Fig.1, the key points 6, 16, and 26 on the web plate were chosen to analyze the variation rules of temperature, residual stress, and welding deformation and their mapping relationship.For the welding assembly characteristics under the first and second conditions, their variation trends and results during any change in welding direction are shown in Fig.4.PT-6, PT-16, and PT-26 denote the key points 6, 16, and 26, respectively, on web plates 1, 2, and 3 of the parallel T-shaped thin-walled part.Meanwhile, PTr-6, PTr-16, and PTr-26 represent the key points 6, 16, and 26, respectively, on the web plate under reversed welding direction, that is, the opposite welding direction of web plate 2.
(a)
(b)

(c)
Fig.4 Temperature, residual stress, and deformation curve diagram for simultaneous welding when changing welding direction and temperature distribution nephogram.(a)Temperature curve diagram;(b)Residual stress curve diagram;(c)Welding deformation curve diagram
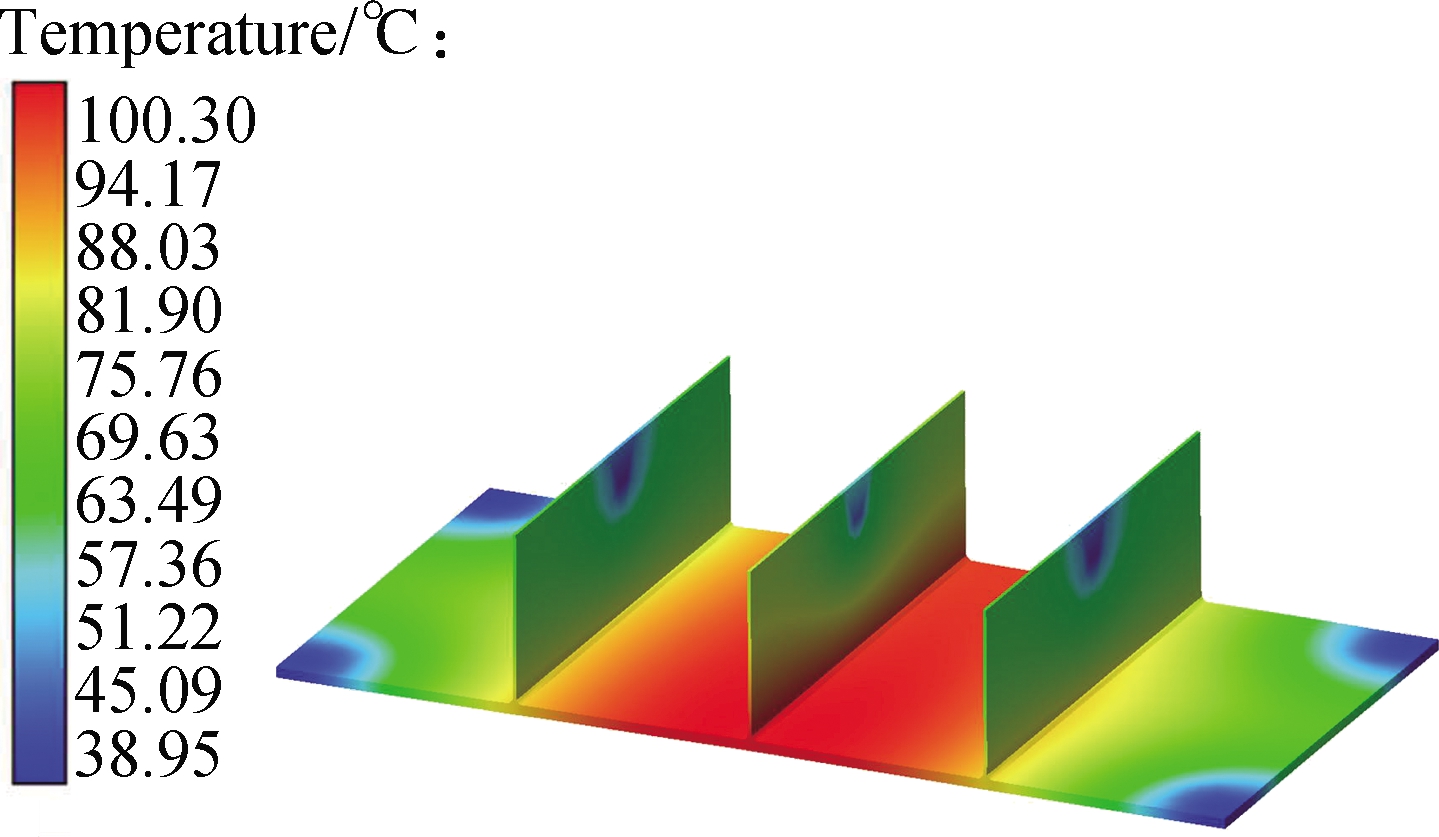
As shown in Fig.4(a), when the welding direction of the web plate was changed, an approximate temperature variation trend was observed under the first and second conditions.In the preliminary welding stage of the thin-walled part, the welding temperature of thin-walled parts was basically at the ambient temperature of 20 °C.With the increase in welding time, the temperature sharply increased and then decreased.At the 240th s, the clamping constraint of fixtures was released, and the temperature of the selected points 6, 16, and 26 on the thin-walled part slightly increased, then slightly dropped, and finally reached the ambient temperature after cooling.On the basis of the temperature distribution nephogram at the 240th s in Fig.5, the welding assembly has a greater impact on the temperature distribution of web plate 2 compared with that of web plates 1 and 3.This result can be partially attributed to the coupling effect and mutual influence of the welding temperature field on the three web plates together with the base plate.However, the temperature curve diagram in Fig.4(a)also shows that the difference in welding direction has a slight influence on the variation of the welding temperature of the thin-walled parts.

(a)
(b)
Fig.5 Temperature distribution nephogram at the 240th s under the first two conditions corresponding to Fig.4(a).(a)Temperature nephogram under the first condition;(b)Temperature nephogram under the second condition
As shown in Fig.4(b), when the welding direction was changed, the residual stress of thin-walled parts was also greatly altered, especially from an overall perspective.The residual stress of key points 6 and 26 under the first condition was less than that under the second condition.Owing to the coupling effect and mutual influence of welding assembly, the residual stress of key point 16 on the web plate also varied under the first two conditions.When the fixtures were released at the 240th s, the residual stress of key point 16 under the first condition sharply declined until it reached a steady state.Meanwhile, the residual stress of key point 16 under the second condition slightly decreased and then slightly increased to reach a steady state.Moreover, the residual stress fluctuated by increasing and reaching the peak value at 60th s and then sharply declining and increasing again to a small peak value at about 90th s.After fluctuating, the residual stress continued to decline until the fixtures were released to reach a steady state.These results showed that the welding residual stress is not only affected by the welding direction to a great degree but also by the fixture release and the coupling effect and mutual influence of the welding assembly of the multiple thin-walled parts.
As shown in Fig.4(c), the welding deformation of key point 6 under two conditions exhibited a significant change within 60 to 70 s.At the 240th s, the clamping constraint of fixtures on web plate 2 was released, and the welding deformation of key points 6, 16, and 26 on the thin-walled parts sharply increased and then stabilized.Owing to the difference in the welding deformations among the key points, the different welding directions influenced the welding deformation to a certain extent, as indicated by the variations in the welding deformation curve for different key points.However, the release of fixture constraints had a great impact on the spring-back of welding deformation in the later welding assembly stage.Therefore, welding deformation is affected by single factors and the combined effects of multiple factors.
On the basis of the above results, the different welding directions have an influence on temperature, residual stress, and welding deformation.Before the clamping constraint of fixtures was released at the 240th s, no specific one-to-one correspondence was observed among temperature, residual stress, and welding deformation, as shown in their variable curves.However, after the release of the clamping constraint of fixtures at the 240th s due to the existence of residual stress for the welding assembly between the web and base plates, the welding temperature increased in a shorter time, and the residual stress declined, and the welding deformation intensified.When the welding temperature dropped, the residual stress of key points also generally declined, and the welding deformation slowly increased until it reached equilibrium.These results reveal a variation relationship between temperature, residual stress, and welding deformation over a period of time.
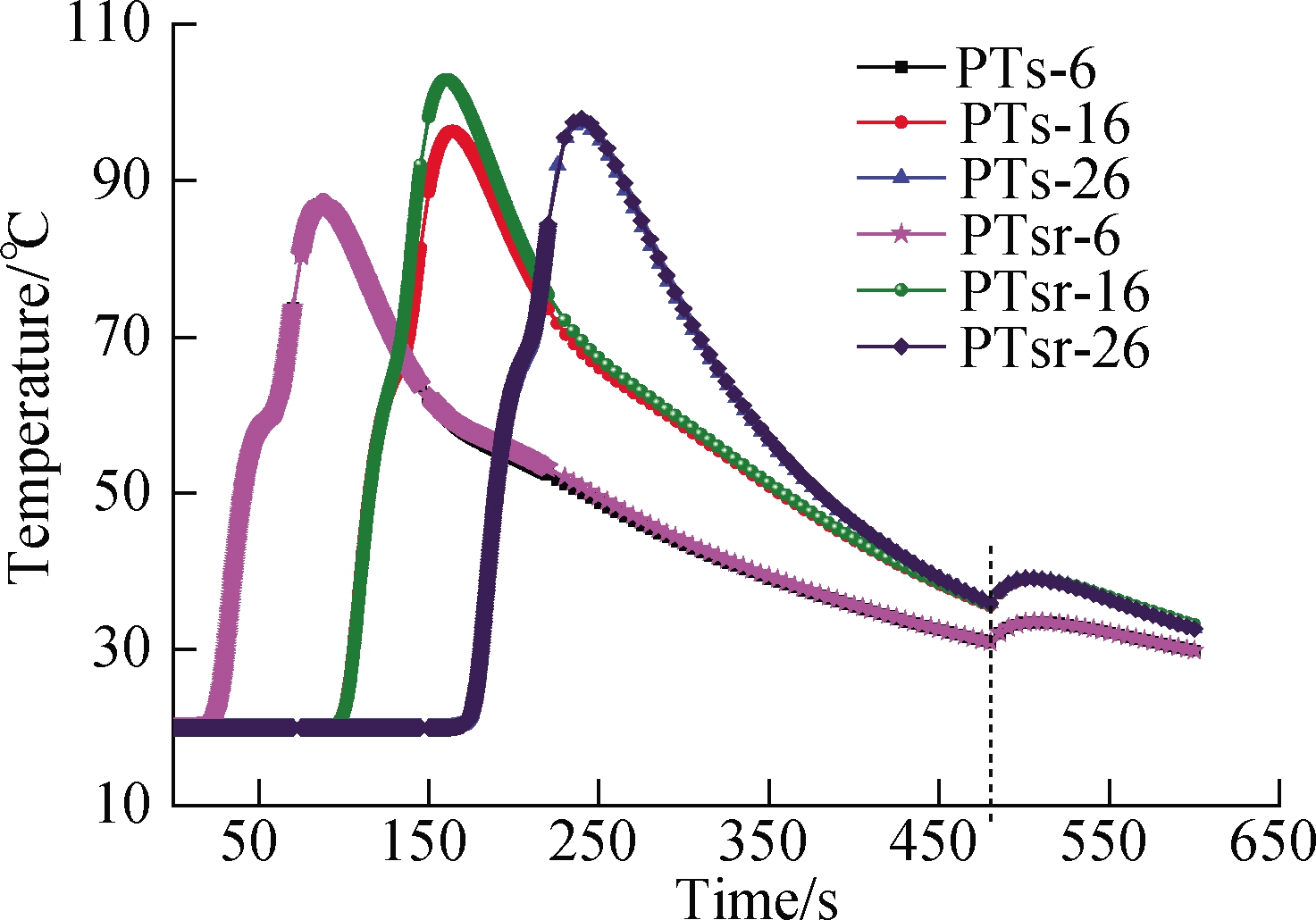
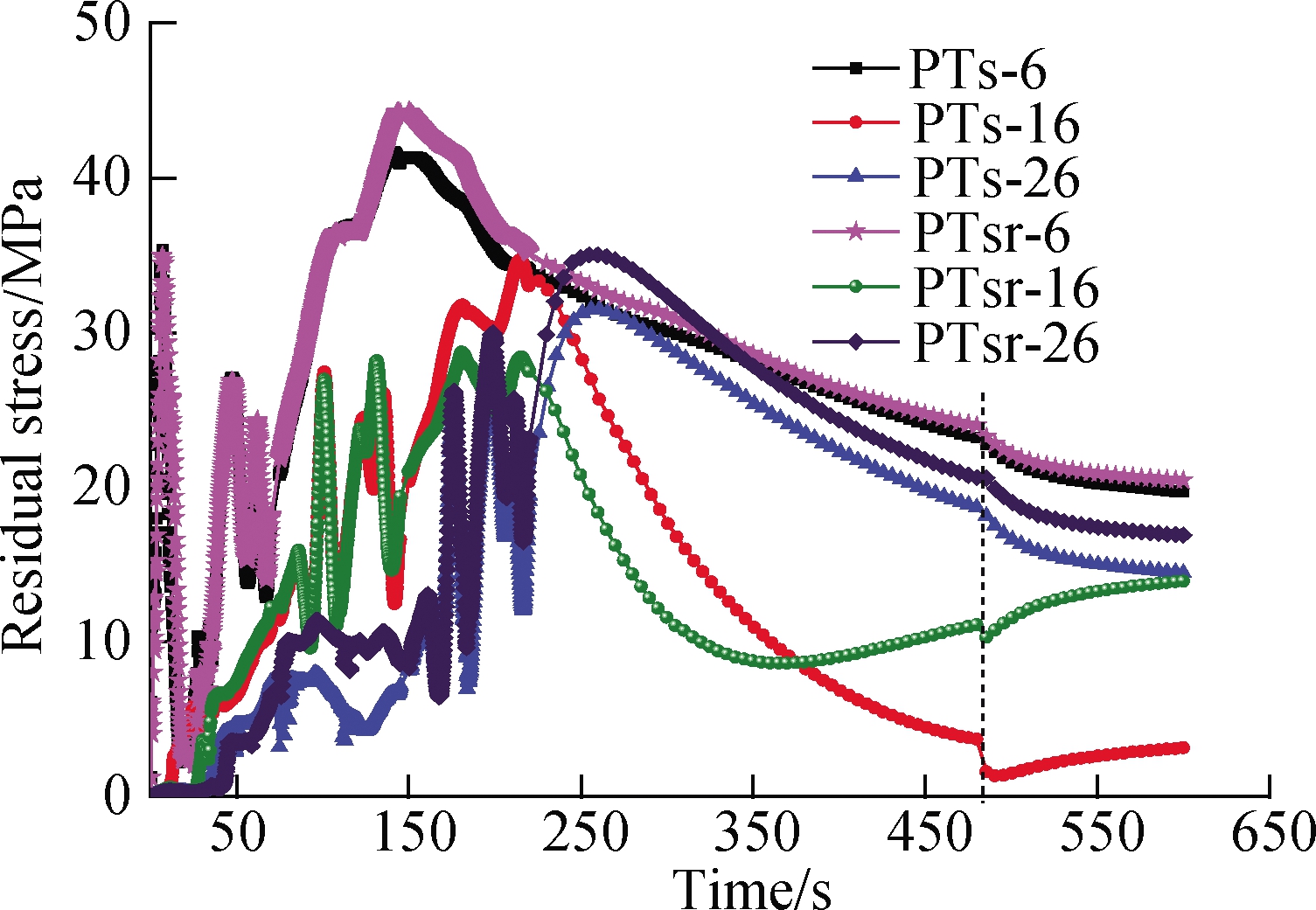
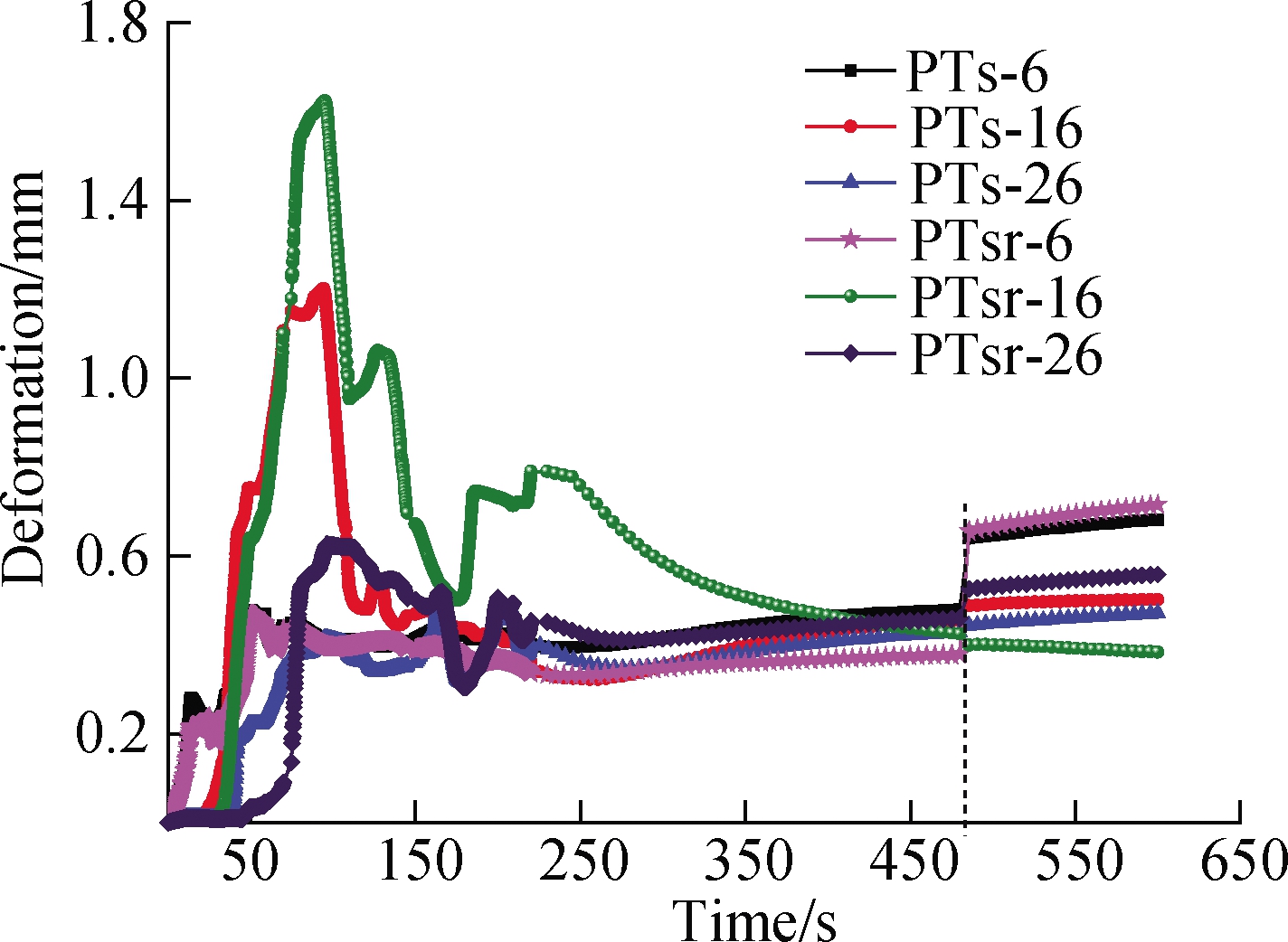
Under the third and fourth conditions in Fig.6, PTs-6, PTs-16, and PTs-26 denote the key points 6, 16, and 26, respectively, on web plates 1, 2, and 3 for the same sequential welding assembly of the parallel T-shaped thin-walled part.PTsr-6, PTsr-16, and PTsr-26 represent the key points 6, 16, and 26, respectively, on the web plate under reversed welding direction.Moreover, three web plates were sequentially welded, and the total welding time was extended.
As shown in Fig.6(a), from an overall perspective, the difference between the temperature variation curve of key points was smaller, regardless of before or after the release of the clamping constraint of fixtures.This finding revealed that the welding direction has a minimal impact on temperature variation.However, the clamping constraint of fixtures was released at 480th s, and the tem-perature curve first increased and then declined to ambient temperature.This result showed the effect of the clamping constraint of fixtures on the welding temperature.As shown in Fig.6(b), for the overall welding assembly process, the residual stress of PTs-6 was less than that of PTsr-6, and that of PTsr-26 was higher than that of PTs-26.Owing to the coupling effect of multiple factors, no difference in residual stress was found between PTs-16 and PTsr-26 in the early stage.However, in the later stage, especially after the release of the clamping constraint of fixtures at the 480th s, the residual stress of PTsr-26 was higher than that of PTs-26, indicating that the residual stress on web plate 2 was larger than that before the clamping fixtures were released.As shown in Fig.6(c), when the clamping fixtures were not released, the welding deformation of PTs-6 was slightly larger than that of PTsr-6, and that of PTs-16 was less than that of PTsr-16, and that of PTsr-26 was overall slightly larger than that of PTs-26.When the clamping fixtures were released at the 480th s, the welding deformation sharply changed and then reached equilibrium.The welding deformation results of PTs-6/PTsr-6 and PTs-16/PTsr-16 were opposite to those before the release of the clamping fixtures.At this point, the welding deformation of PTsr-26 was always larger than that of PTs-26.These results can be attributed to the contributions of the method of sequential welding assembly, the different welding directions, and the constraint of clamping fixtures.Web plate 3 was the last to be welded.The comparison results for the welding deformation of key points PTs-26 and PTsr-26 in Fig.6(c)were greatly similar to those for web plate 3 in Fig.4(c).
(a)
(b)
(c)
Fig.6 Temperature, residual stress, and deformation curve diagram when changing welding direction.(a)Temperature curve diagram;(b)Residual stress curve diagram;(c)Welding deformation curve diagram
Before the clamping fixtures were released, the variation curves of temperature, residual stress, and welding deformation for each key point all exhibited a peak value.For some local areas, the curves of residual stress and welding deformation fluctuated.However, from the overall perspective, all of these curves firstly increased to the peak value and then declined.Therefore, when the temperature increased, the residual stress and welding deformation also increased with time.Conversely, when the temperature dropped, the other two parameters showed the corresponding changes.After the release of the clamping fixtures at the 480th s, the temperature in the local area increased, the residual stress declined, and the welding deformation increased with time.After the rising stage of the temperature curve, the temperature and residual stress declined on the whole, and the welding deformation slightly increased with time.On the basis of the variation curve in Fig.6, a mapping relationship exists between temperature, residual stress, and welding deformation over a period of time.
1.2 Effect of the releasing time of the clamping fixtures and assembly sequence on welding assembly characteristics
In order to better understand and qualitatively analyze the mapping relationship between multiple properties for welding assembly, for the first and third conditions, they have the same welding direction and welding parameters, but the former is the synchronous welding assembly, and the latter is the sequential welding assembly which has different welding start time for three web plates together with a base plate.Moreover, the releasing time of the clamping fixtures are also different.In this work, the effect of the releasing time of the clamping fixtures and assembly sequence on welding characteristics is expounded and analyzed.The comparative curve diagrams for different releasing times and assembly sequences and the deformation nephogram are shown in Fig.7.

(a)

(b)

(c)
Fig.7 Comparative curve diagram for different releasing times and assembly sequence, and the deformation nephogram.(a)Temperature curve diagram;(b)Residual stress curve diagram;(c)Welding deformation curve diagram
As shown in Fig.7, PT-6, PT-16, PT-26, PTs-6, PTs-16, and PTs-26 were explained in the above-mentioned section.When the released time of clamping fixtures on the web plates was changed to the 240th and 480th s, the welding temperature sharply increased and then declined after the release of the clamping fixtures.Simultaneously, the residual stress and welding deformation retained in the thin-walled parts were all liberated.Thus, the releasing time of the clamping fixtures and assembly sequence has a great impact on welding temperature, residual stress, and welding deformation.Moreover, the released clamping fixtures can effectively reduce residual stress, ensure assembly quality, and relieve the instability of the welding structure caused by welding residual deformation.At that moment, when the temperature declined from the overall perspective, the residual stress decreased, and the welding deformation increased with time.Moreover, the residual stress also dropped, and the welding deformation slowly increased within the range of 240 to 480 s.However, before the release of clamping fixtures, the residual stress of the key point PT-16 and the welding deformation of PTs-16 were most affected by the coupling effect of multiple factors involving the welding assembly effect of web plates 1 and 3, together with the base plate, as shown in Figs.7(b)and(c).Meanwhile, this result can be also clearly seen from Fig.8 that the variation and distribution of welding deformation for simultaneous welding or sequential welding assembly at the 90th, 240th, and 480th s.Therefore, these results further confirmed that a mapping relationship exists between temperature, residual stress, and welding deformation over a period of time.
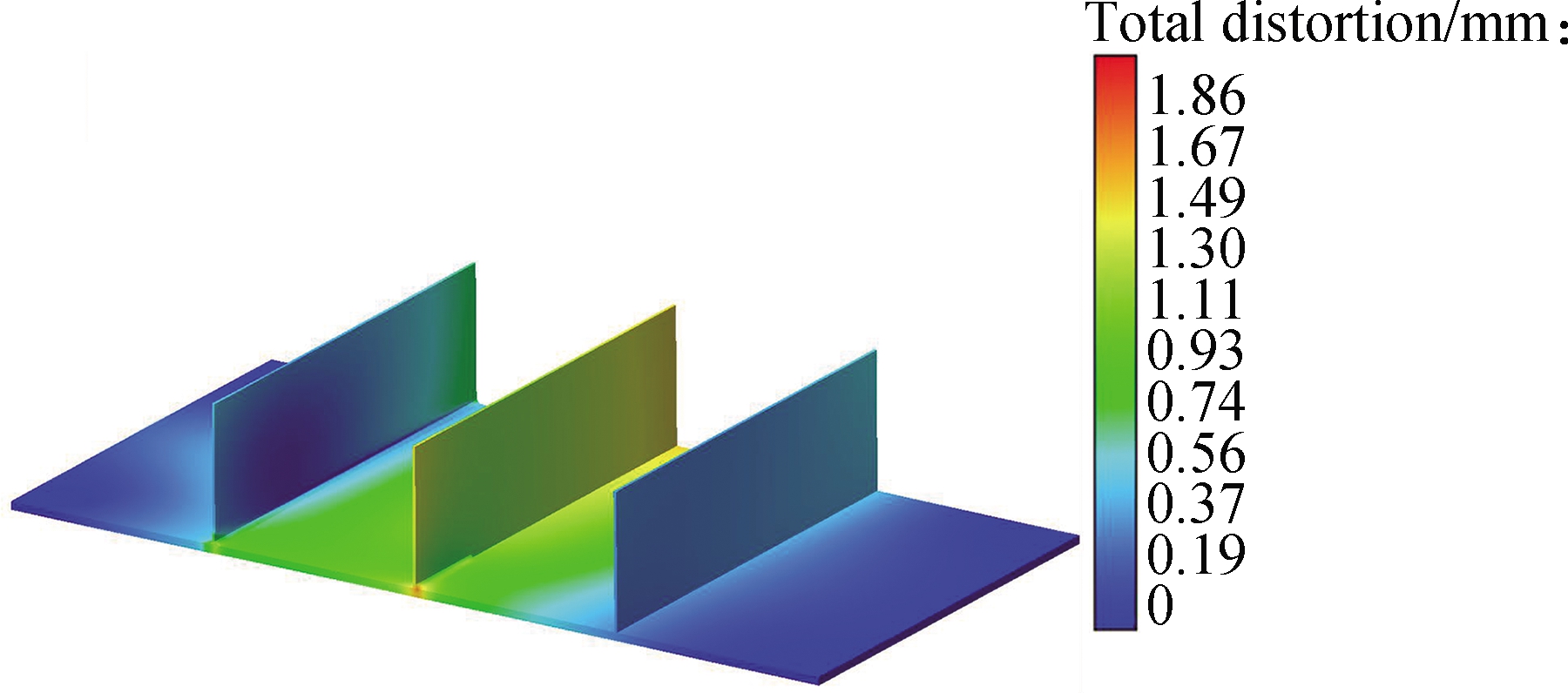
(a)

(b)

(c)
Fig.8 The deformation nephogram at different time corresponding to Fig.7(c).(a)Deformation nephogram for sequential welding at the 90th s;(b)Deformation nephogram for simultaneous welding at the 240th s;(c)Deformation nephogram for sequential welding at the 480th s
2 Prediction of Welding Assembly Characteristics for Thin-Walled Parts with Machine Learning Algorithms
In this work, in order to effectively and accurately predict the welding deformation, the change of temperature distribution, and residual stress for thin-walled parts, the machine learning algorithms of GRNN, WNN, and FNN are adopted.In addition, the obtained welding deformation, residual stress value, and temperature value for key points on the thin-walled parts through FE simulation are taken as the training data and testing data of the neural network.
When these machine learning algorithms are designed, they are all divided into the input layer and output layer.Different neural networks also have hidden layers, model layers, summation layers, and fuzzification layers.The input layers are respectively the welding deformation value, temperature value, and residual stress value of the key points on the thin-walled part, and the output layers are the welding deformation prediction value, temperature prediction value, and prediction value of residual stress for key points.The deformation, temperature, and residual stress data of welding simulation are also divided into training data and testing data.Three different neural networks mentioned above are used to predict them in order to verify the prediction effectiveness of the machine learning algorithms.
The GRNN algorithm is a kind of probabilistic neural network approach with a forward neural network method, and it can evaluate the response based on the output response and the input parameters[15-16].Its theoretical basis is nonlinear regression analysis; if the joint probability density function of the random variables x and y is f(x,y), and the observation value of x is X, then the regression of y relative to X, namely, the conditional mean value is
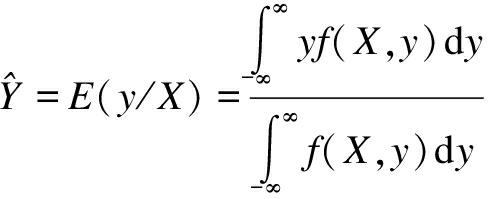
(1)
where ![]() is the prediction output under the condition of input X.
is the prediction output under the condition of input X.
Simultaneously, the nonparametric estimation method is used to estimate the density function ![]()

(2)
where Xi and Yi are respectively the sample observation value of random variables x and y, and it is the sample of(X,Y); n is the sample size; p is the dimension of random variable x; and σ denotes the smooth factor.
By replacing ![]() with f(X,y), Eq.(2)is substituted to Eq.(1).The prediction value is obtained as follows[15-16]:
with f(X,y), Eq.(2)is substituted to Eq.(1).The prediction value is obtained as follows[15-16]:
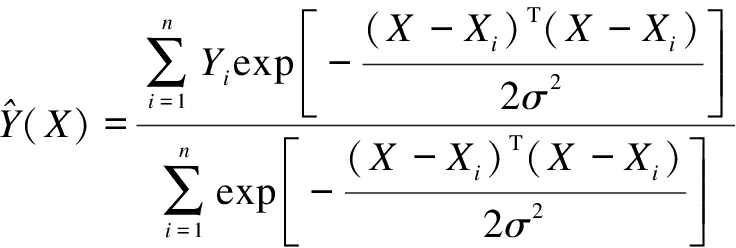
(3)
Hereby, the loss function of GRNN is the following mean square error function.
(4)
where yn is the desired output, and ![]() is the network prediction output result.
is the network prediction output result.
In this study, the cross validation method is used to train this neural network, which can accurately find the best expansion factor SPREAD of radial basis function.Through the method of cyclic training, a better prediction effect is achieved for welding assembly characteristics.Meanwhile, the dimensions of the input layer and output layer are 3 and 1, respectively; the cross-validation fold for the training data is 4 in this work.
For the WNN algorithm, it is a novel neural network combining wavelet theory and backpropagation neural network, and the wavelet basis function is taken as the transfer function of hidden layer nodes[17-18].It can make full use of the localization property of wavelet transform and the self-learning ability of the neural network.Meanwhile, it has a stronger fault-tolerant ability, fast convergence speed, and good prediction accuracy.According to Refs.[17-18], in this work, the Morlet function is taken as the wavelet basis function, and its equation is
y=e-x2/2cos(1.75x)
(5)
In addition, the calculated network prediction error equation of the WNN method is[17]
(6)
where ym(k)is the desired output result, y(k)is the prediction output result.The network prediction error equation can judge the prediction effect of WNN.
In this work, the number of hidden layer nodes for WNN is 6, and the number of the input layer and output layer is also 3 and 1, respectively.Furthermore, the iteration number is 100.When the weight parameter is updated, for the random initialization of the network connection weight, the learning rate is 0.01; for the random initialization of the expansion factor and translation factor of the wavelet function, its learning rate is 0.001 in this work.
The FNN algorithm is a T-S fuzzy neural network presented by Takagi and Sugeno; this algorithm can describe the input-output mapping relationship with fuzzy if-then rules and has a stronger nonlinear approximation capability[19-20], and its fuzzy rules are as follows: Ri:if x1 is ![]() x2 is
x2 is ![]() …, xn is
…, xn is ![]() The final output value of the fuzzy model using fuzzy calculation is as follows:
The final output value of the fuzzy model using fuzzy calculation is as follows:

(7)
where ![]() is the parameters of the fuzzy system;ωi is the multiplication operator.
is the parameters of the fuzzy system;ωi is the multiplication operator.
In addition, the loss function of FNN is as the following[20]:
(8)
where yn(k)is the desired output result.
According to the input and output dimensions of the training samples, the number of input and output nodes is also determined.In this work, the dimension of the input data is 3; that is, three groups of original simulation data of welding deformation, temperature, and residual stress are selected and used as the input data.And the dimension of output data is 1, and the number of input and output layer nodes are 3 and 1.Moreover, the number of the fuzzy membership functions is set to 6; therefore, the network structure for FNN is 3-6-1, and the number of network training is 100 in this work.
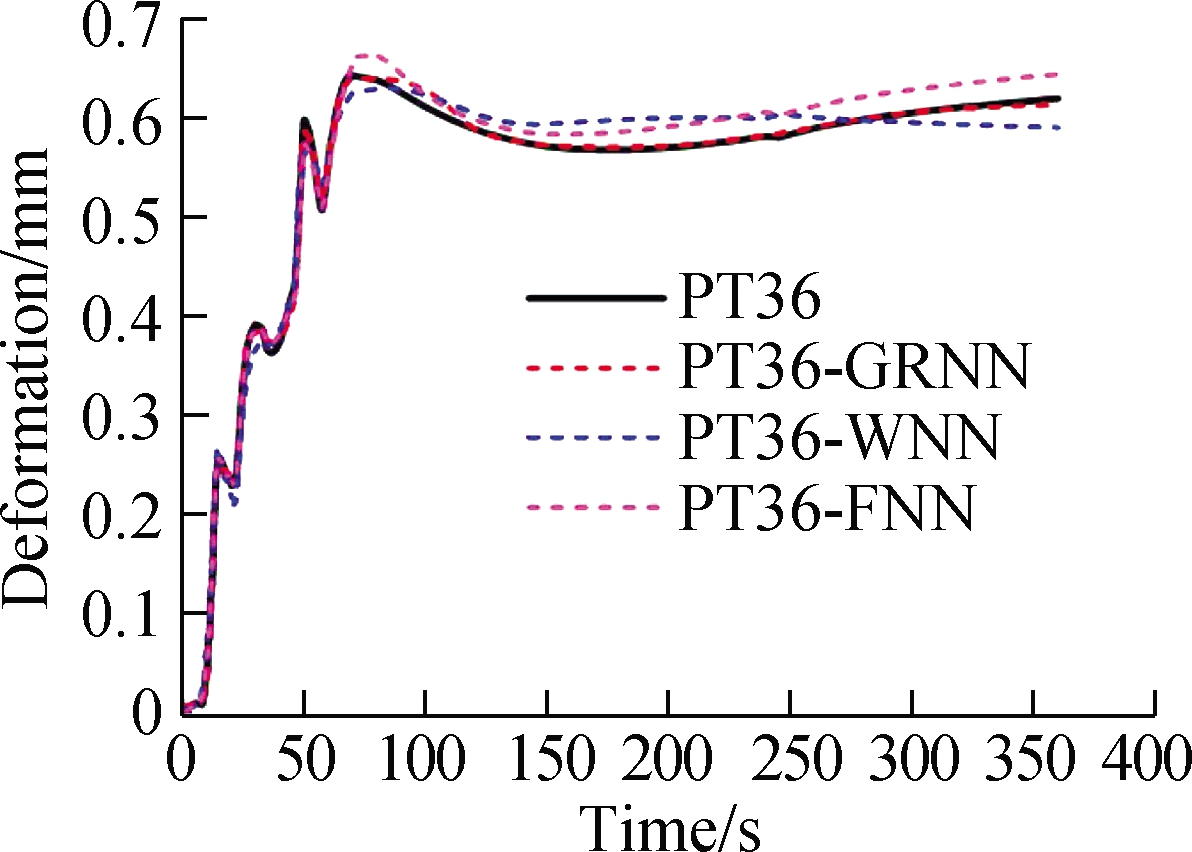
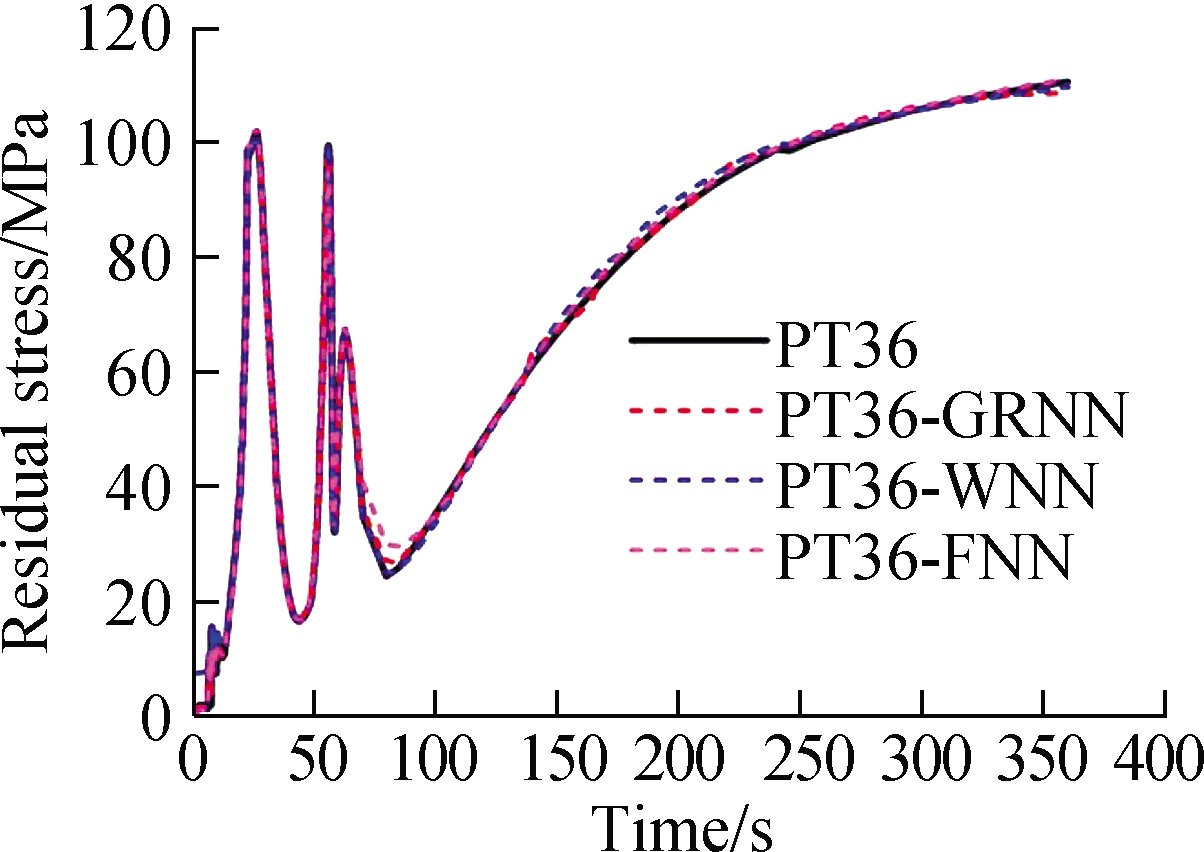
According to the above three machine learning algorithms, in this work, the prediction results are carried out through MATLAB programs.In addition, the welding characteristics data of the key points 6 and 36 on the thin-walled parts are chosen to be taken as original data, which is being used for training data and testing data to predict these welding assembly characteristics.Through comparing with the original change results, the contrast curve of prediction results for welding deformation, temperature, and residual stress of key points 6 and 36 are shown in Fig.9.
In Fig.9, PT-6 and PT-36 represent the original data of welding assembly characteristics which are obtained by FE simulation.Meanwhile, PT-6-GRNN, PT-6-WNN, and PT-6-FNN denote the prediction values of welding assembly characteristics through GRNN, WNN, and FNN, respectively.In Figs.9(a)to(c), the welding deformation, temperature, and residual stress of key point 6 on the web plate are predicted with GRNN, WNN, and FNN.Key point 36 on the base plate is also so, as shown in Figs.9(d)to(f).As illustrated in the comparison curve, the prediction curves obtained by three different machine learning algorithms were close to the original data curves, and their changing trend was greatly similar to the original variation trend for all the three characteristics of the key points on the thin-walled parts.In addition, the prediction variation curves also mirrored the mapping relationship among welding deformation, temperature, and residual stress of thin-walled parts to a great extent.These results indicated that the employed machine learning algorithms are feasible and effective for predicting the welding assembly properties of thin-walled parts.

(a)

(b)
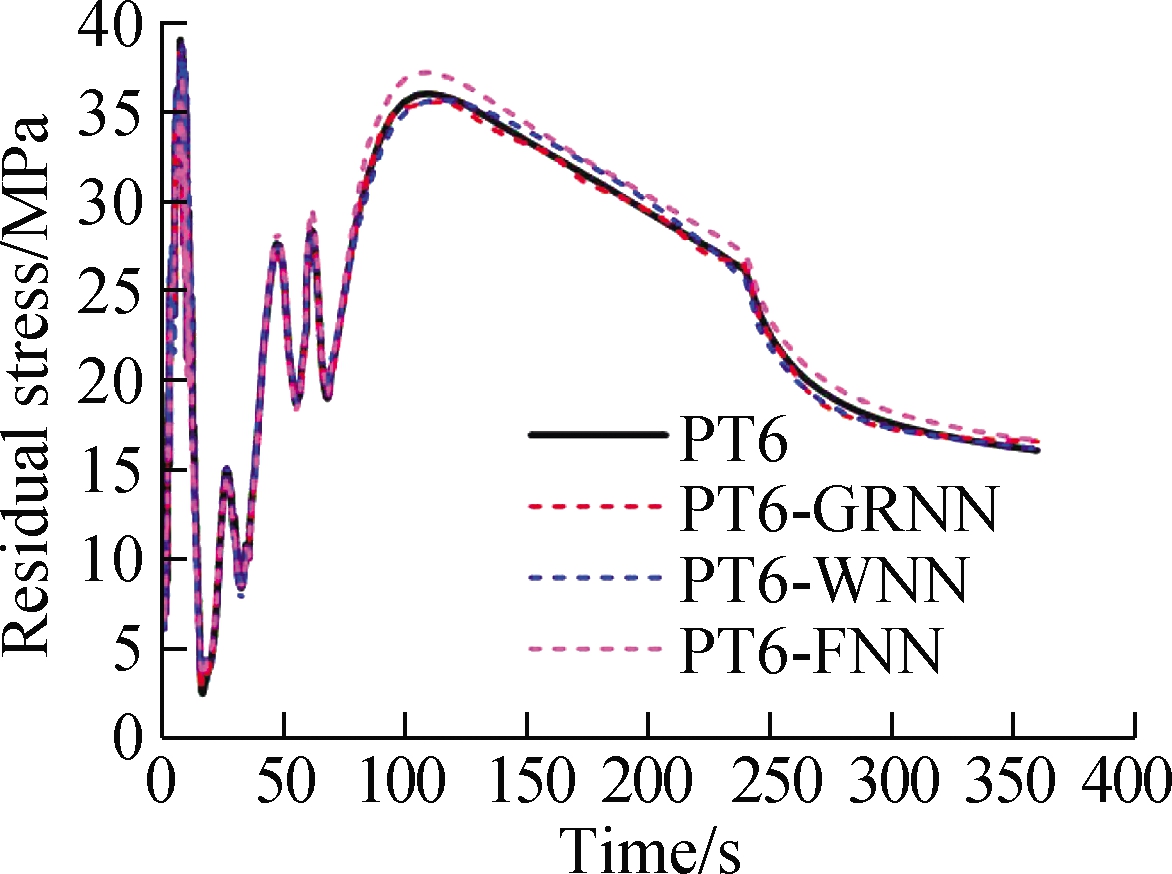
(c)
(d)

(e)
(f)
Fig.9 Comparison curve between prediction value and original value for key points.(a)Deformation comparison curve of key point 6;(b)Temperature comparison curve of key point 6;(c)Residual stress comparison curve of key point 6;(d)Deformation comparison curve of key point 36;(e)Temperature comparison curve of key point 36;(f)Residual stress comparison curve of key point 36
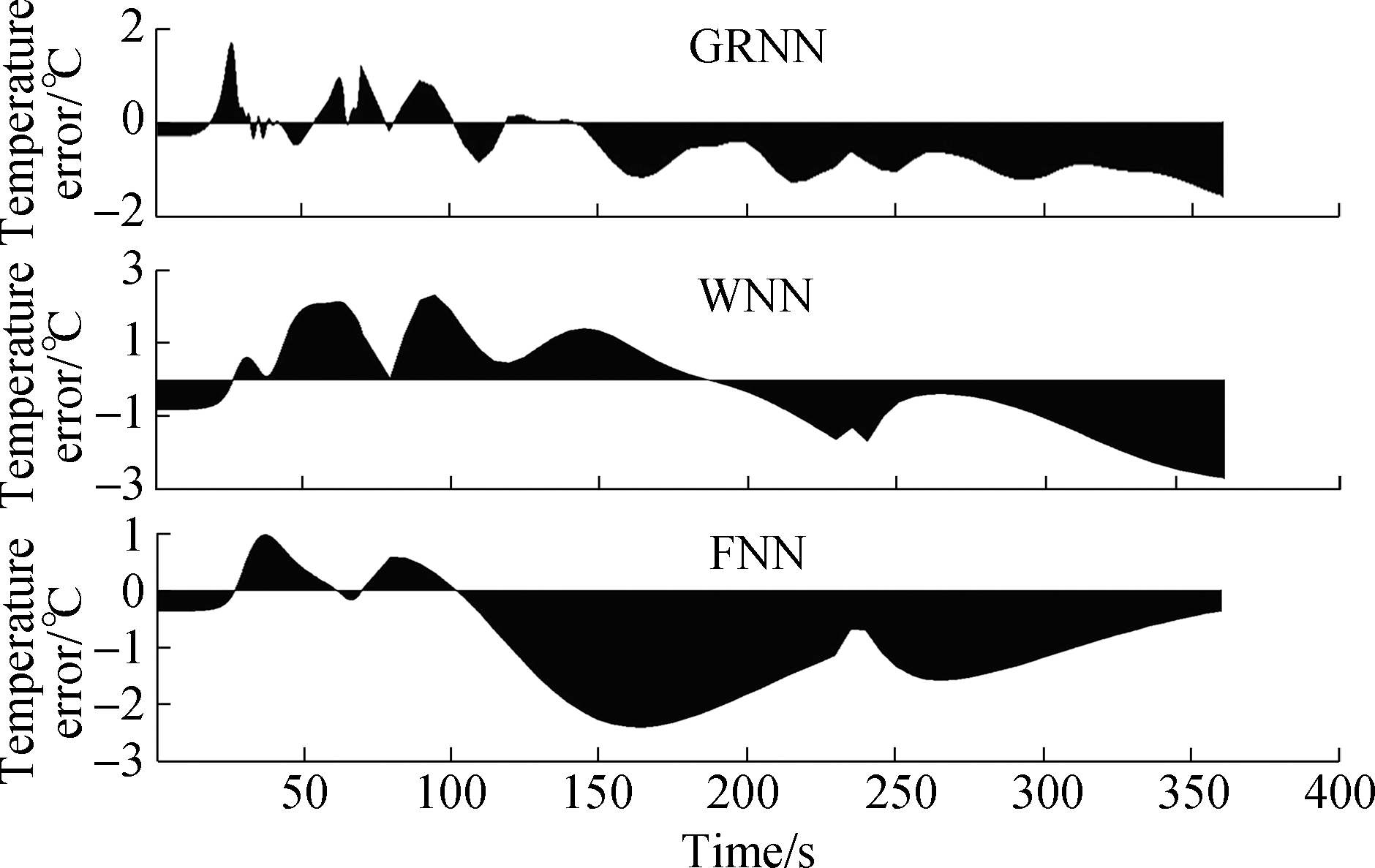
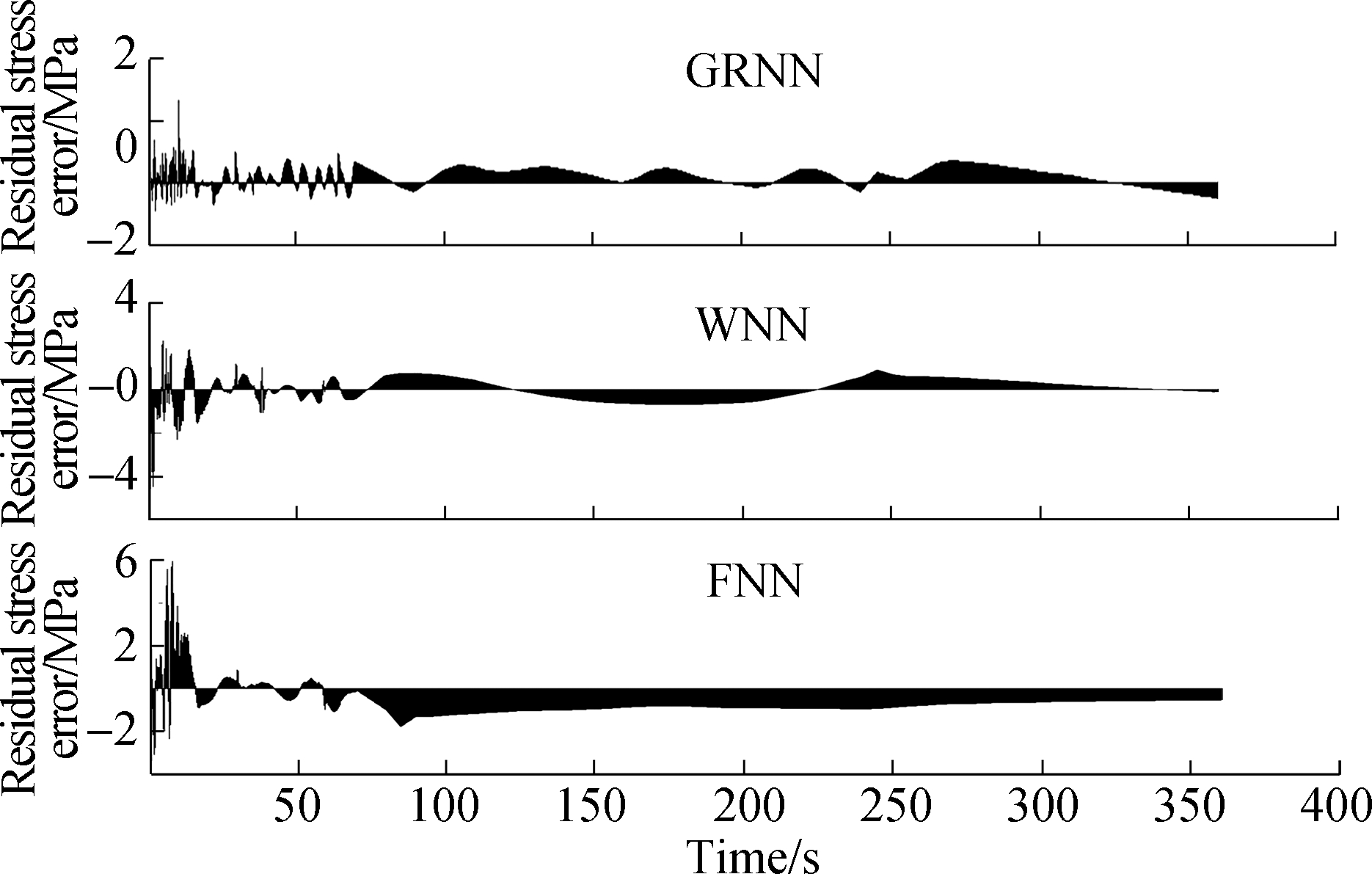
Key point 6 was taken as an example to illustrate the variety of different to intuitively understand the errors between original simulation and prediction values for welding assembly properties.The error area diagrams between original values and prediction values from different mach- ine learning algorithms are shown in Fig.10.These diagrams can reflect the changing patterns of the errors.The errors between the original value and prediction value were not large.Especially, those for deformation were relatively minor, regardless of the algorithm used for prediction.This result further verified the prediction effectiveness of the machine learning algorithms.

(a)
(b)
(c)
Fig.10 Error area diagrams between the original value and prediction value for key point 6 with different machine learning algorithms.(a)Deformation error area diagram;(b)Temperature error area diagram;(c)Residual stress error area diagram
The mean of relative errors of the prediction values was obtained using three different machine learning algorithms(see Tab.2)to quantify and compare the prediction of the welding characteristics of different key points on the thin-walled parts.A comparison of the mean relative error for the predicted values of welding deformation, temperature, and residual stress for key point 6 revealed that the employed FNN method had the best prediction effect.Its mean value of relative error was less than 3%, which was better than those of the other two methods.Moreover, the GRNN prediction results were relatively better than those from WNN.According to the mean relative error for another key point in Tab.2, the employed FNN method had the best effect, and the maximum mean relative error was no greater than 4.8%.In addition, the prediction effect of the GRNN method was also relatively better.However, from an overall perspective, the mean relative error for predicting welding deformation was relatively larger than that for the other parameters.In addition, the mean relative error for predicting the welding assembly of different key points on the thin-walled parts using the three prediction methods was less than 9%, thus further verifying their prediction effectiveness.Among all the prediction methods, the employed FNN method was proven to be the best.
Tab.2 Prediction results of the welding characteristics with machine learning algorithms %
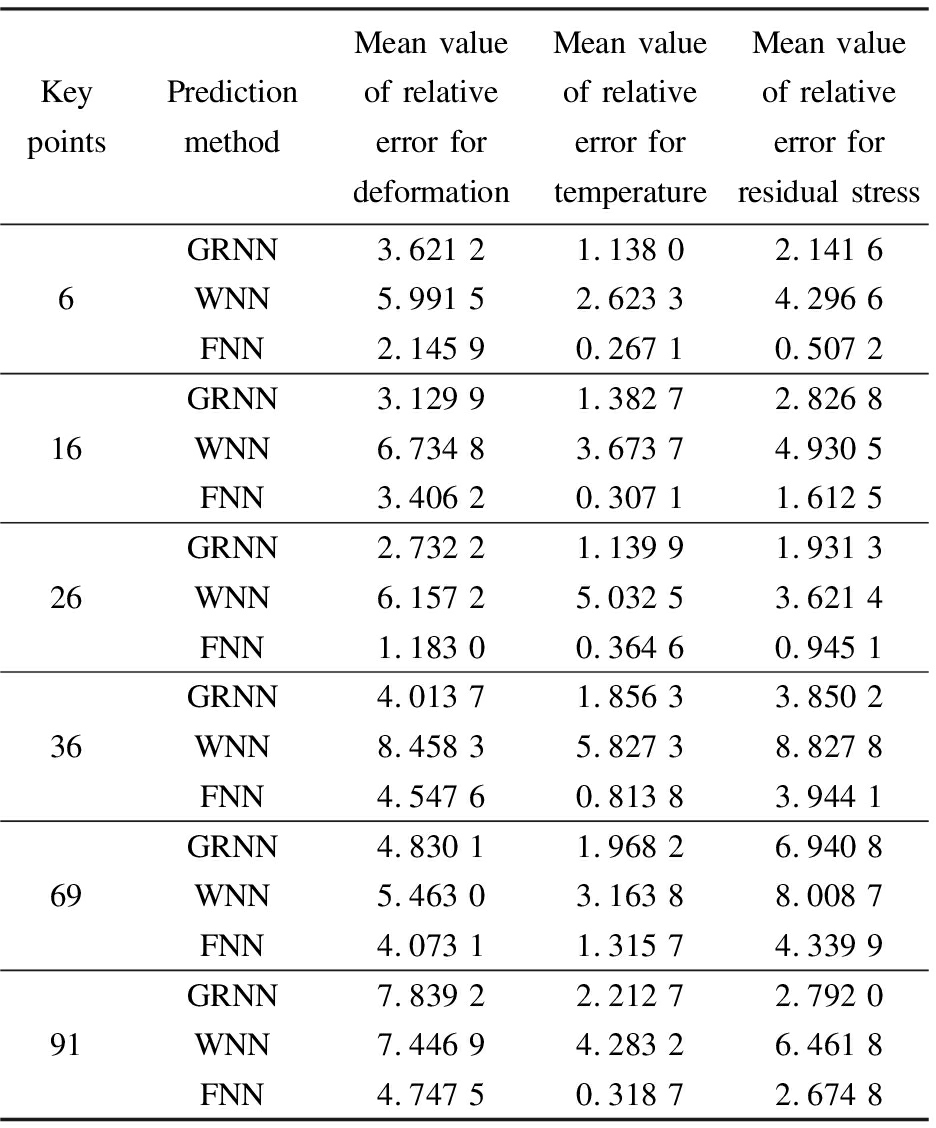
Key pointsPrediction methodMean value of relative error for deformationMean value of relative error for temperatureMean value of relative error for residual stress6GRNN3.621 21.138 02.141 6WNN5.991 52.623 34.296 6FNN2.145 90.267 10.507 216GRNN3.129 91.382 72.826 8WNN6.734 83.673 74.930 5FNN3.406 20.307 11.612 526GRNN2.732 21.139 91.931 3WNN6.157 25.032 53.621 4FNN1.183 00.364 60.945 136GRNN4.013 71.856 33.850 2WNN8.458 35.827 38.827 8FNN4.547 60.813 83.944 169GRNN4.830 11.968 26.940 8WNN5.463 03.163 88.008 7FNN4.073 11.315 74.339 991GRNN7.839 22.212 72.792 0WNN7.446 94.283 26.461 8FNN4.747 50.318 72.674 8
3 Conclusions
1)The employed FE method can effectively simulate and analyze the effect of various factors and conditions on welding assembly characteristics.A certain mapping relationship occurs between temperature, residual stress, and welding deformation to some extent over a period of time.
2)The prediction results of the multiple properties for the welding assembly of thin-walled parts are well in agreement with the FE simulation results as confirmed by different machine learning algorithms, including GRNN, WNN, and FNN.Moreover, the mean value of relative error for prediction with different machine learning algorithms is within 9%.
3)The employed FNN algorithm is the best prediction method from the perspective of quantitative analysis.This result distinctly verified the effectiveness of the employed machine learning algorithms.
[1] Ma N S, Wang J C, Okumoto Y.Out-of-plane welding distortion prediction and mitigation in stiffened welded structures[J].The International Journal of Advanced Manufacturing Technology, 2016, 84(5/6/7/8): 1371-1389.DOI:10.1007/s00170-015-7810-y.
[2] Li Y W, Zou W F, Lee B, et al.Research progress of aluminum alloy welding technology[J].The International Journal of Advanced Manufacturing Technology, 2020, 109(5/6): 1207-1218.DOI:10.1007/s00170-020-05606-1.
[3] Murakawa H, Deng D A, Ma N S, et al.Applications of inherent strain and interface element to simulation of welding deformation in thin plate structures[J].Computational Materials Science, 2012, 51(1): 43-52.DOI:10.1016/j.commatsci.2011.06.040.
[4] Ma N S, Huang H, Murakawa H.Effect of jig constraint position and pitch on welding deformation[J].Journal of Materials Processing Technology, 2015, 221: 154-162.DOI:10.1016/j.jmatprotec.2015.02.022.
[5] Ma N S, Cai Z P, Huang H, et al.Investigation of welding residual stress in flash-butt joint of U71Mn rail steel by numerical simulation and experiment[J].Materials & Design, 2015, 88: 1296-1309.DOI:10.1016/j.matdes.2015.08.124.
[6] Bhatti A A, Barsoum Z, Murakawa H, et al.Influence of thermo-mechanical material properties of different steel grades on welding residual stresses and angular distortion[J].Materials & Design, 2015, 65: 878-889.DOI:10.1016/j.matdes.2014.10.019.
[7] Chen B Q, Hashemzadeh M, Garbatov Y, et al.Numerical and parametric modeling and analysis of weld-induced residual stresses[J].International Journal of Mechanics and Materials in Design, 2015, 11(4): 439-453.DOI:10.1007/s10999-014-9269-7.
[8] Xia J, Jin H.Numerical study of welding simulation and residual stress on butt welding of dissimilar thickness of austenitic stainless steel[J].The International Journal of Advanced Manufacturing Technology, 2017, 91(1/2/3/4): 227-235.DOI:10.1007/s00170-016-9738-2.
[9] Cheon J, Na S J.Prediction of welding residual stress with real-time phase transformation by CFD thermal analysis[J].International Journal of Mechanical Sciences, 2017, 131/132: 37-51.DOI:10.1016/j.ijmecsci.2017.06.046.
[10] Mondal A K, Biswas P, Bag S.Prediction of welding sequence induced thermal history and residual stresses and their effect on welding distortion[J].Welding in the World, 2017, 61(4): 711-721.DOI:10.1007/s40194-017-0468-3.
[11] Lee J M, Seo H D, Chung H.Efficient welding distortion analysis method for large welded structures[J].Journal of Materials Processing Technology, 2018, 256: 36-50.DOI:10.1016/j.jmatprotec.2018.01.043.
[12] Ahmad A S, Wu Y X, Gong H, et al.Numerical simulation of thermal and residual stress field induced by three-pass TIG welding of Al 2219 considering the effect of interpass cooling[J].International Journal of Precision Engineering and Manufacturing, 2020, 21(8): 1501-1518.DOI:10.1007/s12541-020-00357-1.
[13] Arunkumar M, Dhinakaran V, Siva Shanmugam N.Numerical prediction of temperature distribution and residual stresses on plasma arc welded thin titanium sheets[J].International Journal of Modelling and Simulation, 2021, 41(2): 146-162.DOI:10.1080/02286203.2019.1700089.
[14] Pan M H, Tang W C, Xing Y.Welding thermal characteristics analysis with numerical simulation for thin-wall parts assembly under different conditions[J].Journal of Southeast University(English Edition), 2018, 34(2):199-207.DOI:10.3969/j.issn.1003-7985.2018.02.009.
[15] Majumder H, Maity K P.Predictive analysis on responses in WEDM of titanium grade 6 using general regression neural network(GRNN)and multiple regression analysis(MRA)[J].Silicon, 2018, 10(4): 1763-1776.DOI:10.1007/s12633-017-9667-1.
[16] Saravanakumar A, Rajeshkumar L, Balaji D, et al.Prediction of wear characteristics of AA2219-Gr matrix composites using GRNN and Taguchi-based approach[J].Arabian Journal for Science and Engineering, 2020, 45(11): 9549-9557.DOI:10.1007/s13369-020-04817-8.
[17] Pan M H, Tang W C, Xing Y.The deformation analysis, prediction, and experiment verification for thin-wall part assembly based on the fractal theory model with WNNM[J].The International Journal of Advanced Manufacturing Technology, 2017, 92(9/10/11/12): 4145-4159.DOI:10.1007/s00170-017-0497-5.
[18] Yao R H, Zhang W S, Zhang L H.Hybrid methods for short-term traffic flow prediction based on ARIMA-GARCH model and wavelet neural network[J].Journal of Transportation Engineering, Part A: Systems, 2020, 146(8): 04020086.DOI:10.1061/jtepbs.0000388.
[19] Han Y F, Zeng W D, Zhao Y Q, et al.A study on the prediction of mechanical properties of titanium alloy based on adaptive fuzzy-neural network[J].Materials & Design, 2011, 32(6): 3354-3360.DOI:10.1016/j.matdes.2011.02.009.
[20] Li W, Qiao J F, Zeng X J, et al.Identification and simplification of T-S fuzzy neural networks based on incremental structure learning and similarity analysis[J].Fuzzy Sets and Systems, 2020,394:65-86.DOI:10.1016/j.fss.2019.10.003.