Studies are ongoing for determining the importance measures of components in mechatronic systems.A well-known study is the theory of binary coherent systems[1-3].Zio et al.[4] improved the Birnbaum importance measure in binary and multistate systems by using the Markov or semi-Markov process.Subsequently, several other studies on multistate systems have been reported.Recently, methods for determining component importance have been extended to various variants considering different scenarios, such as cost-based importance measures considering the cost of maintaining each component[5], importance measures for systems with degrading components[6], importance measures for components with reconfigured systems[7], and many others[8-10].
Although studies on component importance measures have received considerable interest, some challenges still remain.For example, a serious drawback of the Birnbaum importance measure is that it ranks only individual components.The differential importance measure overcomes this challenge, but it does not consider component aging.For the state-space model, the expenditure to analyze a mechatronic system with a large state space is extremely high.Moreover, existing studies assume that the system components are independent, and none of these studies considers the influence of functional dependency.
Recently, studies on complex networks have gradually received research attention.Li et al.[11]systematically reviewed the literature to investigate the applications of complex networks in the manufacturing field.They found that the following two issues are their main negative factors: 1)Most previous studies on importance measures did not consider the coupling strength among components[12].Moreover, past research only considered models with unweighted networks.Alternatively, each edge was equally weighted.2)According to previous studies, the roles of neighboring nodes may affect a node’s degree of importance[13-14].That is, the importance of a node can be greatly affected by its neighbors, but it was not considered in previous studies.
To address the limitations in past research, this study investigates the dependency-based importance measures of components in mechatronic systems with complex network theory.Its main contributions are to:
1)Address the issue of characterizing functional dependencies among components.Although considerable efforts have been made to model functional dependencies among components, their adequate representations and calculations are still needed.
2)Model a mechatronic system as a functional dependency network(FDN), which is weighted and directional; the components of a mechatronic system are represented with nodes by considering their weights, and the dependencies among components are represented by edges.Furthermore, edge weights are represented by dependency strengths, and the dependencies are directional.
3)Propose a method to identify the important nodes in FDN, considering the functional dependencies among components with an improved PageRank importance measure(IPIM)algorithm.IPIM considers the contributions of the neighbor’s importance.
The paper illustrates the component functional dependency analysis referring to the example from Ref.[15]at first.Next, the mechatronic system is modeled as an FDN and the functional dependencies among components are represented as edge weights.The node weights by combining the functional roles of components in the system and the topological positions of the corresponding nodes are analyzed.Afterwards, an approach called IPIM to find the most important node in FDN is proposed.Finally, the validity of the methodology is given.
1 Component Functional Dependency Analysis
To clarify the dependencies of components in a mechatronic system, we present an example adapted from a previous study as follows[16]:
Suppose supported component Cj is a widget production machine, and supporting component Ci supplies coolant and lubricant fluids to Cj.Pi and Pj are the actual operability levels of components Ci and Cj, respectively, on the condition of dependency linkage from Ci to Cj.Suppose that Cj is completely operable when it produces 120 widgets per hour, then Pj(Pi=120)=100 utils.In the case of no supply of fluids from Ci, Cj can only produce 80 widgets per hour.Suppose the production rate of 80 widgets per hour is worth 55 utils, then Pj(Pi=80)=55 utils when no support is obtained from Ci.This situation implies that the baseline operability level of Cj is 55 utils.Suppose the fluids from Ci are ideal for lowering the operating temperature of the engine and increasing the output of Cj.Without these fluids, the engine’s temperature would rise, resulting in part wearing.Cj would also decline from its baseline operability level of 55 utils and eventually become completely inoperable(0 utils).
In the example cited above, the authors introduce a conceptual word “util” to express the value of functioning performance for a component, which is a dimensionless number similar to the von Neumann-Morgenstern utility.Dependency strength parameter αij is defined to represent the reliance degree of component Cj on Ci, and pj is the baseline operability level of component Cj.Thus,
(1)
where Pi and Pj are the actual operability levels of components Ci and Cj, respectively.Eq.(1)reveals that if the dependency strength αij from Ci to Cj is 0, then Cj can only function at its baseline level Pj.Moreover, if αij equals 1, then Cj can function with 100 utils.
However, the support from component Ci to Cj may be intermittent; that is, the interactive relationship between components Ci and Cj is not always continuously effective.Under this condition, two additional indicators, contact frequency and duration, are used to depict dependency strengths accurately.According to a previous study[15], another time-related parameter βij is defined as follows:
(2)
where dij represents the empirical contact duration of the type of functional dependency between components Ci and Cj, and fij denotes their contact frequency.s(Ci)is the number of times the operation state of Ci changes, whereas s(Ci|Cj)is the number of times the operation state of Cj arising from Ci changes.Thus, the normalized dependency strength between components Ci and Cj can be expressed as
(3)
2 FDN Modeling and Node Weight Analysis
2.1 FDN modeling and edge weight
As discussed in the introduction section, if the components of a mechatronic system are treated as nodes and the dependencies among components as edges, the mechatronic system can be represented as an FDN.To facilitate FDN modeling, we first transfer the bidirectional dependence among components into a one-way dependence, as illustrated in Fig.1.
(a)
(b)
Fig.1 Conversion of bidirectional to one-way dependence.(a)Bidirectional link exists between components vi and vj;(b)Transferring the bidirectional link into a one-way link.
In Fig.1, a bidirectional link exists between components vi and vj with the dependencies of eij and eji, respectively.Virtual node vk is inserted into the network to help transfer the bidirectional link into a one-way one.In Fig.1(a), eij is the dependency from nodes vi to vj indicated by a right arrow, whereas eji is that from nodes vj to vi pointed out by a left arrow.To avoid the bidirectional link, virtual node vk is inserted into the network to help transfer the bidirectional link into a one-way one, as displayed in Fig.1(b)where eij is the dependency from nodes vi to vj indicated by a right arrow.ejk is set to be equal to eji, whereas eki is set as 1.Thus, the dependency from nodes vj to vi can be calculated as ejk*1=eji.We define an FDN as a networked organization of components connected by functional dependencies.Functional dependencies among components are represented by directional edges.Considering the importance of components and the strengths of functional dependencies, an analytical model is established as follows:
FDN=(V, E, W)
(4)
and
(5)
where V is the set of nodes representing components; n is the total number of nodes; E is the set of edges; eij represents the functional dependency strength(edge weight)between nodes vi and vj; W is the set of node weights for V, and W(vi)represents the weight for node vi.The edge weight between nodes vi and vj can be calculated using Eq.(3)with αij and βij introduced in Section 1.
2.2 Node weight analysis
The node weight of a component in a mechatronic system is determined by the functional role of the component in the system and the topological position of the corresponding node in the FDN, as shown in Fig.2.
Fig.2 Factors influencing the node weight
The indexes to evaluate the functional role of a component include the expense, lifetime, mean time between failure(MTBF), and failure probability(FB).These indexes can be obtained through a statistical analysis of failure maintenance data or basic performance parameters in the datasheet for the component.
The topological positions of nodes in an FDN can be determined using the evaluation metrics of complexity theory.For example, when evaluating the importance of node vi in an FDN, the number of the tail ends(not head ends)linked with node vi is considered, which is called the outdegree of vi, as shown in Fig.3.
Fig.3 Outdegree of vi
The outdegree of node vi can be defined as
(6)
where Vout(vi) represents the set of all nodes directed by node vi.The koutiof vi in Fig.3 is 3.
Other metrics for evaluating the topological importance of nodes from different aspects include clustering coefficient, closeness centrality, and eigenvector centrality.Specifically, these metrics can be used to evaluate the topological importance of nodes on the basis of the actual application requirements.
Herein, we combine the functional roles of components in a system and the topological positions of the corresponding nodes in an FDN by using an aggregation operator(AO)[17].An AO is a generalized operator that aggregates multiple generalized importance measure indexes into a single comprehensive one to identify the key components in a system.Assuming that set A={a1, a2,…,ai,…, an} exists and the basic measure set of each element ai in A is {αi1, αi2,…, αim}, the comprehensive value of ai can be expressed as follows:
Ti=AO(αi1, αi2,…, αim)
(7)
Herein, we use the Choquet integral(CI)as the AO because it considers the importance of the critical factors of components and the interrelated and restrictive influences of the factors.On this basis and by combining each importance measure metric shown in Fig.2, CI is used to evaluate the weight of node vi as follows:
i=1,2,…,N
(8)
where Ti={αi1, αi2,…, αim} is the importance index set for node vi; N is the number of nodes in the FDN; j represents the j-th importance index(j=1, 2, …, m, where m is the number of importance indexes for node vi); αi(j)-αi(j-1)is the vector transformation for αi(j), such that αi(1)<αi(2)< … <αi(m); and μ(Ai(j))is the weight of each importance index for node vi.
3 IPIM Method
Herein, we propose an approach called IPIM to determine the most important node in an FDN.IPIM is used for evaluating the importance of a component by considering functional dependency eij described using αij and βij and node weight W(vi), which are introduced in Section 1 and Section 2.
The PageRank algorithm is used by Google Search and has recorded huge success in sorting websites on the Internet.It is expressed as follows[18-19]:
(9)
where PR(pi)is the PageRank value of the evaluated webpage pi; PR(pj)is the PageRank value of the neighboring webpage pj linked with webpage pi; p1, p2, …, pN are the considered pages; N is the number of pages; M(pi)represents the set of pages; Cout(pj)shows the number of outbound links on page pj; and d is the damping factor.Notably, when calculating the Page-Rank value, pages with no outbound links are assumed to be linked to all other pages in the collection.Therefore, the PageRank values are divided evenly among all other pages.Alternatively, to be fair to pages that have no links, random transitions are added to all nodes on the website, usually with a d that is equal to 0.85, estimated from the frequency with which users continuously follow a link[20].
The PageRank algorithm can be applied to any collection of entities with reciprocal quotations or links.However, when used to evaluate important nodes in an FDN, the algorithm cannot analyze or measure the coupling strength among components.Herein, we introduce IPIM for importance measures to assess node importance in an FDN, which is a directed-weighted complex network.IPIM considers the node weights and edge weights and has three improvements compared with that in Eq.(9).
1)Item 
in Eq.(9)represents the importance factor from webpage pi itself and is a constant value for every webpage pi.However, it is not the case for the components in a mechatronic system, for each component has a different functional role in the system and a different topological position.We add the node weight to express the importance factor from webpage pi.Thus, Eq.(9)can be modified as
(10)
where w(vi)is the normalized value of W(vi), which is the node weights calculated using Eq.(8).The expression of w(vi)is given as follows:
(11)
2)Item 
in Eq.(9)represents the influence from the neighboring webpage pj on the evaluated webpage pi.The influence the neighboring webpage pj can bring to the evaluated webpage pi is its own influence PR(pi)divided by the number(Cout(pj))of outgoing links.That is, the neighboring webpage pj evenly distributes its influence PR(pi)to its out-linked webpages(including the evaluated webpage pi), taking no consideration of the linking strength.To compensate for this drawback, Eq.(10)can be modified as
(12)
where eji is the strength of dependence of the evaluated webpage pi on webpage pj, and ∑ejk is the sum of all the dependency strengths between webpage pj and its out-linking webpage pk.
3)In Eq.(9), d is the damping factor indicating the probability that the user reaches the evaluated webpage pi and continues to browse the neighboring webpage pj linked with pi.It is also a constant value.However, the influence of a component on others in the FDN owing to functional dependencies may vary and spread in a large scope, blocking or even paralyzing the whole network operation.We define the influence propagation probability of node vi as follows[15]:
(13)
where FR(vi)is the functional influence of node vi, and it can be obtained by adding the normalized values of expense, lifetime, MTBF, and FB.Vi+ is the set of neighboring nodes connected to node vi.Thus, the influence propagation damping of node vi can be calculated as
d(vi)=1-Fp(vi)
(14)
Moreover, IPIM synthetically considers the functional dependency, the node weight of each component, the component functional influence, and the topological structure of the FDN.To calculate the importance of node vi, the IPIM algorithm is expressed as follows:
(15)
where IPIM(vi)is the IPIM ranking value of vi; d(vi)is the influence propagation damping; w(vi)is the normalized value of W(vi)calculated using Eq.(11).
4 Case Study
4.1 System description and network modeling
A case study on an elevator system is conducted to investigate the proposed models and methods.The core units of an elevator include traction subsystem, guide subsystem, car and door subsystem, electrical control subsystem, and safety protection subsystem, as shown in Fig.4.All subsystems have various functional components.Herein, we consider only the traction(a typical example of mechanical subsystems)and safety protection subsystems(a typical example of electrical subsystems)to demonstrate component dependency modeling and its network models.
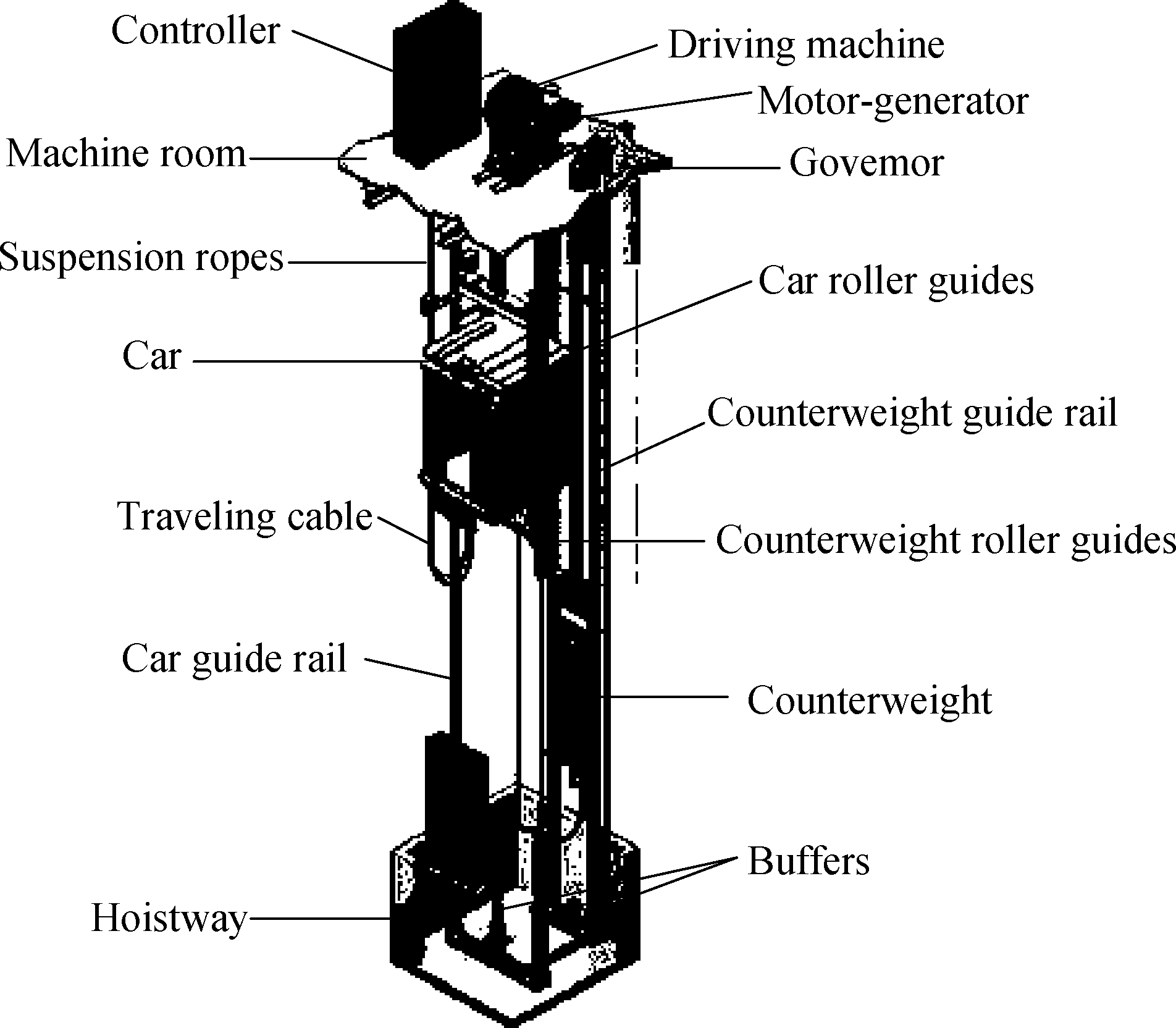
Fig.4 Core units of an elevator
When all subsystems are devoted to constituting an elevator system and the dependencies among the components in different subsystems are considered, the FDN of the elevator system is obtained, as depicted in Fig.5.
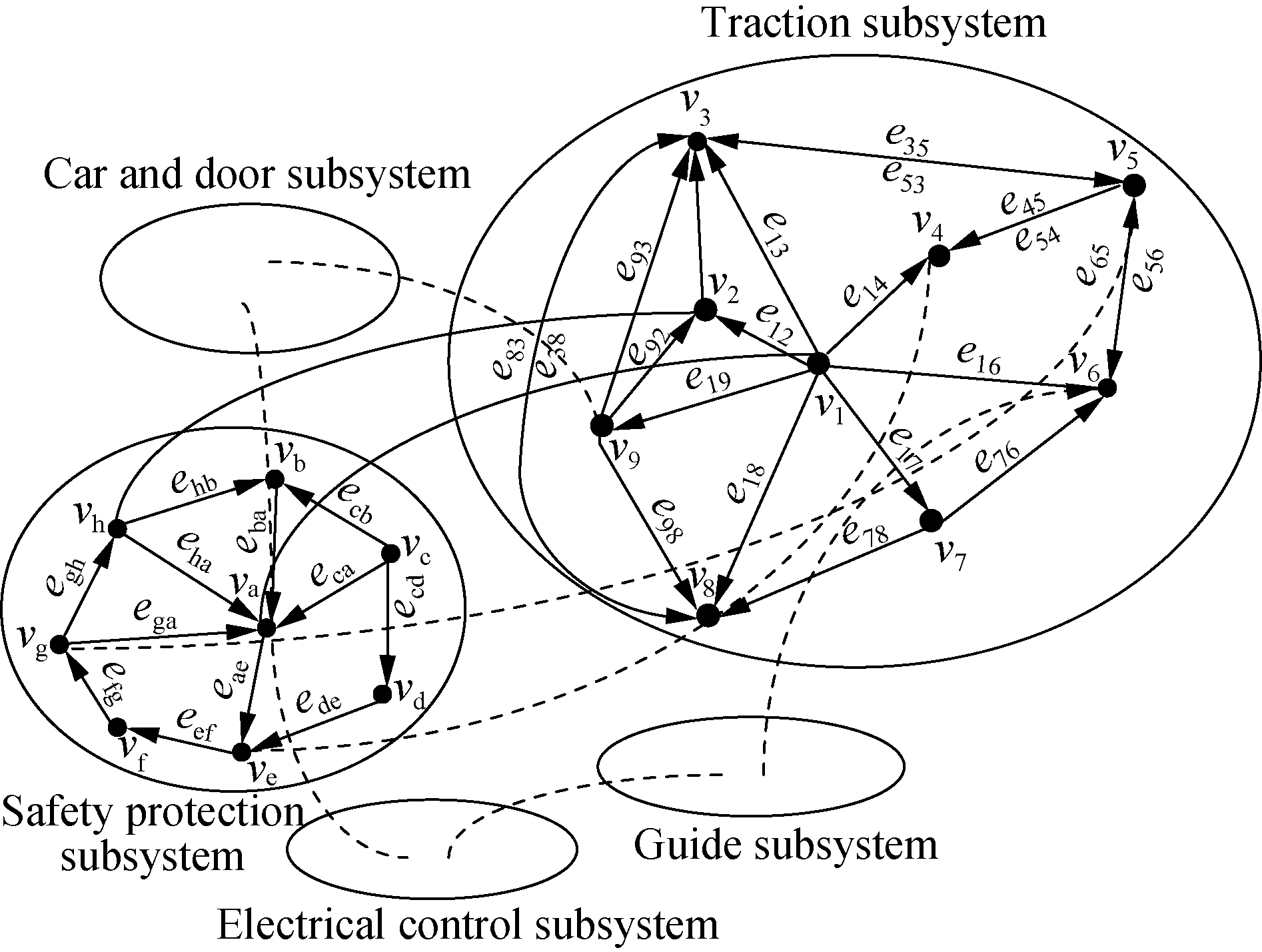
Fig.5 FDN for an elevator system
4.2 Component importance evaluation
In the component dependency network of the elevator system, the strength of the functional dependency of each component is represented as eij.eij is determined using parameters α and β, where α represents the reliance degree among components in their operation states, and β represents the interactive frequency and contact duration of functional dependencies among components.Herein, α can be collected from the design or manufacturing datasheets or the repair and maintenance databases of the elevator system, and β can be obtained from experience.As reported in a previous study[15], linguistic terms are used to describe the fuzzy probabilities regarding the interactive frequency and contact duration of functional dependencies by triangular fuzzy numbers.Reliance degree parameter α and the fuzzy probabilities of β are listed in Tab.1.Here, α and β are derived from the original data collected by Elevator World, Inc., Educational Division.The data must be selected and cleared before use.
Tab.1 Parameters for determining functional dependency strength
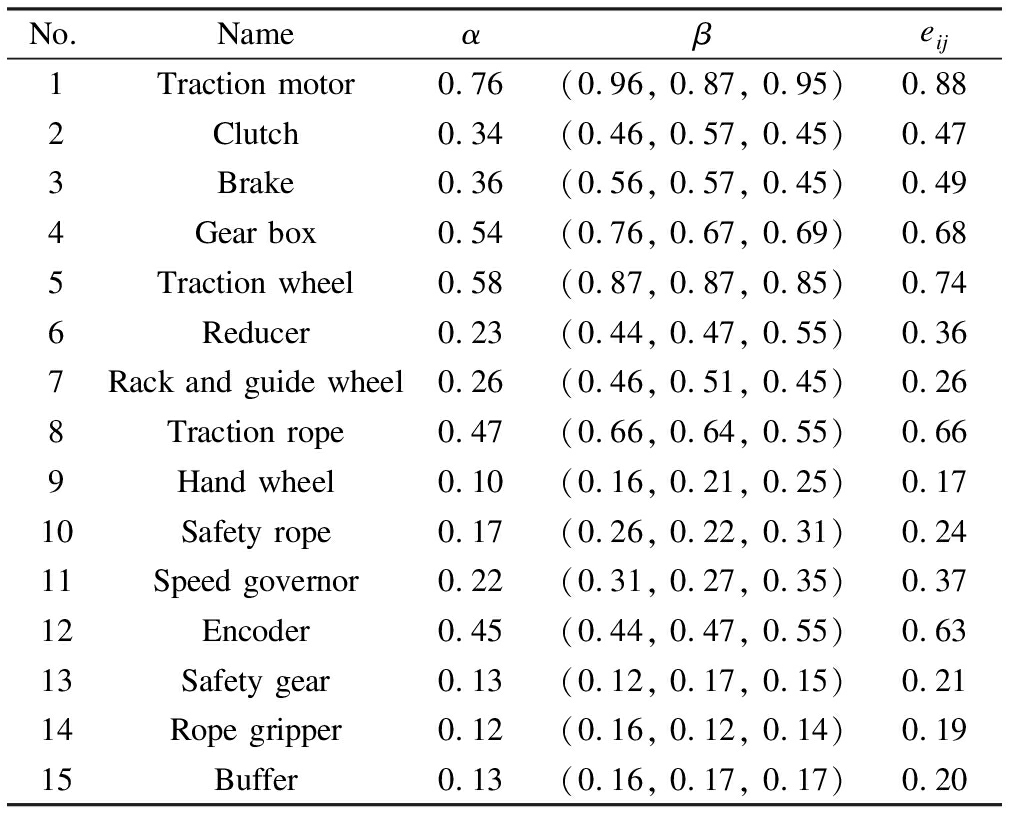
No.Nameαβeij1Traction motor0.76(0.96, 0.87, 0.95)0.882Clutch0.34(0.46, 0.57, 0.45)0.473Brake0.36(0.56, 0.57, 0.45)0.494Gear box0.54(0.76, 0.67, 0.69)0.685Traction wheel0.58(0.87, 0.87, 0.85)0.746Reducer0.23(0.44, 0.47, 0.55)0.367Rack and guide wheel0.26(0.46, 0.51, 0.45)0.268Traction rope0.47(0.66, 0.64, 0.55)0.669Hand wheel0.10(0.16, 0.21, 0.25)0.1710Safety rope0.17(0.26, 0.22, 0.31)0.2411Speed governor0.22(0.31, 0.27, 0.35)0.3712Encoder0.45(0.44, 0.47, 0.55)0.6313Safety gear0.13(0.12, 0.17, 0.15)0.2114Rope gripper0.12(0.16, 0.12, 0.14)0.1915Buffer0.13(0.16, 0.17, 0.17)0.20
The factors used for assessing the functional roles of components include their expense, lifetime, MTBF, and FB, as shown in Fig.2.Such information is collected from the historical databases of the elevator system.The data is studied by eliminating irrelevant items, and the result is presented in Tab.2.The topological positions of components in the elevator system can be evaluated using metrics such as the outdegree and betweenness centrality of the FDN.With the FDN of the elevator system, the metric values for each component can be calculated using Pajek toolkits(a set of tools for complex network parameter calculations)[21], and the outcome is presented in Tab.3.Herein, an iteration termination condition is set as follows:
Tab.2 Historical data assessing the functional roles of components
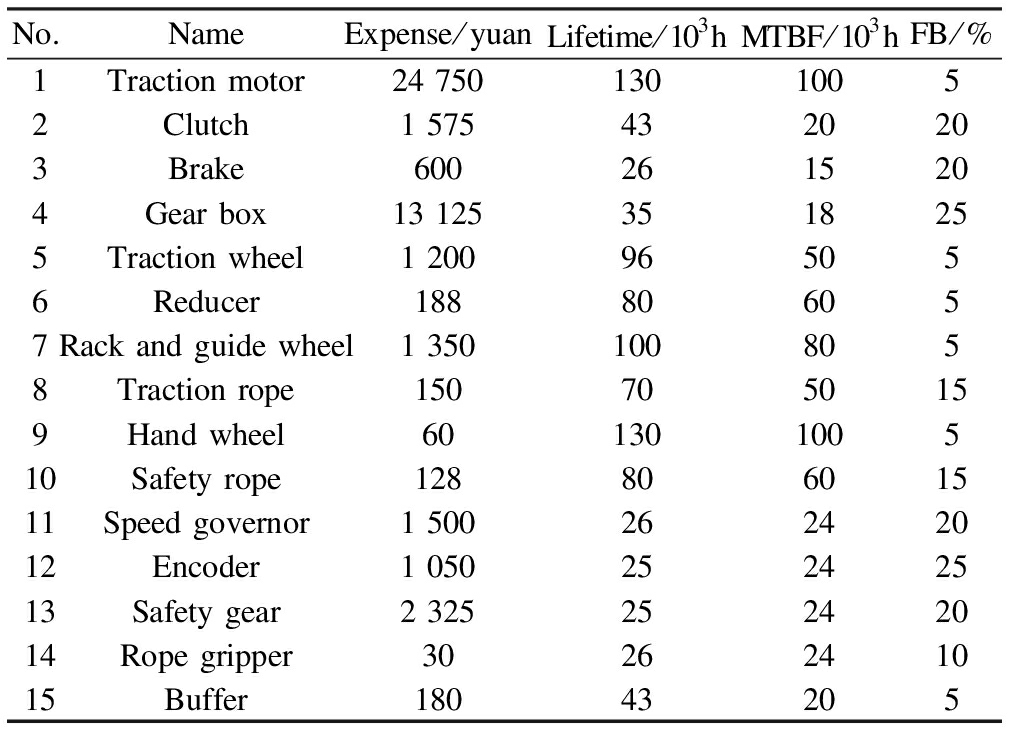
No.NameExpense/yuanLifetime/103hMTBF/103hFB/%1Traction motor24 75013010052Clutch1 5754320203Brake6002615204Gear box13 1253518255Traction wheel1 200965056Reducer188806057Rack and guide wheel1 3501008058Traction rope1507050159Hand wheel60130100510Safety rope12880601511Speed governor1 50026242012Encoder1 05025242513Safety gear2 32525242014Rope gripper3026241015Buffer18043205
Tab.3 FDN metric values for components
No.NameOut-degreeBetweenness centrality1Traction motor80.672Clutch20.103Brake30.124Gear box40.165Traction wheel30.116Reducer30.137Rack and guide wheel20.118Traction rope20.119Hand wheel20.1210Safety rope20.1111Speed governor30.1412Encoder20.1013Safety gear40.1614Rope gripper20.1115Buffer20.10
|IPIM(vn)-IPIM(vn-1)|≤ε
(16)
where ε is a small value to terminate the iterative arithmetic.When ε= 0.01, the calculation is performed in 15 seconds on a MATLAB platform in a Windows 10 operating system.
When IPIM is used to calculate the importance of a node in an FDN(considering the functional dependency of each node, the node weight of each component, component functional influence, and the topological structure of the FDN), the number of iterations must be determined because the computing complexity increases drastically as the number of components increases.
We compare the importance ranking results obtained using IPIM with those using the Birnbaum binary importance measure reported in Ref.[3], the Birnbaum measure for multistate components in Ref.[4], and the ranking results obtained from the maintenance records of Shanghai Aoan Elevator Co., Ltd.The comparison is shown in Fig.6.
Fig.6 Comparison of ranking results
The x-axis represents the component number, standing for each component(15 components), whereas the y-axis represents the ranking order(1 to 15).The smaller the ranking order, the more important the component is.
The curve presenting the importance ranking obtained from IPIM coincides with that of the maintenance records of Shanghai Aoan Elevator Co.Ltd., indicating a high evaluation accuracy of the IPIM method.Moreover, all the methods identify the traction motor as the most important component, which is consistent with the result obtained from the maintenance records.
However, considerable differences are observed among the ranking results for the reducer, traction rope, and speed governor(Nos.6, 8, and 11, respectively)obtained using different methods.Taking the traction rope(No.8)as an example, IPIM ranks it as important with a ranking of 10, the Birnbaum binary importance measure ranks it as important with a ranking of 2, and the Birnbaum measure for multistate components ranks it as important with a ranking of 6.This discrepancy can be attributed to the Birnbaum binary importance measure method considering only two states for each component, including perfect and completely invalid states.As the traction rope drives the traction wheel to lift the elevator car, the binary importance measure method ranks it high.The Birnbaum measure for multistate components evaluates the traction rope through a stochastic process considering the set of all possible states, the so-called state space.Thus, it provides the traction rope with a fair ranking.However, when we investigate the functional strength of the traction rope with other components, its eij is only 0.66.Furthermore, the expense, lifetime, MTBF, and FB are 150 yuan, 7×104 h, 5×104 h, and 15%, whereas the outdegree and betweenness centrality are 2 and 0.11, respectively.This results in a small W(vi)value.All these factors make the IPIM method rank the traction rope as a relatively unimportant component.The close agreement with the ranking results of the maintenance records of Shanghai Aoan Elevator Co., Ltd.validates the correctness of IPIM.
5 Conclusions
1)A complex network-based method is proposed for determining importance by combining the functional role of each component of a system and their topological position in the mechatronic system based on an FDN.
2)In the FDN, the components of the mechatronic system are treated as nodes by considering their weights and the dependencies among components; the dependencies are represented by edges.An IPIM algorithm is established to identify important components by considering the importance of the neighboring components.
3)A case study is conducted to investigate the accuracy of the proposed method, and the results indicate that the method can effectively determine the importance measures of components.
4)Although the results of the proposed method are satisfactory, further studies must obtain:(i)a more accurate model, such as networks of networks, for complex mechatronics and(ii)more parameters for models considering the node weights of components in a system.
[1] Namkung M, Loubenets E R.Two-sequential conclusive discrimination between binary coherent states via indirect measurements[J].Physica Scripta, 2021, 96(10): 105103.DOI:10.1088/1402-4896/ac0c56.
[2] DiMario M T,Kunz L,Banaszek K, et al.Optimized communication strategies with binary coherent states over phase noise channels[J].Npj Quantum Information, 2019, 5:1-7.DOI: 10.1038/s41534-019-0177-4.
[3] Wu S M, Coolen F P A.A cost-based importance measure for system components: An extension of the Birnbaum importance[J].European Journal of Operational Research, 2013, 225(1): 189-195.DOI:10.1016/j.ejor.2012.09.034.
[4] Zio E, Podofillini L.Importance measures of multi-state components in multi-state systems[J].International Journal of Reliability, Quality and Safety Engineering, 2003, 10(3): 289-310.DOI:10.1142/s0218539303001159.
[5] Dui H Y, Si S B, Yam R C M.A cost-based integrated importance measure of system components for preventive maintenance[J].Reliability Engineering & System Safety, 2017, 168: 98-104.DOI:10.1016/j.ress.2017.05.025.
[6] SiS B, Zhao J B, Cai Z Q, et al.Recent advances in system reliability optimization driven by importance measures[J].Frontiers of Engineering Management, 2020, 7(3): 335-358.DOI: 10.1007/s42524-020-0112-6.(in Chinese)
[7] Si S B,Levitin G, Dui H Y, et al.Importance analysis for reconfigurable systems[J].Reliability Engineering & System Safety, 2014, 126: 72-80.DOI:10.1016/j.ress.2014.01.012.
[8] Li G J,Xie C Y, Wei F Y.The moment-independence importance measure for fuzzy failure criterion and its Kriging solution[C]//2016 Prognostics and System Health Management Conference(PHM-Chengdu).Chengdu, China, 2016: 1-6.DOI:10.1109/PHM.2016.7819898.
[9] Kuttler E, Barker K, Johansson J.Network importance measures for multi-component disruptions[C]//2020 Systems and Information Engineering Design Symposium(SIEDS).Charlottesville, VA, USA, 2020: 1-6.DOI:10.1109/SIEDS49339.2020.9106662.
[10] Cao Y S, Liu S F, Fang Z G.Importance measures for degrading components based on cooperative game theory[J].International Journal of Quality & Reliability Management, 2019, 37(2): 189-206.DOI:10.1108/ijqrm-10-2018-0278.
[11] Li Y F, Tao F, Cheng Y, et al.Complex networks in advanced manufacturing systems[J].Journal of Manufacturing Systems, 2017, 43: 409-421.DOI:10.1016/j.jmsy.2016.12.001.
[12] Ruan Y R, Lao S Y, Wang J D.Node importance measurement based on neighborhood similarity in complex network[J].Acta Physica Sinica, 2017, 3: 038902.doi:10.7498/aps.66.038902.(in Chinese)
[13] Xu J, Liang Z L, Li Y F, et al.Generalized condition-based maintenance optimization for multi-component systems considering stochastic dependency and imperfect maintenance[J].Reliability Engineering & System Safety, 2021, 211: 107592.DOI:10.1016/j.ress.2021.107592.
[14] He X Q, Zhang S, Liu Y G.An adaptive spectral clustering algorithm based on the importance of shared nearest neighbors[J].Algorithms, 2015, 8(2): 177-189.DOI:10.3390/a8020177.
[15] Wang Y H, Bi L F, Lin S, et al.A complex network-based importance measure for mechatronics systems[J].Physica A: Statistical Mechanics and Its Applications, 2017, 466: 180-198.DOI:10.1016/j.physa.2016.09.006.
[16] Paul R, Ariel C.Introduction to functional dependency network analysis[C]//Second Internation Symposium in Engineering Systems.Cambridge, MA, USA, 2009: 1-17.
[17] Das S,Guha D.Power harmonic aggregation operator with trapezoidal intuitionistic fuzzy numbers for solving MAGDM problems[J].Iranian Journal of Fuzzy Systems, 2015, 12(6): 41-74.
[18] Markus S.The PageRank algorithm[EB/OL].(2002-03-01)[2019-10-21].http://pr.efactory.de/e-pagerank-algorithm.shtml.
[19] Yao W B,Shen Y, Wang D B.A weighted PageRank-based algorithm for virtual machine placement in cloud computing[J].IEEE Access, 2019, 7: 176369-176381.DOI:10.1109/ACCESS.2019.2957772.
[20] Wu G, Wang Y C, Jin X Q.A preconditioned and shifted GMRES algorithm for the PageRank problem with multiple damping factors[J].SIAM Journal on Scientific Computing, 2012, 34(5): A2558-A2575.DOI:10.1137/110834585.
[21] Mrvar A, Batagelj V.Analysis and visualization of large networks with program package Pajek[J].Complex Adaptive Systems Modeling, 2016, 4: 6.DOI:10.1186/s40294-016-0017-8.