The structural and working parameters of a double drum have an important impact on the mixing uniformity of a recycled asphalt mixture.Accordingly, many scholars have conducted considerable research on this topic.Ma et al.[1] analyzed the influence of the single factor of structure parameter and working parameter on the mixing uniformity.Liu et al.[2] analyzed the inclination installation range of double-drum blades.Zhao et al.[3] matched the blade parameters of an asphalt mixer based on the discrete element method(DEM).Simons et al.[4] studied the characterization of granular mixing in a helical ribbon blade blender.Sakai et al.[5] evaluated the uniformity of solid mixing in an industrial blender based on discrete element simulation.Milstead[6] improved the shape of agitation blades on the outer wall of an inner cylinder to improve the uniformity of a mixture.Larry et al.[7] proposed a mixing chain device that can reduce the adhesion of an asphalt mixture on the outer surface of an inner cylinder to prevent the adhered aging materials from cracking and falling into a mixing chamber and hence contaminating the mixture.Wallevik et al.[8] analyzed shear rates within a concrete truck mixer.In addition, scholars have conducted relevant research on the mechanical properties, production processes, and structural characteristics of double-drum regeneration equipment[9-13].Other studies on the structural parameters of mixed equipment using the DEM have also been conducted[14-17].
The above-mentioned studies focused on the optimization and improvement of the performance of double-drum mixing plants.The limited literature on the effect of structural parameters and working parameters on the mixing uniformity only covered the influence of a single parameter.In the actual mixing process, the uniformity of mixing is affected by the interaction of parameters, such as drum rotation speed, drum inclination angle, blade axial installation angle, blade radial installation angle, and mixing-arm phase angle.
Therefore, based on the DEM, a simulation model with actual working conditions was established in this study.By analyzing the influence of every single factor on the uniformity of aggregate mixing, the response surface method(RSM)was used to establish a mathematical model between the discrete coefficient of aggregates and the factors.Then, the significant relationship between each factor and its interaction on the uniformity of the aggregate was analyzed.This study provides a reference for the further understanding of the mixing mechanism and reveals the movement law of particles on mixing blades.
1 Main Influencing Parameters and Value Range
A double drum, as shown in Fig.1, is the core component of a double-drum recycling mixing plant.
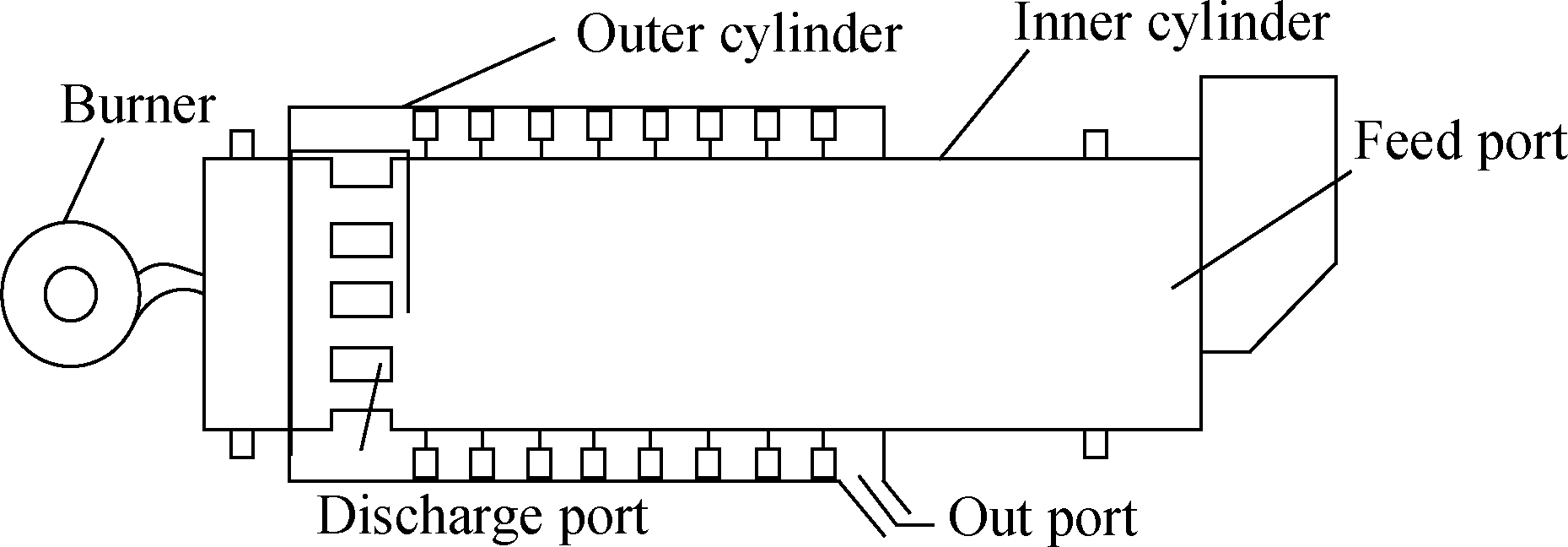
Fig.1 Structure diagram of a double drum
It consists of an inner cylinder and a number of outer cylinders, and the outer wall of the inner cylinder is equipped with mixing blades.New aggregates enter the inner cylinder from the feed port after proportioning and move toward the burner with the rotation of the inner cylinder.Then, the heated aggregate falls into the outer cylinder.Recycled materials, new asphalt, and powder were heated and stirred in the outer cylinder of the recycled mixture, which realizes the recycling of old recycled materials.The mixing uniformity and mixing efficiency of the asphalt mixture have many influencing factors.In addition to the characteristics of the mixture itself, the other main factors are the axial installation angle of the blade(β), blade radial installation angle(α), mixing-arm phase angle(φ), drum inclination angle(γ), drum rotation speed(n), and their influence on each other.
According to the normal production requirements of the double-drum recycling mixing plant and Ref.[1], the parameters’ value ranges are as follows: α=31.54°~39.36°, β=33.54°~45.36°, φ=20°~60°, γ=2°~6°, and n=6~10 r/min.
2 Simulation Analysis
2.1 DEM contact model
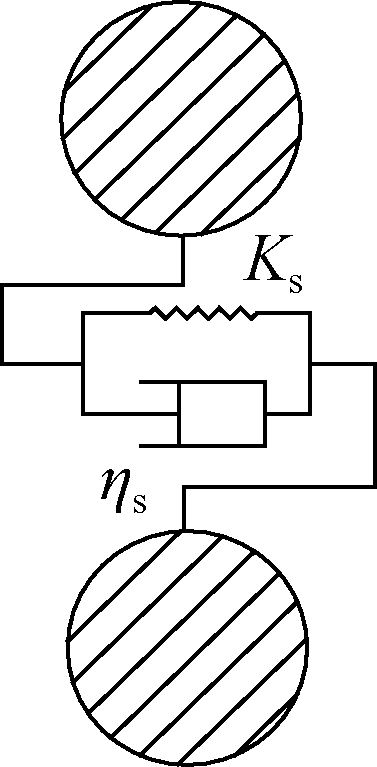
The simulation model was established based on the DEM.The contact relationship of the DEM generally includes particle to particle and particle to geometry, as shown in Fig.2.The displacement change of particles in contact is shown in Fig.3.For example, particle i is in contact with particle j at point C.The dotted line is the initial contact position; a is the tangent overlap; and δ is the normal overlap.The vibration equation can be used to express the contact problem of the particle model in the DEM.The contact relationship of particles is represented by the vibration model, as shown in Fig.4.

Fig.2 Particle contact diagram

Fig.3 Particle contact displacement

(a)
(b)
(c)
Fig.4 Vibration model.(a)Normal vibration model;(b)Tangent vibration model;(c)Sliding model
The vibration motions of particles are disintegrated into the normal and tangential directions in the process of contact.The vibration equation is
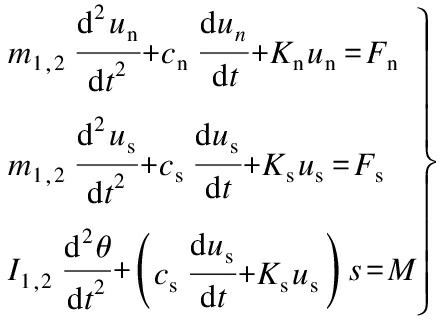
(1)
where m1,2 is the equivalent mass of particles; I1,2is the equivalent moment of inertia; un is the normal relative displacement; us is the tangential one; θ denotes the rotational angle; Fn is the normal components of particles acted on by the outside force; Fs is the tangential one; M is the external moment of particles; Kn is the normal elastic coefficient in the contact model; Ks is the tangential one; cn is the normal damping coefficient; cs is the tangential one.
The friction force between contacting particles has an effect on the tangential sliding and rolling of particles.Through the sliding model, the limiting conditions of tangential sliding and rolling can be obtained by
(2)
where μ is the friction coefficient.
2.2 Simulation parameter settings
The simulation model of the double-drum regeneration mixing equipment was established by the EDEM software.To improve the simulation speed, the aggregate in the mixture was simplified as a single spherical particle model.Three kinds of aggregate with different particle size ranges were used to simulate the mixture.The particle size ranges of the aggregates A1, A2, and A3 were 2.36 to 4.75, 4.75 to 9.50, and 9.50 to 19.00 mm, respectively.Based on the production efficiency and gradation, the production rates of the particle factory, aggregate A1, and aggregate A2 are 1.51, 14.73, and 20.21 kg/s, respectively.
The complex contact forces between the asphalt and mineral aggregate, the mineral aggregate and mineral aggregate covered with asphalt, and the mineral aggregate and mixing plant include the intermolecular van der Waals force, acid-base force based on the chemical reaction, and meshing friction force.To simulate the adhesion of asphalt, Hertz Mindlin with Johnson-Kendall-Roberts cohesion contact model in the EDEM software was selected.The intrinsic parameters and contact parameters of the mixing device and material particles are set according to the guidelines in the literature[1].
3 Influencing Factor Analysis
3.1 Effect of n on the mixing uniformity
In this study, β=40°,α=36°,φ=40°,γ=4°, and n=6~10 r/min.After the material flow became stable, the distribution data of the three kinds of aggregate at the outlet were extracted.The relationship between Cv(the coefficient of variation of the aggregate)and n is shown in Fig.5.

Fig.5 Relationship between Cv and n
As shown in Fig.5, n has a great influence on the mixing uniformity of the mixture.When n increases from 6 to 9 r/min, Cv of the three kinds of aggregate decreases, and Cv of A1 and A3 decrease.Because A1 and A3 were relatively fine and coarse particles and the number of particles was relatively small, segregation could be easily produced.When n is low, the distribution of particles is less disturbed.With n increases, the aggregate throwing increases correspondingly, the large-scale cross movement among particles becomes more intense, and the renewal frequency of the particle position increases.Because the number of particles in A2 is relatively large and the particle size is moderate, its particle distribution has a strong anti-interference ability and a small fluctuation range of the dispersion coefficient.When n changes from 9 to 10 r/min, the decrease range of the Cv of A1 and A3 becomes smaller, and the Cv of A2 slightly increases; that is, the influence of n on the uniformity of the aggregate is nonlinear.When n reaches a certain value, the mixture distribution tends to be stable, and the further increase of n will not have a great positive effect on the improvement of the mixing uniformity.
3.2 Effect of γ on the mixing uniformity
In this study, β=40°,α=36°,φ=40°,n=8 r/min, and γ=2°~6°.The relationship between Cv and γ is shown in Fig.6.
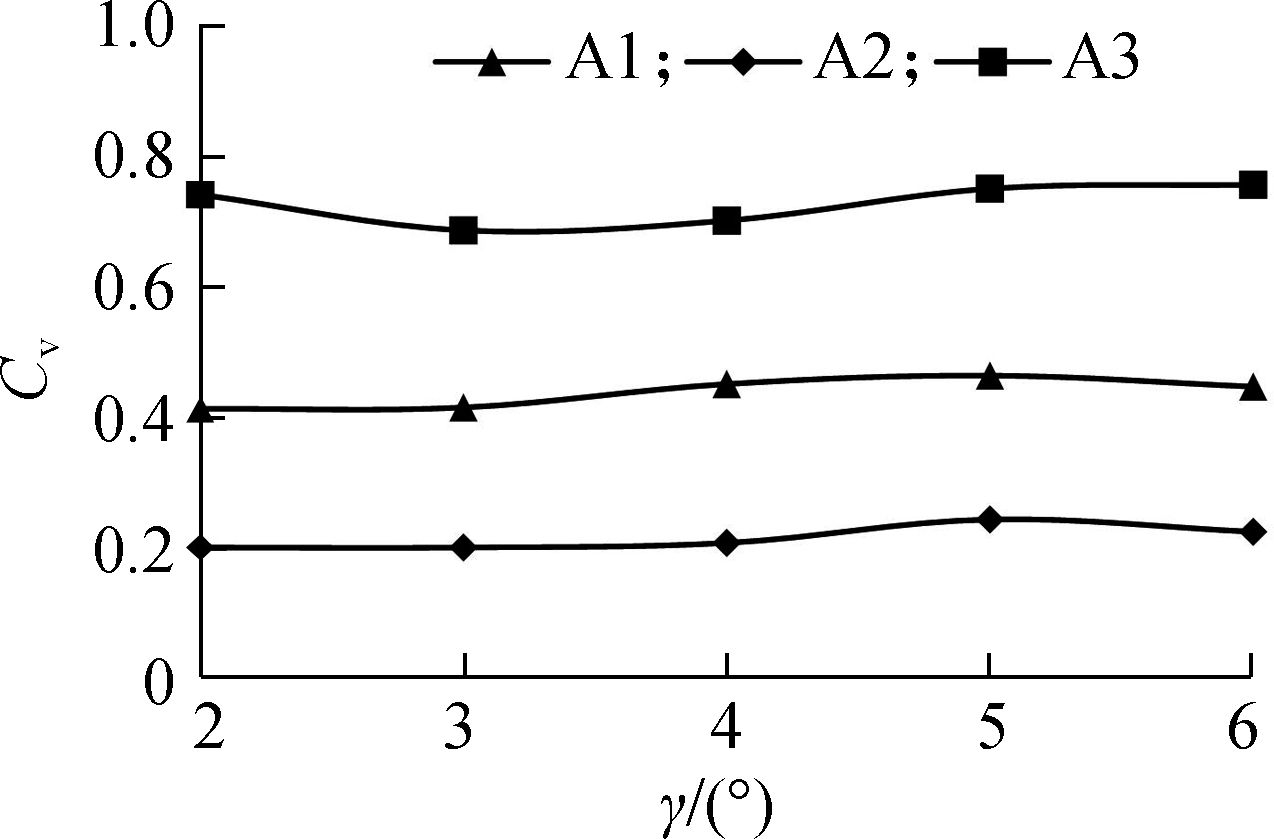
Fig.6 Relationship between Cv and γ
As shown in Fig.6, with the change in γ, the Cv of A1 and A2 fluctuates less, and the Cv of A3 relatively fluctuates more, but it is also limited within the range of 0.07.This result indicates that the change in γ has less influence on the uniformity of the mixture.Theoretically, increasing γ can prolong the retention time of the mixture in the mixing drum and increase the mixing times.However, as shown in Fig.6, the greater the γ, the greater the segregation of the mixture.
The feed rate of the particle factory was reduced by 30%, but other parameters remained unchanged.The uniformity of the mixture was analyzed when the inclination of the roller was 6°.The Cv of A1, A2, and A3 were 0.427, 0.184, and 0.683, respectively, which are lower than those before the feed rate was reduced.This finding shows that the filling ratio of the mixing chamber is high when γ is 6° without the decrease in the feeding rate.Therefore, increasing γ can prolong the mixing time of the mixture.However, the retained mixture can easily result in a large filling ratio in the mixing drum, which is not conducive to mixing.
When γ is 4° and n is 9 r/min, the Cv of the three aggregates is smaller than that when γ is 2°and n is 8 r/min.Therefore, to address the increase in the filling ratio of the mixing drum caused by the increase in γ, n can be properly increased without reducing the productivity.
3.3 Effect of β on the mixing uniformity
In this study, α=36°,φ=40°,γ=4°,n=8 r/min, and β=31°, 34°, 37°, 40°, 43°, 46°.The relationship between the Cv of the aggregate and β is shown in Fig.7.

Fig.7 Relationship between Cv and β
As shown in Fig.7, β has a great influence on the mixing uniformity.When β increases from 34° to 46°, the Cv of the three aggregates all increase.When β decreases from 34° to 31°, the Cv of A1 and A3 increase slightly.Overall, when β=34°, the uniformity of the mixture is the best.
β affects the intensity of the axial and circumferential movements of the mixture, which in turn affects the mixing uniformity.The axial average velocity(Va)and circumferential average velocity(Vc)of all particles were collected at different values of β to analyze the effect of β on the motion speed of the aggregate, as shown in Fig.8.

Fig.8 Average velocity of particles with different β
As shown in Fig.8, when β increases from 31° to 46°, the average axial velocity of the particles increases first and then decreases, and the maximum value is obtained when β=40°.The average circumferential velocity of the particles in the mixture reaches the maximum value when β=34° and decreases when β increases.As shown in Figs.7 and 8, when β=34°, the circumferential movement of the mixture is sufficient, which is conducive to the mixing of aggregates; the axial movement speed of the mixture is slow, which is conducive to the extension of the mixing time.
The feed rate of the particle plant was reduced by 30%, and other parameters were unchanged.The uniformity of the mixture was analyzed when β=31°.The dispersion coefficients of A1, A2, and A3 were 0.363, 0.145, and 0.626, respectively, which are lower than those before the feed rate was reduced.This finding shows that the filling ratio of the mixing drum is high when β=31° without a decrease in the feeding rate.As shown in Fig.8, compared with β=34°, when β=31°, the axial movement speed of the mixture is slower, and the filling ratio of the mixing drum is higher, which is not conducive to the cross movement between particles.The circumferential velocity of the mixture was decreased, and the particle throwing was weakened.Therefore, the axial installation angle should take into account the axial and circumferential movements of the mixture.
3.4 Effect of φ on the mixing uniformity
In this study, β=40°, α=36°, γ=4°, and n=8 r/min, φ=20°, 30°, 40°, 50°, 60°.The relationship between the Cv of the aggregate and φ is shown in Fig.9.

Fig.9 Relationship between Cv and φ
As shown in Fig.9, the Cv of A1 changes slightly, and the Cv of A2 and A3 vary greatly.When φ=30°, Cv of A2 and A3 are at the minimum.When φ increases from 30° to 60°, Cv of A2 and A3 increases gradually, but Cv of A3 increases exponentially.This finding shows that φ has a significant impact on the uniformity of large particles in the mixture.An excessively large φ is unfavorable to the mixing of the coarse aggregate.
The feed rate of the particle plant was reduced by 30%, whereas other parameters were unchanged.The uniformity of the mixture was analyzed when φ=60°.The Cv of A1, A2, and A3 were 0.451, 0.316, and 1.038, respectively, which are lower than those before the feed rate was reduced.Hence, when the feed rate is constant and φ is 60°, the filling ratio of the mixing drum is on the high side.
3.5 Effect of α on the mixing uniformity
β=40°,φ=40°,γ=4°,n=8 r/min, and α=32°, 34°, 36°, 38°, 40°.The relationship between the Cv of the aggregate and α is shown in Fig.10.

Fig.10 Relationship between Cv and α
As shown in Fig.10, the Cv of A1 and A2 has little change.The Cv of A3 is largely influenced by α, but its fluctuation range is also less than 0.11.Hence, α has little influence on the uniformity of the mixture.
α can separate the mixture from the inner wall of the outer cylinder, shorten the rolling distance, and reduce the segregation of the coarse particles in the rolling process.Therefore, the uniformity of A3 is greatly affected by α.When α is 36° and the other parameters remain unchanged, the uniformity of the aggregate is compared when φ is 60° and 40°.The results show that the Cv of A1, A2, and A3 are 0.464, 0.363, and 1.298, respectively, when φ is 60°, which are higher than that when φ is 40°.
In addition, α will affect the movement speed of the mixture particles.To study the influence of α on the mixture moving speed, we collected the average speed of all particles and determined the average moving speed of particles with different α, as shown in Fig.11.
Fig.11 Change in the average particle velocity with different α
As shown in Fig.11, the average velocity of particles has little change; that is, α has little influence on the velocity of the mixture.When α is 36°, the average veloci-ty of particles in the mixture is relatively large, and the homogeneity of the mixture is relatively good.When α is 40°, the average velocity of particles is slow, which is not conducive to the mixing of the mixture.
4 RSM Analysis
To analyze the interaction between various factors and find the best parameter match, the RSM was used for further research.
4.1 Simulation scheme design
Referring to the design of the structural parameters and motion parameters of the double-drum mixing equipment in the previous paper, the value ranges of five factors are set as follows: 34°≤α≤46°,32°≤β≤40°,20°≤φ≤60°,2°≤γ≤6°, and 6 r/min≤n≤10 r/min.
Taking α, β, φ, γ, and n as the influencing factors and Cv as the response value, according to the design method of the response surface experiment, the simulation scheme of the five factors and three levels was designed, as shown in Tab.1.
Tab.1 Influencing factors and level value

Influencing factorslevel -1level 0level 1α/(°)344046β/(°)323640φ/(°)204060γ/(°)246n/(r·min-1)6810
4.2 Simulation results and analysis
According to the range of the influencing factors in Tab.1, the simulation scheme and results were obtained by the Box-Behnken design test method.The simulation results are analyzed by RSM.Each factor of aggregates is

(3)
where Cv1,Cv2,Cv3are the coefficients of variation of A1, A2, and A3, respectively.The significant factors and the significant relationship of Cv1 are n>β>φ.In the interaction term, φ and γ, φ and β have a significant influence.The significant factors and the significant relationship of Cv2 are n>β>γ>φ, and among the interaction terms, φ and γ, φ and α, φ and β have significant influences.The significant factors and significant relationship of Cv3are φ>n>β>γ, and among the interaction terms, φ and γ, φ and n, φ and α have significant effects.
4.3 Interaction factor analysis
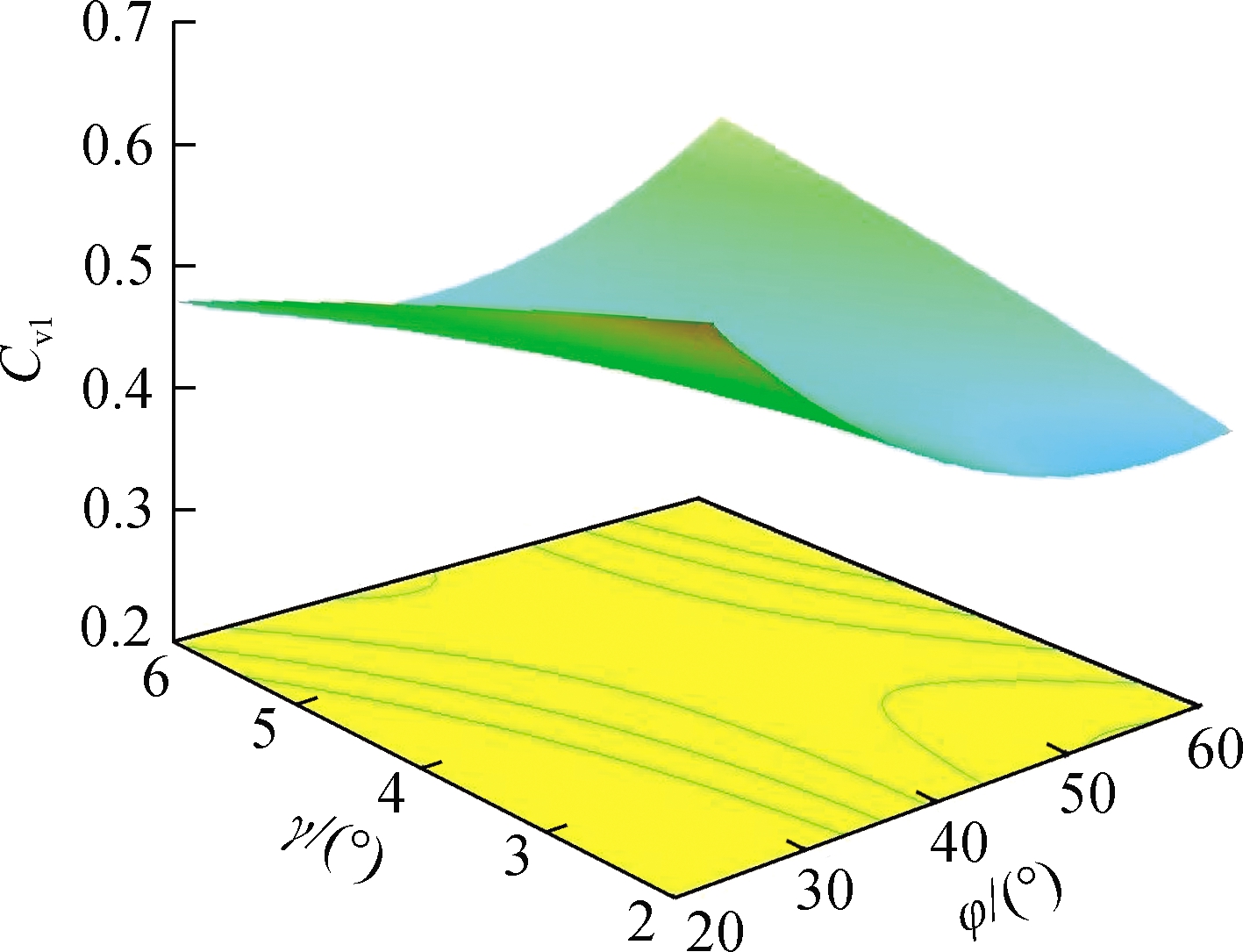
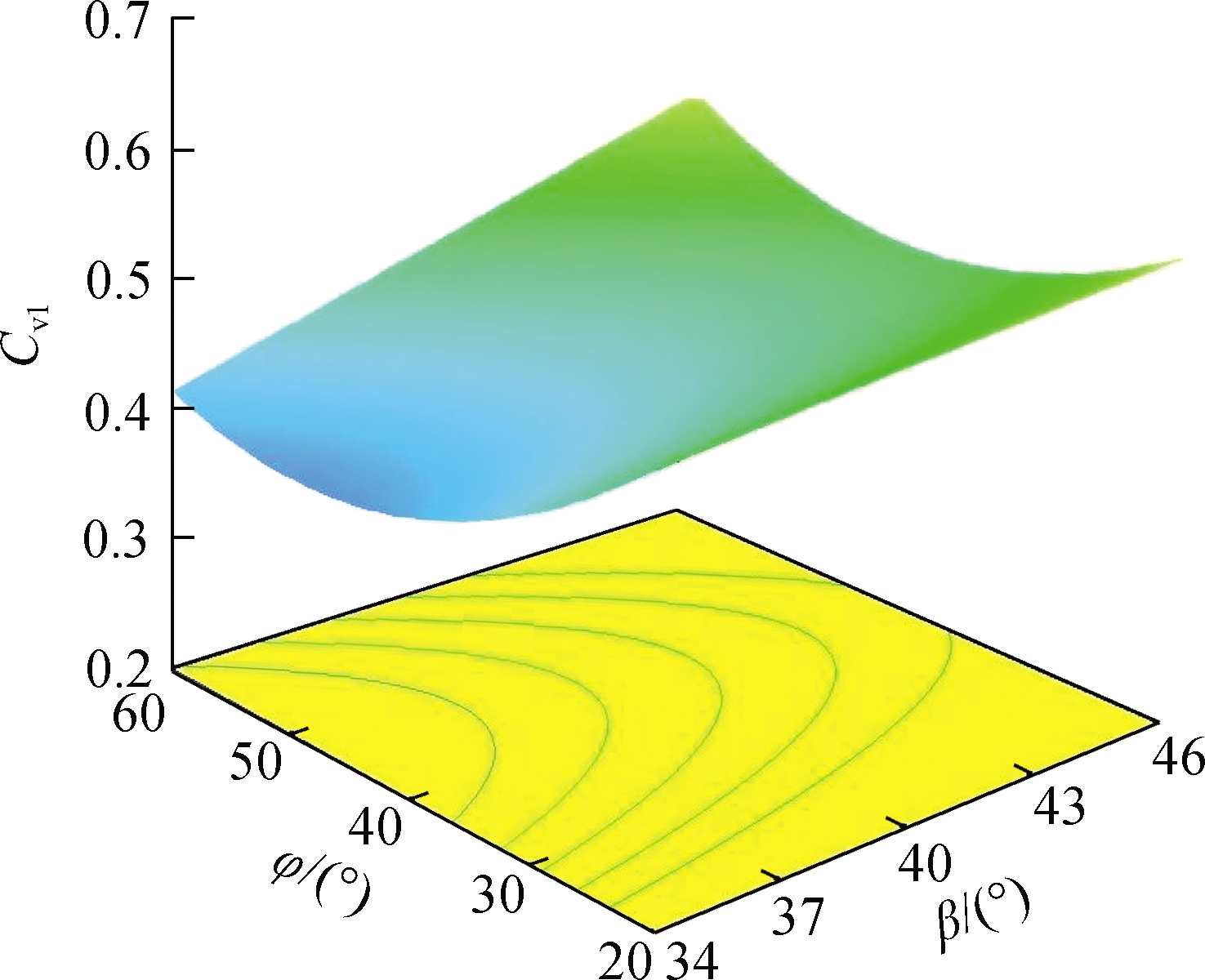
Among the interaction factors, the interactions of γ and φ, β and φ have a significant effect on Cv1.The response surface relationship between Cv1 and the significant interaction factor of A1 is shown in Fig.12.
The response surface relationship between the discrete coefficient and interaction factor is shown in Fig.12(a).When the phase angle of the mixing arm is 20°, Cv1 decreases when γ increases.When φ is 60°, Cv1 increases when γ increases.As shown in Fig.12(b), if φ is any value, Cv1 will decrease when β decreases.Among them, when φ is 60°, Cv1 decreases faster.
(a)
(b)
Fig.12 Relationship between Cv1 and interaction factors.(a)Significant effect of γ and φ on Cv1;(b)Significant effect of φ and β on Cv1
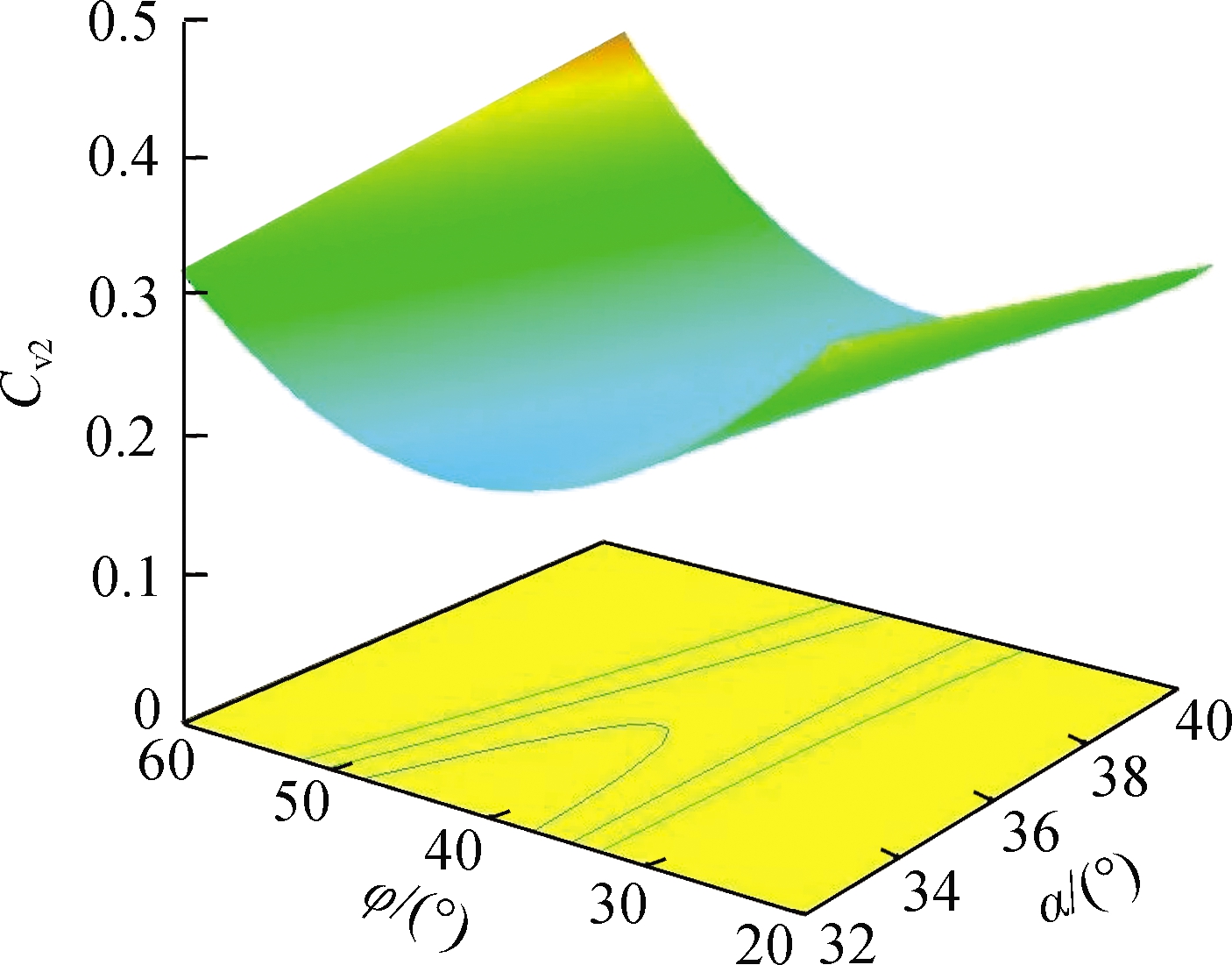
Among the interaction factors, the interactions of φ and β,α and φ, γ and φ have a significant effect on Cv2.The response surface relationship between Cv2and the significant interaction factor of A2 is shown in Fig.13.
As shown in Fig.13, the interaction between φ and α,β has a similar effect on the uniformity of A2.When φ is constant, the change in α,β has little influence on Cv1.In particular, when φ is 60°, the effect is relatively obvious.With changes in φ, γ has a great influence on the uniformity of A2.When φ is 20°, Cv2 decreases when γ increases.When φ is 60°, Cv2 increases when γ increases.

(a)
(b)

(c)
Fig.13 Relationship between Cv2 and interaction factors.(a)Significant effect of φ and β on Cv1;(b)Significant effect of φ and α on Cv2;(c)Significant effect of γ and φ on Cv2
Among the interaction factors, the interactions of β and φ, γ and φ, n and φ have a significant effect on Cv3.The response surface relationship between Cv3 and the significant interaction factors of A3 is shown in Fig.14.
As shown in Fig.14, when φ is 20°, β, γ, and n have little influence on Cv3.When φ is 60°, Cv3 increases when β increases, decreases when γ decreases, and increases when n decreases.Therefore, when φ is large, n, γ, and β have an obvious influence on the uniformity of A3.As shown in Fig.14(c), when n is 10 r/min, Cv3 decreases first and then increases when φ increases, and the change range is small.When n is 6 r/min, Cv3 greatly increases when φ increases.The results show that when φ is large and n is reduced, the segregation of A3 easily increases.
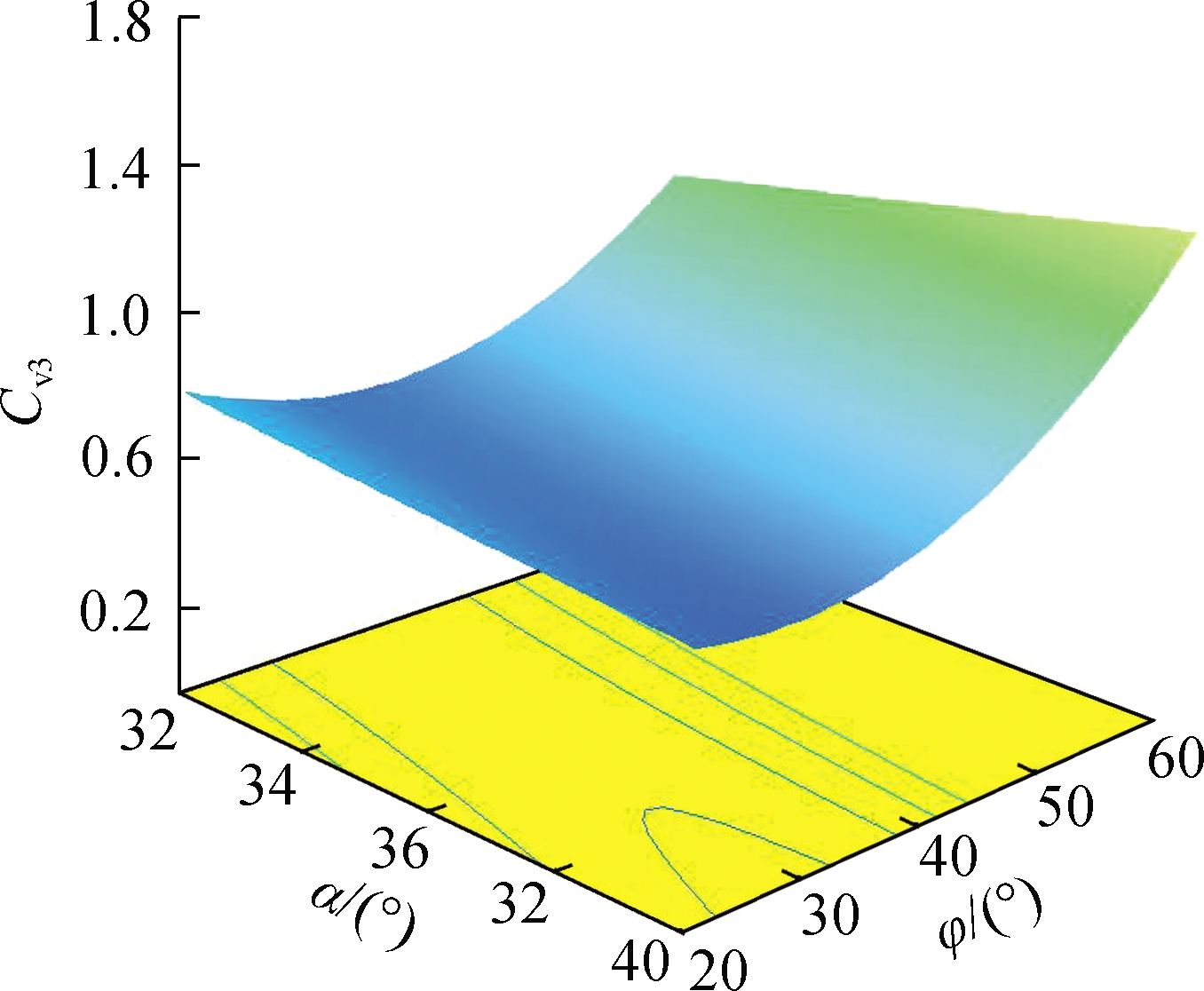
(a)

(b)

(c)
Fig.14 Relationship between Cv3 and interaction factors.(a)Significant effect of α and φ on Cv3;(b)Significant effect of γ and φ on Cv3;(c)Significant effect of n and φ on Cv3
As shown in Figs.12(a), 13(c), and 14(b), the interaction between γ and φ has a significant effect on the Cv of the three kinds of aggregates.To improve the mixing uniformity, when γ is large, φ should be smaller than γ.When γ is constant, φ corresponding to the low point of the response surface of the Cv of the aggregate decreases in turn; that is, a small value of φ should be arranged for the mixing of large particles.
Taking the minimum value of Cv as the optimization objective, the following values of each parameter are obtained: β=35°, α=38°, φ=32°, γ=6°, and n=10 r/min.
5 Conclusions
1)Increasing the speed and reducing the axial installation angle of the blade within the design range can reduce the discrete coefficient of the aggregates.
2)In the case of a certain feeding rate, increasing the phase angle alone can easily cause the mixing lag of the mixture, so the filling rate of the mixing chamber is increased.
3)To obtain a good mixing uniformity, when γ is large, φ should be a small value, and conversely, a large value should be taken.φ should be set to a large value when mixing large particles.
4)Through the RSM, the significant relationship between the influence of every single factor and its interaction on the Cv of the aggregates is obtained.Taking the minimum value of Cv as the goal, the best parameter matching is as follows: α=38°, β=35°, γ=6°, n=10 r/min, and φ=32°.
[1] Ma D C, Liu K.Modeling and simulation of mixing uniformity of double drum regenerative mixing equipment[J].Journal of Huazhong University of Science and Technology(Natural Science edition), 2020, 29(3):17-21.DOI:10.13245/j.hust.200302.(in Chinese)
[2] Liu B, Li Z G, Da Y F.Study on the inclination angle of outer cylinder mixing blade of double drum continuous mixing equipment[J].Highways & Automotive Applications,2014(4):150-152.(in Chinese)
[3] Zhao L J, Shen Y, Deng X, et al.Parameters matching of mixing blades for asphalt mixture mixer based on EDEM[J].Journal of Zhengzhou University(Engineering Science edition), 2019,40(3):79-84.DOI:10.13705/j.issn.1671-6833.2018.06.005(in Chinese)
[4] Simons T A H, Bensmann S,Zigan S, et al.Characterization of granular mixing in a helical ribbon blade blender[J].Powder Technology, 2016, 293(5):1-11.DOI:10.1016/j.powtec.2015.11.041
[5] Sakai M, Shigeto Y, Basinskas G, et al.Discrete element simulation for the evaluation of solid mixing in an industrial blender[J].Chemical Engineering Journal,2015,279(11):821-839.DOI:10.1016/j.cej.2015.04.130
[6] Milstead J.Asphalt drum mixer with curved scoop-like mixing tips:US5380082[P].Chattanooga, TN, USA: Astec Inductries, Inc.,1995-10-01.
[7] Larry W, Hudman J, Michael C.Method and apparatus for adapting asphalt dryer/mixer to minimize asphalt build-up: US8172448[P].Chattanooga, TN, USA: Astec Inductries, Inc.,2009-09-03.
[8] Wallevik J E, Wallevik O H.Analysis of shear rate inside a concrete truck mixer[J].Cement and Concrete Research,2017,95: 9-17.DOI:10.1016/j.cemconres.2017.02.007
[9] Mohajeri M, Molenaar A A A.Blending of virgin bitumen and RA binder in mixtures with high amounts of RA[J].Advances in Asphalt Materials, 2015:363-392.DOI:10.1080/14680629.2019.1663244
[10] Zhao L Y, Gu H R, Ye M.Differential double drum agitation uniformity modeling and multi-target parameter optimization[J].Journal of Huazhong University of Science and Technology, 2021,49(12):1-7.DOI:10.13245/j.hust.220205.(in Chinese)
[11] Ma D C.Lan F.Numerical simulation analysis on multi-layer low-temperature heating method of asphalt pavement in hot in-place recycling[J].Journal of Central South University,2020, 27(12):3793-3806.DOI: 10.1007/S11771-020-4577-6.
[12] Gao X.The dust removal system research of double drum type continuous regeneration asphalt mixing equipment[D].Changsha: Changsha University of Science and Technology,2015.(in Chinese)
[13] Zhong P H.Research on metering system in the continuous drum asphalt mixing plant[D].Xi’an: Chang’an University, 2013.(in Chinese)
[14] Huang K, Xu T, Li G F.The feasibility of DEM to analyze the temperature field of asphalt mixture[J].Construction and Building Materials,2016,106:592-599.DOI:10.1016/j.conbuildmat.2015.12.192.
[15] Zhang C G, Jiao S J, Xie L Y, et al.Modeling and simulation of material curtain density for asphalt mixing plant rotary dryer[J].Journal of Huazhong University of Science and Technology(Natural Science Edition),2017,45(5):55-60.DOI:10.13245/j.hust.170511(in Chinese)
[16] Shi H Q.Simulation of mixing asphalt mixture based on EDEM[D].Xi’an: Chang’an University,2017.(in Chinese)
[17] Zhang S J.Study and simulation analysis of the twin horizontal shaft mixer for asphalt mixture mixing experiment[D].Xi’an: Chang’an University, 2018.(in Chinese)