The development of reliability theory in geotechnical engineering has made it possible to establish a probabilistic limit state design method of pile foundation, represented by partial coefficients of load and resistance based on this theory.In recent years, the application of such a design based on reliability theory has become a development trend in the field of engineering structure codes.Therefore, many scholars have calibrated the calculation formulas of axial resistance for different pile types in code standards.
For instance, Luo[1] used the calibration method to calculate the reliability index of pile foundation in code for designs used in railway bridges and culverts.The author identified the expression of the design value of the axial-bearing capacity of bored cast-in-place piles and driven piles under the target reliability and obtained the corresponding partial coefficient of resistance.Bian et al.[2] systematically studied the reliability design method of pile foundation and proposed the calculation formula of the reliability index in a serviceability limit state.Many scholars have also conducted calibration and research for different pile types.For example, Fortier[3] developed a database according to the collected pile test data from Louisiana and Mississippi and then calibrated the resistance coefficient in AASHTO using the MC method.Tang et al.[4] collected the static load test data of 149 H-shaped steel piles and obtained the statistical variables of model factors.Using such information, they modified the design resistance coefficient of the vertical bearing capacity limit state of the H-shaped steel pile.
Some scholars have investigated the factors affecting the reliability index of pile foundation bearing capacity.For example, Wang et al.[5] clarified the influence of the effective internal friction angle of soil and the uncertainty of variable load on reliability design.Huang et al.[6] and Zhang et al.[7] analyzed the reliability indexes of bored cast-in-place pile before and after grouting.Their results indicated that post grouting can reduce the influence on the reliability of bearing layer characteristics and pile foundation construction.
In summary, many scholars have studied the reliability of axial resistance design methods for several types of piles.Thus, the corresponding data processing methods, reliability calibration procedures, and recommended values of partial coefficients were obtained.However, research on the probabilistic limit state design method for post grouting piles remains lacking.
In this paper, the probabilistic limit state design method of the axial resistance of post grouting pile was analyzed based on the statistical data for the axial resistance of 103 post grouting piles.The partial coefficient of total resistance was further calibrated under the determined target reliability, after which the recommended values of partial coefficients for load and resistance were obtained based on the probabilistic limit state design method of the vertical bearing capacity of the post grouting pile.
1 Calibration of the Design Method for Axial Resistance
1.1 Limit state equation
Assuming that the function of the structure is determined by n factors, then the function of the structure is given by
Z=g(X)
(1)
where X={X1,X2,…,Xn}T.
Generally, the basic equation of the limit state is defined as follows:
Z=g(R,G,Q)=R-G-Q=0
(2)
where R is the resistance of pile foundation; G is the dead load; Q is the live load.
To normalize the resistance caused by differences in pile specifications and soil properties, the dimensionless variables λR, λG and λQ are respectively introduced as follows[7-9]:
(3)
(4)
(5)
where RM, GM, and QM are the measured values of resistance, dead, and live loads, respectively; RK, GK, and QK are the calculated values of ultimate bearing capacity, as well as dead and live loads according to the code standards, respectively.
Thus, Eq.(2)is transformed into
Z=λRRK-λGGK-λQQK=0
(6)
In addition, reliability indexes were investigated for different live to dead load ratios or different partial coefficients contained in the code standard formulas.The ratio of live load to dead load, ρ=QK/GK, and the limit state design formulas are determined as follows:
(7)
where ρ is the ratio of live load to dead load; γR, γG, and γQ are the partial coefficients of total resistance, as well as dead and live loads, respectively.
1.2 Partial coefficient of resistance
Using Eq.(7)and the collected statistical data of field test piles, the reliability indexes of the pile axial resistance design formula can be obtained for different partial resistance coefficients and live to dead load ratios.
In this study, the JC method is used for conducting the reliability analysis[6].The results obtained by splitting the ratios of end and side resistance are equal to the partial coefficient of total resistance obtained by calibration:
(8)
where γb, γs, and γu are the partial coefficients of the end, side, and total resistance, respectively; ηs and ηbare the ratios of the mean values of side and end resistance to the mean value of the total resistance, respectively.
1.3 Target reliability index of bridge pile foundation
The target reliability index of a highway bridge structure is 4.7[10].Therefore, the reliability index contained in the probabilistic limit state calculation formula, which is represented by the resistance partial coefficient, should not be lower than 4.7.
2 Calculation Model and Data Analysis of Post Grouting Pile
2.1 Calculation method
In this paper, the limit value of the vertical bearing capacity of post grouting pile is obtained, in accordance with the specifications for the design of foundation for highway bridges and culverts(JTG 3363—2019)[11]:
Ru=Rus+Rub=u∑βsiqikli+2βpqrAp
(9)
where Ru, Rus, and Rub are the ultimate bearing capacities of the total, side, and end resistance, respectively; u is the perimeter of the pile; qik is the standard value of the ultimate side resistance of the ith soil layer; li is the thickness of the i-th soil layer; qr is the standard value of ultimate end resistance; Ap is the cross-sectional area of pile end; βsi and βp are the enhancement coefficients of side and end resistance, respectively.
Then the corresponding probabilistic limit state design formula is given by
2.2 Statistical analysis
A total of 103 post grouting pile test data were collected in this study[12-15], of which 73 piles were loaded to the limit state in the field static load test.Additionally, even though 30 field test piles were not loaded to the limit state, the detailed load and settlement data could be predicted by the polynomial, hyperbolic, and modified hyperbolic models[16-19].
After screening these data[20], the numbers of test piles that can be predicted by the polynomial, hyperbolic, and modified hyperbolic models are 29, 28, and 26, respectively.The prediction results of each model are listed in Tab.1.
Tab.1 Statistical information on the prediction results of different models
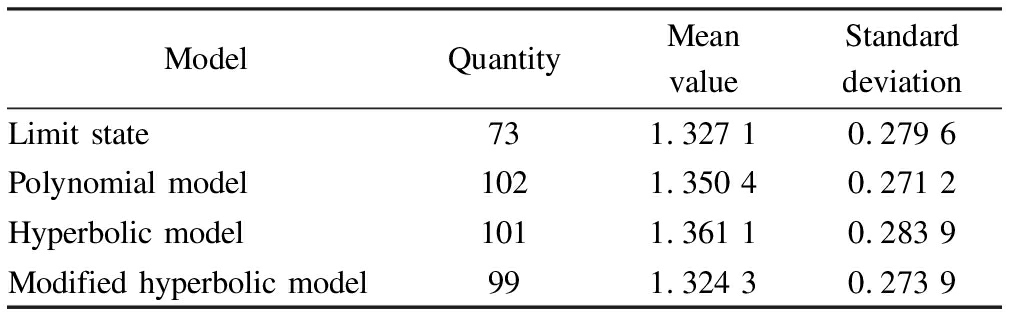
ModelQuantityMeanvalueStandarddeviationLimit state731.327 10.279 6Polynomial model1021.350 40.271 2Hyperbolic model1011.361 10.283 9Modified hyperbolic model991.324 30.273 9
3 Reliability Design Formula
3.1 Effect of predictive models on the reliability index of axial resistance
The statistical data of the axial resistance of post grouting pile under different prediction models are given in Tab.1.Then, the reliability indexes of the design formula of the axial resistance of post grouting pile for a highway bridge under the conditions of γR=2, γG=1.2, and γQ=1.4 were calculated.The results are shown in Fig.1.As shown in the figure, the calculated results of the three prediction models are higher compared with the test results loaded to the limit state, while the results obtained from the modified hyperbolic prediction model are closest to the results of the static load test.
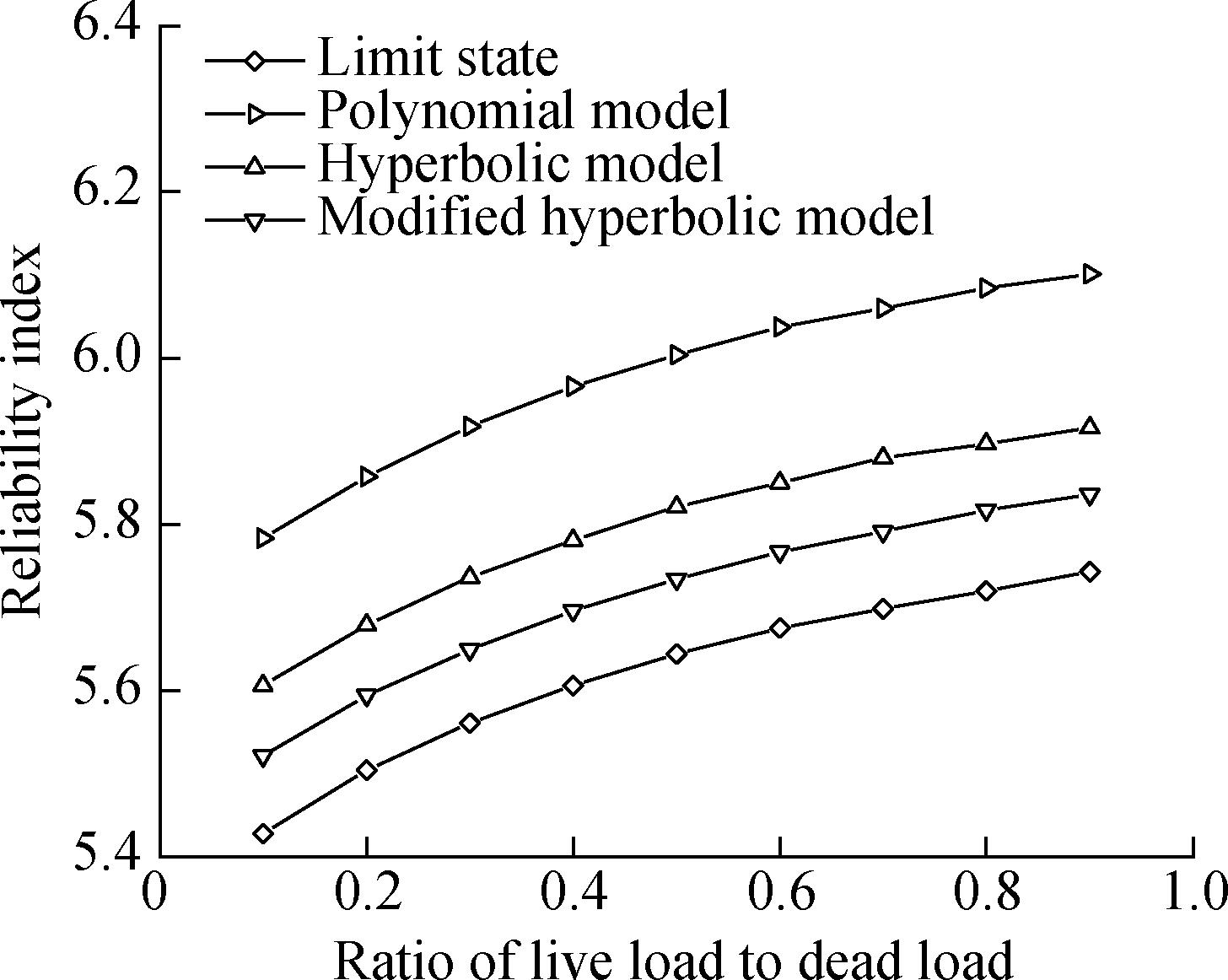
Fig.1 Reliability index of the axial resistance of post grouting pile under different prediction models
3.2 Factors influencing the reliability index
The influence of different factors, such as the operating condition of the vehicles on the bridge and the ratio of live to dead load on the reliability index is considered in this section based on two sets of partial coefficient values; namely, γR=2, γG=1.2, γQ=1.4 and γR=2, γG=1.1, γQ=1.4.The calculation results of the axial resistance reliability index of the post grouting pile based on Eq.(9)are plotted in Fig.2.As shown in the figure, the influence degree of the operating state of vehicles on the reliability index shows a trend of increasing, decreasing, and then increasing again as the ratio of live to dead load changes.
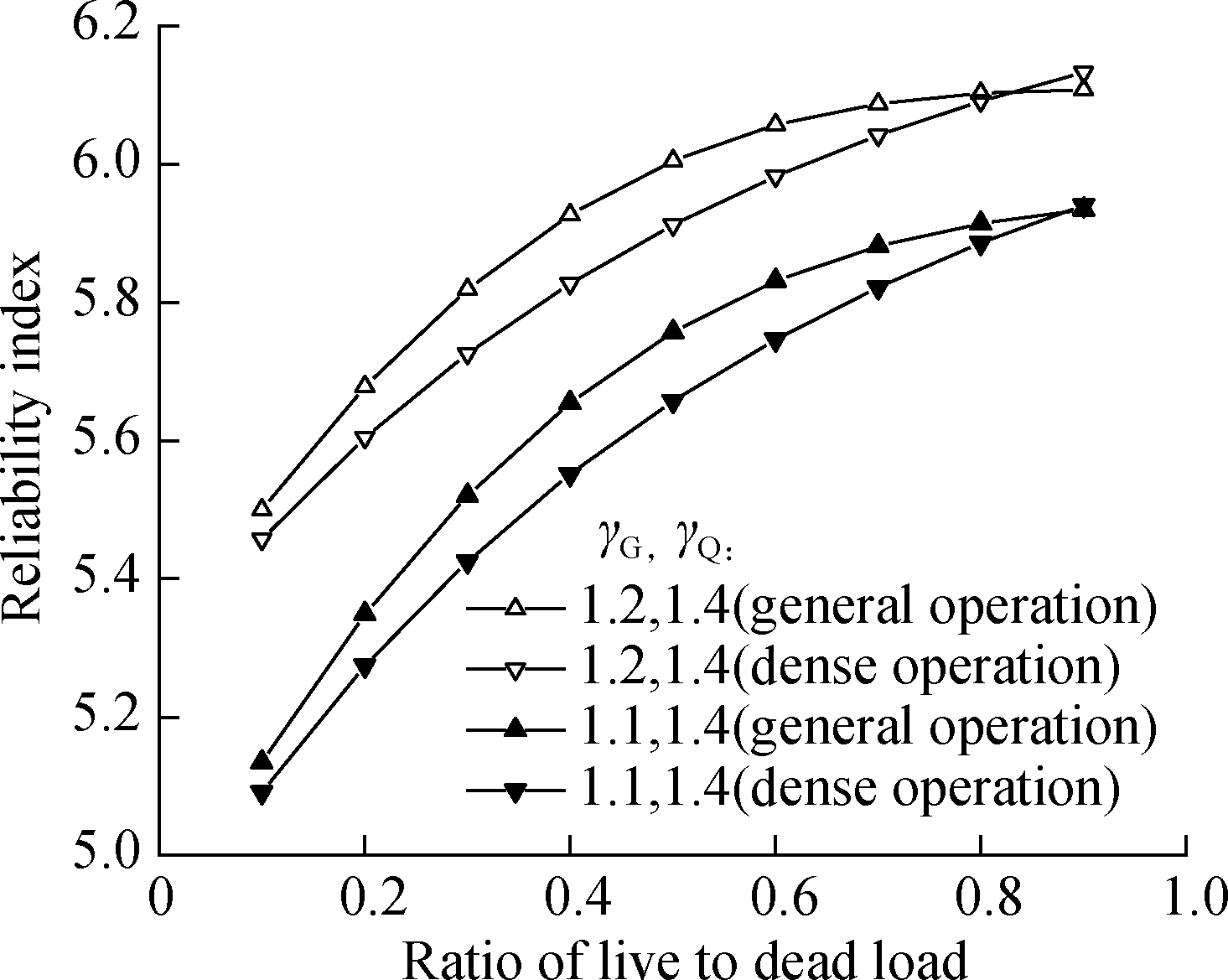
Fig.2 Reliability indexes of the axial resistance of post grouting pile under different operation conditions
Additionally, under the condition that the partial coefficient of the live load is 1.4, the partial coefficients of dead load are 1.1 and 1.2, respectively.Furthermore, the calculated reliability indexes are greater than the target reliability index of 4.7, and the reliability index also increases gradually with the change of the ratio of live to dead load.Thus, it is necessary to calibrate the reliability.
3.3 Partial coefficient of the resistance of grouting pile
The partial coefficients of the total resistance of post grouting pile under different operating conditions are calibrated, and the target reliability is determined as 4.7.The calibration results for the corresponding partial coefficients of different loads are shown in Fig.3.

Fig.3 Partial coefficients of the total axial resistance of post grouting pile
Based on Eq.(8), the partial coefficients of the total axial resistance of post grouting pile are equivalently divided under different operating conditions.The partial coefficients of the side and end resistance of the post grouting pile are obtained by setting the ratio of live to dead load as 0.1.The calculation results are listed in Tab.2.
Tab.2 Partial coefficients of the axial load and resistance of post grouting pile

Operation statusγGγQγuγsγbGeneral operation1.11.41.821.652.681.21.41.691.552.30Dense operation1.11.41.841.662.731.21.41.701.562.34
Tab.2 shows that the operation state has little effect on the total resistance and the side and end resistance partial coefficients of the grouting pile under the same partial coefficients of dead and live loads.Therefore, in order to facilitate, unify, and ensure the safety of bridge foundation piles, the resistance partial coefficient under dense operation can be determined based on the load partial coefficient.
3.4 Verification based on engineering case
Suramadu Bridge in Indonesia is located on Madura Strait in East Java Province, Indonesia.The No.45 pile of the approach bridge was selected as an engineering case in this study to illustrate and verify the feasibility of the probabilistic limit state design method of axial resistance for the post grouting pile.
The pile is 2.2 m in diameter and 80.708 m in length.The side resistance within 11 m above the pile end is enhanced, and the enhancement coefficients of side and end resistance are taken as βsi=1.3 and βP=1.6, respectively[11].Then, based on Eq.(9), the calculated values of ultimate side resistance and ultimate end resistance of the test pile are Rus=26.636 MN and Rub=7.347 MN, respectively.
According to the proposed probabilistic limit state design method for the axial resistance of the post grouting pile,γG=1.2 and γQ=1.4 are considered, and the design value of the bearing capacity of the test pile is calculated from the post grouting pile’s partial coefficient of resistance.The bearing capacity calculated from the total partial coefficient is 19.990 MN, and the corresponding value for the sum of the partial coefficients of end and side resistance is 20.214 MN.
The measured pile top load-displacement equivalent curve of the No.45 pile is shown in Fig.4.As can be seen, the load at the maximum displacement is determined as the ultimate bearing capacity.As shown in Fig.4, the measured bearing capacity of the test pile is 39.717 MN, while the end resistance and side resistance corresponding to the level of load are 9.580 and 30.137 MN, respectively.The safety factor is taken as 2.0.Then, the design value of the bearing capacity of the test pile, which is calculated by using the probabilistic limit state design method of axial resistance, is slightly higher than the measured value.Given that the test pile is not loaded to failure, the design value obtained according to the method given in this study is relatively safe.
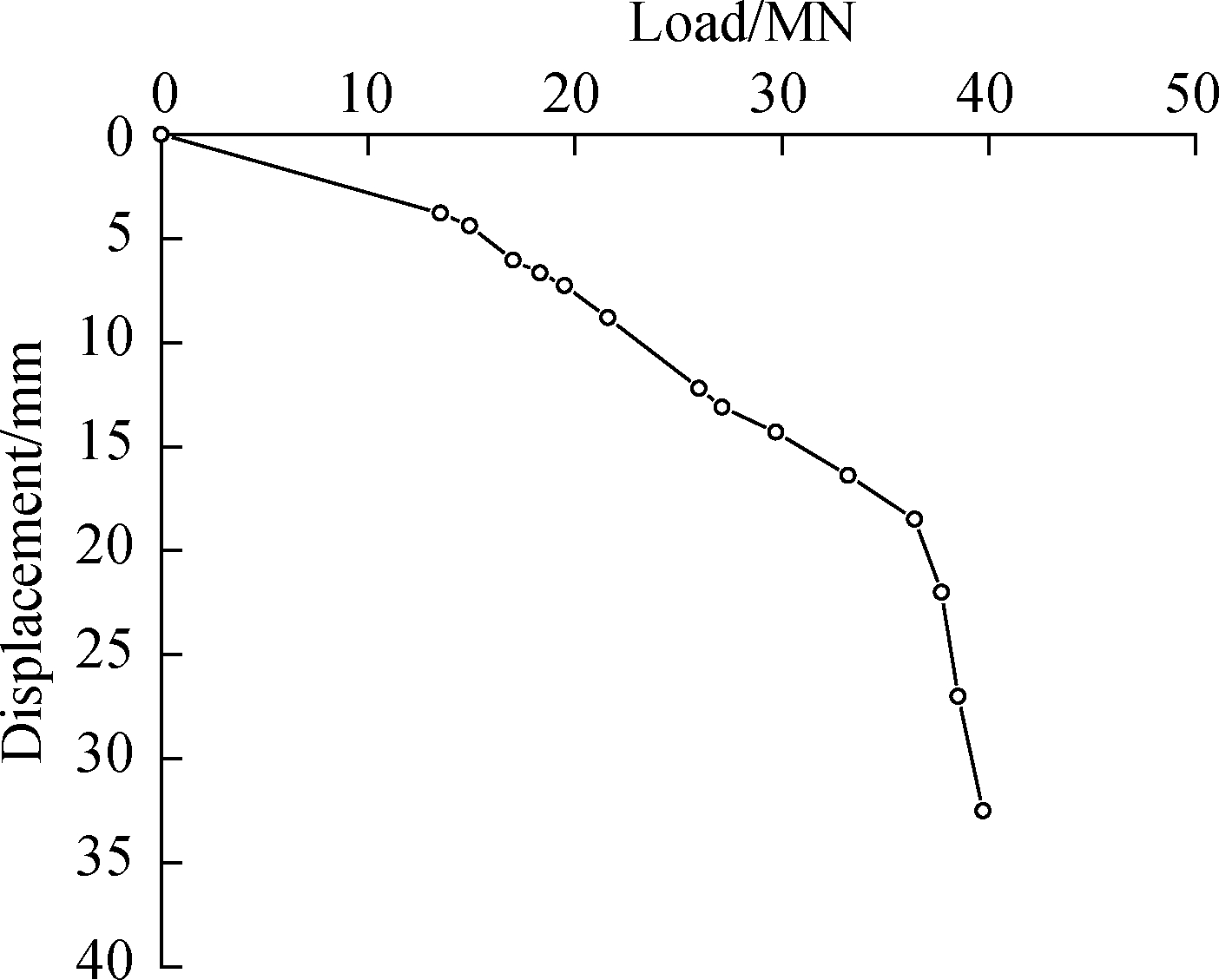
Fig.4 Load-displacement curve of the test pile of Suramadu Bridge
4 Conclusions
1)Compared to the calculated values based on the data on the static load test for the limit state, the three ultimate bearing capacity prediction models produced higher values.Furthermore, the results obtained from the modified hyperbolic prediction model are closest to that of the static load test.
2)The reliability index of the axial resistance of the post grouting pile increases gradually with the increase in the ratio of live to dead load.Furthermore, the influence degree of the operating state of vehicles on the reliability index shows a trend of increasing, decreasing, and then increasing again as the ratio of live to dead load changes.
3)The corresponding partial coefficient of total resistance was obtained based on the target reliability index value of 4.7.Assuming that γG=1.1 and γQ=1.4, the corresponding partial coefficients of the total resistance, side resistance, and end resistance are 1.84, 1.66, and 2.73, respectively.Meanwhile, upon assuming that γG=1.2 and γQ=1.4, the corresponding partial coefficients of the total, side, and end resistance are 1.70, 1.56, and 2.34, respectively.
4)The engineering case results show that the design value obtained using the proposed method is relatively safe.
[1] Luo S X.Research and engineering application on probability limit states design method of pile foundation[D].Chengdu: Southwest Jiaotong University, 2004.(in Chinese)
[2] Bian X Y, Zheng J J, Xu Z J, et al.Target reliability index for serviceability limit state of single piles[J].Journal of Central South University, 2015, 22(1): 310-316.DOI: 10.1007/s11771-015-2523-9.
[3] Fortier A R.Calibration of resistance factors needed in the LRFD design of drilled shafts[D].Baton Rouge, LA, USA: Louisiana State University, 2016.
[4] Tang C, Phoon K K.Evaluation of model uncertainties in reliability-based design of steel H-piles in axial compression[J].Canadian Geotechnical Journal, 2018, 55(11): 1513-1532.DOI: 10.1139/cgj-2017-0170.
[5] Wang J M, Xiao F, Chen J J, et al.A reliability analysis method for pile foundation based on Bayesian theory and Monte Carlo simulation[J].Chinese Journal of Underground Space and Engineering, 2017, 13: 85-90.(in Chinese)
[6] Huang S G, Shen J H, Li M.Reliability analysis of bearing capacity of post-grouted bored piles[J].Rock and Soil Mechanics, 2019, 40(5): 1977-1982.DOI: 10.16285/j.rsm.2018.0332.(in Chinese)
[7] Zhang Z T, Gong W M, Dai G L.Calculation and analysis of bearing capacity reliability index of post-grouting pile[J].Japanese Geotechnical Society Special Publication, 2020, 8(10): 404-409.DOI: 10.3208/jgssp.v08.c30.
[8] Phoon K K, Kulhawy F H.Characterization of geotechnical variability[J].Canadian Geotechnical Journal, 1999, 36(4): 612-624.DOI: 10.1139/t99-038.
[9] Dithinde M, Phoon K K, De W M, et al.Characterization of model uncertainty in the static pile design formula[J].Journal of Geotechnical and Geoenvironmental Engineering, 2011, 137(1): 70-85.DOI: 10.1061/(ASCE)GT.1943-5606.0000401.
[10] CCCC Highway Consultants Co., Ltd.Unified standard for reliability design of highway engineering structures: JTG 2120—2020[S].Beijing: China Communications Press, 2020.(in Chinese)
[11] CCCC Highway Consultants Co., Ltd.Specifications for design of foundation of highway bridges and culverts: JTG 3363—2019[S].Beijing: China Communications Press, 2020.(in Chinese)
[12] Li X M, Zhang X W, Guo J S et al.Study on bearing behavior of post grouting super long bored pile of Dongming Yellow River Bridge[J].Journal of China & Foreign Highway, 2014, 34(3): 88-92.DOI: 10.14048/j.issn.1671-2579.2014.03.038.(in Chinese)
[13] Zhang Z T, Gong W M, Dai G L, et al.Enhancement of load bearing of post-grouted drilled shafts based on in situ tests[J].Arabian Journal of Geosciences, 2021, 14(1): 1-13.DOI: 10.1007/s12517-020-06332-4.
[14] Wan Z H, Dai G L, Gong W M.Field and theoretical analysis of response of axially loaded grouted drilled shafts in extra-thick fine sand[J].Canadian Geotechnical Journal, 2020, 57(3): 391-407.DOI: 10.1139/cgj-2018-0382.
[15] Chu C F, Li X C, Lu L H, et al.Load bearing behavior of pile tip post-grouting super-long large-diameter bored piles in cohesionless soil[J].Chinese Journal of Geotechnical Engineering, 2011, 33(S2): 388-391.DOI: 1000-4548(2011)S2-0388-04.(in Chinese)
[16] Zhang Q Q, Li S C, Liang F Y, et al.Simplified method for settlement prediction of single pile and pile group using a hyperbolic model[J].International Journal of Civil Engineering, 2014, 12(2): 146-159.
[17] Gao X J, Zhu X.Forecasting ultimate bearing capacity of single squeezed branch pile by hyperbola method[J].Rock and Soil Mechanics, 2006, 27(9): 1596-1600.DOI: 10.16285/j.rsm.2006.09.035.(in Chinese)
[18] Zhao M H, Hu Z Q.Adjusting hyperbola method for estimating ultimate bearing capacity of test pile[J].Building Structure, 1995(3): 47-52.DOI: 10.19701/j.jzjg.1995.03.012.(in Chinese)
[19] Luo X G, Ren W X, Yin Y G, et al.A modified hyperbolicity-based load transfer model for nonlinear settlement analysis of root piles in multilayered soils[J].Acta Geotechnica, 2022, 17: 303-317.DOI: 10.1007/s11440-021-01215-8.
[20] Xu Z J.Reliability analysis of bearing capacity and reliability design optimization of piles[D].Wuhan: Huazhong University of Science & Technology, 2012.(in Chinese)