High-speed maglev transportation is the fastest ground transportation system worldwide.The high-speed maglev guideway is an important part of the maglev transportation line that undergoes many changes under transverse, vertical, and longitudinal static and dynamic loads.With the development of high-speed railways, more studies on the vibration characteristics of railway bridges and vehicles have been conducted [1].However, the dynamic interaction response characteristics of high-speed maglev vehicles running on flexible guideways have received less research attention.When a high-speed maglev vehicle is running, the guideway and vehicle are easily affected by the external natural environment and the coupling vibrations.Meanwhile, the maglev transportation system has strict requirements for the deformation control of the guideway and the vehicle.The dynamic response is not only related to the vehicle but also to the guideway system; thus, it is of great significance to the analysis and research of the dynamic response of high-speed maglev vehicles on a flexible guideway.Furthermore, the dynamic response can provide reference and guidance for the health monitoring of guideways and for avoiding the so-called “frequency resonance effect” in the design of high-speed maglev vehicle components.
As an inherent property of a structure, frequency reflects the changes in the dynamic characteristics of the structure[2-3].The fast Fourier transform is a widely used signal frequency domain processing technology.However, for most multi-degree-of-freedom(multi-DOF)systems, the system frequency cannot be accurately obtained, the frequency domain identification accuracy is low, and the signal cannot be analyzed in the time-frequency domain simultaneously, resulting in the loss of signal time information [4-5].The wavelet transform, which is a time-scale signal analysis method, has the characteristics of multi-resolution and a good ability to characterize the local characteristics of signals in the time and frequency domains.Therefore, this method is not only suitable for detecting transient phenomena in normal signals and showing their components but also has a good effect on detecting and diagnosing dynamic system faults using wavelet transform [6-7].In practice, the measured signal of the structure is inevitably mixed with noise and interference.Related to this, wavelet transform can simultaneously analyze signals in the time and frequency domains, distinguish the effective and noise interference components in the signal and effectively realize the preprocessing of signal noise elimination [8].
As presented in the literature, the method of modal identification using the wavelet transform achieved good results.For example, phase and amplitude information is used to extract the ridgeline of the wavelet.However, these two methods are only accurate in the case of a relatively high signal-to-noise(SNR)ratio.Furthermore, both methods are only suitable for cases in which the signal contains a single component.Even if each component can be clearly distinguished on the wavelet transform plane, multiple ridges cannot be extracted simultaneously when the signal contains multiple components.However, the two methods mentioned above cannot meet the requirements of vibration response characteristics analysis because the dynamic response of a high-speed maglev vehicle on a flexible guideway has the characteristics of a low SNR and multiple frequency components.Therefore, to solve the shortcomings of the above two methods, this study uses a method based on the maximum slope method to extract the wavelet ridge.Doing so can simultaneously meet the situation of low SNR and multi-frequency components and effectively improve the accuracy of wavelet ridge extraction.
In the current study, a high-speed maglev guideway was taken as the research object, and a finite element model of the guideway was established.The method of extracting the wavelet ridgeline using the maximum slope method was used.The effectiveness of the method was proven by taking the simulated real response signal as an example.At the same time, the data collection of the vibration acceleration response of the guideway was conducted based on the 600 km/h high-speed maglev vehicle and high-speed maglev test line.We also analyzed the frequency parameters and vibration modes of the interaction vibration characteristics of the guideway and the 600 km/h maglev vehicle.Furthermore, the objective function of the finite element model was established due to the inconsistency between the finite element model of the guideway and its measured modal parameters.The initial guideway finite element model was also updated and modified using the iterative parameter method in order to obtain the model of the high-speed maglev guideway, consistent with the actual guideway.Combined with the maglev vehicle/guideway coupling dynamic model with 18 DOF, we verified the accuracy of the updated guideway in the dynamic response calculation.This lays the foundation for the analysis of the high-speed maglev vehicle/guideway coupling dynamic response and the design of the maglev control system.
1 Extraction of the Wavelet Ridgeline Based on the Maximum Slope Method
The signal distribution on the continuous wavelet plane is similar to the ridge in the topographic map.The parameters distributed along the ridgeline in the time-frequency plane of the wavelet transform share a strong similarity with the original signal, which can be used to describe the original signal’s important parameters.The amplitude or phase of the wavelet transform can be extracted from the ridgeline in the time-frequency plane.The steps of the extraction of wavelet ridgelines based on the phase information of the Morlet wavelet and the amplitude information can be found in a previous study [9].The phase and amplitude information methods based on the wavelet coefficient are particularly sensitive to noise.The ridgeline of the signal wavelet transform can be extracted accurately only when the real response signal contains a single component and when the SNR is relatively high.To overcome the shortcomings of the above two methods, this study thus adopts the maximum slope method to extract the wavelet ridgeline under the condition of a non-stationary signal with a low SNR and multi-frequency components [10].
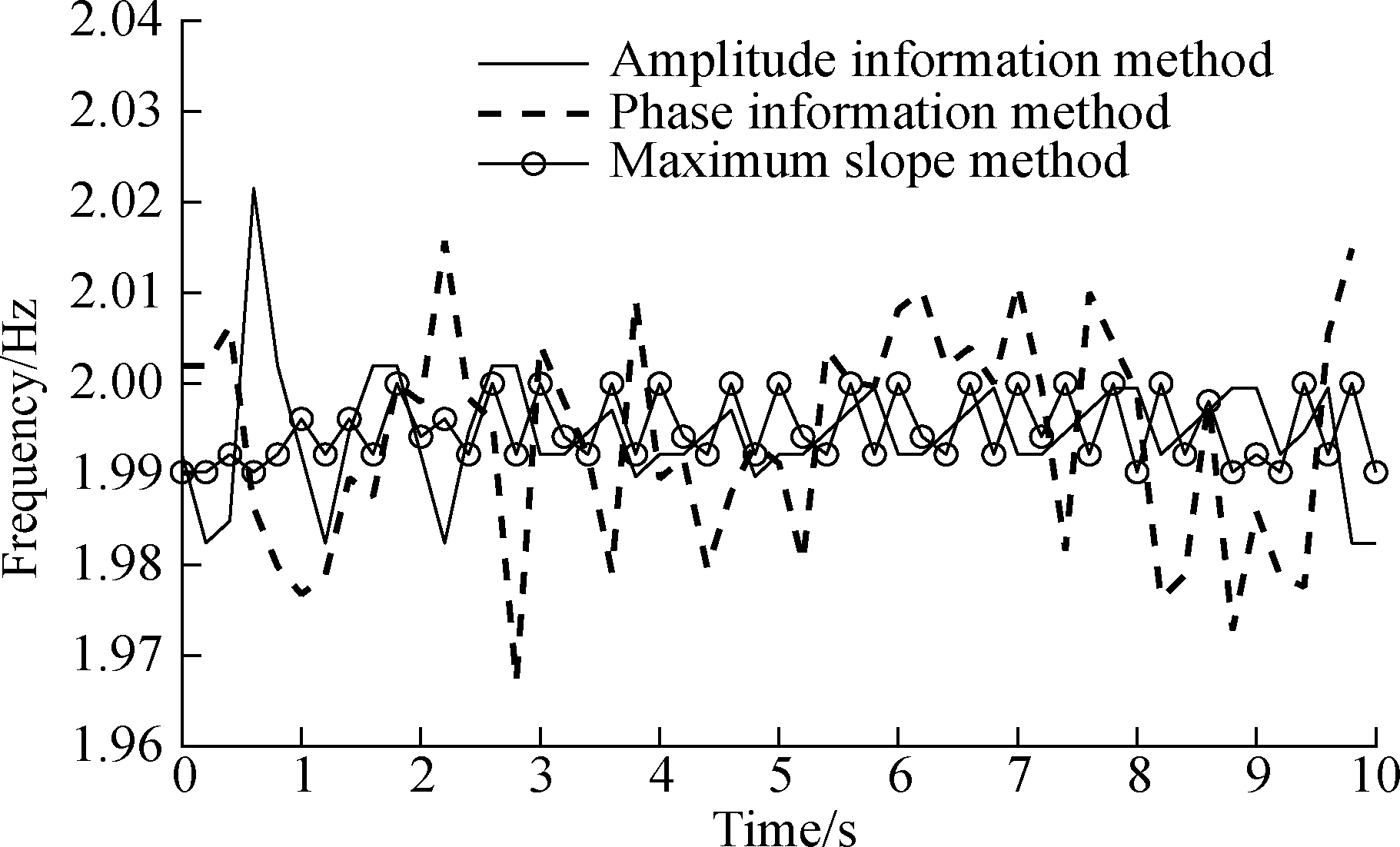
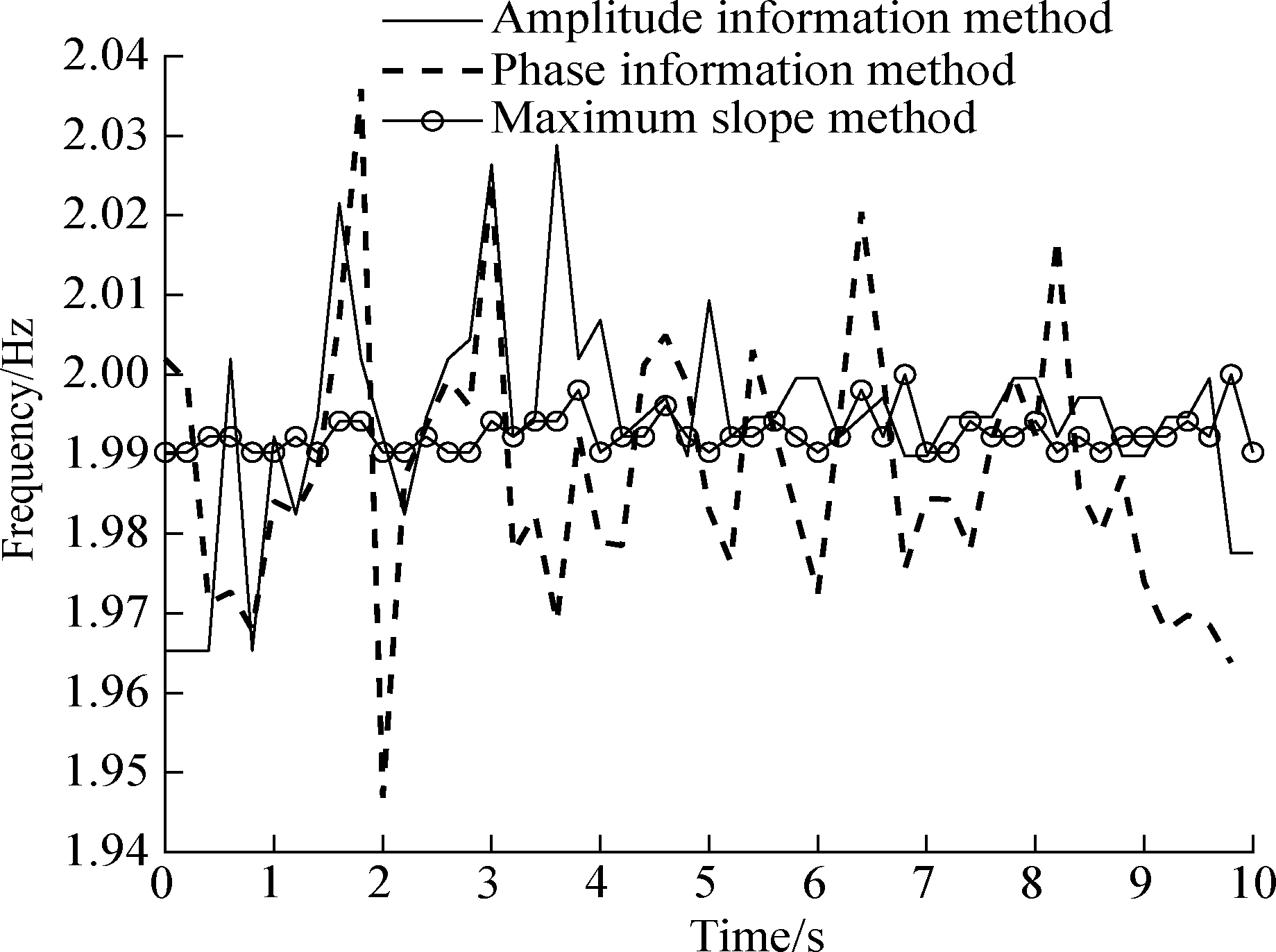
Here, we used the maximum slope method to extract the wavelet ridge of the original signal x(t)=cos(4πt)with the addition of a 25% noise signal.The specific extraction results of the wavelet ridge compared to the amplitude and phase information methods are shown in Figs.1(a)and(b).The results of the frequency identification reveal that the noise level has little effect on the accuracy of the frequency extraction.The maximum and minimum errors of the three methods were also compared and analyzed.The results indicate that the maximum errors of the phase information, the amplitude information, and the maximum slope methods are 2.655%, 1.735%, and 0.400%, respectively.Furthermore, compared to the phase and amplitude information methods, the accuracy of the maximum slope method improved by 2.255% and 1.335%, respectively.Therefore, the method of extracting wavelet ridges based on the maximum slope method overcomes the shortcomings of the amplitude and phase information while also reducing the influence of signal noise level on the accuracy of wavelet ridge extraction.Moreover, the maximum slope method can effectively extract the instantaneous frequency of various non-stationary signals, and the identified instantaneous frequency values are consistent with the theoretical results.Finally, the recognition accuracy is better than that of the wavelet phase information and amplitude information methods.
(a)
(b)
Fig.1 Comparison of the frequency recognition results of different methods.(a)No noise signal added;(b)25% noise signal added
2 Modal Identification of the High-speed Maglev Guideway Structure
2.1 Field data measurement of the guideway structure
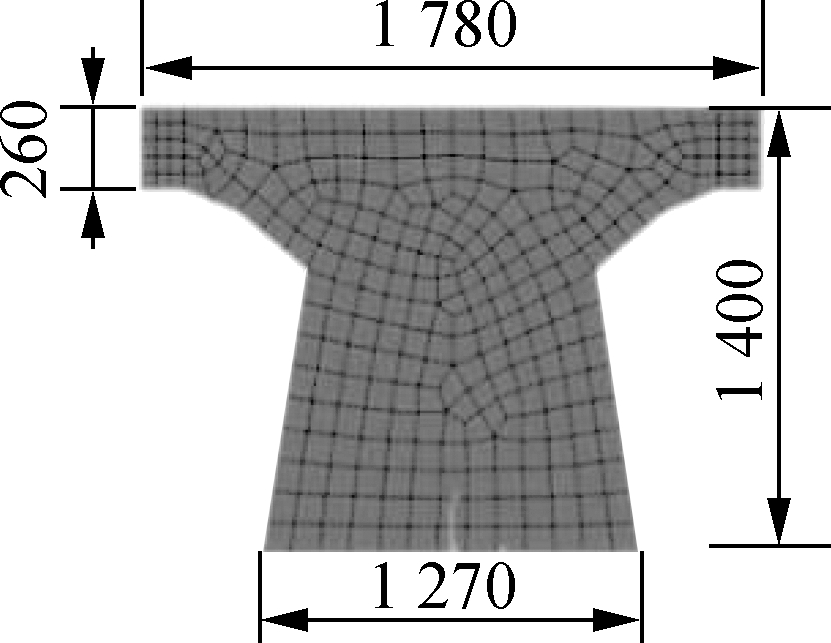
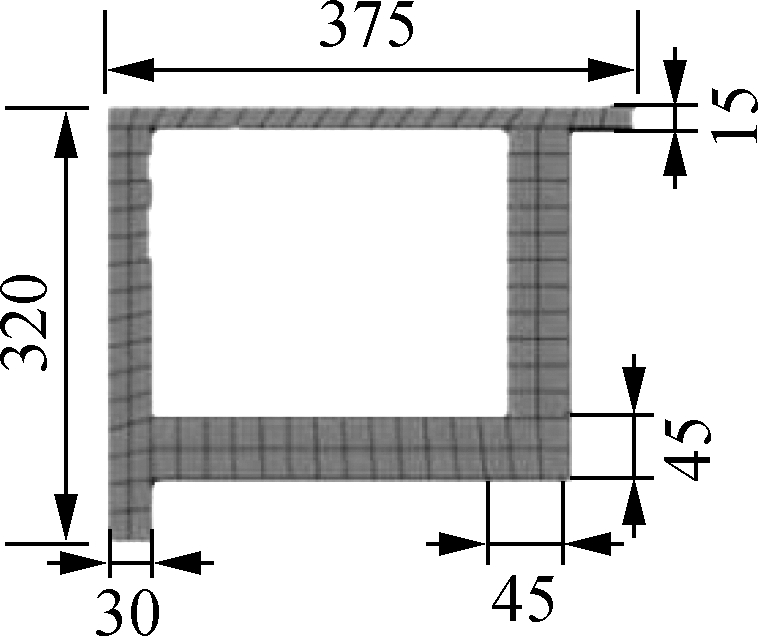
As the basic structure of a high-speed maglev vehicle, the guideway bears the load generated by a high-speed maglev vehicle and transmits the load to the ground.The upper structure is a prestressed concrete guideway, each comprising of a concrete beam and two steel reaction rails.The sectional diagrams are shown in Fig.2.The concrete beam and reaction rail were connected using a steel support.To ensure stable and reliable cooperation between the concrete beam and the reaction rail, one end of the steel support was embedded in the guide rail beam, while the other end was connected to the reaction rail through high-strength bolts.The high-speed maglev test line, located inside the Jiading Campus of Tongji University, Shanghai, has a total length of 1 475 m.The overall configuration of this line is shown in Fig.3.There are four types of maglev track lines: turnout, straight, horizontal curve, and vertical curve.The 12.384 m guideway at the straight section was taken as the test object.The linear guideway of the test section consisted of a single-span beam, the two ends of which were supported using elastic supports.The tie constraint was used to simulate the rigid connection between the reaction rail and the concrete beam.The density of the concrete beam structure was 2 500 kg/m3, the elastic modulus was 36.5 GPa, and the cross-sectional area was 1.550 m2.Furthermore, the structural density of the reaction rail was 7 850 kg/m3, the elastic modulus was 310 GPa, and the cross-sectional area was 0.038 m2.
(a)
(b)

(c)
Fig.2 Structure of the 12.384 m high-speed maglev guideway.(a)Cross-section view of the guideway structure;(b)Cross-section view of the reaction rail structure;(c)The model of the 12.384 m guideway structure
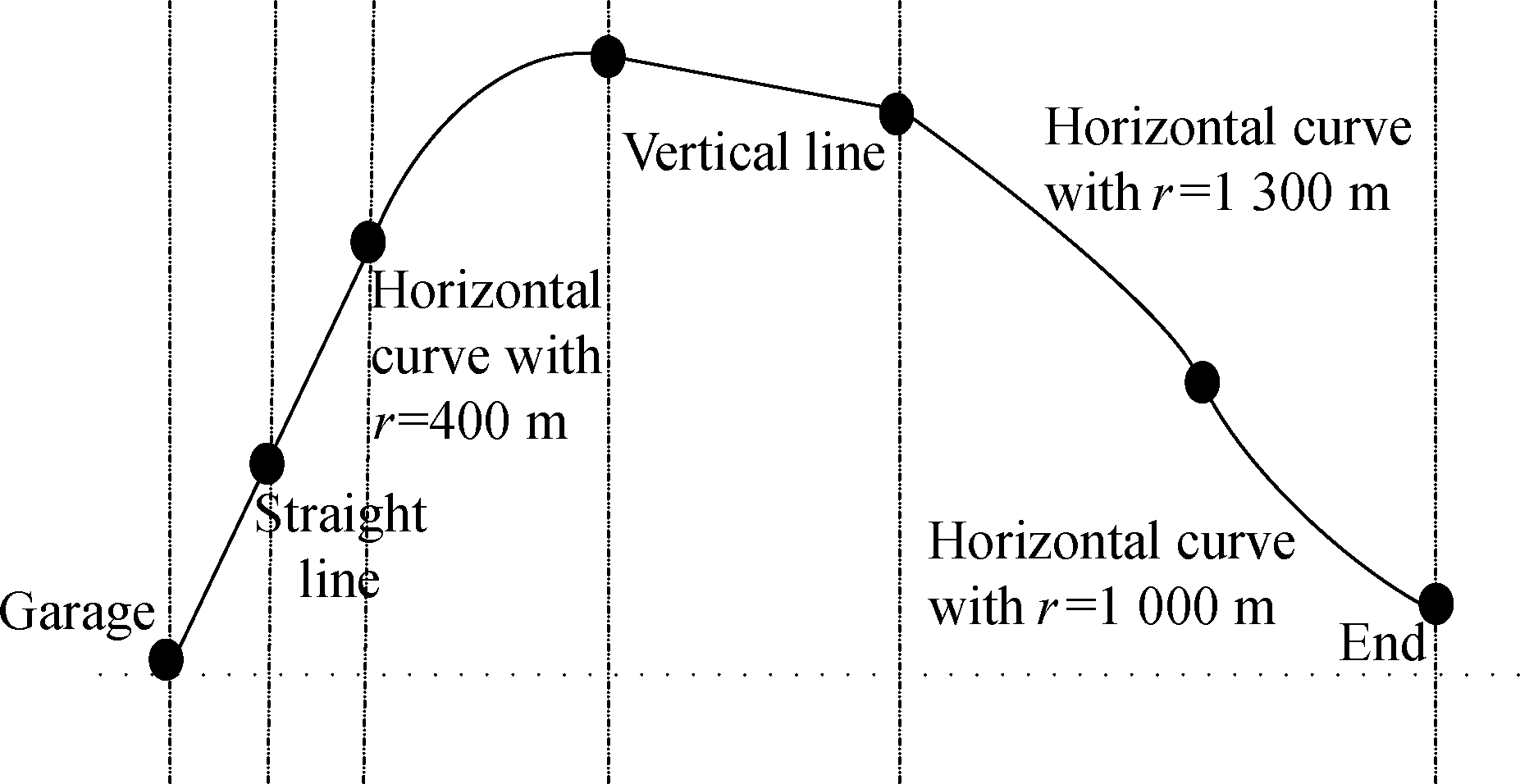
Fig.3 High-speed maglev test line at Tongji University
Relying on the 600 km/h high-speed maglev test vehicle, a field vibration test of a 12.384 m guideway was conducted on the high-speed maglev test line.The speed of the high-speed maglev vehicle was 30 km/h, and the weight of the vehicle was 60 t.Seven sensors were arranged on each side of the guideway to measure the vibration frequency of the guideway as much as possible.Among these, measuring sensors V7 and V8 served as the midpoints of the guideway; sensors V1, V3, and V5 were on the left side; sensors V9, V11, and V13 were on the right side; and sensors V2, V4, V6, V8, V10, V12, and V14 were arranged on the other side of the guideway.The arrangement of the field sensors is illustrated in Fig.4.As can be seen, the z-direction acceleration sensors were arranged at each measuring point, while the y-direction acceleration sensor was set at an odd number measuring point.The acceleration sensor adopted a 941 B-type vibration pick-up.The field layout and installation of the z-and y-direction acceleration sensors are shown in Fig.5(a).The z-direction sensor was arranged and installed separately, as shown in Fig.5(b).A laser velocimeter was used to measure the speed of the 600 km/h maglev vehicle passing through the guideway.The device is shown in Fig.5(c).The field test guideway is shown in Fig.5(d), and the signal acquisition equipment is shown in Fig.5(e).The sampling frequency of the field acquisition instrument was set to 1 024 Hz.
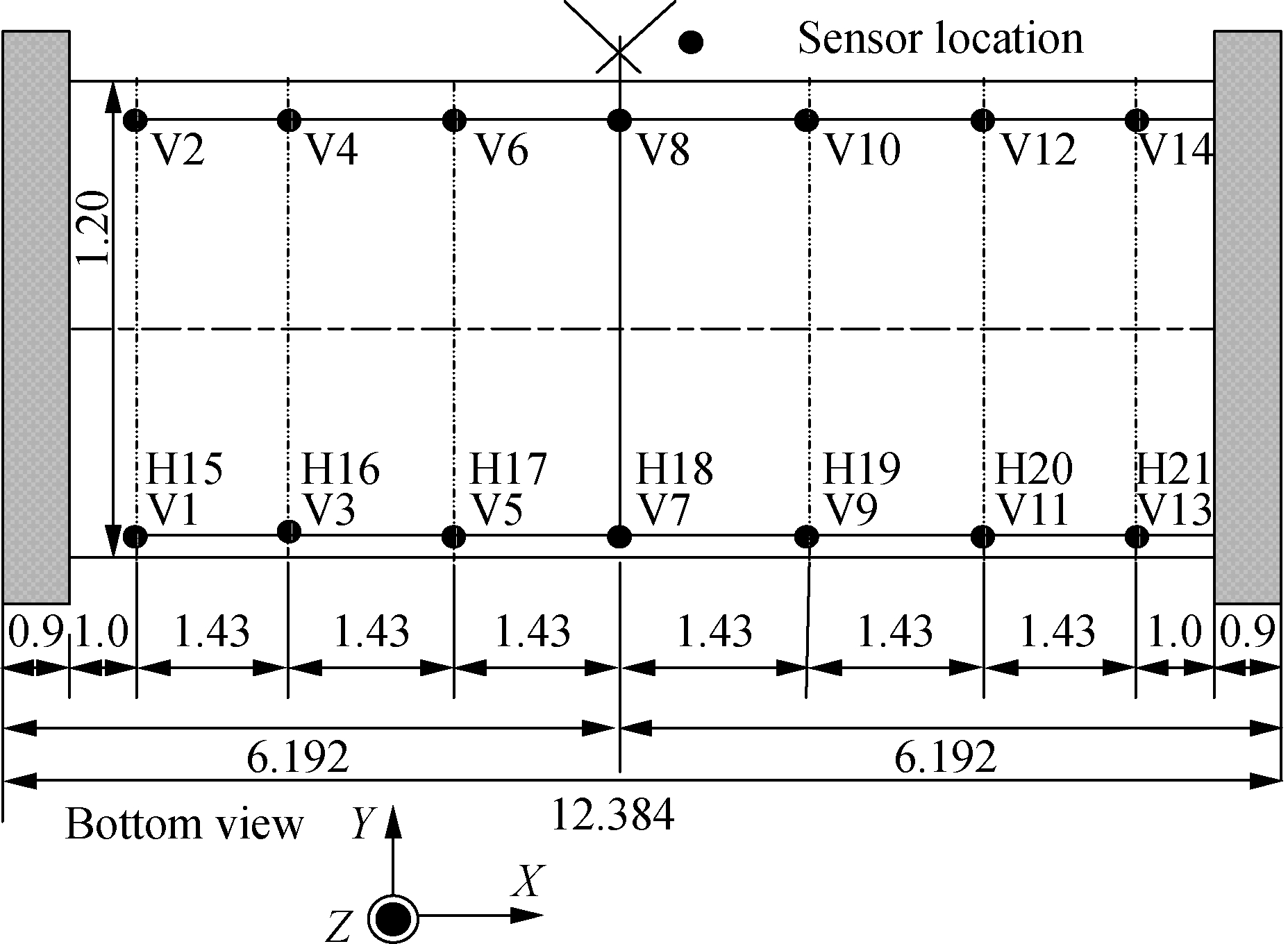
Fig.4 Schematic diagram of site measuring point layout of the guideway structure(unit: m)

(a)

(b)

(c)

(d)

(e)
Fig.5 High-speed maglev test site and test equipment.(a)Sensor arrangement in the z-and y-directions;(b)Sensor arrangement in the z-direction;(c)Laser velocimeter;(d)Field test structure of guideway;(e)Field acquisition equipment
2.2 Modal identification of the guideway structure based on wavelet transform
In the measured data of the high-speed maglev guideway, the sampling frequency was 1 024 Hz, the sampling time was 10 s, and each measuring point had 10 240 data.Taking as an example the measurement sensors V7, V8, and H18 in the middle of the high-speed maglev guideway, the power spectrum curve is relatively smooth, and the modal frequency identification results are relatively accurate.Next, we calculated the correlation function curves among sensors V7, V8, and H18.The correlation between V7 and V8 is large because they are located on both sides of the same section of the guideway, and all vertical accelerations are highly correlated in the low-frequency range.However, the correlation between V7 and H18 and that between V8 and H18 shows a significant decrease, especially at the low-frequency special vibration frequency.Furthermore, the correlation function is lower than 0.4, indicating that the coupling degree of the lateral vibration and vertical vibration of the guide rail is not significant.The peak values of the guideway response excited by the maglev vehicle in the middle of the guideway ranged 0.6 to 0.8 m/s2, while those of the lateral acceleration ranged 0.8 to 1.0 m/s2.
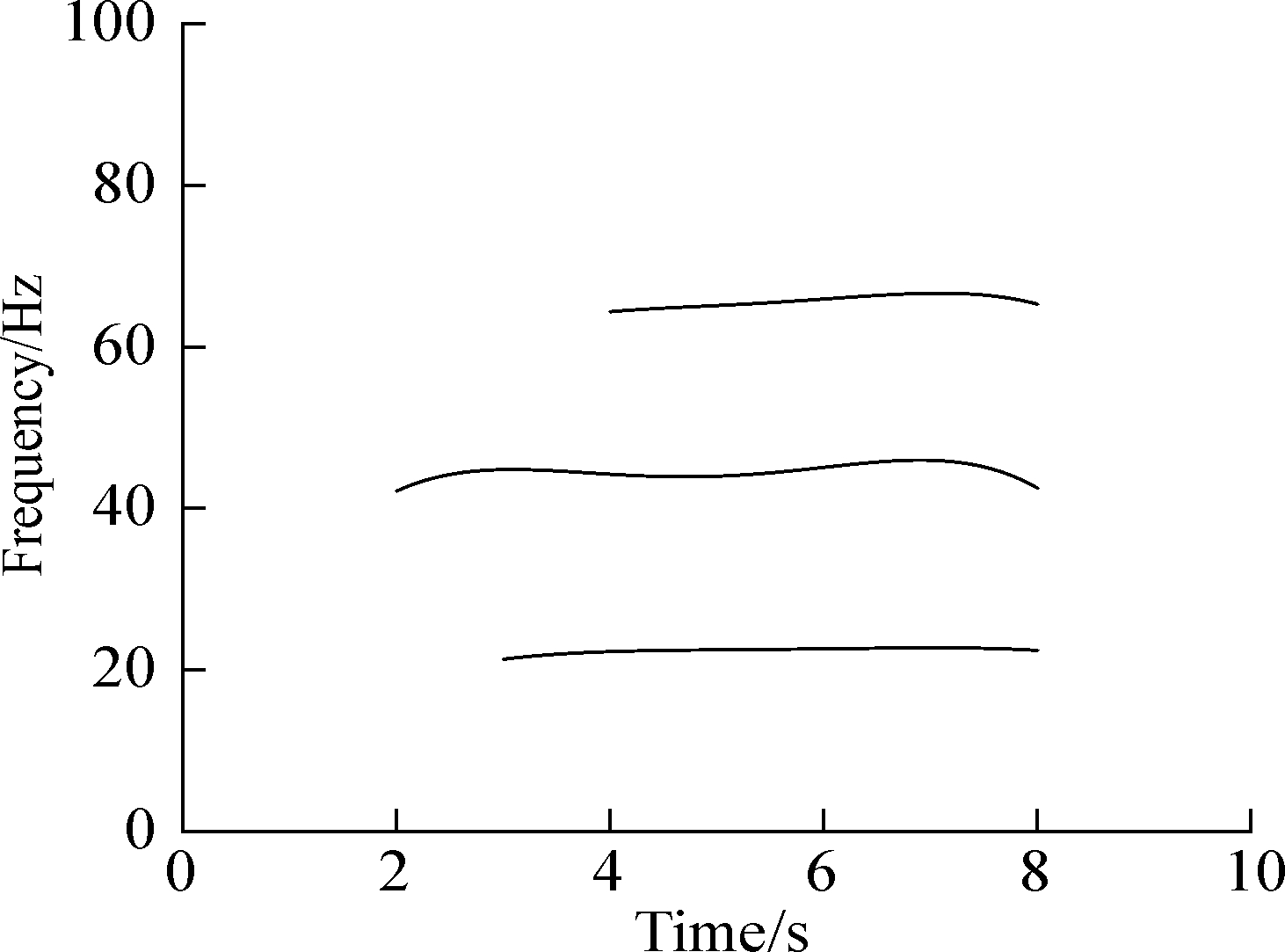
Based on wavelet transform theory, a continuous wavelet transform was applied to the free vibration response data of the guideway at the above sensors.To identify the modal frequencies of the sensor V7, the maximum slope method was used.The time-frequency wavelet diagram is shown in Fig.6(a).The frequency domains of the measuring point 7V from low to high frequency are[20, 23],[42, 46],[60, 70].The frequency identification of sensor V7 based on the maximum slope method is shown in Fig.6(b).Meanwhile, the frequency identification values from low to high frequency are 22.89, 44.98, and 66.65 Hz, respectively, which can also be used for the frequency identification of other sensors.

(a)
(b)
Fig.6 Time-frequency wavelet diagram and frequency identification based on maximum slope method of measurement point V7.(a)Time-frequency wavelet diagram;(b)Frequency identification based on the maximum slope method
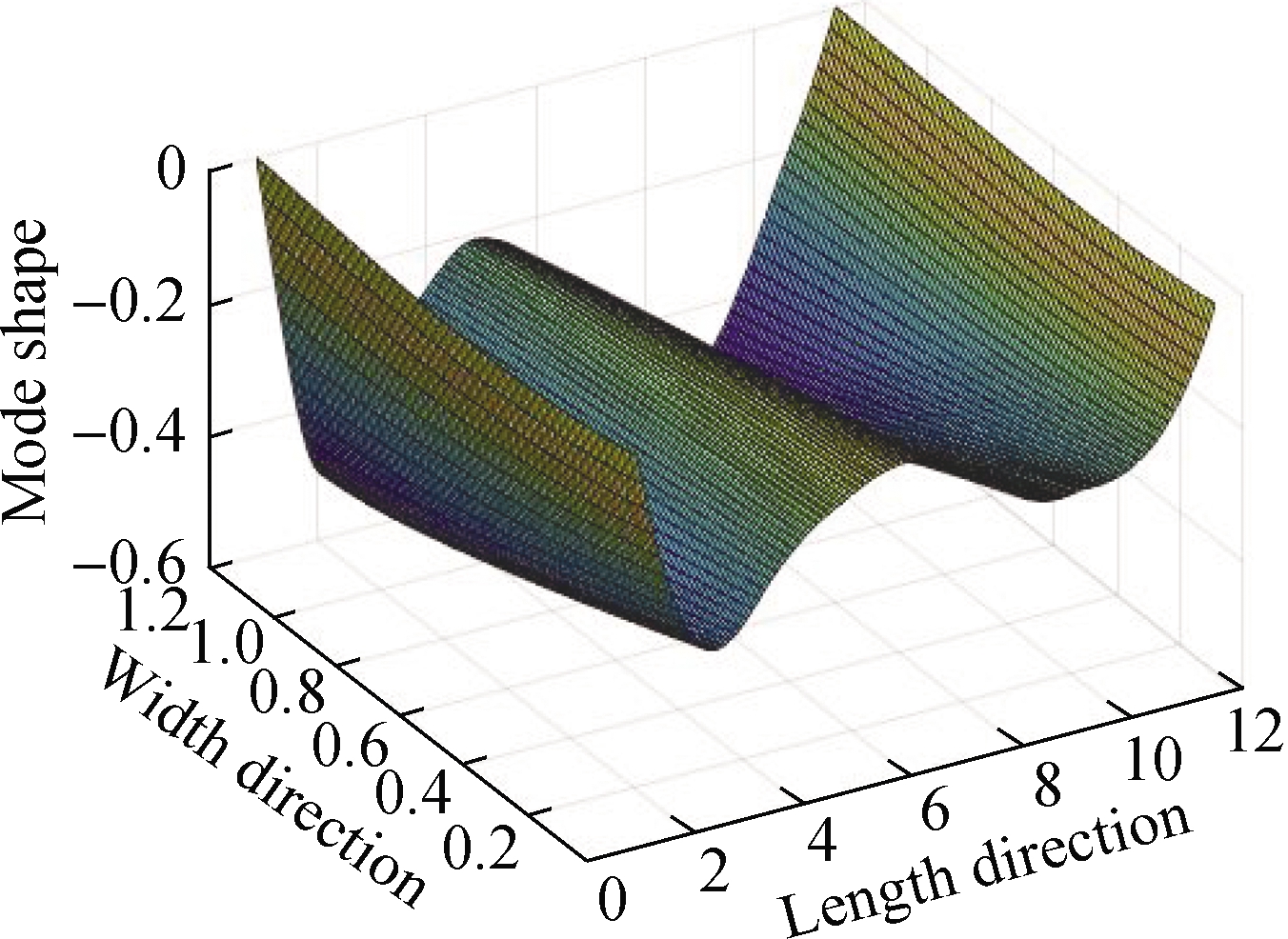
The first-order transverse vibration mode curve of the high-speed maglev guideway was obtained through the analysis and calculation of the wavelet coefficients and the least square fitting of the analysis results of each measuring point, as shown in Fig.7(a).As can be seen, the first and last points represent the end nodes of the high-speed maglev guideway, and their values are constant at zero.Similarly, the acceleration data of 14 vertical sensors of the high-speed maglev guideway were processed using the same wavelet transform.We also used the surface fitting method to obtain the first-and second-order vertical vibration modes of the high-speed maglev guideway, as shown in Figs.7(b)and(c), respectively.The first-order torsional vibration mode is shown in Fig.7(d).According to the measured data of the high-speed maglev guideway, the first-order transverse, first-order vertical, second-order vertical, and first-order torsional damping ratios are 1.68%, 2.68%, 0.76%, and 0.25%, respectively.

(a)

(b)
(c)

(d)
Fig.7 Frequency parameters and mode shapes.(a)First-order transverse mode shape;(b)First-order vertical mode shape;(c)Second-order vertical mode shape;(d)First-order torsional mode shape
3 Updating Method of the High-Speed Maglev Guideway Structure
3.1 Updating method of the guideway structure
In the existing maglev guideway, the concrete elastic modulus(Ec)causes large errors in the finite element model structure due to the influence of the embedded parts and other complex factors.In addition, the elastic support stiffness value(Ky)of the guideway has not been clearly defined in previous studies [3].Therefore, the current study selected Ec and Ky as the adjustment and correction parameters, respectively, to update and modify the guideway model.Based on the relevant research data, the value range of the concrete elastic modulus Ec is 34.5 to 50.0 GPa, and the value range of the elastic support stiffness Ky is 1 to 100 GN/m.The initial vertical stiffness of the elastic bearing was defined as 1×1011 GN/m, while the initial elastic modulus of concrete was 34.5 GPa.Therefore, based on the finite element model of the guideway, the modal frequency parameters of the initial guideway(fm,i)and experimental modal frequency parameters(fc,i)are listed in Tab.1.
Tab.1 Modal frequency parameters of the initial guideway and the experimental modal

Frequency/Hzfm,ifc,ifc,i-fm,ifc,i%First-order vertical20.95622.8978.45First-order transverse38.08840.2905.47First-order torsional40.51944.9809.92Second-order vertical74.00266.65011.03
Based on the experimental modal parameters, the parameter iteration method was used to update and modify the guideway so that the error between the experimental modal parameters and finite element guideway modal parameters can meet the accuracy requirements of the model.The definition of objective function G for updating and modifying the guideway model is given by
(1)
where fc,i and fm,i are the i-th natural vibration modes obtained from the test and calculation of the guideway model, respectively; Ky is the vertical stiffness of the elastic boundary; Ec is the elastic modulus of concrete; and wi is the weight function of the ith mode.In this study, the value of wi is 1, and n is the number of vibration modes identified in the process of updating the guideway model.Here, n=4 was selected and combined with the actual modal test because the vibration of the maglev guideway was mainly concentrated in the low-frequency band below 100 Hz.Based on the iterative parameter calculation, when Ky is 4.5 GN/m and Ec is 42 GPa, the objective function G is less than 0.005, which meets the accuracy requirements of the guideway model.Furthermore, compared to the original model, the errors of the first-order transverse, first-order vertical, second-order vertical, and first-order torsional frequency parameters of the updated guideway model are reduced by 2.85%, 5.15%, 8.89%, and 10.933%, respectively, based on the experimental modal frequency parameters of the guideway.
3.2 Validating the results of the updating of the guideway structure
An 18-DOF dynamic numerical model of a high-speed maglev vehicle and guideway with one carriage, four suspension frames, and eight electromagnets was established, including the control model of the magnet, in order to verify the validity of the finite element model and evaluate the accuracy of the updated model [11-12].In this study, the suspension frame, the elastic deformations of the carriage, and the electromagnet were ignored, and only the rigid carriage motion of the maglev carriage was considered.The carriage and each suspension frame included a vertical translational DOF and rotational DOF in the vertical plane, while each electromagnet included a vertical translational DOF.The structural, mechanical model of the maglev carriage is shown in Fig.8.The maglev vehicle was connected to four suspension frames through eight air-spring damping units, thus forming a secondary suspension system.Each suspension frame was connected to two electromagnets by two rubber spring damping units.The four suspension frames were then connected to eight spring damping units to form a primary suspension system.

Fig.8 Mechanical model of the high-speed maglev system with 18 DOF
The relevant dynamic parameters of the 600 km/h high-speed maglev vehicle are listed in Tab.2.We also compared the dynamic response of the initial model of the guideway, the updated guideway model, and the test, as shown in Fig.9.The maximum displacement of the initial guideway model is 0.501 9 mm, whereas the maximum displacement of the updated guideway model is 0.437 7 mm.Therefore, compared to the displacement calculation results of the field test, the maximum errors of the initial and updated models are 14.18% and 0.42%, respectively.
Tab.2 Dynamic model parameters of the 600 km/h high-speed maglev vehicle

ParameterValueCarriage mass Mc/kg39 000 Suspension frame mass Ml/kg1 500 Electromagnet mass Mm/kg1 000 Moment of inertia of carriage mass Jc/(kg·m2)2×106Moment of inertia of suspension frame mass Jl/(kg·m2)1.2×106Vertical spring stiffness of primary suspension Kp/(MN·m-1)40Vertical damping of primary suspension Cp/(kN·s·m-1)10Vertical spring stiffness of secondary suspension Ks/(kN·m-1)400Vertical damping of secondary suspension Cs/(kN·s·m-1)10
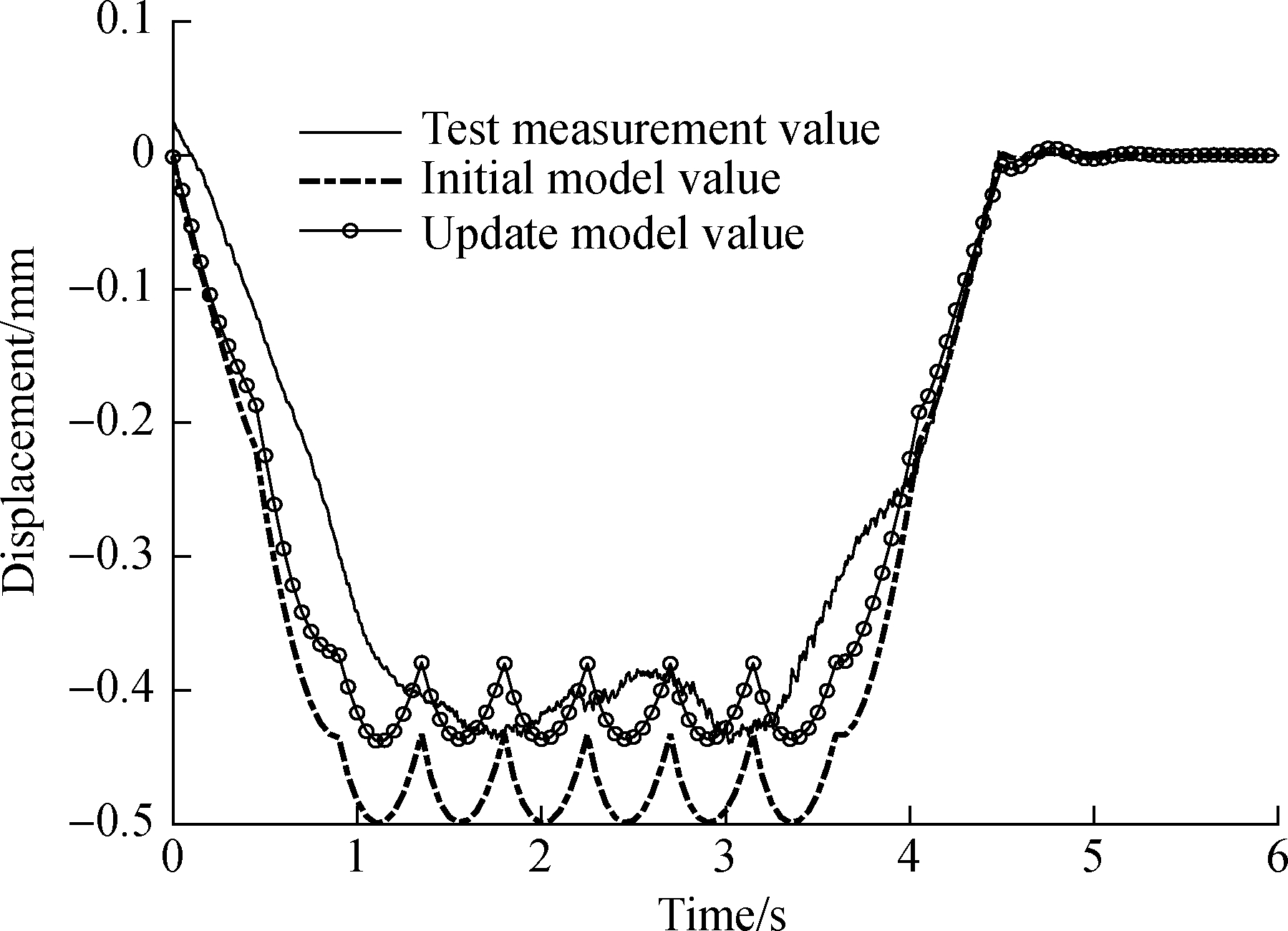
Fig.9 Comparison of the test results and the numerical model results of the displacement of the guideway structure
4 Conclusions
1)Regarding frequency identification, the maximum errors of the phase and amplitude information methods are 2.655% and 1.735%, respectively, whereas that of the maximum slope method is 0.4%.Compared to the phase and amplitude information methods, the accuracy of the maximum slope method improved by 2.255% and 1.335%, respectively.
2)The frequency of the first transverse mode is 40.29 Hz; the frequencies of the first and second vertical modes are 22.89 and 66.65 Hz, respectively; and the frequency of the first torsional mode is 44.98 Hz, based on the measured data of the guideway.The vibration of the high-speed maglev guideway is mainly concentrated in the low-frequency band below 100 Hz.Compared to the original model, the errors of the first-order transverse, first-order vertical, second-order vertical, and first-order torsional frequency parameters of the updated guideway model are reduced by 2.85%, 5.15%, 8.89%, and 10.933%, respectively.
3)When the vehicle’s running speed is 30 km/h, the guideway response excited by the maglev vehicle in the middle of the guideway span is evident.At this resonance speed, the peak vertical acceleration ranges from 0.6 to 0.8 m/s2, while the peak value of lateral acceleration is from 0.8 to 1.0 m/s2.
4)The vertical vibration and transverse vibration of the 12.384 m high-speed maglev guideway have a low coupling degree.Compared to the displacement calculation results of the field test, the maximum errors of the initial guideway and the updated guideway are 14.18% and 0.42%, respectively.Therefore, the calculation results of the updated guideway in terms of the dynamic response are more accurate.
[1] Yau J D, Yang Y B.Vibration of a suspension bridge installed with a water pipeline and subjected to moving trains[J].Engineering Structures, 2008, 30(3):632-642.DOI: 10.1016/j.engstruct.2007.05.006.
[2] Yuen K V, Kuok S C.Ambient interference in long-term monitoring of buildings[J].Engineering Structures, 2010, 32(8):2379-2386.DOI:10.1016/j.engstruct.2010.04.012.
[3] Ren W X, Chen H B.Finite element model updating in structural dynamics by using the response surface method[J].Engineering Structures, 2010, 32(8):2455-2465.DOI: 10.1016/j.engstruct.2010.04.019.
[4] Fernández-García V, Marcos E, Fernández-Guisuraga J M, et al.Multiple endmember spectral mixture analysis(MESMA)applied to the study of habitat diversity in the fine-grained landscapes of the cantabrian mountains[J].Remote Sensing, 2021, 13(5):979.DOI: 10.3390/rs13050979.
[5] Zhou X.Automatic detection of short-term atrial fibrillation segments based on frequency slice wavelet transform and machine learning techniques[J].Sensors, 2021, 21(16):5302.DOI:10.3390/s21165302.
[6] Pasin D, Cawley A, Bidny S,et al.Current applications of high-resolution mass spectrometry for the analysis of new psychoactive substances: A critical review[J].Analytical and Bioanalytical Chemistry, 2017, 409(25):5821-5836.DOI: 10.1007/s00216-017-0441-4.
[7] Deighan A J, Watts D R.Ground-roll suppression using the wavelet transform[J].Geophysics, 2012, 62(6):1896-1903.DOI: 10.1190/1.1444290.
[8] Karami K, Fatehi P, Yazdani A.On-line system identification of structures using wavelet Hilbert transform and sparse component analysis[J].Computer-Aided Civil and Infrastructure Engineering, 2020, 35:870-886.DOI: 10.1111/mice.12552.
[9] Cheng J.Research on wavelet ridge extraction algorithm and application[D].Dalian:Dalian University of technology, 2014.(in Chinese)
[10] Liu L, Ren W X, Wang C,et al.Extraction of wavelet ridges and instantaneous frequencies of non-stationary signals based on the maximum slope method[J].Engineering Mechanics, 2018, 35(2): 30-37, 46.(in Chinese)
[11] Zhang L, Huang J Y.Stiffness of coupling connection and bearing support for high-speed maglev guideways[J].Journal of Bridge Engineering, 2018, 23(9):04018064.DOI:10.1061/(ASCE)BE.1943-5592.0001284.
[12] Zhang L, Huang J Y.Dynamic interaction analysis of the high-speed maglev vehicle/guideway system based on a field measurement and model updating method[J].Engineering Structures, 2019, 180:1-17.DOI: 10.1016/j.engstruct.2018.11.031.