G lobal navigation satellite system(GNSS)uses static measurement for deformation monitoring[1-2].Weakening the multipath effect through difference is difficult because of its low correlation between stations[3-4].The repetitive correction method has an efficient weakening effect on the multipath error in GNSS deformation monitoring because of the diurnal repeatability of the multipath effect[5-6], in which multipath error separation plays a key role in the whole method.Satirapod et al.[7] and Su et al.[8] used wavelet to separate the multipath error from GPS signal data, and their results verify the effectiveness of wavelet.However, the wavelet effect is limited by choice of wavelet basis, threshold, and decomposition order, which are usually determined by experience[6,9].Huang et al.[10] proposed empirical mode decomposition(EMD)to adaptively decompose a signal into a series of intrinsic mode functions(IMFs)and a residual, allowing useful information to be extracted quickly from the decomposition without prior information[11-12].Dai et al.[13] used EMD to separate GPS multipath errors, and they found that EMD can separate multipath errors more directly and effectively than wavelet.Yan et al.[14] proposed a combination of EMD and recursive least squares(RLS)filtering to separate the multipath error from GNSS data, maximizing the advantages of EMD and RLS.However, EMD is easily susceptible to the mode aliasing problem, resulting in degraded decomposition accuracy[15].Wu et al.[16] proposed ensemble empirical mode decomposition(EEMD)to overcome mode aliasing, but the effect of EEMD is limited by the amount of white noise added[17].Therefore, this paper proposed a novel method that combines wavelet and EEMD to weaken the multipath errors more effectively.In this paper, the principle of the proposed method is introduced first, and then its results, as evaluated by GNSS data, are presented.
1 Multipath Effect
Fig.1 shows that the multipath effect is caused by the interference between direct and reflected signals.With the assumption that the receiver receives a set of signals from a satellite, the superimposed signal formed by the reflected signal and the direct signal in this set of signals can be expressed as
S=AScos(ωt+φ)
(1)
where AS is the amplitude of the superimposed signal; ω is the angular frequency; φ is the multipath error, and its formula is
(2)
where α is the reflection factor of the reflector, and Δ is the phase delay caused by the path difference between the reflected signal and the direct signal, which can be obtained according to Fig.1.

Fig.1 Principle of multipath effect
(3)
where λ is the wavelength of the signal; θ is the reflection angle; and H is the receiver height.
The typical frequency f of the multipath effect can be expressed as
(4)
where D is the reflection distance, and ![]() is the variation rate of the satellite incident angle, which takes 7×10-5 rad/s, while θ takes 45°.
is the variation rate of the satellite incident angle, which takes 7×10-5 rad/s, while θ takes 45°.
As a result of signal attenuation, the reflected signal can be neglected at a reflected distance greater than 50 m, implying a low multipath effect in the frequency domain[3].The operation cycle of GNSS satellites is basically maintained at 12 sidereal times.The multipath effect for two consecutive days shows a strong correlation[4], i.e., diurnal repeatability, when the surrounding environment of the station receiver changes slightly.
2 Improved EEMD-Wavelet Combined Filter
2.1 Wavelet analysis
According to the principle of wavelet, the wavelet basis is stretched and shifted, and the wavelet basis is used to fit the signal to be processed at multiple scales.The wavelet transform for a signal series f(t)can be expressed as[7]
W(a,b)=〈f(t),ψa,b(t)〉![]()
(5)
where a is the stretch factor; b is the shift factor; ψ(t)is the wavelet basis; and ψ*(t)is the conjugate function of ψ(t).
f(t)can be reconstructed by using inverse wavelet transform, which is expressed as
(6)
where Cψ is the admissibility condition of the wavelet basis.
The following are the specific steps for separating the multipath error from the GNSS signal using wavelet:
1)The wavelet basis and decomposition layers are determined and are used to decompose the GNSS signal.
2)The rule for estimating threshold is determined and is used for soft thresholding of the high-frequency wavelet coefficients of each layer; the low-frequency wavelet coefficients of each layer are not processed.
3)The high-frequency wavelet coefficients after soft thresholding and the low-frequency wavelet coefficients are combined to reconstruct the useful signal, i.e., multipath error.
Knowing the characteristics of the signal in advance and determining the optimal wavelet parameters according to experience are generally necessary because wavelet lacks adaptive processing ability.Typically, the GNSS signal exhibits multiscale characteristics because of the superposition of various noises, leading to a significantly increased workload of multipath error separation by wavelet.
2.2 Ensemble empirical mode decomposition
EEMD is an improved EMD method based on the characteristics of non-correlation, zero-mean, and uniform distribution of Gaussian white noise in time-frequency space.The EEMD effectively overcomes mode mixing with the addition of Gaussian white noise and multiple EMD processing[16].
The following are the specific steps for separating the multipath error from the GNSS signal by using EEMD:
1)Gaussian white noise is added to the GNSS signal to obtain the signal to be processed.
Ym(t)=Y(t)+nm(t)
(7)
where nm(t)is the Gaussian white noise series, and Y(t)is the GNSS signal series.
2)The signal series are decomposed into a series of IMFs and one residual by EMD[10].
(8)
where n is the order of EMD decomposition, i.e., the number of IMFs.
3)Steps 1 and 2 are repeated N times to obtain N sets of IMFs and residuals.
4)The average values of IMFs and residuals are calculated as the final decomposition result.
(9)
(10)
where ![]() are the i-th IMF and the residual obtained by the j-th EMD processing, respectively.
are the i-th IMF and the residual obtained by the j-th EMD processing, respectively.
5)The useful signal(multipath error)is reconstructed by analyzing the frequency and amplitude characteristics of the decomposition result.
According to Chen et al.[17], EEMD works best when the amplitude factor of white noise is 0.01 to 0.5, and the number of EMD processing is 100 to 300.However, theoretical and data support for determining the above two parameters in multipath error separation is lacking, which most likely will lead to an unsatisfactory separation.
2.3 Improvement of EEMD-wavelet combined filter
In accordance with the characteristics and shortcomings of wavelets and EEMD, a combined filter was proposed for GNSS multipath error weakening, and its process is shown in Fig.2.
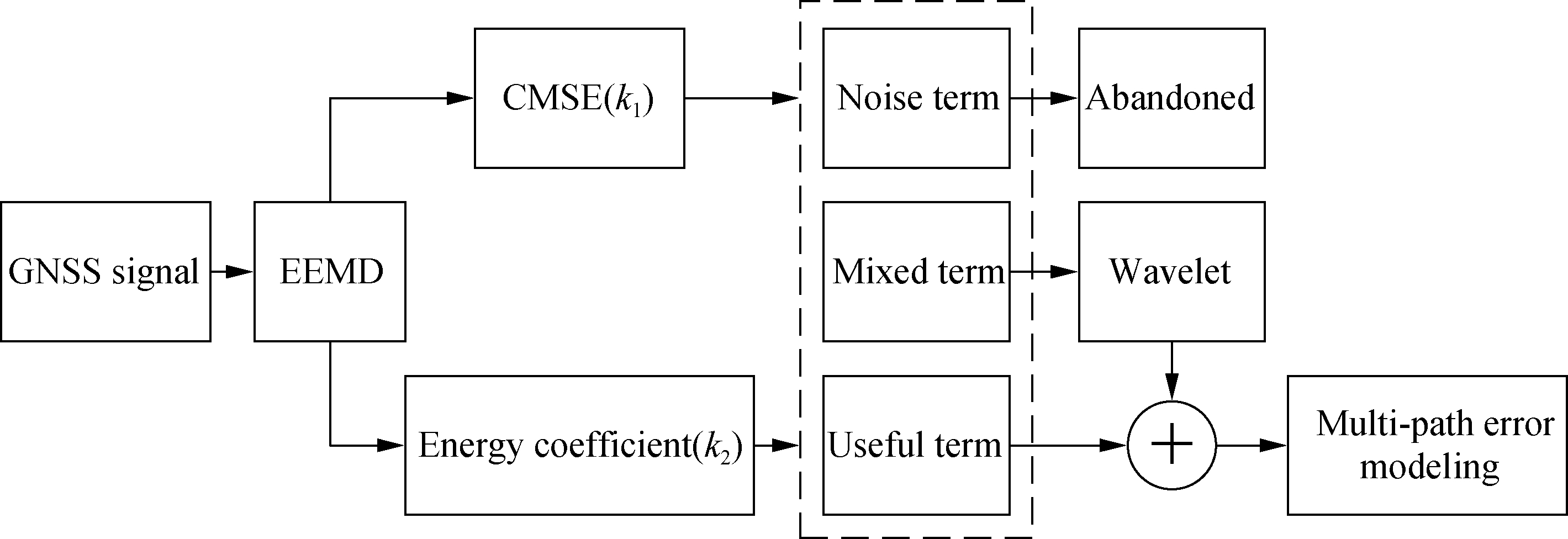
Fig.2 Process of the proposed method
The steps of the process are as follows:
1)The GNSS signal is decomposed into several IMFs and a residual using EEMD, and the decomposition is subdivided into noise Y(t)noise, mixed Y(t)mixed and useful terms Y(t)useful.
(11)
where t=1,2,…,m, m is the epochs.
2)Y(t)noise is abandoned, and wavelet is used to filter Y(t)mixed.Then, the Y(t)mixed after filtering and Y(t)useful are reconstructed to obtain the useful signal, i.e., the multipath error.
(12)
3)The multipath error for the first day is separated in accordance with the above steps and taken as the reference signal Yr(t).Then, the recovery factor of the amplitude between Yr(t)and the extracted multipath error ![]()
4)The amplitude of multipath error is recovered by ![]() and the multipath error model is taken to correct the GNSS signal data.
and the multipath error model is taken to correct the GNSS signal data.
In Eq.(11), k1 and k2 are the combined classification criterion indexes proposed in this paper, which are calculated as follows.
The reconstructed signal can be expressed as
(13)
where k=1, 2, …, n.
The continuous mean square error(CMSE)criterion[11] is used to determine the first index k1 of the classification criteria.CMSE criterion is defined as follows:
![]()
![]()
(14)
where k=1, 2, …, n-1; N is the signal length.
Eq.(14)indicates that CMSE measures the squared Euclidean distance between two consecutive reconstructions of the signal, which is equivalent to the energy density of the k-th IMF.With this quantity, the IMF order where the first significant change in energy occurs can be determined because the energy of the mixed and useful terms is much higher than that of noise.k is taken as the starting point of the mixed term when the value of the k-th CMSE is the first local minimum, k1=k.
(15)
The second index k2 is determined by the energy coefficient, which is defined by the product of energy density and average period, where the calculation for the k-th IMF’s product of energy density and average period is as follows
(16)
where k=1, 2,…, n; Ek is the energy density of the k-th IMF; ![]() is the mean period of the k-th IMF.The formulas of Ek and
is the mean period of the k-th IMF.The formulas of Ek and ![]() respectively are
respectively are
(17)
(18)
where N is the length of the k-th IMF; Ok is the number of extreme points of the k-th IMF.
The energy coefficient Ck is defined as[12]

(19)
where k=2,3,…, n.
The product of the IMF dominated by white noise is a constant.Ck is greater than the given threshold σ when Pk increases geometrically compared with the previous one, which implies the k-th IMF is non-constant whilst the previous IMFs are mainly dominated by noise.Accordingly, k serves as the starting point of the useful term, k2=k, as shown in Fig.3.In this paper, σ=3[13].

Fig.3 Determination process of k2
3 GNSS Measured Data Analysis
3.1 Data sources and analysis
The analysis in this subsection employed the GNSS data from three stations(CUT0, CUTB and CUTC)from July 5 to 7, 2020(DOY187, DOY188, DOY189).They were collected at 30 s intervals with millimeter accuracy and can be downloaded for free from the Curtin GNSS Research Center.First, we calculated the baseline vectors of CUTB-CUT0 and CUTB-CUTC by using the processing strategy shown in Tab.1.Then, we obtained the residual series by subtracting the true values of the baseline vectors.
Tab.1 GNSS data processing strategy
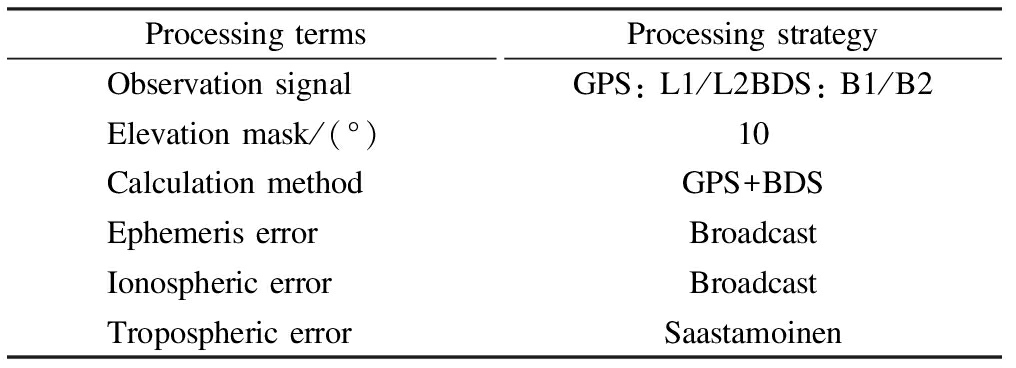
Processing termsProcessing strategyObservation signalGPS: L1/L2BDS: B1/B2Elevation mask/(°)10Calculation methodGPS+BDSEphemeris errorBroadcastIonospheric errorBroadcastTropospheric errorSaastamoinen
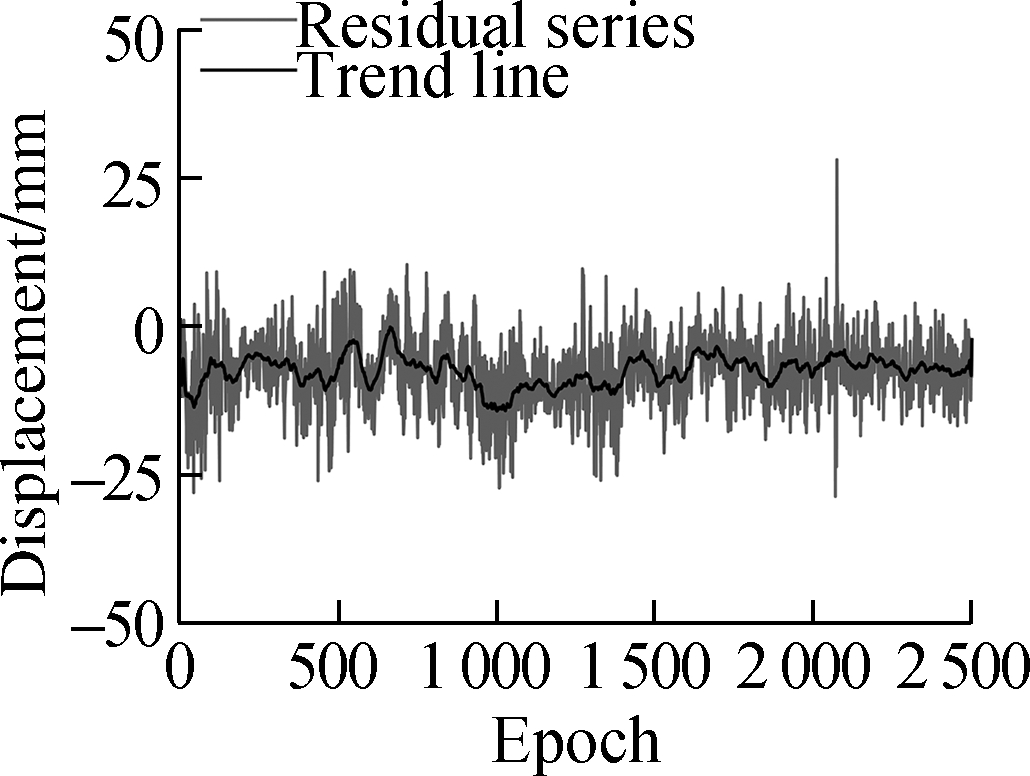
The residual series can be considered to consist of only multipath error and noise because CUTB-CUT0 and CUTB-CUTC are ultra-short baselines with lengths of 4.27 and 6.15 m, respectively.In this work, we considered only the residual series with a length of 2 500 epochs in the vertical direction because the height accuracy is the most interesting and important part of the deformation monitoring, where each residual series has a length of 2 500 epochs.We also calculated the trend of the residual series by using the moving average method with a moving window of 50 epochs.The residual series and their trend lines are shown in Fig.4.
Fig.4 shows that the residual series contains high-frequency noise and low-frequency multipath error, and some abnormal jump phenomena occur randomly.We calculated the Pearson’s correlation coefficient R of the residual series in Fig.4 for correlation analysis, and the results are shown in Tab.2.

(a)

(b)

(c)

(d)

(e)
(f)
Fig.4 Residual series(vertical direction)and trend line.(a)CUTB-CUT0 at DOY187;(b)CUTB-CUT0 at DOY188;(c)CUTB-CUT0 at DOY189;(d)CUTB-CUTC at DOY187;(e)CUTB-CUTC at DOY188;(f)CUTB-CUTC at DOY189
Tab.2 Correlation analysis results for residual series

BaselineR valuesDOY187-188DOY188-189DOY187-189CUTB-CUT00.810 40.742 00.668 3CUTB-CUTC0.807 10.809 00.693 8
According to Tab.2, the R values of the residual series for two adjacent days are maintained at around 0.8, and the R values of the residual series with an interval of 1 d are maintained at around 0.68.This condition indicates the existence of significant diurnal repeatability among the residual series.
3.2 Multipath error separation and analysis
In this subsection, wavelet, EEMD, and the proposed method were used to separate the multipath from the residual series, and their results were compared.Wavelet adopted the Sym6 wavelet basis with five decomposition layers and the soft threshold function based on the Heursure rule.EEMD combined the mean of the standardized accumulated mode criterion[6].The proposed method is consistent with the above in the wavelet part.We used the root-mean-square error(RMSE)to evaluate the separation effect.
(20)
where N is the length of the residual series; y(t)is the residual series; and u(t)is the filtered noise series in this subsection.
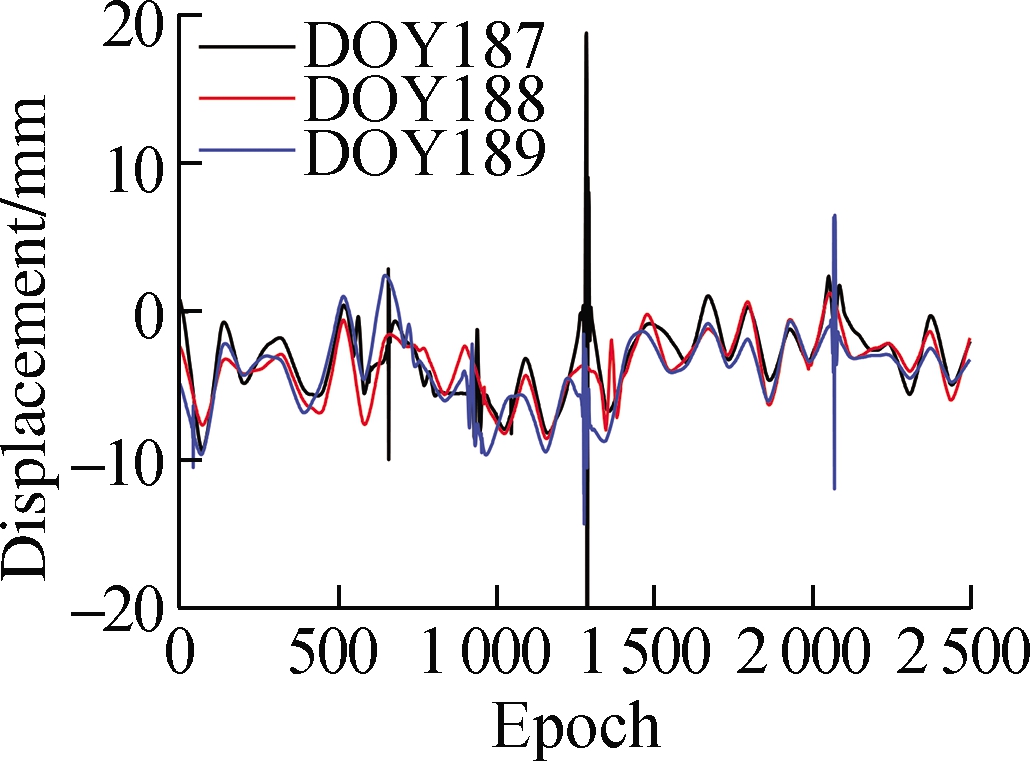
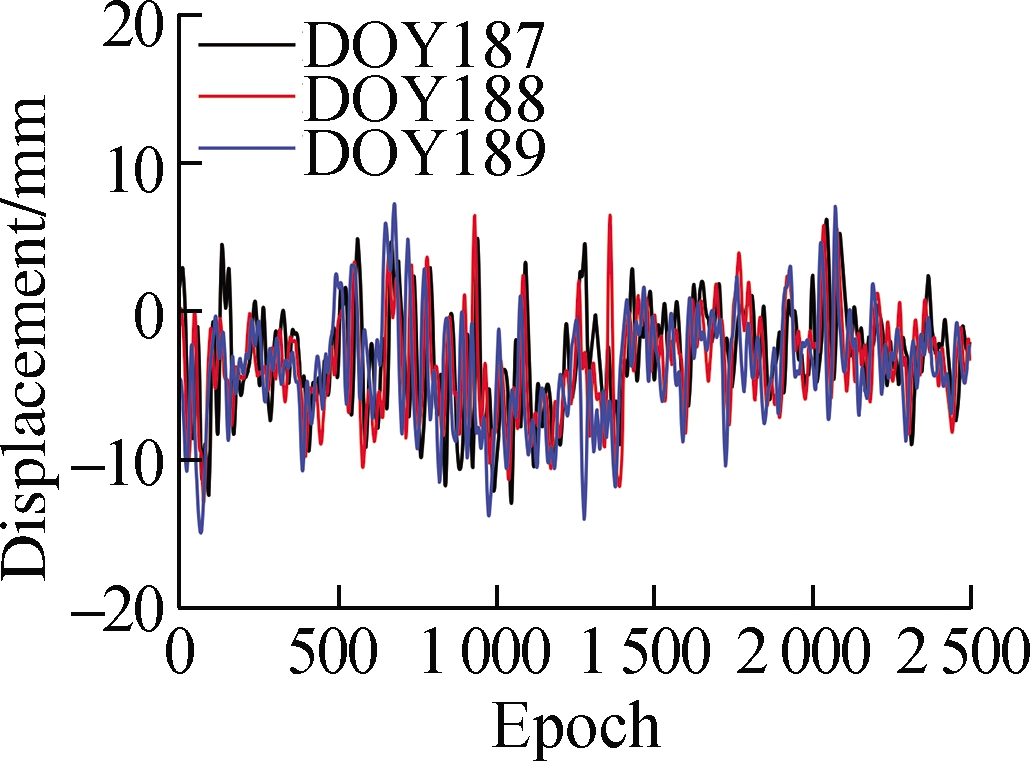
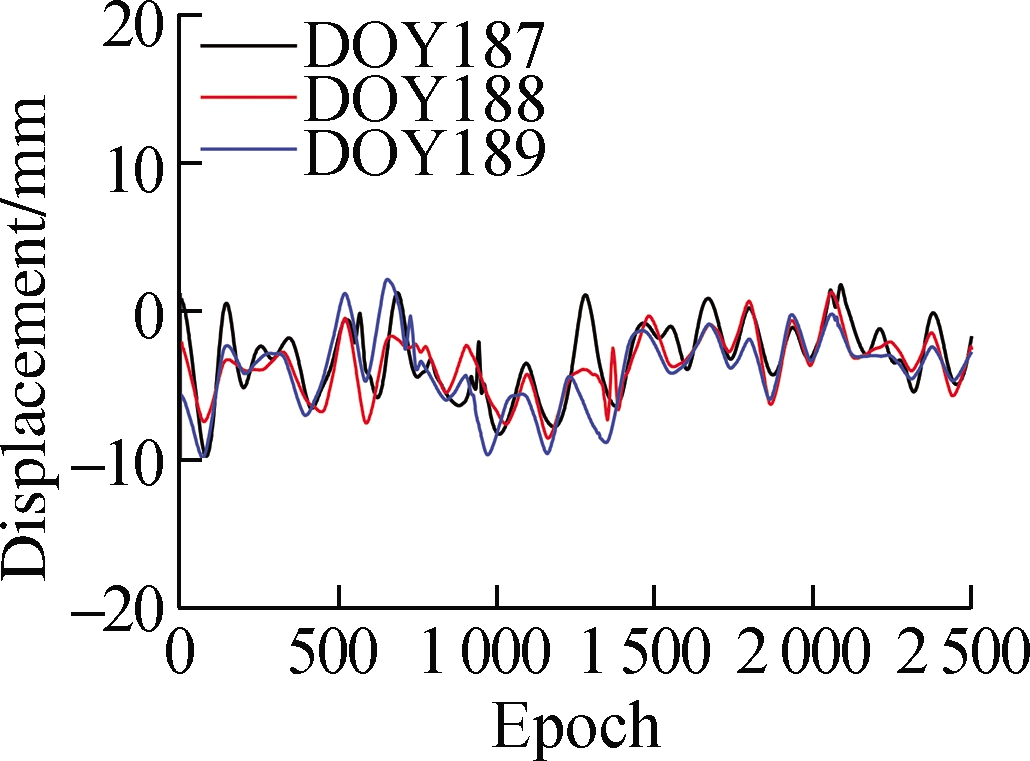
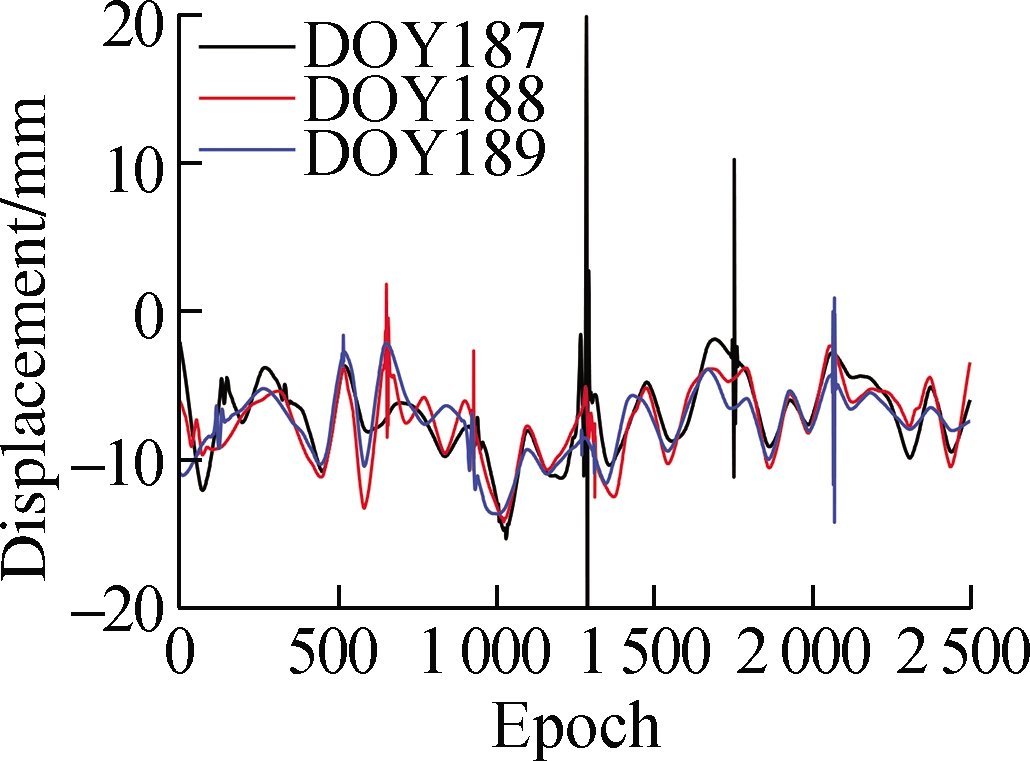
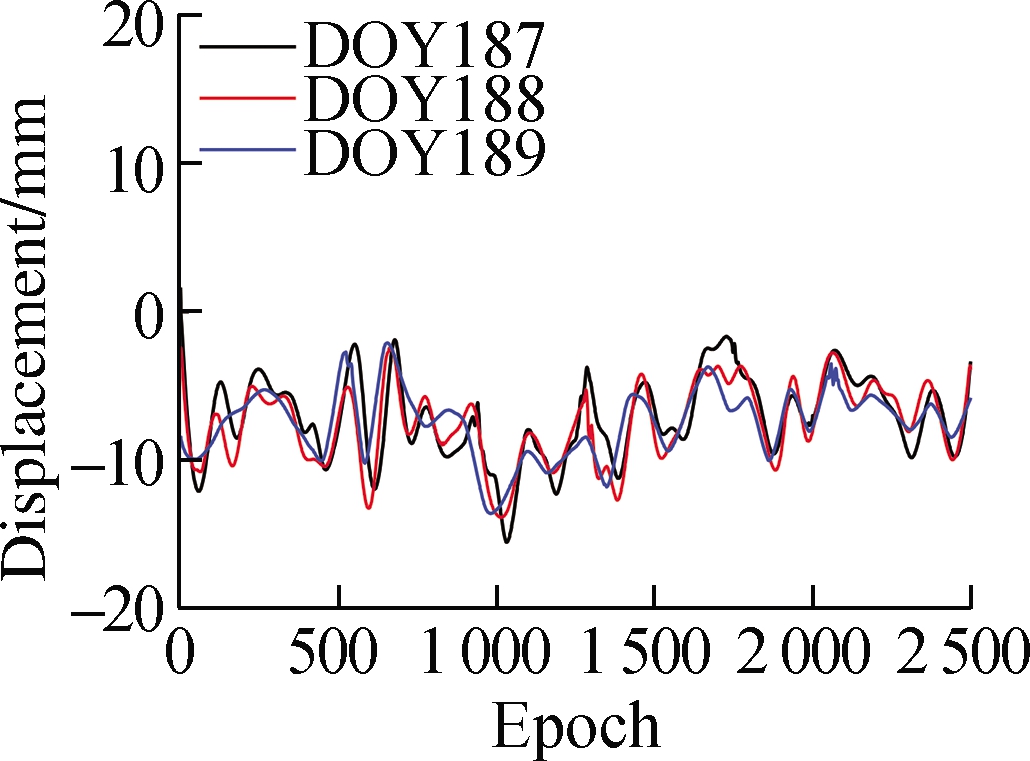
The separated multipath error series is shown in Fig.5.The trend of the multipath error series obtained by the proposed method is closer to that obtained by wavelet; their multipath errors are smoother than those of EEMD.The multipath error series obtained by wavelet exhibits some significant jump phenomena, whereas the multipath error series obtained by the proposed method does not exhibit such jump phenomena.
(a)
(b)
(c)
(d)

(e)
(f)
Fig.5 Multipath error separation results.(a)Multipath error of CUTB-CUT0 obtained by wavelet;(b)Multipath error of CUTB-CUT0 obtained by EEMD;(c)Multipath error of CUTB-CUT0 obtained by the proposed method;(d)Multipath error of CUTB-CUTC obtained by wavelet;(e)Multipath error of CUTB-CUTC obtained by EEMD;(f)Multipath error of CUTB-CUTC obtained by the proposed method
The RMSE values of residual series before and after filtering are shown in Tab.3.The ratio of RMSE before and after filtering of the three methods remains at 0.6-0.9, indicating that the multipath effect dominates in the residual series.The RMSE values of wavelet and the proposed method are lower than those of EEMD, with some RMSE values of the proposed method being slightly greater than those of wavelet.
Tab.3 RMSE of residual series before and after filtering

RMSE values of CUTB-CUT0/mmRMSE values of CUTB-CUTC/mmTimeNo filterWaveletEEMDProposedmethodNo filterWaveletEEMDProposedmethodDOY1876.694.044.703.959.327.558.047.62DOY1886.454.154.924.119.507.808.407.89DOY1896.994.645.374.669.507.848.317.80
The aforementioned analysis cannot fully determine which approach is the most effective in multipath error separation because the true value of the multipath error in the residual series used is unknown.Therefore, further analysis was performed on the separation effect of the three methods according to the low-frequency and diurnal repeatability of the multipath effect.
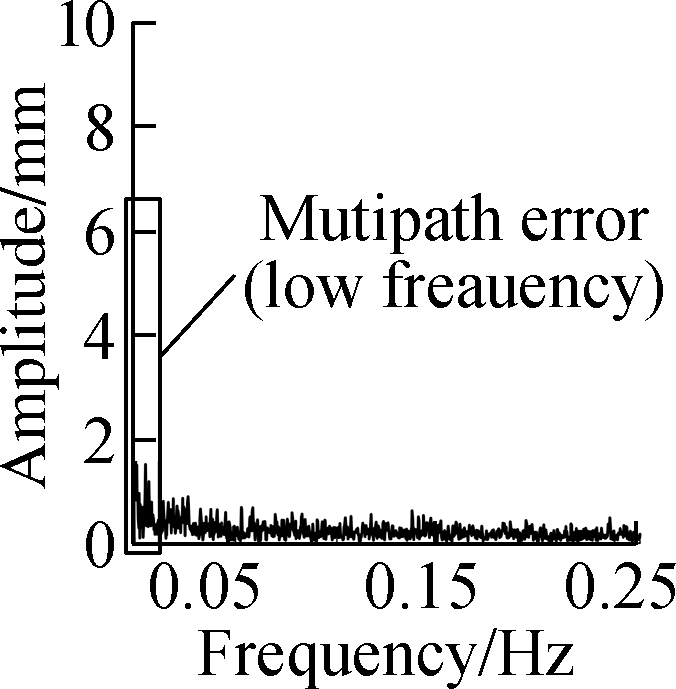
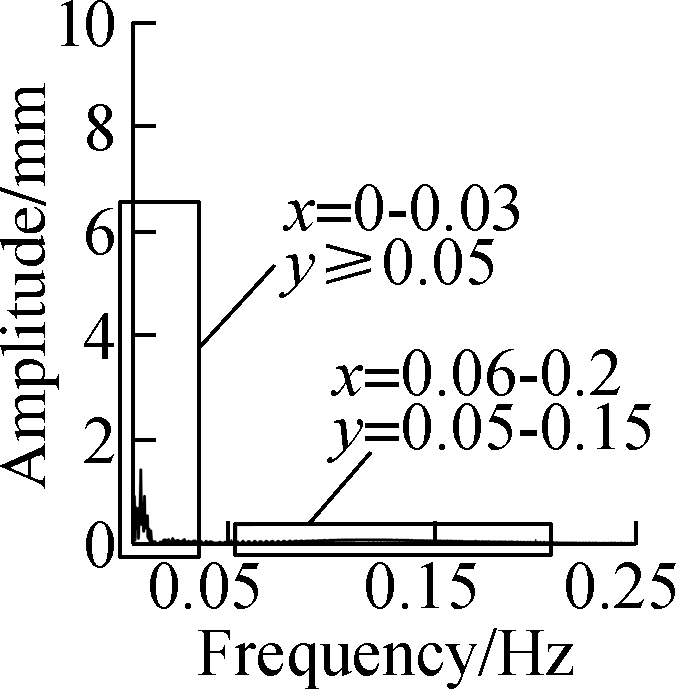
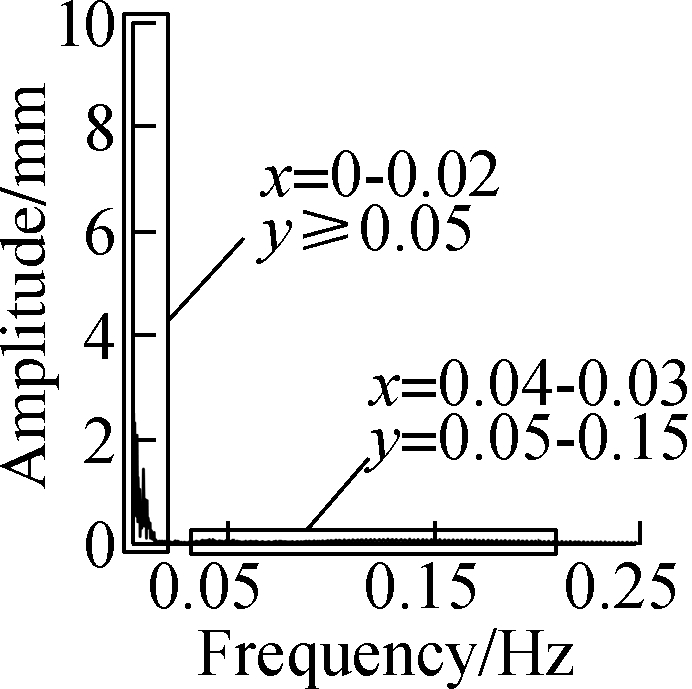
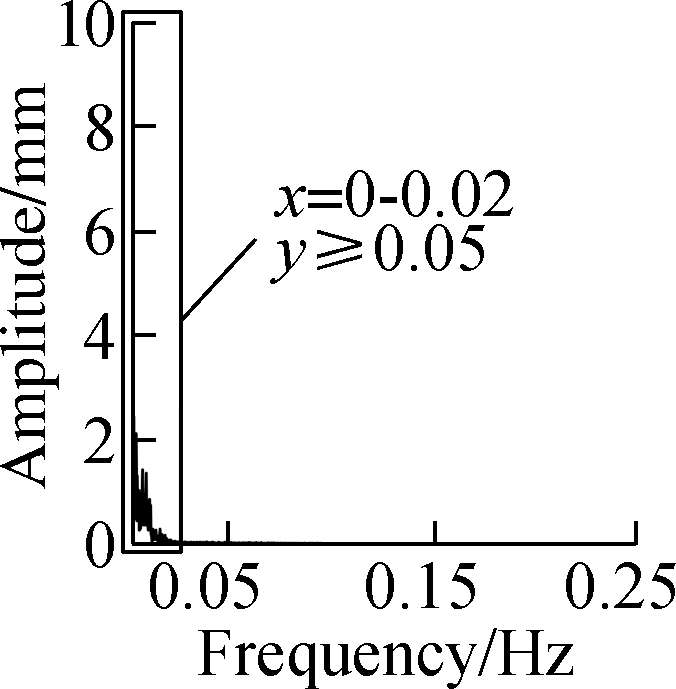
Spectrum analysis was conducted for the residual series and its multipath error series, and the results of DOY187 are shown in Fig.6.The spectrogram of the residual series shows the presence of obvious noise in the whole frequency domain, while the multipath error is mainly concentrated in the low-frequency part of the rectangular window and its amplitude value is significantly greater than that of noise.The spectrum analysis results of the three methods in the window suggests that the multipath error of wavelet is mainly distributed at 0-0.02 and 0.06-0.2 Hz, and the multipath error of EEMD is mainly distributed at 0-0.06Hz.The multipath error of the proposed method is the lowest among the three, being mainly distributed at 0-0.02Hz.
(a)
(b)

(c)

(d)

(e)
(f)

(g)
(h)
Fig.6 Spectrum analysis results.(a)CUTB-CUT0’s residual series;(b)CUTB-CUT0’s multipath error obtained by wavelet;(c)CUTB-CUT0’s multipath error obtained by EEMD;(d)CUTB-CUT0’s multipath error obtained by the proposed method;(e)CUTB-CUTC’s residual series;(f)CUTB-CUTC’s multipath error obtained by wavelet;(g)CUTB-CUTC’s multipath error obtained by EEMD;(h)CUTB-CUTC’s multipath error obtained by the proposed method
The correlation analysis of the multipath error series is shown in Tab.4.The multipath effect is highly reproducible for the two adjacent days.The R values of the proposed method remain at 0.66-0.85, where the R value between the second and third days of CUTB-CUTC is slightly lower than that of wavelet.
Tab.4 Correlation analysis results for multipath errors

R values of CUTB-CUT0R values of CUTB-CUTCTimeWaveletEEMDProposed methodWaveletEEMDProposed methodDOY187-1880.736 90.510 80.782 80.744 10.559 10.841 1DOY188-1890.745 60.538 90.763 90.810 60.558 00.797 3DOY187-1890.648 60.173 40.674 10.644 20.249 40.683 0
In summary,the proposed method has better performance than wavelet and EEMD in multipath error separation, as indicated by an analysis based on intuition, low-frequency, and diurnal repeatability.
3.3 Multipath error correction
The correction effect of the proposed method on multipath error was determined by first using the multipath error series of the first day for modeling to correct the residual series of the second and third days.Then, the multipath error series for the first two days was used for mean modeling to correct the third day.In this subsection, we used Eq.(20)to calculate the RMSE to evaluate the correction effect, where u(t)is the separated multipath error series.
The RMSE values of the residual series after multipath error correction are shown in Tab.5.The correction effect for the second day is better than that for the third day, indicating that repetitive modeling based on the three methods can effectively correct the multipath error at a relatively short time interval of multipath error.The correction effect of the multipath error begins to decline as the time interval increases, while the mean modeling further corrects the multipath error compared with the former.Thus, repetitive modeling based on mean processing can effectively suppress the effect of time interval extension.The RMSE values after correction by the proposed method are lower than those of wavelet and EEMD, and we can calculate that the proposed method attains about 21.07% and 41.90% multipath error correction in the residual series of CUTB-CUT0 and CUTB-CUTC, respectively.Compared with wavelet and EEMD, the proposed method improves the correction of the residual series of CUTB-CUT0 and that of CUTB-CUTC by 5.50% and 4.45% on average, respectively.
Tab.5 RMSE of residual series before and after multipath correction

RMSE values of CUTB-CUT0/mmRMSE values of CUTB-CUTC/mmTimeNo correctionWaveletEEMDProposedmethodNocorrectionWaveletEEMDProposedmethodDOY1886.455.265.395.049.505.765.845.50DOY1896.995.656.495.619.505.786.495.59DOY1895.506.025.485.585.915.47 Note: The last row of data is the RMSE values of residual series after mean modeling correction.
4 Conclusions
1)The shortcomings of EEMD and wavelet on multipath weakening were analyzed in this work.A filter method that combines EEMD and wavelet was proposed for multipath error weakening.
2)According to the GNSS data analysis, the evaluation indices show that the effect of the proposed method on multipath separation and correction is better than that of EEMD and wavelet.
3)The proposed method achieved good results on multipath error weakening but has an unclear improvement effect on multipath error correction.Its effectiveness in practical application is limited to a certain extent, and thus it needs further improvement in terms of theory and algorithm.
[1] Shen N, Chen L, Liu J B, et al.A review of global navigation satellite system(GNSS)-based dynamic monitoring technologies for structural health monitoring[J].Remote Sensing, 2019, 11(9): 1001.DOI:10.3390/rs11091001.
[2] Niu Y B, Xiong C B.Analysis of the dynamic characteristics of a suspension bridge based on RTK-GNSS measurement combining EEMD and a wavelet packet technique[J].Measurement Science and Technology, 2018, 29(8): 085103.DOI:10.1088/1361-6501/aacb47.
[3] Li C, Liu X, Shi M W, et al.Characteristic analysis and reducing method of GPS multipath errors[J].Journal of Navigation and Positioning, 2017,5(1): 103-107.(in Chinese)
[4] Avram A, Schwieger V, El Gemayel N.Experimental results of multipath behavior for GPS L1-L2 and Galileo E1-E5b in static and kinematic scenarios[J].Journal of Applied Geodesy, 2019, 13(4): 279-289.DOI:10.1515/jag-2019-0010.
[5] Zheng K, Zhang X H, Li P, et al.Multipath extraction and mitigation for high-rate multi-GNSS precise point positioning[J].Journal of Geodesy, 2019, 93(10): 2037-2051.DOI:10.1007/s00190-019-01300-7.
[6] Zhao L, Gao J X, Li Z K, et al.GPS multipath correction algorithm based on CEEMD-wavelet-SavGol model[J].Bulletin of Surveying and Mapping, 2017(11): 1-5.(in Chinese)
[7] Satirapod C, Rizos C.Multipath mitigation by wavelet analysis for GPS base station applications[J].Survey Review, 2005, 38(295): 2-10.DOI:10.1179/sre.2005.38.295.2.
[8] Su M K, Zheng J S, Yang Y X, et al.A new multipath mitigation method based on adaptive thresholding wavelet denoising and double reference shift strategy[J].GPS Solutions, 2018, 22(2): 1-12.DOI:10.1007/s10291-018-0708-z.
[9] Kankanamge Y, Hu Y F, Shao X Y.Application of wavelet transform in structural health monitoring[J].Earthquake Engineering and Engineering Vibration, 2020, 19(2): 515-532.DOI:10.1007/s11803-020-0576-8.
[10] Huang N E, Shen Z, Long S R, et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London Series A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995.DOI:10.1098/rspa.1998.0193.
[11] Boudraa A O, Cexus J C.EMD-based signal filtering[J].IEEE Transactions on Instrumentation and Measurement, 2007, 56(6): 2196-2202.DOI:10.1109/TIM.2007.907967.
[12] Flandrin P, Rilling G, Goncalves P.Empirical mode decomposition as a filter bank[J].IEEE Signal Processing Letters, 2004, 11(2): 112-114.DOI:10.1109/LSP.2003.821662.
[13] Dai W J, Ding X L, Zhu J J, et al.EMD filter method and its application in GPS multipath[J].Acta Geodaetica et Cartographica Sinica, 2006, 35(4): 321-327.DOI: 10.3321/j.issn: 1001-1595.2006.04.005.(in Chinese)
[14] Yan C, Wang Q, Yang G C, et al.EMD-RLS combination algorithm and its application in weakening BDS multipath error[J].Journal of Chinese Inertial Technology, 2019, 27(2): 190-198.DOI:10.13695/j.cnki.12-1222/o3.2019.02.008.(in Chinese)
[15] Wei D D, Tang W C.A method for constraining the end effect of EMD based on sequential similarity detection and adaptive filter[J].Journal of Southeast University(English Edition), 2021, 37(1): 14-21.DOI: 10.3969/j.issn.1003-7985.2021.01.003.
[16] Wu Z H, Huang N E.Ensemble empirical mode decomposition: A noise-assisted data analysis method[J].Advances in Adaptive Data Analysis, 2009, 1(1): 1-41.DOI:10.1142/s1793536909000047.
[17] Chen R X, Tang B P, Ma J H.Adaptive de-noising method based on ensemble empirical mode decomposition for vibration signal[J].Journal of Vibration and Shock, 2012, 31(15): 82-86.DOI: 10.3969/j.issn.1000-3835.2012.15.016.(in Chinese)