The Korteweg-de Vries(KdV)equation was derived by Korteweg and de Vries[1] in 1895 and has a history of more than 130 years.The KdV equation is one of the classical mathematical physics equations.The KdV equation plays an important role in nonlinear dispersive waves and has a wide range of applications.Many scholars have investigated its solutions from the point of view of analysis and numerical value.Moreover, the general solutions of the KdV equation are difficult to obtain.Therefore, many numerical methods, such as the finite difference method[2-6], finite element method[7-10], spectral method[11-12], and meshless method[13-16], have been applied to solve the KdV equation.Among them, the finite difference method is simple and easy to implement on computers.The finite difference method is an important method for solving nonlinear evolution equations.Meanwhile, the theoretical analysis of the difference scheme is relatively difficult, particularly for the initial-boundary value problem.Consequently, we will use the finite difference method to solve the initial-boundary value problem of the KdV equation in this study.
When solving nonlinear evolution equations, we need to consider the corresponding initial and boundary value conditions.The three main types of problems are the initial, periodic boundary, and initial-boundary value problems.Currently, many studies on solving nonlinear evolution equations using the finite difference method have been conducted.Some of them analyzed the initial value problems.For this class of problems, difference schemes were conveniently established by adding homogeneous boundary conditions to the boundary in the practical computation, which is a Dirichlet boundary value problem.If the highest order of the spatial derivative of the equation for the space variable x is two, then the addition of homogeneous boundary conditions will not affect the construction and analysis of difference schemes, such as Burgers’ equation:
ut+uux=νuxx
where ν is a positive constant.The difference scheme has the same form at all inner grid points.If the highest order of the spatial derivatives is over two, then the difference will be significant because of the presence of derivative boundary conditions, such as the KdV equation:
ut+γuux+uxxx=0
where γ is a constant whose boundary conditions[17] are
u(0,t)=u(L,t)=ux(L,t)=0 t≥0
The boundary condition is asymmetric, which means that the difference scheme will also be asymmetric.Therefore, for the initial-boundary value problem of the KdV equation, the construction and analysis of difference schemes need to be more detailed.Studies of the periodic boundary problems of the KdV equation using the finite difference method have also been conducted.However, because of the existence of derivative boundary conditions, similarly generalizing the method for the periodic boundary value problems to the initial-boundary value problems of the KdV equation is difficult.
Recently, we established two finite difference schemes for the KdV equation with the initial-boundary value conditions in Ref.[5].One was a nonlinear difference scheme and the other was a linearized difference scheme.The nonlinear difference scheme was proven to be unconditionally convergent, whereas the linearized difference scheme was conditionally convergent.The accuracy of these two finite difference schemes was the first order in space.Subsequently, in Ref.[6], we established a nonlinear difference scheme and proved that its spatial convergence order was two.In the numerical examples, we solved the nonlinear difference scheme using the Newton iterative method, which increased the computational cost at each time level.To improve computational efficiency and keep the convergence order unchanged, we consider establishing a linearized difference scheme for solving the initial-boundary problem of the KdV equation.
In this study, we construct a three-level linearized difference scheme for the following problem:
ut+γuux+uxxx=0 0<x<L, 0<t≤T
(1a)
u(x,0)=φ(x) 0<x<L
(1b)
u(0,t)=u(L,t)=ux(L,t)=0 0≤t≤T
(1c)
where φ(0)=φ(L)=φ′(L)=0, γ is a constant.We also establish the difference scheme and illustrate the truncation errors in detail.Then, we will present its conservation law, prove its unique solvability and conditional convergence, and provide some numerical simulations to verify our theoretical results and compare them with those of the nonlinear difference scheme in Ref.[6].
1 Difference Scheme
In this section, we will use the method of reduction of order to establish the difference scheme for Problem(1)and illustrate the truncation errors in detail.
1.1 Notation
Before presenting the difference scheme, we introduce the notations used.
We take two positive integers m and n.Then, we let h=L/m, xj=jh, 0≤j≤m; τ=T/n, tk=kτ, 0≤k≤n; Ωh={xj|0≤j≤m}.Ωτ={tk|0≤k≤n}.Moreover, we let
![]() be the grid function of Ωh},
be the grid function of Ωh},
Vh={v|v∈Uh and v0=vm=0}
For any u,v∈Uh, we introduce the following notations:
Then, we let
![]() be the grid function of Ωτ}
be the grid function of Ωτ}
For any w∈Sτ, we introduce the following notations:
It is easy to know that
1.2 Derivation of the difference scheme
We construct the difference scheme using the method of reduction of order.
Let
v=ux 0≤x≤L, 0≤t≤T
Then Problem(1)is equal to the following problem of coupled equations:
ut+γuux+vxx=0 0<x<L, 0<t≤T
(2a)
v=ux 0<x<L, 0<t≤T
(2b)
u(x,0)=φ(x) 0≤x≤L
(2c)
u(0,t)=u(L,t)=0 0<t≤T
(2d)
v(L,t)=0 0≤t≤T
(2e)
Then, we denote
0≤j≤m, 0≤k≤n
Considering Eq.(2a)at points(xj,t1/2)and(xj,tk)and using the Taylor expansion, we obtain
1≤j≤m-1
(3)
and
1≤j≤m-1, 1≤k≤n-1
(4)
The constant c1>0 exists, such that
1≤j≤m-1, 1≤k≤n-1
(5)
We consider Eq.(2b)at points(xj+1/2,tk)and use the Taylor expansion to obtain
For the discrete error ![]() in Eq.(6), we obtain the following results.
in Eq.(6), we obtain the following results.
Lemma 1[6] We denote
0≤j≤m-2, 0≤k≤n
The constant c2>0 exists, such that
Considering the initial and boundary value conditions expressed in Eqs.(2c)to(2e), we obtain
(7)
(8)
(9)
By omitting the small terms in Eqs.(3),(4), and(6)and combining them with Eqs.(7)to(9), we construct a three-level linearized difference scheme for Problem(2), as follows:
(10a)
1≤j≤m-1, 1≤k≤n-1
(10b)
(10c)
(10d)
(10e)
(10f)
1.3 Calculation of the difference scheme
For ease of calculation, we separate the variables for Eq.(10).
Theorem 1 The difference scheme expressed in Eq.(10)is equivalent to the following system of equations:
1≤j≤m-2
(11a)
(11b)
1≤j≤m-2, 1≤k≤n-1
(11c)
1≤k≤n-1
(11d)
(11e)
(11f)
and
(12a)
j=m-1,m-2,…,0; 0≤k≤n
(12b)
Proof Ⅰ)Based on Eqs.(10)to(12), first, we determine that Eqs.(10d)and(10e)are equivalent to Eqs.(11e)and(11f), respectively, and Eq.(10f)is equivalent to Eq.(12a).Moreover, Eq.(10c)is equivalent to Eq.(12b), and Eq.(10a)is equivalent to
(13a)
(13b)
Based on Eq.(10c), we derive
(14)
By substituting Eq.(14)into Eq.(13a), we derive Eq.(11a).
Similarly,based on Eq.(10f), we derive
Then, we obtain
By substituting the obtained equality into Eq.(13b)and using Eq.(14), we derive Eq.(11b).
Similarly, we obtain Eqs.(11c)and(11d)from Eqs.(10b),(10c), and(10f).
Ⅱ)Based on Eqs.(10)to(12), we determine that Eqs.(11e)and(11f)are equivalent to Eqs.(10d)and(10e), respectively, and Eq.(12a)is equivalent to Eq.(10f).Based on Eq.(12), we derive Eq.(10c)and
(15a)
(15b)
Based on Eq.(15), we obtain
By substituting the obtained equation into Eq.(11b), we derive
(16)
which is Eq.(10a)with j=m-1.By substituting Eq.(15b)into Eq.(11a), we obtain
that is
By combining the obtained equation with Eq.(16), we derive
which is Eq.(10a)with 1≤j≤m-2.
Similarly, we obtain Eq.(10b)from Eqs.(11c),(11d), and(12).
The proof is completed.
The difference scheme expressed in Eq.(11)contains only the unknown quantity ![]() Thus, calculating u from Eq.(11)is easier than that from Eq.(10).Next, we describe in detail how to solve the difference scheme expressed in Eq.(11).
Thus, calculating u from Eq.(11)is easier than that from Eq.(10).Next, we describe in detail how to solve the difference scheme expressed in Eq.(11).
We denote
Based on Eq.(11e), we obtain u0.Then, we compute u1 using Eqs.(11a),(11b), and(11f).We let w=u1/2.If we determine w, then we can obtain u1 using the following expression:
u1=2w-u0
Based on Eqs.(11a),(11b), and(11f), we can obtain the system of equations for w, as follows:
The value of w can be obtained by solving the aforementioned system of quatic diagonal linear equations using the double-sweep method.
Assuming that we already know uk and uk-1, we solve the value of uk+1.We let ![]() If we determine w, then we can obtain uk+1 using the following expression:
If we determine w, then we can obtain uk+1 using the following expression:
uk+1=2w-uk-1
Based on Eqs.(11c),(11d), and(11f), we can obtain the system of equations for w, as follows:
The value of w can be obtained by solving the aforementioned system of quadratic diagonal linear equations using the sweep method.
Furthermore,Theorem 1 illustrates that analyzing Eq.(10)is equivalent to analyzing Eq.(11).
2 Theoretical Analysis
In this section, we will analyze the conservation, unique solvability, and convergence of the difference scheme expressed in Eq.(10).
2.1 Conservation and Unique solvability
First, we provide several lemmas, which will be subsequently used.
Lemma 2[18] For ∀u∈Uh and v∈Vh, we have
(ψ(u,v),v)=0
Lemma 3[6] We let v∈Uh and u∈Vh satisfy
vm=0, vj+1/2=δxuj+1/2 0≤j≤m-1
Then, we derive
For the continuous problem expressed in Eq.(1), conservation exists.
Theorem 2[5] Supposing that u(x,t)is the solution to Problem(1), we denote
Then, we derive
Similarly,the difference scheme expressed in Eq.(10)has an invariant.
Theorem 3 Supposing that ![]() is the solution to Eq.(10), we denote
is the solution to Eq.(10), we denote
1≤k≤n
Then, we derive
Ek=‖u0‖2 1≤k≤n
Proof Ⅰ)Taking the inner product of Eq.(10a)with u1/2, we obtain
Together with Lemmas 2 and 3, we derive
That is,
(17)
Ⅱ)Taking the inner product of Eq.(10b)with ![]() we obtain
we obtain
1≤k≤n-1
Together with Lemmas 2 and 3, we derive
1≤k≤n-1
That is,
1≤k≤n-1
By adding the equality expressed in Eq.(17)to the obtained equality, we derive
0≤k≤n-1
This completes the proof.
Then, we prove the unique solvability.
Theorem 4 The difference scheme expressed in Eq.(10)has a unique solution.
Proof We obtain u0 using Eq.(10d)and v0 using Eqs.(10c)and(10f).
Based on Eqs.(10a),(10c),(10e), and(10f), we derive u1 and v1.Considering the system of homogeneous equations, we obtain
(18a)
(18b)
(18c)
(18d)
Taking the inner product of Eq.(18a)with u1, we derive
Together with Lemmas 2 and 3, we obtain
Then, we have
‖u1‖=0
which follows
From Eq.(18b)and Eq.(18d), we can get
That is, Eqs.(10a),(10c),(10e)and(10f)have the unique solutions u1 and v1.
We suppose that uk, uk-1 and vk,vk-1 are known.Based on Eqs.(10b),(10c),(10e)and(10f), we determine uk+1 and vk+1.Considering the system of homogeneous equations, we obtain
1≤j≤m-1
(19a)
(19b)
(19c)
(19d)
Taking an inner product of Eq.(19a)with 2uk+1, we get
Using Lemmas 2 and 3, we obtain
Then, we have
‖uk+1‖=0
which follows
Based on Eqs.(19b)and(19d), we obtain
That is, Eqs.(10b), Eq.(10c), Eq.(10e), and Eq.(10f)have the unique solutions uk+1 and vk+1.
This completes the proof.
2.2 Convergence
Assuming that {u(x,t),v(x,t)|(x,t)∈[0,L]×[0,T]} is the solution to Problem(2)and ![]() is the solution to the difference scheme expressed in Eq.(10), we denote
is the solution to the difference scheme expressed in Eq.(10), we denote
0≤j≤m, 0≤k≤n
By subtracting Scheme(10)from Eqs.(3),(4), and(6)to(9), we derive the following system of error equations:
(20a)
1≤j≤m-1
(20b)
(20c)
(20d)
(20e)
(20f)
Before obtaining the convergence result, we present the following two lemmas.
Lemma 4 From the proof of Theorem 4.3 in Ref.[5], it follows that the following equality holds:
Lemma 5 From the proof of Theorem 4.1 in Ref.[6], it follows that the following equality holds:
We denote
Theorem 5 We let
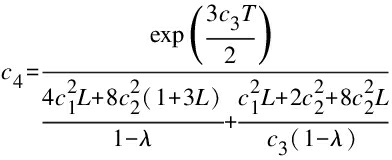
If λ<1, then we have
‖ek‖≤c4(τ2+h2) 0≤k≤n
Proof Ⅰ)It follows from Eq.(20d)that
‖e0‖=0
(21)
Taking the inner product of Eq.(20a)with 2e1/2, we derive
That is,
(22)
It follows from Lemma 5 that
![]()
By substituting the previously derived equality into Eq.(22)and combining it with Lemma 1, Lemma 5, and the truncation error expressed in(5), we obtain
![]()
That is,
(23)
Ⅱ)Taking the inner product of Eq.(20b)with ![]() we derive
we derive
That is,
1≤k≤n-1
(24)
It follows from Lemma 5 that
By substituting the previously derived equality into Eq.(24)and combining it with Lemmas 4 and 1, we obtain
Then, we derive
Using the truncation error expressed in Eq.(5), we obtain
![]() 2)+
2)+
![]()
![]() ·
·
(25)
We let
It follows that
If λ<1, then we derive
It follows from inequality(25)that
![]() (Ek+1-Ek)≤c3(Ek+1+Ek)+
(Ek+1-Ek)≤c3(Ek+1+Ek)+
That is,
(1-c3τ)Ek+1≤(1+c3τ)Ek+
1≤k≤n-1
Using the Gronwall inequality, we obtain
By substituting Eqs.(21)and(23)into the previously derived inequality, we obtain
It is easy to know that
Consequently,
‖ek‖≤c4(τ2+h2) 1≤k≤n
This completes the proof.
3 Numerical Examples
In this section, we present two numerical examples.The numerical results illustrate the efficiency of the difference scheme expressed in Eq.(11).
In Ref.[6], we presented the following two-level nonlinear difference scheme:
(26a)
(26b)
(26c)
(26d)
and solved it using the Newton iterative method.
We make the numerical solution corresponding to the step size h and τ be ![]() 0≤k≤n}.
0≤k≤n}.
We denote the error as follows:
When τ is sufficiently small, the spatial convergence order is defined as follows:
When h is sufficiently small, the temporal convergence order is defined as follows:
Example 1 In Problem(1), we take T=1, L=1, γ=-6, φ(x)=x(x-1)2(x3-2x2+2).The exact solution is unknown.
The difference scheme expressed in Eq.(11)will be employed to numerically solve this problem.The numerical accuracy of the difference scheme in space and time will be verified.
By varying step size h with the sufficiently small step size τ=1/12 800 and varying step size τ with the sufficiently small step size h=1/12 800, the numerical errors and convergence orders for Scheme(11)are listed in Tabs.1 and 2.From these tables, we determine that the numerical convergence orders of Scheme(11)can achieve O(τ2+h2), which is consistent with Theorem 5.
Tab.1 Errors and space convergence orders of Example 1(τ=1/12 800)
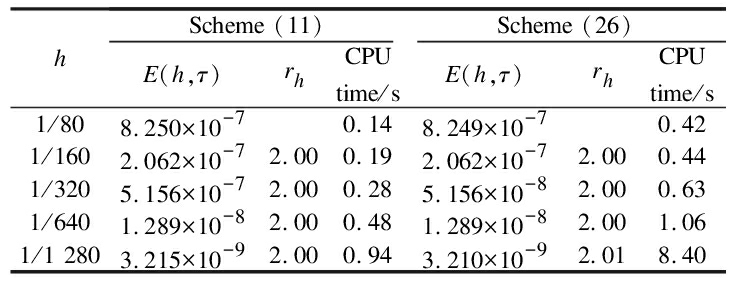
hScheme (11)Scheme (26)E(h,τ)rhCPUtime/sE(h,τ)rhCPUtime/s1/808.250×10-70.148.249×10-70.421/1602.062×10-72.000.192.062×10-72.000.441/3205.156×10-72.000.285.156×10-82.000.631/6401.289×10-82.000.481.289×10-82.001.061/1 2803.215×10-92.000.943.210×10-92.018.40
Tab.2 Errors and time convergence orders of Example 1(h=1/12 800)

τScheme (11)Scheme (26)F(h,τ)rhCPUtime/sF(h,τ)rhCPUtime/s1/801.410×10-20.094.445×10-34.601/1604.363×10-31.690.161.030×10-32.119.111/3201.005×10-32.120.322.508×10-42.0417.351/6402.451×10-42.040.637.133×10-51.8132.651/1 2807.068×10-51.801.241.843×10-51.9563.29
Furthermore, we observe that the difference scheme expressed in Eq.(11)is more computationally efficient than the nonlinear difference scheme expressed in Eq.(26).
Fig.1 indicates that the energy of Scheme(11)is conserved for Example 1.

Fig.1 Energy conservation law of Example 1
We denote
and
Example 2 We conduct a numerical experiment with the exact solution of a solitary wave[19], as follows:
u(x,t)=4sech2(x-4t-4)
0≤x≤20, 0≤t≤1
The corresponding parameter is γ=3.
Similarly, we compute the example using the difference scheme expressed in Eq.(11)and observe the convergence.First, we fix the time step size as 1/3 200 and calculate the errors and convergence orders in the space directions, as shown in Tab.3.Then, we fix the space step size as 1/3 200 and calculate the errors and convergence orders in the time directions, as shown in Tab.4.
Tab.3 Errors and space convergence orders of Example 2
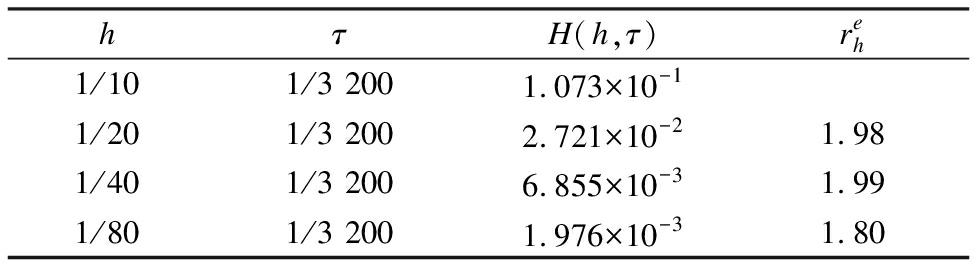
hτH(h,τ)reh1/101/3 2001.073×10-11/201/3 2002.721×10-21.981/401/3 2006.855×10-31.991/801/3 2001.976×10-31.80
Tab.4 Errors and time convergence orders of Example 2

hτH(h,τ)reτ1/3 2001/106.082×10-11/3 2001/201.643×10-11.891/3 2001/404.196×10-21.971/3 2001/801.057×10-21.99
Notably, the numerical results are consistent with the theoretical analysis.In Fig.2, the numerical and exact solution curves are plotted for t=0.25,0.5,0.75,1.0.Fig.2 shows that the numerical solutions are consistent with the exact solutions.

(a)

(b)
Fig.2 Curves of Example 2(h=τ=1/40).(a)Numerical solution;(b)Exact solution
4 Conclusions
In this study, we consider the numerical solution to the initial-boundary value problem of the KdV equation using the finite difference method.With the use of the method of reduction of order, we establish a three-level linearized difference scheme and show that it is more computationally efficient than the two-level nonlinear difference scheme through numerical simulations while retaining the same convergence orders.Using the energy analysis method, we prove the conservation, unique solvability, and conditional convergence of the difference scheme.
In Theorem 5, the convergence of the difference scheme was proven under the constraint of the step size ratio.This difference scheme may be unconditionally convergent.Indeed, we found from Example 1 that the restriction of step size ratio is unnecessary for ensuring that the convergence result holds.However, we have not yet discovered a better method to prove the unconditional convergence and will continue our research in future work.
[1] Korteweg D J, de Vries G.On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves[J].The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1895, 39(240): 422-443.DOI:10.1080/14786449508620739.
[2] Kuo P Y, Wu H M.Numerical solution of K.D.V.equation[J].Journal of Mathematical Analysis and Applications, 1981, 82(2): 334-345.DOI:10.1016/0022-247X(81)90199-2.
[3] Zhu S H.A scheme with a higher-order discrete invariant for the KdV equation[J].Applied Mathematics Letters, 2001, 14(1): 17-20.DOI:10.1016/S0893-9659(00)00105-1.
[4] Taha T R, Ablowitz M J.Analytical and numerical aspects of certain nonlinear evolution equations.Ⅰ.Analytical[J].Journal of Computational Physics, 1984, 55(2): 192-202.DOI:10.1016/0021-9991(84)90002-0.
[5] Shen J Y, Wang X P, Sun Z Z.The conservation and convergence of two finite difference schemes for KdV equations with initial and boundary value conditions[J].Numerical Mathematics: Theory, Methods and Applications, 2020, 13(1): 253-280.DOI:10.4208/nmtma.oa-2019-0038.
[6] Wang X P, Sun Z Z.A second order convergent difference scheme for the initial-boundary value problem of Korteweg-de Vires equation[J].Numerical Methods for Partial Differential Equations, 2021, 37(5): 2873-2894.DOI:10.1002/num.22646.
[7] Alexander M E, Morris J L.Galerkin methods applied to some model equations for non-linear dispersive waves[J].Journal of Computational Physics, 1979, 30(3): 428-451.DOI:10.1016/0021-9991(79)90124-4.
[8] Yan J,Shu C W.A local discontinuous Galerkin method for KdV type equations[J].SIAM Journal on Numerical Analysis, 2002, 40(2): 769-791.DOI:10.1137/s0036142901390378.
[9] Xu Y, Shu C W.Error estimates of the semi-discrete local discontinuous Galerkin method for nonlinear convection-diffusion and KdV equations[J].Computer Methods in Applied Mechanics and Engineering, 2007, 196(37/38/39/40): 3805-3822.DOI:10.1016/j.cma.2006.10.043.
[10] Shen J.A new dual-petrov-Galerkin method for third and higher odd-order differential equations: Application to the KDV equation[J].SIAM Journal on Numerical Analysis, 2003, 41(5): 1595-1619.DOI:10.1137/s00361429-02410271.
[11] Feng B F, Wei G W.A comparison of the spectral and the discrete singular convolution schemes for the KdV-type equations[J].Journal of Computational and Applied Mathematics, 2002, 145(1): 183-188.DOI:10.1016/S0377-0427(01)00543-X.
[12] Zhang Z Q, Ma H P.A rational spectral method for the KdV equation on the half line[J].Journal of Computational and Applied Mathematics, 2009, 230(2): 614-625.DOI:10.1016/j.cam.2009.01.025.
![]() Dereli Y.Numerical solutions of KdV equation using radial basis functions[J].Applied Mathematical Modelling, 2008, 32(4): 535-546.DOI:10.1016/j.apm.2007.02.001.
Dereli Y.Numerical solutions of KdV equation using radial basis functions[J].Applied Mathematical Modelling, 2008, 32(4): 535-546.DOI:10.1016/j.apm.2007.02.001.
[14] Shen Q.A meshless method of lines for the numerical solution of KdV equation using radial basis functions[J].Engineering Analysis With Boundary Elements, 2009, 33(10): 1171-1180.DOI:10.1016/j.enganabound.2009.04.008.
[15] Dehghan M, Shokri A.A numerical method for KdV equation using collocation and radial basis functions[J].Nonlinear Dynamics, 2007, 50(1/2): 111-120.DOI:10.1007/s11071-006-9146-5.
[16] Bhatta D D, Bhatti M I.Numerical solution of KdV equation using modified Bernstein polynomials[J].Applied Mathematics and Computation, 2006, 174(2): 1255-1268.DOI:10.1016/j.amc.2005.05.049.
[17] Zhang B Y.Boundary stabilization of the Korteweg-de Vries equation[C]//Control and Estimation of Distributed Parameter Systems: Nonlinear Phenomena, 1994: 371-389.DOI:10.1007/978-3-0348-8530-0_21.
[18] Sun H, Sun Z Z.On two linearized difference schemes for Burgers’ equation[J].International Journal of Computer Mathematics, 2015, 92(6): 1160-1179.DOI:10.1080/00207160.2014.927059.
[19] Mohamad M N B.Exact solutions to the combined KdV and mKdV equation[J].Mathematical Methods in the Applied Sciences, 1992, 15(2): 73-78.DOI:10.1002/mma.1670150202.