In 2008, Nakamoto[1] first proposed an electronic cash system constructed with blockchain technology. Blockchain technology has made it possible to directly use Bitcoin for transactions between entities that do not trust each other without any centralized trusted third party for management. In 2013, Buterin et al.[2-3] created the Ethereum platform inspired by Bitcoin to apply smart contract technology to blockchain and improve the scalability of a blockchain system. The Linux Foundation launched the Hyperledger Fabric open-source project for developing enterprise-level applications[4]. Blockchain technology has allowed the direct use of Bitcoin for transactions between entities that do not trust each other without any centralized trusted third party for management. The consensus algorithm, one of the core technologies of blockchain, is the mechanism of how mutually independent nodes in a blockchain system can reach consistency. Consequently, the consensus algorithm is a significant factor in determining the operational efficiency of the blockchain system.
Recently, consensus protocols can be categorized into three categories based on whether or not they are fault tolerant: the non-fault-tolerant proof of X class of schemes represented by the proof of work[5], general fault-tolerant CFT class of schemes represented by Raft[6], and byzantine fault-tolerant (BFT) class of schemes represented by the PBFT[7]. Each type of consensus protocol has its drawbacks, which limit its application to specific scenarios. BFT class protocols have a long history, are the most widely used, and can tolerate partially faulty nodes and evil nodes. However, the performance of these protocols is poor, so the improvement of PBFT has become a crucial research direction for consensus protocols used in various enterprise-level applications, including BFT-SmaRT[8], G-PBFT[9], and LibraBFT[10] consensus. Li et al.[11] proposed a PBFT-optimized consensus protocol named scalable hierarchical byzantine fault tolerance (SHBFT), which improves the efficiency of internode negotiation by designing a hierarchical structure. Li et al.[12] proposed a scalable multilayer PBFT-based consensus mechanism by hierarchically grouping nodes into different layers.
In the PBFT consensus protocol, all nodes have to communicate with one another to reach consensus, and the communication complexity is O(N2). PV-PBFT uses the threshold signature, where the threshold is set to 2f+1 and f is the number of malicious nodes. The main communication is between the primary and replica nodes, and phase voting is used, which brings the communication complexity down to O(N).
1 PV-PBFT Protocol
1.1 PV-PBFT consensus protocol
The PV-PBFT consensus protocol includes five phases with the same phase number as the original PBFT consensus protocol, and they can correspond to one another. The specific process is shown in Fig. 1. The following are the detailed processes.
1)Request phase: Similar to the request phase of the original PBFT. ClientC sends a request message to the primary node P. The format of the request message is m=[o,t,cid,csig], where m is the request message, o is the operation to be executed, t is the timestamp, cid is the client ID, and csig is the client’s signature. The timestamp ensures that the command is only executed once, and the client signature ensures that the message is correct.
2)Preparation phase: PV-PBFT is different from the original PBFT as the prepare phase of the sequence number distribution focuses mainly on distributing messages from the primary node to the replica nodes. PV-PBFT not only distributes messages from the primary node to the replica nodes in this phase but also performs voting after the replica node acknowledges the message. The replica node completes its own threshold signature and sends its signed part back to the primary node. After receiving a request from client C, primary node P assigns a sequence number s to message m, constructs a prepare message [v,s,psig,m], and broadcasts it to all replica nodes, where v is the view number, s is the sequence number, psig is the signature of the primary node, and m is the request message. The sequence number s is the order of request execution, the view number allows the replica node to record the current view, and the primary node signature ensures the authentication of the replica node to the primary node’s identity. After the correctness check of the prepare message from the primary node, the replica node i first calculates the hash digest h=H(v,s,m) and then signs h using the subkey to obtain ξ(h)i, where ξ(h)i is the partial threshold signature generated by the replica node i. The prepare-vote message is constructed [v,s,ξ(h)i] to the primary node P.
3)Precommit phase: In the precommit phase of the original PBFT, the replica nodes each confirm the correctness of the message and then broadcast the confirmation information to all other nodes[13]. However, PV-PBFT already performs replica node message confirmation in the previous phase. In this phase, the primary node combines messages containing signatures, completes a round of consensus, sends the consensus results to all replica nodes, and opens another round of consensus. When the primary node receives 2f+1 prepare-vote messages, it calculates the resulting overall threshold signature ξ(h) and constructs a precommit message [v,s,ξ(h)] to broadcast to all replica nodes. The replica node verifies the correct precommit message from the primary node by verifying the public key k and then computes the hash digest d=H(v,s,ξ(h)). Then, it signs d with the subkey to obtain σ(d)i, where σ(·)i is the partial threshold signature generated by the replica node. Eventually, the replica node constructs the precommit-vote message [v,s,σ(d)i] to the primary node P.
4)Commitment phase: The sequence number confirmation phase of the original PBFT starts to confirm the consensus, whereas the PV-PBFT has already performed the second round of consensus confirmation. After receiving 2f+1 precommit-vote messages, the primary node calculates the resulting overall threshold signature σ(d) and constructs a commit message [v,s,σ(d)] to broadcast to the replica node. After verifying the correctness of the commit message from the primary node by verifying the public key k′, the replica node i executes the request message with the sequence number s, updates the state machine state to χ, and computes the hash digest τ=H(χ). Then, it signs τ with the subkey to obtain π(τ)i, where π(·)i is the partial threshold signature. Eventually, the replica node generates the commit-vote message [v,s,π(τ)i] to the primary node P.
5)Reply phase: While all nodes in the response phase of the original PBFT send the consensus result to the client,the PV-PBFT is a broadcast of the consensus result by the primary node, including the client. After the primary node receives 2f+1 commit-vote messages and successfully computes the resulting overall threshold signature π(τ). It indicates that the request message has been successfully executed by enough nodes, constructs a reply message [v,s,π(τ)] to broadcast to all replica nodes, and responds to the client. The replica node ends this consensus after the reply message from the primary node is verified to be correct.
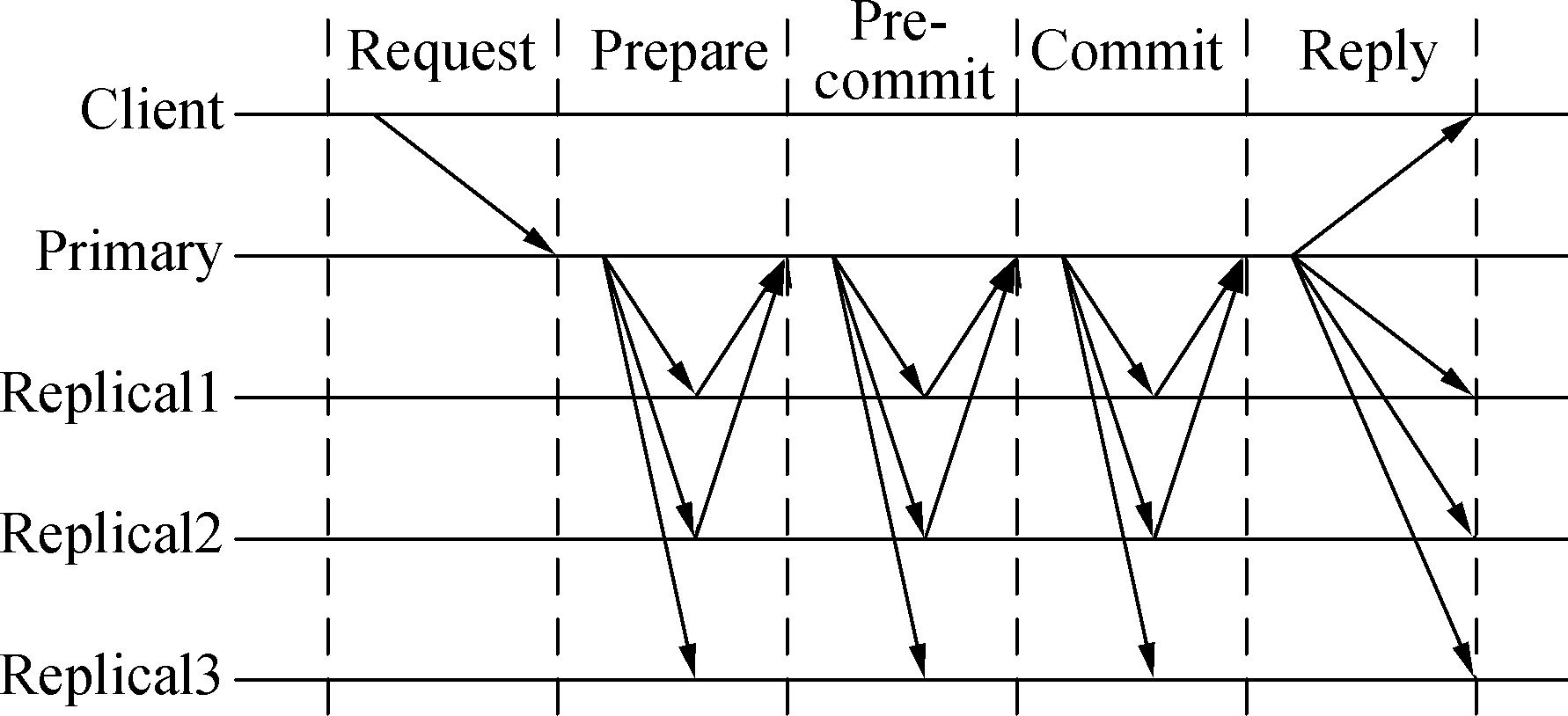
Fig.1 PV-PBFT consensus protocol process
1.2 PV-PBFT view-change protocol
The node weight wi is added to the PV-PBFT view-change protocol. This value will directly affect the election of the primary node. For any node i, its weight value is calculated as follows:
wi=Nlevel-αnprimary
(1)
where Nlevel is the weight level of the node, which can be set by the user; α is the adjustment coefficient; and nprimary is the number of times the node has been elected as the primary node in history, whose value increases by 1 each time the node is elected.
A node with a higher weight level has a higher probability of being elected as the primary node. If each node is initially elected as the primary node with the same probability, the weight level of all nodes can be set to the same value. If a node is elected as the primary node too many times, it can likely become the target of the attacker’s priority attack. Therefore, the number of times the node has been elected as the primary node in the history of the node is used as the influencing factor to reduce the probability of the same node being elected as the primary node multiple times, thereby reducing the attacker’s attention.
Similarly to the trigger condition of the PBFT view-change protocol, the replica node does not receive a message from the primary node for a long time. For example, in the prepare phase, the replica node does not receive the prepare message from the primary node within the timer time. In contrast, in the precommit phase, the primary node does not. After calculating the overall threshold signature, the information that 2f+1 replica nodes have confirmed to receive the prepare message to the replica nodes is broadcasted. The view-change protocol of the PV-PBFT is shown in Fig. 2. The detailed process is as follows.
1)View-change phase: The replica node i stops receiving requests, constructs a view-change message and broadcasts it to all other nodes in the format [wi,x,C,S,i], where wi is the weight value of node i in the current view, x is the latest stable checkpoint message sequence number of node i, C is the set of 2f+1 valid checkpoint messages saved by node i, and S is the set of messages after the sequence number x.
2)View-change-Ack phase: After the replica node i receives 2f+1 view-change messages, after the correctness check, the size of wi in all the messages is compared, the node with the largest weight value is compared and determined, and the hash value is calculated. Hash h=H(wa,a) is computed, where a is the unique identifier of the replica node with the largest weight value and wa is its corresponding weight value. Then, the subkey is used to sign to obtain ξ(h)i, where ξ(·)i is the partial threshold signature generated by the replica node. A view-change-Ack message is constructed and sent to node a in the format [i,ξ(h)i].
3)New-view phase: After the replica node a receives 2f+1 view-change-ack messages, it calculates the obtained overall threshold signature ξ(h), constructs a new-view message, and broadcasts it to all replica nodes. Its format is [v+1,a,ξ(h),O], where O is the set of prepare messages received by node a under view v. After receiving the new-view message, the other replica nodes verify the correctness of the public key k and approve the node a as the new primary node, and the view replacement protocol ends.
Based on the specific process of the PV-PBFT view-change protocol above, the replica node needs to propose a candidate primary node according to the node with the largest weight value in the received view-change
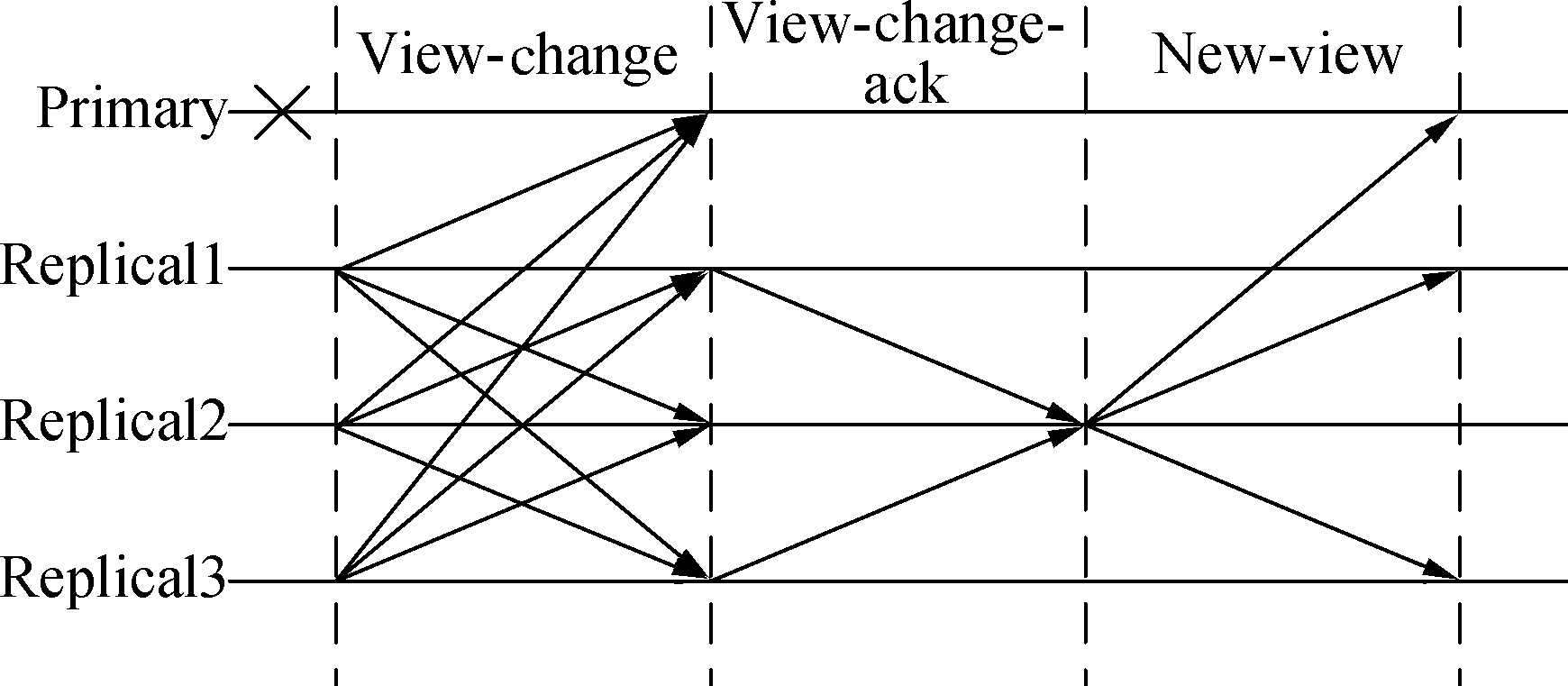
Fig.2 PV-PBFT view-change protocol process
message. The candidate primary node is confirmed as the primary node after receiving 2f+1 proposal messages. Compared with the PBFT view-change protocol, where the primary node is directly determined by the current view number, that is, (v+1)mod n, where n is the total number of nodes, the election security of the primary node in the PV-PBFT view-change protocol is significantly improved.
2 Performance Analysis
In this section, the communication overheads of the PV-PBFT and PBFT protocols were first analyzed and compared. Then, the performance of three consensus protocols, namely, PV-PBFT, SHBFT, and PBFT, was tested in terms of throughput and consensus latency. The consensus protocols were written in Go language for experimental simulation.
2.1 Communication overhead analysis
Assuming that the total number of nodes in the system is n, the number of Byzantine malicious nodes is f=(n-1)/3. During the various phases of consensus execution, as long as each node can receive n-f messages, the normal operation of the system can be guaranteed. For the received n-f messages, there may be false messages spread by f malicious nodes at most, so to ensure that most messages are reliable, n-f-f>f must be satisfied, n>3f, n≥3f+1, and the maximum number of BFT nodes is f=(n-1)/3. The BFT requirement for n≥3f+1 was first demonstrated by Pease et al.[14] in 1980. The detailed proof process can look over Ref.[14].
w1=2n2-n-1+p(n2-1)=18f 2+9f+p(9f 2+6f)
(2)
where w1 is the number of PBFT communications, and p is the trigger view replacement protocol probability. In the PBFT consensus protocol, the number of communications is (n-1)+2n(n-1)=2n2-n-1=18f 2+9f. If the view replacement protocol is triggered, the additional number of communications can be calculated as n(n-1)+(n-1)=n2-1=9f 2+6f.
w2=6(n-1)+p(n2+n-2)=18f+p(9f 2+9f)
(3)
where w2 is the number of PV-PBFT communications. In the PV-PBFT consensus protocol, the number of communications is 6(n-1)=18f. If the view replacement protocol occurs, the additional number of communications is n(n-1)+2(n-1)=n2+n-2=9f 2+9f.
The resulting ratio R of the number of PV-PBFT communications to the number of PBFT communications can be obtained as follows:
(4)
MATLAB is used to make a visual graph of the variation of R with f and p, as shown in Fig. 3, where f takes values from 4 to 20 in steps of 2 and p takes values from 0 to 1 in steps of 0.1.
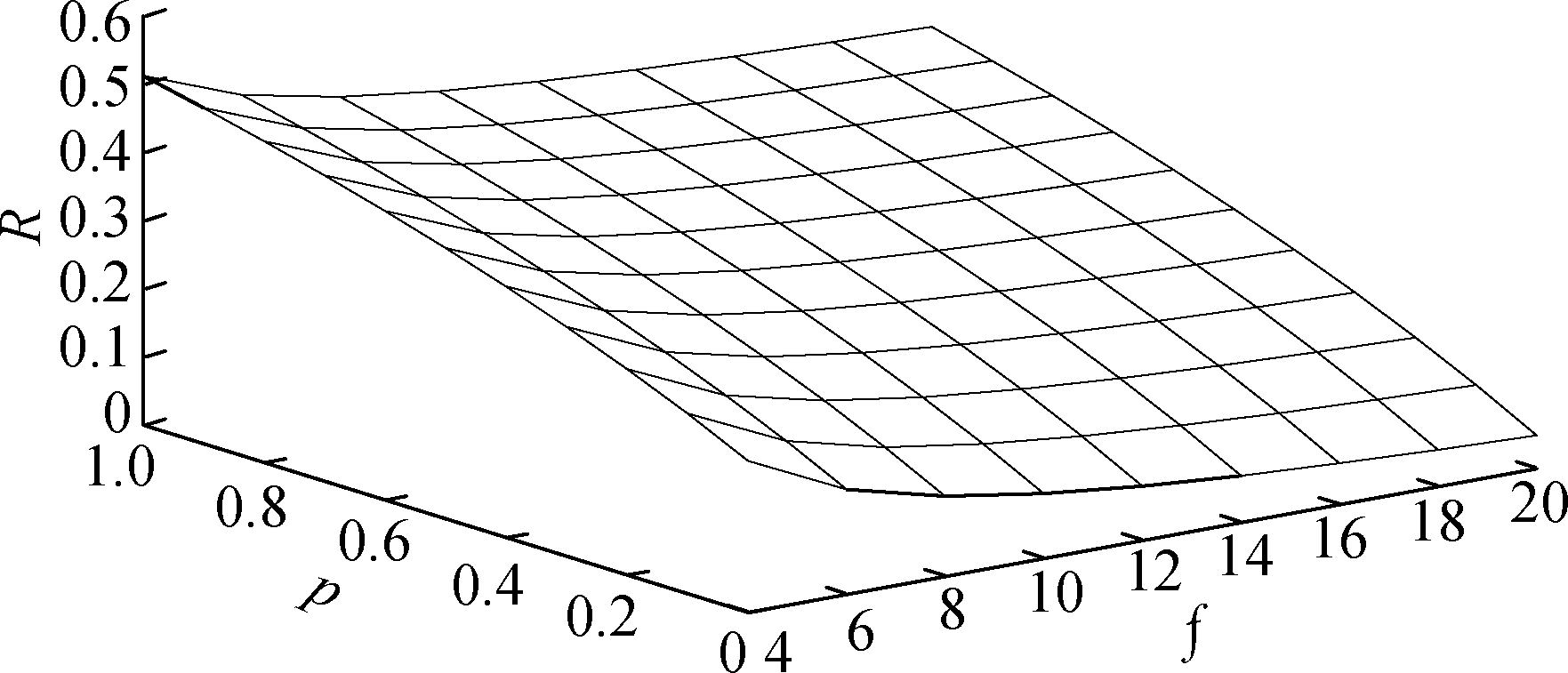
Fig.3 Ratio graph of the PV-PBFT to the PBFT communication overheads
As shown in Fig. 3, the value of R is always less than 1 in the given range of f and p; i.e., the PV-PBFT communication overhead is always less than the communication overhead of the PBFT. In addition, with the same view replacement probability, the PV-PBFT communication overhead decreases more significantly as the number of nodes in the system increases. When the number of Byzantine malicious nodes is 20 and the view switching probability is 0.1, the value of R is only approximately 0.1. That is, the PV-PBFT protocol makes the communication overhead significantly decrease, only approximately 10% of the PBFT protocol.
2.2 Throughput test
The consensus protocols’ throughput is the maximum rate of agreement on the values done to verify the transactions in a blockchain network[15]. In the blockchain system, the throughput can be expressed in terms of the number of transactions processed in each second (TPS), i.e.,
(5)
where Ntran is the number of transactions processed by the system in the block generation time, and Δt is the block-out time.
To test the throughput of the PV-PBFT, this section first conducted experiments on the variation of the PV-PBFT with the SHBFT and PBFT throughput with the number of nodes in the system. The total number of nodes in the system was set to increase from 10 to 60 in steps of 5, the number of Byzantine error nodes always did not exceed one-third, and the number of transaction requests initiated in each experiment was 2 000. After performing ten experiments for each of the three algorithms at different numbers of nodes, the average value was taken as the throughput at different numbers of nodes, and the results are shown in Fig. 4.
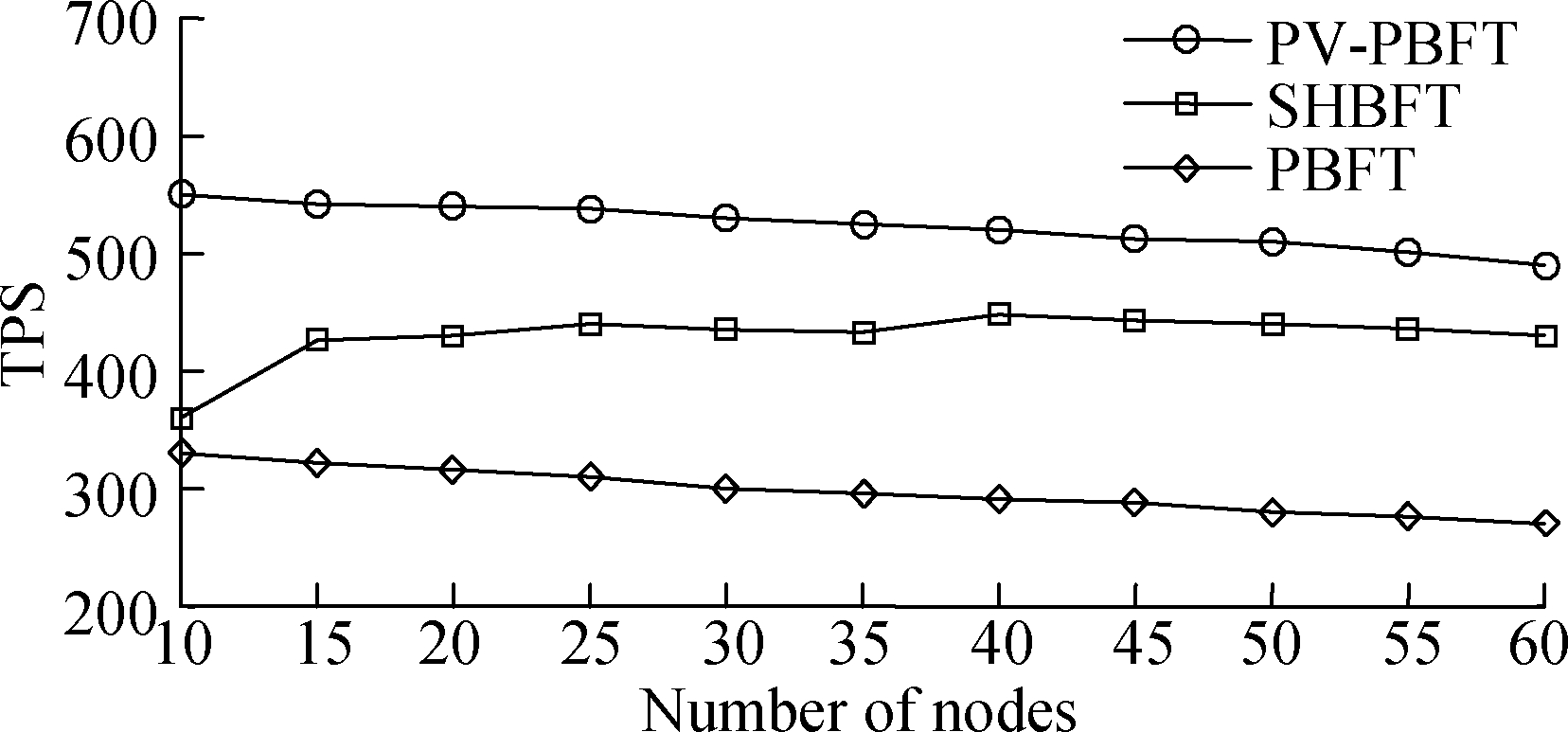
Fig.4 Comparison of the PV-PBFT, SHBFT, and PBFT throughput changes with the number of nodes
On the whole, the throughput of the PV-PBFT is significantly higher than that of the PBFT and SHBFT. With the same number of nodes, the throughput of the PV-PBFT is nearly double that of the PBFT. According to the definition of the throughput, i.e., the number of transactions processed in the block-out time of the system, the number of recent transactions in the new blocks generated by the three consensus protocols is the same. However, there was no process of all replica nodes broadcasting communication with one another in the PV-PBFT; the consensus efficiency was substantially improved, the block-out time was reduced, and the throughput was increased. Although the SHBFT was optimized for the PBFT consensus by the node hierarchy, all tertiary nodes still need to make O(N2) broadcast communication. As the number of nodes in the blockchain system increased, the throughput of the three consensus protocols basically remained within a stable range. As the number of nodes increased, with Byzantine error nodes, for the PV-PBFT and PBFT, the time to collect 2f+1 messages in each phase of the protocol became longer and may trigger the view replacement protocol, resulting in a longer processing time for transactions in the current block and a certain decrease in the throughput occurs. The number of tertiary nodes in the SHBFT is relatively stable, so the consensus protocol time consumption is less affected by the total number of nodes. The throughput of the SHBFT is basically not degraded.
2.3 Consensus latency test
Consensus latency is the total time from the time the client launched the transaction request to the time the consensus is completed, and the transaction information is stored in the new block. It is also an important parameter to evaluate the performance of the consensus protocol. The lower the consensus time delay, the more efficient the system is in processing transactions and the better the performance. The consensus time delay Tdelay is defined as follows:
Tdelay=Ttx+Tcon+Tblock
(6)
where Ttx is the time from when the client initiates a transaction to when the primary node takes out the transaction message from the transaction pool, which is the propagation time for a transaction message to enter the execution phase of the consensus protocol; Tcon represents the time of the consensus protocol execution in the consensus protocol; and Tblock is the confirmation time of the new block in all replica nodes.
To test the consensus latency of the three protocols, the total number of nodes in the system was set to increase incrementally from 10 to 60 with steps of 5, and the Byzantine error nodes did not exceed one-third of the total nodes. The experiment was repeated ten times for each of the three protocols with different numbers of nodes to measure the total time between the initiation of a single request and the receipt of a sufficient confirmation response by the client. Then, the average value is taken as the consensus latency with different numbers of nodes. The results are shown in Fig. 5.
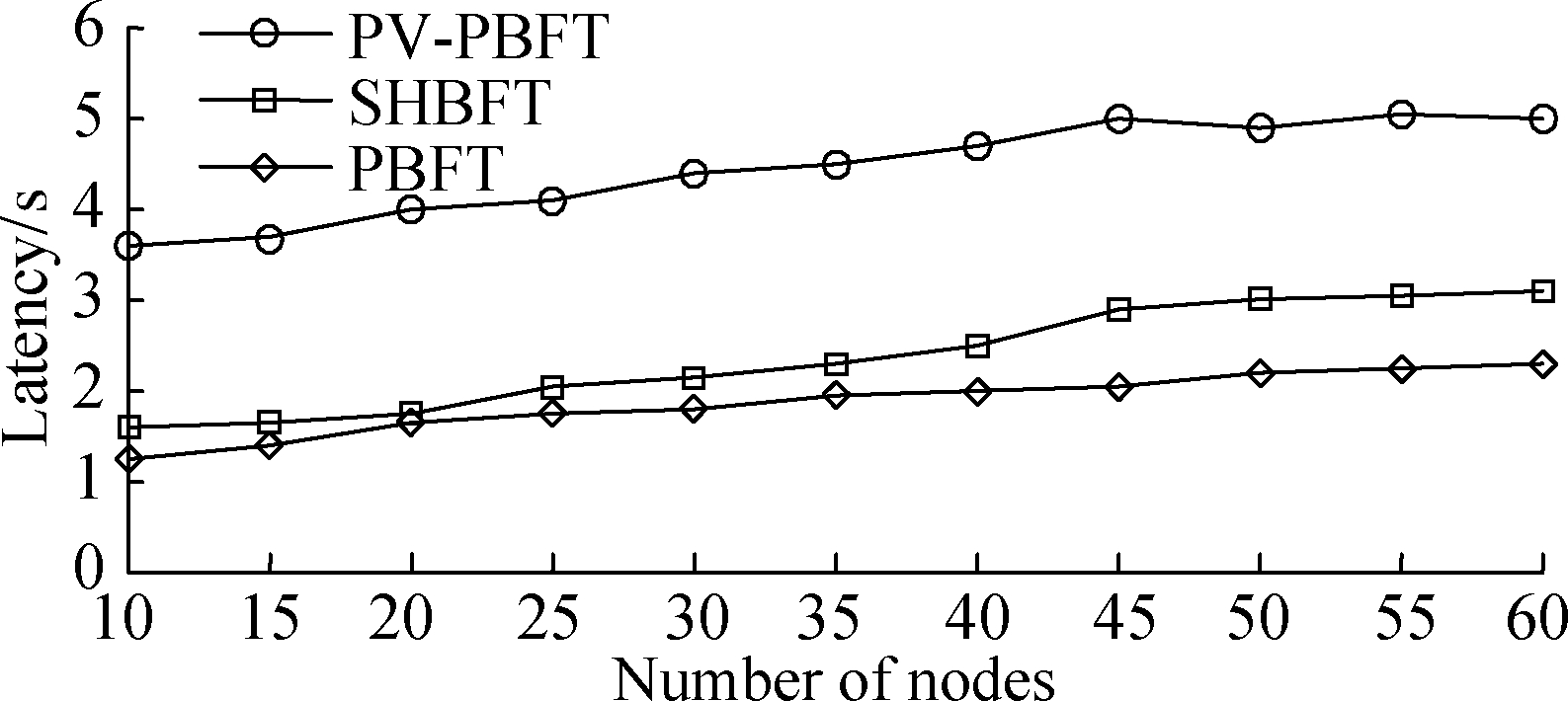
Fig.5 Comparison of the PV-PBFT, SHBFT, and PBFT consensus delays with the number of nodes
Based on the experimental results in Fig. 5,on the whole, the consensus latency of the PV-PBFT protocol is lower than that of the SHBFT protocol with the same number of nodes and significantly lower than that of the PBFT protocol, which is only approximately one-third of the consensus latency of the PBFT protocol. By using the primary node as the communication intermediary in the PV-PBFT protocol, the broadcast communication process between all replica nodes is omitted, which not only makes the completion efficiency of the protocol better than SHBFT and PBFT but also reduces the consensus delay. As the number of nodes increases, in the presence of Byzantine error nodes, the time for nodes to receive 2f+1 messages during communication increases, which makes the consensus protocol completion time increase and consensus latency rise. However, the growth rate of the consensus latency of the PV-PBFT protocol with the increasing number of nodes is lower than that of the PBFT protocol.
3 Conclusions
1) We propose an improved PBFT consensus protocol, including the PV-PBFT consensus protocol and view-change protocol, which reduces the communication complexity to O(N) and extends the scope of use of the protocol.
2) The PV-PBFT uses the threshold signature technique, which improves the fault tolerance of the system and prevents Byzantine nodes and primary nodes from committing errors. Multi-phase voting, with multiple consensus, further reduces the node consensus error rate.
3) We implemented a prototype of the PV-PBFT and compared it with two consensus protocols, i.e., SHBFT and PBFT. The theoretical performance analysis and simulation experimental results demonstrate that the PV-PBFT protocol outperforms the PBFT protocol in terms of the communication overhead and significantly outperforms the SHBFT and PBFT protocols in terms of throughput and consensus latency.
[1] Nakamoto S. Bitcoin: A peer-to-peer electronic cash system [EB/OL]. (2008)[2021-10-06] http: //www.bitcoin.org/bitcoin.pdf.
[2] Wood G.Ethereum: A secure decentralised generalised transaction ledger [EB/OL]. (2013)[2021-10-06] http://yellowpaper.io/.
[3] Buterin V. A next-generation smart contract and decentralized application platform [EB/OL]. (2014-01)[2021-10-06] https://github.com/ethereum/wiki/wiki/White-Paper.
[4] Cachin C. Architecture of the hyperledger blockchain fabric [C]// IBM Research. Zurich, Switzerland, 2016: 310.
[5] Tschorsch F, Scheuermann B. Bitcoin and beyond: A technical survey on decentralized digital currencies [J]. IEEE Communications Surveys & Tutorials, 2016, 18(3): 2084-2123. DOI: 10.1109/COMST.2016.2535718
[6] Thai Q T,Yim J C, Yoo T W, et al. Hierarchical Byzantine fault-tolerance protocol for permissioned blockchain systems [J]. The Journal of Supercomputing, 2019, 75(11): 7337-7365. DOI: 10.1007/s11227-019-02939-x
[7] Xiao Y, Zhang N, Lou W, et al.A survey of distributed consensus protocols for blockchain networks [J]. IEEE Communications Surveys & Tutorials, 2020, 22(2): 1432-1465. DOI: 10.1109/COMST.2020.2969706.
[8] Belotti M, Bozic N, Pujolle G, et al. A vademecum on blockchain technologies: When, which, and how [J]. IEEE Communications Surveys & Tutorials, 2019, 21(4): 3796-3838. DOI: 10.1109/COMST.2019.2928178.
[9] Lao L, Dai X,Xiao B, et al. G-PBFT: A location-based and scalable consensus protocol for IoT-blockchain applications [C]//International Parallel and Distributed Processing Symposium. New Orleans, LA, USA, 2020: 664-673. DOI:10.1109/IPDPS47924.2020.00074.
[10] Ali S, Wang G, White B, et al. Libra critique towards global decentralized financial system [C]//International Conference on Smart City and Informatization. Singapore: Springer, 2019: 661-672. DOI:10.1007/978-981-15-1301-5_52.
[11] Li Y,Qiao L, Lü Z. An optimized byzantine fault tolerance algorithm for consortium blockchain [J]. Peer-to-Peer Networking and Applications, 2021, 14(5): 2826-2839. DOI:10.1007/s12083-021-01103-8
[12] Li W, Feng C, Zhang L, et al. A scalable multi-layer PBFT consensus for blockchain [J]. IEEE Transactions on Parallel and Distributed Systems, 2021, 32(5): 1146-1160. DOI:10.1109/TPDS.2020.3042392.
[13] Wang Y,Cai S, Lin C, et al. Study of blockchains’s consensus mechanism based on credit[J]. IEEE Access, 2019, 7: 10224-10231. DOI10.1109/ACCESS.2019.2891065
[14] Pease M,Shostak R, Lamport L. Reaching agreement in the presence of faults [J]. Journal of the ACM, 1980, 27(2):228-234. DOI:10.1145/322186.322188
[15] Bamakan S M H, Motavali A, Babaei A B. A survey of blockchain consensus algorithms performance evaluation criteria [J]. Expert Systems with Applications, 2020, 154: 113385. DOI:10.1016/j.eswa.2020.113385