Permanent magnet synchronous motors (PMSMs) are widely used in servo and high-performance speed regulation systems due to their high efficiency, high power, and low loss[1-2]. Vector control and direct torque control are two typical control strategies for a PMSM. However, as vector control, its closed-loop performance is restricted due to the conflict between the linearity of the proportional-integral (PI) controller adopted in its current loop and the rotation speed loop and nonlinearity of the PMSM. For the direct torque control, the hysteresis loop controller adopted in its inner loop results in an increased ripple of the electromagnetic torque and three-phase current. In recent years, with the rapid development of microprocessors, predictive control has become a novel nonlinear control strategy for PMSMs, owing to its fast dynamic response and high control precision. Model predictive control (MPC) has become a high-performance control scheme because of its merits such as fast dynamic response, simplicity, and no requirement for the parameter tuning of the current loop[3-6]. MPC mainly includes model predictive torque control and MPCC. Compared with the former control, MPCC has a value function whose control variable only involves current. Without considering the weight of different control variables, it can achieve the fast tracking of current overshoot, which is highly favorable for actual control. To further improve the static performance of the PMSM control system, domestic and foreign scholars have performed a substantial amount of research on the two-vector model predictive current control (TV-MPCC) strategies of PMSMs[7-9].
APMSM is a typical nonlinear multi-variable strongly coupled system. Its predictive current control system generally adopts a PI controller as its rotation speed loop controller. However, due to the complexity of the PMSM’s rotation speed control model, a mathematical model is not precise enough. Moreover, PI control is sensitive to the parameter changes of the PMSM model, resulting in the poor dynamic performance and robustness of the speed regulation system. In response to the inherent defects of the conventional PI, Han[10] proposed active disturbance rejection control (ADRC), which is characterized by simple regulation, high accuracy, real-time estimation, and compensation of internal and external disturbances without the need for an accurate and controlled mathematical model system. In recent years, ADRC has been widely applied to the PMSM’s control system. Zhou et al.[11] suggested that a speed control system with ADRC showed better dynamic and static performance than the speed control system with PI control in the vector control of PMSMs. Hezzi et al.[12] investigated the speed tracking capability and elastic control performance of the ADRC technique under different operating conditions based on a five-phase PMSM for electric vehicles. Accordingly, ADRC can ensure higher dynamic performance and robustness of a system than PI control. Zhang et al.[13] proposed an extended state observer (ESO)-based predictive control strategy for a PMSM’s active disturbance rejection model to reduce the ripple of electromagnetic torque, which demonstrates a satisfactory performance of the rotation speed tracking and disturbance rejection. However, ADRC cannot be widely applied due to its complex parameter calibration and nonlinear function. Accordingly, Gao[14] simplified nonlinear ADRC into linear ADRC (LADRC), which has been applied to power systems[15].
This paper attempts to design a one-order LADRC controller that consists of the following parts: linear extended state observer (LESO) and linear state error feedback (LSEF)[16]. The innovative LADRC controller provides intuitive parameter calibration and significantly reduces computational effort, achieving the same high performance as nonlinear ADRC, making it more suitable for PMSM speed loop control system[17-18]. The proposed control strategy can increase the disturbance rejection capacity and robustness of the PMSM’s predictive current control system.
1 PMSM Mathematical Model
Based on the magnetic field orientation theory, ignoring the hysteresis loss of the PMSM, the state equation of the stator current for the table-posted PMSM in the synchronous rotation coordinate system is
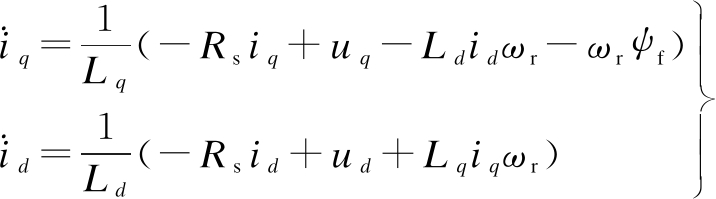
(1)
where id and iq are the stator current, ud and uq are the stator voltage, respectively; Ld=Lq=Ls denote the stator’s winding inductance; Rs is the stator resistance; ψf is the permanent magnet flux linkage; and ωr is the rotor electrical angular velocity.
The mechanical motion equation of the motor is
(2)
where TL and Te are the load torque and electromagnetic torque, respectively; J is the rotational inertia; and F is the rotor viscous friction coefficient. In ωr=pωm, ωm refers to the rotor mechanical angular velocity, and p is the number of pole pairs.
The electromagnetic torque equation is
Te=1.5pψfiq
(3)
2 PMSM TV-MPCC
A two-level three-phase voltage source inverter may generate eight basic switch states: Six valid voltage vectors U1(001), U2(010), U3(011), U4(100), U5(101), U6(110) and two zero vectors U0(000) and U0(111). They can determine the limited number of output current possibilities for the next sampling interval. A traditional MPCC only selects one optimal voltage vector Vopt1 as the output voltage. However, the electromagnetic torque and stator current demonstrate obvious ripples. With TV-MPCC, another voltage vector is selected within one control period to determine the second optimal voltage vector Vopt2. The optimal voltage vector Vopt1 and the eight voltage vectors are combined and pre-allocated to the action time of two voltage vectors in each combination. Therefore, the selected voltage vector is accurate. It can effectively improve the current tracking accuracy and obtain good static performance. TV-MPCC aims to minimize the error between the prediction current value and the set current value by calculating the value function. With d-q axis currents as the control quantities, the value function can be established as follows:
(4)
where 
are the given values of the d and q axis currents, respectively. The seven voltage vectors of the voltage source inverter correspond to the values of the seven value functions.
For state Eq.(1), the Eulerian method is adopted to obtain the discretized d-q phase current prediction equation:
(5)
where tg1 and tg2 are the action times of Vopt1 and Vopt2 within a control cycle TS, respectively, tg1=Ts-tg2; i′d1(k), i′d2(k), i′q1(k) and i′q2(k) denote the current slope of d and q axis components with the actions of Vopt1 and Vopt2. The calculation is as follows:
(6)
(7)
where n=1,2，udn and uqn denote the d and q axis voltages of Vopt1 and Vopt2, respectively. Combining the equation above, the action time of Vopt1 is obtained:
(8)
tg2=TS-tg1
(9)
When the motor is started, there may be circumstances where the calculation results of tg1and tg2 do not fall within 0 and Ts. At this time, tg1 and tg2 should be reallocated. There are mainly two circumstances: if tg1<0, then, tg1=0; if tg1>Ts, then, tg1=Ts. The structure block diagram of the PMSM TV-MPCC is shown in Fig.1.
Fig.1 Structure block diagram of the PMSM TV-MPCC
3 Design of the LADRC Controller
3.1 LADRC rotation speed loop controller
For the surface-mount PMSM (id=0) with the given Ld=Lq, the following expression is obtained from Eqs.(2) and (3):
(10)
where 
is the torque current coefficient.
The disturbance is set as
(11)
Eq.(10) can be rewritten as
(12)
where 
is the compensation coefficient.
This paper utilizes the TV-MPCC controller as the current loop of the PMSM control system and the LADRC controller as the speed loop. The input of the rotation speed loop controller is the given rotation speed 
and feedback rotation speed ωr, and the output is the given torque current 
In Eqs.(2) and (3), the input and output of the rotation speed loop are a one-order differential equation, so only one-order LADRC is needed. The structure diagram of the designed one-order LADRC is shown in Fig.2, where z1 refers to the rotation tracking speed, z2 is the observed value of the total disturbance, z2/b0 denotes the compensation for internal and external disturbances. u0 is the initial signal of the LSEF’s control object, u is the final control signal after disturbance compensation, d is the external disturbance, and P is the controlled object.
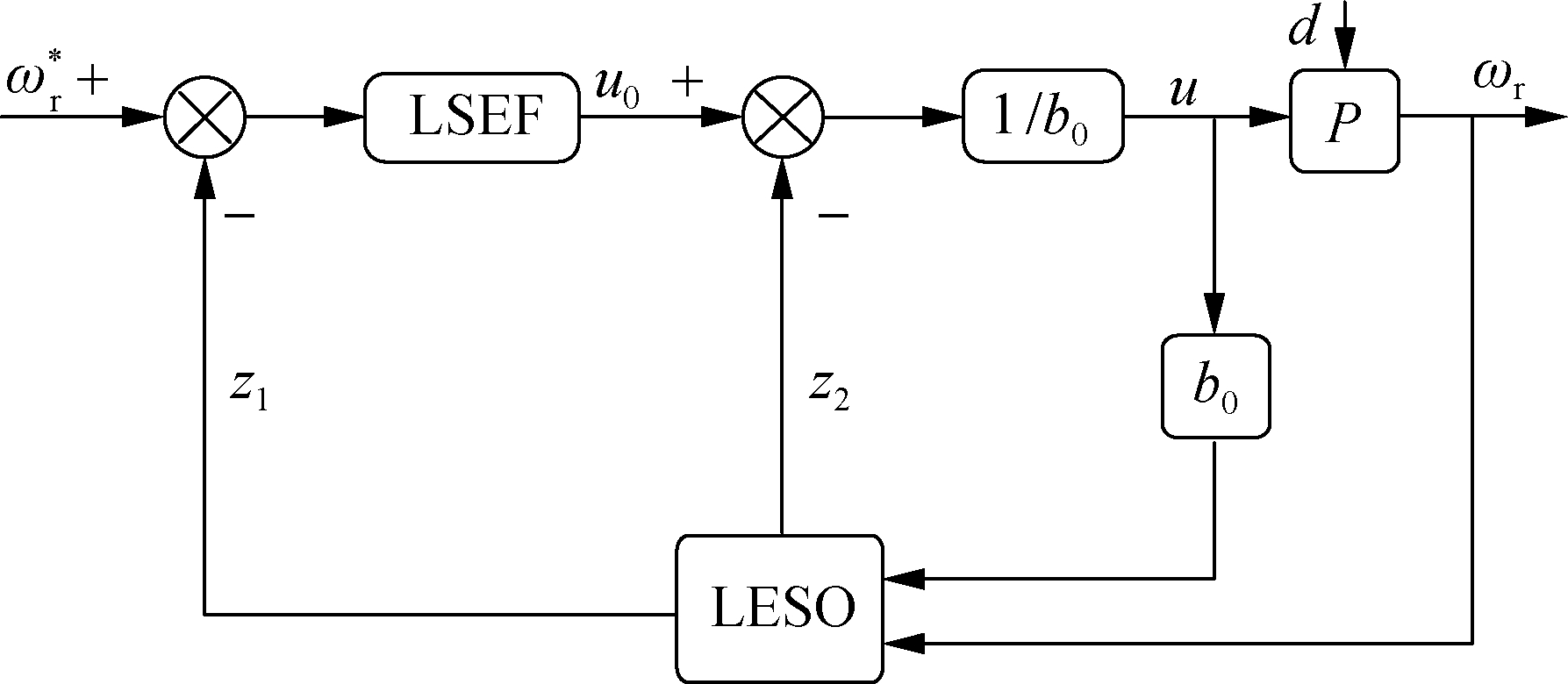
Fig.2 Structure diagram of the designed one-order LADRC
3.2 LESO
LESO is the core part of the LADRC controller. It is mainly applied to observe the actual value of the disturbance actions inside and outside the system and compensate for the feedback to eliminate the influence of disturbances and improve the performance of the control system.
The equation of the controlled object is set as follows:
(13)
where y and u denotes the output and input; t is the system’s time-varying state; and b is the gain of the controlled variable. The true value of b is hard to estimate in real systems. Therefore, Eq.(13) can be written as
f1(y,ω,t)=b0u+f(y,ω,t)
(14)
where f (y,ω,t) is the total internal and external disturbances.
The state variables are selected as follows:x1=y, x2=f, 
Then, Eq.(14) can be converted into a state-space equation:
(15)
The corresponding LESO is
(16)
where z is the state variable of the observer (z→x). L refers to the error feedback gain matrix of the observer as in 
where ωo denotes the bandwidth of the observer and can be exported through the pole assignment.
Substitute the parameters for A, B, L and C into Eq.(16), and the LESO equation can be obtained as follows:
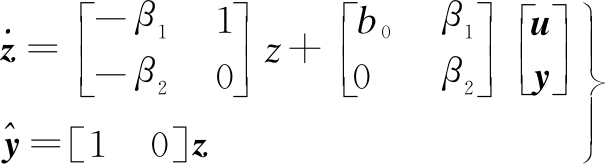
(17)
3.3 LSEF
The traditional proportional-integral-derivative (PID) is a simple weighted sum of the error’s proportion, integral, and differential. As the LESO can achieve real-time estimation and compensate for internal and external disturbances, there is no need to employ traditional PID integration to eliminate residual errors under constant disturbances. Similar to a PI controller, the LSEF is mainly used to control the reference input, error feedback, and offset disturbance. It converts a complex mathematical model into an integral series model, thus eliminating the negative influence of the integrator. The control law can be expressed as
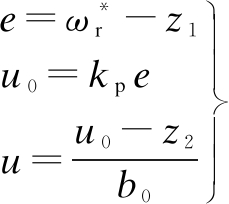
(18)
where kp is the gain coefficient. Supposing that ωc is the bandwidth of the LADRC controller, the high-performance tracking of the signal can be achieved when kp=ωc.
3.4 Parameter calibration strategy
In a rotation speed loop’s one-order LADRC controller, only three parameters need to be calibrated: bandwidth ωc of the controller, bandwidth ωo of the observer, and compensation coefficient b0. ωc determines the controller’s response speed. Moreover, the greater the ωc, the better the control effect. However, excessiveness may cause system divergence. ωo determines the tracking speed of the LESO, where the greater the ωo, the faster the LESO’s estimation of disturbance. However, the system is still sensitive to noise. Therefore, a balance between the observer’s parameters and the system’s sensitivity to noise must be found. b0 represents the characteristics of the controlled object and can be directly exported based on those characteristics.
Gao[14] proposed a strategy that simplifies the LADRC parameter adjustment to the bandwidth parameter adjustment problem. Therefore, for most engineering projects, the relationship between ωo and ωc can be set as ωo≈(3～5)ωc. In simulations, appropriate parameters can be found through multiple comparative analyses using cut-and-try methods.
4 Simulation Results and Analysis
To verify the correctness and effectiveness of the proposed control strategy, the performance test of the PMSM system with the TV-MPCC as the current loop and the LADRC controller as the speed loop was performed on the MATLAB/Simulink platform, and the results were compared with those of the TV-MPCC PMSM where the speed loop adopts a PI controller. The general block diagram of the PMSM’s control system is shown in Fig.3. The selected main parameters of the PMSM are shown in Tab.1. The system sampling cycle Ts is 50 μs, and the base frequency of both systems is 133.33 Hz. The LADRC parameters are as follows: ωo=1 950, ωc=480, and b0=1 734.5.
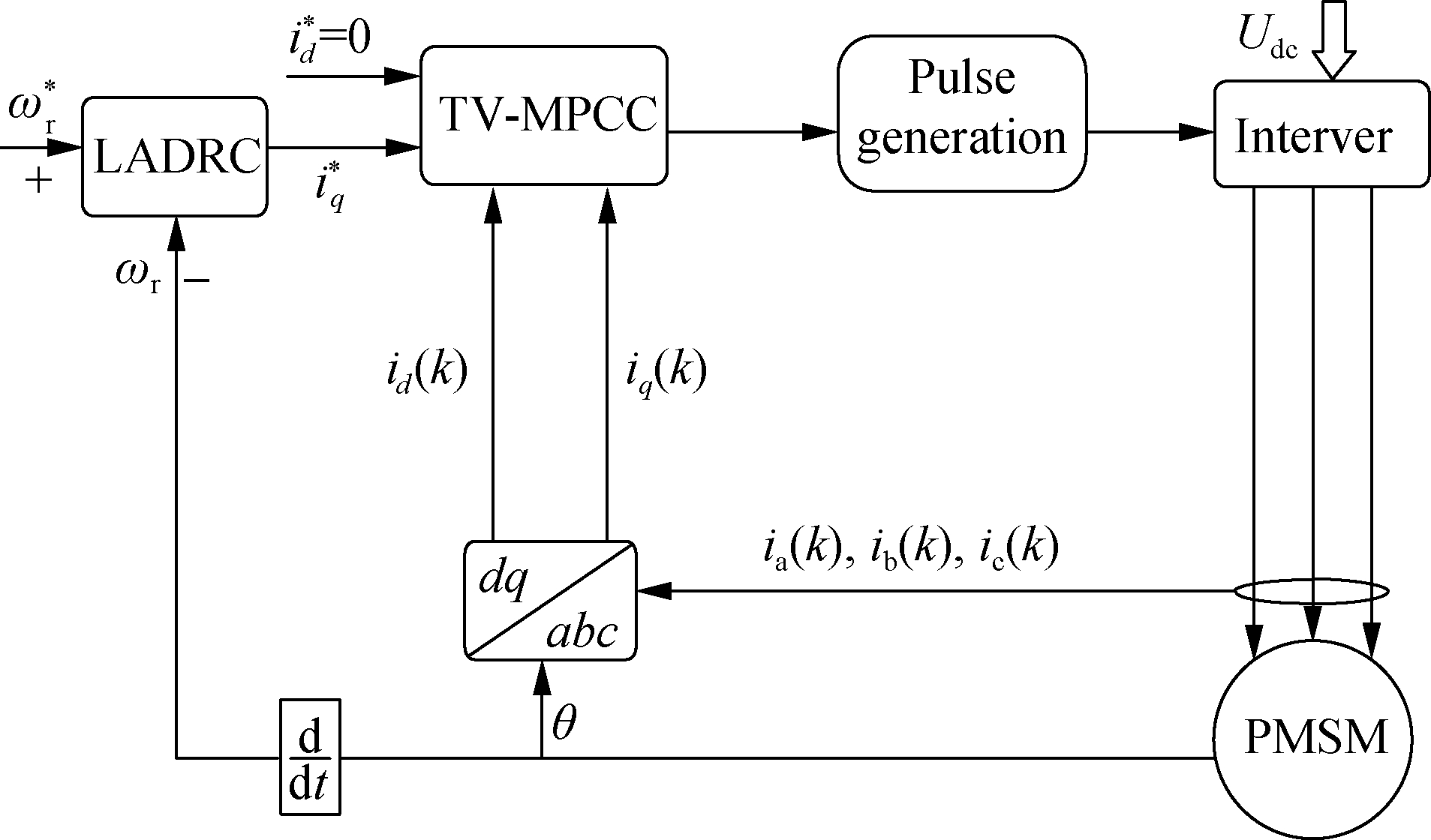
Fig.3 General block diagram of the PMSM’s control system
Tab.1 Selected main parameters of the PMSM
ParametersvalueDC bus voltage Udc/V300Rotor flux ψf/Wb0.182 7d-q coordinate inductance Ls/H0.005 25Stator resistance Rs/Ω0.958 5Friction coefficient F/(10-6N·m·s) 3Number of pole pairs p4Rotational inertia J/(g·m2)0.632
The PI parameters were adjusted at the same simulation conditions so that the two TV-MPCC PMSM systems that adopt PI and LADRC achieve the same dynamic performance as much as possible. Accordingly, kp=0.20 and ki=0.014 can be obtained. Fig.4 shows the system response of the TV-MPCC PMSM with PI.
4.1 Simulation results with the PMSM parameter match
To solidly and comparatively analyze the dynamic performance of the two systems, the PI parameters were
(a)
(b)
(c)
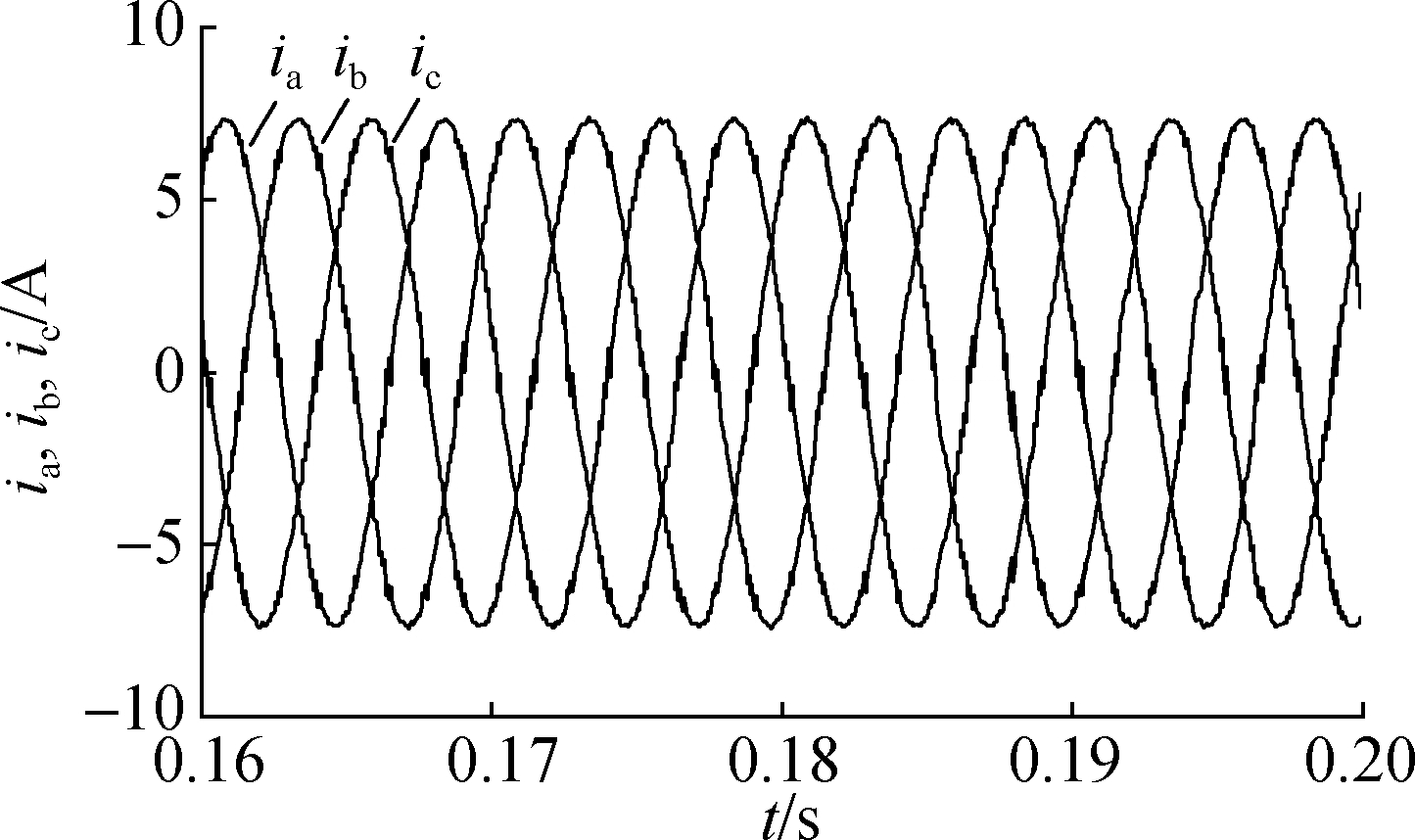
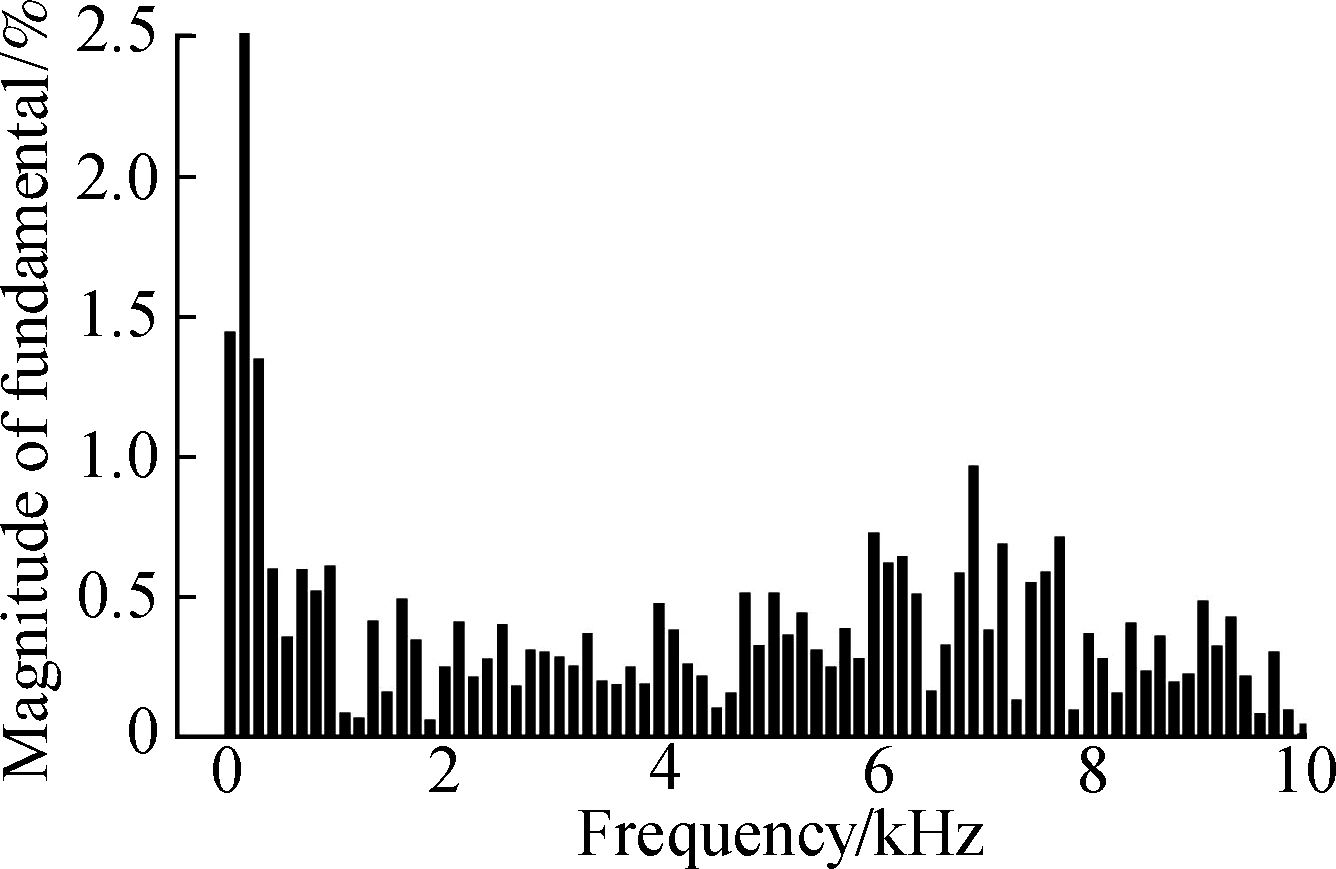
Fig.4 System response of the TV-MPCC with PMSM parameter match based on PI(kp=0.90 and ki=0.70). (a) Speed response; (b) Three-phase current response of the PMSM in the steady state; (c) FFT analysis of the PMSM phase current(THD=3.61%)
adjusted so that the two TV-MPCC PMSM systems using PI and LADRC can achieve the same anti-interference performance as much as possible. Accordingly, kp= 0.90 and ki= 0.70 can be obtained. The simulation conditions are as follows: When the motor operated at a stable speed of 2 000 r/min without load, 8 N·m load disturbance was abruptly added at 0.1 s. Figs.4 and 5 show the corresponding response curves of the two systems.
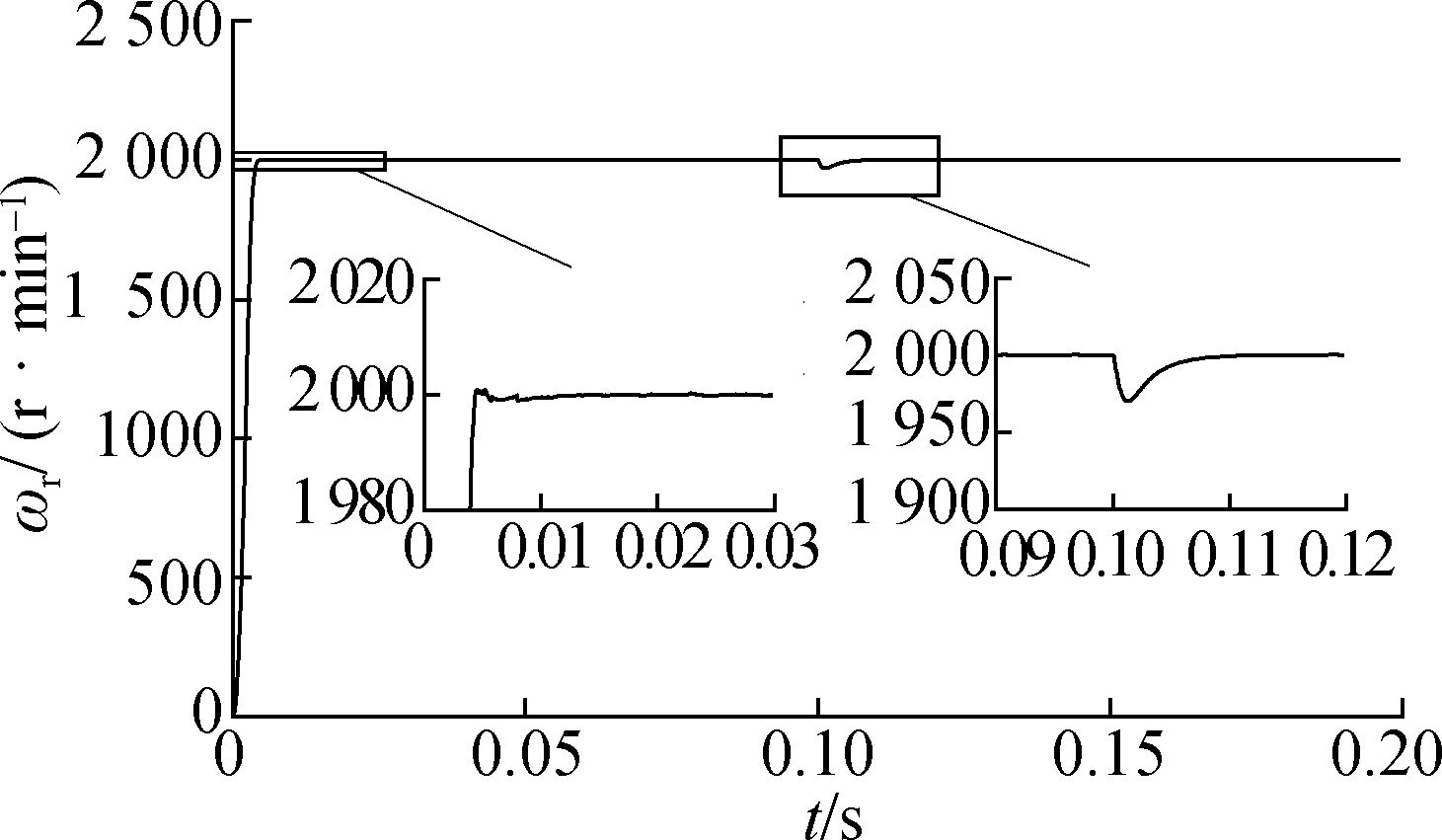
Figs.4 and 5 show that when the rotation speed loop has the same anti-load disturbance capacity, the fluctuation of the rotation speed wave and the overshoot are great with the PI controller during the initial startup period of the motor. It takes a long transition time when Ts= 16 ms. However, as the LADRC controller was adopted, the overshoot was smaller with the transition time (Ts=8 ms), and the response was faster. Figs.4(b) and 5(b) show the waves of the three-phase current (ia, ib, and ic) under the control of the PI and LADRC, respectively, in a stable state after 0.16 s. A fast Fourier transform (FFT) analysis was conducted for ia, and one cycle after 0.16 s was selected. As shown in Figs.4(c) and 5(c), the THDs controlled by the PI and LADRC are 3.61% and 3.32%, respectively.
The robustness of the LADRC and PI controllers are compared in Figs.5 and 6. When the speed loop basically has the same dynamic performance, the rotation speed controlled by PI was reduced by 3.35% as an abrupt 8 N·m load was added at 0.1 s, as shown in Fig.6(a). At the same time, when the rated rotation speed was resumed, there was a 2.4% steady-state error. In Fig.5(a), however, the rotation speed is reduced by only 1.62%. Furthermore, when the rated rotation speed is resumed, there is no steady-state error. Figs.5(b) and 6(b) show the wave of three-phase current (ia, ib, and ic), respectively, under the control of the LADRC and PI in a stable state after 0.16 s. The FFT analysis was conducted for ia, and one cycle after 0.16 s was selected.
(a)
(b)
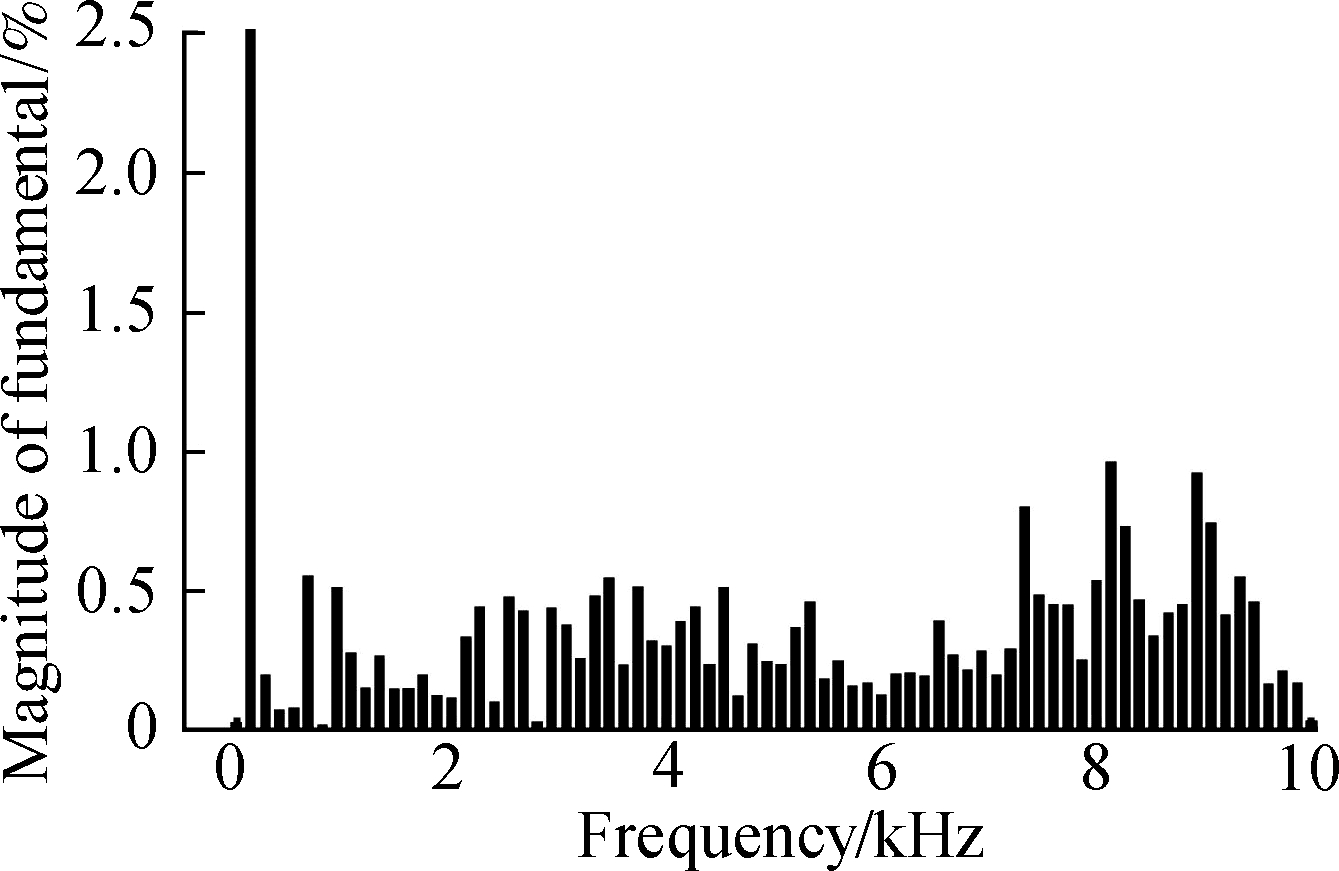
(c)
Fig.5 System response of the TV-MPCC with PMSM parameter match based on LADRC. (a) Speed response; (b) Three-phase current response of the PMSM in the steady state; (c) FFT analysis of the PMSM phase current(THD=3.32%)
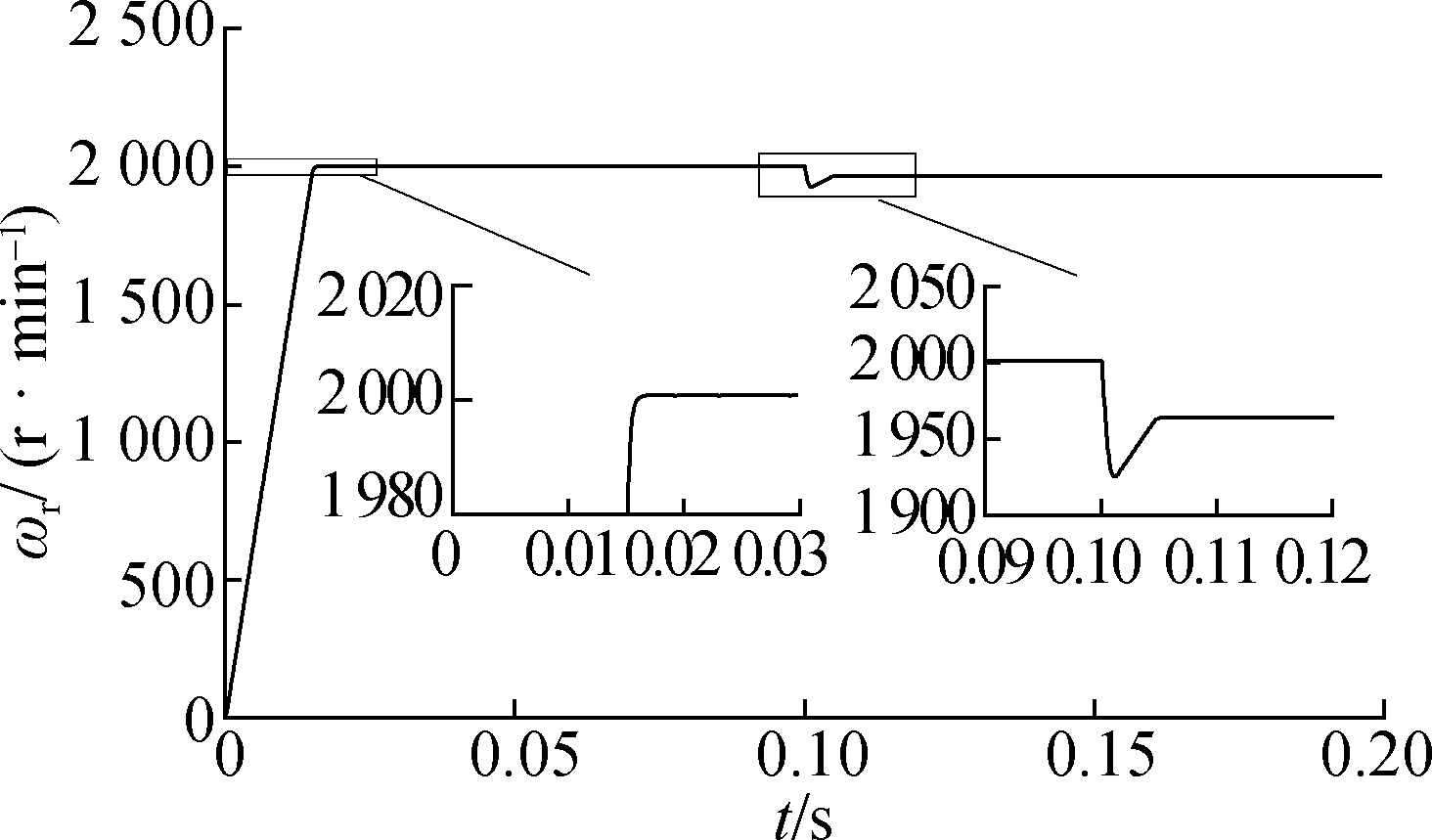
(a)
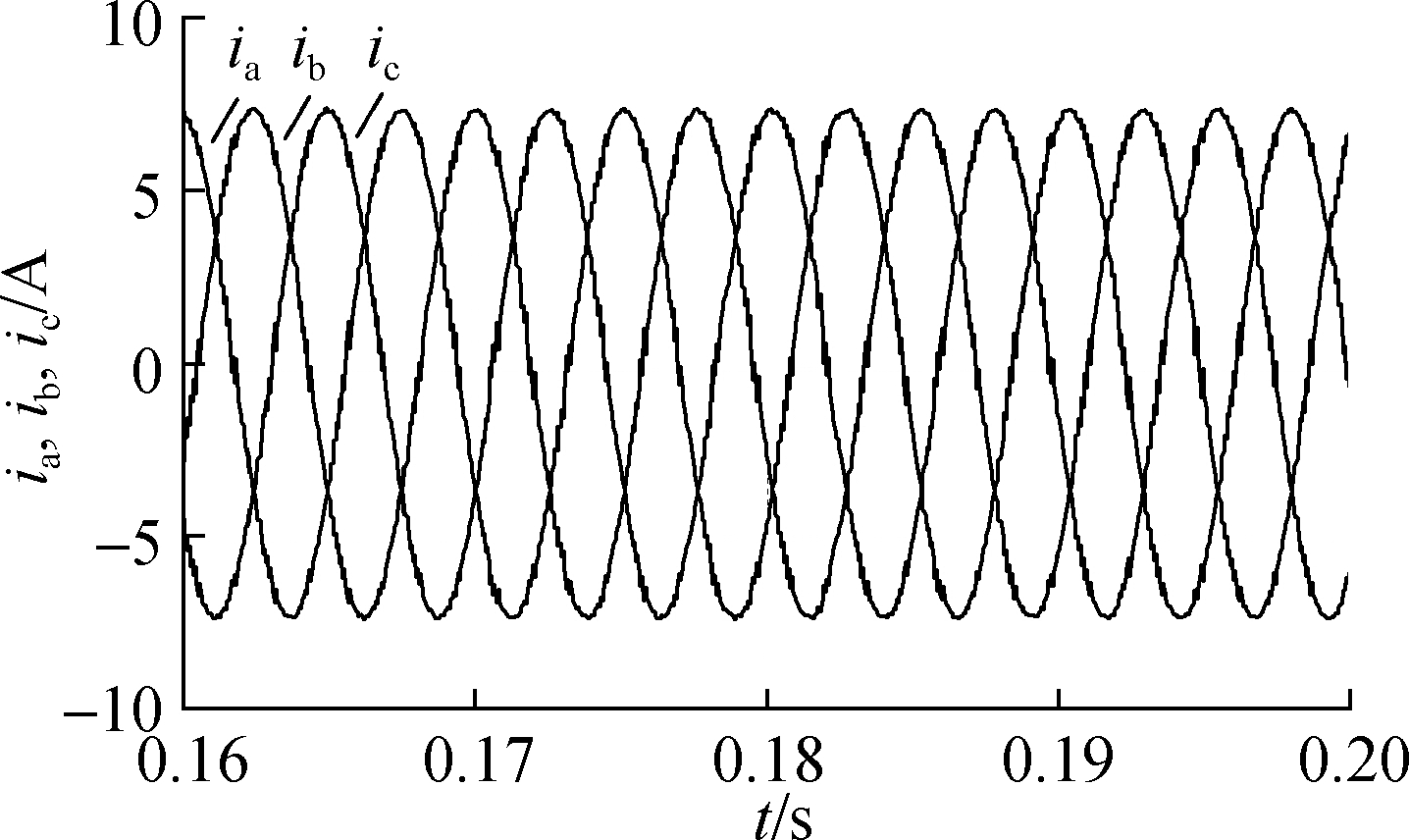
(b)
(c)
Fig.6 System response of the TV-MPCC with PMSM parameter match based on PI(kp=0.20 and ki=0.014). (a) Speed response; (b) Three-phase current response of the PMSM in a steady state; (c) FFT analysis of the PMSM phase current(THD=4.17%)
The THDs controlled by the PI and LADRC were 4.17% and 3.32%, respectively.
To further test the application of the designed LADRC in the high-performance PMSM speed regulation system, the control strategy was simulated in comparison with that presented in Ref.[13], in which the control strategy speed loop employs the conventional active disturbance rejection controller under the same simulation conditions. The PMSM system response of Ref.[13] is shown in Fig.7.
(a)
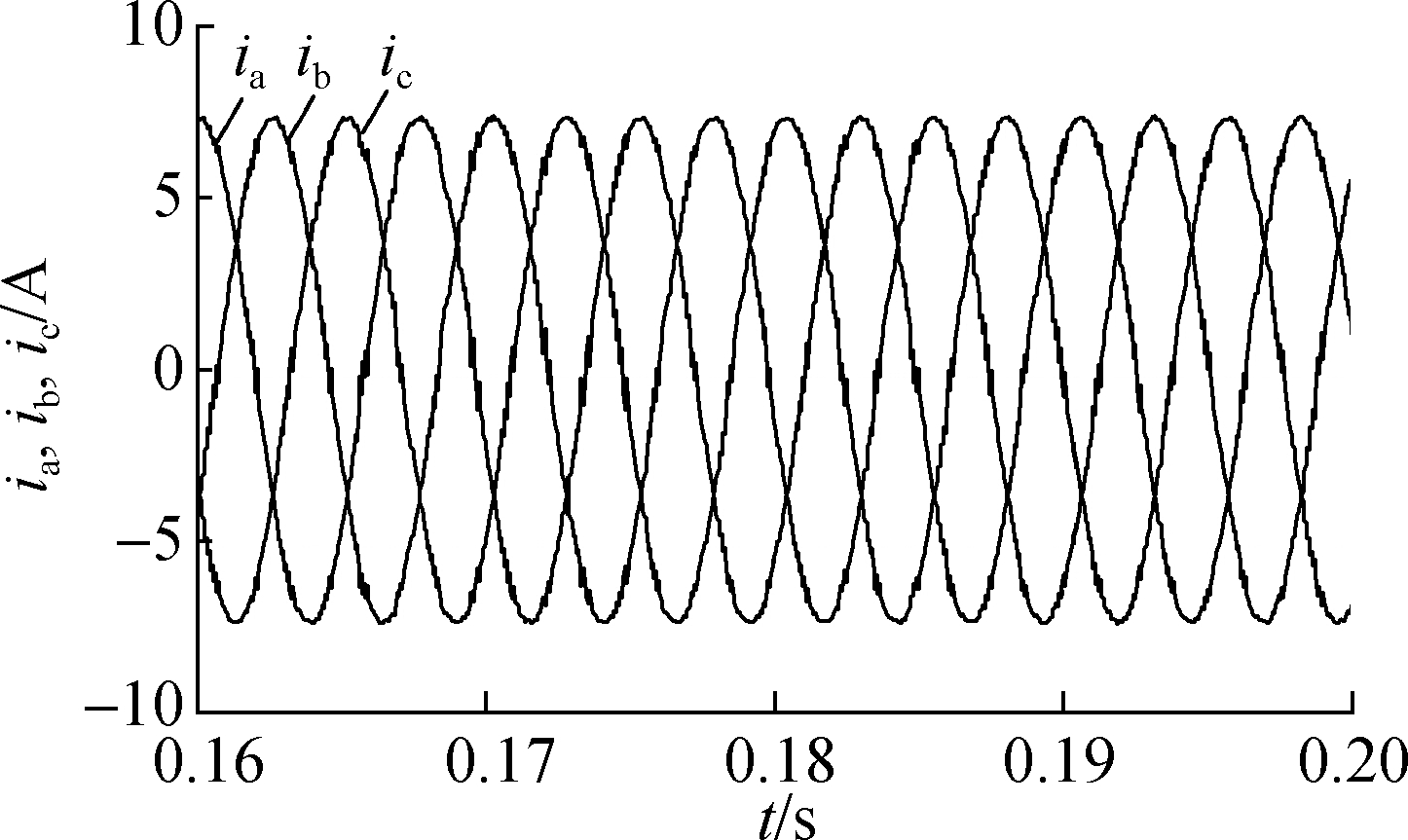
(b)
(c)
Fig.7 PMSM system response of the control strategy in Ref. [13]. (a) Speed response; (b) Three-phase current response of the PMSM in a steady state; (c) FFT analysis of the PMSM phase current(THD=4.01%)
Comparing Figs.5(a) and 7(a), the proposed control strategy demonstrates better transient response features and disturbance rejection control than that of Ref.[13]. Figs.5(b) and 7(b) show the three-phase currents (ia, ib, and ic) of the proposed control strategy and those in Ref. [13] in a steady state after 0.16 s, respectively. The FFT analysis also demonstrates that the THD of the phase current is small. Tab.2 presents the control system performance of the speed loop with different control strategies.
Tab.2 Control system performances of the rotation speed loop adopting different control strategies
Control strategyTransition time/msStart overshootTHD of ia/%Steady-state error/%PI (kp=0.90, ki= 0.70)16Yes3.612.35PI (kp= 0.20, ki= 0.014)16No4.173.35Ref.[13]14No4.012.75LADRC8No3.321.62
4.2 Simulation results with the PMSM parameter mismatch
During the actual running of the motor, due to factors such as temperature rise and magnetic saturation, the PMSM parameters may deviate. To verify the effectiveness of the proposed LADRC controller in the case of mismatched motor parameters, under the same conditions as in Section 4.1, the actual values of the inductance, rotor flux linkage, and stator resistance in the control strategy are set to be 1.5, 1.2, and 0.8 times their nominal values, respectively. Fig.8 shows the response of the PI-based TV-MPCC PMSM system, where kp=0.90 and ki=0.70. Fig.9 presents the corresponding response when kp=0.20 and ki=0.014.
Fig.10 shows the corresponding system response of the LADRC-based TV-MPCC PMSM system in the case of a motor parameter mismatch. Comparing Figs.8 and 9, the motor speed response time of the proposed control strategy is short, the steady-state error is small, and the simulation is close to the nominal value of the motor parameters. Based on the FFT analysis on ia (see Fig.10(c)), the THD of the phase current is small. Hence, the system under the proposed control strategy has good performance, can effectively deal with the changes in motor parameters, and has good robustness when the motor parameters do not match.
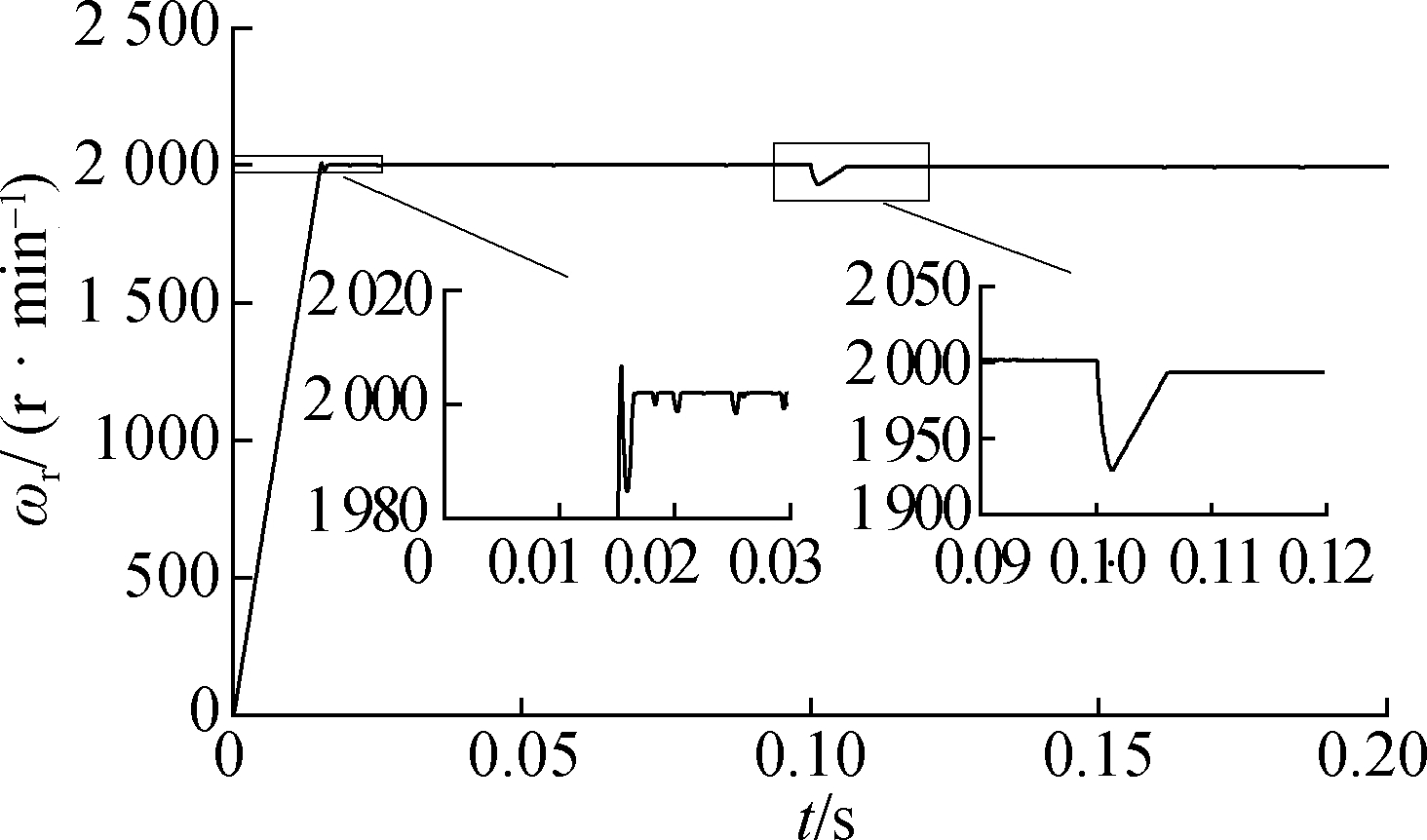
(a)
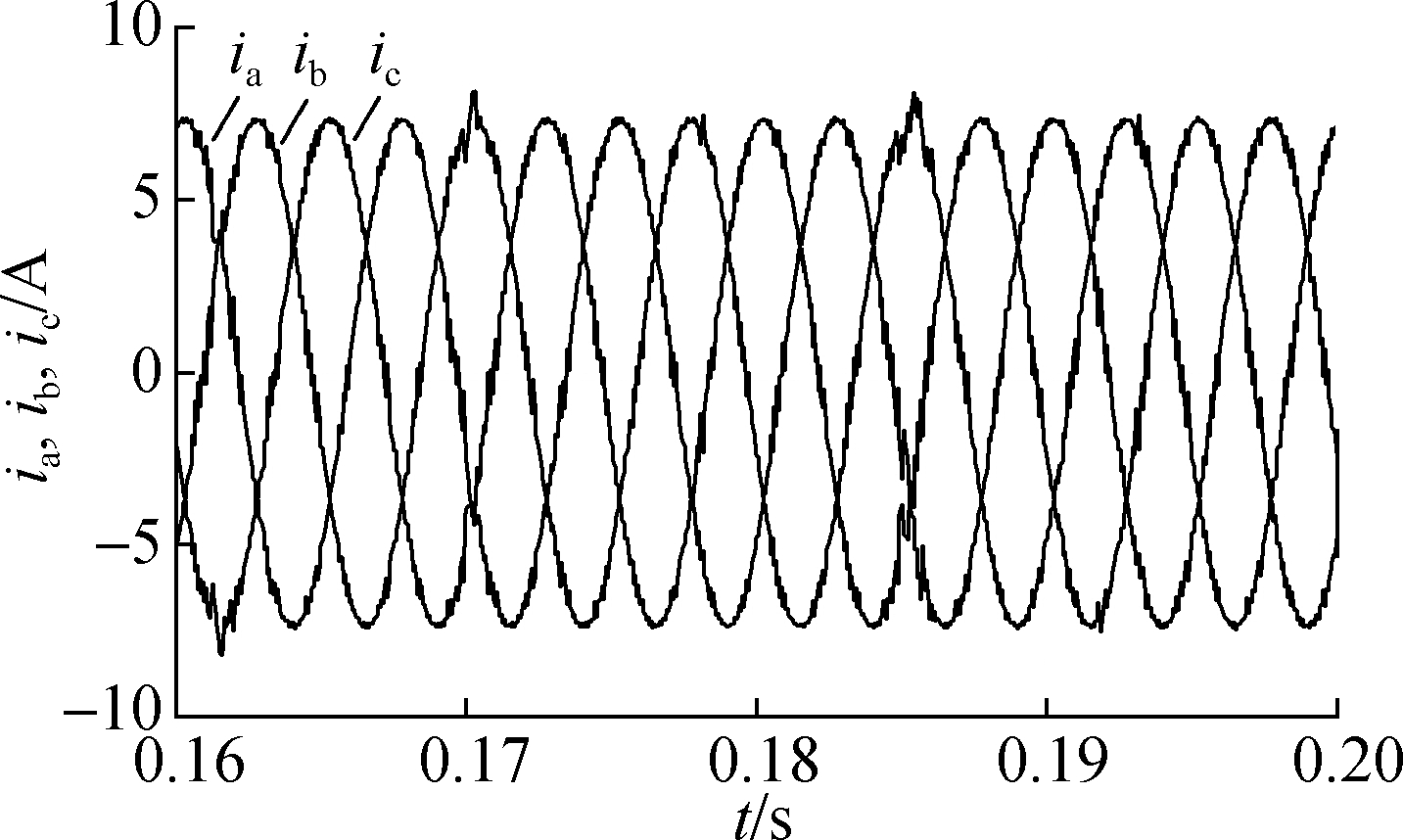
(b)
(c)
Fig.8 System response of the TV-MPCC with PMSM parameter mismatch based on PI(kp=0.90 and ki=0.70). (a) Speed response; (b) Three-phase current response of the PMSM in a steady state; (c) FFT analysis of the PMSM phase current(THD=5.13%)
(a)
(b)
(c)
Fig.9 System response of the TV-MPCC with PMSM parameter mismatch based on PI(kp=0.20 and ki=0.014). (a) Speed response; (b) Three-phase current response of the PMSM in a steady state; (c) FFT analysis of the PMSM phase current(THD=4.55%)
(a)
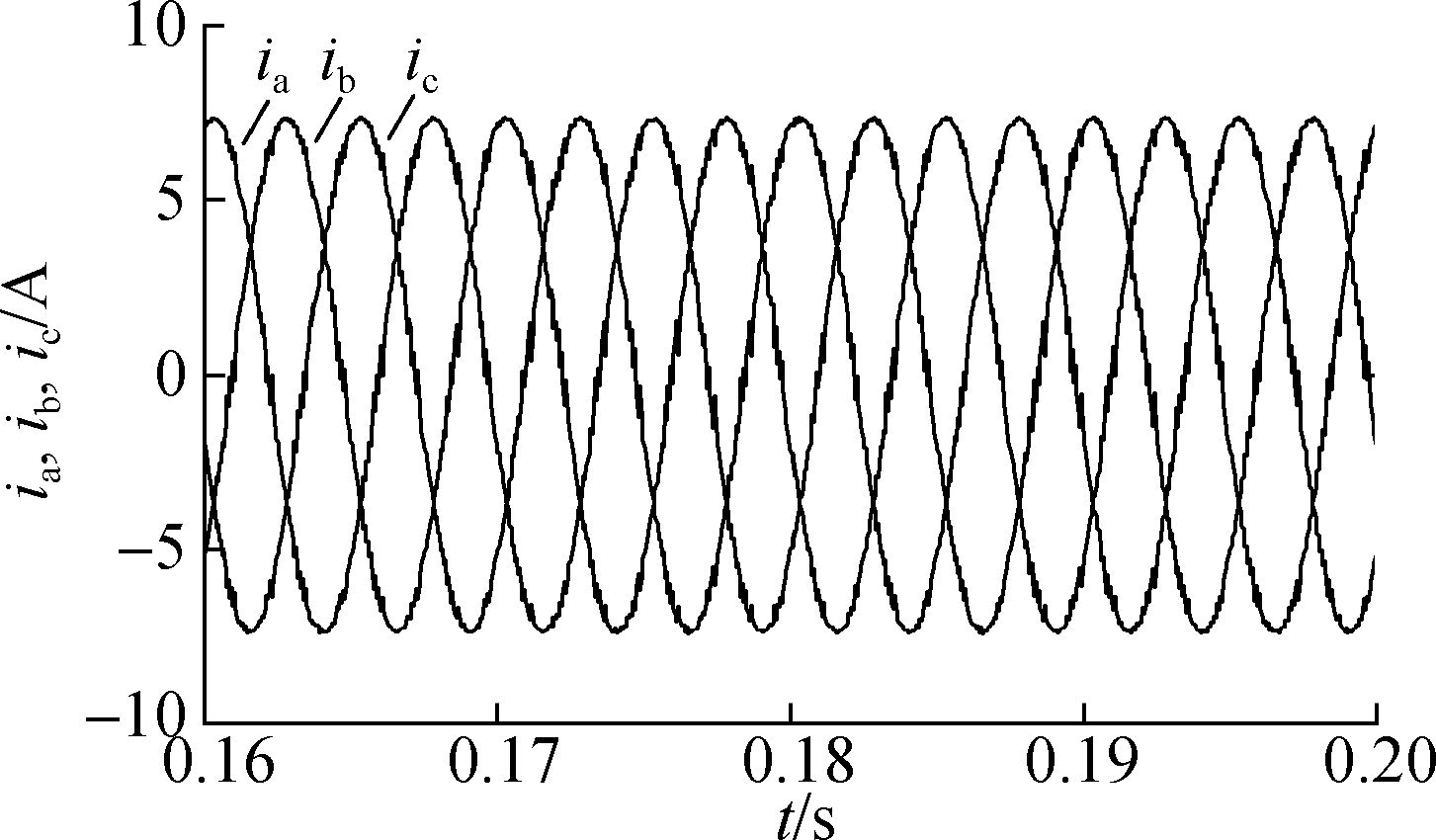
(b)
(c)
Fig.10 System response of the TV-MPCC with PMSM parameter mismatch based on LADRC under motor parameter mismatch. (a) Speed response; (b) Three-phase current response of the PMSM in a steady state; (c) FFT analysis of the PMSM phase current(THD=4.18%)
5 Conclusions
1) A control strategy employing the LADRC controller as the speed loop of the PMSM predictive current control system is proposed, which effectively overcomes the contradiction between PI control robustness and dynamic performance. The proposed LADRC controller is of simple design with intuitive parameters without reliance on precise mathematical models. Moreover, it improves the disturbance rejection capacity and robustness of the PMSM’s predictive current control system.
2) Based on the simulation and comparative analysis results of two TV-MPCC PMSM systems based on PI and LADRC, the comprehensive performance of the rotation speed loop based on the LADRC is better than that of the PI controller in terms of its fast response speed, low startup overshoot, high disturbance rejection performance, and non-steady-state error. The LADRC achieves more satisfactory results than the PI controller in controlling speed and current.
3) The proposed control strategy can be applied in the fields of aerospace, wind power systems, new energy vehicles, home appliances, and elevator control. However, due to the addition of the LADRC controller in the proposed control strategy, the computational complexity of the sampling period is increased. Nonetheless, the parameter setting of the LADRC controller is relatively vague, and further research is required.
[1] Kang K, Song J, Kang C, et al. Real-time detection of the dynamic eccentricity in permanent-magnet synchronous motors by monitoring speed and back EMF induced in an additional winding[J].IEEE Transactions on Industrial Electronics, 2017, 64(9): 7191-7200. DOI:10.1109/TIE.2017.2686376.
[2] Hussain S, Bazaz M A. Comparative analysis of speed control strategies for vector controlled PMSM drive[C]//2016 International Conference on Computing, Communication and Automation (ICCCA). Greater Noida, India, 2016: 1314-1319. DOI:10.1109/CCAA.2016.7813950.
[3] Teng Q F, Luo W D. Model predictive torque control for PMSM systems fed by three level inverter based on compound control strategy[J]. Acta Energiae Solaris Sinica, 2020, 41(7): 173-182. (in Chinese)
[4] Lan Z Y, Wang B, Xu C, et al. A novel three-vector model predictive current control for permanent magnet synchronous motor[J]. Proceedings of the CSEE, 2018, 38(S1): 243-249. DOI:10.13334/j.0258-8013.pcsee.181100. (in Chinese)
[5] Niu F, Han Z D, Huang X Y, et al. Model predictive flux control for permanent magnet synchronous motor[J]. Electric Machines and Control, 2019, 23(3): 34-41. DOI:10.15938/j.emc.2019.03.005.(in Chinese)
[6] Zhang B, Yang L B, Liu X, et al. Model predictive torque control of PMSM system driven by three phase eight switch fault-tolerant inverter[J]. Acta Energiae Solaris Sinica, 2019, 40(4):1076-1084. (in Chinese)
[7] Xu Y P, Zhang B C, Zhou Q. Two-vector based model predictive current control for permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 222-230. DOI:10.19595/j.cnki.1000-6753.tces.160308.(in Chinese)
[8] Park S Y, Kwak S. Comparative study of three model predictive current control methods with two vectors for three-phase DC/AC VSIs[J]. IET Electric Power Applications, 2017, 11(7): 1284-1297. DOI:10.1049/iet-epa.2016.0687.
[9] Tu Z, Zhao Y, Yu J J, et al. Two-vector-based model predictive current control of permanent magnet synchronous motor[J]. Engineering Journal of Wuhan University, 2020, 53(8):721-727. DOI:10.14188/j.1671-8844. 2020-08-010. (in Chinese)
[10] Han J Q. From PID technique to active disturbances rejection control technique[J]. Control Engineering of China, 2002, 9(3): 13-18. DOI:10.14107/j.cnki.kzgc.2002.03.003. (in Chinese)
[11] Zhou K, Sun Y C, Wang X D, et al. Active disturbance rejection control of PMSM speed control system[J]. Electric Machines and Control, 2018, 22(2): 57-63. DOI:10.15938/j.emc.2018.02.008.(in Chinese)
[12] Hezzi A, Ben Elghali S, Bensalem Y, et al. ADRC-based robust and resilient control of a 5-phase PMSM driven electric vehicle[J]. Machines, 2020, 8(2): 17. DOI:10.3390/machines8020017.
[13] Zhang B, Wen X, Li K Q. Active disturbance rejection control FCS-MPC strategy based on ESO of PMSM system[J]. Journal of Measurement Science and Instrumentation, 2018, 9(2): 140-147. DOI:10.3969/j.issn.1674-8042.2018.02.007.
[14] Gao Z Q. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the 2003 American Control Conference. Denver, CO, USA, 2003: 4989-4996. DOI:10.1109/ACC.2003.1242516.
[15] Barva A V, Bhavsar P R. Design and simulation of four-leg based three-phase four-wire shunt active power filter[C]//2018 International Conference on Communication information and Computing Technology (ICCICT). Mumbai, India, 2018: 1-6. DOI:10.1109/ICCICT.2018.8325868.
[16] Ahi B,Haeri M. Linear active disturbance rejection control from the practical aspects[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(6): 2909-2919. DOI:10.1109/TMECH.2018.2871880.
[17] Zhang H, Wang Y Y, Zhang G W, et al. Research on LADRC strategy of PMSM for road-sensing simulation based on differential evolution algorithm[J]. Journal of Power Electronics, 2020, 20(4): 958-970. DOI:10.1007/s43236-020-00090-y.
[18] Cao Z C, Chu Y B. Active disturbance rejection vector control system for PMSMs[J]. Engineering Journal of Wuhan University, 2020, 53(1):67-71. DOI: 10.14188/j.1671-8844. 2020-01-011. (in Chinese)