The turbine flow sensor has widely been used for its high precision, repeatability, and dynamic performance. Researchers have done active research on turbine flow sensors to improve the accuracy of the turbine flow sensor. The main research methods include experimental research, theoretical analysis, and computational fluid dynamics (CFD) simulation with flow-field analysis. Lee et al.[1] established the mathematical model of turbine flow sensors based on the law of conservation of momentum. The “Hump” on the impeller blade surface caused by the transition from laminar to turbulent flow is consistent with the experimental results. Xu[2] developed a turbine model that considers the drag caused by tip leakage and the drag caused by fluid boundary layer separation. Nam et al.[3] conducted experimental research on the influence of temperature on the performance of turbine flow sensors. Zhang et al.[4] used particle image velocimetry measurement technology to obtain the velocity distribution information of the turbine flow sensor blade inlet and obtained a prediction result closer to the real response of the turbine flow sensor. Sun et al.[5] proposed a multi-parameter quantitative optimization method for the impeller of a liquid turbine flow sensor to reduce the influence of sensor characteristics on the viscosity change of the measured liquid. By investigating the effect of pulsation amplitude on the turbine flow sensors, Lee et al.[6] reduced the measurement error. Tonkonogij et al.[7] established a new semi-experimental method for predicting the response and dynamic error of turbine flow sensors in transient flow regimes with varying flow rates. 
et al.[8] studied the acceleration and deceleration performance of turbine flow sensors under transient conditions. The results showed that the turbine flow sensor has an excellent dynamic response to accelerating flow. López-González et al.[9] established a dynamic characteristic model of a gas flowmeter according to the law of conservation of mass, linear momentum, energy, and angular momentum.
The potential physical mechanism can be better understood using the CFD technology, and the velocity field and phase distribution with a high spatial-temporal resolution for engineering flow applications can be provided[10]. Wang et al.[11] studied the method of predicting the measurement performance of the tangential turbine flow sensor using CFD simulation. Guo et al.[12] used CFD software to simulate the internal flow field of the sensor and explained the mechanism of the influence of fluid viscosity change on measurement performance. Sun et al.[13] used CFD numerical simulation to analyze the effect of different structural parameters of the front deflector on the performance of the turbine flow sensor. Further, Wu et al.[14] used the dynamic grid method, sliding grid method, and dynamic coordinate system method to simulate the separated transient incompressible flow in the starting process of the cross blade. The results show that the sliding grid method has higher computational efficiency and accuracy.
Currently, the standard simulation method is not suitable for studying the dynamic performance of turbine flow sensors. In this research, the 6-DOF simulation method is adopted, and a UDF is used to limit the degree of freedom so that the impeller can only rotate in response to the fluid. The position of the impeller at each moment is recorded during the simulation process to obtain information on the impeller speed. The method is verified by steady and unsteady experiments; it simulates the flow of the turbine flow sensor in pulsating and step flow.
1 Theoretical Basis
1.1 Working principle of the turbine flow sensor
The impeller is the core component of the turbine flow sensor. It starts to rotate under the driving torque of the fluid and is also influenced by various resistances. Fig.1 depicts the torques on the impeller of the turbine flow sensor. In Fig.1, Td is the impeller driving torque; Tb is the journal bearing retarding torque; Th is the impeller hub retarding torque due to fluid drag; Tm is the resistance torque of the magnetoelectric signal detector; Tt is the blade tip clearance drag torque; Tw is the hub disks retarding torque due to fluid drag.
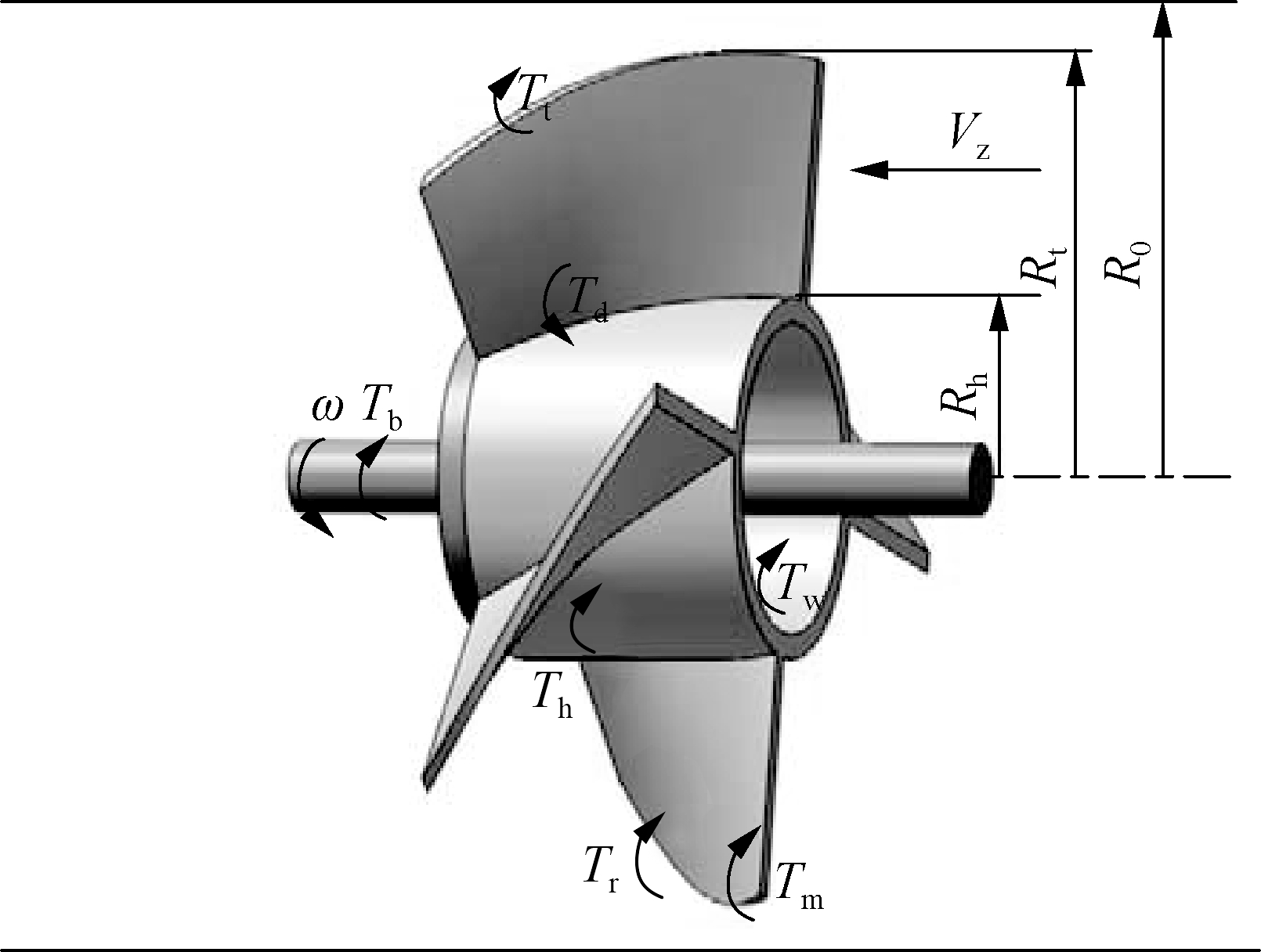
Fig.1 Schematic of torques on the impeller of the turbine flow sensor
According to Newton’s First Law of Motion, the impeller’s equation of motion is as follows:
(1)
where J is the rotational inertia of the impeller; ω is the rotational angular velocities of the impeller.
1.2 6-DOF model
The 6-DOF equation of motion is used to simulate the movement state of the turbine flow sensor impeller. Two coordinate systems are established to facilitate the calculation: the body coordinate system where the impeller is located and the inertial coordinate system connected to the impeller. According to Newton’s laws of motion, the equation of motion of a rigid body in the inertial system is given as
(2)
where m is the mass of the rigid body; v is the translation speed of the rigid body; F is the combined external force of the rigid body.
In this system, the rigid body rotation equation is given. The momentum torque of the impeller is defined as
L=Iω
(3)
where I is the inertia tensor.
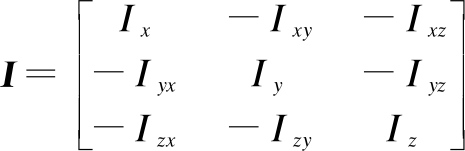
(4)
According to the theorem of momentum:
=T
(5)
Eqs. (2) to (5) are the mathematical models of the 6-DOF method.
Then
I
+ω×(Iω)=T
(6)
where ω is the rotational angular velocity of the rigid body in the system; T is the resultant torque acting on the blades in the system, including driving torque and resistance torque.
In the simulation, the mass, moment of inertia, and direction of rotation of the impeller are governed by UDF to control the six degrees of freedom of the impeller during movement. The rotational angular velocity of the impeller and the fluid velocity distribution are then calculated using superposition.
2 Simulation Method Based on 6-DOF
2.1 Simulation method
In this study, the passive method was used to simulate the internal flow field of the turbine flow sensor based on the working principle of the turbine flow sensor and the 6-DOF model. A UDF program was written to control the six degrees of freedom of the impeller, allowing the impeller to only rotate in the direction of the fluid while remaining fixed in other directions. The rotational inertia of the impeller was obtained using the SolidWorks software and then loaded into a target program so that the impeller could adjust its angular acceleration in response to the force impact by the fluid. During the simulation process, the force and position information of the impeller can be monitored, and the change of the impeller speed and force information can be observed in real-time.
Fig.2(a) depicts the flowchart of the impeller active rotation simulation method, and the flow chart of the impeller passive rotation simulation method studied in this research is shown in Fig.2(b).
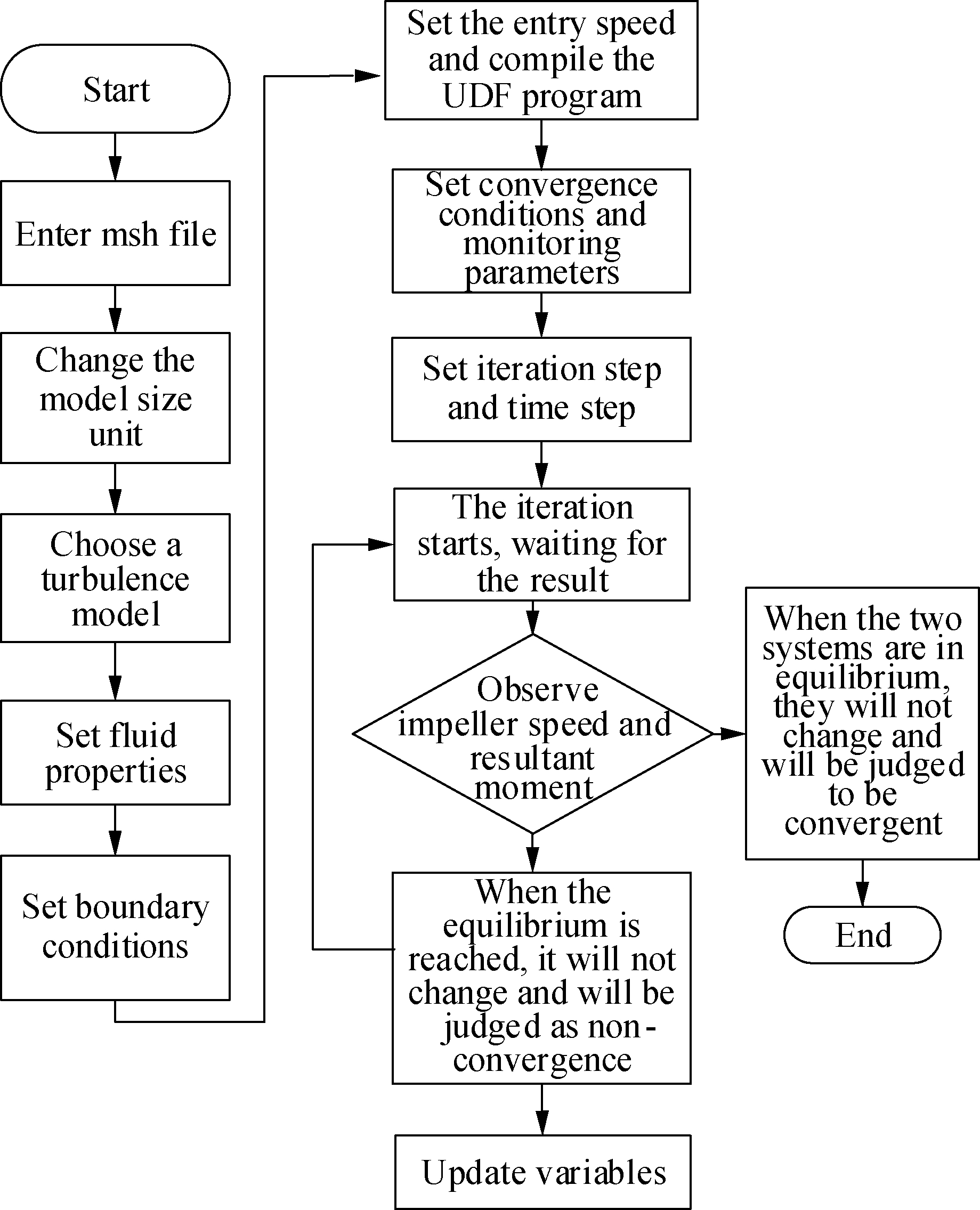
(a)
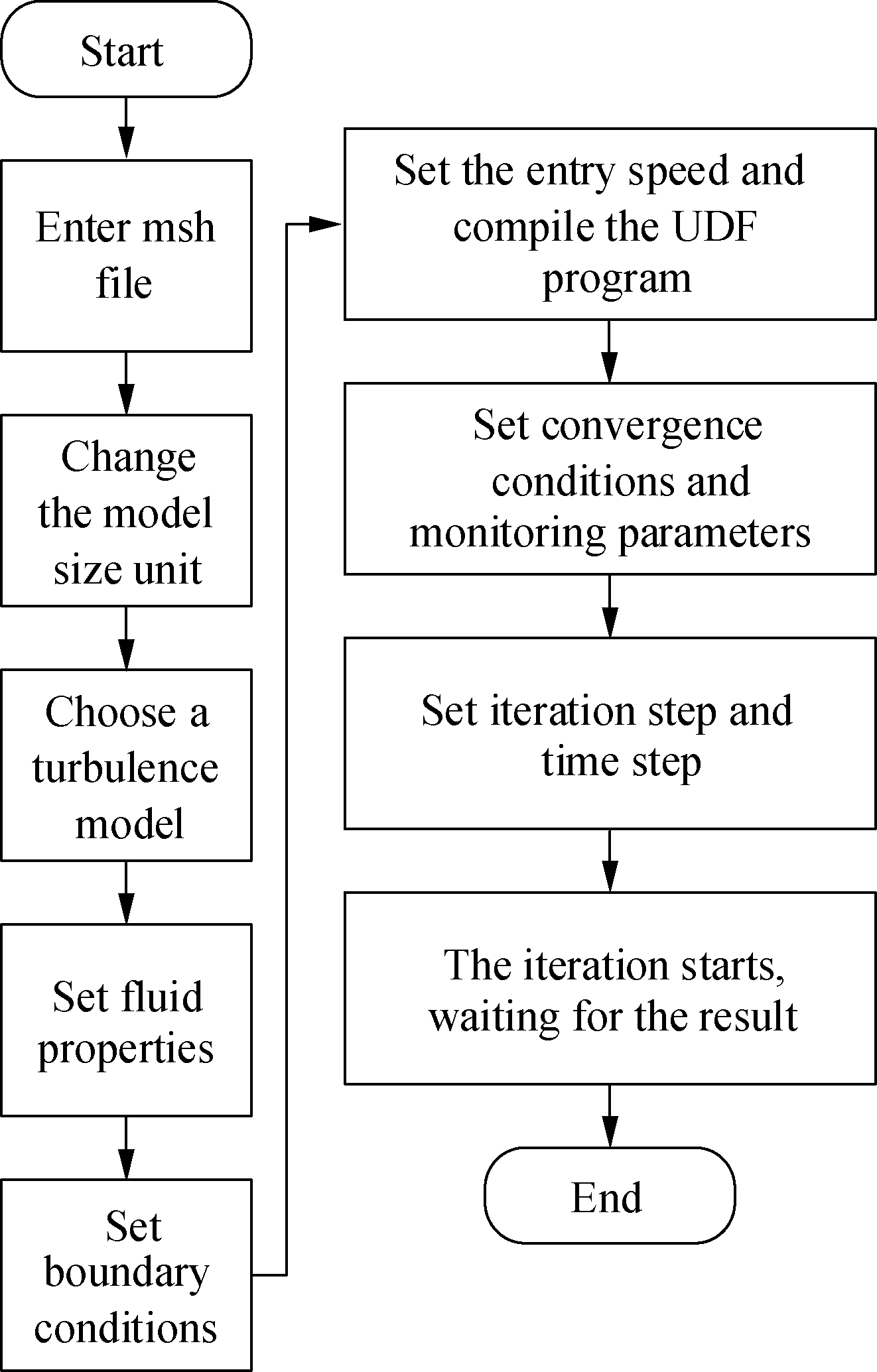
(b)Fig.2 Comparison of simulation flow chart. (a) Impeller active rotation simulation method; (b) Impeller passive rotation simulation method
When the active simulation method is used to simulate the inner flow field of the turbine flow sensor, the impeller rotational speed must be set manually according to the real-time torques observed until the torques reach a balanced state. In order to obtain the appropriate impeller speed, the operator needs to constantly monitor changes in torque and adjust the speed of the impeller all the time. The operator must judge the equilibrium state of the torque, which introduces significant subjective influences.
After the inlet velocity of the turbine flow meter is set using the passive simulation method proposed in this study, the rotational speed of the impeller can be automatically adjusted based on the force acting on the impeller and Newton’s law of motion. The simulation result depends on the fluid nature, flow rate, the diameter of the sensor, the structure and material of the impeller, and so on, with no human intervention. Thus, the working process of the passive simulation method is more scientific.
2.2 Steady-state simulation
The DN25 liquid turbine flow sensor manufactured by Jinxin Machinery Manufacturing Co., Ltd. was selected as the research prototype in this study. Fig.3 presents the internal structure of the turbine flow sensor.
Fig.3 Internal structure of the turbine flow sensor
2.2.1 Establishment of the simulation model
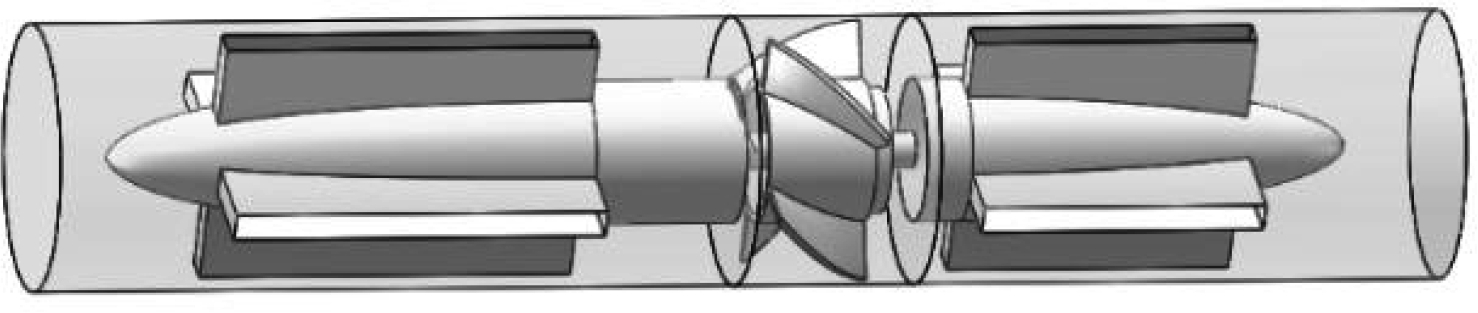
An accurate simulation model was built in this study to precisely predict the performance of the turbine flow sensor. First, the key dimensions of the physical sensor were measured. Next, the structure of the turbine flow sensor was drawn using SolidWorks software based on the measurement results as shown in Fig.4(a).
(a)
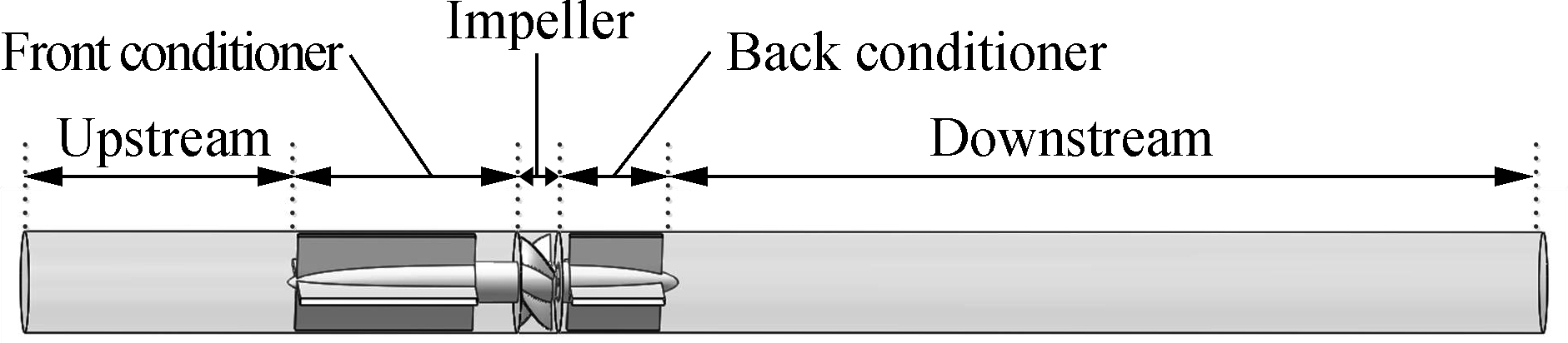
(b)Fig.4 Three-dimensional structure diagram of the turbine flow sensor. (a) Structure diagram; (b) Simulation model
The turbine flow sensor structure was then imported into the Gambit software. In order to reach a fully developed flow state, the 5D and 10D straight pipe sections (D is the inner diameter of the pipe) were added to the upstream and downstream of the sensor, respectively. Fig.4(b) depicts the three-dimensional flow field simulation model of the turbine flow sensor.
2.2.2 Meshing
The meshing technology of Gambit is used to mesh the flow field, which is divided into ten small sections, as shown in Fig.5. The impeller’s section is defined as the rotating section, and the remaining regions are set as stationary parts. Two pairs of interfaces join the rotational and stationary regions. Unstructured grids perform better in dynamic grid sections with complex structures, such as the rotating sections, whereas structured grids are used in sections with simpler structures. Tab.1 presents the grid number and type of each part. To accurately and quickly predict the performance of the turbine flow sensor, three different grid densities are used to find the best matching grid, ensuring that our finding is independent of the computational grid. The same mesh generation strategy is used in all cases. The EquiSize Skew and the AngleSize Skew of all grids are less than 0.80. Tab.2 shows the grid independence analysis results of impeller speed at 4 m3/h volumetric flow rate. Finally, a 0.54×106 grid number simulation model is selected for the following study.
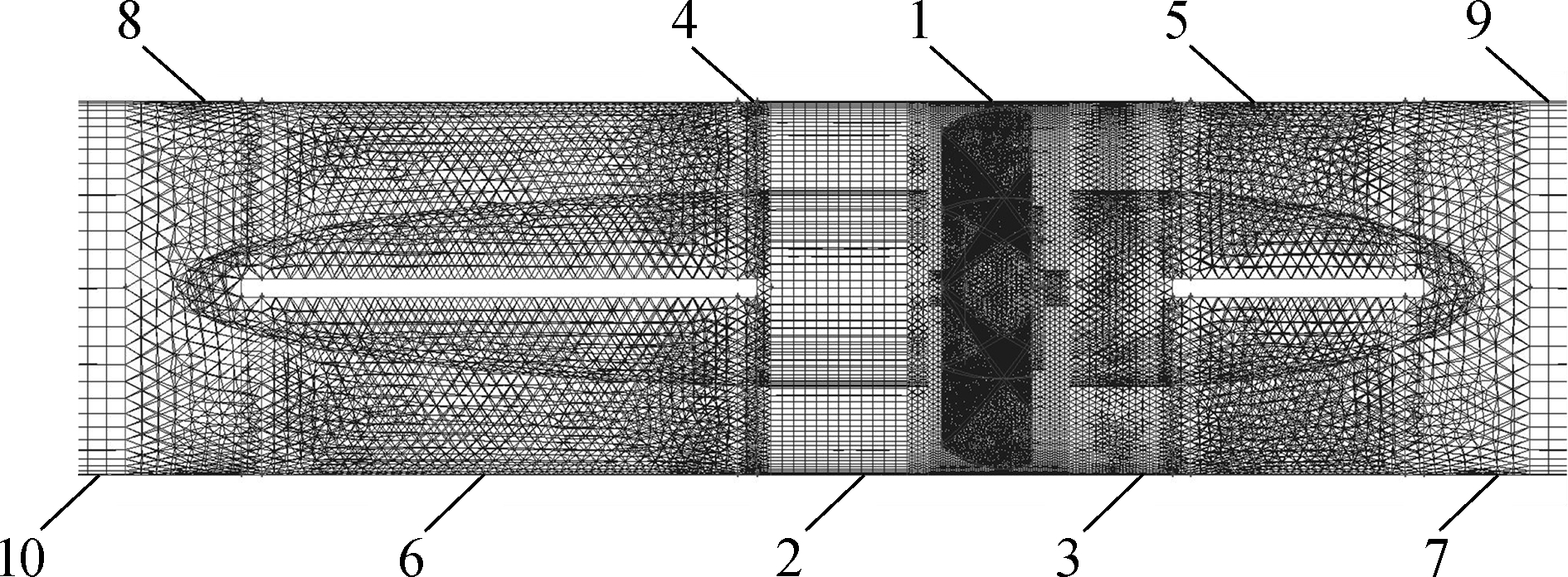
Fig.5 Schematic diagram of the mesh of the turbine flow sensor 3D simulation flow field
Tab.1 Grid number and type of each part
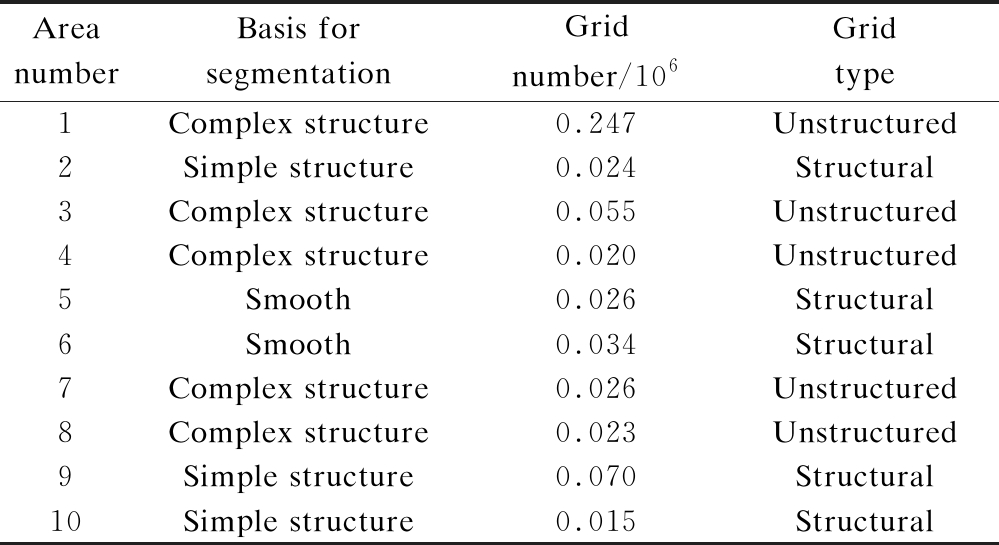
AreanumberBasis forsegmentationGridnumber/106Gridtype1Complex structure0.247Unstructured2Simple structure0.024Structural3Complex structure0.055Unstructured4Complex structure0.020Unstructured5Smooth0.026Structural6Smooth0.034Structural7Complex structure0.026Unstructured8Complex structure0.023Unstructured9Simple structure0.070Structural10Simple structure0.015Structural
Tab.2 Grid independence results in terms of rational speed for 4 m3/h flow rate
Grid cells number/1060.320.540.78Calculated rotational speed/(rad·s-1)357.69368.87369.35
The medium is water at 20 ℃. The simulation results are the closest to the experimental results when the grid number is 0.54×106. The schematic diagram of grid division is shown in Fig.5.
2.2.3 Initial conditions and boundary conditions
Water under standard conditions (20 ℃, 101.325 kPa) was used as the fluid medium. According to the “Turbine Flowmeter”[15] verification regulation, flow rates of 1.0, 2.5, 4.0, 7.0, and 10.0 m3/h were selected. Tab.3 depicts the corresponding inlet velocity and turbulence intensity. The simulation was carried out under a non-steady-state. A dynamic mesh and a 6-DOF model were applied to the impeller part. The time step is calculated with reference to the experimental data, and the corresponding time step for each flow rate is shown in Tab.3. One rotation of the impeller requires 180 steps. To ensure that the impeller rotates smoothly, the number of simulation steps is 2 000.
Tab.3 Setting of initial conditions and boundary conditions
Flow rate/(m3·h-1)Inlet velocity/(m·s-1)Turbulenceintensity/%Timestep/μs1.00.5664.855188.02.51.4054.32575.44.02.2744.07347.87.03.8843.80928.010.05.6623.63419.0
2.3 Selection of turbulence model
Different turbulence models must be adopted for different flow fields, which have a great effect on the calculation of flow properties, velocity changes, pressure changes, and other series of simulation results. Therefore, it is necessary to select an appropriate turbulence model according to the characteristics of the flow field. To select a suitable turbulence model, the simulation was carried out using different turbulence models. The simulation results are compared with the experimental data, and the results are shown in Fig.6. It can be seen from Fig.6 that the simulation results using the Reynolds stress (S-BLS) turbulence model are closer to the experimental results. Therefore, the Reynolds Stress (S-BLS) turbulence model is selected in the later simulation process.
Fig.6 Comparison of the results using different turbulence models with experimental results
2.4 Data processing
The position information is recorded during the simulation. The angular displacement of the impeller in Δθi is calculated at each step. The rotation speed ωi of the impeller in each step can be calculated by
(7)
where Δt is the time step.
Fig.7 presents the torque diagram of the turbine flow sensor at a 2.5 m3/h flow rate. According to the data processing steps, the impeller speed is shown in Fig.8.
(a)
(b)
(c)
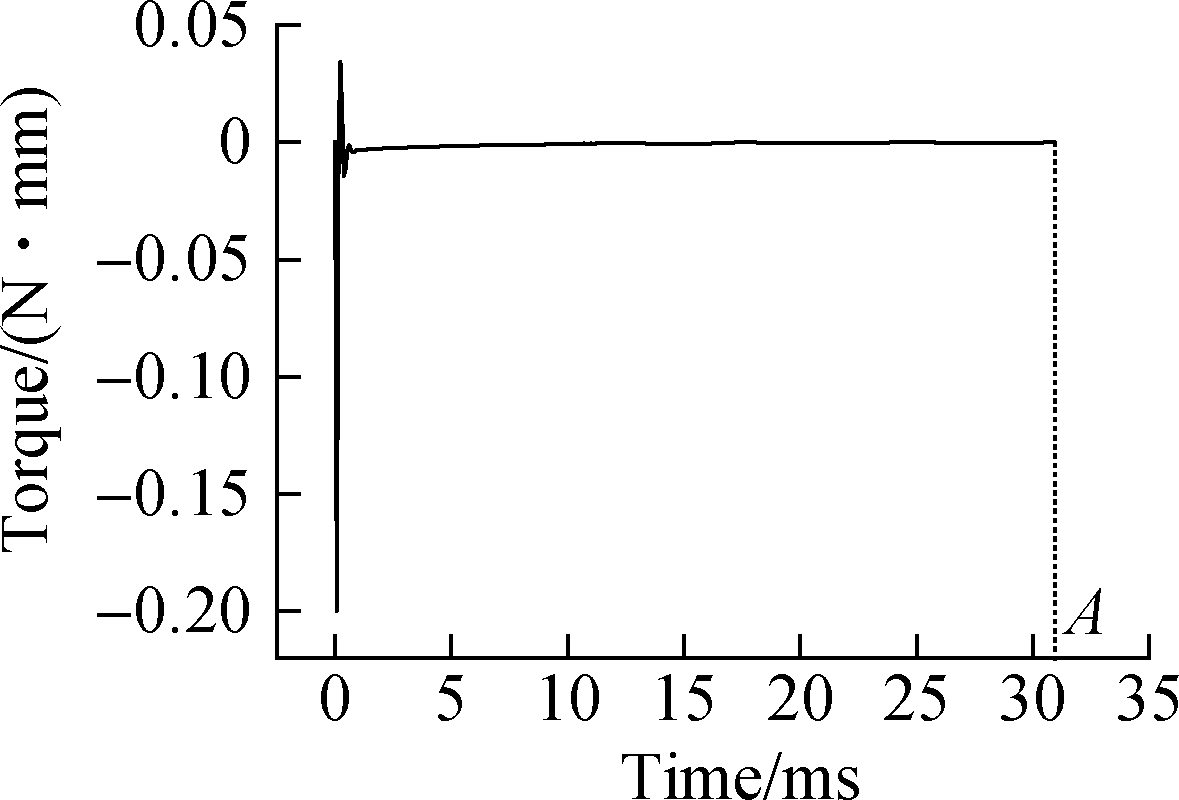
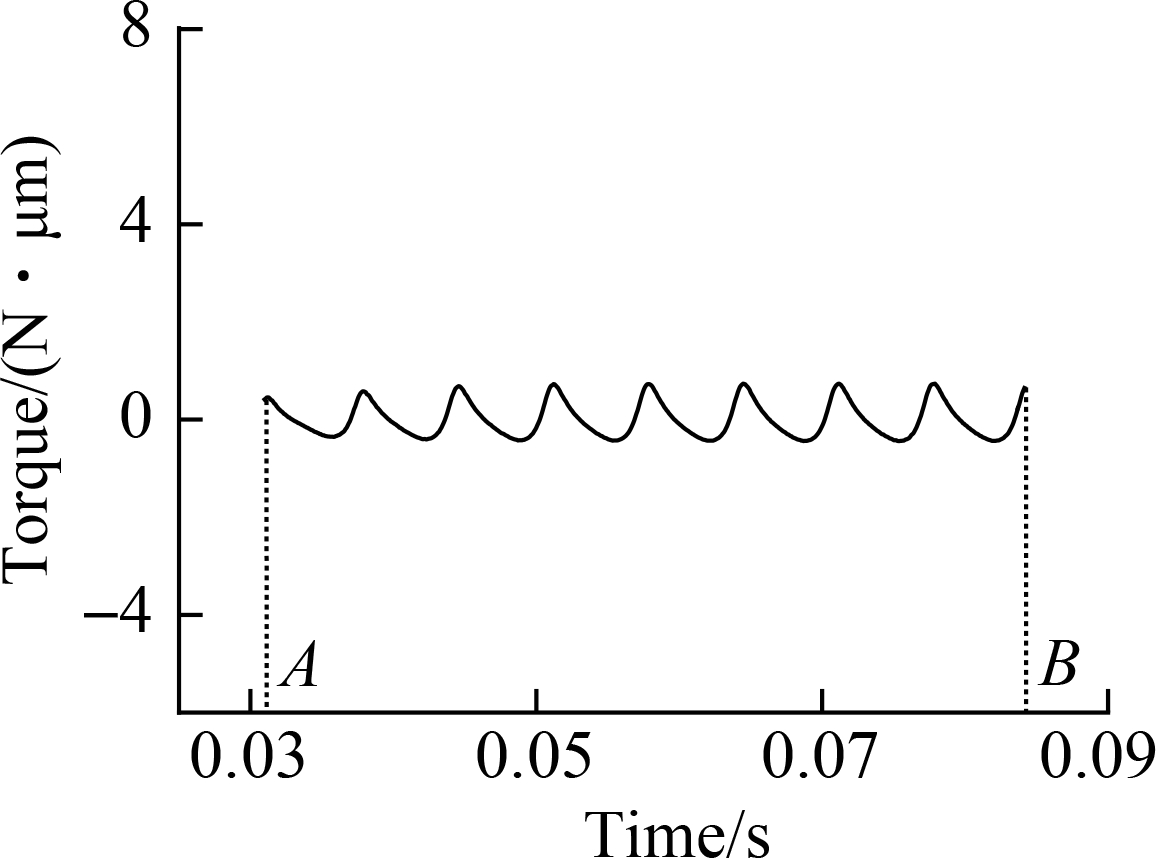
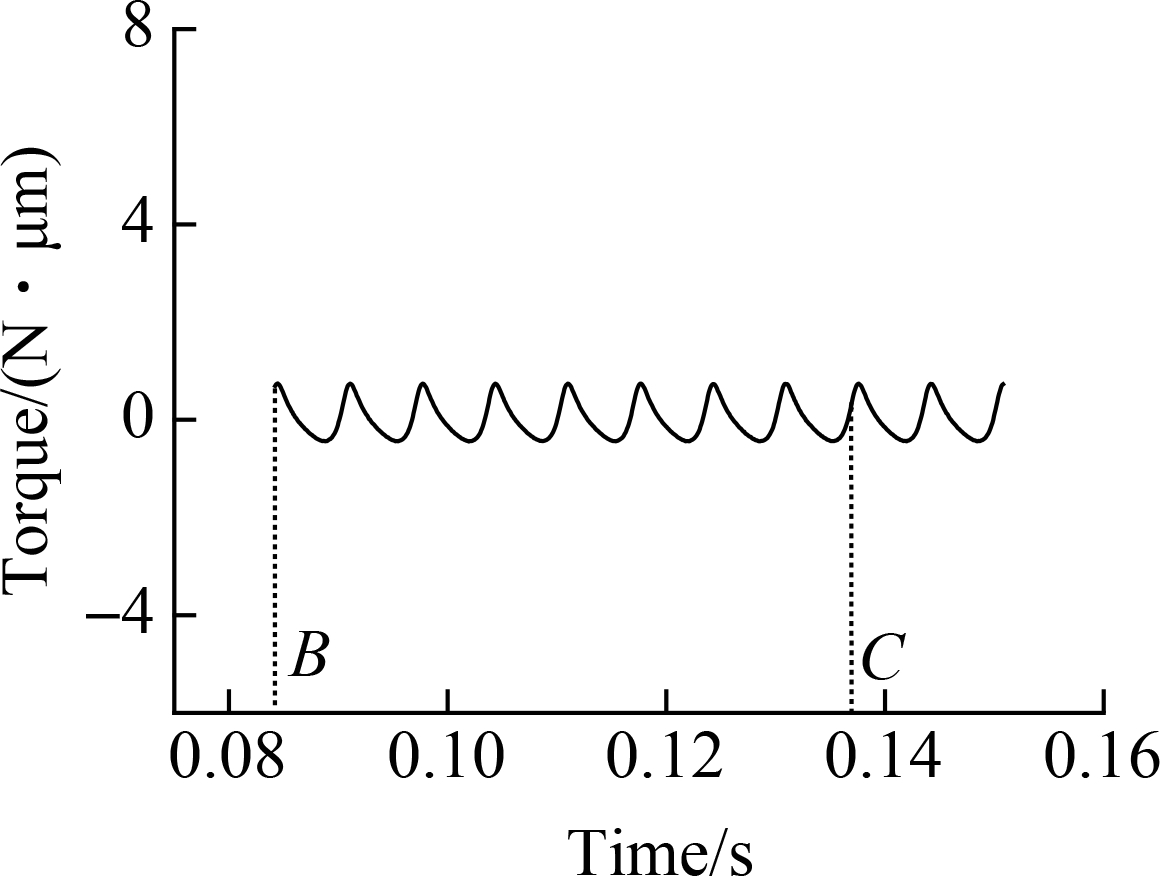
Fig.7 Impeller torque versus time diagram. (a) Time for the impeller to rotate one circle (360°); (b) Time for the impeller to rotate three circles; (c) Time for the impeller to rotate five circles
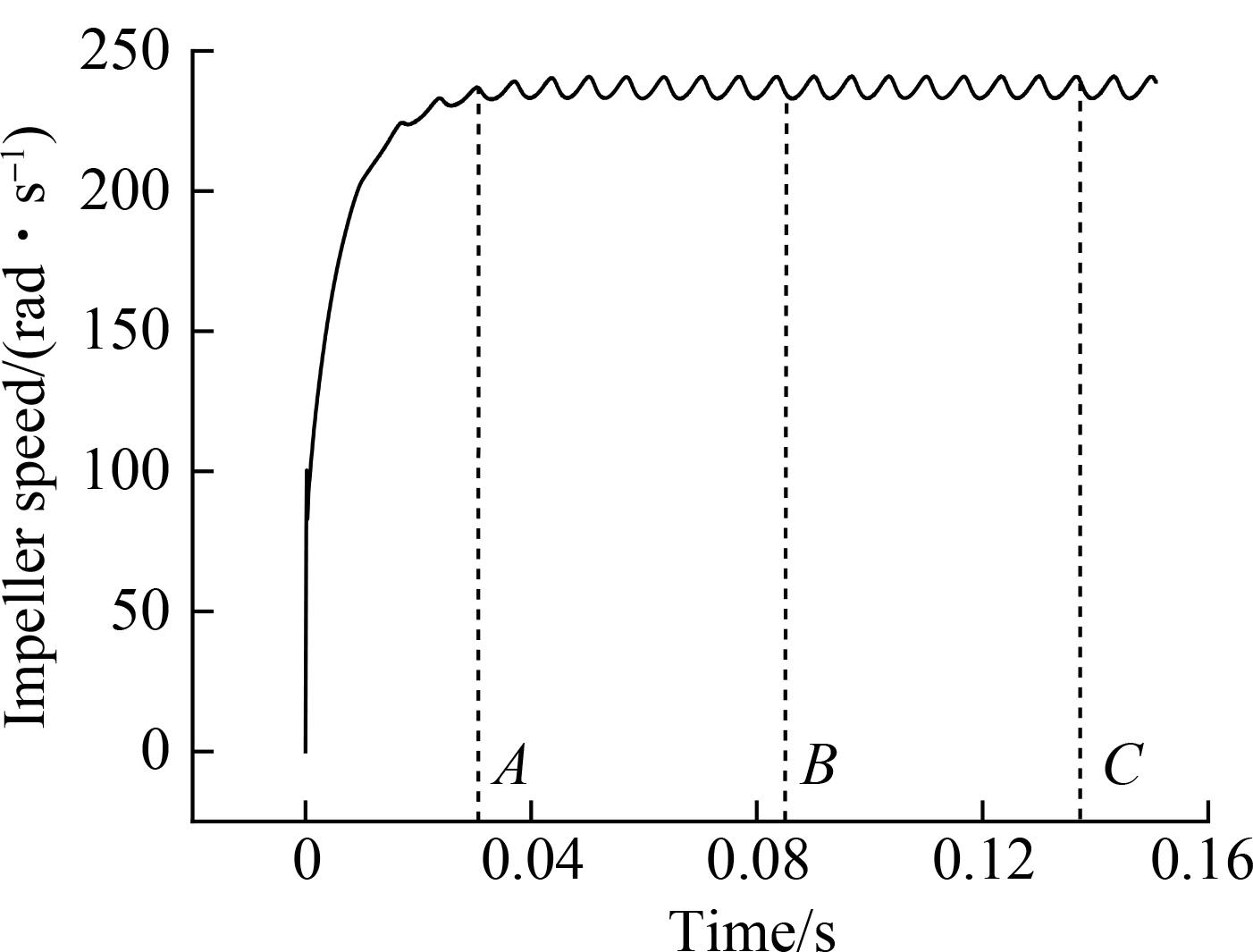
Fig.8 Impeller speed change chart with time
In Fig.7, point A is the time for the impeller to rotate one circle (360°). Point B is the time for the impeller to rotate three circles, and point C is the time for the impeller to rotate five circles.
When the time point A is reached, the impeller rotates for a circle, and the speed of the impeller accelerates obviously with the torque. When time point B is reached, the speed of the impeller rises slowly with the torque until it reaches a stable state. After time point B, the speed of the impeller reaches a dynamic constant state with the torque.
When the impeller speed presents a stable periodic change, it is considered that the impeller has reached a stable state of rotation. This change is mainly caused by the angle of fluid impacting the blade. The average rotation speed of the impeller for one stable circular revolution is used as the corresponding rotation speed of the impeller at this flow rate.
(8)
where n is the number of simulation steps in a cycle.
The impeller rotation frequency f and the meter factor KS of the turbine flow sensor are calculated by
(9)
(10)
where N is the number of impellers.
3 Verification of Passive Simulation Method in the Steady Flow
3.1 Steady flow experiment
To verify the reliability of the above simulation method, the turbine flow sensor was tested in the experimental facility, and the experimental results were compared with the simulation results.
3.1.1 Experimental facility
The experiment was carried out on the water flow standard facility in the Flow Laboratory of Tianjin University. Fig.9 presents the structure of the facility. The static weighing method was used in the experiment, and the overall uncertainty was better than 0.05% (k=2). Water at normal temperature (20 ℃) was used as the fluid medium. The DN25 turbine flow sensor was selected as the experimental prototype (the same prototype as the one measured during simulation).
3.1.2 Experimental data processing methods and results
Each flow rate was measured three times during the experiment, and the meter factor was calculated separately. The average meter factor 
linear error EL, and repeatability error Er of the turbine flow sensor in the entire flow range were calculated according to equations.
The meter factor of the j-th detection at the i-th flow rates is as follows:
(11)
The average meter factor for each flow rate becomes:
(12)
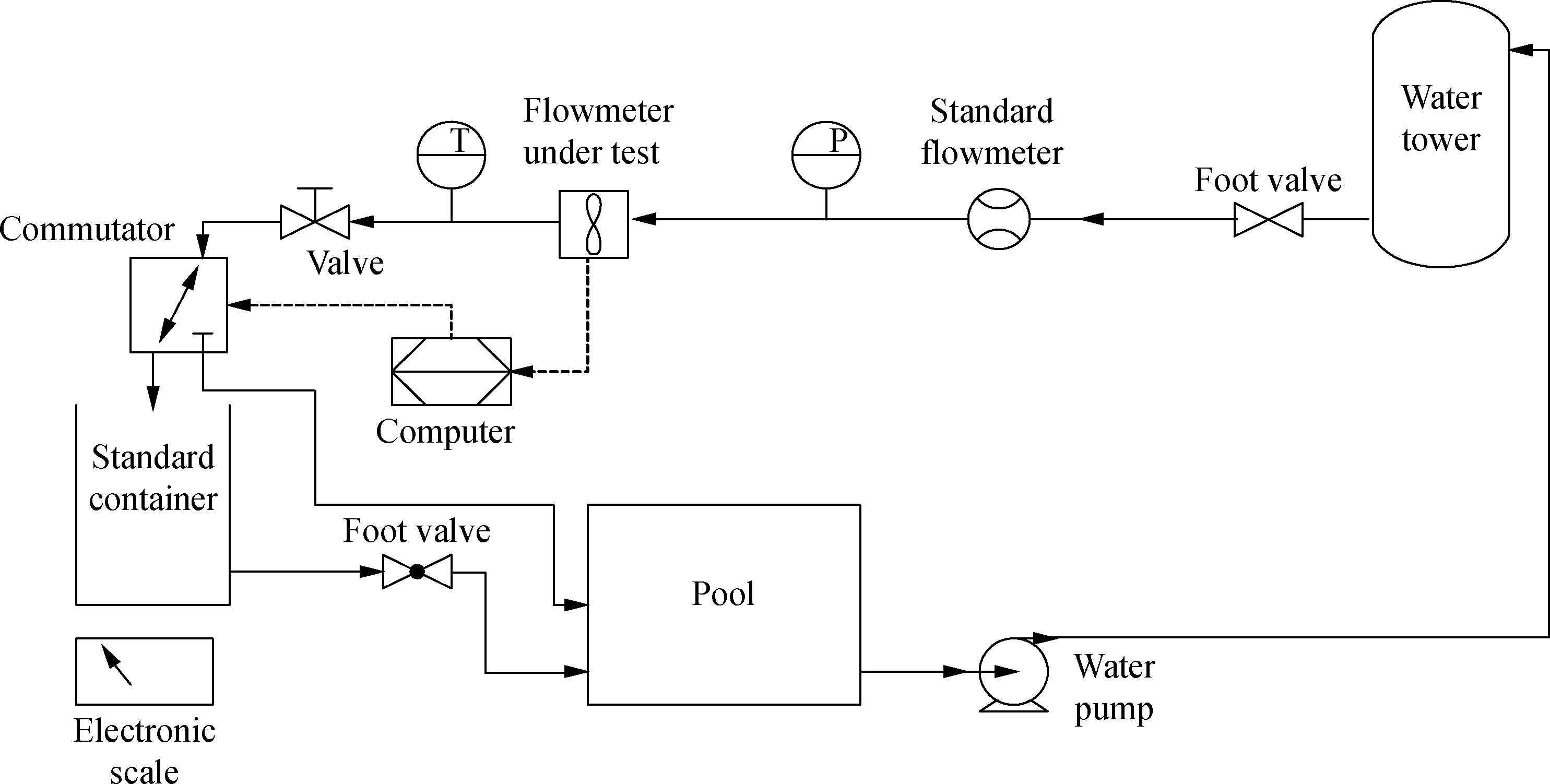
Fig.9 Schematic diagram of the facility
The average meter factor of turbine flow sensor:
(13)
The linearity error is
(14)
The error is
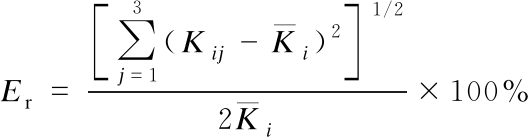
(15)
where Kij is the meter factor of a single measurement; Nij is the number of pulses during a single test; Mij is the electronic scale reading during a single test; ρ is the density of the measured medium.
Tab.4 depicts the experimental results obtained according to the above data processing method. To compare the difference between the simulation data and the experimental data, the deviation is defined as
(16)
where KiS is the simulation meter factor of the i-th flow rate.
Tab.4 Comparison of experimental data and simulation results
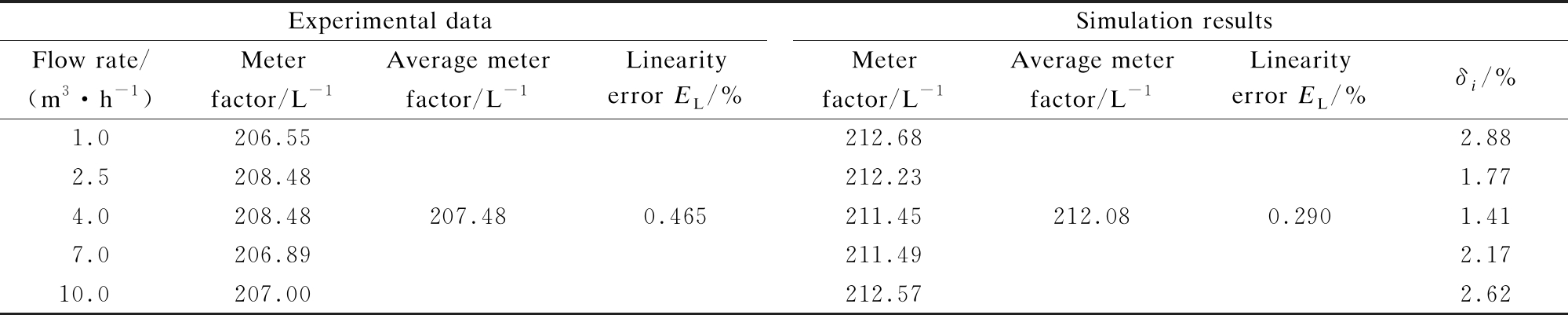
Experimental dataSimulation resultsFlow rate/(m3·h-1)Meterfactor/L-1Average meterfactor/L-1Linearityerror EL/%Meterfactor/L-1Average meterfactor/L-1Linearityerror EL/%δi/%1.0206.552.5208.484.0208.487.0206.8910.0207.00207.480.465212.68212.23211.45211.49212.57212.080.2902.881.771.412.172.62
The data in Tab.4 shows that: 1) The meter factor corresponding to different flow rates is variable. The simulation meter factor of each flow rate fluctuates around the average meter factor as the inlet flow rate increases. The trend is consistent with the experimental results. 2) The simulated data and the experimental data are close. The maximum deviation is 2.88% compared with the experimental data. The reason for the deviation is that the simulation ignores the influence of the friction torque between the shaft and the bearing as well as the electromagnetic drag torque of the signal detector acting on the impeller blades. Since the deviation is within an acceptable range, this simulation method can be considered reliable, and the performance of the turbine flow sensor can be predicted using the above CFD simulation method.
3.2 Comparison of different simulation methods
The simulation method in this study is compared with other simulation methods to illustrate its advantages.Tab.5 presents the description of each simulation method. The active simulation method sets the initial value of impeller speed based on test and experience and requires manual adjustment of impeller speed according to synthetic torque. When the synthetic torque approaches zero, the corresponding impeller speed is considered the steady operating speed of the impeller. Only the steady-state flow field data can be obtained, but not the motion state of the impeller under an instantaneous flow field. The passive simulation method sets the parameters of inlet speed change and the 6-DOF model in the UDF program. During the simulation, the sum of the torques on the impeller is calculated, and the angular speed of rotation is automatically adjusted according to the 6-DOF model. The impeller is detected dynamically in real-time, and its motion state is obtained under an instantaneous flow field.
Tab.5 Description of participating and comparing methods
MethodMethod descriptionMain featureAdvantagesMethod 1(this paper)6 DOF+dynamic meshThe passive simulation method is closer to the real working state of the impel-ler.The impeller speed can be calculated in real-time, and the inlet speed varying with time can be set to obtain the dynamic performance of the tur-bine flowmeter.Method 2[16]Method 3[17]Method 4[18]Method 5[11]Method 6[19]Sliding grid based on a torque balance equationThe impeller actively rotates, and the rotation state of the impeller is simula-ted using an unsteady state method.Steady-state simulation based on a torque balance equationThe impeller actively rotates, and the steady-state method is used to simulate the rotation state of the impeller.The setting is simple and easy to operate.
The flow rates are normalized to facilitate the comparison of the simulation results of different diameter turbine flow sensors in different flow ranges.
(17)
where Q is the relative flow rate; qvi is the simulated flow rate; qvmax is the maximum flow rate.
Fig.10 compares the deviation between the calculated and experimental results when using different simulation methods. The curve in Fig.10 shows that the variation between the simulation result in this study and the experimental results is the smallest, and the trends of the two are the closest.
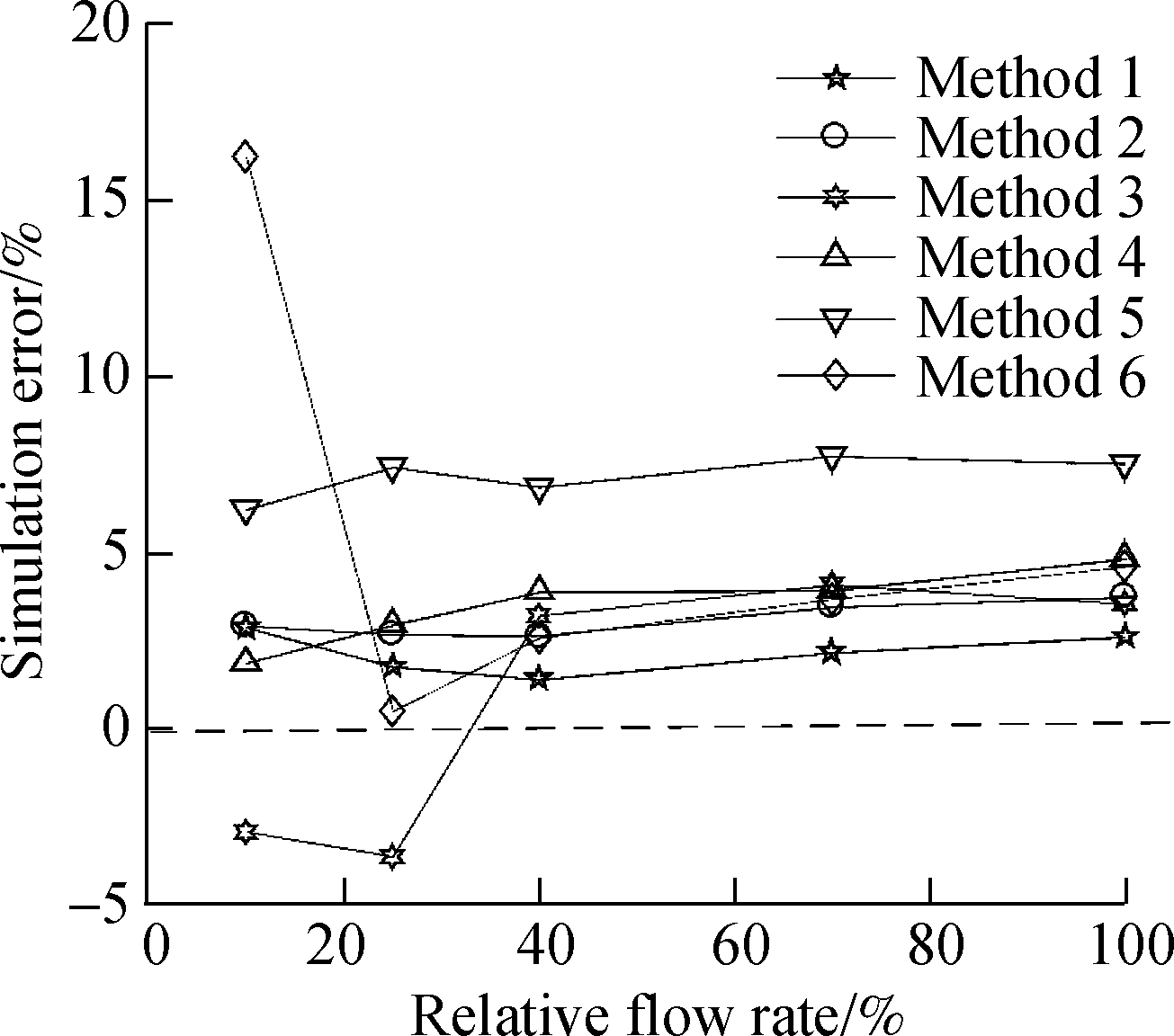
Fig.10 Comparison of the same method and experimental results
4 Application of the Passive Simulation Method in Unsteady Flow
4.1 Reliability verification of the simulation method
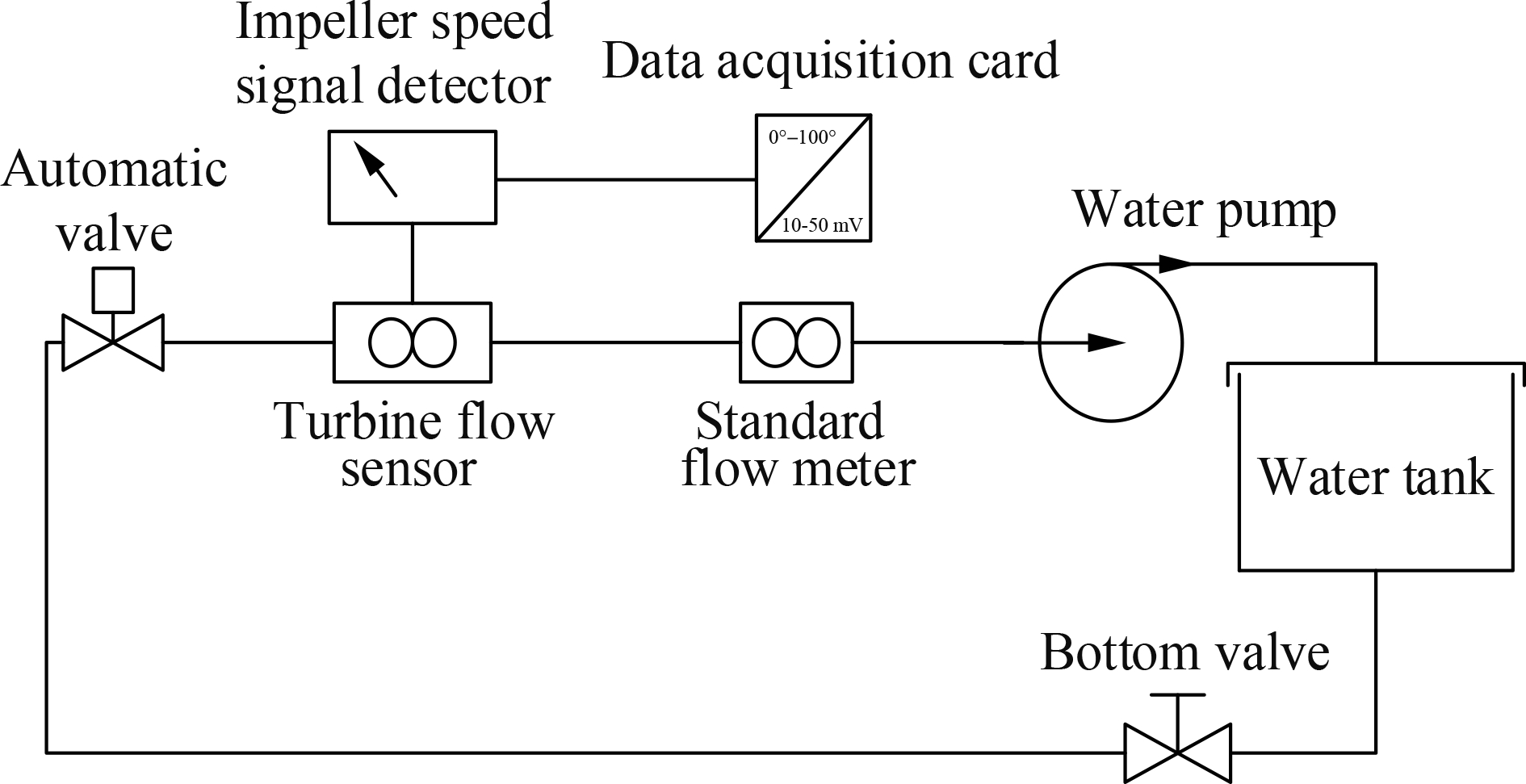
To verify the reliability of the passive simulation method in the unsteady flow, unsteady flow experiments and CFD simulations were carried out. Fig.11(a) depicts a schematic view of the experiment facility.
In this experiment, the steady flow is generated by a standard facility, and then the unsteady flow is obtained by opening and closing the automatic valve. Simultaneously, the data acquisition card receives the frequency signal of the impeller and transmits it to the upper device. The dynamic performance of the turbine flow sensor is obtained. Fig.11(b) shows the main devices of the experiment.
(a)
(b)Fig.11 Experimental diagram. (a) Schematic representation of the experiment facility; (b) Experimental facility diagram
To reduce the error caused by the signal delay, the original signal from the impeller speed signal detector is used without being converted to the standard pulse signal. The output signal of the turbine flow sensor is shown in Fig.12.
The rotational frequency f of the impeller is calculated using the received signal of the turbine flow sensor. According to the principle of the turbine flow sensor, the instantaneous flow rate is calculated by Eq.(10) when the frequency f and meter factor K are known.
Fig.12 The signal of the turbine flow sensor collected
During the experiment, the flow rate was stabilized at the required nominal value q0 first, then the automatic valve was closed, and the impeller of the turbine flow sensor reached a standstill. The automatic valve was reopened about 30 s later. This way, the accelerating flow rate is obtained using the unsteady flow rate. The experimental data are fitted to get the functional equation of flow rates with time, and the functional equation is used as the entrance boundary condition for simulation by the UDF function. Finally, the simulation results are compared with the experimental data, and the compared results are shown in Fig.13.
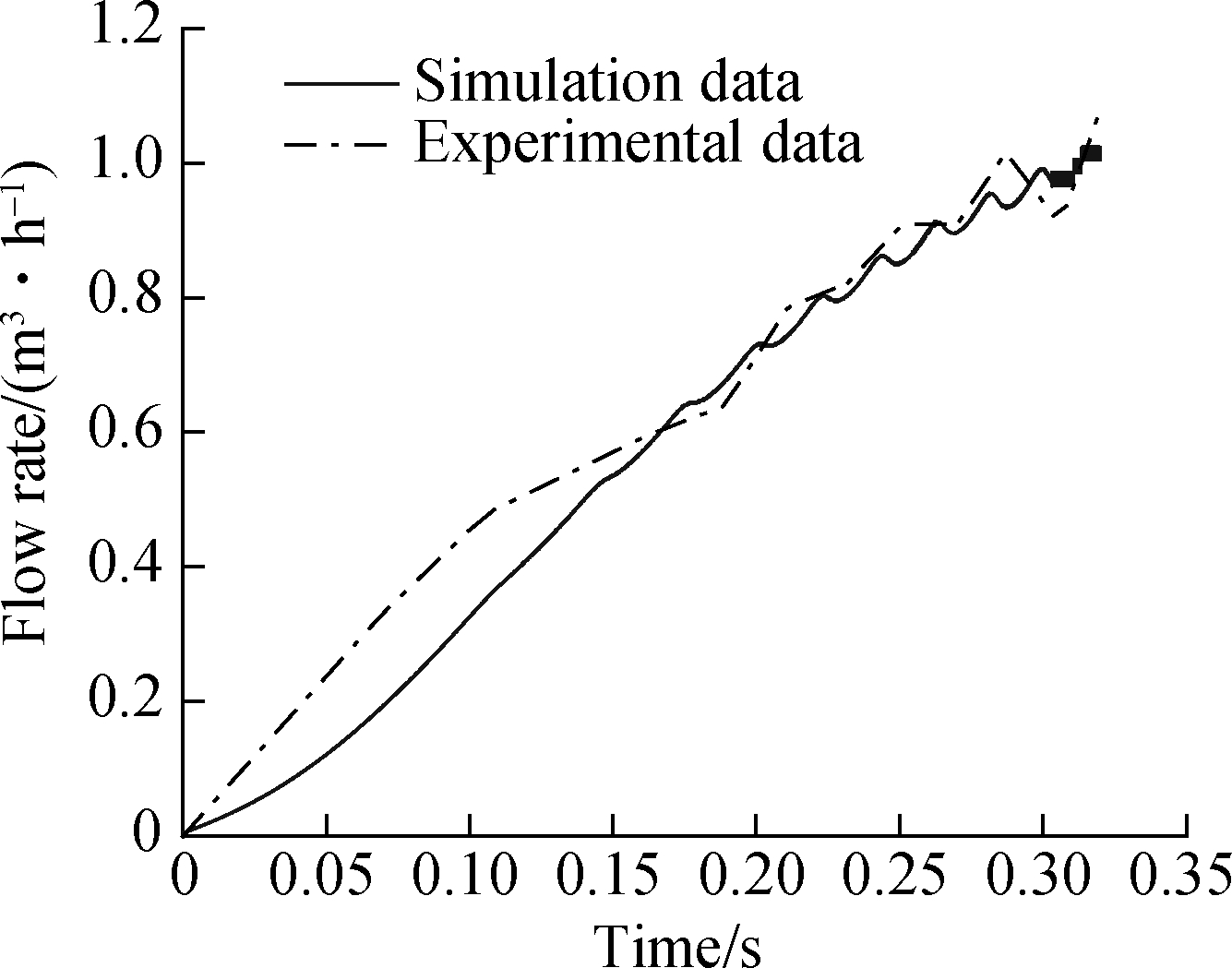
Fig.13 Comparison of experimental data and simulation results
The flow rate variation in the simulation results follows the same trend as the flow rate variation in the experimental process. This means that CFD simulation can accurately simulate the dynamic variation in the actual flow. Thus, the simulation method is suitable for dynamic performance simulation of the turbine flow sensor. The dynamic characteristics of turbine flow sensors in pulsating flow and step flow are studied by flow field simulation below.
4.2 Simulation of turbine flow sensor measuring pulsating flow
Three turbine flow sensors of varying diameters are selected for simulation, along with three flow rates within the range of each sensor. The expression of sinusoidal pulsating flow is
(18)
First, the flow rate is stabilized q0, the sinusoidal pulsating flow is generated at t0, and the flow field is simulated for two periods, where fi is the pulsating frequency and qA is the pulsating amplitude. According to the flow rate of the tested flow sensor, the inlet velocity of the tested flow sensor is calculated as the simulated boundary condition. In the simulation process, the UDF program containing the following equation is loaded to set the inlet velocity.
The UDF program is loaded before initialization to perform the unsteady state simulation. Tab.6 shows the specific working conditions, where two cycles are simulated for each working condition.
The inlet flow rate and impeller speed are obtained, as shown in Fig.14. The impeller speed changes periodically due to the periodic changes of the force acting on the impeller during the rotation, resulting in data fluctuation. There is a phase difference between the inlet flow rate and the impeller frequency. Thus, the dynamic performance of the turbine flow sensor can be analyzed by amplitude-frequency and phase-frequency characteristics.
Tab.6 Values of q0, qA, and fi
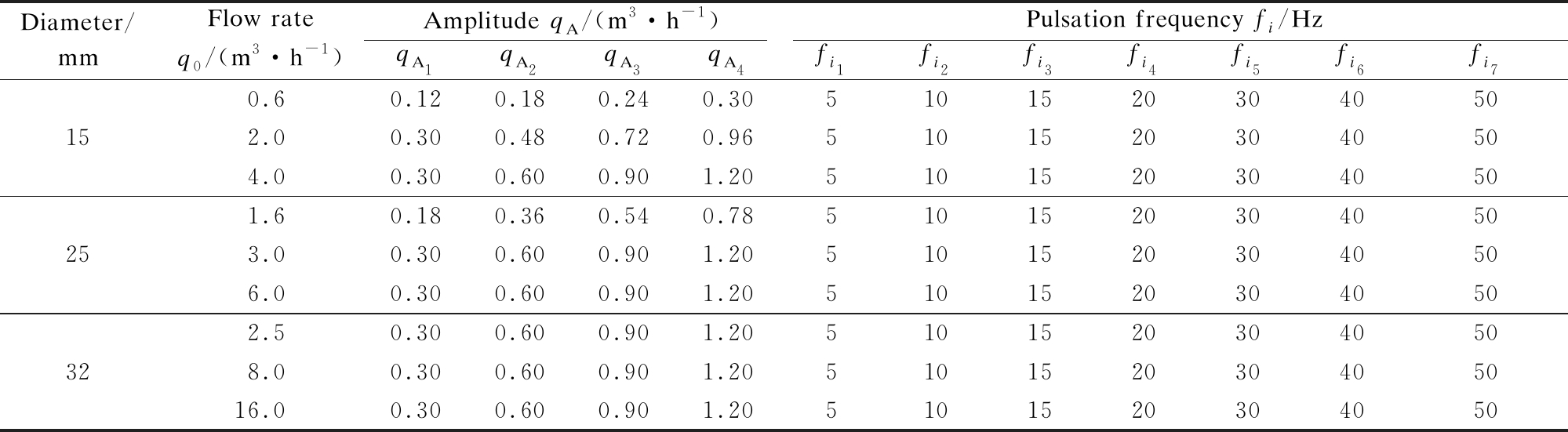
Diameter/mmFlow rateq0/(m3·h-1)Amplitude qA/(m3·h-1)Pulsation frequency fi/HzqA1qA2qA3qA4fi1fi2fi3fi4fi5fi6fi7150.60.120.180.240.3051015203040502.00.300.480.720.9651015203040504.00.300.600.901.205101520304050251.60.180.360.540.7851015203040503.00.300.600.901.2051015203040506.00.300.600.901.205101520304050322.50.300.600.901.2051015203040508.00.300.600.901.20510152030405016.00.300.600.901.205101520304050
4.3 Simulation of turbine flow sensor measuring step flow
In this research, three turbine flow sensors with different diameters were selected for simulation, and five flow rates within the range of each sensor were chosen. After stabilizing the flow rate at q0, a positive or a negative step is generated at t0, where Δq is the step amplitude.
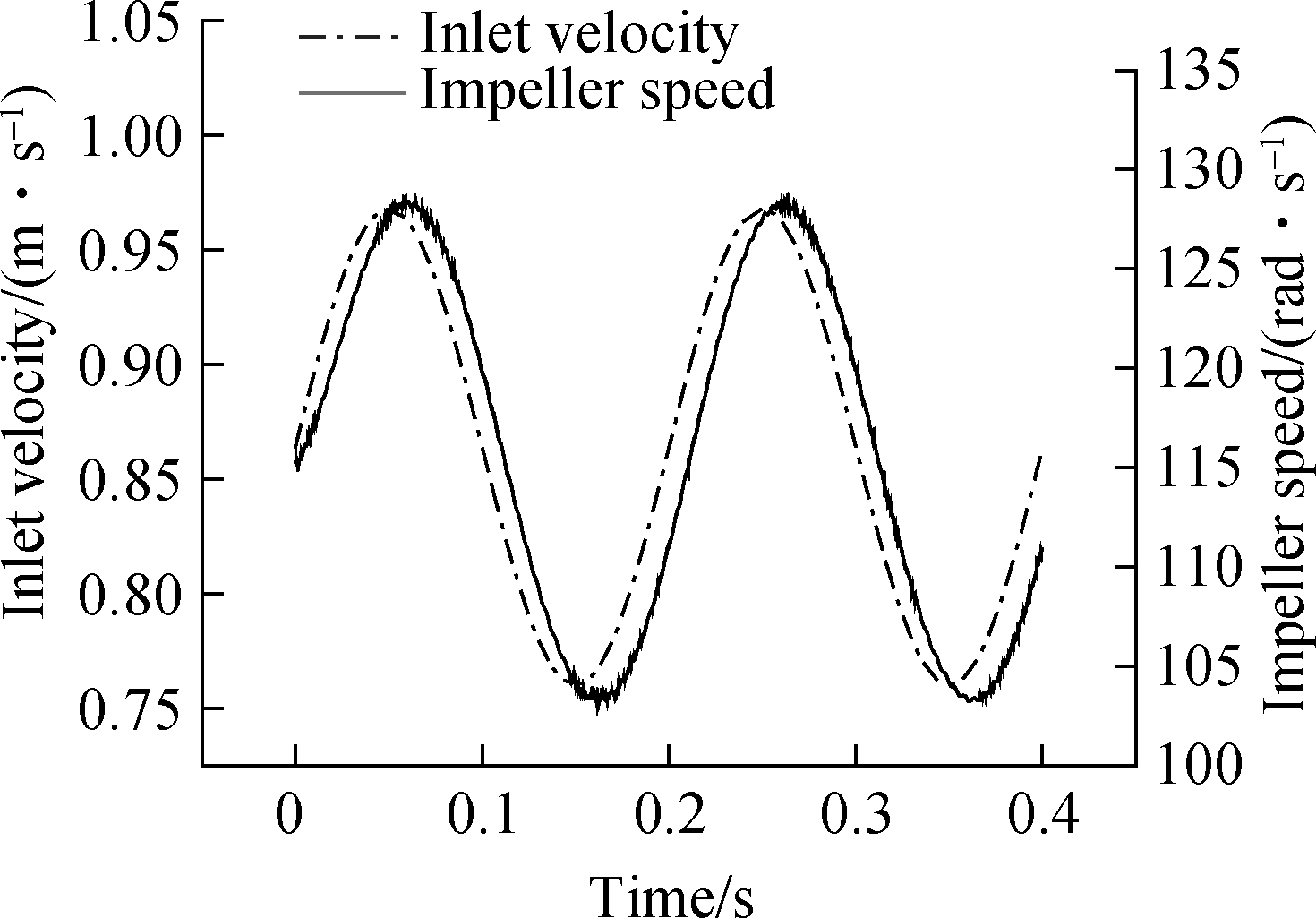
Fig.14 Comparison of the response curve of pulse flow rate and inlet flow rate
When the flow rate is stable, the entire process is complete. The inlet velocity is calculated from the flow rate of the tested flow sensor and is set as the simulated boundary condition. The inlet flow rate expression is shown as follows:
(19)
(20)
Tab.7 depicts the specific working conditions set as data. Fig.15 depicts the inlet flow rate of the turbine flow sensor and obtained impeller speed. The impeller speed changes periodically as the force acting on the impeller changes periodically during the impeller rotation process.
Tab.7 q0 and Δq in step flow
Diameter/mmFlowrateq0/(m3·h-1)Step amplitude Δq/(m3·h-1)Δq1Δq2Δq3Δq4150.60.060.120.180.241.00.100.200.300.401.60.160.320.480.642.80.280.560.841.124.00.400.801.201.60251.60.160.320.480.642.50.250.500.751.004.00.240.600.901.207.00.240.600.901.2010.00.240.600.901.20322.50.240.600.901.204.00.240.600.901.206.40.240.600.901.2011.20.240.600.901.2016.00.240.600.901.20
The analysis of the step response of the turbine flow sensor indicates that the impeller speed of the flow sensor gradually increases and then stabilizes near a small fluctuation value with no obvious overshoot. The step response curve of the turbine flow sensor is more consistent with the step response of the first-order system, allowing the turbine flow sensor to be analyzed as a first-order linear system.
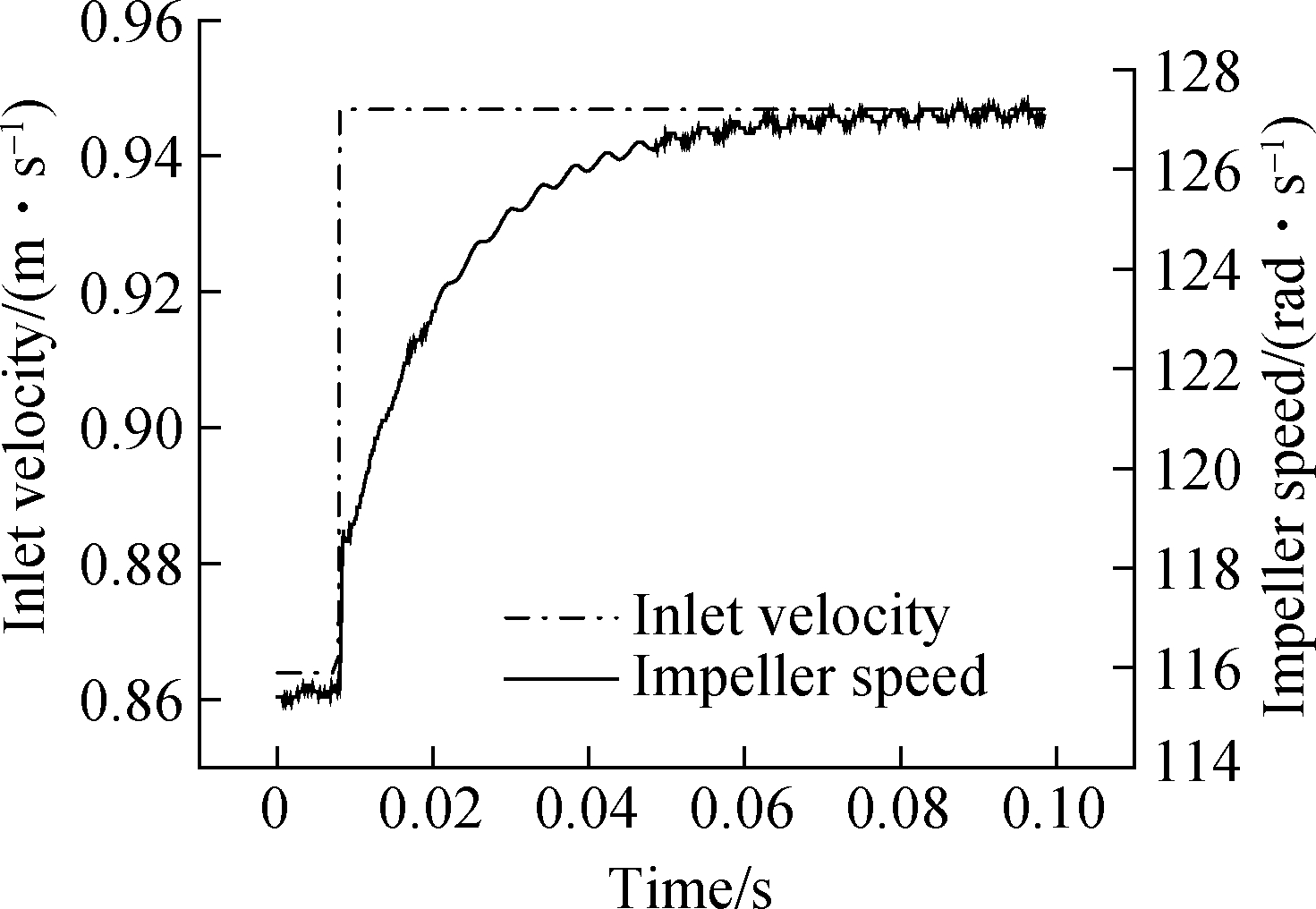
Fig.15 Step response curve of the turbine flow sensor
Therefore, the passive simulation method proposed in this paper can be used to study the dynamic characteristics of the turbine flow sensor.
5 Conclusions
1) In the steady-state experiment and simulation, the variation trend of the simulation meter factor with the flow rate is consistent with the experimental results, and the deviation between the simulation results and the experimental results is better than that between the findings of other simulations methods and the experimental results.
2) The changing trend of the simulated impeller speed in the unsteady state experiment and simulation is consistent with that of the experimental impeller speed, indicating a good follow-up.
3) In the simulation study of pulsating flow state and step flow state, the impeller speed of the simulation results is consistent with the inlet flow change, so this method can be used to predict and examine the dynamic performance of the turbine flow sensor.
[1] Lee W F Z,Karlby H. A study of viscosity effect and its compensation on turbine-type flowmeters[J]. Journal of Basic Engineering, 1960, 82(3): 717-725. DOI:10.1115/1.3662720.
[2] Xu Y. Calculation of the flow around turbine flowmeter blades[J].Flow Measurement and Instrumentation, 1992, 3(1): 25-35. DOI:10.1016/0955-5986(92)90013-U.
[3] Nam K H, Park J H, Kim H J. Performance test of turbine flowmeter according to temperature variation[J].The KSFM Journal of Fluid Machinery, 2017, 20(2): 47-52. DOI:10.5293/kfma.2017.20.2.047.
[4] Zhang G F, Wang L H, Zhu Y J, et al. Turbine flowmeter response analysis based on PIV measurement[J]. Chinese Journal of Scientific Instrument, 2013, 34(10): 2381-2387. DOI:10.19650/j.cnki.cjsi.2013.10.032.(in Chinese)
[5] Sun L J, Zhou Z Y, Zhang T. Quantitative optimization method for rotor geometric parameters of liquid turbine flow sensor[J]. Chinese Journal of Scientific Instrument, 2007, 28(3): 493-498. DOI:10.19650/j.cnki.cjsi.2007.03.021.(in Chinese)
[6] Lee B, Cheesewright R, Clark C. The dynamic response of small turbine flowmeters in liquid flows[J]. Flow Measurement and Instrumentation, 2004, 15(5/6): 239-248. DOI:10.1016/j.flowmeasinst.2004.07.002.
[7] Tonkonogij J, Pedišius A, 
A. The new semi-experimental method for simulation of turbine flow meters rotation in the transitional flow[J]. Proceedings of World Academy of Science Engineering & Technology, 2008: 208-212.
Z, 
irok B, Bizjan B. Turbine flowmeter response to transitional flow regimes[J]. Flow Measurement and Instrumentation, 2018, 59: 18-22. DOI:10.1016/j.flowmeasinst.2017.11.006.
[9] López-González L M, Sala J M, González-Bustamante J A, et al. Modelling and simulation of the dynamic performance of a natural-gas turbine flowmeter[J].Applied Energy, 2006, 83(11): 1222-1234. DOI:10.1016/j.apenergy.2005.12.002.
[10] Zheng D H, He X, Che D F. CFD simulations of hydrodynamic characteristics in a gas-liquid vertical upward slug flow[J].International Journal of Heat and Mass Transfer, 2007, 50(21/22): 4151-4165. DOI:10.1016/j.ijheatmasstransfer.2007.02.041.
[11] Wang Z, Zhang T. Computational study of the tangential type turbine flowmeter[J].Flow Measurement and Instrumentation, 2008, 19(5): 233-239. DOI:10.1016/j.flowmeasinst.2007.11.003.
[12] Guo S N, Sun L J, Zhang T, et al. Analysis of viscosity effect on turbine flowmeter performance based on experiments and CFD simulations[J].Flow Measurement and Instrumentation, 2013, 34: 42-52. DOI:10.1016/j.flowmeasinst.2013.07.016.
[13] Sun H J, Feng Y, Wang B. Numerical simulation and optimal design of front diversion body in gas turbine flowmeter[J]. Journal of Electronic Measurement and Instrumentation, 2016, 30(4): 550-557. DOI:10.13382/j.jemi.2016.04.007.(in Chinese)
[14] Wu D Z, Chen T, Sun Y B, et al. Study on numerical methods for transient flow induced by speed-changing impeller of fluid machinery[J].Journal of Mechanical Science and Technology, 2013, 27(6): 1649-1654. DOI:10.1007/s12206-013-0412-4.
[15] General Administration of Quality Supervision. Verification regulation of turbine flowmeter: JJG 1037—2008 [S]. Beijing: Inspection and Quarantine of the People’s Republic of China, 2008. (in Chinese)
[16] Guo S N, Yang Z H, Wang F, et al. Optimal design of wide viscosity range turbine flow sensor based on flow field analysis[J].Flow Measurement and Instrumentation, 2021, 79: 101909. DOI:10.1016/j.flowmeasinst.2021.101909.
[17] Zhao J L, Sun L J, Zhang T, et al. Experiment and numerical simulation study on the viscosity impact of turbine flowmeter’s performance[J].Advanced Materials Research, 2011, 301/302/303: 1283-1288. DOI:10.4028/www.scientific.net/amr.301-303.1283.
[18] Saboohi Z, Sorkhkhah S, Shakeri H. Developing a model for prediction of helical turbine flowmeter performance using CFD[J]. Flow Measurement and Instrumentation, 2015, 42: 47-57. DOI:10.1016/j.flowmeasinst.2014.12.009.
[19] Wang X. Research on turbine flowmeter for small flow viscous liquid [D]. Lanzhou: Lanzhou University of Technology, 2019. (in Chinese)