Shake tables can be used to reproduce a vibration environment in the laboratory and play an indispensable role in extensive vibration experiments[1-6]. Hydraulic shake tables are typical and largescale shake tables extensively applied in many fields, such as large displacement amplitude and heavy-duty vibration experiments. However, limited by the properties of mechanical and hydraulic components, conventional hydraulic shake tables cannot easily simultaneously meet the heavy load, large displacement, and high acceleration requirements, such as in the strong earthquake resistance test of large buildings[7]. Furthermore, traditional hydraulic shake tables often have low efficiency and high energy consumption during a vibration test. Hence, it is beneficial to develop a novel and efficient shake table to overcome the defects of traditional hydraulic shake tables mentioned above and meet the diverse demands of vibration experiments for modern industrial products and construction structures.
Resonance, in most cases, is detrimental to mechanicaloperations and often seriously affects mechanical properties. Despite the adverse effects, resonance can be utilized to enhance the vibration of exciters in vibration experiments, and it can not only save energy but also filter high-frequency clutters to improve control accuracy[8-9]. Up to now, several resonant shake tables (RSTs) have been built and utilized[7, 10]. Compared with traditional shake tables, RSTs could obtain a higher exciting force with a comparable or even lower input power. However, the natural frequencies of the RSTs were difficult to be adjusted during the vibration experiments, and the resonance can only be achieved in a narrowband frequency. To extend the resonance frequency band, Feng et al.[11-12] made useful attempts. However, limited by the regulation mechanism, resonance cannot be easily realized with a broad frequency band.
This article focuses on the use of resonance technology to enhance vibrations and reduce power consumption in a wide frequency band. Inspired by the resonant and anti-resonant mechanism[13-18], a novel variable stiffness mechanism (VSM) constituted by leaf spring-lever combinations (LSLCs) was designed, and three parallel-connected VSMs were mounted on a hydraulic shake table to constitute an RST. Under specific experimental conditions, the resonant frequency and excitation frequency of the shake table can be altered.
1 VSM
To achieve the nonlinear stiffness characteristics of the VSM, leaf springs were chosen as the stiffness element and structural members. The VSM was mainly constructed by four leaf LSLCs. Two LSLCs were symmetrically installed for the synergy operation to construct a single VSM. To achieve a large displacement amplitude of vibrations, two single VSMs were connected in series via slider guide rail combinations to construct a complete VSM, as shown in Fig. 1. In the LSLC, several pieces of leaf springs were stacked to constitute one leaf spring stack. The leaf spring stacks were in a cantilever state. The lever of the LSLC was L-shaped, and the lengths of the two arms of the lever were different. The middle fulcrum of the lever was hinged to the bracket. The short arm end of the lever was in rolling contact with the surface of the suspended end of the leaf spring stack by bearings. The long arm end of the lever bears the force exerted by the vibration exciter.

Fig.1 Three-dimensional model of the VSM
1.1 VSM model
The working principle of the LSLC is shown in Fig. 2, where the local coordinate system o-v-h is defined. In the initial state, the L-shaped lever is in the A′OB′ position, and the leaf spring remains undeformed. When force Fl is exerted on the lever’s long arm end along the x-axis, the lever revolves to the A′OB′ position. During rotation, the angle between the long arm of the lever and the horizontal plane changes from θ10 to θ1. Applying the principle of torque balance, we can obtain the following expression[19]:
(1)
where l1 and l2 are the lengths of the long and short arms of the lever, respectively; φ is the sum of the angles of the long and short arms with respect to the horizontal plane; ![]() is the force exerted on the short arm end of the L-shaped lever due to the bending of the leaf spring stack; and βB′ is the slope at the free end of the leaf spring stack.
is the force exerted on the short arm end of the L-shaped lever due to the bending of the leaf spring stack; and βB′ is the slope at the free end of the leaf spring stack.

Fig.2 Schematic diagram of the LSLC
The downward displacement of the lever’s long arm end along the x-axis is
x=l1(sinθ10-sinθ1)
(2)
By deducing from Eq. (2), we can obtain
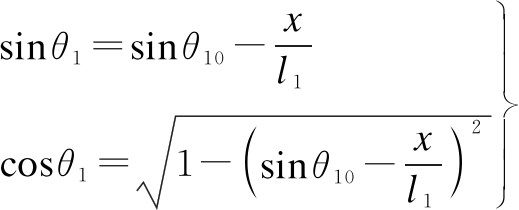
(3)
Rotating the lever to the A′OB′ position, the coordinate of the end point B′ of the lever is marked as (hB′,vB′) among the coordinate system o-v-h. The nonlinear geometric relationship of each component is
(4)
(5)
where d1 and d2 are the horizontal and vertical distances between the fixed end of a leaf spring stack and the fixed fulcrum of the L-shaped lever, respectively.
Based on references [20-21], the relationship between the force and bending deformation of the cantilever end of the leaf spring stack can be obtained as
(6)
(7)
where E is the elastic modulus of the leaf spring stack, and I is the equivalent moment of inertia of the leaf spring stack. Conducting a series of derivations for Eqs. (6) and (7), the following equations can be obtained:
(8)
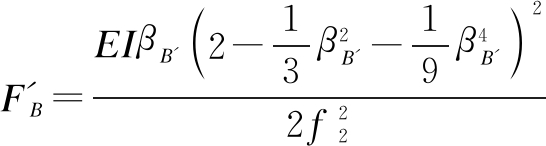
(9)
Combining Eqs. (1), (3), (4), (5), (8), and (9), the vertical force Fl can be expressed as the explicit function of displacement x:
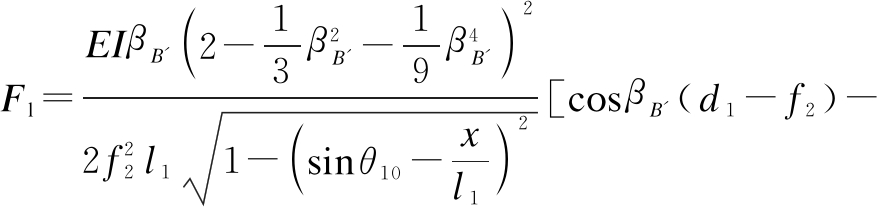
sinβB′(f1+d2)]
(10)
The equivalent dynamic stiffness of the LSLC along the x-axis can be obtained by differentiating Eq. (10) with respect to x. The specific differential process is cumbersome, so it is not shown here. The parameters of the LSLC are as follows: d1=22 cm, d2=78 mm, l1=6 cm, l2=45 mm,φ=70°,θ10=60°, E=2.06 GPa, and I=543.8 mm4. Substituting the parameters into Eq. (10), the restoring force and equivalent dynamic stiffness of the LSLC versus the displacement of the lever’s long arm end along the x axis can be obtained, as shown in Fig. 3. In the figure, the LSLC is a stiffness softening

Fig.3 Restoring force and equivalent stiffness of the LSLC
system whose stiffness rapidly decreases with the displacement increase of the lever’s long arm end.
The RST is composed of three identical VSMs, and each VSM contains two pairs of LSLCs that have identical structural parameters. According to the equivalent force-displacement calculation method of series-parallel springs, taking the symmetrical center of the LSLC pair as a zero point of the RST displacement, the restoring force of three VSMs can be expressed as Eq. (11). Substituting the parameters of the LSLC assigned above into Eq. (11), we can obtain the restoring force of three VSMs versus the RST displacement, as shown in Fig. 4. In the figure, the restoring force of three VSMs nonlinearly varies as the RST moves away from the balancing position. The VSMs exhibit stiffness softening properties. With the increase in the vibration amplitude, the equivalent dynamic stiffness of the RST can decrease, combined with the decrease in the equivalent natural frequency of the system.
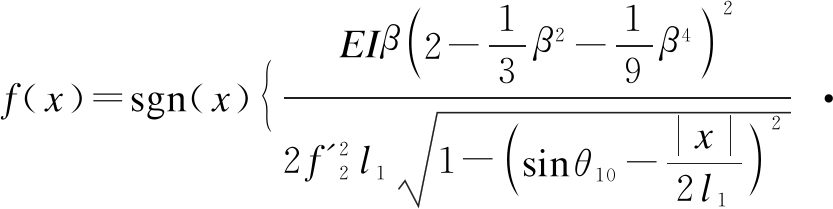
(11)

![]()
![]()
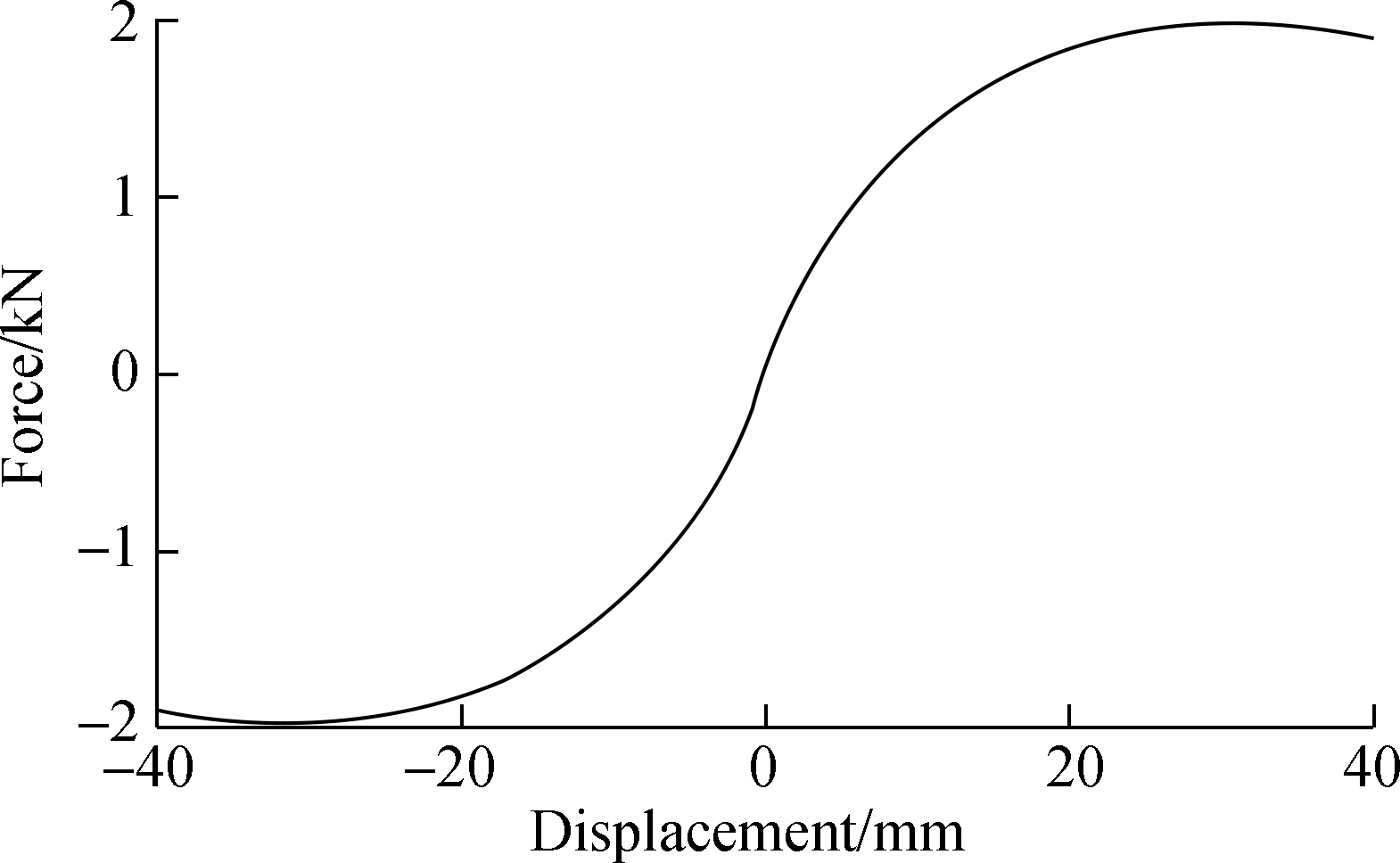
Fig.4 Restoring force of three VSMs versus the RST displacement
1.2 Experimental test on the LSLC’s stiffness
To verify the correctness of the theoretical calculation of the LSLC’s stiffness, the experimental prototype of the VSM comprised of one pair of LSLC was built, as shown in Fig. 5. The leaf spring stack in the VSM is comprised of several leaf springs of the same length and width and different thicknesses. Its stiffness can be adjusted to meet the equivalent stiffness requirements of the shake table. The equivalent moments of inertia of the leaf spring stacks were I=418.3 mm4 and I=543.8 mm4. The vertical displacements of the lever’s long arm end were measured using a grating ruler and dial indicator, and the results were the mean values of two measurement results. Through continuous loading, the relationship between the force exerted on the movable end of the VSM and displacement was determined. The comparisons between the experimental and theoretical results of the force-displacement calculation method are shown in Fig. 6, where Figs. 6(a) and (b) correspond to I=418.3 mm4 and I=543.8 mm4, respectively.

Fig.5 Equivalent stiffness measurement of the LSLC
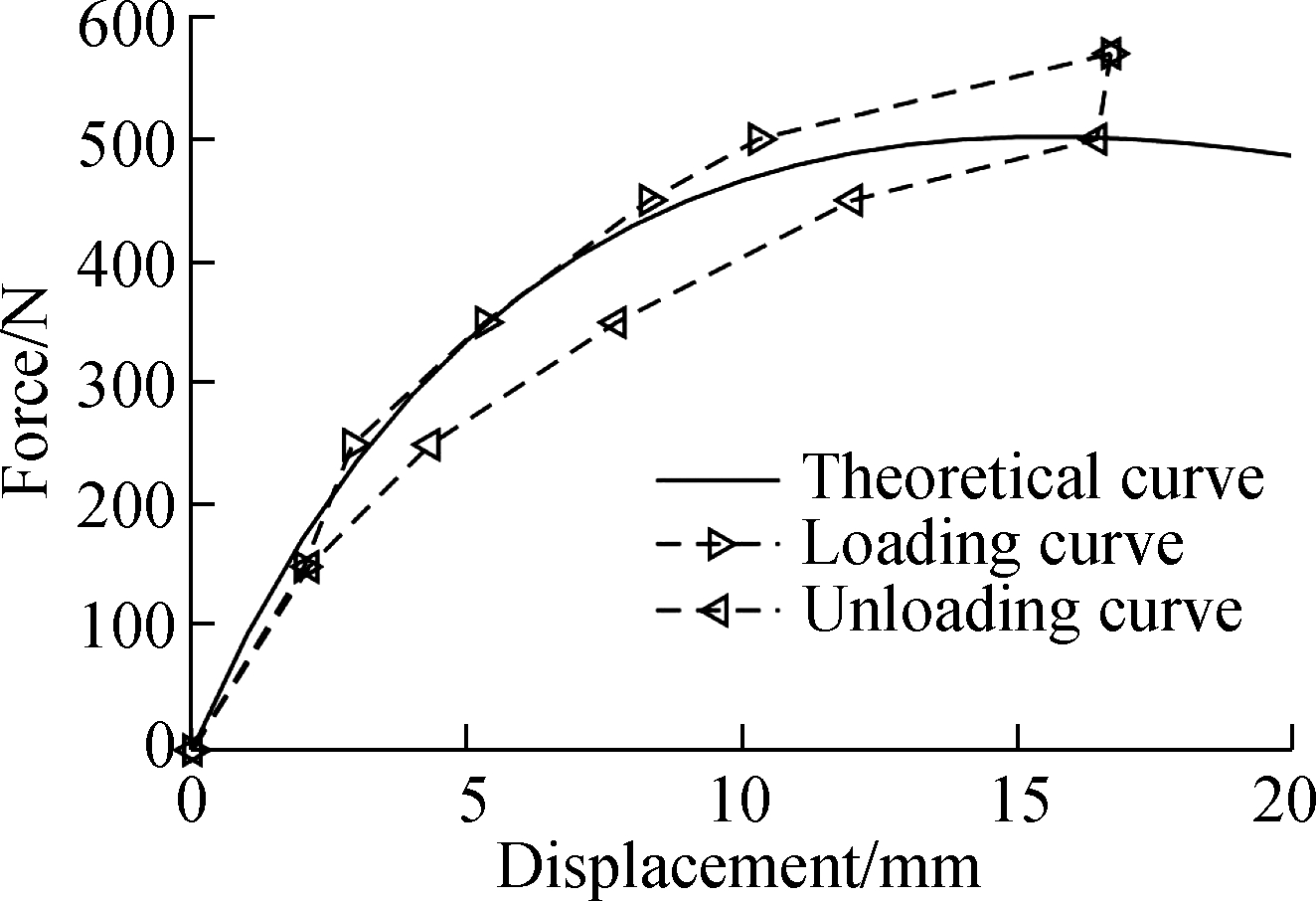
(a)
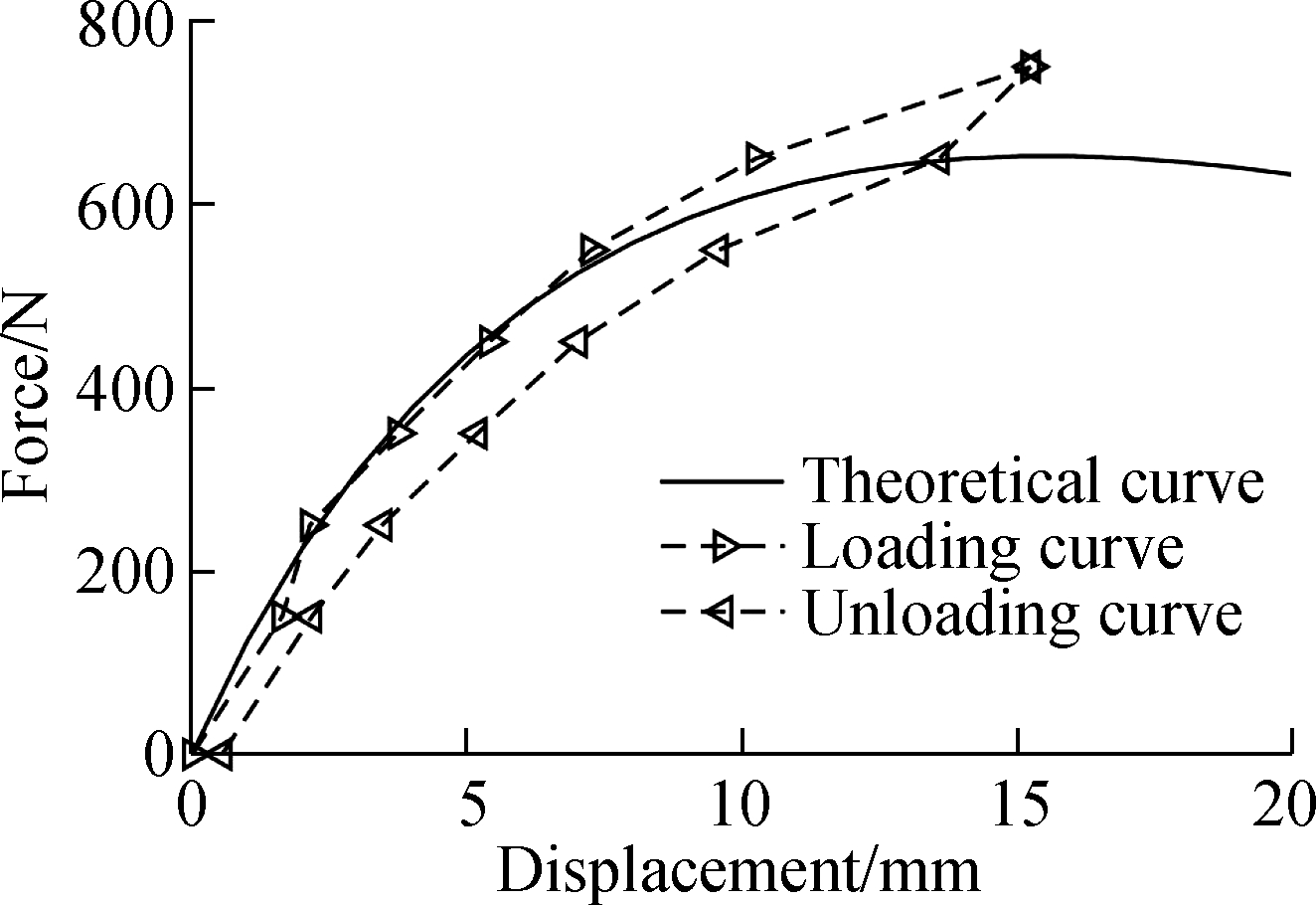
(b)
Fig.6 Experimental and theoretical result comparison of the restoring force of the LSLC. (a) I=418.3 mm4; (b) I=543.8 mm4
In Fig. 6, the experimental results are in good agreement with the theoretical results. The loading and unloading curves do not coincide with each other, hence the existence of hysteresis. Thus, the friction force between the moving parts of the VSM is relatively large.
2 RST
The RST was constructed by connecting three VSMs on the traditional hydraulic shake table. The number of VSMs used in the RST is not limited to three in order to meet actual requirements. Benefiting from the structural advantages, the VSMs can not only broaden the resonant frequency band but also suppress the vibration clutter in non-vibrating directions of the shake table by physically restricting other degrees of freedom except the vertical direction.
2.1 Dynamic modeling of the RST
The RST with VSMs can be simplified as a viscously damped variable stiffness spring-mass system. The dynamic equation of the system can be obtained as
(12)
where m is the total mass of the payload and shake table, specified as 90 kg; c is the equivalent damping coefficient of the RST, specified as 2 262 N·s/m to make the damping factor as about 0.25; and f(x) is the restoring force of three VSMs, as expressed in Eq. (11).
2.2 Simulation study on the RST’s dynamic characteristic
2.2.1 Response of vibrational excitation
To reveal the superior performance of the RST, the comparisons between the displacement responses of the RST with VSMs and conventional shake table with a fixed stiffness mechanism (FSM) were simulated under the same harmonic sweep frequency vibrational excitations. In the simulation, the parameters of the VSMs were set to be the same as those specified in Section 1.1, except that I=669.2 mm4. The stiffness of the FSM was 216.168 kN/m, which gives the shake table an undamped natural frequency of 7.8 Hz. The vibration frequency spanned from 2 to 13 Hz at a rate of 1 Hz/s. The amplitude of the input force was 4 323.36 N, which was expected to excite the displacement amplitude of 20 mm.
The simulation results were obtained, as shown in Fig. 7. Obviously, under the sweep frequency excitation with constant force amplitude, the resonance phenomenon occurs. Specifically, with 4 to 12 Hz (corresponding time is 2 to 10 s), the displacement responses of two shake tables are amplified. In the frequency band of 5.5 to 7.8 Hz (3.5 to 6 s), the RST response displacement is larger than that of the conventional shake table. In the non-resonant frequency band, the displacement responses of the two shake tables are almost the same. Hence, the displacement amplification effect of the RST is better than that of the conventional shake table due to the VSM.
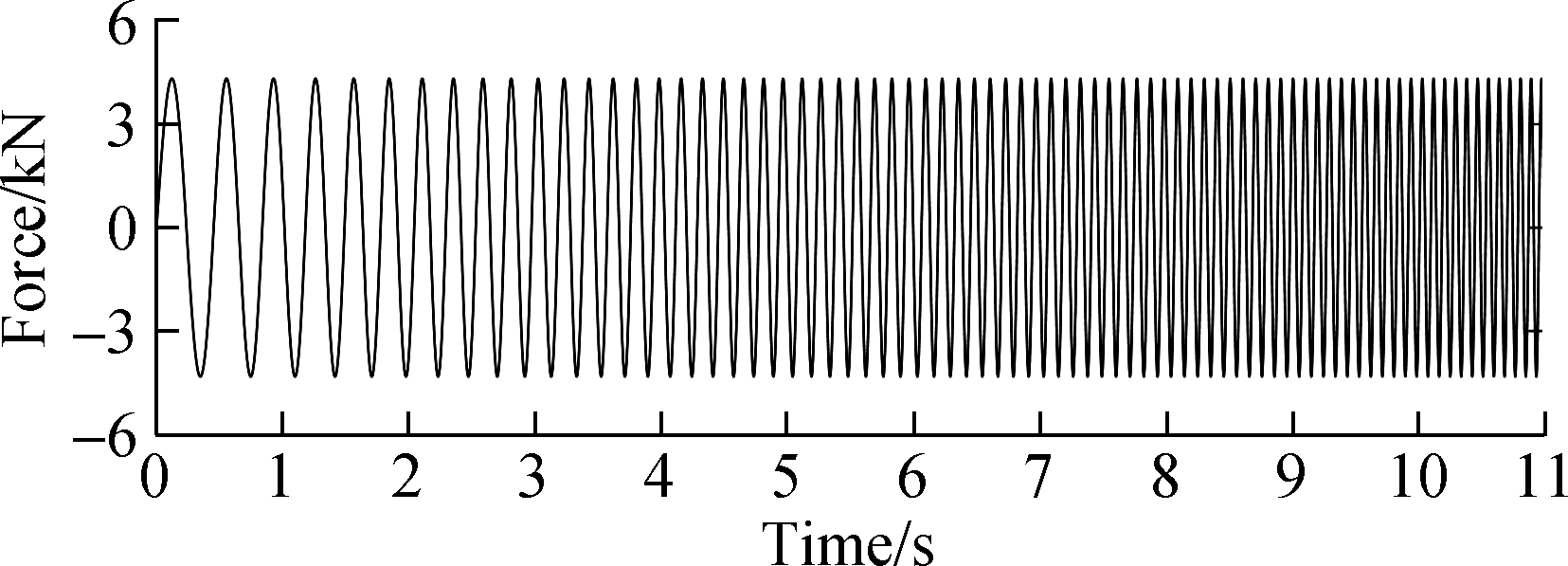
(a)

(b)
Fig.7 Displacement response under sweep frequency excitation from 2 to 13 Hz. (a) Excitation force; (b) Displacement response
2.2.2 Required vibrational excitation force
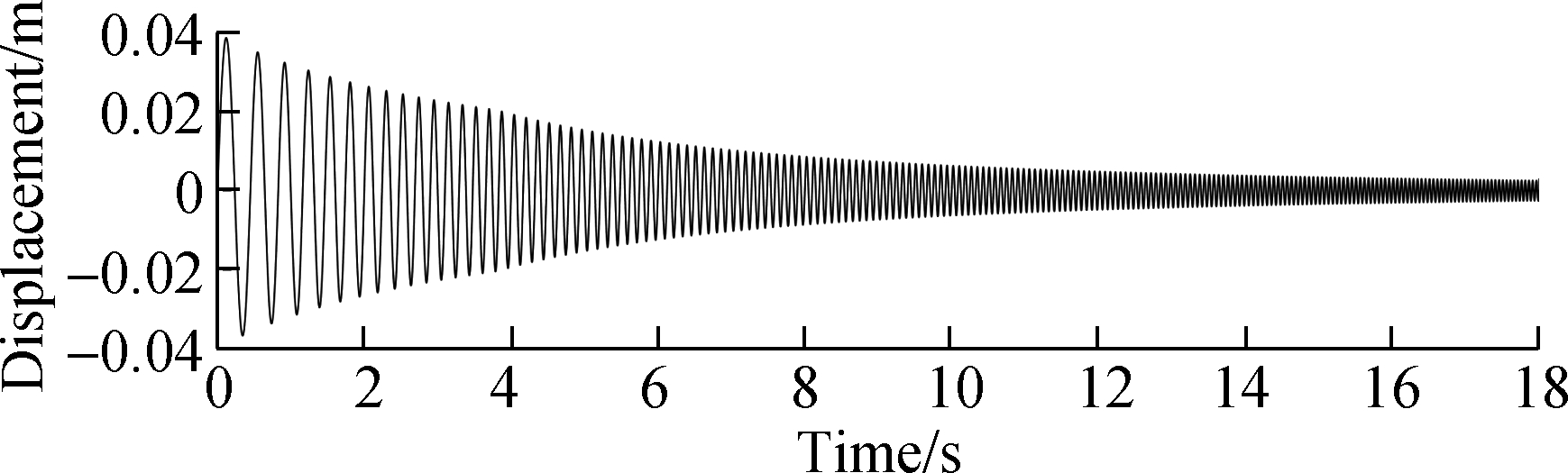
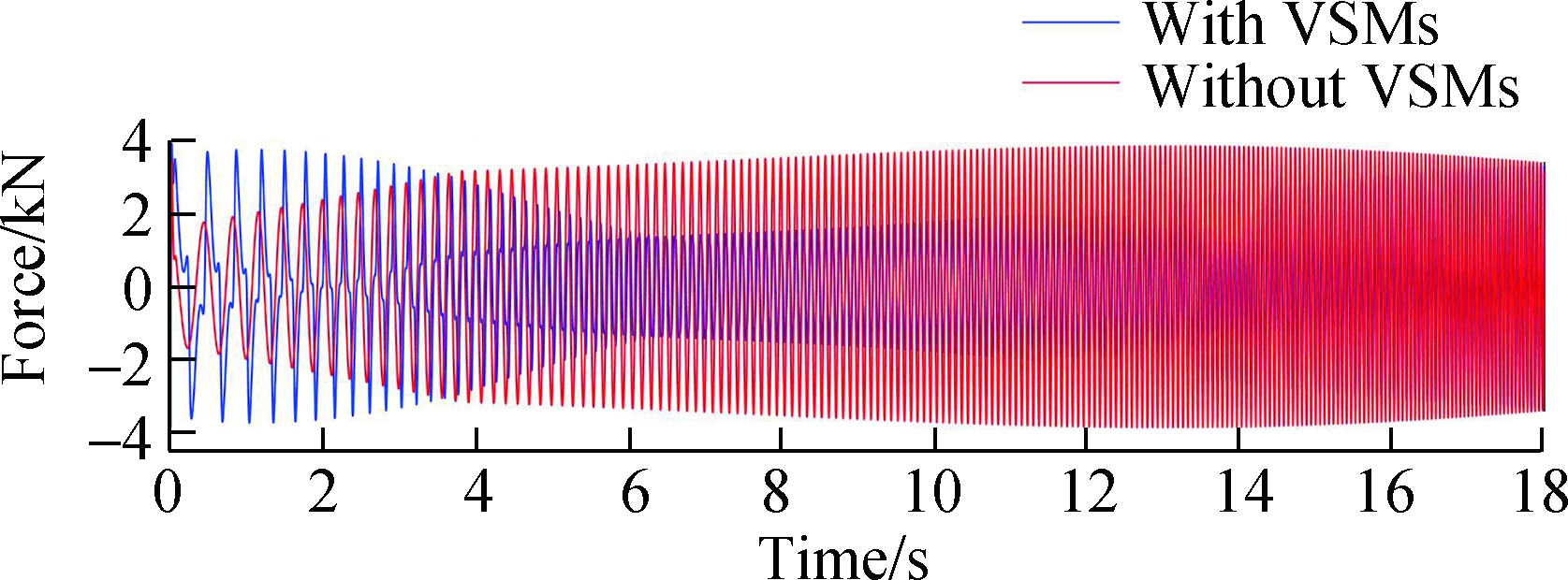
To intuitively present the influence of VSMs on the shake table, harmonically sweep frequency vibrations with rated displacement amplitude response were simulated. By producing a rated displacement response, the input forces of shake tables equipped with and without VSMs were compared. Specifically, the shake tables were required to output sinusoidal sweep frequency vibrations with a constant velocity amplitude of 1 m/s (corresponding to 2 to 7.8 Hz) and a constant acceleration amplitude of 5 g (corresponding to 7.8 to 20 Hz). In particular, the sinusoidal sweep frequency vibration simulated the rated vibrational excitation scenarios, of which 7.8 Hz is the crossover frequency and the required vibrational excitation power is the largest around the crossover frequency. Fig. 8(a) presents the vibration displacement response of the two shake tables, and Fig. 8(b) presents the required excitation force of the shake tables equipped with and without VSMs.
(a)
(b)
Fig.8 Comparison of excitation forces with the same displacement response. (a) Displacement response; (b) Excitation force
Fig. 8 shows that by producing the same displacement response, the excitation force of the shake table with VSMs is higher than that of the shake table without VSMs during 0 to 4 s (2 to 6 Hz). Beneficially, the excitation force of the shake table with VSMs is lower than that of the shake table without VSMs during 4 to 18 s (6 to 20 Hz). With low frequencies, the shake table with VSMs needs to overcome more resistance provided by the equivalent stiffness of VSMs. Conversely, with high frequencies producing a rated vibration response, the broadband resonance caused by the VSMs reduces the excitation force of the RST.
2.3 Experimental study on the RST’s dynamic characteristic
A prototype of the hydraulic shake table equipped with three VSMs was built, as shown in Fig. 9. Among the prototype, the servo cylinder with double piston rods was controlled by one servo valve. The upper piston rod of the cylinder was rigidly fixed on the bottom of the shake table. The movable ends of three VSMs were connected to the shake table to provide a nonlinear restoring force. The three VSMs were mounted on the base through three vertical columns. One displacement sensor (type) was placed on the cylinder to measure the vibration displacement. Two oil pressure sensors were separately installed on the two inlet chambers of the servo cylinder to detect the working pressure of hydraulic oil. The signal acquisition and control circuit based on DSP2812 were used in the experiments.

Fig.9 Experimental shake table with VSMs
2.3.1 Sweep frequency vibration experiment
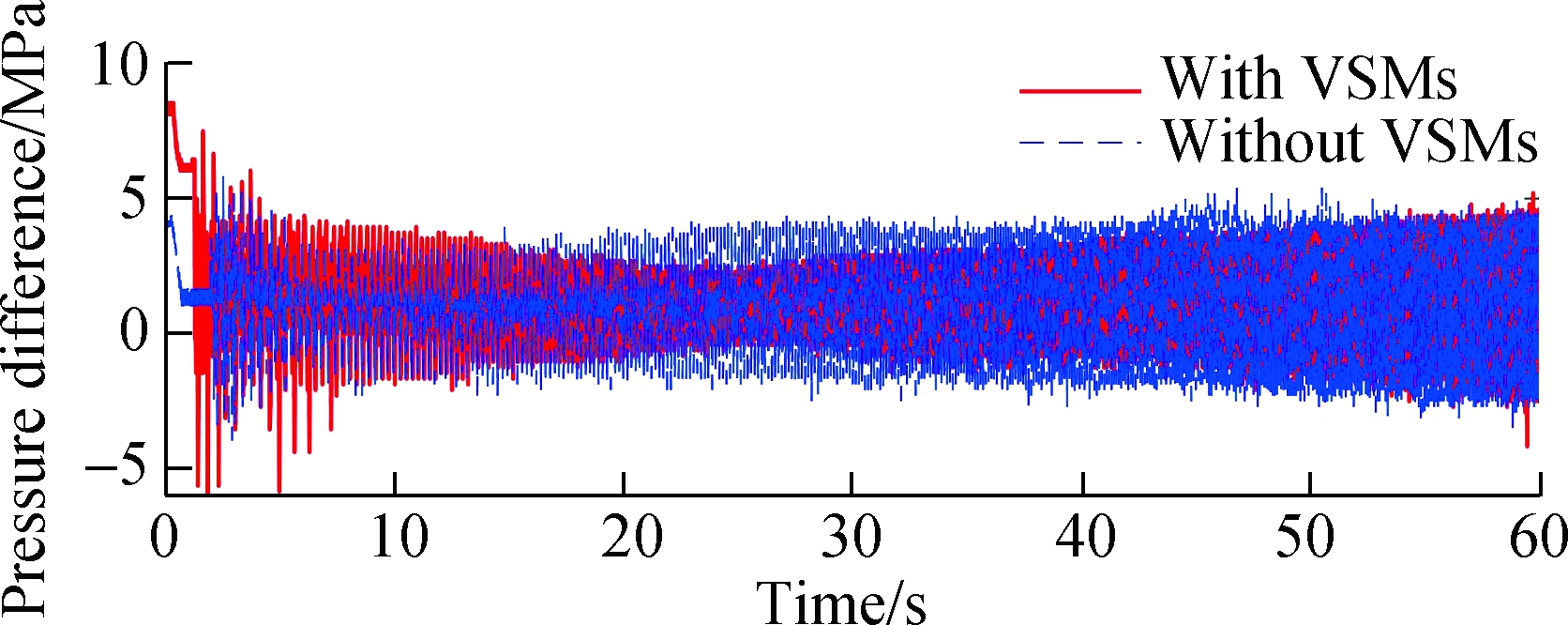
Shake tables equipped with and without VSMs were made to produce 2 to 13 Hz sinusoidal sweep frequency vibration at a rate of 0.2 Hz/s. The parameters of the experimental equipment are the same as specified in the simulation study. The vibration of the shake tables conforms to the constant velocity amplitude (1 m/s) in the frequency band of 2 to 7.8 Hz and constant acceleration amplitude (5 g) in the frequency band of 7.8 to 13 Hz. The vibration displacements of the two shake tables are presented in Fig. 10(b). The pressure difference between the two inlet chambers of the servo cylinder in the shake tables is shown in Fig. 10(a), where the solid and dotted lines represent the pressure difference of the shake tables with and without VSMs, respectively. The fast Fourier transform of the pressure differences is demonstrated in Fig. 11.
(a)

(b)
Fig.10 Oil pressure difference of two cylinder chambers with the same displacement output under sweep frequency vibration. (a) Pressure difference; (b) Displacement

Fig.11 Fast Fourier transform of pressure difference of two cylinder chambers
As shown in Figs. 10 and 11, when outputting the same vibration displacement, compared with the shake table without VSMs, the shake table with VSMs consumes more power in the time interval of 0 to 15 s (2 to 4.5 Hz) and less power in the time interval of 15 to 50 s (4.5 to 10 Hz). The experimental results are in good agreement with the simulation results presented in Section 2.2.2. Hence, the resistance provided by the VSMs plays a major role during the vibration in the low frequencies (2 to 4.5 Hz). In high frequencies (4.5 to 10 Hz), the resonance phenomenon emerges when the exciting frequency is close to the natural frequency of the RST system. The pressure difference of the shake table with VSMs is prominently lower than that of the shake table without VSMs around the frequency of 6.5 Hz.
2.3.2 Fixed-frequency vibration experiment
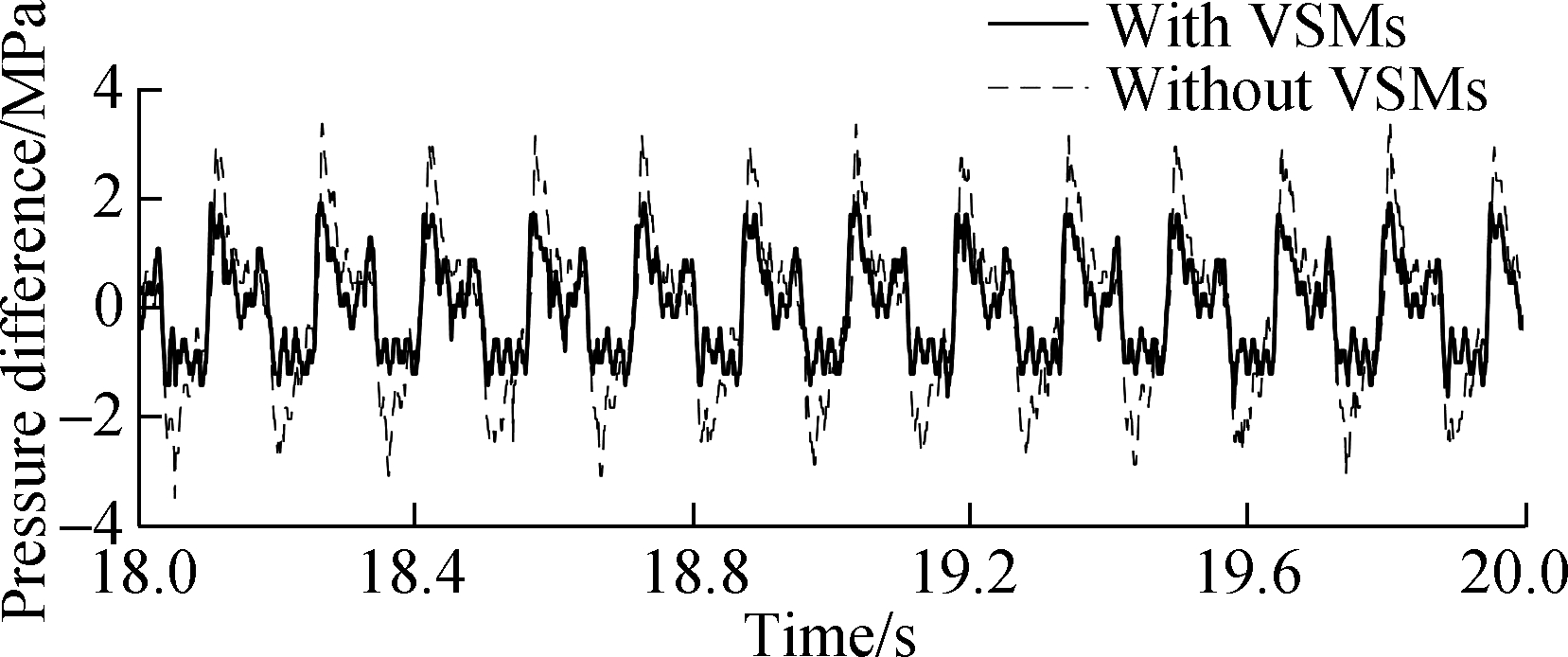
To further verify the influence of the VSMs on the dynamic characteristics of the shake table, fixed-frequency (6.5 Hz) harmonic vibration experiments were carried out. Outputting the same vibration displacement (see Fig. 12(b)), the pressure differences between two cylinder chambers of the shake tables with and without VSMs are shown in Fig. 12(a). In the figure, the input force amplitude of the shake table with VSMs is almost half of the input force of the shake table without VSMs. Producing the same vibration displacement, the power consumed by the shake table with the VSMs is significantly lower (almost 50%) than that of the shake table without the VSMs under a frequency of 6.5 Hz.
(a)
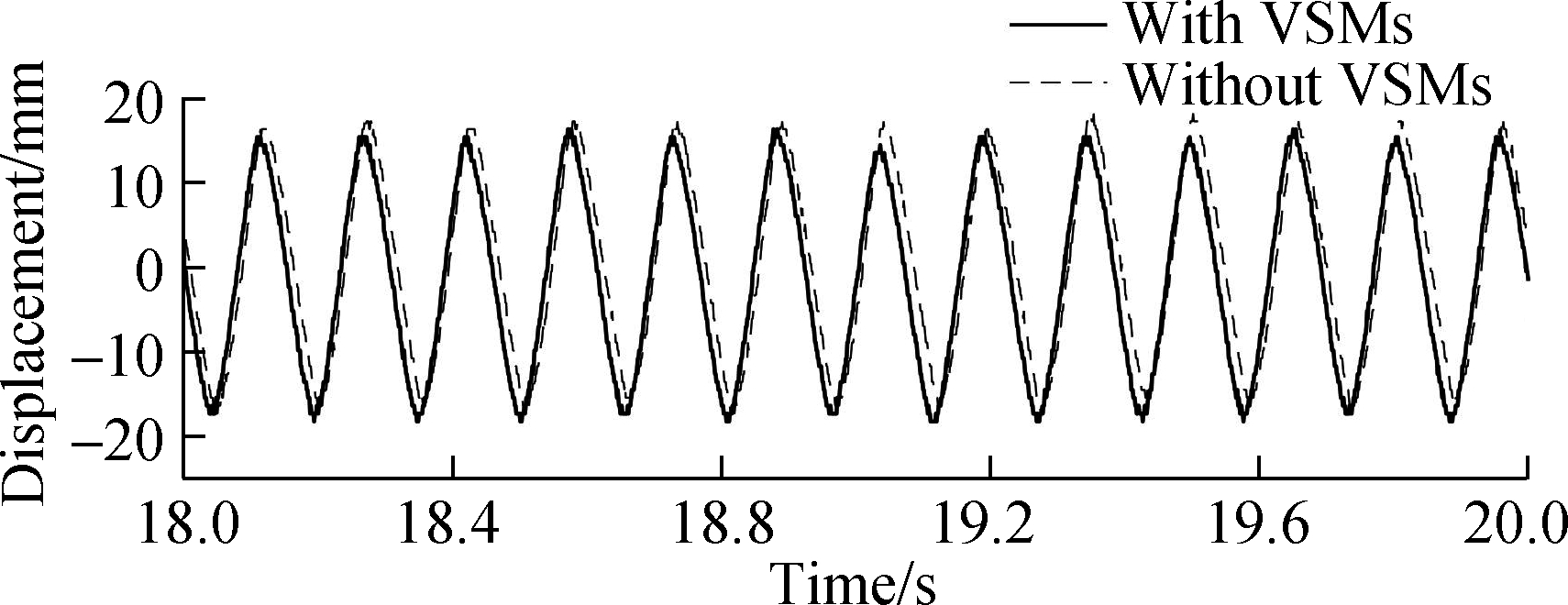
(b)
Fig.12 Oil pressure difference of two cylinder chambers with the same vibration displacement output with a fixed frequency excitation of 6.5 Hz. (a) Pressure difference; (b) Displacement
3 Conclusions
1) Under harmonic vibrational excitation conditions, shake tables with VSMs are effective for vibration enhancement among broadband resonance frequencies and can lower input power to some extent. Specifically, VSMs are effective and efficient for enhancing the vibrations of shake tables when conducting rated harmonic vibration experiments.
2) The nonlinear stiffness characteristics of VSMs comprised of LSLCs are beneficial for achieving broadband resonance, and LSLCs with passive nonlinear stiffness are expected to meet the demands of diverse engineering practices.
3)RSTs inevitably face some challenges, such as the increase in structural complexity and difficulty of precise vibration control. Limited by the properties of vibration exciters, only simple harmonic vibrational excitations were used to verify the RST system. The vibration test on the complex waveform and stability of the RST system will be carried out in subsequent studies.
[1] Xiong Z M, Chen X, Wang Y W, et al. Shaking table tests on braced reinforced concrete frame structure across the earth fissure under earthquake [J]. The Structural Design of Tall and Special Buildings, 2019, 28: 1-15. DOI: 10.1002/tal.1559.
[2] Fiorino L, Macillo V, Landolfo R. Shake table tests of a full-scale two-story sheathing-braced cold-formed steel building [J]. Engineering Structures, 2017, 151: 633-647. DOI: 10.1016/j.engstruct.2017.08.056.
[3] Lu X L,Zou Y, Lu W S, et al. Shaking table model test on Shanghai World Financial Center Tower [J]. Earthquake Engineering & Structural Dynamics, 2007, 36: 439-457. DOI: 10.1002/eqe.634.
[4] Fan Z M, Yu X J, Zhang Q, et al. Fatigue life estimation for simply-supported pipeline of robots under hybrid excitation [J]. International Journal of Fatigue, 2018, 108: 127-139. DOI: 10.1016/j.ijfatigue.2017.11.002.
[5] Mršnik M, Slavi![]() J, Boltežar M. Frequency-domain methods for a vibration-fatigue-life estimation-application to real data [J]. International Journal of Fatigue, 2013, 47: 8-17. DOI: 10.1016/j.ijfatigue.2012.07.005.
J, Boltežar M. Frequency-domain methods for a vibration-fatigue-life estimation-application to real data [J]. International Journal of Fatigue, 2013, 47: 8-17. DOI: 10.1016/j.ijfatigue.2012.07.005.
[6] Lu Z, Chen X Y, Zhang D C, et al. Experimental and analytical study on the performance of particle tuned mass dampers under seismic excitation [J].Earthquake Engineering & Structural Dynamics, 2017, 46: 697-714. DOI: 10.1002/eqe.2826.
[7] Sakai M, Kanazawa K,Ohtori Y. Development of high acceleration shaking table system using resonance vibration [C]//Proceedings of the ASME 2016 Pressure Vessels and Piping Conference. Vancouver, Canada, 2016: 1-6.
[8] Tagawa Y, Kajiwara K. Controller development for the E-defense shaking table [J]. Proceedings of the Institution of Mechanical Engineers, Part Ⅰ: Journal of Systems and Control Engineering, 2007, 221: 171-181. DOI: 10.1243/09596518JSCE331.
[9] Ogawa N,Ohtani K, Katayama T, et al. Construction of a three-dimensional, large-scale shaking table and development of core technology [J]. Phil Trans R Soc Lond A, 2001, 359:1725-1751. DOI: 10.1098/rsta.2001.0871.
[10] Hirose J, Suzuki K,Yoshika N. Seismic capacity tests of motor operated fans in ventilation systems [C]//Proceedings of the ASME 2011 Pressure Vessels & Piping Division Conference. Baltimore , MA, USA, 2011: 1-9.
[11] Feng Z J, Ruan J, Jin D C,et al. Mechanism analysis of high-frequency single-axis electro-hydraulic shaking table’s resonance phenomenon [J]. Hydraulics Pneumatics & Seals, 2016, 4:20-23. DOI: 10.3969/j.issn.1008-0813.2016.04.006. (in Chinese)
[12] Ren Y, Ruan J. Theoretical and experimental investigations of vibration waveforms excited by an electro-hydraulic type exciter for fatigue with a two-dimensional rotary valve [J]. Mechatronics, 2016, 33: 161-172. DOI: 10.1016/j.mechatronics.2015.12.006.
[13] Park Y J, Huh T M, Park D, et al. Design of a variable-stiffness flapping mechanism for maximizing the thrust of a bio-inspired underwater robot [J].Bioinspir Biomim, 2014, 9: 036002. DOI: 10.1088/1748-3182/9/3/036002.
[14] Zhou X H, Sun X, Tang K H, et al. Preliminary study on broadband resonance of shaking table based on the compressibility of gas [J]. Journal of Beijing Institute of Technology(English Edition), 2019, 28: 257-264. DOI: 10.15918/j.jbit1004-0579.17189.
[15] Hu Z, Wang X, Yao H X, et al. Theoretical analysis and experimental identification of a vibration isolator with widely-variable stiffness [J]. Journal of Vibration and Acoustics, 2018, 140: 051014. DOI: 10.1115/1.4039537.
[16] Feng X, Jing X J. Human body inspired vibration isolation: Beneficial nonlinear stiffness, nonlinear damping & nonlinear inertia [J]. Mechanical Systems and Signal Processing, 2019, 117: 786-812. DOI: 10.1016/j.ymssp.2018.08.040.
[17] Heo Y J, Lee W C, Kim T, et al. Active micromechanical motion amplifiers using the mechanical resonance modulated by variable stiffness springs [J]. Sensors and Actuators A: Physical, 2012, 180: 97-104. DOI: 10.1016/j.sna.2012.04.018.
[18] Potekin R, Kim S, McFarland D M, et al. A micromechanical mass sensing method based on amplitude tracking within an ultra-wide broadband resonance [J]. Nonlinear Dynamics, 2018, 92: 287-304. DOI: 10.1007/s11071-018-4055-y.
[19] Park J J, Song J B. A nonlinear stiffness safe joint mechanism design for human robot interaction [J]. Journal of Mechanical Design, 2010, 132:0610051. DOI: 10.1115/1.4001666.
[20] Zhou X H, Sun X, Zhao D X, et al. The design and analysis of a novel passive quasi-zero stiffness vibration isolator [J]. Journal of Vibration Engineering & Technologies, 2021, 9:225-245 DOI: 10.1007/s42417-020-00221-6.
[21] Zhou X H, Zhao D X, Sun X , et al. An asymmetric quasi-zero stiffness vibration isolator with long stroke and large bearing capacity [J].Nonlinear Dynamics, 2022, 108: 1903-1930. DOI: 10.1007/s11071-022-07300-1.