环中的中心clean元和中心Drazin逆

In the research on ring theory, the cleanness of a ring is a basic but important topic. Clean rings originated from the study of exchange rings, which play an important role in the cancellation of modules. The interesting characterizations and properties of clean rings have motivated many scholars to conduct further investigations. The concept of clean rings was first introduced by Nicholson[1] in 1977. Subsequently, Nicholson et al.[2] proved that the linear transformation of a countable vector space over a division ring is clean. In 1999, Nicholson[3] introduced a strongly clean ring and presented some equivalent characterizations of strongly clean elements and rings. In 2001, Han et al.[4] investigated the cleanness of group rings, the ring of formal power series over a ring, and a direct product of rings. In 2011, Hiremath et al.[5] presented some characterizations of strongly clean rings. More details concerning the cleanness of the rings can be found in Refs.[6-12].

Throughout the paper,R denotes an associative ring with unity 1. The center of R is denoted by C(R)={x∈R:ax=xa for all a∈R}. The element e∈R is considered idempotent if e2=e. In contrast, the element e∈R is considered central idempotent if e2=e and e∈C(R). The symbols E(R), CE(R), U(R), and J(R) denote the sets of all idempotents, central idempotents, invertible elements, and Jacobson radicals of R, respectively. Recall that the element a∈R is considered clean if u∈U(R) and e∈E(R) exist such that a=u+e. The element a∈R is considered strongly clean if u∈U(R) and e∈E(R) exist such that a=u+e and ue=eu. In this case, a=e+u is considered a strongly clean decomposition.

Drazin[13] introduced the concept of pseudo-inverse (usually called Drazin inverse) in rings and semigroups. The element a∈R is considered a Drazin invertible if x∈R and the nonnegative integer k exist such that xax=x, ax=xa, xak+1=ak. Such x is unique if it exists and is considered the Drazin inverse of a. The smallest nonnegative integer k satisfying the previously presented equations is called the Drazin index of a. If k=1, then x is considered the group inverse of a.

Further research showed that there is a close connection between clean rings and Drazin inverses. For example, Zhu et al.[14] proved that a∈R is a Drazin invertible if and only if u∈U(R), e∈E(R) and the positive integer n exist such that an=u+e is a strongly clean decomposition and anR∩eR=0. Moreover, many scholars investigated the Drazin invertibility of combinations of idempotents. For instance, Liu et al.[15] analyzed this topic in complex matrices, i.e., Drazin invertibility of aP+bQ+cPQ+dQP+ePQP+fQPQ+gQPQP for idempotent complex matrices P and Q under the conditions (PQ)2=(QP)2. More details concerning Drazin inverses can be found in Refs.[16-26].

In 2019, to analyze the commutative properties of Drazin inverses (see Example 2.8 in Ref.[27]), Wu et al.[28] introduced the concept of central Drazin inverses.

Definition 1[28] Element a∈R is considered a central Drazin invertible if x∈R and the nonnegative integer k exist such that xax=x, xa∈C(R), xak+1=ak. Such x is unique if it exists and is considered the central Drazin inverse of a, denoted by ac. The smallest nonnegative integer k satisfying the previously presented equations is still the Drazin index of a, denoted by ind(a). If k=1, then x is called the central group inverse of a, denoted by a©.

In Ref.[28], a centrally clean element and a centrally clean ring are also introduced.

Definition 2[28] Let a∈R. If u∈U(R) and e∈CE(R) exist such that a=u+e, then a is considered centrally clean. In this case, a=u+e is considered a centrally clean decomposition of a. Thus, centrally clean is clean. If every element of R is centrally clean, then R is considered a centrally clean ring.

Moreover, a∈R is a central Drazin invertible if and only if u∈U(R), e∈CE(R) and the positive integer n exist such that a=u+e is a centrally clean decomposition, and anR∩eR=0, or equivalently, u∈U(R), e∈CE(R) and the positive integer n exist such that a=u+e is a centrally clean decomposition and ae is nilpotent. Subsequently, Zhao et al.[29] investigated the one-sided central Drazin inverses.

Motivated by the previous studies, we investigated centrally clean elements and central Drazin inverses in R. We first give an example and characterizations of centrally clean elements. Then, we analyze the properties of centrally clean rings and provide some equivalent characterizations. Moreover, we present the necessary and sufficient conditions for the existence of central Drazin inverses in terms of centrally clean decompositions. In addition, we investigate the central group invertibility of combinations of two central idempotents. Finally, we calculate all invertible, central group invertible, group invertible, central Drazin invertible elements, and centrally clean elements of the group ring Z2S3.

1 Characterization of Centrally Clean Elements

First, we provide an example of centrally clean elements.

1) Units are centrally clean.

2) The elements in J(R) are centrally clean.

3) Nilpotent elements are centrally clean.

4) Central idempotents are centrally clean.

Proof 1) and 3) are obvious.

2) Let x∈J(R). Notably, J(R)={x∈R: 1-ax is left invertible for any a∈R} and J(R)={x∈R: 1-xa is right invertible for any a∈R}.

Then, we take a=1, and it follows that 1-x∈U(R). Hence, x is centrally clean.

4) Let e∈CE(R). Given that (2e-1)2=1 and (1-e)2=1-e, it follows that 2e-1∈U(R) and 1-e∈CE(R). Then, e=(2e-1)+(1-e). Hence, e is centrally clean.

Let a∈R. Then, we use Ra and aR to denote the left and right ideals generated by a, respectively. We use l(a) and r(a) to denote the left and right annihilators of a, respectively. That is,

Nicholson[3] proved that if e∈E(R) and a∈eRe is strongly clean, then a∈R is also strongly clean. Moreover, he provided some characterizations of strongly clean elements. Then, we investigate the relevant characterizations of centrally clean elements.

Lemma 1[3] Let a∈R and e∈E(R) with ea=ae. Then, the following conditions are equivalent:

2) e∈Ra and l(a)⊆l(e).

3) e∈aR and r(a)⊆r(e).

Theorem 1 Let a∈R. Then, the following conditions are equivalent:

1) a is centrally clean.

2) e∈CE(R) exists such that l(a)⊆R(1-e)⊆R(1-a) and l(1-a)⊆Re⊆Ra.

3) e∈CE(R) exists such that r(a)⊆(1-e)R⊆(1-a)R and l(1-a)⊆eR⊆aR.

4) e∈CE(R) exists such that ea∈U(eR) and (1-e)(1-a)∈U((1-e)R).

5) e∈CE(R) exists such that ea is centrally clean in eR and (1-e)(1-a) is centrally clean in (1-e)R.

6) e∈CE(R) exists such that ea is centrally clean in eR and (1-e)a is centrally clean in (1-e)R.

7) The decomposition 1=e1+e2+…+en exists, where n is a positive integer, e is a centrally orthogonal idempotent, and eia is centrally clean in eiR for each positive integer i.

Proof 1)⟹2). Given that a is centrally clean, we can suppose that a=(1-e)+u, where e∈CE(R) and u∈U(R). If ra=0, then r(1-e)+ru=0, and it follows that r=ruu-1=[-r(1-e)]u-1∈R(1-e), i.e., l(a)⊆R(1-e). Moreover, from ae=[(1-e)+u]e=ue, we derive e=u-1ae=u-1ea∈Ra, i.e., Re⊆Ra.

Rewrite a=(1-e)+u as 1-a=e+(-u). Then, by a similar argument, we can obtain l(1-a)⊆Re and R(1-e)⊆R(1-a).

2)⟹4). From e∈Re⊆Ra and l(a)⊆R(1-e)=l(e), we can obtain ea∈U(eR) based on Lemma 1. Similarly, we can derive (1-e)(1-a)∈U((1-e)R).

1)⟹3)⟹4) are similar to 1)⟹2)⟹4).

4)⟹5). This is obvious from 1) of Example 1.

5)⟹6). Given that (1-e)(1-a) is centrally clean in (1-e)R, it follows that (1-e)a=(1-e)-(1-e)(1-a) is also centrally clean in (1-e)R.

6)⟹7) Write e1=e and e2=1-e. Then, e1e2=0 and 1=e1+e2. Moreover, eia is centrally clean in eiR for each i.

7)⟹1). For each positive integer i, eia is centrally clean in eiR. Then, we suppose that eia=fi+ui, where fi∈CE(eiR) and ui∈U(eiR), and it follows that vi∈eiR exists such that viui=uivi=ei. Given that ei is a centrally orthogonal idempotent, we derive f=∑fi∈CE(R), u=∑ui∈U(R), and u-1=∑vi. Hence, a=∑eia=∑(fi+ui)=∑fi+∑ui=f+u. Therefore, a is centrally clean.

Proposition 1 Let a∈R. Then, the following conditions are equivalent:

1) a is centrally clean.

2) v∈U(R) and f∈CE(R) exist such that f=fva and 1-f=-(1-f)v(1-a).

3) u∈U(R) and f∈CE(R) exist such that f=fua and 1-f=(1-f)u(1-a).

4) f∈CE(R) and x,y∈R exist such that f=fxa, 1-f=(1-f)y(1-a), and fx-(1-f)y∈U(R).

Proof 1)⟹2). Let a=u+e, where u∈U(R) and e∈CE(R). Write f=1-e and v=u-1. Then,

2)⟹1). Write e=1-f. Then, v(a-e)=[fv+(1-f)v](a-1+f)=fva-fv+fv-(1-f)v(1-a)=f+1-f=1. Hence, a-e=v-1, i.e., a is centrally clean.

2)⟹3). Write u=(2f-1)v. Then, f=fva=fua and 1-f=-(1-f)v(1-a)=(1-f)u(1-a).

3)⟹2) is similar to 2)⟹3).

2)⟹4). Write x=v and y=-v. Then, f=fxa and 1-f=(1-f)y(1-a).

4)⟹2). Write v=fx-(1-f)y∈U(R). Then, fx=fv and -(1-f)y=(1-f)v, and it follows that f=fxa=fva and 1-f=(1-f)y(1-a)=-(1-f)v(1-a).

2 Characterizations of Centrally Clean Rings

Recall that if R/J(R) is a division ring, then R is considered a local ring.

Proposition 2 Every local ring is a centrally clean ring.

Proof Let a∈R. If a∈J(R), then a is centrally clean based on 2) of Example 1. If a∉J(R), then a+J(R)∈U(R/J(R)). Hence, x+J(R)∈R/J(R) exists such that

and it follows that ax+J(R)=1+J(R), i.e., ax-1∈J(R). Therefore, ax=1-(1-ax)∈U(R). Then, a is right invertible in R. Similarly, we can deduce that a is left invertible in R. It follows that a∈U(R), and hence, it is centrally clean.

In 2004, Nicholson et al.[12] proved that if R≠0, then R[x] is not clean. Then, it is obvious that R[x] is not centrally clean when R≠0.

Proposition 3 The following conditions are equivalent:

1) 2∈U(R), and R is centrally clean.

2) For any a∈R, u∈U(R) and x∈C(R) exist, with x2=1, such that a=u+x.

Proof 1)⟹2). Let a∈R. Given that R is centrally clean, u∈U(R) and e∈CE(R) exist such that

and it follows that a=(2e-1)+2u. From 2∈U(R), we derive 2u∈U(R). Moreover, (2e-1)2=1 and 2e-1∈C(R).

2)⟹1). Hypothetically, we have 1=x+v, where v∈U(R), x2=1 and x∈C(R). Then, (1-v)2=x2=1, and it follows that v2=2v. Hence, from v∈U(R), we derive 2=v∈U(R). Let a∈R. Then, 2a-1=y+w, where w∈U(R), y2=1 and y∈C(R). Therefore,

is centrally clean.

Then, we provide some characterizations of centrally clean rings.

Theorem 2 The following conditions are equivalent:

1) R is centrally clean.

2) Every element x∈R can be written as x=u-e, where u∈U(R) and e∈CE(R).

3) Every element x∈R can be written as x=u+e, where u∈U(R)∪0 and e∈CE(R).

4) Every element x∈R can be written as x=u-e, where u∈U(R)∪0 and e∈CE(R).

Proof 1)⟹2). Let x∈R. Then, -x=e+v, and it follows that x=-v-e, u=-v∈U(R) and e∈CE(R).

2)⟹3) and 3)⟹4) are similar to 1)⟹2).

4)⟹1). Let x∈R. Then, we derive -x=u-e based on the assumption, where u∈U(R)∪0 and e∈CE(R). Hence, x=(-u)+e. The case when u=0 follows from 4) of Example 1.

Recall that if e∈E(R) exists such that e∈aR and 1-e∈(1-a)R for any a∈R, then R is an exchange ring. Moreover, if every idempotent of R is central, then R is called abelian.

Theorem 3 The following conditions are equivalent:

1) R is centrally clean.

2) R is an exchange and abelian.

3) R is clean and abelian.

4) For any a∈R, e∈CE(R) exists such that e∈aR and 1-e∈(1-a)R.

Proof 1)⟹3). It suffices to prove that every idempotent of R is central. Let e∈E(R). Then, we derive e=f+u, where f∈CE(R) and u∈U(R), and it follows that if f+u=(f+u)2=f+2fu+u2, then 1=u+2f. Hence, we obtain e=f+u=f+1-2f=1-f∈CE(R).

3)⟹4). Given that clean rings are exchange rings, it follows that, for any a∈R, e∈E(R) exists such that e∈aR and 1-e∈(1-a)R. Given that R is abelian, we derive e∈CE(R).

4)⟹2). This is enough to show that R is abelian. Let f∈E(R). Then, according to the assumption, e∈CE(R) exists such that e∈fR and 1-e∈(1-f)R. Hence, we obtain fe=e and (1-f)(1-e)=1-e. Then, f=e∈CE(R). Therefore, R is abelian.

2)⟹1). Let x∈R. Given that R is an exchange ring, e∈E(R) exists such that e∈xR and 1-e∈(1-x)R. Let e=xa′, where a′∈R. Then, e=e2=xa′xa′. Write a=a′xa′, and it follows that e=xa and ae=a′xa′xa′=a′xa′=a. Then, axa=a. Given that R is abelian, we derive ax=axax=xa(ax)=xaxa=xa. By a similar argument, we can obtain (1-e)=(1-x)b, b(1-e)=b, and (1-x)b=b(1-x). Furthermore, we can obtain [x-(1-e)](a-b)=xa-xb-(1-e)a+(1-e)b=e+(1-x)b=1 and (a-b)[x-(1-e)]=1. That is, [x-(1-e)]-1=a-b. Then, x=x-(1-e)+(1-e). Hence, R is centrally clean.

Proposition 4 Let p∈CE(R). Then, a∈pR is centrally clean in R if and only if a is centrally clean in pR.

Proof The necessity is clearly stated in Theorem 1. Conversely, assume a∈pR is centrally clean in R. Then, e∈CE(R) and u∈U(R) exist such that a=e+u, and it follows that pa=pe+pu, pe∈CE(pR), and pu∈U(pR). From pa=a, we derive a=pe+pu. Hence, a is centrally clean in pR.

Corollary 1 Let p∈CE(R). If R is a centrally clean ring, then so is pR.

Han et al.[4] proved that when e∈E(R), if eRe and (1-e)R(1-e) are clean rings, then so is R. Here, we consider the case of e∈CE(R).

Corollary 2 Let e∈CE(R). If eR and (1-e)R are centrally clean, then so is R.

Proof This is clearly stated in Theorem 1.

Han et al.[4] also investigated the cleanness of group rings, the ring of formal power series over a ring, and a direct product of rings. Then, we analyze the relevant results of R[[x]] and ∏Rα.

Proposition 5 The ring R[[x]] is centrally clean if and only if R is centrally clean.

Proof Let f=a+bx+cx2+…∈R[[x]]. Given that R is centrally clean, we can suppose that a=u+e, where e∈CE(R) and u∈U(R). Then, f=e+(u+bx+cx2+…), e∈CE(R[[x]]), and u+bx+cx2+…∈U(R[[x]]). Therefore, R[[x]] is centrally clean.

Conversely, we know that R[[x]]/(x) is centrally clean because R[[x]] is centrally clean. Hence, R≅R[[x]]/(x) is centrally clean.

Lemma 2 Let R, S be two rings and φ: R→S be a surjective ring homomorphism. If R is centrally clean, then so is S.

Proof It is obvious.

Proposition 6 A direct product R=∏Rα is centrally clean if and only if Rα is centrally clean.

Proof Given that πα: ∏Rα→Rα is a surjective ring homomorphism, it follows that Rα is centrally clean based on Lemma 2.

Conversely, suppose that Rα is centrally clean. Let x=(xα)∈∏Rα. Then, for each α, we derive xα=uα+eα, where uα∈U(Rα) and eα∈CE(Rα). Hence, we obtain x=e+u, u=(uα)∈U(∏Rα) and e=(eα)∈CE(∏Rα), and it follows that R=∏Rα is centrally clean.

Let L be a two-sided ideal of R. We suppose that the idempotents can be lifted modulo L if, given that x∈E(R/L), e∈E(R) exists such that e-x∈L. Similarly, we can define the concept that the central idempotents can be lifted modulo L if e∈CE(R) exists such that e-x∈L for x∈CE(R/L).

Proposition 7 R is centrally clean if and only if R/J(R) is centrally clean, and the central idempotent can be lifted modulo J(R).

Proof Based on Lemma 2, we confirm that the factor ring of a centrally clean ring is centrally clean. Then, R/J(R) is centrally clean. Given that a centrally clean ring is exchange, it follows that the idempotents can be lifted modulo J(R). Based on Theorem 3, we determine that the idempotents of R are central. Then, the sufficiency is proven.

Conversely, let x∈R and

Then, r1,r2∈J(R) exist such that uv=1+r1 and vu=1+r2. Hence, u∈U(R). Given that the central idempotents can be lifted modulo J(R), we suppose that p∈CE(R) and p-e∈J(R), and it follows that r∈J(R) exists such that x=p+u+r=p+u(1+u-1r). Given that u-1r∈J(R), we derive 1+u-1r∈U(R). Hence, R is centrally clean.

3 Characterizations of Central Drazin Inverses

In this section, we mainly provide some characterizations for the existence of central Drazin inverses.

Theorem 4 Let a∈R. Then, the following conditions are equivalent:

1) a is central Drazin invertible.

2) u∈U(R), e∈CE(R), and the positive integer m exist such that am=eu and au=ua.

3) v∈U(R) and f∈CE(R) exist such that a=f+v and af∈Rnil.

4) p∈CE(R) exists such that ap∈U(pR) and a(1-p)∈Rnil.

Proof 1)⟹2). Write e=aac. Then, e∈CE(R). Given that a is central Drazin invertible, and it follows that the positive integer m exists such that am=amaac=ame. Write u=am+(1-e). Then, [am+(1-e)][(ac)me+(1-e)]=am(ac)me+am(1-e)+(1-e)(ac)me+(1-e)2=e+1-e=1. Hence, we have u∈U(R) and u-1=(ac)me+(1-e), and it follows that am=ame=[u-(1-e)]e=eu and au=a[am+(1-e)]=am+1+a(1-e)=am+1+(1-e)a=[am+(1-e)]a=ua.

2)⟹3). Write f=1-e. Then, f∈CE(R). Given that (am-f)(u-1e-f)=1, we derive am-f∈U(R). Then, (a-f)(am-1+am-2f+…+af+f)=am-f∈U(R). Hence, we obtain v=a-f∈U(R) and (af)m=amf=eu(1-e)=0, i.e., af∈Rnil.

3)⟹4). Write p=1-f. Then, p∈CE(R), ap=pa=pv∈U(pR) and a(1-p)=af∈Rnil.

4)⟹1). Based on this assumption, it follows that w∈U(pR) exists such that apw=pwa=p. From pw=w, we derive aw=wa=p∈C(R), waw=pw=w, and a-a2w=a(1-aw)=a(1-p)∈Rnil. Hence, a is central Drazin invertible.

Zhu et al.[14] showed that a is Drazin invertible if and only if u∈U(R), e∈E(R), and the positive integer m exist such that am=u+e is strongly clean decomposition and amR∩eR=0. Here, we investigate the relevant results of central Drazin inverses.

Theorem 5 Let a∈R. Then, the following conditions are equivalent:

1) a is central Drazin invertible.

2) u∈U(R), e∈CE(R), and the positive integer n exist such that an=u+e and anR∩eR=0.

3) u∈U(R), e∈CE(R), and the positive integer n exist such that an=u-e and anR∩eR=0.

Proof 1)⟹2). Given that a is central Drazin invertible, we derive u=an-1+aac∈U(R) for any positive integer n>ind(a). Write e=1-aac. Then, an=u+e is the centrally clean decomposition. Let x∈anR∩eR. Then, y,z∈R exist such that x=any=ez=eany=0. Hence, anR∩eR=0.

2)⟹1). From e∈CE(R), it follows that the positive integer m exists such that:

i.e., ane∈Rnil. Let m be the nilpotent index of ane. Then, (an)m=um(1-e). In fact,

um(1-e)+(ane)m=um(1-e)

Hence, (an)m is central group invertible derived by Theorem 3.6 in Ref.[28]. Then, a is central Drazin invertible derived by Theorem 3.3 in Ref.[28].

1)⟺3). This is similar to the proof of 1)⟺2).

From Theorem 5, we derive the following corollary.

Proposition 8 Let a∈R. Then, the following conditions are equivalent:

1) a is central Drazin invertible.

2) e∈CE(R) and the positive integer n exist such that ane=0 and an-e∈U(R).

3) e∈CE(R) and the positive integer n exist such that ane=0 and an+e∈U(R).

Proof 1)⟹2). Given that a is central Drazin invertible, we derive u=an-1+aac∈U(R) for any positive integer n>ind(a). Write e=1-aac. Then, ane=0 and an-e∈U(R).

2)⟹1). Let x∈anR∩eR. Then, y,z∈R exist such that x=any=ez=eany=aney=0. Hence, anR∩eR=0. According to Theorem 5, the proof is completed.

1)⟺3). This is similar to the proof of 1)⟺2).

For the central group inverses, we also obtain the following relevant results.

Proposition 9 Let a∈R. Then, the following conditions are equivalent:

1) a is central group invertible.

2) u∈U(R) and e∈CE(R) exist such that a=u+e and aR∩eR=0.

3) v∈U(R) and f∈CE(R) exist such that f=fva, 1-f=(1-f)v(1-a), and af=a.

Proof 1)⟺2). This is given in Corollary 4.6 in Ref.[28].

2)⟹3). Write f=1-e and v=u-1(1-2e). Then, v∈U(R) and f∈CE(R), and it follows that fva=(1-e)u-1(1-2e)(u+e)=(1-e)(1-2e)=1-e=f and a(1-f)=(u+e)e∈aR∩eR=0. Hence, af=a and

3)⟹2). Write u=v-1(2f-1) and e=1-f. Given that 1-f=(1-f)v(1-a)=(1-f)v-(1-f)va=(1-f)v-va+fva=(1-f)v-va+f, it follows that a=v-1(1-f)v+v-1(2f-1)=1-f+v-1(2f-1)=e+u. Let x∈aR∩eR. Then, r,t∈R exist such that x=ar=et, and it follows that fr=fvar=fv(et)=fv(1-f)t=0, i.e., r=(1-f)r. Then, x=ar=a(1-f)r=(a-af)r=0. Therefore, aR∩eR=0.

4 Central Group Invertibility of Combinations of Two Central Idempotents

Motivated by the study conducted by Liu et al.[15], we investigate the central group invertibility of combinations of two central idempotents in this section.

In this section, F denotes a field and A denotes the algebra over F.

Theorem 6 Let p,q∈A be the central idempotent and a=d1p+d2q+d3pq, where di∈F, i=1,2,3. Then, a is central group invertible, and

Proof Let

which suffices to prove that x is the central group inverse of a.

Given that p,q∈CE(R), we derive xa∈C(R). By computation, it follows that

[d1dd†-d1+d2dd†-d2+d3dd†]pq=

Hence, x is the central group inverse of a, and

where

Let d1=1, d2=1, d3=0. Then, we obtain the following results according to Theorem 6.

Corollary 3 Let 2∈U(R) and p,q∈A be the central idempotents. Then, p+q is central group invertible, and

If pq=p, then we obtain the following results according to Theorem 6. That is, we take d3=0 in Theorem 6.

Corollary 4 Let p,q∈A be the central idempotent and pq=p. Then, d1p+d2q is central group invertible, and

If pq=q, then we obtain the following results according to Theorem 6.

Corollary 5 Let p,q∈A be the central idempotent and pq=q. Then, d1p+d2q is central group invertible, and

5 An Example

In this section, we present all invertible, central group invertible, group invertible, central Drazin invertible elements, and centrally clean elements of Z2S3. For convenience, we write g1=(1), g2=(12), g3=(13), g4=(23), g5=(123), g6=(132), and

By computation, we obtain the following results:

E(Z2S3)={0,g1,g5+g6,g1+g5+g6,g2+g3+g5,g2+

g3+g6,g2+g4+g5,g2+g4+g6,g3+g4+g5,g3+

g4+g6,g1+g2+g3+g5,g1+g2+g3+g6,g1+g2+

g4+g5,g1+g2+g4+g6,g1+g3+g4+g5,g1+g3+

C(Z2S3)={0,g1,g5+g6,g1+g5+g6,g2+g3+g4,

Example 2 All invertible, central group invertible, group invertible, central Drazin invertible elements, and centrally clean elements of Z2S3 are listed as follows.

For convenience, we use CG(Z2S3), G(Z2S3), CD(Z2S3), and CC(Z2S3) to denote the sets of all central group invertible, group invertible, central Drazin invertible elements, and centrally clean elements of Z2S3, respectively.

U(Z2S3)={g1,g2,g3,g4,g5,g6,e+g1,e+g2,e+g3,

CG(Z2S3)={0,U(Z2S3),g2+g3,g2+g4,g3+g4,

G(Z2S3)={CG(Z2S3),g1+g2+g5,g1+g2+g6,

g1+g3+g5,g1+g3+g6,g1+g4+g5,g1+g4+g6,

g2+g3+g5,g2+g3+g6,g2+g4+g5,g2+g4+g6,

g3+g4+g5,g3+g4+g6,e+g4+g6,e+g4+g5,

e+g3+g6,e+g3+g5,e+g2+g6,e+g2+g5,e}

CD(Z2S3)={CG(Z2S3),g1+g2,g1+g3,g1+g4,

g1+g2+g3,g1+g2+g4,g1+g3+g4,g2+g5+g6,

g3+g5+g6,g4+g5+g6,e+g3+g4,e+g2+g4,

e+g2+g3,e+g1+g4,e+g1+g3,e+g1+g2,e}

CC(Z2S3)={0,U(Z2S3),g1+g2,g1+g3,g1+g4,

g1+g5,g1+g6,g5+g6,g2+g3,g2+g4,g3+g4,

g1+g2+g3,g1+g2+g4,g1+g3+g4,g2+g3+g4,

g1+g5+g6,g2+g5+g6,g3+g5+g6,g4+g5+g6,

g2+g3+g4,e+g1+g6,e+g1+g5,e+g1+g4,

e+g1+g3,e+g1+g2,e+g3+g4,e+g2+g4,

e+g2+g3,e+g6,e+g5,e}

Proof Given that Z2S3 is finite, it follows that Z2S3 is strongly π-regular. Hence, the elements in Z2S3 are Drazin invertible.

Then, we calculate the units of Z2S3.

Let α=x1g1+x2g2+x3g3+x4g4+x5g5+x6g6 and β=y1g1+y2g2+y3g3+y4g4+y5g5+y6g6. From αβ=g1, we can obtain

which has a unique solution.

Denote

Notably, x1+x2+x3+x4+x5+x6=1. Hence, we can obtain

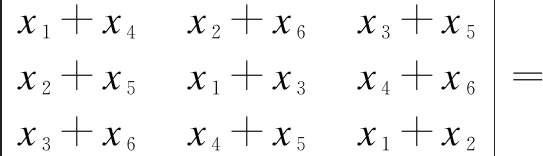
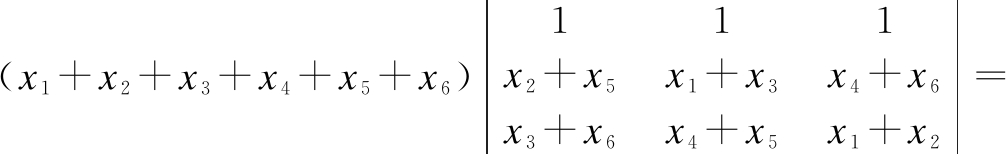
(1+x4+x6)(1+x4+x5)+(1+x1+x3)(1+x1+x2)

Then, from |A+B|≠0, it follows that xi=0 for certain i∈{1,2,…,6} and the others are 1, or xi=1 for certain i∈{1,2,…,6} and the others are 0. Hence, we have

Therefore,based on Theorem 3.6 in Ref.[28], Proposition 8.24 in Ref.[30], Theorem 4.5 in Ref.[28], and the definition of centrally clean elements, we can present the sets of CG(Z2S3), G(Z2S3), CD(Z2S3), and CC(Z2S3), respectively.

[1] Nicholson W K. Lifting idempotents and exchange rings[J].Transactions of the American Mathematical Society, 1977, 229: 269-278. DOI:10.1090/s0002-9947-1977-0439876-2.

[2] Nicholson W K, Varadarajan K. Countable linear transformations are clean[J]. Proceedings of the American Mathematical Society, 1998, 126(1): 61-64. DOI:10.1090/s0002-9939-98-04397-4.

[3] Nicholson W K. Strongly clean rings and fitting’s lemma[J]. Communications in Algebra, 1999, 27(8): 3583-3592. DOI:10.1080/00927879908826649.

[4] Han J, Nicholson W K. Extensions of clean rings[J].Communications in Algebra, 2001, 29(6): 2589-2595. DOI:10.1081/agb-100002409.

[5] Hiremath V A, Hegde S. On strongly clean rings [J]. International Journal of Algebra, 2011, 5(1): 31-36.

[6] Camillo V P, Yu H P. Exchange rings, units and idempotents[J].Communications in Algebra, 1994, 22(12): 4737-4749. DOI:10.1080/00927879408825098.

[7] Chen J L, Cui J. Two questions of L.Vaš on *-clean rings[J]. Bulletin of the Australian Mathematical Society, 2013, 88(3): 499-505. DOI:10.1017/s0004972713000117.

[8] Cui J, Wang Z. A note on strongly*-clean rings[J]. Journal of the Korean Mathematical Society, 2015, 52(4): 839-851. DOI:10.4134/jkms.2015.52.4.839.

[9] Li C N, Zhou Y Q. On strongly*-clean rings[J]. Journal of Algebra and Its Applications, 2011, 10(6): 1363-1370. DOI:10.1142/s0219498811005221.

[10] Vaš L. *-clean rings; some clean and almost clean Baer *-rings and von Neumann algebras[J]. Journal of Algebra, 2010, 324(12): 3388-3400. DOI:10.1016/j.jalgebra.2010.10.011.

[11] Zhang H B, Camillo V. On clean rings[J].Communications in Algebra, 2016, 44(6): 2475-2481. DOI:10.1080/00927872.2015.1053899.

[12] Nicholson W K, Zhou Y Q. Rings in which elements are uniquely the sum of an idempotent and a unit[J]. Glasgow Mathematical Journal, 2004, 46(2): 227-236. DOI:10.1017/s0017089504001727.

[13] Drazin M P. Pseudo-inverses in associative rings and semigroups[J]. The American Mathematical Monthly, 1958, 65(7): 506-514. DOI:10.1080/00029890.1958.11991949.

[14] Zhu H H, Zou H L, Patrício P. Generalized inverses and their relations with clean decompositions[J]. Journal of Algebra and Its Applications, 2019, 18(7): 1950133. DOI:10.1142/s0219498819501330.

[15] Liu X J, Wu L L, Yu Y M. The group inverse of the combinations of two idempotent matrices[J]. Linear and Multilinear Algebra, 2011, 59(1): 101-115. DOI:10.1080/03081081003717986.

[16] Cao Q H, Xie T, Zuo K Z. Discussions on the group inverses of combinations of two idempotent matrices [J]. Journal of Wuhan University (Natural Science Edition), 2018, 64(3): 262-268. (in Chinese)

[17] Chen J L. Algebraic theory of generalized inverses: Group inverses and Drazin inverses[J]. Journal of Nanjing University Mathematical Biquarterly, 2021, 38(1): 1-113. DOI:10.3969/j.issn.0469-5097.2021.01.01.

[18] Chen J L, Gao Y F, Li L F. Drazin invertibility in a certain finite-dimensional algebra generated by two idempotents[J]. Numerical Functional Analysis and Optimization, 2020, 41(14): 1804-1817. DOI:10.1080/01630563.2020.1813167.

[19] Chen J L, Zhuang G F, Wei Y M. The Drazin inverse of a sum of morphisms[J]. Acta Mathematica Scientia: Series A, 2009, 29(3): 538-552.(in Chinese)

D S, Wei Y M. Algebraic properties of generalized inverses [M]. Singapore: Springer, 2017: 89-93.

[21] Guo L, Chen J L, Zou H L. Representations for the Drazin inverse of the sum of two matrices and its applications[J]. Bulletin of the Iranian Mathematical Society, 2019, 45(3): 683-699. DOI:10.1007/s41980-018-0159-x.

[22] Xie T, Zuo K Z, Zheng L Z. Group inverse of combinations of two idempotent matrices[J]. Journal of Jilin University (Science Edition), 2016, 54(1): 45-53. (in Chinese)

[23] Zhang D

D, Guo L. The Drazin inverse of the sum of four matrices and its applications[J]. Linear and Multilinear Algebra, 2020, 68(1): 133-151. DOI:10.1080/03081087.2018.1500518.

[24] Zou H L,

D, Chen J L. The existence and representation of the Drazin inverse of a 2 × 2 block matrix over a ring[J]. Journal of Algebra and Its Applications, 2019, 18(11): 1950212. DOI:10.1142/s0219498819502128.

[25] Zhu H H, Chen J L. Additive and product properties of Drazin inverses of elements in a ring[J]. Bulletin of the Malaysian Mathematical Sciences Society, 2017, 40(1): 259-278. DOI:10.1007/s40840-016-0318-2.

[26] Zhou M M, Chen J L, Zhu X. The group inverse and core inverse of sums of two elements in a ring[J]. Communications in Algebra, 2020, 48(2): 676-690. DOI:10.1080/00927872.2019.1654497.

[27] Drazin M P. Commuting properties of generalized inverses[J]. Linear and Multilinear Algebra, 2013, 61(12): 1675-1681. DOI:10.1080/03081087.2012.753593.

[28] Wu C, Zhao L. Central Drazin inverses[J]. Journal of Algebra and Its Applications, 2019, 18(4): 1950065. DOI:10.1142/s0219498819500658.

[29] Zhao L, Wu C, Wang Y. One-sided central Drazin inverses[J]. Linear and Multilinear Algebra, 2022, 70(7): 1193-1206. DOI:10.1080/03081087.2020.1757601.

[30] Bhaskara Rao K P S. The theory of generalized inverses over commutative rings [M]. London: Taylor and Francis, 2002: 144-146.

Centrally clean elements and central Drazin inverses in a ring

1 Characterization of Centrally Clean Elements

2 Characterizations of Centrally Clean Rings

3 Characterizations of Central Drazin Inverses

4 Central Group Invertibility of Combinations of Two Central Idempotents

5 An Example

环中的中心clean元和中心Drazin逆