Let H be a Hopf algebra. Schauenburg^[1] obtained a braided monoidal category equivalence between the category of right-right Yetter-Drinfeld modules over H and the category of two-sided two-cosided Hopf modules over H under some suitable assumption. This yields new sources of braiding by which one can obtain the solutions to the Yang-Baxter equation, which plays a fundamental role in various areas of mathematics^[2-3].

In 1997, Doi^[4] studied the duality of any finite-dimensional Hopf modules in the left-left Yetter-Drinfeld category 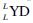where L denotes any ordinary Hopf algebra over the ground field k with a bijective antipode.

The most well-known examples of Hopf algebras are the linear spans of(arbitrary)groups. Dually, also the vector space of linear functionals on a finite group carries the structure of a Hopf algebra. In the case of quasigroups(nonassociative groups), however, it is no longer a Hopf algebra, but more generally, a Hopf quasigroup^[5-10], which is a specific case of the notion of unital coassociative bialgebra^[11].

Motivated by these notions and structures, this paper aims to construct Sweedler's dual of infinite-dimensional Hopf algebras in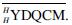

Throughout this paper, let k be a fixed field. We will work over k. Let C be a coalgebra with a coproduct Δ. We will use Heyneman-Sweedler's notation^[12], Δ(c)=∑c₁c₂ for all c∈C, for coproduct.

Recall from Ref.[5] that a Hopf coquasigroup is a unital associative algebra H,armed with three linear maps: Δ:H→HH,ε:H→K and S:H→H satisfying the following equations for all a,b∈H:

Δ(ab)=Δ(a)Δ(b)

ε(ab)=ε(a)ε(b)

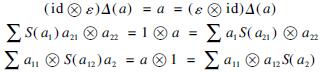
Recall from Ref.[6], the authors gave the notion of a left H-quasimodule over a Hopf quasigroup H. Duality, a left H-quasicomodule over a Hopf coquasigroup H is a vector space M with a linear map ρ:M→HM, where ρ(m)=∑m_-1m₀ such that ∑ε(m_-1)m₀=m and

∑S(m_-1)m_0-1m₀₀=∑m_-1S(m_0-1)m₀₀=1m

for all m∈M.

Moreover, the authors studied the notion of the left-left Yetter-Drinfeld quasimodule M=(M, ·,ρ)over a Hopf quasigroup H.

Duality, a left-left Yetter-Drinfeld quasicomodule M=(M, ·,ρ)over a Hopf coquasigroup H is a left H-module(M,·)and a left H-quasicomodule(M,·)satisfying the following equations:

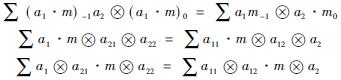
for all a∈H,m∈M.

Remark that the first equation is equivalent to the following formula:

We use ^H_HYDQCM to denote the category of the left-left Yetter-Drinfeld quasicomodules over a Hopf coquasigroup H. Moreover, if we assume that M is an ordinary left H-comodule, we say that M is a left-left Yetter-Drinfeld module over H. Obviously, the left-left Yetter-Drinfeld modules with the obvious morphisms is a subcategory of ^H_HYDQCM. We denote it by ^H_HYDCM.

Note that if the antipode S of Hopf quasigroup H is bijective, then the category ^H_HYDCM is a braided monoidal category with a “pre-braiding” defined as

for any M,N∈^H_HYDCM, m∈M and n∈N.

One can check the following lemmas and Corollary 1.

Lemma 1 Let H be a Hopf coquasigroup. Then,(^H_HYDQCM,,k)is a monoidal category.

Lemma 2 Let H be a Hopf coquasigroup with a bijective antipode S. Then, the monoidal category(^H_HYDQCM,k)with the pre-braiding defined above is a braided monoidal category if and only if the following identity holds:

For any M,N,P∈^H_HYDQCM, m∈M, n∈N and p∈P, this category will be denoted as(^H_HYDQC,,k).

Corollary 1 Let H be a Hopf coquasigroup with a bijective antipode S. If the following equations hold:

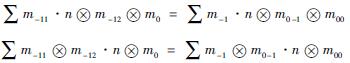
for any M,N∈^H_HYDQCM, m∈M,n∈N, then(^H_HYDQCM,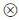,k)is a braided monoidal category, and we denote it as(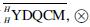,k).

Let H be a Hopf coquasigroup with a bijective antipode S. Under the hypotheses of the above results, we have the relationship:

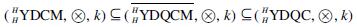
In what follows, let L denote a Hopf coquasigroup with a bijective antipode S_L. Let H be a Hopf algebra in i.e., explicitly, it is both a L-algebra and a L-coalgebra with comultiplication Δ and counit ε, and the following identities hold:

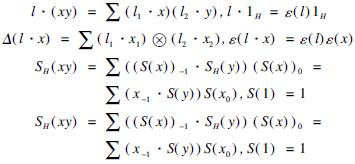
for any x,y∈H and l∈L.

In this section, let H be a Hopf coquasigroup with a bijective antipode S, and B an infinite-dimensional Hopf algebra in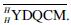

Let(A,m_A,μ_A)be an associative algebra. Then, we have coalgebra A⁰ given in Ref.[13] as

A⁰={f∈A^*|Kerfan ideal of A of cofinite dimension}

Let(B,m_B,μ_B,D_B,ε_B)be a bialgebra in 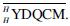Recall that B⁰ is the subspace of all b^*∈B^* vanishing on some cofinite ideal I of B. Let i:B^*B^*→(BB)^* be the natural embedding, defined as(i(fg))(a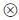b)=f(a)g(b)for f,g∈B^* and a,b∈B. For all f∈B^*, the following statements are equivalent:

f∈B⁰=(m^*_B)^-1(A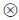^*A^*), dim(Bf)<∞

dim(fB)<∞,dim(BfB)<∞

For any f∈B^* and a,b∈B, we define(af)(b)=f(ba)and(fa)(b)=f(ab). This defines a B-B bimodule structure on B^*.

We consider the action of H on B^* given by(h ·f)(b)=f(S(h)·b)and the quasicoaction of H on B^* defined by ρ(f)(b)=for all h∈H, b∈B and f∈B^*.

Let A, B be algebras in 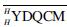. Then, we have the braided tensor product algebra AB with the product for all x,a∈A and y,b∈B.

It is not difficult for one to check the following two lemmas.

Lemma 3 The action 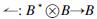is a left H-linear and the action 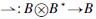is a left H^cop-linear.

Lemma 4 B⁰ is an H-submodule of(B^*, Δ^*_B, ε^*_B).

Proposition 1 B⁰ is a subalgebra of(B^*, Δ^*_B, ε^*_B).

Proof By Lemma 3, for any f, g∈B^* and a, b∈B, we obtain

Thus,

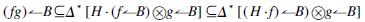
Combining f∈B⁰ with Lemma 4, we can conclude that H ·f∈B⁰. Moreover, since f,g∈B⁰, the left-hand side of the above containment is finite dimensional. Hence, fg∈B⁰. Finally, it is easy to check that ε^*_B(1)∈B⁰.

Lemma 5 We have that 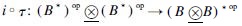is an algebra map in

Proof Applying the quasicoaction of H on B^*, the proof is complete.

Now, we obtain the main result of this paper which gives a characterization of Sweedler's dual of Hopf algebras in ^H_HYD.

Theorem 1 Let H be any Hopf coquasigroup with a bijective antipode S. If(B,m_B,μ_B, Δ_B, ε_B)be a Hopf algebra in 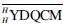with antipode S_B, then(B⁰,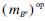))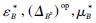is a Hopf algebra in 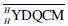with antipode .

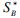Proof According to Ref.[13], we check that

1)B⁰ is an H-subquasicomodule of B^*.

2)Observe that . It is morphism in ^H_HYDQCM. Obviously, is. Thus,(B⁰,)is an algebra in _HM.

3)Observe that 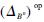is the composite map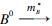 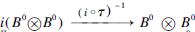. It is a morphism in ^H_HYDQCM. Obviously, 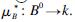Thus,(B⁰,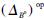,)is a coalgebra in _HM.

4) is an algebra map.

5)

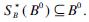
6)

^op=ε^*_Bμ^*_B.In the setting of Hopf coquasigroups, the notion of the left H-module is exactly the same as that for ordinary Hopf algebras since it only depends on the algebra structure of H. Thus, the proof of these assertions is either trivial or will become trivial after acquainting the Hopf coquasigroup calculus developed above.